Решение биквадратных уравнений: Решение биквадратных уравнений

Содержание

Решение биквадратных уравнений — онлайн калькулятор

Справочник
Онлайн-калькуляторы
Тесты с ответами

Биквадратное уравнение имеет вид ax4+bx2+c=0. Суть решения состоит в приведении уравнения к квадратному с помощью подстановки новой переменной.

Решение биквадратных уравнений онлайн – это быстрый способ получить ответ, не совершая преобразований и расчетов. Вам потребуется только ввести условие задачи в калькулятор. Наш сервис выполнит необходимые вычисления по нужным формулам. Автоматические расчеты исключают ошибки, опечатки, использование неверного алгоритма.

Введите данные в соответствующие поля. Отправьте уравнение на вычисление кнопкой
«Рассчитать». Получите решение и ответ.

Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:

Решение квадратных уравнений: формула корней, примеры
Уравнение и его корни: определения, примеры
Теорема Виета, формулы Виета
Нахождение неизвестного слагаемого, множителя: правила, примеры, решения
Квадратные неравенства, примеры, решения
Решение квадратных неравенств методом интервалов

Ответ:

Решение

Ответ:

Похожие калькуляторы:

Решение квадратных уравнений

Решение систем линейных уравнений методом Крамера
Решение систем линейных уравнений методом Гаусса
Решение систем линейных уравнений матричным методом

Решение систем линейных уравнений методом подстановки

Как решать биквадратное уравнение

Калькулятором на сайте пользуются школьники и студенты для самопроверки. Так в самостоятельных вычислениях можно найти и исправить недочеты.

Чтобы решить биквадратное уравнение, необходимо выполнить следующие действия:

Ввести новую переменную y=x2 для упрощения исходного уравнения до квадратного.
Подставить полученную переменную в первоначальное уравнение.
Вычислить неизвестные в квадратном уравнении.
Найденные корни (y1,y2) подставить в переменную y=x2 и получить решение биквадратного уравнения.

Нахождение ответов для биквадратных уравнений через калькулятор также понадобится родителям для проверки домашних заданий, преподавателям для быстрой подготовки учебных материалов.

Сервис выдает не только готовый ответ, но и подробное решение. Используя его можно изучать новую тему, закреплять уже полученные знания. Чтобы найти ответ, не надо платить или регистрироваться. Вы бесплатно получаете решение нужного количества задач в любое время суток.

На сайте доступны калькуляторы на разные виды уравнений. Поэтому задача по алгебре не останется без решения. На время зачетов, контрольных, экзаменов вы можете заказать услугу онлайн-помощи. Напишите об этом консультанту и получите скидку.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Решение матриц
Точка, прямая, плоскость
Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами
Периметр фигур

Поможем с любой работой

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Решение задач
Отчеты по практике

Все наши услуги

Не получается написать работу самому?

Доверь это кандидату наук!

Найти корни биквадратного уравнения решить.

Мы получили снова четыре корня:

Вот так решаются все биквадратные уравнения. Конечно, это не самый быстрый способ, зато он самый надежный. Попробуйте самостоятельно прорешать такие же примеры, как и в этом видео. В ответе значения иксов нужно записывать через точку с запятой — вот так, как я записывал. На этом урок закончен. Удачи!

Инструкция

Способ подстановкиВыразите одну переменную и подставте ее в другое уравнение. Выражать можно любую переменную по вашему усмотрению. Например, выразите «у из второго уравнения:
х-у=2 => у=х-2Затем подставьте все в первое уравнение:
2х+(х-2)=10Перенесите все без «х в правую часть и подсчитайте:
2х+х=10+2
3х=12 Далее, чтобы «х, разделите обе части уравнения на 3:
х=4.Итак, вы нашли «х. Найдите «у. Для этого подставьте «х в то уравнение, из которого вы выразили «у:
у=х-2=4-2=2
у=2.

Сделайте проверку. Для этого подставьте получившиеся значения в уравнения:
2*4+2=10
4-2=2
Неизвестные найдены верно!

Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.

Если нет четко выраженных переменных, то необходимо немного преобразовать уравнения.
В первом уравнении имеем «2х, а во втором просто «х. Для того, чтобы при сложении или «х сократился, второе уравнение умножьте на 2:
х-у=2
2х-2у=4Затем вычтите из первого уравнения второе:
2х+у-(2х-2у)=10-4Заметим, если перед скобкой стоит минус, то после раскрытия поменяйте на противоположные:
2х+у-2х+2у=6
3у=6
у=2«х найдите, выразив из любого уравнения, т. е.

Видео по теме

Уравнение , в общем виде записанное ах+bу+с=0, называется линейным уравнением с двумя переменными . Такое уравнение само по себе содержит бесконечное множество решений, поэтому в задачах оно всегда чем-либо дополняется – еще одним уравнением или ограничивающими условиями. В зависимости от условий, предоставленных задачей, решать линейное уравнение с двумя переменными следует разными способами.

Вам понадобится

— линейное уравнение с двумя переменными;
— второе уравнение или дополнительные условия.

Инструкция

Если дана система из двух линейных уравнений, решайте ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными поменьше и выразите одну из переменных, например, х. Затем подставьте это значение, содержащее у, во второе уравнение. В полученном уравнении будет лишь одна переменная у, перенесите все части с у в левую часть, а свободные – в правую.

Решить систему из двух уравнений можно и другим способом. Умножьте одно из уравнений на число, чтобы коэффициент перед одной из переменных, например, перед х, был одинаков в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть аналогично и правые части). Вы увидите, что переменная х исчезла, и осталась только одна переменная у. Решите полученное уравнение, и подставьте найденное значение у в любое из первоначальных равенств. Найдите х.

Третий способ решения системы двух линейных уравнений – графический. Начертите систему координат и изобразите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставляйте любые два значения х в уравнение и находите соответствующие у – это будут координаты точек, принадлежащих прямой. Удобнее всего находить пересечение с осями координат – достаточно подставить значения х=0 и у=0. Координаты точки пересечения этих двух линий и будут задачи.

Если в условиях задачи лишь одно линейное уравнение, значит, вам даны дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными х и у обозначены расстояние, скорость, вес – смело ставьте ограничение х≥0 и у≥0. Вполне возможно, под х или у скрывается количество , яблок, и т.д. – тогда значениями могут быть только . Если х – возраст сына, понятно, что он не может быть старше отца, поэтому укажите это в условиях задачи.

Источники:

как решить уравнение с одной переменной

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

— система из трех уравнений с тремя неизвестными.

Инструкция

Если два из трех системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными . Ваша цель при этом – превратить его в обычное уравнение с неизвестной. Если это , дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные.

Некоторые системы уравнений можно вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из на или переменную так, чтобы сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.

Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными . Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрице свободных членов, то есть А*Х=В.

Найдите матрицу А в степени (-1) предварительно отыскав , обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.

Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.

Источники:

решений уравнений с тремя неизвестными

Решение системы уравнений сложно и увлекательно. Чем сложнее система, тем интереснее ее решать. Чаще всего в математике средней школы встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть и больше. Решать системы можно несколькими методами.

Инструкция

Самый распространенный метод решения системы уравнений — это подстановка. Для этого необходимо выразить одну переменную через другую и подставить ее во второе уравнение системы, таким образом приведя уравнение к одной переменной. Например, дана уравнений:2х-3у-1=0;х+у-3=0.

Из второго выражения удобно выразить одну из переменных, перенеся все остальное в правую часть выражения, не забыв при этом сменить знак коэффициента:х=3-у.

Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.

В первом выражении все члены 2, можно вынести 2 за скобку распределительному свойству умножения:2*(2х-у-3)=0. Теперь обе части выражения можно сократить на это число, а затем выразить у, так как коэффициент по модулю при нем равен единице:-у=3-2х или у=2х-3.

Так же, как и в первом случае, подставляем данное выражение во второе уравнение и получаем:3х+2*(2х-3)-8=0;3х+4х-6-8=0;7х-14=0;7х=14;х=2. 2 ? 4ac. При этом переменные a, b, c являются коэффициентами нашего уравнения.

Найдите корни биквадратного уравнения. Для этого возьмите корень квадратный из полученных решений . Если решение было одно, то будет два – положительное и отрицательное значение корня квадратного. Если решений было два, у биквадратного уравнения будет четыре корня.

Видео по теме

Одним из классических способов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований переводится в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.

Инструкция

Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. Мысленно определите коэффициенты, стоящие перед каждой неизвестной, а также коэффициенты в правой части каждого уравнения.

Всем еще со школы известно такое понятие, как уравнения. Уравнение — это равенство, содержащее одну или несколько переменных. Зная то, что одна из частей данного равенства равна другой, можно вычленять отдельные части уравнения, перенося те или иные его составляющие за знак равенства по четко оговоренным правилам. Можно упростить уравнение до необходимого логического завершения в виде х=n, где n — это любое число.

С начальной школы все дети проходят курс изучения различной сложности. Позже в программе появляются более сложные линейные уравнения — квадратные, затем идут кубические уравнения. Каждый последующий вид уравнений имеет новые методики решения, становится труднее в изучении и повторении.

Однако после этого возникает вопрос о решении такого вида уравнений, как биквадратные уравнения. Данный вид, несмотря на кажущуюся сложность, решается достаточно просто: главное — уметь привести такие уравнения в должный вид. Их решение изучается за один-два урока вместе с практическими заданиями, если у учащихся имеются базовые знания о решении квадратных уравнений.

Что необходимо знать человеку, столкнувшемуся с этим типом уравнений? Для начала то, что они включают в себя только четные степени переменной «икс»: четвертая и, соответственно, вторая. Чтобы биквадратное уравнение было решаемо, необходимо привести его к виду Как это сделать? Достаточно просто! Нужно всего лишь заменить «икс» в квадрате на «игрек». Тогда устрашающий для многих школьников «икс» в четвертой степени превратится в «игрек» в квадрате, а уравнение примет вид обычного квадратного.

Далее оно решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение таинственного «игрека». Чтобы решить биквадратное уравнение до конца, нужно найти из числа «игрек» — это и будет искомая величина «икс», после нахождения значений которого можно будет поздравить себя с успешным завершением расчетов.

Что же следует помнить, решая уравнения данного вида? Первое и самое главное: игрек не может быть отрицательным числом! Само условие, что игрек — это квадрат числа икс, исключает подобный вариант решения. Поэтому если при первичном решении биквадратного уравнения одно из значений «игрек» получается у вас положительным, а второе — отрицательным, необходимо взять только его положительный вариант, иначе биквадратное уравнение будет решено неверно. Лучше сразу ввести правило, что переменная «игрек» больше либо равна нулю.

Второй немаловажный нюанс: число «икс», являясь квадратным корнем числа «игрек», может быть как положительным, так и отрицательным. Допустим, если «игрек» равен четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но отличного знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом немаловажном моменте, иначе можно попросту потерять один или несколько ответов уравнения. Лучше всего сразу писать, что «икс» равен плюс-минус квадратному корню от «игрек».

В общем и целом, решение биквадратных уравнений — это достаточно просто и не требует больших временных затрат. На изучение этой темы в школьной программе хватает двух академических часов — не считая, конечно, повторений и контрольных работ. Биквадратные уравнения стандартного вида решаются очень легко, если соблюдать перечисленные выше правила. Их решение не составит для вас никакого труда, потому что оно подробно расписано в учебниках математики. Удачной вам учебы и успехов в решении любых, не только математических, задач!

Найти корни биквадратного уравнения решить. Биквадратное уравнение, решение биквадратных уравнений

Инструкция

Способ сложения или вычитания уравненийИзбавьтесь сразу от -нибудь перемененной. В нашем случае это проще сделать с «у.
Так как в «у со знаком «+ , а во втором «- , то вы можете выполнить операцию сложения, т.е. левую часть складываем с левой, а правую с правой:
2х+у+(х-у)=10+2Преобразуйте:
2х+у+х-у=10+2
3х=12
х=4Подставьте «х в любое уравнение и найдите «у:
2*4+у=10
8+у=10
у=10-8
у=2По 1-ому способу можете , что найдены верно.

Видео по теме

Вам понадобится

— линейное уравнение с двумя переменными;
— второе уравнение или дополнительные условия.

Инструкция

Источники:

как решить уравнение с одной переменной

Вам понадобится

— система из трех уравнений с тремя неизвестными.

Инструкция

Источники:

решений уравнений с тремя неизвестными

Инструкция

Раскрываем скобки: 6-2у-3у-1=0;-5у+5=0;у=1.Полученное значение у подставляем в выражение:х=3-у;х=3-1;х=2.

Видео по теме

Инструкция

Сначала приведите систему уравнений в такой вид, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные Х будут стоять первыми в каждой строке, все Y – после X, все Z — после Y и так далее. В правой части каждого уравнения неизвестных быть не должно. {2}}=\frac{1}{4} \\& \left[ \begin{align}& x=\frac{1}{2} \\& x=-\frac{1}{2} \\\end{align} \right. \\\end{align}\]

Мы получили снова четыре корня:

Перед тем, как решать биквадратные уравнения, необходимо разобраться, что собой являет данное выражение. Итак, это уравнение четвертой степени, которое можно записать в таком виде: «(ах 4) + (bx 2) + с = 0 ». Его общий вид можно записать в виде «ах ». Чтобы решить уравнение подобного рода, необходимо применить метод под названием «подстановка неизвестных». Согласно ему, выражение «х 2 » необходимо заменить другой переменной. После такой подстановки получается простое квадратное уравнение, решение которого в дальнейшем не составляет особого труда.

Необходимо:

— чистый лист бумаги;
— пишущая ручка;
— элементарные математические навыки.

Инструкция:

Итак, необходимо изначально записать выражение на листке бумаги. Первый этап его решения состоит в простой процедуре замены выражения «х 2 » на простую переменную (например «к »). После того, как Вы это сделали, у Вас должно получиться новое уравнение: «(ак 2) – (bк) + с = 0 ».
Далее, чтобы правильно решить биквадратное уравнение, нужно вначале найти корни для «(ак 2 ) – (bк) + с = 0 », которое у Вас получилось после замены. Чтобы это сделать, необходимо будет посчитать значение дискриминанта по известной формуле: «D = (b 2 ) − 4*ас ». При этом все эти переменные (а , b и с ) являются коэффициентами вышеприведенного уравнения.
В ходе расчета дискриминанта мы можем узнать, имеет ли решение наше биквадратное уравнение, ведь если в итоге данное значение получится со знаком минус, то оно просто-напросто может не иметь решения в дальнейшем. В случае же если дискриминант будет равняться нулю, тогда у нас будет одно единственное решение, определенное такой формулой: «к = — (b / 2 * а) ». Ну и в случае, если наш дискриминант окажется больше нуля, тогда у нас получится два решения. Для нахождения двух решений необходимо будет взять квадратный корень от «D » (то есть с дискриминанта). Полученное значение нужно будет записать в виде переменной «QD ».
Следующий шаг – непосредственное решение квадратного уравнения , которое у Вас получилось. Для этого Вам необходимо будет подставить в формулу уже известные значения. Для одного из решений: «к1 = (-b + QD) / 2 * а », а для другого: «к2 = (-b — QD) / 2 * а ».
И, наконец, завершающий этап – нахождение корней биквадратного уравнения . Для этого необходимо будет взять квадратный корень из полученных до этого решений обычного квадратного уравнения. Если же дискриминант был равен нулю, и у нас было только одно решение, тогда в этом случае корней получится два (с отрицательным и с положительным значением квадратного корня). Соответственно, если дискриминант был больше нуля, то наше биквадратное уравнение будет иметь целых четыре корня.

Впервые квадратные уравнения сумели решить математики древнего Египта. Вавилоняне умели решать неполные квадратные уравнения, так же частные виды полных квадратных уравнений около 2 тысяч лет до нашей эры. Древнегреческие математики умели решать некоторые виды квадратных уравнений, сводя их к геометрическим построениям. Примеры решения уравнений без использования геометрических знаний дает Диофант Александрийский (3 век). Диофант в своих книгах «Арифметика» изложил способ решения полных квадратных уравнений, однако эти книги не сохранились. В Европе формулы для решения квадратных уравнений были впервые изложены итальянским математиком Леонардо Фибоначчи в 1202 году.

Общее правило решения квадратных уравнений, преобразованных в вид х 2 + bх = с , было описано немецким математиком М. Штифелем. Он и сформулировал в 1544 году общее правило решения квадратных уравнений, приведенных к единому каноническому виду
х 2 + bх + с = 0 при всевозможных вариациях знаков и коэффициентов b и с.

Франсуа Виет вывел формулы квадратного уравнения в общем виде, однако он работал только с положительными числами.

Тарталья, Кардано, Бомбелли – итальянские ученые, которые среди первых в XVI веке учитывают кроме положительных еще и отрицательные корни.

Выводом формулы решения квадратных уравнений общего вида занимался Виет. Одно свое утверждение он высказывал лишь для положительных корней (отрицательных чисел он не признавал).

После трудов нидерландского математика Альберта Жирара, а также Декарта и Ньютона, методы решения квадратных уравнений приняли современный вид.

Квадратные уравнения

1. Вспомним уже знакомые способы решения и исследования квадратных уравнений:

выделение полного квадрата;
по формуле корней для квадратного уравнения;
по теореме Виета;
на основании свойств квадратичной функции.

В процессе решения уравнений необходимо следить за множеством допустимых значений неизвестного, т. к. оно может изменяться. В случае его расширения следует проверять найденное решение, не является ли оно посторонним для данного уравнения. В случае, если произошло сужение, необходимо убедиться, не являются ли потерянные значения неизвестных решениями данного уравнения. Процесс нахождения выпавших решений не всегда легко выполним, поэтому желательно избегать сужение множества допустимых значений неизвестных уравнения.

2. Типичные ошибки при решении уравнений.

По правилам можно преобразовывать исходное уравнение в равносильное ему, при этом, вы знаете, что: обе части уравнения можно делить или умножать на одно и то же, отличное от нуля, число.

1) Если уравнение имеет вид f(х) · g(х) = p(х) · g(х), то деление обеих частей на одинаковый множитель g(x), как правило, недопустимо. Данное действие может привести к потере корней: могут быть потеряны корни уравнения g(х) = 0, если ни существуют.

Пример 1.

Решить уравнение 2(х – 3) = (х – 3)(х + 5).

Решение.

Здесь нельзя сокращать на множитель (х – 3).

2(х – 3) – (х – 3)(х + 5) = 0, вынесем общую скобку:

(х – 3)(-х – 3) = 0, теперь

х – 3 = 0 или -х – 3 = 0;

х = 3 или х = -3.

Ответ: -3; 3.

2) Уравнение вида f(х) / g(х) = 0 можно заменить системой:

{f(x) = 0,
{g(x) ≠ 0.

Она равносильна исходному уравнению.

Или можно решить уравнение f(x) = 0, а уже затем исключить найденных корней те, которые обращают в нуль знаменатель g(x).

Встречаются дробно-рациональные уравнения, которые сводятся к квадратным уравнениям.

Пример 2.

Решить уравнение: (х + 3) / (х – 3) + (х – 3) / (х + 3) = 10/3 + 36/(х – 3)(х + 3).

Решение.

Умножив обе части уравнения на общий знаменатель и заменив исходное уравнение целым, получим равносильную систему:

{3(х + 3) 2 + 3(х – 3) 2 = 10(х – 3)(х + 3) + 3 · 36;
{(х – 3)(х +3) ≠ 0.

В результате получим два корня: х = 3 или х = -3, но х ≠ 3 и х ≠ -3.

Ответ: уравнение корней не имеет.

Пример 3.

Решить уравнение: (х + 5)(х 2 + 4х — 5)/(х + 5)(х + 2) = 0.

Решение.

Часто ограничиваются таким решением:

(х 2 + 4х – 5) / (х + 2) = 0.
{х = -5, х = 1,
{х ≠ -2.

Ответ: -5; 1.

Правильный ответ: 1.

Пример 4.

При выполнении распространенных заданий на исследование квадратного уравнения следующего вида: «Не вычисляя действительных корней х 1 и х 2 уравнения 2х 2 + 3х + 2 = 0, найти значение х 1 2 + х 2 2 » банальная невнимательность приводит к грубой ошибке.

Действительно, по теореме Виета,

х 1 2 + х 2 2 = (х 1 + х 2) 2 – х 1 х 2 = (-3/2) 2 – 2 · 1 = 1/4.

Однако, теоремой можно было воспользоваться при существовании действительных корней. В данном примере D

Ответ: значение х 1 2 + х 2 2 не существует.

Пример 5.

Вычислить отрицательный коэффициент b и корни уравнения х 2 + bх – 1 = 0, если с увеличением каждого из этих корней на единицу они становятся корнями уравнения х 2 – b 2 х – b = 0.

Решение.

Пусть х 1 и х 2 – корни уравнения х 2 + bх – 1 = 0. Тогда по т. Виета

х 1 + х 2 = -b и х 1 х 2 = -1 (*). С другой стороны, по условию

(х 1 + 1) + (х 2 + 1) = b 2 и (х 1 + 1)(х 2 + 1) = -b.

Перепишем:

х 1 + х 2 = b 2 – 2 и (х 1 + 1)(х 2 + 1) = -b.

Теперь, учитывая условия (*), получим b 2 – 2 = -b, следовательно,

b 1 = -2, b 2 = 1. По условию подходит b 1 = -2.

Значит, исходное уравнение имеет вид х 2 – 2х – 1 = 0, корнями являются числа х 1,2 = 1 ± √2.

Ответ: b 1 = -2, х 1,2 = 1 ± √2.

Уравнения, приводимые к квадратным. Биквадратные уравнения

Уравнения вида ах 4 + bх 2 + c = 0, где а ≠ 0 , называются биквадратными уравнениями с одной переменной.

Для решения биквадратного уравнения нужно сделать подстановку х 2 = t, найти корни t 1 и t 2 квадратного уравнения аt 2 + bt + c = 0 и решить уравнения х 2 = t 1 и х 2 = t 2 . Они имеют решения лишь в случае, когда t 1,2 ≥ 0.

Пример 1.

Решить уравнение х 4 + 5х 2 – 36 = 0.

Решение.

Подстановка: х 2 = t.

t 2 + 5t – 36 = 0. По т. Виета t 1 = -9 и t 2 = 4.

х 2 = -9 или х 2 = 4.

Ответ: В первом уравнении корней нет, из второго: х = ±2.

Пример 2.

Решить уравнение (2х – 1) 4 – 25(2х – 1) 2 + 144 = 0.

Решение.

Подстановка: (2х – 1) 2 = t.

t 2 – 25t + 144 = 0. По т. Виета t 1 = 9 и t 2 = 16.

(2х – 1) 2 = 9 или (2х – 1) 2 = 16.

2х – 1 = ±3 или 2х – 1 = ±4.

Из первого уравнения два корня: х = 2 и х = -1, из второго тоже: х = 2,5 и х = -1,5.

Ответ: -1,5; -1; 2; 2,5.

Таким образом, процесс решения любых уравнений состоит в последовательной замене данного уравнения другим, равносильным ему и более простым уравнением.

Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!

blog. сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение биквадратных уравнений. Решение уравнений с параметром

Представление об уравнениях с двумя переменными впервые формируется в курсе математики за 7 класс. Рассматриваются конкретные задачи, процесс решения которых приводит к такому виду уравнений.

При этом они изучаются довольно поверхностно. В программе главный акцент делается на системах уравнений с двумя неизвестными.

Это стало причиной того, что задачи, в которых на коэффициенты уравнения накладываются определенные ограничения, практически не рассматриваются. Недостаточно внимания уделено методам решения заданий типа «Решить уравнение в натуральных или целых числах». Известно, что материалы ЕГЭ и билеты вступительных экзаменов часто содержат такие упражнения.

Какие именно уравнения определяются как уравнения с двумя переменными?

ху = 8, 7х + 3у = 13 или х 2 + у = 7 – примеры уравнений с двумя переменными.

Рассмотрим уравнение х – 4у = 16. Если х = 4, а у = -3, оно будет правильным равенством. Значит, эта пара значений – решение данного уравнения.

Решение любого уравнения с двумя переменными – множество пар чисел (х; у), которые удовлетворяют это уравнение (превращают его в верное равенство).

Часто уравнение преобразовывают так, чтобы из него можно было получить систему для нахождения неизвестных.

Примеры

Решить уравнение: ху – 4 = 4х – у.

В данном примере можно воспользоваться методом разложения на множители. Для этого нужно сгруппировать слагаемые и вынести общий множитель за скобки:

ху – 4 = 4х – у;

ху – 4 – 4х + у = 0;

(ху + у) – (4х + 4) = 0;

у(х + 1) – 4(х + 1) = 0;

(х + 1)(у — 4) = 0.

Ответ: Все пары (х; 4), где х – любое рациональное число и (-1; у), где у – любое рациональное число.

Решить уравнение: 4х 2 + у 2 + 2 = 2(2х — у).

Первый шаг – группирование.

4х 2 + у 2 + 2 = 4х – 2у;

4х 2 + у 2 + 1 — 4х + 2у + 1 = 0;

(4х 2 – 4х +1) + (у 2 + 2у + 1) = 0.

Применив формулу квадрата разности, получим:

(2х — 1) 2 + (у + 1) 2 = 0.

При суммировании двух неотрицательных выражений ноль получится только в том случае, если 2х – 1 = 0 и у + 1 = 0. Отсюда следует: х = ½ и у = -1.

Ответ: (1/2; -1).

Решить уравнение (х 2 – 6х + 10)(у 2 + 10у + 29) = 4.

Рационально применить оценочный метод, выделив полные квадраты в скобках.

((х — 3) 2 + 1)((у + 5) 2 + 4) = 4.

При этом (х — 3) 2 + 1 ≥ 1, а (у + 5) 2 + 4 ≥ 4. Тогда левая часть уравнения всегда не меньше 4. Равенство возможно в случае

(х — 3) 2 + 1 = 1 и (у + 5) 2 + 4 = 4. Следовательно, х = 3, у = -5.

Ответ: (3; -5).

Решить уравнение в целых числах: х 2 + 10у 2 = 15х + 3.

Можно записать это уравнение в таком виде:

х 2 = -10у 2 + 15х + 3. Если правую часть равенства делить на 5, то 3 – остаток. Из этого следует, что х 2 не делится на 5. Известно, что квадрат числа, которое не делится на 5, должен дать в остатке или 1, или 4. Значит, уравнение корней не имеет.

Ответ: Решений нет.

Не стоит расстраиваться из-за трудностей в поиске верного решения для уравнения с двумя переменными. Упорство и практика обязательно принесут свои плоды.

Предлагаем вам удобный бесплатный онлайн калькулятор для решения квадратных уравнений. Вы сможете быстро получить и разобраться, как они решаются, на понятных примерах.
Чтобы произвести решение квадратного уравнения онлайн , вначале приведите уравнение к общему виду:
ax 2 + bx + c = 0
Заполните соответственно поля формы:

Как решить квадратное уравнение:

Виды корней:

1. Привести квадратное уравнение к общему виду:
Общий вид Аx 2 +Bx+C=0
Пример: 3х — 2х 2 +1=-1 Приводим к -2х 2 +3х+2=0

2. Находим дискриминант D.
D=B 2 -4*A*C .
Для нашего примера D= 9-(4*(-2)*2)=9+16=25.

3. Находим корни уравнения.
x1=(-В+D 1/2)/2А.
Для нашего случая x1=(-3+5)/(-4)=-0,5
x2=(-В-D 1/2)/2А.
Для нашего примера x2=(-3-5)/(-4)=2
Если В — четное число, то дискриманант и корни удобнее считать по формулам:
D=К 2 -ac
x1=(-K+D 1/2)/А
x2=(-K-D 1/2)/А,
Где K=B/2

1. Действительные корни. Причем. x1 не равно x2
Ситуация возникает, когда D>0 и A не равно 0.

2. Действительные корни совпадают. x1 равно x2
Ситуация возникает, когда D=0. Однако при этом, ни А, ни В, ни С не должны быть равны 0.

3. Два комплексных корня. x1=d+ei, x2=d-ei, где i=-(1) 1/2
Ситуация возникает, когда D
4. Уравнение имеет одно решение.
A=0, B и C нулю не равны. Уравнение становиться линейным.

5. Уравнение имеет бесчисленное множество решений.
A=0, B=0, C=0.

6. Уравнение решений не имеет.
A=0, B=0, C не равно 0.

Для закрепления алгоритма, вот еще несколько показательных примеров решений квадратных уравнений .

Пример 1. Решение обычного квадратного уравнения с разными действительными корнями.
x 2 + 3x -10 = 0
В этом уравнении
А=1, B = 3, С=-10
D=B 2 -4*A*C = 9-4*1*(-10) = 9+40 = 49
квадратный корень будем обозначать, как число 1/2 !
x1=(-В+D 1/2)/2А = (-3+7)/2 = 2
x2=(-В-D 1/2)/2А = (-3-7)/2 = -5

Для проверки подставим:
(x-2)*(x+5) = x2 -2x +5x – 10 = x2 + 3x -10

Пример 2. Решение квадратного уравнения с совпадением действительных корней.
х 2 – 8x + 16 = 0
А=1, B = -8, С=16
D = k 2 – AC = 16 – 16 = 0
X = -k/A = 4

Подставим
(x-4)*(x-4) = (x-4)2 = X 2 – 8x + 16

Пример 3. Решение квадратного уравнения с комплексными корнями.
13х 2 – 4x + 1 = 0
А=1, B = -4, С=9
D = b 2 – 4AC = 16 – 4*13*1 = 16 — 52 = -36
Дискриминант отрицательный – корни комплексные.

X1=(-В+D 1/2)/2А = (4+6i)/(2*13) = 2/13+3i/13
x2=(-В-D 1/2)/2А = (4-6i)/(2*13) = 2/13-3i/13
, где I – это квадратный корень из -1

Вот собственно все возможные случаи решения квадратных уравнений.
Надеемся, что наш онлайн калькулятор окажется весьма полезным для вас.
Если материал был полезен, вы можете

В этой статье мы будем учиться решать биквадратные уравнения.

Итак, уравнения какого вида называются биквадратными?
Все уравнения вида ах 4 + bx 2 + c = 0 , гдеа ≠ 0 , являющиеся квадратными относительно х 2 , и называются биквадратными уравнениями. Как видите, эта запись очень похожа на запись квадратного уравнения, поэтому и решать биквадратные уравнения будем используя формулы, которые мы применяли при решении квадратного уравнения.

Только нам необходимо будет ввести новую переменную, то есть обозначим х 2 другой переменной, например, у или t (или же любой другой буквой латинского алфавита).

Например, решим уравнение х 4 + 4х 2 ‒ 5 = 0.

Обозначим х 2 через у (х 2 = у ) и получим уравнение у 2 + 4у – 5 = 0.
Как видите, такие уравнения вы уже умеете решать.

Решаем полученное уравнение:

D = 4 2 – 4 (‒ 5) = 16 + 20 = 36, √D = √36 = 6.

у 1 = (‒ 4 – 6)/2= ‒ 10 /2 = ‒ 5,

у 2 = (‒ 4 + 6)/2= 2 /2 = 1.

Вернемся к нашей переменной х.

Получили, что х 2 = ‒ 5 и х 2 = 1.

Замечаем, что первое уравнение решений не имеет, а второе дает два решения: х 1 = 1 и х 2 = ‒1. Будьте внимательны, не потеряйте отрицательный корень (чаще всего получают ответ х = 1, а это не правильно).

Ответ: — 1 и 1.

Для лучшего усвоения темы разберем несколько примеров.

Пример 1. Решите уравнение 2х 4 ‒ 5 х 2 + 3 = 0.

Пусть х 2 = у, тогда 2у 2 ‒ 5у + 3 =0.

D = (‒ 5) 2 – 4· 2 · 3 = 25 ‒ 24 = 1, √D = √1 = 1.

у 1 = (5 – 1)/(2· 2) = 4 /4 =1, у 2 = (5 + 1)/(2· 2) = 6 /4 =1,5.

Тогда х 2 = 1 и х 2 = 1,5.

Получаем х 1 = ‒1, х 2 = 1, х 3 = ‒ √1,5 , х 4 = √1,5.

Ответ: ‒1; 1; ‒ √1,5; √1,5.

Пример 2. Решите уравнение 2х 4 + 5 х 2 + 2 = 0.

2у 2 + 5у + 2 =0.

D = 5 2 – 4 · 2 · 2 = 25 ‒ 16 = 9, √D = √9 = 3.

у 1 = (‒ 5 – 3)/(2 · 2) = ‒ 8 /4 = ‒2, у 2 = (‒5 + 3)/(2 · 2) = ‒ 2 /4 = ‒ 0,5.

Тогда х 2 = ‒ 2 и х 2 = ‒ 0,5. Обратите внимание, ни одно из этих уравнений не имеет решения.

Ответ: решений нет.

Неполные биквадратные уравнения — это когда b = 0 (ах 4 + c = 0) или же c = 0

(ах 4 + bx 2 = 0) решают как и неполные квадратные уравнения.

Пример 3. Решить уравнение х 4 ‒ 25х 2 = 0

Разложим на множители, вынесем х 2 за скобки и тогда х 2 (х 2 ‒ 25) = 0.

Получим х 2 = 0 или х 2 ‒ 25 = 0, х 2 = 25.

Тогда имеем корни 0; 5 и – 5.

Ответ: 0; 5; – 5.

Пример 4. Решить уравнение 5х 4 ‒ 45 = 0 .

х 2 = ‒ √9 (решений не имеет)

х 2 = √9, х 1 = ‒ 3, х 2 = 3.

Как видите, умея решать квадратные уравнения, вы сможете справиться и с биквадратными.

Если же у вас остались вопросы, записывайтесь на мои уроки. Репетиор Валентина Галиневская.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Цели:

Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.

Тип урока : комбинированный.

Оборудование: графопроектор.

Наглядность: таблица «Теорема Виета».

Ход урока

1. Устный счет

а) Чему равен остаток от деления многочлена р n (х) = а n х n + а n-1 х n-1 + … + а 1 х 1 + a 0 на двучлен х-а?

б) Сколько корней может иметь кубическое уравнение?

в) С помощью чего мы решаем уравнение третьей и четвертой степени?

г) Если b четное число в квадратном уравнение, то чему равен Д и х 1 ;х 2

2. Самостоятельная работа (в группах)

Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»

1 группа

Корни: х 1 = 1; х 2 = -2; х 3 = -3; х 4 = 6

Составить уравнение:

B=1 -2-3+6=2; b=-2

с=-2-3+6+6-12-18= -23; с= -23

d=6-12+36-18=12; d= -12

е=1(-2)(-3)6=36

х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)

Решение . Целые корни ищем среди делителей числа 36.

р = ±1;±2;±3;±4;±6…

р 4 (1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера

р 3 (x) = х 3 -х 2 -24x -36

р 3 (-2) = -8 -4 +48 -36=0, х 2 =-2

р 2 (x) = х 2 -3х -18=0

х 3 =-3, х 4 =6

Ответ: 1;-2;-3;6 сумма корней 2 (П)

2 группа

Корни: х 1 = -1; х 2 = х 3 =2; х 4 =5

Составить уравнение:

B=-1+2+2+5-8; b= -8

с=2(-1)+4+10-2-5+10=15; с=15

D=-4-10+20-10= -4; d=4

е=2(-1)2*5=-20;е=-20

8+15+4х-20=0 (это уравнение решает на доске 3 группа)

р = ±1;±2;±4;±5;±10;±20.

р 4 (1)=1-8+15+4-20=-8

р 4 (-1)=1+8+15-4-20=0

р 3 (x) = х 3 -9х 2 +24x -20

р 3 (2) = 8 -36+48 -20=0

р 2 (x) = х 2 -7х +10=0 х 1 =2; х 2 =5

Ответ: -1;2;2;5 сумма корней 8(Р)

3 группа

Корни: х 1 = -1; х 2 =1; х 3 =-2; х 4 =3

Составить уравнение:

В=-1+1-2+3=1;в=-1

с=-1+2-3-2+3-6=-7;с=-7

D=2+6-3-6=-1; d=1

е=-1*1*(-2)*3=6

х 4 — х 3 — 7х 2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)

Решение. Целые корни ищем среди делителей числа 6.

р = ±1;±2;±3;±6

р 4 (1)=1-1-7+1+6=0

р 3 (x) = х 3 — 7x -6

р 3 (-1) = -1+7-6=0

р 2 (x) = х 2 -х -6=0; х 1 =-2; х 2 =3

Ответ:-1;1;-2;3 Сумма корней 1(О)

4 группа

Корни: х 1 = -2; х 2 =-2; х 3 =-3; х 4 =-3

Составить уравнение:

B=-2-2-3+3=-4; b=4

с=4+6-6+6-6-9=-5; с=-5

D=-12+12+18+18=36; d=-36

е=-2*(-2)*(-3)*3=-36;е=-36

х 4 + 4х 3 – 5х 2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)

Решение. Целые корни ищем среди делителей числа -36

р = ±1;±2;±3…

р(1)= 1 + 4-5-36-36 = -72

р 4 (-2) = 16 -32 -20 + 72 -36 = 0

р 3 (х) = х 3 +2х 2 -9х-18 = 0

р 3 (-2)= -8 + 8 + 18-18 = 0

р 2 (х) = х 2 -9 = 0; x=±3

Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)

5 группа

Корни: х 1 = -1; х 2 =-2; х 3 =-3; х 4 =-4

Составить уравнение

х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)

Решение . Целые корни ищем среди делителей числа 24.

р = ±1;±2;±3

р 4 (-1) = 1 -10 + 35 -50 + 24 = 0

р 3 (х) = x- 3 + 9х 2 + 26x+ 24 = 0

p 3 (-2) = -8 + 36-52 + 24 = О

р 2 (х) = x 2 + 7x+ 12 = 0

Ответ:-1;-2;-3;-4 сумма-10 (И)

6 группа

Корни: х 1 = 1; х 2 = 1; х 3 = -3; х 4 = 8

Составить уравнение

B=1+1-3+8=7;b=-7

с=1 -3+8-3+8-24= -13

D=-3-24+8-24= -43; d=43

х 4 — 7х 3 — 13х 2 + 43 x — 24 = 0 (это уравнение решает потом 1 группа на доске)

Решение . Целые корни ищем среди делителей числа -24.

р 4 (1)=1-7-13+43-24=0

р 3 (1)=1-6-19+24=0

р 2 (x)= х 2 -5x — 24 = 0

х 3 =-3, х 4 =8

Ответ: 1;1;-3;8 сумма 7 (Л)

3. Решение уравнений с параметром

1. Решить уравнение х 3 + 3х 2 + mх — 15 = 0; если один из корней равен (-1)

Ответ записать в порядке возрастания

R=Р 3 (-1)=-1+3-m-15=0

х 3 + 3х 2 -13х — 15 = 0; -1+3+13-15=0

По условию х 1 = — 1; Д=1+15=16

Р 2 (х) = х 2 +2х-15 = 0

х 2 =-1-4 = -5;

х 3 =-1 + 4 = 3;

Ответ:- 1;-5; 3

В порядке возрастания: -5;-1;3. (Ь Н Ы)

2. Найти все корни многочлена х 3 — 3х 2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.

Решение: R=Р 3 (1) = Р 3 (-2)

Р 3 (1) = 1-3 + а- 2а + 6 = 4-а

Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а

x 3 -Зх 2 -6х + 12 + 6 = х 3 -Зх 2 -6х + 18

x 2 (x-3)-6(x-3) = 0

(х-3)(х 2 -6) = 0

3) а=0, х 2 -0*х 2 +0 = 0; х 2 =0; х 4 =0

а=0; х=0; х=1

а>0; х=1; х=а ± √а

2. Составить уравнение

1 группа . Корни: -4; -2; 1; 7;

2 группа . Корни: -3; -2; 1; 2;

3 группа . Корни: -1; 2; 6; 10;

4 группа . Корни: -3; 2; 2; 5;

5 группа . Корни: -5; -2; 2; 4;

6 группа . Корни: -8; -2; 6; 7.

Решение биквадратных уравнений

Репетиторы ❯ Математика ❯ Решение биквадратных уравнений

Автор: Валентина Галиневская

●

11. 08.2015

●

Раздел: Математика

В этой статье мы будем учиться решать биквадратные уравнения.

Итак, уравнения какого вида называются биквадратными?
Все уравнения вида ах⁴ + bx² + c = 0, гдеа ≠ 0, являющиеся квадратными относительно х², и называются биквадратными уравнениями. Как видите, эта запись очень похожа на запись квадратного уравнения, поэтому и решать биквадратные уравнения будем используя формулы, которые мы применяли при решении квадратного уравнения.

Только нам необходимо будет ввести новую переменную, то есть обозначим х²^{другой переменной, например, у или t (или же любой другой буквой латинского алфавита).}

Например, решим уравнение х⁴+ 4х²‒ 5 = 0.

Обозначим х²^{через у (х²= у) и получим уравнение у²+ 4у – 5 = 0.
Как видите, такие уравнения вы уже умеете решать.}

Решаем полученное уравнение:

D = 4²– 4 (‒ 5) = 16 + 20 = 36, √D = √36 = 6.

у₁= ( ‒ 4 – 6)/2= ‒ 10 /2 = ‒ 5,

у₂= ( ‒ 4 + 6)/2= 2 /2 = 1.

Вернемся к нашей переменной х.

Получили, что х²= ‒ 5 и х²= 1.

Замечаем, что первое уравнение решений не имеет, а второе дает два решения: х₁= 1 и х₂= ‒1. Будьте внимательны, не потеряйте отрицательный корень (чаще всего получают ответ х = 1, а это не правильно).

Ответ: — 1 и 1.

Для лучшего усвоения темы разберем несколько примеров.

Пример 1. Решите уравнение 2х⁴ ‒ 5 х² + 3 = 0.

Пусть х² = у, тогда 2у² ‒ 5у + 3 =0.

D = (‒ 5)²– 4· 2 · 3 = 25 ‒ 24 = 1, √D = √1 = 1.

у₁ = (5 – 1)/(2· 2) = 4 /4 =1, у₂ = (5 + 1)/(2· 2) = 6 /4 =1,5.

Тогда х²= 1 и х²= 1,5.

Получаем х₁= ‒1, х₂= 1, х₃= ‒ √1,5 , х₄= √1,5.

Ответ: ‒1; 1; ‒ √1,5; √1,5.

Пример 2.Решите уравнение 2х⁴ + 5 х² + 2 = 0.

х² = у

2у² + 5у + 2 =0.

D = 5²– 4 · 2 · 2 = 25 ‒ 16 = 9, √D = √9 = 3.

у₁ = (‒ 5 – 3)/(2 · 2) = ‒ 8 /4 = ‒2, у₂ = (‒5 + 3)/(2 · 2) = ‒ 2 /4 = ‒ 0,5.

Тогда х²= ‒ 2 и х²= ‒ 0,5. Обратите внимание, ни одно из этих уравнений не имеет решения.

Ответ: решений нет.

Неполные биквадратные уравнения — это когда b = 0 (ах⁴ + c = 0) или же c = 0

(ах⁴ + bx² = 0) решают как и неполные квадратные уравнения.

Пример 3. Решить уравнение х⁴ ‒ 25х² = 0

Разложим на множители, вынесем х² за скобки и тогда х²(х²‒ 25) = 0.

Получим х²= 0 или х²‒ 25 = 0, х²= 25.

Тогда имеем корни 0; 5 и – 5.

Ответ: 0; 5; – 5.

Пример 4. Решить уравнение 5х⁴‒ 45 = 0.

5х⁴ = 45

х⁴ = 45 / 5

х⁴ = 9

х² = ‒ √9 (решений не имеет)

х² = √9, х₁= ‒ 3, х₂= 3.

Как видите, умея решать квадратные уравнения, вы сможете справиться и с биквадратными.

Если же у вас остались вопросы, записывайтесь на мои уроки. Репетиор Валентина Галиневская.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Биквадратные уравнения — примеры с решениями

Впервые с решением биквадратных уравнений сталкиваются на уроках алгебры. Степенные равенства высокого порядка решаются по аналогии с квадратными уравнениями. Существует несколько способов, позволяющих найти ответ, но чаще используется метод введения новой переменной. Такой подход простой и разобраться с ним будет под силу даже семикласснику. При этом существуют и онлайн-сервисы, проводящие вычисление корней квадратичного равенства.

Содержание

Появление методики
Основные понятия
Решение равенств
Примеры уравнений
Разложение на множители

Появление методики

Уравнения начали составлять ещё в Древнем Вавилоне. Это было вызвано потребностью находить площади земельных участков, выполнять инженерные работы. Составляли равенства и астрономы, высчитывая расстояния до обнаруживаемых космических тел. Квадратные равенства встречаются в клинописных текстах греков и вавилонян. При этом в этих записях попадаются уравнения, содержащие кубическую или биквадратную степень.

Несмотря на довольно хорошее развитие алгебры в стародавнее время, находимые упоминания о равенствах содержат только ответы, без указаний способов решений. Задачи с примерами решения биквадратных уравнений встречаются у астронома Ариабхатта и индийского учёного Брахмапутра. Формулы для решения сложных уравнений были изложены в сборнике «Книга абака», написанной в 1202 году итальянцем Фибоначчи. Это издание способствовало развитию математики, в частности, алгебре, в Италии, Германии, Франции. Большой вклад в развитие теории решения внесли и советские учёные-математики: Чеботарев, Четаев.

В XVI веках в Китае был разработан способ нахождения корней равенств высшей степени методом Цинь Цзю-шао, после успешно применявшимся в работах Руффини и Горнера.

Этот метод использовал способ подбора, но применим был только для случаев, когда в ответе присутствовали только целые числа.

Все способы решения биквадратных уравнений сводились к приведению их к простому квадратному равенству. Была найдена формула, позволяющая решать уравнения с помощью радикалов (корней). Впервые этот метод предложил Виета, но он был рассчитан только на положительные ответы. Итальянские же учёные Тарталья, Кордано, Бомбелли стали учитывать и отрицательные корни. В итоге Декарт, Жирар и Ньютон привели способы решения к современному виду.

Биквадратные выражения стали разделять на полные и неполные. В алгоритмическом языке корнями уравнения начали называть такие значения неизвестной составляющей, при которой решаемое выражение обращается в правильное числовое равенство. То есть чтобы решить задачу, нужно найти всевозможные его корни или доказать, что решения быть не может.

Основные понятия

Биквадратным уравнением будет называться равенство вида: a*p ⁴ + b*p ² + c = 0. Переменные a, b, c могут быть различными числами, при этом A не должно равняться нулю. Символ C называют свободным членом. За P принимают неизвестную переменную, требующую вычисления. Решение уравнений сводится к поиску чисел, которые при подстановке вместо P сделают равенство верным.

Согласно теореме Безу, число корней многочлена, не равного нулю, не может превосходить величину его степени. При этом любой многочлен с коэффициентами ненулевой степени должен иметь хотя бы одно решение. Тут следует отметить, что корень уравнения может быть комплексным. То есть таким выражением, степень которого равна w^x = z, где x — степень, а w — комплексное число. Понятие комплексного числа уже относится к высшей математике. Обозначают его символом (z)^1/x.

Для того чтобы доказать справедливость утверждения Безу, нужно за корень многочлена f принять c1 и составить равенство f = (p — c1) f¹. Тогда (f 1 Є K [p]), где К — является элементом поля многочлена, но лишь при условии, что f можно разделить на (p — c). Если принять за c2 корень f1, то f1 = (p — c 2)* f 2 (f 2 Є K [ p ]), а это значит что будет верным выражение: f = (p — c 1) * (p — c 2) * f2. Для длинного многочлена вида: f = (p — c 1) * (p — c 2) *…* (p — c) * s, где многочлен (s Є K [p]) не имеет решений.

Так как значения с1, с2… Cm — это все возможные корни f, то для любого поля будет верным: f (p) = (c — c1) * (c — c2)…(c — cm) * s (p). Учитывая, что s (p) не равно нулю, а f (p) = 0 только в том случае, если C равно некоторому числу I, величина корней многочлена f не может быть более значения m.

Таким образом, уравнение может иметь четыре, три, два, или одно решение. При этом есть вероятность, что ответа может совсем и не быть. Принцип, по которому решаются биквадратные уравнения, следующий:

вводят новую переменную y = p²;
подставляют используемую переменную в решаемое уравнение;
используя методы решения квадратных уравнений, находят корни равенства;
найденные величины подставляют в выражение y = p²и вычисляют исходные корни.

Квадратные уравнения можно решать любым удобным способом. Типичная схема состоит всего из четырёх шагов и редко вызывает трудности понимания. Пожалуй, сложности могут возникнуть только при нахождении комплексных корней.

Решение равенств

Без знания методов нахождения корней в квадратных уравнениях решить самостоятельно биквадратное равенство не удастся, так как исходное неравенство в итоге приводится к виду квадратичного. Существует несколько способов, позволяющих быстро найти нужные корни или доказать невозможность существования равенства.

К основным относят:

разложение части уравнения с неизвестной на множители;
вынос за скобки полного квадрата;
использование специальных формул;
графический метод;
теорему Виета.

Разложение многочлена на множители основано на группировании и нахождении дискриминанта, то есть знака, по виду которого можно судить о существовании корней. Для решения используется формула: a * p ² + b * p + c = a * (p — p 1) * (p — p 2), где p и являются корнями уравнения. Этот способ понятен и используется при обучении учащихся решению задач такого типа.

Нахождение корней методом выделения полного квадрата требует опыта использования формул сокращённого умножения, особенно если коэффициентами являются рациональные числа. При решении используется выражение: (a + b)² = a ² + 2* a * b + b ² и (a — b)² = a ² — 2* a * b + b ².

Существуют специальные формулы нахождения корней квадратного, а значит, и биквадратного уравнения. Выглядят они следующим образом: p 1 = (- b — (b ²— 4 ac)^½) / (2* a) и p 2 = (- b + (b ² + 4 ac)^½) / (2* a). С их помощью можно решить любое уравнение. При этом часто для упрощения решения вводят замену подкоренному выражению (b ²— 4 ac) обозначая его буквой D — дискриминант. Если D больше нуля, то есть два корня, если меньше — решений нет. Если же D = 0, то существует только один корень.

Франсуа Виет, проводя математические исследования, смог обнаружить зависимость между корнями уравнения и его коэффициентами. Он установил, что если p1 и p2 являются решениями равенства, то их сумма будет равна второму коэффициенту с другим знаком, а произведение свободному члену. То есть для уравнения вида: p2 +r*p + k = 0, будет справедливо записать, что p1 + p2 = — r, p1 * p2 = k.

Графическое решение требует построения зависимостей. График первой представляет собой параболу, проходящую через начало координат, а второй — прямую. Для того чтобы выделить зависимости используют перенос. В результате получается две функции: y = a * p ² и y = -(r * p+k). Построение функций и нахождение точек пересечения занимает много времени, поэтому этот метод практически никогда не используется.

Примеры уравнений

Решения любым из способов имеют свои достоинства и недостатки. По мнению математиков, проще решать уравнения, используя теорему Виета. Например, пусть дано выражение: 4p⁴ — 5p + 1 = 0, необходимо найти все бинарные корни. В первую очередь задание нужно привести к виду квадратного равенства. Для этого вводится переменная m = p². Тогда заданное уравнение можно записать как 4 m² — 5m + 1 = 0.

Теперь можно определить дискриминант: D = (-5)² — 4 * 4 * 1 = 9. Используя формулы нахождения корней, вычисляют: m1 = (5+3) / 8 = 1, m2 = (5−3) / 8 = ¼. Оба ответа удовлетворяют условию, то есть больше нуля. Подставив полученные значения в исходные выражения, решают неполные квадратные уравнения: p1 = 1; p2 = -1; p3 = ½; p4 = -½. Это цифры и будут искомыми корнями.

Довольно легко решаются уравнения с помощью метода Виета. Вероятность допущения ошибки при определении корней в этом случае стремится к нулю. Например, p⁴ — 10 * p² + 9 = 0. Чтобы избавиться от четвёртой степени, вводят переменную p.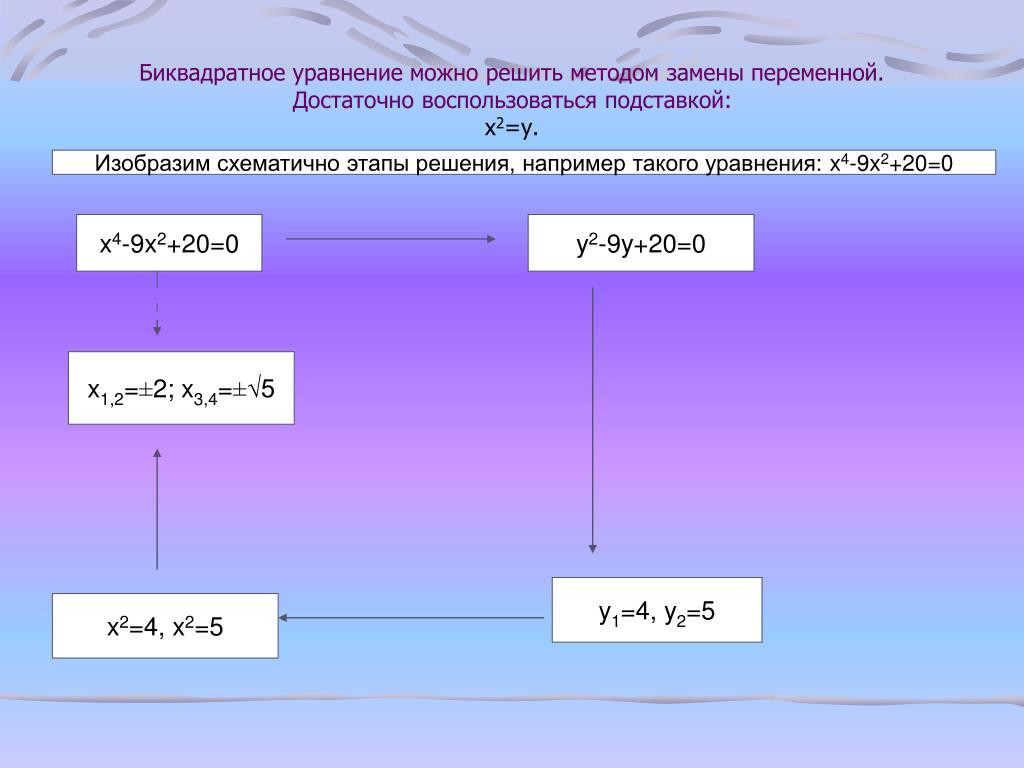 В результате уравнение принимает вид: p² — 10 * p² + 9 = 0. Теперь можно найти корни, используя обратную теорему Виета: p 1 = 9, p 2 = 1. Так как оба ответа больше нуля, то действительными корнями уравнения будут: p 1 = 3, p 2 = -3, p 3 = 1, p 2 = -1.

Определить, что решать биквадратное уравнение не имеет смысла, можно, используя комбинаторный анализ. Например, p⁴ + 11*p² + 10 = 0. Для его решения необходимо расписать каждые члены уравнения, используя определение равенства. Так как каждый член p⁴, 11*p², 10 должен быть больше либо равен нулю, то справедливым будет выражение: p⁴ + 11*p² + 10 > 0.

Отсюда можно сделать вывод, что p⁴ + 11*p² + 10 решения не имеет, ведь сумма неотрицательных чисел с положительным не может быть равной нулю. И также можно разложить и доказать бесперспективность поиска для задания с одними минусами, например, -2 p⁴ — 45 p² — 12 = 0.

Но не всегда уравнение будет иметь четыре корня. Например, p ⁴ +4 *p ² — 21=0. Если принять p²= m, квадратное уравнение изменится до вида: m ²+4*m -21=0, отсюда m 1 = -7, m 2 =3. Теперь нужно решить первоначальное уравнение. Первый ответ не имеет действительных корней, из второго же находят решение. Им будут корни: m 1 = (3)^½ и m 2 = -(3)^½.

Разложение на множители

Самостоятельная работа, дающаяся в школе, часто предполагает решение биквадратных равенств методом разложения на множители. Связанно это с тем, что этот способ позволяет понять принцип нахождения корней для многочлена любой степени.

Например, нужно разложить уравнение p⁴ + p³ — 6p² на множители. В первом действии неизвестное выносится за скобки p² (p² + p — 6). Во втором, используя формулу нахождения решений, вычисляют: p 1 = (-1 + (1² — 4 * (-6))^½) / 2, p 2 = (-1 — (1² — 4 * (-6))^½) / 2. Отсюда корни уравнения будут p1 = -3, p2 = 2. Подставив полученные значения в заданное выражение, можно записать: p 2 + p — 6 = (p — p 1)*(p — p 2) = (p + 3) * (p-2).

Пошагово описать разложение многочлена можно на следующем примере: p⁴ + 2p³ + 3p² + 4p +2. Решают его в следующей последовательности:

Предположив, что решение имеет хотя бы один рациональный корень, можно утверждать, что он и будет делителем второго члена. Значит, он будет любым из цифр: -2, -1, 1, 2.
Подставив эти числа в уравнение, получим четыре ответа: 6, 0, 12, 54. То есть одним из корней будет -1.
Разделив многочлен на (p- p1), запишем уравнение p³+ p² + 2p + 2.
Теперь можно составить равенство: p⁴ + 2p³ + 3p² + 4p +2 = (p + 1) * (p ³+ p² + 2p + 2).
Для решения уравнения, стоящего во второй части произведения, делают предположение, что кубический многочлен имеет целый корень числа 2, а значит, его ответом будет так же -1.
Сгруппировав члены, можно записать: (p + 1) * p² + 2 * (p + 1) = (p + 1) * (p² + 2).
Из-за того, что уравнение p² + 2 = 0 не может иметь действительных корней, разложение будет иметь вид: p⁴ + 2p³ + 3p² + 4p +2 = (p + 1)² * (p² + 2).

Вычисление корней требует внимательности и усердия. Для проверки своих навыков можно использовать онлайн-калькуляторы. Это сервисы, использующие специальное программное обеспечение, часто написанное на Паскале, умеют быстро и безошибочно рассчитывать корни любого примера.

Чтобы решить биквадратное уравнение онлайн, особых умений или знаний правил не нужно. Всё, что требуется — это ввести в предложенную форму параметры решаемого равенства. Из наиболее популярных интернет-порталов выделяют Allcalc. Используя его, можно проверить свои знания, исправить допущенные ошибки при самостоятельном расчёте. Причём свои услуги сайт предлагает совершенно бесплатно.

МатематикаРешение кубических уравнений — методы и примеры вычислений

МатематикаПараллелограмм — его основные свойства, признаки и формулы

биквадратных уравнений | Superprof

Полиномиальные уравнения очень трудно решить. Наиболее часто используемым методом нахождения факторов полиномиального уравнения является метод проб и ошибок, который не только отнимет у вас много времени, но и разочарует любого. Математика была открыта для того, чтобы облегчить нашу жизнь, а не усложнить ее, поэтому мы пытаемся использовать метод «биквадратных уравнений» для решения полиномиальных уравнений.

Биквадратные уравнения являются разновидностью полиномиальных уравнений, однако это означает, что не все полиномиальные уравнения являются биквадратными уравнениями. Суть в том, чтобы проверить, есть ли в полиномиальном уравнении член нечетной степени? Если вы увидели член с нечетной степенью, это означает, что биквадратичный метод неприменим к этому уравнению, к сожалению, вам нужно использовать метод проб и ошибок, чтобы решить это уравнение.

Например, вот уравнение, проверьте, есть ли в уравнении члены нечетной степени, , не торопитесь и подумайте, можно ли применить к этому уравнению метод биквадратов? Если ваш ответ нет, то поздравляем! Вы узнали, когда использовать этот метод. Причина довольно проста, если вы проверите третий член (то есть ), это член нечетной степени. Как упоминалось выше, вы не можете применять этот метод, если уравнение имеет член нечетной степени. Вот еще один пример, чтобы проверить себя, можем ли мы применить метод биквадратичного уравнения к этому уравнению? Да, конечно! Потому что нет термина нечетной степени. Слово нечетное не означает, что мы говорим о нечетных числах, не путайте нечетные числа и нечетные термины. Это последний пример, выясним, можем ли мы использовать этот метод или нет, ответ — нет, потому что он уже в форме квадратного уравнения. Мы используем метод биквадратичного уравнения для преобразования полиномиальных уравнений в квадратные уравнения, чтобы мы могли легко решать их, нарушая метод среднего члена или используя квадратную формулу.

Найдите репетитора по математике на Superprof.

Решение биквадратных уравнений

Теперь вы знаете первое, что касается биквадратичного метода, а именно, что его нельзя применять к уравнениям с членами нечетной степени. Следующее, что вам нужно понять, это преобразование уравнения полинома в биквадратное уравнение. Для этого мы используем метод, который мы называем предположением . Это очень простая техника, вам нужно положить переменную с определенной степенью на другую переменную. Например, вот полиномиальное уравнение:

Здесь предположим, что уравнение преобразуется в квадратное уравнение. Лучшая часть предположения заключается в том, что вы можете предположить что угодно, однако убедитесь, что оно соответствует вашей системе. Проще говоря, вы можете предположить что угодно, но не в пределе, чтобы вы могли работать над своим уравнением. Для вышеприведенного уравнения предположим . Вы можете использовать любую другую переменную, кроме t, это может быть a,b,c,d и т. д. Давайте подставим наше предположение в приведенное выше уравнение:

Теперь это уравнение было преобразовано в квадратное уравнение, что означает, что наше предположение было верным, но это еще не конец. Вам нужно решить приведенное выше уравнение и получить его множители, к счастью, мы его уже решили, и вот множители. Почему бы вам не взглянуть на исходное уравнение? Вы что-то заметили? Переменная в уравнении была , однако переменная в ответе . Это произошло потому, что мы подставили переменную, помните? Не забывайте об этом! Это очень распространенная ошибка. Учащиеся оставляют свои ответы в терминах, которые не являются ответом. Как только вы найдете коэффициенты , пришло время вернуть исходное значение, которое было . Вы сделаете что-то вроде этого:

Укореняясь с обеих сторон:

*Потому что корень из отрицательного числа означает мнимое число.

Еще одна распространенная ошибка заключается в том, что студенты забывают добавить, когда берут корни факторов. Помните, что обычно биквадратные уравнения имеют четыре ответа, но в некоторых случаях они могут иметь и два ответа.

Найдите различные курсы по математике онлайн на Superprof.

Доступны лучшие репетиторы по математике

Поехали

Примеры

Пусть:

Вы можете использовать оба метода (метод среднего члена и квадратную формулу) для решения этого уравнения, здесь мы будем использовать метод среднего члена для решения нашего уравнения:

Замена

Такая же процедура может быть использована для решения уравнений:

Supposing

Using the quadratic formula to get factors:

Substituting

Пусть:

Используя метод разбиения среднего члена, чтобы найти множители:

Substituting

Taking root on both sides

Let :

Using quadratic formula to find factors

Замещающий

Укореняющийся с обеих сторон

Let :

Using the middle term breaking method to find factors

Substituting

Let :

Использование квадратичной формулы для нахождения коэффициентов0003

Замена

Повысьте скорость обучения и понимания с репетитором по математике на Superprof.

Алгебраическое решение уравнений кубической и четвертой степени

Обзор

Решение уравнений кубической и четвертой степени было одним из главных достижений алгебры эпохи Возрождения. Публикация результатов в книге Джироламо Кардано «Великое искусство » вызвала обвинения в том, что Кардано нарушил свое обещание, данное Тарталье, который утверждал, что сделал главное открытие в кубическом случае. Попытки идентифицировать все решения уравнений кубического, четвертого и более высоких порядков потребовали бы изобретения комплексных чисел и привели бы к открытию теории групп — одной из важнейших идей современной абстрактной алгебры.

Исходная информация

Наше слово «алгебра» происходит от арабского Kitab al-jabr w’almuqabala, книги арабского математика Мухаммада ибн Мусы аль-Хорезми (ок. 780-ок. 850), которая описал искусство «восстановления и сокращения», то есть нахождения значения неизвестных величин в равенстве путем перестановки членов. Книга была переведена на латынь в 1145 году как Liber алгебра и альмукабала Робертом Честерским (эт. 1145), английским ученым, жившим в мусульманской Испании. В христианской Западной Европе математика находилась в гораздо менее развитом состоянии, чем в странах, находящихся под контролем мусульман. Греческая научная традиция продолжилась в Византийской империи, которая, однако, подвергалась частым нападениям со стороны своих соседей. В 1543 году турецкие войска захватили его столицу Константинополь. Византийские ученые нашли убежище в Италии, где богатые и влиятельные семьи, такие как Медичи, добавили ученых в свое окружение и рукописи в свои библиотеки. Появление печатного станка Гутенберга сделало математические идеи гораздо более доступными. До 1500 г. в Италии появилось более 200 новых книг по математике9.0003

В 1545 году вышла книга итальянского математика Джироламо Кардано (1501-1576) под названием Ars Magna, или The Great Art, . В эту работу вошли важные новые результаты — решение уравнений кубической и четвертой степени. В современной трактовке алгебры квадратное уравнение — это любое уравнение формы

, где A — число, отличное от нуля, а B и C — константы, которые могут быть положительными, отрицательными или нулевыми. Буква x , конечно же, неизвестное, которое нужно найти. Однако до недавнего времени у математиков не было инструментов для работы со случаями, когда 90 255 A, B 90 256 и 90 255 C 90 256 являются положительными числами. Кроме того, существовала тенденция избегать появления отрицательных чисел. Метод решения некоторых квадратных уравнений был разработан древними вавилонянами на основе процесса, который теперь преподают как «заполнение квадрата». В al-jabr обсуждаются шесть возможных вариантов квадратного уравнения, которые можно записать без отрицательных чисел или нуля, например, Ax ² = Bx или Ax ² + Bx = C . В последнем случае есть два возможных решения, даваемые квадратичной формулой, которая включает в себя обычные арифметические операции: сложение, вычитание, умножение и деление, а также извлечение квадратного корня.

Кубическое уравнение имеет современную форму

Когда B установлено равным нулю, это известно как сокращенное кубическое уравнение. Уравнение четвертой или биквадратной формы имеет вид

Как и в случае с предыдущим решением квадратного уравнения, при обработке этих уравнений Кардано должен был учитывать множество особых случаев, чтобы избежать отрицательных величин и необходимости извлечения квадратного корня из отрицательного числа. Как и в случае с квадратичным, решение Кардано для кубического и квартического чисел включало добавление вычитания, умножения, деления и извлечения корней, в данном случае включая кубические корни, а также квадратные корни.

Кардано открыто признал, что представленные им решения не были его первоначальным открытием. Решение редуцированного кубического уравнения x ³ + Ax = B были найдены в 1515 году Сципионом дель Ферро (1465-1526), профессором Болонского университета. Примерно 20 лет спустя он сообщил об этом решении своему ученику Антонио Фиору. Итальянский математик Никколо Фонтана, более известный как Тарталья (1500?-1557), затем объявил, что он нашел решение кубического уравнения, в котором отсутствует член первого порядка, x ³ + Ax ² = Б , а также решение дела дель Ферро. Фиор сомневался, что Тарталья мог найти такое решение, и устроил соревнование, в котором он и Тарталья обменялись наборами из 30 задач. По истечении оговоренного времени Тарталья решил все проблемы Фиора, в то время как Фиор не смог решить ни одну из проблем Тартальи. Кардано пригласил Тарталью к себе домой, намекнув, что, возможно, сможет познакомить его с возможным покровителем. Там Тарталья раскрыл свой метод Кардано в обмен на заверения, что он не будет опубликован.

Решение квартики было получено итальянцем Людовико Феррари (1522-1565), который был секретарем Кардано и станет его зятем. Кардано писал, что Ferrari разработала его по его просьбе. Суть решения заключалась в том, чтобы определить новую переменную, связанную с неизвестным, таким образом, чтобы квартику можно было записать в виде кубической, которую затем можно было решить.

Тарталья отреагировал на книгу Кардано, опубликовав одну из своих собственных, описав собственное исследование кубического уравнения и напав на честность Кардано за нарушение своего обещания. Встреча Кардано и Тартальи произошла в 1539 году.. Однако Кардано узнал о решении дель Ферро в 1542 году и почувствовал, что больше не связан своим обещанием, поскольку дель Ферро в значительной степени предвидел результаты Тартальи. Феррари встал на защиту Кардано и бросил Тарталье публичный математический вызов, на который Тарталья ответил. После шести таких обменов мнениями Ферраро и Тарталья вступили в публичные устные дебаты в миланской церкви в 1548 году.

Несмотря на спор о том, правильно ли действовал Кардано, есть важные открытия, которые, несомненно, принадлежат Кардано. Именно Кардано открыл систематический метод преобразования общего кубического уравнения в сокращенную форму, чтобы можно было использовать решение дель Ферро. Кардано был также первым, кто показал, что кубическое уравнение может иметь три действительных решения. Он также был одним из первых математиков, использовавших мнимые числа для выражения решений алгебраических уравнений, хотя полного понимания их свойств не было в течение почти трех столетий.

Воздействие

Чрезвычайная конкуренция математиков, занимающихся решением уравнений кубической и четвертой степени, согласуется с агрессивным индивидуализмом эпохи Возрождения. Кардано был более ярким, чем большинство. Незаконнорожденный сын юриста, он играл в кости и шахматы, чтобы получить доход. Он получил медицинскую степень в Падуанском университете в 1526 году, но до 1534 года ему не разрешали практиковать в родном Милане из-за незаконнорожденности. Хотя среди его пациентов когда-то был Папа Римский, в 1570 году он попал в тюрьму за ересь за составление гороскопа Иисуса, а год спустя стал папским астрологом. Тарталья тоже занимался сомнительной практикой. Он опубликовал перевод Архимеда, сделанный бельгийским ученым Вильгельмом Мербеке (ок. 1220–1286), таким образом, что можно предположить, что это его собственная работа. Феррари, вероятно, тоже был замешан в интригах. Сообщается, что его отравил родственник.

Важным шагом вперед в алгебре стала работа французского юриста и писателя Франсуа Виета (1540-1620). Хотя приведенное выше обсуждение соответствует современной практике использования букв для обозначения как известных, так и известных чисел, это достигается только в работе Виете. В al-jabr вообще не использовались математические символы, в то время как в работе Кардано буквы использовались для известных величин, но не для неизвестных. С новыми обозначениями Виета стало легче думать о решении алгебраического уравнения как о нахождении значений 9.0255 x , для которого определенная функция переменной x равнялась бы нулю. Это подготовило почву для изучения самих функций и изучения преобразований функций, вызванных введением новых переменных, идей, важных в современной алгебре, тригонометрии и исчислении.

Решение уравнений со степенями неизвестных величин неоднократно служило источником вдохновения для новых разработок в математике. Греческий математик Диофант (ок. 3 в. н. э.) поставил вопрос о существовании целочисленных решений уравнений с целыми степенями различных неизвестных. Французский математик Пьер де Ферма (1601-1665) предположил, что целых чисел не существует, A, B, C, к уравнениям вида

Когда n больше двух. Поиски доказательства гипотезы Ферма займут математиков на века.

Введение комплексных чисел, то есть чисел вида а + ib , где «мнимая» единица i обладает тем свойством, что i ² = -1, было отчасти мотивировано изучением алгебраических уравнений. Если в качестве решений допускаются комплексные числа, то каждое квадратное уравнение имеет два решения, каждое кубическое — три, а каждое четверное — четыре. Понимание природы комплексных чисел было источником многих новых идей в математике девятнадцатого века.

При известных решениях уравнений кубической и четвертой степени может показаться, что решение уравнения пятой степени, которое включает пятую степень неизвестного, и уравнения даже более высокого порядка, в конечном итоге будет достигнуто. Несмотря на несколько столетий усилий, эти решения так и не были найдены. То, что такие точные решения, включающие только корни и арифметические операции, невозможны, было продемонстрировано в 1824 году норвежским математиком Нильсом Хенриком Абелем (1802–1829). Результаты Абеля были обобщены французским математиком Эваристом Галуа (1811-1832) на все уравнения со степенями неизвестного выше четвертой. Изучение алгебраических преобразований этими двумя математиками привело бы к общей теории преобразований, теперь известной как теория групп, которая считается одной из основных областей как абстрактной, так и полезной математики современными математиками и учеными.

ДОНАЛЬД Р. ФРАНЧЕТТИ

Дополнительная литература

Белл, Эрик Темпл. Развитие математики . Нью-Йорк: McGraw-Hill, 1945.

Бойер, Карл Б. История математики . Нью-Йорк: Wiley, 1968.

Клайн, Моррис. Математическая мысль от древности до современности . Нью-Йорк: Издательство Оксфордского университета, 1972.

Наука и ее времена: понимание социальной значимости научных открытий 9Уравнение 2+q=0$ имеет четыре решения, которые являются последовательными членами арифметического уравнения.

Ответ: root из $q / p = -3/10$, но я понятия не имею, что здесь происходит, и хотел бы знать. Все, что я мог сделать до того, как увидел ответ, это то, что $p<0$ и $q>0$. Буду признателен, если кто-то, кто может решить эту проблему, ответит и поможет. Спасибо

квадратика
арифметическая прогрессия

$\endgroup$

$\begingroup$

Вы хотите, чтобы корни вашего полинома были $a$, $a+r$, $a+2r$, $a+3r$ для некоторого $r$. 92} \ \ = \ \ \frac34 \ · \ \left(-\frac25 \right) \ \ = \ \ -\frac{3}{10} \ \ . $$

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Решение кубических и четвертых уравнений | Марко Тавора, доктор философии.

Выходя за рамки квадратных полиномов

Image par Pete Linforth de Pixabay

Все мы учимся решать квадратные уравнения в старшей школе. Квадратные уравнения представляют собой полиномиальные уравнения второго порядка, включающие только одну переменную. Однако задачи решения уравнений кубической и четвертой степени в школе не преподаются, хотя для их решения требуются лишь базовые математические приемы. В этой статье я покажу, как получить решения этих двух типов полиномиальных уравнений. Точные решения (или корни полинома) можно найти с помощью методов алгебры или тригонометрии (эта статья, однако, будет ограничена только алгебраическими методами).

Я начну с краткого обзора истории предмета.

Кубические уравнения

Кубические уравнения изучались на протяжении столетий, начиная с древних вавилонян, греков, китайцев, индийцев и египтян (подробнее см. в статье Wiki). Самым старым изучаемым кубическим уравнением была алгебраическая версия знаменитой геометрической задачи удвоения куба, так называемой задачи Делоса (которая в алгебраическом смысле эквивалентна решению уравнения 9).0492 х ³=2).

Рисунок 1: Неудачные попытки Леонардо да Винчи решить делосскую проблему (источник).

Несколько известных математиков решили частные случаи кубических уравнений, но общее решение было найдено только в 1500-х годах. Это решение было впервые опубликовано итальянским эрудитом Джероламо Кардано в его важной книге по алгебре Ars Magna (1545 г.). Версию книги на латыни можно найти здесь.

Рисунок 2: Титульная страница Ars Magna ( источник ).

Однако Кардано не был первооткрывателем этого результата. Первым, кто нашел решение кубического уравнения, был итальянский математик эпохи Возрождения Шипионе дель Ферро. Дель Ферро передал свою формулу своему ученику, математику Антонио Фиоре (когда тот был на смертном одре).

Рисунок 3: Сципионе дель Ферро, Никколо Тарталья и Джероламо Кардано, слева направо.

Итальянский математик и инженер Никколо Тарталья также нашел решение (независимо). Позже Кардано убедил его раскрыть свой секрет (решение) при условии, что Кардано поклялся никогда его не публиковать. Однако, когда Кардано узнал, что дель Ферро самостоятельно нашел решение раньше Тартальи, он решил включить его в свой Ars Magna (хотя Кардано приписывал первоначальное открытие и Тарталье, и дель Ферро, Тарталья не был доволен тем, что его секрет был раскрыт! ).

Однако Кардано заметил, что решение Тартальи иногда включало то, что мы теперь называем комплексными числами, поэтому он не осознавал всех последствий результата. Позднее этим вопросом подробно занимался итальянский математик Рафаэль Бомбелли. По этой причине многие считают Бомбелли первооткрывателем комплексных чисел.

Уравнения четвертой степени

Уравнение четвертой степени было решено в 1540 году математиком Людовико Феррари. Однако, как мы увидим, для решения уравнений четвертой степени требуется решение кубических уравнений. Следовательно, он был опубликован только позже, в Ars Magna Кардано.

Рисунок 4: Математик Людовико Феррари (источник).

Сейчас мы покажем, как найти решения. Начнем с кубических уравнений, так как они нужны для решения квартик.

Наша цель — показать, как решить следующее кубическое уравнение:

Уравнение 1: Наша цель в этом разделе — решить кубическое уравнение.

Это уравнение называется депрессивной кубической. Хотя они проще, чем общие кубические уравнения (которые имеют квадратичный член), любое кубическое уравнение можно свести к вдавленному кубическому (через замену переменных).

Рисунок 5: Пример кубического полинома (источник).

Левая часть уравнения. 1 приведен пример полиномиальной функции p ( z ), которая представляет собой выражение, включающее сумму степеней переменных, умноженных на коэффициенты. уравнение 1 представляет собой полиномиальное уравнение , соответствующее полиномиальной функции p ( z ). Как упоминалось ранее, нули уравнения называются корнями.

Чтобы найти z в уравнении. 1 сначала выберем две вспомогательные переменные u и v так, что u + v = z , и подставьте это выражение в уравнение 1. Удобная группировка терминов дает:

Уравнение 2: Результат подстановки u + v = z в уравнение. 1.

Теперь u и v могут принимать любые значения, если их сумма равна z . Наиболее очевидный выбор для u и против здесь должен подчиняться

Уравнению 3: Более очевидный выбор для u и против

, поскольку при таком выборе средний член уравнения 2 исчезает. Мы получаем систему двух уравнений:

Уравнение 4: Подставляя uv =- p /3 в уравнение. 2 средний член исчезает, и мы получаем эту систему уравнений.

Теперь определите:

Уравнение 5: Определение z и w.

Система уравнений становится:

Уравнение 6: Система в уравнении.

4 с использованием уравнения. 5.

уравнение 6 представлены решения квадратного уравнения. Переменные z и w тогда равны:

Уравнение 7: Квадратное уравнение, соответствующее решениям, которые подчиняются уравнению. 6.

Используя u + v = z , мы получаем искомые решения:

Уравнение 8: Решения уравнения. 1.

Напомним, что это решение предполагает уравнение. 3 нужно соблюдать. Давайте теперь посмотрим, как решать полиномы четвертой степени.

Стратегия, которой мы будем следовать здесь, состоит в том, чтобы получить решения уравнения четвертой степени через решения кубического уравнения (которое мы знаем, как решать). Этот подход был разработан Леонгардом Эйлер, один из величайших математиков в истории. Поскольку уравнение четвертой степени без члена x ³, известное как редуцированное уравнение четвертой степени, может быть получено из общего уравнения четвертой степени с использованием только тривиальной замены переменных, нам нужно решить только первое (сокращенное уравнение).

Рисунок 6: Портрет Леонарда Эйлера работы Якоба Эмануэля Хандманна (источник).

Следуя Эйлеру, наша цель — доказать, что редуцированное уравнение четвертой степени

Уравнение 9: Пример уравнения четвертой степени.

имеет следующие корни:

Уравнение 10: Решения уравнения. 9.

при условии, что три θ с являются нулями следующего кубического полинома:

Уравнение 11: Уравнение, корни которого задаются θ с.

Как упоминалось ранее, это уравнение можно тривиально преобразовать в депрессивное кубическое уравнение, которое мы знаем, как решить (см. раздел выше).

Рисунок 7: Пример многочлена четвертой степени (источник).

Чтобы найти наше доказательство, поступим следующим образом. Суммируя четыре уравнения в формуле. 10 или по одной из формул Виета (устанавливающих связь коэффициентов многочлена с его нулями) находим, что з.с. уравнения. 10 удовлетворяют:

Уравнение 12: Формуле подчиняются zs уравнения.

10.Рис. 8: Французский математик Франсуа Виет (источник).

Теперь дадим следующие определения:

Уравнение 13: Определение θ₁, θ₂ и θ₃.

Решая четыре z с в этой системе уравнений, мы получаем уравнение. 10. Подставляя уравнение. 10 в уравнение 9 получаем:

Уравнение 14: Полученные соотношения Подставляя уравнение. 13 в уравнение. 9.

Прямое применение формул Виета означает, что θ с в уравнении. 12 являются корнями кубического многочлена

Уравнение 15: θ s являются корнями этого кубического многочлена.

, которую мы ранее научились решать. На этом наше доказательство заканчивается.

Спасибо за внимание и до скорой встречи! Как всегда, конструктивная критика и отзывы всегда приветствуются!

На моем Github и личном веб-сайте www.marcotavora.me есть другие интересные материалы как по математике, так и по другим темам, таким как физика, машинное обучение, глубокое обучение и финансы!

Найдите корни биквадратного уравнения, которое нужно решить.

Биквадратное уравнение, решение биквадратного уравнения

На предыдущих уроках мы научились решать квадратные уравнения. Это потребовало введения нового математического объекта — дискриминанта. Если вы не помните, что это такое, рекомендую вернуться к уроку «Как решать квадратные уравнения».

Начнем с того, что биквадратичное уравнение — это любое выражение, в котором переменная присутствует только в 4-й и 2-й степенях. 9(2))-5t+4=0\]

Это обычное квадратное уравнение, вычисляем его с помощью дискриминанта:

Это хорошее число. Корень равен 3.

Теперь найдем значение $t$:

\[\begin(array)((35)(l))

((t)_(1))\text()=\ text()\frac(5+3)(2)=\text()\frac(8)(2)\text()=\text() 4 \\((t)_(2))\text( )=\frac(5-3)(2)=\text()\frac(2)(2)\text(= )1 \\\end (массив)\]

Но будьте осторожны, мы нашли только $ t$ — это не решение, это только третий шаг. Переходим к четвертому шагу — вспомним, что такое $t$ и решим: 9(2))-\frac(5)(4t)+\frac(1)(4)=0\]

Умножим обе части на 4, чтобы избавиться от дробных коэффициентов:

Найдите $D$:

Корень дискриминанта равен трем:

\[\begin(array)((35)(l))

((t)_(1))\text()=\text()\frac(5+ 3)(2\cdot 4)=\text()\frac(8)(8)\text()=\ text()1 \\((t)_(2))\text()=\frac( 5-3)(2\cdot 4)=\text()\frac(2)(8)=\text()\frac(1)(4) \\\end(array)\]

Считаем X . (2))=1 \\& \left[ \begin(align)& x=1 \\& x=-1 \\\end(выравнивание) \right . \\\конец(выравнивание)\] 9(2))=\frac(1)(4) \\& \left[ \begin(align)& x=\frac(1)(2) \\ & x=-\frac(1)(2) \ \\конец(выравнивание) \вправо. \\\end(align)\]

Мы снова получили четыре корня:

Вот так все делается биквадратными уравнениями. Конечно, это не самый быстрый способ, но зато самый надежный. Попробуйте сами решить те же примеры, что и в этом видео. В ответе значения x надо писать через точку с запятой — я так и записал. Этот урок окончен. Удачи!

Инструкция

Метод подстановки Выразите одну переменную и подставьте ее в другое уравнение. Вы можете выразить любую переменную, которую хотите. Например, выразите «y» из второго уравнения:
x-y=2 => y=x-2 Затем подставьте все в первое уравнение:
2x+(x-2)=10 Переместите все без x вправо и посчитайте:
2x+x=10+2
3x=12 Затем для «x» разделите обе части уравнения на 3:
x=4. Итак, вы нашли «x. Найдите «у. Для этого подставьте «х» в уравнение, из которого вы выражали «у:
у=х-2=4-2=2
у=2.

Сделать чек. Для этого подставляем полученные значения в уравнения:
2*4+2=10
4-2=2
Неизвестное найдено правильно!

Как складывать или вычитать уравнения Избавьтесь сразу от любой переменной. В нашем случае это проще сделать с «у.
Так как в «у» стоит «+», а во втором «-«, то можно выполнить операцию сложения, т.е. левую часть прибавляем к левой, а правая часть вправо:
2x+y+(x-y)=10+2Convert:
2x+y+x-y=10+2
3x=12
x=4 Подставьте «x» в любое уравнение и найдите «y:
2*4+y=10
8+y=10
y=10-8
y=2 По 1-му способу можно найти то, что нашли правильно

Если нет четко определенных переменных, то необходимо немного преобразовать уравнения
В первом уравнении имеем «2x», а во втором просто «x. Для того, чтобы сложение или «x уменьшилось», умножьте второе уравнение на 2:
x-y=2
2x-2y=4 Затем вычтите второе уравнение из первого уравнения:
2x+y-(2x-2y)=10-4
2x+y-2x+2y=6
3y=6
найти y = 2″x, выразив из любого уравнения, т. е.
x=4

Родственные видео

Уравнение , записанное в общем виде ax+by+c=0, называется линейным уравнением с двумя переменными . Само это уравнение содержит бесконечное множество решений, поэтому в задачах его всегда чем-то дополняют — другое уравнение или предельные условия.В зависимости от условий, предусмотренных задачей, решить линейное уравнение с двумя переменные должны по-разному.

Вам понадобится

— линейное уравнение с двумя переменными;
— второе уравнение или дополнительные условия.

Инструкция

Дана система двух линейных уравнений. Решите ее следующим образом. Выберите одно из уравнений, в котором коэффициенты перед переменными меньше и выражают одну из переменных, например, х. Затем подставьте это значение, содержащее y, во второе уравнение. В полученном уравнении будет только одна переменная у, переместите все части с у в левую часть, а свободные в правую. Найдите у и подставьте в любое из исходных уравнений, найдите х.

Есть еще один способ решить систему двух уравнений. Умножьте одно из уравнений на число так, чтобы коэффициент перед одной из переменных, например, перед х, был одинаковым в обоих уравнениях. Затем вычтите одно из уравнений из другого (если правая часть не равна 0, не забудьте вычесть правую часть таким же образом). Вы увидите, что переменная x исчезла и осталась только одна переменная y. Решите полученное уравнение и подставьте найденное значение y в любое из исходных равенств. Найдите х.

Третий способ решения системы двух линейных уравнений — графический. Нарисуйте систему координат и начертите графики двух прямых, уравнения которых указаны в вашей системе. Для этого подставьте в уравнение любые два значения x и найдите соответствующие y — это будут координаты точек, принадлежащих прямой. Удобнее всего найти пересечение с осями координат — достаточно подставить значения x=0 и y=0. Координаты точки пересечения этих двух линий и будут задачами.

Если в условиях задачи есть только одно линейное уравнение, то вам даются дополнительные условия, благодаря которым можно найти решение. Внимательно прочитайте задачу, чтобы найти эти условия. Если переменными x и y являются расстояние, скорость, вес — смело устанавливайте предел x≥0 и y≥0. Вполне возможно, что x или y скрывает количество , яблок и т. д. — тогда значения могут быть только . Если х — возраст сына, то понятно, что он не может быть старше своего отца, поэтому укажите это в условиях задачи.

Источники:

как решить уравнение с одной переменной

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего его дополняют еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

— система из трех уравнений с тремя неизвестными.

Инструкция

Если две из трех систем имеют только две из трех неизвестных, попробуйте выразить некоторые переменные через другие и подставить их в уравнение с тремя неизвестными .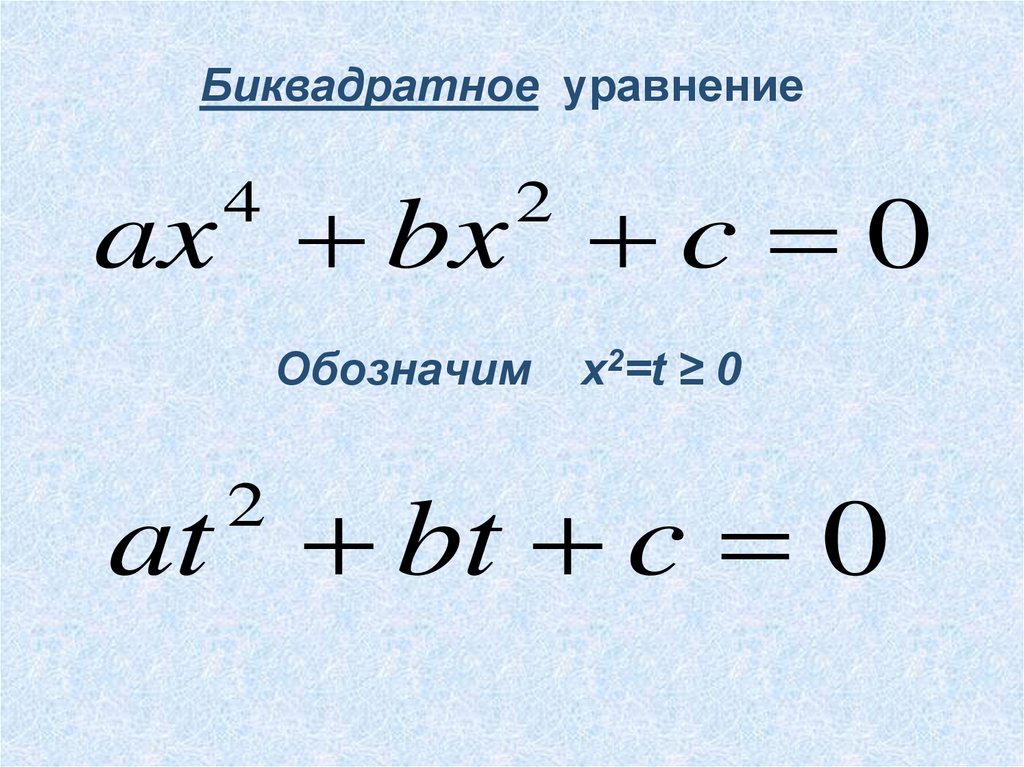 Ваша цель состоит в том, чтобы превратить его в обычное уравнение с неизвестным. Если это , то дальнейшее решение достаточно простое — подставить найденное значение в другие уравнения и найти все остальные неизвестные.

Некоторые системы уравнений могут быть вычтены из одного уравнения другим. Посмотрите, можно ли умножить одну из переменных на или на переменную так, чтобы сразу две неизвестные уменьшились. Если есть такая возможность, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число нужно умножать и левую, и правую часть. Точно так же, вычитая уравнения, помните, что правая часть также должна быть вычтена.

Если предыдущие способы не помогли, используйте в общем виде решения любых уравнений с тремя неизвестными . Для этого перепишем уравнения в виде а11х1 + а12х2 + а13х3 = b1, а21х1 + а22х2 + а23х3 = b2, а31х1 + а32х2 + а33х3 = b3. Теперь составим матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, матрицу свободных членов, то есть А*Х=В.

Найдите матрицу A в степени (-1) после нахождения , обратите внимание, что она не должна быть равна нулю. После этого умножьте полученную матрицу на матрицу B, в результате вы получите искомую матрицу X с указанием всех значений.

Вы также можете найти решение системы трех уравнений методом Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя значения свободных членов вместо значений соответствующих столбцов. Теперь найдем x: x1=∆1/∆, x2=∆2/∆, x3=∆3/∆.

Источники:

решения уравнений с тремя неизвестными

Решение системы уравнений сложное и увлекательное. Чем сложнее система, тем интереснее ее решать. Чаще всего в средней школе математики встречаются системы уравнений с двумя неизвестными, но в высшей математике переменных может быть больше. Системы могут быть решены несколькими способами.

Инструкция

Наиболее распространенным методом решения системы уравнений является подстановка. Для этого нужно выразить одну переменную через другую и подставить ее во вторую уравнения системы, тем самым сводя уравнение к одной переменной. Например, учитывая уравнения: 2x-3y-1=0; х+у-3=0.

Одну из переменных удобно выразить из второго выражения, перенеся все остальные в правую часть выражения, не забывая при этом менять знак коэффициента: х = 3-у.

Раскрываем скобки: 6-2у-3у-1=0; -5у+5=0; у = 1. Полученное значение у подставляется в выражение: х = 3-у; х = 3-1; х = 2,

В первом выражении все члены равны 2, можно вынести 2 за скобку к распределительному свойству умножения: 2 * (2x-y-3) = 0. Теперь обе части выражения можно сократить по этому числа, а затем выразить у, так как коэффициент по модулю для него равен единице: -у = 3-2х или у = 2х-3.

Так же, как и в первом случае, подставляем это выражение во второе уравнение и получаем: 3x+2*(2x-3)-8=0;3x+4x-6-8=0;7x- 14=0;7х=14;х=2. Подставляем полученное значение в выражение: y=2x -3;y=4-3=1. 92 ? 4ас. В этом случае переменные a, b, c являются коэффициентами нашего уравнения.

Найдите корни биквадратного уравнения. Для этого извлеките квадратный корень из полученных решений. Если было одно решение, то их будет два — положительное и отрицательное значение квадратного корня. Если бы было два решения, биквадратное уравнение имело бы четыре корня.

Видео по теме

Одним из классических методов решения систем линейных уравнений является метод Гаусса. Он заключается в последовательном исключении переменных, когда система уравнений с помощью простых преобразований преобразуется в ступенчатую систему, из которой последовательно находятся все переменные, начиная с последних.

Инструкция

Сначала приведем систему уравнений к такому виду, когда все неизвестные будут стоять в строго определенном порядке. Например, все неизвестные X будут идти первыми в каждой строке, все Y будут идти после X, все Z будут идти после Y и так далее. В правой части каждого уравнения не должно быть неизвестных. В уме определите коэффициенты перед каждым неизвестным, а также коэффициенты в правой части каждого уравнения.

Все со школы знают такое понятие, как уравнения. Уравнение – это равенство, содержащее одну или несколько переменных. Зная, что одна из частей этого равенства равна другой, можно вычленять отдельные части уравнения, переводя ту или иную его составную часть за знак равенства по четко определенным правилам. Можно упростить уравнение до нужного логического вывода в виде x=n, где n — любое число.

С начальной школы Все дети проходят курс обучения разной сложности. Далее в программе более сложные линейные уравнения — квадратные, затем идут кубические уравнения. Каждый последующий тип уравнений имеет новые методы решения, становится сложнее изучать и повторять.

Однако после этого встает вопрос о решении такого типа уравнений, как биквадратные уравнения. Этот тип, несмотря на кажущуюся сложность, решается достаточно просто: главное уметь приводить такие уравнения к надлежащему виду. Их решение изучается на одном-двух уроках вместе с практическими заданиями, если у учащихся есть базовые знания о решении квадратных уравнений.

Что нужно знать человеку, который сталкивается с уравнениями такого типа? Начнем с того, что в них входят только четные степени переменной «х»: четвертая и, соответственно, вторая. Для того, чтобы биквадратное уравнение было решено, необходимо привести его к виду Как это сделать? Достаточно просто! Вам просто нужно заменить «х» в квадрате на «у». Тогда пугающая многих школьников «х» в четвертой степени превратится в «у» в квадрате, и уравнение примет вид обычного квадрата.

Далее решается как обычное квадратное уравнение: раскладывается на множители, после чего находится значение загадочной «игры». Чтобы решить биквадратное уравнение до конца, нужно найти из числа «у» — это и будет искомое значение «х», после нахождения значений которого можно поздравить себя с успешным завершением расчетов.

Что следует помнить при решении уравнений этого типа? Прежде всего: Y не может быть отрицательным числом! Само условие, что y является квадратом x, исключает аналогичные варианты решения. Поэтому, если при первоначальном решении биквадратного уравнения одно из значений «у» окажется для вас положительным, а второе отрицательным, нужно взять только его положительный вариант, иначе биквадратное уравнение будет решено неправильно. Лучше сразу ввести правило, что переменная «у» больше или равна нулю.

Второй важный нюанс: число «х», являющееся квадратным корнем из числа «у», может быть как положительным, так и отрицательным. Допустим, если «у» равно четырем, то биквадратное уравнение будет иметь два решения: два и минус два. Это происходит по той причине, что отрицательное число, возведенное в четную степень, равно числу того же модуля, но другого знака, возведенному в ту же степень. Поэтому всегда стоит помнить об этом важном моменте, иначе можно просто потерять один или несколько ответов на уравнение. Лучше сразу написать, что «х» равно плюс-минус квадратному корню из «йиг».

В общем случае решение биквадратных уравнений довольно простое и не требует много времени. Для изучения этой темы в школьной программе достаточно двух академических часов, кроме, конечно, повторений и контрольных работ. Стандартный вид биквадратичных уравнений Их очень легко решить, если следовать приведенным выше правилам. Их решение не составит для вас труда, ведь оно подробно описано в учебниках по математике. Удачи в учебе и успехов в решении любых, не только математических, задач!

страница не найдена — Williams College

’62 Центр театра и танца, ’62 Center
Касса	597-2425
Магазин костюмов	597-3373
Менеджер мероприятий/помощник менеджера	597-4808	597-4815 факс
Производство		597-4474 факс
Магазин сцен	597-2439
’68 Центр изучения карьеры, Мирс	597-2311	597-4078 факс
Академические ресурсы, Парески	597-4672	597-4959 факс
Служба поддержки инвалидов, Парески	597-4672
Приемная, Уэстон Холл	597-2211	597-4052 факс
Позитивные действия, Хопкинс Холл	597-4376
Африканские исследования, Голландия	597-2242	597-4222 факс
Американские исследования, Шапиро	597-2074	597-4620 факс
Антропология и социология, Холландер	597-2076	597-4305 факс
Архивы и специальные коллекции, Sawyer	597-4200	597-2929 факс
Читальный зал	597-4200
Искусство (История, Студия), Spencer Studio Art/Lawrence	597-3578	597-3693 факс
Архитектурная студия, Spencer Studio Art	597-3134
Студия фотографии, Spencer Studio Art	597-2030
Студия печати, Spencer Studio Art	597-2496
Скульптурная студия, Spencer Studio Art	597-3101
Senior Studio, Spencer Studio Art	597-3224
Видео/фотостудия, Spencer Studio Art	597-3193
Азиатские исследования, Голландия	597-2391	597-3028 факс
Астрономия/астрофизика, Физика Томпсона	597-2482	597-3200 факс
Отделение легкой атлетики, физического воспитания, отдыха, Ласелл	597-2366	597-4272 факс
Спортивный директор	597-3511
Лодочная пристань, озеро Онота	443-9851
Вагоны	597-2366
Фитнес-центр	597-3182
Хоккейный каток Ice Line, Lansing Chapman	597-2433
Очные занятия, Спортивный центр Чендлера	597-3321
Физкультура	597-2141
Мокрая линия бассейна, Спортивный центр Чендлера	597-2419
Информация о спорте, Хопкинс-холл	597-4982	597-4158 факс
Спортивная медицина	597-2493	597-3052 факс
Корты для сквоша	597-2485
Поле для гольфа Taconic	458-3997
Биохимия и молекулярная биология, Биология Томпсона	597-2126
Биоинформатика, геномика и протеомика, Бронфман	597-2124
Биология, Биология Томпсона	597-2126	597-3495 факс
Безопасность и безопасность кампуса, Хопкинс-холл	597-4444	597-3512 факс
Карты доступа/Системы сигнализации	597-4970/4033
Служба сопровождения, Хопкинс-холл	597-4400
Офицеры и диспетчеры	597-4444
Секретарь, удостоверения личности	597-4343
Распределительный щит	597-3131
Центр развития творческого сообщества, 66 Stetson Court	884-0093
Центр экономики развития, 1065 Main St	597-2148	597-4076 факс
Компьютерный зал	597-2522
Вестибюль	597-4383
Центр экологических исследований, выпуск 1966 г. No related posts. Навигация по записям Предыдущая статьяТаблица степени брадиса: синусы и косинусы, тангенсы, котангенсы Следующая статьяЗадачи по основным фондам с решением: Задачи по теме: Основные фонды предприятия с решением и пояснениями \| Консультация на тему: Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Найти: Рубрики Геометрия Математика Физика Химия Школьная жизнь Разное © 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа» Карта сайта

Решение биквадратных уравнений — онлайн калькулятор

Теоретические статьи из справочника, которые помогут вам лучше разобраться в теме:

Как решать биквадратное уравнение

Чтобы решить биквадратное уравнение, необходимо выполнить следующие действия:

Найти корни биквадратного уравнения решить.

Найти корни биквадратного уравнения решить. Биквадратное уравнение, решение биквадратных уравнений

Необходимо:

Инструкция:

Решение биквадратных уравнений. Решение уравнений с параметром

Решение биквадратных уравнений

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Курсы по математике 10 класс

Курсы по математике 9 класс

Математика 11 класс

Курсы по геометрии 7 класс

Курсы по алгебре 7 класс

Алгебра 8 класс

Курсы по геометрии 8 класс

Курсы французского языка для начинающих

Биквадратные уравнения — примеры с решениями

Появление методики

Основные понятия

Решение равенств

Примеры уравнений

Разложение на множители

биквадратных уравнений | Superprof

Решение биквадратных уравнений

Примеры

Алгебраическое решение уравнений кубической и четвертой степени

Твой ответ

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Решение кубических и четвертых уравнений | Марко Тавора, доктор философии.

Выходя за рамки квадратных полиномов

Кубические уравнения

Уравнения четвертой степени

Найдите корни биквадратного уравнения, которое нужно решить.

страница не найдена — Williams College

Добавить комментарий Отменить ответ