Линейная функция
Функция называется
линейной, если ее можно записать в виде \(y=kx+b\), где \(k\) и \(b\) -некоторые числа.Примеры:
|
\(y=\frac{1}{3}x-5\) |
\(k=\frac{1}{3}\), \(b=-5\) |
|
|
\(y=2x\) |
\(k=2\), \(b=0\) |
|
|
\(y=8\) |
\(k=0\), \(b=8\) |
Функция не всегда сразу задана в виде \(y=kx+b\), иногда такой вид получится только после преобразований. Например, \(y=6(x-1)+10x\) — это линейная функция, потому что если раскрыть скобки и привести подобные слагаемые мы получим \(y=16x-6\).
Чтобы в этом убедиться построим графики функций \(y=2x\), \(y=\frac{1}{3}x-5\), \(y=8\).
Если вы вдруг забыли, как строить графики, можете прочитать об этом здесь.
Как меняется график при разных \(k\)?
Чтобы определить, как влияет на график коэффициент \(k\), построим несколько функций разными \(k\): \(\frac{1}{3}\),\(-\frac{1}{3}\),\(2\),\(-2\) и \(0\). При этом во всех функциях сделаем \(b\) одинаковым (равным нулю), чтобы убрать его влияние.
То есть, построим графики для функций: \(y=\frac{1}{3}x\), \(y=-\frac{1}{3}x\), \(y=2x\), \(y=-2x\), \(y=0\).
Заметьте, что при \(k=2\) и \(\frac{1}{3}\) — функция возрастает, а при \(k=-2\) и \(-\frac{1}{3}\) — убывает. На самом деле:
При любом \(k>0\) функция возрастает и при любом \(k<0\) — убывает.
Когда же \(k=0\) — она не возрастает и не убывает, а идет параллельна оси \(x\) (или совпадает с ней).
Так же можно заметить, чем больше модуль \(k\), тем «круче» график.
Как по графику определить коэффициент k?
- Сначала определим, возрастает или убывает функция. Если возрастает – знак коэффициента \(k\) плюс, если убывает – минус.
- Дальше надо построить на прямой прямоугольный треугольник, так чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Примерно вот так:
Чтобы определить значение \(k\) по модулю (то есть, без учета знака), надо вертикальную сторону треугольника поделить на горизонтальную. Можно использовать правило для запоминания: «стоячий бьет лежачего». В данных случаях \(|k|=\frac{AC}{BC}\). То есть на первом графике \(k=2\),а на втором \(k=-\frac{1}{4}\).
Как меняется график при разных значениях \(b\)?
Чтобы определить, как \(b\) влияет на график, построим несколько функций с разными \(b\): \(6\), \(2\), \(0\), \(-3\) и \(-8\).
При этом \(k\) пусть во всех функциях будет равен \(2\).
Не сложно заметить, что прямая либо поднимается на \(b\) (если \(b>0\)) либо опускается на \(|b|\) если
Как по графику функции определить значение \(b\)?
Очень просто — прямая пересекает ось \(y\) всегда в точке \(b\). Вы можете это увидеть на предыдущем графике.
Пример (ОГЭ): На рисунке изображены графики функций вида \(y=kx+b\). Установите соответствие между графиками функций и знаками коэффициентов \(k\) и \(b\).
A. B.C.
Коэффициенты
| 1) \(k>0\),\(b>0\) | 2) \(k<0\), \(b>0\) | 3) \(k<0\), \(b<0\) | 4) \(k>0\), \(b<0\) |
Решение:
А.
– функция убывает, поэтому \(k<0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 2).
B. — функция возрастает — \(k>0\). Точка пересечения оси \(y\) и прямой находится выше нуля, значит \(b>0\). Подходит вариант под цифрой 1).
C. – функция убывает — \(k<0\). Точка пересечения оси \(y\) и прямой находится ниже нуля, значит \(b<0\). Подходит вариант под цифрой 3).
Ответ: 213.
«Читерский» способ строить график линейной функции
Можно конечно строить график линейной функции по точкам, как описано
здесь, но можно и быстрее, буквально в три шага:
-
Отмечаем точку \(b\) на оси игреков.
-
От неё идем вправо на количество клеточек равное знаменателю \(k\), и вверх на количество клеточек равное числителю \(k\) (если \(k>0\)) или вниз на тоже количество (если \(k<0\)).
-
Проводим через эти две точки прямую.
Пример: Построить график функции \(y=3x+1\).
|
Шаг 1. \(b=1\), поэтому отмечаем точку с этим значением на оси \(y\)
|
Шаг 2. \(k=3\), а тройка это тоже самое, что \(\frac{3}{1}\). При этом \(k>0\). Поэтому идем вправо на единицу и вверх на \(3\). Ставим точку. |
Шаг 3. Проводим через эти две точки прямую. |
Пример: Построить график функции \(y=-\frac{1}{4} x-3\).
|
Шаг 1. \(b=-3\) отмечаем точку с этим значением на оси \(y\).
|
Шаг 2. \(k=-\frac{1}{4}\), \(k<0\), числитель \(1\), знаменатель \(4\). Значит, идем вправо на \(4\) и вниз на единицу. |
Шаг 3. Проводим через эти две точки прямую. |
Немного потренируйтесь и вы сами поймете, какой это классный способ строить линейную функцию.
Линейная функция — определение, основные свойства, график.
Если функция задана формулой , где и — некоторые числа, называется линейной функцией.
Линейная функция областью определения имеет множество всех действительных чисел, потому что выражение имеет смысл при всех значениях . Все частные виды линейной функции можно записать общей формулой . Линейные функции изучаются в школьном курсе математики 7 класса. О том какие они бывают, как построить их графики мы поговорим в этой статье. Вы получите все ответы на тему линейной функции, потому что мы с вами разберем примеры определения ее вида, построения графика и его анализа. Почитать о функции, что это такое и как ее можно задать можно здесь.
Содержание
Определение линейной функции
Вот так выглядит график линейной функции:
Линейная функция y=kx+b и ее график
Примеры линейных функций:
- ,
- ,
Обратите внимание, что уравнение — описывает общий вид, есть и частные виды, линейной функции, например, (когда ) и , когда .
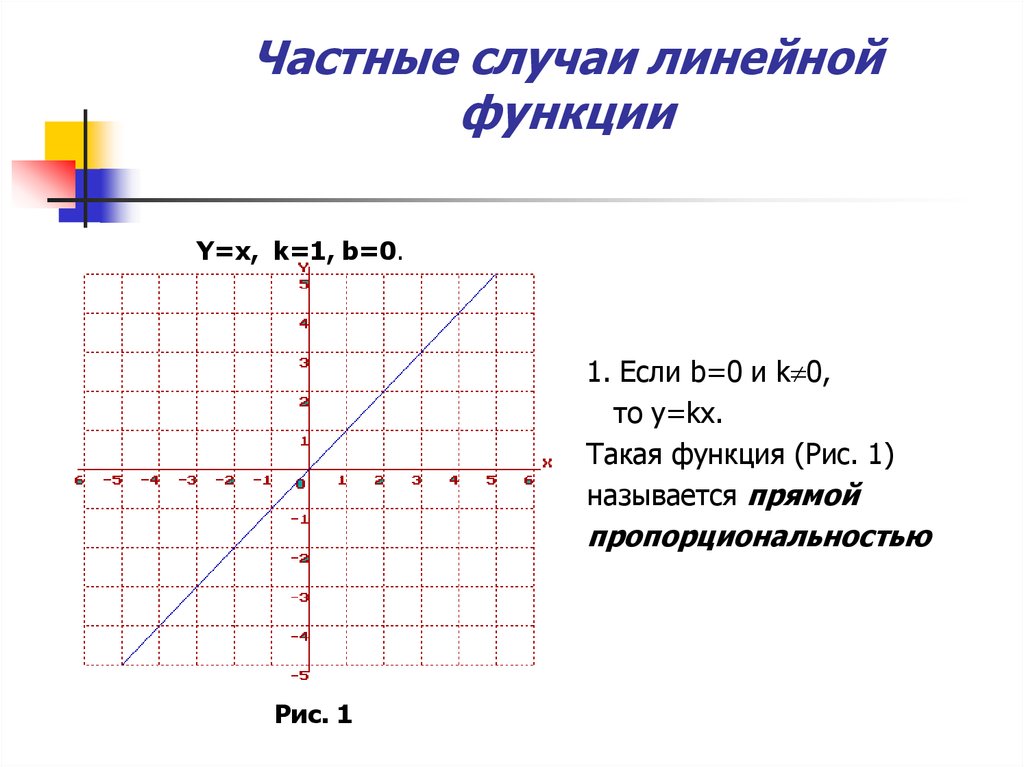
Частный случай линейной функции y=b
Частный вид линейной функции y=kx
Стоит заметить, что уравнение задает прямую пропорциональность между значением и аргументом .
Прямая пропорциональность — это зависимость вида , она изучается в курсе алгебры.
Для построения графика линейной функции достаточно двух точек.
Коэффициенты k и b
Коэффициент характеризует угол, который образует прямая с положительным направлением оси . Поэтому коэффициент k линейной функции называется угловым коэффициентом.
Частный случай линейной функции y=x
- Если , то угол между графиком линейной функции и осью острый.
- Если , то угол между графиком линейной функции и осью тупой.
- Если , то прямая совпадает с осью .
Коэффициент — показывает сдвиг графика вдоль оси .
У коэффициентов и есть геометрический смысл. Коэффициент показывает длину отрезка, которую прямая отсекает по оси , начало отрезка находится в точке . Геометрический смысл коэффициента — тангенс угла наклона прямой линии к положительному направлению оси . По данному коэффициенту можно определить угол наклона прямой линии, например, , это означает и .
То есть угол наклона прямой к оси будет 450.
Примеры
Определите коэффициенты и функций и результаты запишите в таблицу.
| Линейная функция | Коэффициент | Коэффициент |
| 1 | 0 | |
| 3 | 5 | |
| 0 | 6 | |
| -1 | 3 | |
| 2 | -5 | |
| -3 | -1 |
Обратите внимание, что данная функция может быть задана и числом, например, , это означает, что угловой коэффициент равен нулю, то есть , а значит и прямая параллельна оси . Коэффициенты и могут принимать любые числовые значения, то есть могут быть и 0, и 1, и отрицательным числом.
Попробуем записать функцию y=kx+b, зная только значения коэффициентов.
Пример 1
Запишите линейную функцию, если известно, что , .
Решение: сначала запишем общий вид линейной функции: , теперь вместо и подставим указанные значения: .
Упростим выражение и получим:
.
Ответ:
Пример 2
Запишите линейную функцию, если известны коэффициенты и .
Решение: .
Ответ: .
Область определения и область значений
Проанализируем и определим область определения линейной функции. Смотрим на уравнение, очевидно, что в это уравнение можно подставить любое значение . Это значит, что областью определения является вся числовая ось: .
Так как и может принимать любые значения, то мы можем говорить о том, что область значений линейной функции — все числа: .
График линейной функции
Если вы видите прямую линию — например, прямую дорогу или столб, дерево, то знайте — линии эти могут быть описаны с помощью функции, которая называется линейной.
Чтобы построить график функции необходимо и достаточно взять всего две точки. Построим таблицу координат точек:
| x | 0 | -b/k |
| y | b | 0 |
Таким образом, мы можем построить график любой линейной функции вида .
График прямой в общем виде
Примеры построения графика линейной функции
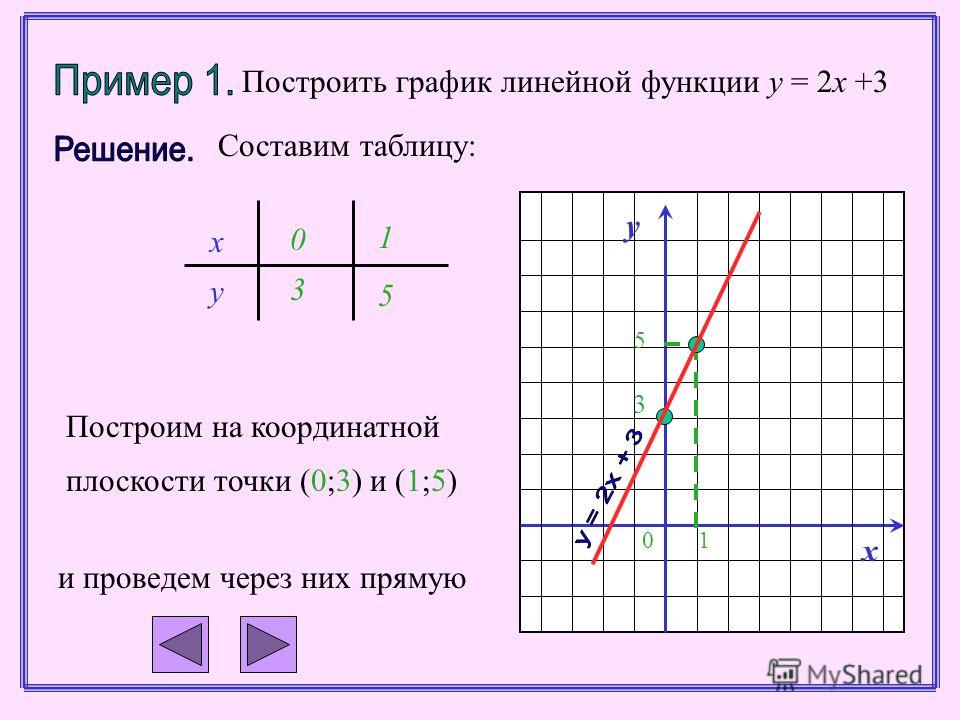
Пример 1
Построим график линейной функции .
Графиком функции является прямая линия. Для построения прямой достаточно взять две точки.
Возьмем точки и . Кстати, эти точки являются одновременно и точками пересечения графика с осями и соответственно.
Нарисуем координатные оси, покажем масштаб и отметим точки и , затем их соединим, получим прямую. Эта прямая и будет графиком функции .
График функции y=2x+1
Итак, мы научились с вами строить график функции, зная ее уравнение. Алгоритм построения графика линейной функции прост:
- Найти координаты двух точек, удовлетворяющих данному уравнению прямой. Для этого берем произвольное значение аргумента и подставляем его в уравнение, вычисляем значение . Можно действовать и наоборот — задать определенное значение и решить уравнение относительно .
- Рисуем координатные оси, указываем их направление, определяем масштаб.
- Наносим найденные точки на координатную плоскость.
- Проводим прямую, через две эти точки.
Совет: если точки взяты близко друг к другу, то при продлении прямой можно получить погрешность рисования — отклонение на несколько градусов, поэтому старайтесь брать точки подальше друг от друга, или же возьмите пару контрольных точек, опираясь на уравнение прямой линии.
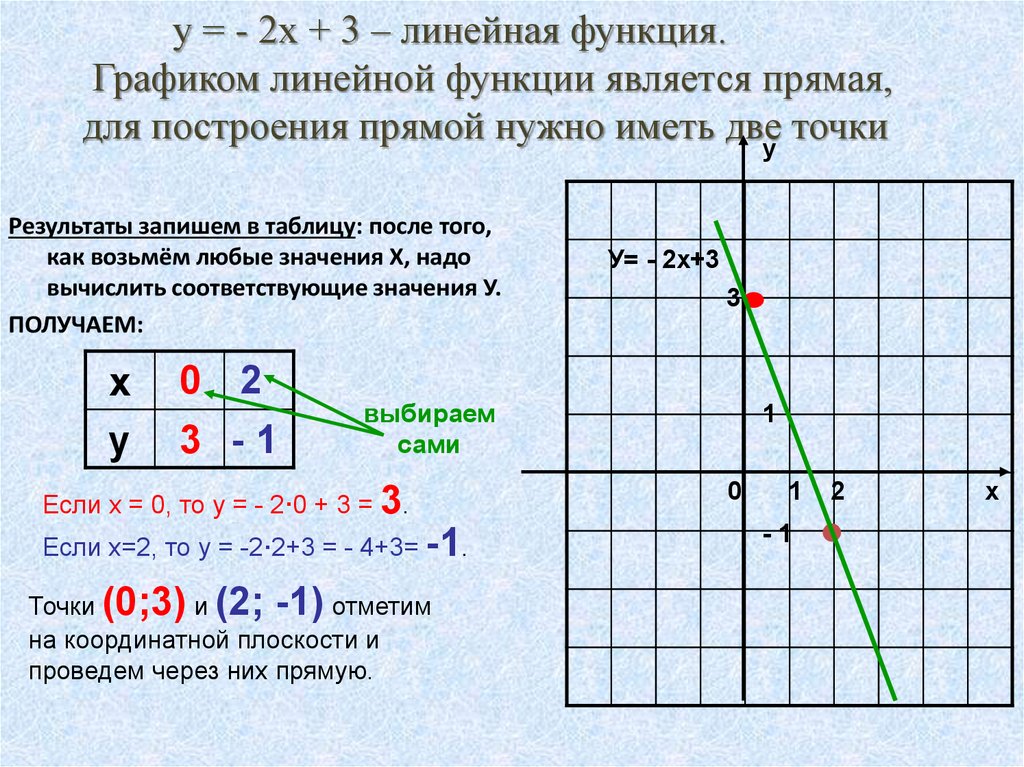
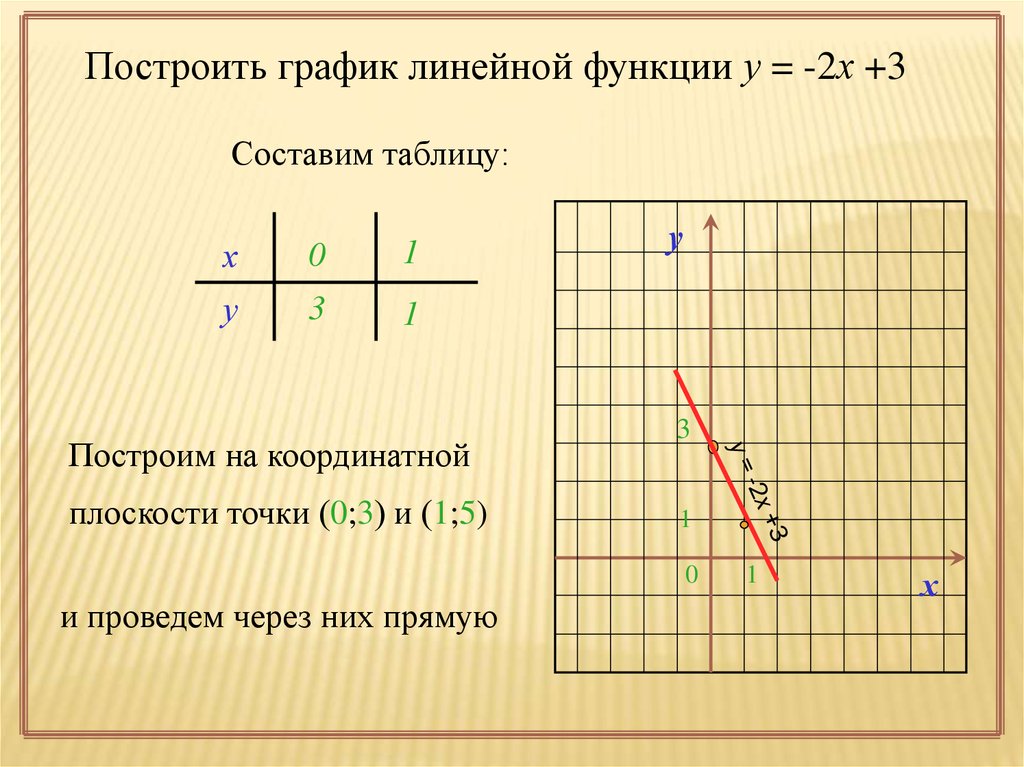
Пример 2
Построим новый график линейной функции. Пусть нам дано уравнение: .
Находим две точки. Пусть , тогда подставим в формулу функции ноль вместо , получим: . Вторую точку возьмем немного подальше — пусть , тогда .
Итак, мы получили две точки: и . Построим график прямой.
График функции y=-x-2
Убывает или возрастает
Функция прямой является убывающей или возрастающей функцией? Вопрос не корректен. Все функции прямых разные, одни убывают, другие возрастают, надо обращать внимание при оценке убывания или возрастания функции на поведение ее при изменении аргумента.
Существует такое правило:
Если при увеличении аргумента значение функции возрастает, то функция является возрастающей, если значение функции при возрастании аргумента уменьшается, то функция является убывающей. Давайте посмотрим как это выглядит на графике.
Перед вами два графика функции, — на каком графике функция убывает, а на каком возрастает, можно понять по тому увеличивается или уменьшается значение функции при движении в положительном направлении оси .
График возрастающей линейной функции
Теперь легко увидеть, почему ниже приведен график убывающей линейной функции:
График убывающей линейной функции
Как мы видим — при увеличении значения аргумента значение функции уменьшается.
Свойства линейной функции
Функция y = x называется линейной функцией, так как переменная x находится в первой степени. Графиком такой функции будет прямая.
Построение графика функции y = x
Для того, чтобы построить график линейной функции нам необходимо задать две точки.
Берем их произвольно. Пусть , тогда . И вторая точка , тогда .
Отмечаем эти точки на координатной плоскости и проводим через них прямую. Это и есть график функции y = x.
Свойства функции
Выпишем свойства функции y = x:
- Функция y = x является линейной, непрерывной и монотонно возрастающей на всем протяжении координатной плоскости, со скоростью 1, так как производная функции равна 1.
- Любое значение переменной будет равно такому же значению функции.
- График функции проходит через начало координат.
- График функции располагается в первой и четвертой четвертях.
- Функция принимает отрицательные значения при отрицательных значениях переменной и положительные значения при положительных значениях переменной.
- Функция y = x является нечетной, так как (условие нечетности функции).
Обратная функция
Обратная функция совпадает с функцией y (x)=x и тоже записывается y = x.
Данная функция также является осью симметрии для всех обратных функций.
Графики обратных функций симметричны относительно оси симметрии y=x.
Что такое линейная функция? Как решить линейную функцию?|Mathhelp
18 декабря 2017 г.
Автор: StudyGate
Теги: Помощь по алгебре, Помощь с домашним заданием
Что такое линейная функция? Как решить линейную функцию?
Если вы ранее научились решать линейные уравнения, вы готовы перейти к решению линейных функций . Они очень похожи, и в процессе также используются простые шаги, поэтому, если вы решаете линейных уравнений во сне, функции будут на одном дыхании!
Шаг 1: Определите, что вы действительно смотрите на линейную функцию.
Если вы еще не знали, линейная функция всегда будет начинаться с f(x) =, за которой следует остальная часть уравнения. Это достаточно легко запомнить, так как f означает функцию . Линейная функция
часто точно следует формуле пересечения наклона, которую вы изучили ранее в алгебре: y = mx + b.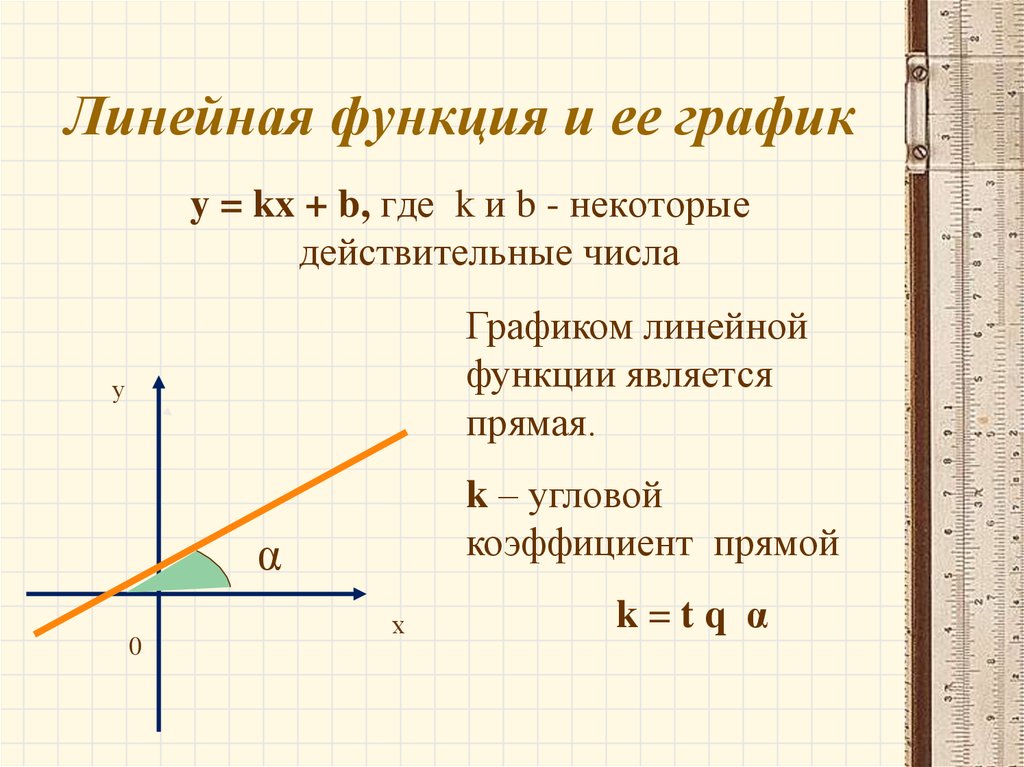
Шаг 2: Замените значения переменными в соответствии с инструкциями.
Когда вы впервые познакомитесь с линейными функциями , вам, скорее всего, дадут значение для замены вашей переменной. Другие функции попросят вас найти уравнение линии, а затем решить соответствующую функцию. В любом случае замените значения, которые вам даны для решения, для вашей переменной.
Шаг 3: Решите свою переменную и проверьте свою работу.
Решите функцию так же, как линейное уравнение ; изолируйте свою переменную, сделайте все, что вы делали с одной частью уравнения, с другой, и упростите свои термины до их наименьших значений. Вы можете проверить свою работу, решив функцию с полученным значением. Как и с
Если этот процесс не так прост, как вы думали, сделайте шаг назад и освежите свою память с помощью домашнего задания по уравнениям.
Ничего страшного, если вам нужно больше практики. Как только вы освоите линейные уравнения, решение линейных функций станет для вас самым простым занятием!
Список категорий
- Карьерные советы (10)
- Образование (17)
- Справка по английскому языку (1)
- Инновации (7)
- Справка по математике (7)
- Онлайн-обучение (52)
- Онлайн-репетиторство (55)
- Советы по исследованиям (3)
- Научная помощь (4)
- Делать заметки (8)
- Технология (3)
- Советы родителям (37)
- Советы студентам (71)
- Подготовка к испытаниям (10)
- советов для достижения успеха (27)
- Советы репетиторам (18)
- Блоги репетиторов (3)
- Советы по обучению (23)
- Репетиторы (20)
- Без рубрики (6)
Популярные теги
Справка по алгебре карьерный совет Справка по химии колледж образование Советы по образованию для родителей Финляндия Веселье Будущее образования Справка по геометрии домашнее задание Помощь с домашним заданием как выбрать колледж информация для учителей Инновации младший год обучение Лайфхаки Справка по математике Онлайн обучение Онлайн-репетиторство Вакансии онлайн-репетитора Советы для родителей общественный колледж Риверсайд Руководство StudyGate Учебные привычки Советы по учебе Технологии Советы по подготовке к экзамену Советы для студентов Советы репетиторам Советы по обучению Калифорнийский университет Риверсайд
Определение, уравнение, пример и график
Простейшая функция, которую мы можем изобразить на -плоскости, это линейная функция .
Несмотря на то, что они просты, линейные функции по-прежнему важны! В AP Calculus мы изучаем линии, которые касаются (или касаются) кривых, и когда мы достаточно увеличиваем кривую, она выглядит и ведет себя как линия!
В этой статье мы подробно обсудим, что такое линейная функция, ее характеристики, уравнение, формулу, график, таблицу и рассмотрим несколько примеров.
- Определение линейной функции
- Уравнение линейной функции
- Формула линейной функции
- График линейной функции
- Таблица линейной функции
- Примеры линейной функции
- Линейные функции — ключевые выводы
Определение линейной функции
Что такое линейная функция ?
Линейная функция представляет собой полиномиальную функцию со степенью 0 или 1. Это означает, что каждый член функции является либо константой, либо константой, умноженной на одну переменную, показатель которой равен либо 0, либо 1.
На графике линейная функция представляет собой прямую линию в координатной плоскости.
По определению, линия прямая, поэтому говорить «прямая линия» излишне. В этой статье мы часто используем слово «прямая линия», однако достаточно просто сказать «линия».
Характеристики линейной функции
На изображении ниже показаны:
- график линейной функции и
- таблица примерных значений этой линейной функции.
График и таблица выборочных значений линейной функции, StudySmarter Originals
Обратите внимание, что при увеличении на 0,1 значение увеличивается на 0,3, то есть увеличивается в три раза быстрее, чем .
Следовательно, наклон графика , 3, можно интерпретировать как скорость изменения по отношению к .
Линейная функция может быть возрастающей, убывающей или горизонтальной линией.
Возрастающие линейные функции имеют положительный наклон .
Убывающие линейные функции имеют отрицательный наклон .
Горизонтальные линейные функции имеют наклон нуля .
Линейные и нелинейные функции
Линейные функции представляют собой особый тип полиномиальных функций. Любая другая функция, которая не образует прямую линию при отображении на координатной плоскости, называется -нелинейной -функцией.
Некоторые примеры нелинейных функций:
- любые полиномиальные функции степени 2 или выше, например,
- квадратичные функции
- кубические функции
- рациональные функции
- экспоненциальные и логарифмические функции
Когда мы думаем о линейной функции в алгебраических терминах, На ум приходят две вещи:
Уравнение и
Формулы
Уравнение линейной функции
Линейная функция является алгебраической функцией, и
0011 родительская линейная функция :
Это линия, проходящая через начало координат.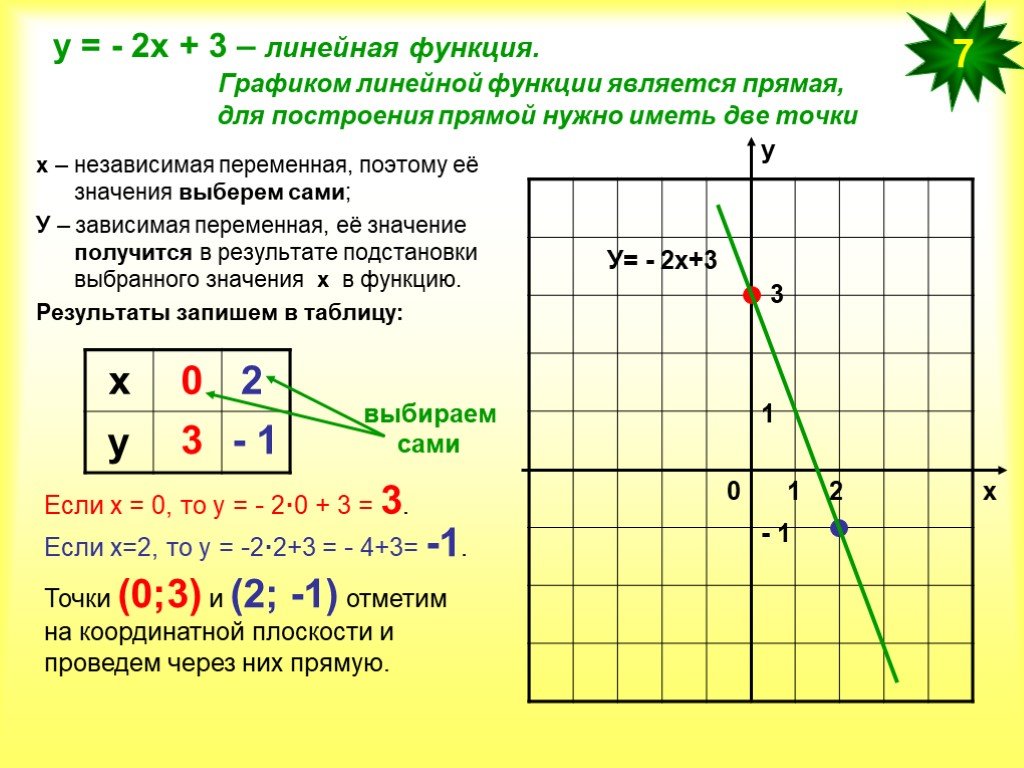
В общем случае линейная функция имеет вид:
Где и — константы.
В этом уравнении
- — это наклон линии
- — точка пересечения по оси Y линии
- — независимая переменная 9 0045 или является зависимой от переменной
Формула линейной функции
Существует несколько формул, представляющих линейные функции. Все они могут быть использованы для нахождения уравнения любой линии (кроме вертикальных линий), и какое из них мы используем, зависит от доступной информации.
Поскольку вертикальные линии имеют неопределенный наклон (и не проходят тест на вертикальные линии), они не являются функциями!
Стандартная форма
Стандартная форма линейной функции:
Где константы.
Откос-перехват Форма
Форма линейной функции с точкой пересечения:
Где:
Форма точки-наклона
Форма точки-наклона линейной функции:
Где: 900 03
Форма перехвата
Форма пересечения линейной функции:
Где:
График линейной функции
График линейной функции довольно прост: это прямая линия на координатной плоскости.
На изображении ниже линейные функции представлены в форме пересечения наклона. (число, на которое умножается независимая переменная ), определяет наклон (или градиент) этой линии и определяет, где линия пересекает ось y (известную как точку пересечения y).
Графики двух линейных функций, StudySmarter Originals
График линейной функции
Какая информация нам нужна для построения графика линейной функции? Итак, исходя из приведенных выше формул, нам нужно либо:
Использование двух точек
Чтобы построить график линейной функции с использованием двух точек, нам нужно либо задать две точки для использования, либо нам нужно подставить значения для независимой переменной и решить для зависимой переменной, чтобы найти две точки.
Если нам даны две точки, построение графика линейной функции — это просто построение двух точек и их соединение прямой линией.
Если, однако, нам дали формулу линейного уравнения и попросили изобразить ее в виде графика, необходимо выполнить еще несколько шагов.
Нарисуйте график функции:
Решение:
- Найдите две точки на прямой, выбрав два значения для .
- Примем значения и .
- Подставьте выбранные нами значения в функцию и найдите соответствующие им значения y.
- Итак, наши две точки: и .
- Нанесите точки на координатную пластину и соедините их прямой линией.
- Обязательно продлите линию за две точки, так как линия никогда не заканчивается!
- Итак, график выглядит так:
График линии по двум точкам, StudySmarter Originals
Использование наклона и точки пересечения по оси y
Чтобы построить график линейной функции с использованием ее наклона и точки пересечения с осью y, мы откладываем точку пересечения с осью y на координатной плоскости и используем наклон, чтобы найти вторую точку для построения графика.
Постройте график функции:
Решение:
- Постройте точку пересечения по оси y, которая имеет вид: .
- Y-отрезок для этой линейной функции:
- Запишите наклон в виде дроби (если он уже не один!) и определите «подъем» и «набег».
- Для этой линейной функции наклон равен .
- Итак, и.
- Для этой линейной функции наклон равен .
- Начиная с точки пересечения с осью y, двигайтесь вертикально по «подъему», а затем двигайтесь по горизонтали по «бегу».
- Обратите внимание: если рост положительный, мы движемся вверх, а если рост отрицательный, мы движемся вниз.
- И обратите внимание: если пробег положительный, мы движемся вправо, а если пробег отрицательный, мы двигаемся влево.
- Для этой линейной функции
- «Поднимаемся» вверх на 1 единицу.
- «Убегаем» вправо на 2 единицы.
- Соедините точки прямой линией и протяните ее за обе точки.
- SO, график выглядит как:
с использованием наклона и y-перехватчика для графика a линии, StemySmarter Originals
Домен
Любая линейная функция может принимать любое действительное значение в качестве входных данных и давать действительное значение в качестве выходных данных.
В этом можно убедиться, посмотрев на график линейной функции. По мере продвижения по функции каждому значению соответствует только одно значение .
Следовательно, пока проблема не дает нам ограниченную область, область определения линейной функции равна:
Диапазон
Кроме того, выходы линейной функции могут находиться в диапазоне от отрицательной до положительной бесконечности , что означает, что диапазон также является набором всех действительных чисел. В этом также можно убедиться, посмотрев на график линейной функции. По мере продвижения по функции каждому значению соответствует только одно значение .
Следовательно, пока задача не дает нам ограниченного диапазона и , диапазон линейной функции равен:
Когда наклон линейной функции равен 0, это горизонтальная линия. В этом случае домен по-прежнему является набором всех действительных чисел, но диапазон равен просто b.
Таблица линейных функций
Линейные функции также могут быть представлены таблицей данных, содержащей пары значений x и y.
Чтобы определить, является ли данная таблица этих пар линейной функцией, мы делаем три шага:0003
Вычислить разницу в значениях x.
Вычислите разницу значений y.
Сравните соотношение для каждой пары.
Мы также можем проверить, представляет ли таблица значений x и y линейную функцию, определив, остается ли скорость изменения относительно (также известная как наклон) постоянной.
Обычно таблица, представляющая линейную функцию, выглядит примерно так:
| значение x | значение y |
| 1 | 4 |
| 2 | 5 |
| 3 | 6 |
| 4 | 7 |
Идентификация a Линейная функция
Чтобы определить, является ли функция линейной, зависит от того, как эта функция представлена.
Если функция представлена алгебраически:
Если функция представлена графически:
Если функция представлена с помощью таблицы:
Определите, представляет ли данная таблица линейную функцию.
| значение x | значение y |
| 3 | 15 |
| 5 | 23 |
| 7 | 31 |
| 11 | 47 |
| 13 | 55 |
Решение:
Чтобы определить, представляют ли значения, приведенные в таблице, линейную функцию, нам необходимо выполнить следующие шаги:
- Вычислить разницу между значениями x и y.
- Вычислите отношение разницы x к разнице y.
- Убедитесь, что соотношение одинаково для всех пар X,Y.
- Если отношение всегда одинаковое, функция линейная!
Давайте применим эти шаги к данной таблице:
Определение того, представляет ли таблица значений линейную функцию, StudySmarter Originals
Поскольку все числа в зеленом поле на изображении выше одинаковы, данная таблица представляет линейная функция.
Специальные типы линейных функций
Существует несколько специальных типов линейных функций, с которыми мы, вероятно, будем иметь дело в исчислении.
Это:
Кусочно-линейные функции
В нашем изучении исчисления нам придется иметь дело с линейными функциями, которые не могут быть определены единообразно во всех областях их определения. Возможно, они определены двумя или более способами, поскольку их домены разделены на две или более частей.
В этих случаях они называются кусочно-линейные функции .
Нарисуйте следующую кусочно-линейную функцию:
Символ ∈ выше означает «является элементом».
Решение:
Эта линейная функция имеет две конечные области определения:
- и
Вне этих интервалов линейная функция не существует. Таким образом, когда мы рисуем эти линии, мы на самом деле просто рисуем сегменты линий, определяемые конечными точками доменов.
- Определите конечные точки каждого сегмента линии.
- Вычислите соответствующие значения y в каждой конечной точке.
- В домене:
значение x значение y -2 1
- В домене:
значение x значение y 1 2
- В домене:
- Нанесите точки на координатную плоскость и соедините сегменты прямой линией.
График кусочно-линейной функции, StudySmarter Originals
Обратные линейные функции
Точно так же мы будем иметь дело с обратными линейными функциями, которые являются одним из типов Обратных функций. Кратко объясним, если линейная функция представлена:
Тогда обратное к нему представлено:
таким образом, что
Верхний индекс, -1 , не степень . Это означает «обратное значение», , а не «f в степени -1».
Найдите обратную функцию:
Решение:
- Замените на .
- Заменить на и на .
- Решите это уравнение для .
- Заменить на .
Если изобразить оба и на одной и той же координатной плоскости, мы заметим, что они симметричны относительно линии . Это характеристика обратных функций.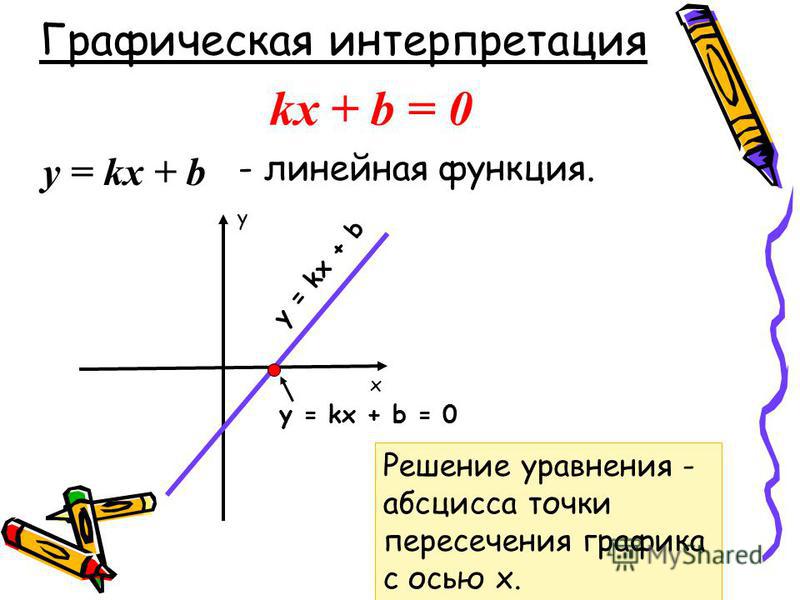
График пары обратных линейных функций и их линия симметрии, StudySmarter Originals
Примеры линейных функций
Реальные приложения линейных функций
В реальном мире линейные функции используются по-разному. Вот некоторые из них:
Задачи расстояния и скорости в физике
Вычисление размеров
Определение цен на вещи (например, налоги, сборы, чаевые и т. д., которые добавляются к цене вещей)
90 073- Запишите данную функцию в виде упорядоченных пар.
- Рассчитайте уклон по формуле: , где соответствуют соответственно.
- , поэтому наклон функции равен 1 .
- Используя формулу наклона, вычислите наклон линейной функции.
- Используя значения, заданные двумя точками, и наклон, который мы только что вычислили, мы можем написать уравнение линейной функции, используя форму точка-наклон .
- — точечно-наклонная форма линии.
- — замена значений для .
- — распределить знак минус.
- — распределите 4.
- — упростите.
- — уравнение прямой.
- Для начала, мы можем выбрать любые две пары эквивалентных значений из таблицы. Это точки на линии.
- Выберем и .
- Вычислите наклон линии между двумя выбранными точками.
- , поэтому наклон равен 9/5.
- Напишите уравнение прямой, используя форму точка-наклон.
- — точечно-наклонная форма линии.
- — замена значений для .
- — распределить фракцию и отменить сроки.
- — упростить.
- Обратите внимание, что на основе таблицы
- Мы можем заменить независимую переменную на , для градусов Цельсия, и
- Мы можем заменить зависимую переменную на , для градусов Фаренгейта.
- Итак, мы имеем:
- — это линейная зависимость между градусами Цельсия и Фаренгейта .
- Подставить в заданную функцию.
- — заменитель.
- — упростить.
- — заменить известные значения.
- — объединить похожие термины.
- — разделить на 30 и упростить.
- Итак, Джейк арендовал машину на 15 дней .
- — переместить все члены, кроме зависимой переменной, в одну сторону уравнения.
- — разделите на -2 для упрощения.
- Теперь мы можем видеть, что независимая переменная имеет степень 1. Это говорит нам о том, что это является линейной функцией .
- Мы можем проверить наши выводы, нарисовав график:
- График линии, StudySmarter Originals
- Перекомпонуйте и упростите функцию, чтобы получить лучшую визуализацию.
- — распространять файлы .
- — переместить все члены, кроме зависимой переменной, в одну сторону.
- — разделите на 2 для упрощения.
- Теперь мы можем видеть, что поскольку независимая переменная имеет степень 2, это не является линейной функцией .
- Мы можем убедиться, что функция является нелинейной, построив ее график:
- График нелинейной функции, StudySmarter Originals
- A линейная функция
- Функция любой другой формы является нелинейной функцией.
- Существуют формы, которые может принимать формула линейной функции:
- Стандартная форма:
- Форма пересечения наклона:
- Форма точки-наклона:
- Форма пересечения:
- Если наклон линейной функции 0, это горизонтальная линия , известная как постоянная функция .
- A вертикальная линия является , а не линейной функцией , потому что она не проходит тест вертикальной линии.
Скажи, что тебе нравится играть в видеоигры.
Вы подписываетесь на игровой сервис, который взимает ежемесячную плату в размере 5,75 долларов США плюс дополнительную плату в размере 0,35 долларов США за каждую загружаемую игру.
Мы можем записать вашу фактическую ежемесячную плату, используя линейную функцию:
Где указано количество игр, которые вы скачиваете за месяц.
Линейные функции: решенные примеры задач
Запишите данную функцию в виде упорядоченных пар.
Решение:
Упорядоченные пары: и .
Найдите наклон линии для следующего.
Решение:
Найдите уравнение линейной функции, заданной двумя точками:
Решение:
Связь между градусами Фаренгейта и Цельсия линейная.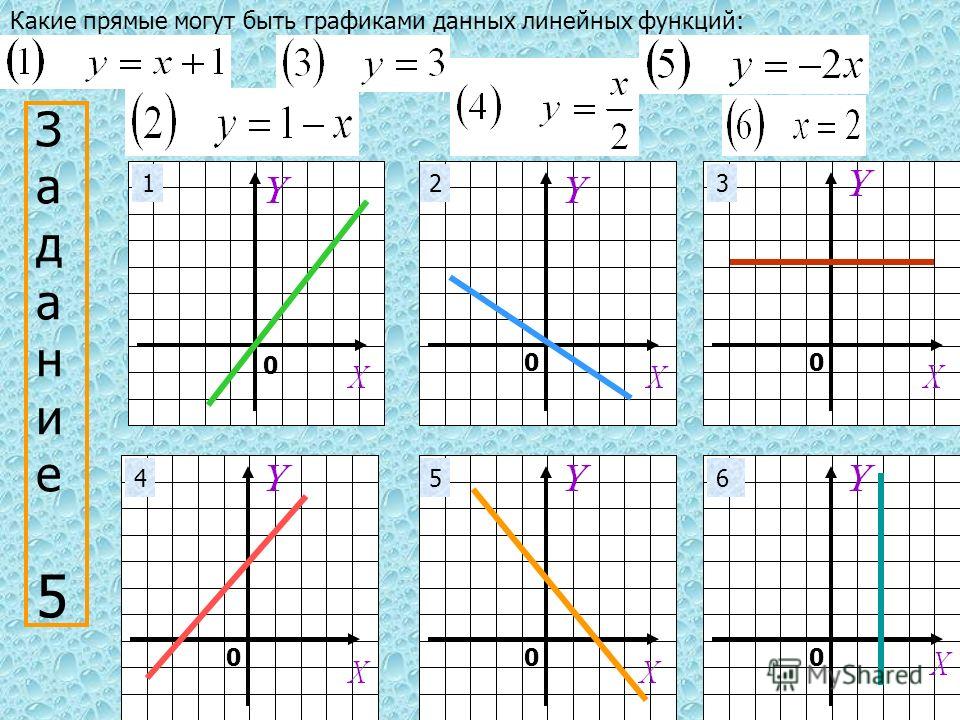
В таблице ниже показаны некоторые из их эквивалентных значений. Найдите линейную функцию, представляющую данные в таблице.
| Цельсия (°C) | Фаренгейты (°F) |
| 5 | 41 |
| 10 | 50 |
| 15 90 460 | 59 |
| 20 | 68 |
Решение:
Допустим, стоимость аренды автомобиля может быть представлена линейной функцией:
Где — количество дней аренды автомобиля.
Сколько стоит аренда автомобиля на 10 дней?
Решение:
Итак, стоимость аренды автомобиля на 10 дней составляет 320 долларов.
Чтобы добавить к последнему примеру. Допустим, мы знаем, сколько кто-то заплатил за аренду автомобиля, используя ту же линейную функцию.
Если Джейк заплатил 470 долларов за аренду машины, на сколько дней он ее арендовал?
Решение:
Мы знаем, что , где количество дней аренды автомобиля. Итак, в этом случае мы заменяем на 470 и находим .
Определите, является ли функция линейной функцией.
Решение:
Нам нужно изолировать зависимую переменную, чтобы визуализировать функцию. Затем мы можем проверить, является ли он линейным, построив график.
Определите, является ли функция линейной функцией.
Решение:
