Решение логических выражений: Математическая логика · oнлайн с подробным объяснением

Законы алгебры логики. Упрощение логических выражений.

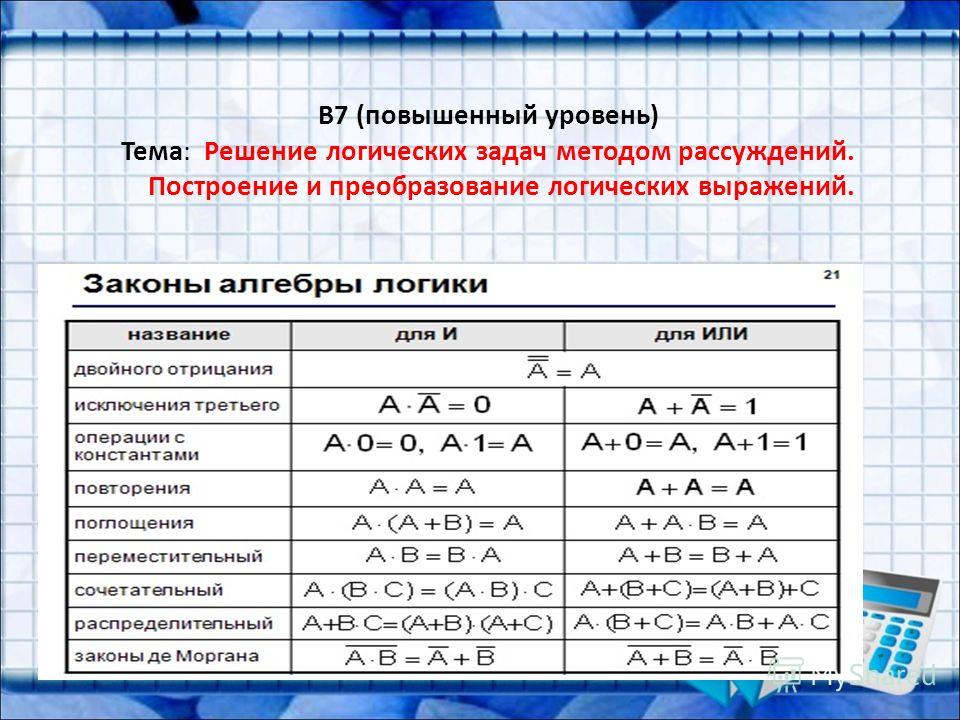
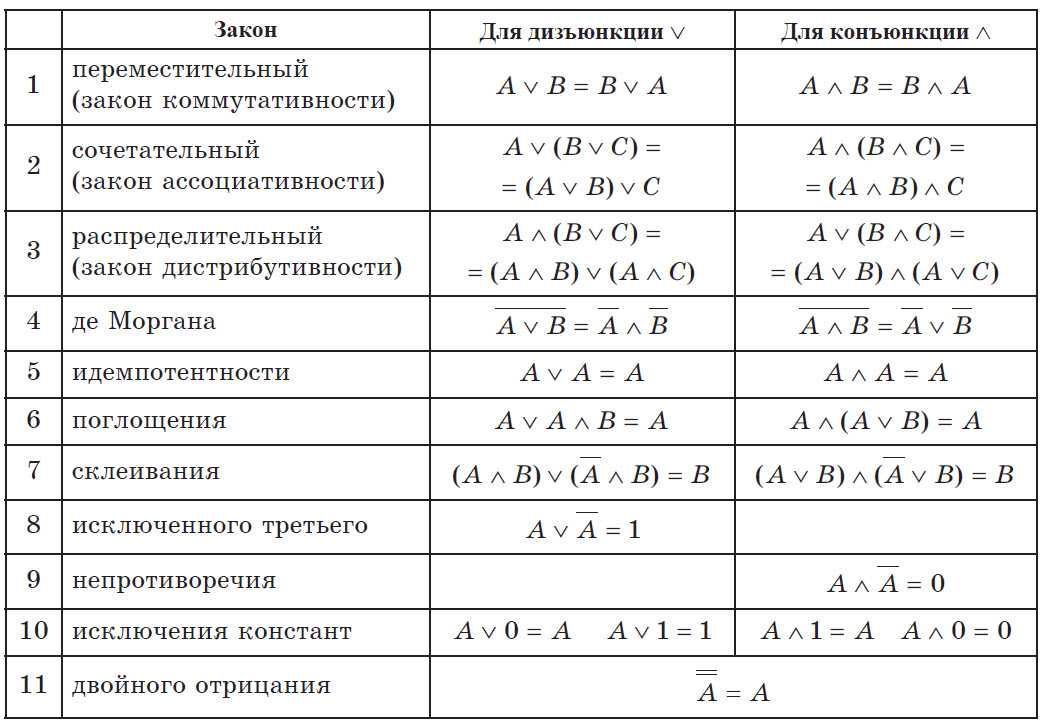
Так же как и в привычной нам алгебре есть законы упрощения выражений, в алгебре логики действуют законы алгебры логики. Для удобства обработки информации алгебраические и логические выражения принято упрощать или приводить к нормальному виду. Большинство законов обеих алгебр схожи и уже знакомы вам. И лишь несколько вы узнаете впервые и, возможно, удивитесь. Упрощение сложных высказываний — это замена их на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы.  Нормальная форма выражений — это выражение где нет знаков операций импликации и эквивалентности, а инверсия применена только к отдельным высказываниям. Для обрабатывания выражений вы должны свободно ориентироваться между обозначениями операций. Основные три из них имеют следующие варианты обозначений: Инверсия (отрицание):   Ø ,`A ,  не . Конъюнкция (умножение): & , L ,  × . Дизъюнкция (сложение): V,  +. Для удобства записи и большей наглядности можно записывать знаки операций в логических выражениях в более привычной нам форме: умножение — знаком ×,  а сложение — знаком +.  Иначе говоря, упростить выражение — это найти в нём законы логики и их применить! Первое, что надо знать для упрощения — формулы замены операций (которых не должно быть в нормальной форме записи логических выражений): Итак, а теперь сами законы алгебры логики: Чтобы ими пользоваться их надо знать, т.е. выучить. Но на самом деле эти законы во многом повторяю законы обычной алгебры.  Закон двойного отрицания напоминает нам ситуацию, когда «минус на минус даёт плюс», хотя так говорить и не грамотно, но зато именно так ученики его запоминают быстрее всего! Законы исключения третьего, операции с константами и законы повторения следуют из определения самих логических операций сложения (дизъюнкции) и умножения (конъюнкции).   Переместительный, сочетательный и распределительный законы нам встречались и в обычной алгебре. Они и в алгебре логики работают точно так же! Правда распределительный закон относительно умножения на уроках математики применять никак нельзя, а в алгебре логики пожалуйста: a + b × c = (a + b)× (a + c) И последнее и самое интересное — это законы де Моргана (или двойного отрицания). Никак нельзя допускать при упрощении выражений оставлять знак отрицания более чем над одним высказыванием! С этой проблемой нам помогают бороться именно законы де Моргана.  Запомнить их просто: отрицание раздается каждому высказыванию, находящемуся под общей чертой, а знаки + меняются на × , и наоборот ×  на +. Упрощение нескольких логических выражений представлено в следующем видео. Вы можете его ставить на паузу и сверяться с формулами законов в любом удобном для вас месте:

Упрощение логических выражений. Решение задач

Похожие презентации:

Элементы алгебры логики. Математические основы информатики. Логические задачи

Алгоритм решения задач средствами алгебры логики

Элементы алгебры логики. Математические основы информатики. (8 класс)

Упрощение логических выражений

Элементы алгебры логики. Математические основы информатики

Преобразование логических выражений. Тема 3

Законы булевой алгебры и упрощение логических выражений. 9 класс

Элементы алгебры логики. Математические основы информатики

Построение таблиц истинности

Методика решения задания ЕГЭ на преобразование логических выражений. (Задание 18)

Упрощение логических
выражений. Решение
задач
Законы алгебры логики
Докажите правильность законов для
операции И:
1. Закон двойного отрицания
2. Закон исключения третьего
3. Закон де Моргана
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
Шаг 2. Расрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключения третьего.
Задание №1
Q M X H M X H (M M ) X H X H
Задание №2
Какое логическое выражение равносильно выражению
A ¬(¬B C)?
1) ¬A ¬B ¬C

1)A B C
2) A ¬B ¬C
2) A B C
3) A B ¬C
3) A B C
4) A ¬B C
4) A B C
A ( B C) A B C A B C
Задание №3
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
раскрыли
распределительный
исключения третьего
повторения
поглощения
Задание №4
Задача. Коля, Вася и Серёжа гостили летом у бабушки.
Однажды один из мальчиков нечаянно разбил любимую
бабушкину вазу.
На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася: 3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля: 5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её
внуков (правдивый), оба раза сказал
правду; второй (шутник) оба раза
сказал неправду; третий (хитрец) один
раз сказал правду, а другой раз неправду. Назовите имена правдивого,
шутника и хитреца.
Кто из внуков разбил вазу?
K
B
C
Утверждение
Серёжи
Утверждение
Васи
Утверждение
Коли
K
C
0
0
0
1
1
1
0
1
0
0
0
1
0
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
1
1
0
0
0
0
1
1
1
0
0
1
1
1
1
0
0
1
0
1
0
1
0
1
0
1
1
1
0
1
0
1
1
0
0
1
1
1
0
0
0
1
0
1
Задание №5
Домашнее задание
Подготовиться к проверочной работе. Для подготовки
можно прорешать примерный вариант работы

English     Русский Правила

Логика и выражения

Использование и изучение логики включает поиск нового факта путем анализа того, могут ли некоторые другие факты вместе оказаться истинными. Некоторые факты или условия, рассматриваемые вместе, могут доказать, что другой факт является истинным, а может быть, и ложным.

Если на улице минусовая температура и у вас нет пальто, вам будет холодно. Если вы не больны, то будете чувствовать себя хорошо. Если вы умеете плавать или кататься на лодке по воде, вы останетесь на плаву. Это утверждения о фактах, которые являются результатом истинности некоторых условий.

Взяв некоторые факты и приведя их к логической форме, мы можем произвести арифметические действия, которые помогут нам проанализировать их и сделать вывод. Используя только что упомянутые примеры, давайте превратим их в некоторые логические словесные уравнения:

• Температура снаружи замерзает И У меня нет пальто = Мне холодно
• НЕ болен = чувствую себя хорошо
• я умею плавать ИЛИ Я в лодке = Я плаваю

Вы видите И, НЕ и ИЛИ в примерах словесных уравнений? Это наши логические операторы . Каждый день мы принимаем решения, когда вместе обдумываем один или несколько фактов, используя эти операторы. Иногда необходимо, чтобы все факты были верными, чтобы вывод был верным. Это тот случай, когда используется оператор AND. При анализе фактов с помощью оператора ИЛИ только факт должен быть верным, чтобы вывод также был верным.

Для принятия решения может потребоваться больше, чем один или два факта. Когда это происходит, требуется другой оператор, чтобы объединить факты вместе, чтобы сделать вывод. В последнем словесном уравнении вы на самом деле не можете быть плавающим, если только эти два условия верны. Чтобы правильно доказать, что вы на самом деле плаваете, вам нужно указать, что вы тоже находитесь в воде.

• ( Я умею плавать ИЛИ Я в лодке ) И Я в воде = Я плаваю

Чтобы доказать, что вы плаваете, два факта, что вы умеете плавать или что вы находитесь в лодке, должны быть объединены в один факт, объединенный с другим фактом, что вы также находитесь в воде. В противном случае, если вы умеете плавать, но все еще на суше, или в лодке, стоящей на берегу, вы не плаваете.

Булева алгебра

Чтобы привести условия, или факты, как мы их назвали, к более компактной форме, была изобретена алгебра. Джордж Буль разработал тип арифметики (булева алгебра), в которой используются символы для условий, операторов и результата. Условия рассматриваются как переменные, которые имеют значение либо

истина или ложь . такие операторы, как И, ИЛИ и НЕ, являются односимвольными символами. Если мы хотим преобразовать утверждение «Я счастлив, когда солнечно или когда я ем пончик» в логическое уравнение, мы могли бы начать с превращения условий в переменные.

• Переменная A = "Солнечно"
• Переменная B = "Я съел пончик"

Результатом является переменная с именем Q , которая истинна, когда вы счастливы, и является значением операции А с В . Это операция ИЛИ, которая представлена ​​символом + .

Q = A + B

Результатом Q будет true , когда либо солнечно, либо вы съели пончик. Если другие вещи делают вас счастливыми, например, отпуск, вы можете добавить это к уравнению.

• Переменная C = "Я в отпуске"

Q = А + В + С

Возможно, вам легко угодить, и вам просто нужно хорошо себя чувствовать, чтобы быть счастливым. Итак, вы счастливы, когда НЕ больны. Мы будем использовать ~ для обозначения НЕ в нашем уравнении.

• Переменная A = «Я болен»

Q = ~A

В ситуации, когда все условия должны быть истинными, чтобы результат был истинным, в условиях используется операция И. Чтобы солнце светило на вас, небо должно быть ясным и должно быть дневное время. Мы соединяем эти два факта с помощью символа AND 9.0012 · .

• Переменная A = "Небо чистое"
• Переменная B = "Сейчас день"
• Результат Q = "Солнце светит"

Q = A · B

Выражения

Иногда разные операции при одних и тех же условиях могут дать одинаковые результаты. Если мы возьмем случай, противоположный последнему примеру, когда солнце не светит, переменные для этого будут следующими:

• Переменная A = "Небо чистое"
• Переменная B = "Сейчас день"
• Результат Q = "Солнце светит"
• Результат ~Q = "Солнце НЕ светит"

Чтобы сделать противоположным "солнце светит" , мы отрицаем, используем символ НЕ в обеих частях уравнения.

~Q = ~(А · В)

Теперь давайте подумаем, что солнце НЕ светит из-за неблагоприятных условий. Если небо не чистое ИЛИ сейчас не день, значит, солнце не светит. Таким образом, перед переменными для каждого условия ставится символ НЕ, так что "солнце НЕ светит" имеет другое уравнение, подобное этому: стороны с переменными A и B в обоих уравнениях эквивалентны друг другу, поскольку они оба равны ~Q :

~(A · B) = ~A + ~B

Логическое уравнение теперь не включает результирующую переменную Q , но вместо этого есть два выражения , которые логически эквивалентно с каждой стороны.

Таблицы истинности

Таблица истинности позволяет увидеть все возможные условия для переменных в логическом выражении и представить результаты в виде диаграммы. Используя утверждение о том, когда на улице мороз, а у вас нет пальто, вот таблица истинности, показывающая возможные условия и их результаты:

Холодно	У меня нет пальто	Мне холодно
ложь	ложь	ложь
ложный	правда	ложь
правда	ложь	ложь
правда	правда	правда

Поскольку вам холодно только тогда, когда оба условия истинны, оператор становится выражением И в булевой алгебре.

• Переменная A = "замерзает"
• Переменная B = «У меня нет пальто»

A · B = Q

Таблица истинности для переменных в выражении имеет те же значения, что и таблица для утверждения истинности ( верно и неверно сокращены до T и3 Ф ).

А	Б	Вопрос
Ф	Ф	Ф
Ф	Т	Ф
Т	Ф	Ф
Т	Ф	Т

Что произойдет, если мы изменим условие «У меня нет пальто» на «У меня есть пальто» ? Как это влияет на таблицу истинности того, насколько вам холодно?

Холодно	У меня есть пальто	Мне холодно
ложь	ложь	ложь
ложный	правда	ложь
правда	ложь	правда
правда	правда	ложь

А	Б	В
Ф	Ф	Ф
Ф	Т	Ф
Т	Ф	Т
Т	Ф	Ф

Чтобы написать логическое уравнение для случая, когда вам холодно, мы находим условия в таблице, где Q равно true . Здесь мы видим, что вам будет холодно только в одном ряду, когда условие A равно true и условие B это ложь . Логическое уравнение для этих условий выглядит следующим образом:

A · ~B = Q

Изменить эту страницу на GitHub
Изменить шаблон этой страницы на GitHub

Упрощение логических выражений

Упрощение логических выражений

Упрощение логических выражений

Примеры булевой алгебры   Двоичный/булев основной индекс

[Примеры таблиц истинности] [Упрощение логических выражений] [Примеры логических вентилей]

Вот несколько примеров упрощений булевой алгебры. Каждая строка дает форму выражения, а правило или правила используется для получения его от предыдущего. Как правило, есть несколько способов достичь результата. Вот список правил упрощения.

• Упрощение: C + BC:

  Выражение	Используемые правила
  C + BC	Исходное выражение
  С + (Б + С)	Закон Де Моргана.
  (С + С) + В	Коммутативные, ассоциативные законы.
  Т + Б	Закон о дополнениях.
  Т	Закон о личности.

• Упрощение: AB(A + B)(B + B):

  Выражение	Используемые правила
  AB(A + B)(B + B)	Исходное выражение
  АВ(А+В)	Закон о дополнении, Закон о личности.
  (А + В) (А + В)	Закон Де Моргана
  А + ВВ	Распределительное право. Этот шаг использует тот факт, что или распределяет по а также. Это может выглядеть немного странно так как сложение не распределяется над умножением.
  А	Дополнение, Идентификация.

• Упростить: (A + C)(AD + AD) + AC + C:

  Выражение	Используемые правила
  (A + C)(AD + AD) + AC + C	Исходное выражение
  (А + С)А(Д + Д) + АС + С	Распределительный.
  (А + С)А + АС + С	Дополнение, Идентификация.
  А((А + С) + С) + С	Коммутативный, Распределительный.
  А(А + С) + С	Ассоциативный, идемпотентный.
  АА + АС + С	Распределительный.
  А + (А + Т )С	Идемпотент, Тождество, Распределение.
  А + С	Личность дважды.

  Вы также можете использовать распределение или более и начиная с A(A+C)+C для достижения того же результата другим путем.

• Упрощение: A(A + B) + (B + AA)(A + B):

  Выражение	Правил(а) использовано
  А(А + В) + (В + АА)(А + В)	Исходное выражение
  АА + АВ + (В + А)А + (В + А)В	Идемпотент (от АА до А), затем Дистрибутив, используется дважды.
  АВ + (В + А)А + (В + А)В	Дополнение, затем Идентификация. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт