Решение неопределенного интеграла онлайн с подробным решением: ∫ Решение несобственного интеграла — Калькулятор Онлайн

2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

∫∫ Двойной интеграл — Калькулятор Онлайн

Калькуляторы онлайн/ Решение интегралов/ Двойной интеграл

Препод очень удивится увидев твоё верное решение интеграла😉

	d		d

Примеры

Введите подинтегральную функцию,

для которой надо найти двойной интеграл

Найдём подробное решение для двойного интеграла от функции f(x, y).

Введите вверхние и нижние пределы для области интегрирования и подинтегральную функцию. 2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от

x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

1 dx интеграл

1 dx интеграл

Вы искали 1 dx интеграл? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 x 2 интеграл, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 dx интеграл».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 dx интеграл,1 x 2 интеграл,1 x 3 интеграл,1 х интеграл,2 x интеграл,4 x 2 первообразная,dx x,dx x 2 интеграл,dx x интеграл,dx интеграл,x 1 интеграл,x 2 интеграл,x dx,x dx интеграл,x exp x интеграл,xdx,xdx интеграл,вычисление интеграла онлайн,вычисление интеграла онлайн с подробным решением,вычисление интегралов калькулятор онлайн,вычисление интегралов онлайн,вычисление неопределенных интегралов онлайн,вычисление неопределенных интегралов онлайн с подробным решением,вычисление первообразной онлайн,вычислите интеграл,вычислите интеграл онлайн,вычислите интегралы,вычислите интегралы онлайн,вычислить интеграл x 2 x,вычислить интеграл калькулятор онлайн,вычислить интеграл онлайн,вычислить интеграл онлайн бесплатно с подробным решением,вычислить интеграл онлайн калькулятор,вычислить интегралы,вычислить интегралы онлайн,вычислить интегралы онлайн с решением,вычислить неопределенные интегралы,вычислить неопределенный интеграл,вычислить неопределенный интеграл онлайн,вычислить первообразную онлайн,интеграл 1 dx,интеграл 1 x,интеграл 1 x 1 3,интеграл 1 x 2,интеграл 1 x 2 dx,интеграл 1 x 3,интеграл 1 x dx,интеграл 1 х 2,интеграл 2 x,интеграл 2 x 3 dx,интеграл 2 x 3 x dx,интеграл 2 x 5 x,интеграл 2 x dx,интеграл 2x,интеграл 3 x dx,интеграл dx,интеграл dx 1,интеграл dx 1 x,интеграл dx 1 x 2,интеграл dx x,интеграл dx x 1,интеграл dx x 1 2,интеграл dx x 2,интеграл dx x 2 1,интеграл dx x 2 x 1,интеграл dx x 5,интеграл dx по dx,интеграл x,интеграл x 1,интеграл x 1 2,интеграл x 1 dx,интеграл x 1 x 2,интеграл x 2,интеграл x 2 1,интеграл x 2 1 dx,интеграл x 2 3 x,интеграл x 2 dx,интеграл x 2 x dx,интеграл x 3 1,интеграл x 3 dx,интеграл x 3 x 2,интеграл x 3 x dx,интеграл x 5 dx,интеграл x dx,интеграл x exp x,интеграл x в степени x,интеграл x корень x dx,интеграл x корень из x dx,интеграл x по x,интеграл xdx,интеграл xdx равен,интеграл y dy,интеграл икс от икс,интеграл калькулятор,интеграл калькулятор онлайн,интеграл неопределенный онлайн с решением,интеграл онлайн,интеграл онлайн калькулятор,интеграл онлайн калькулятор с подробным решением,интеграл онлайн калькулятор с подробным решением неопределенный,интеграл онлайн решение,интеграл онлайн с подробным,интеграл онлайн с решением,интеграл от,интеграл от 0,интеграл от 1,интеграл от 1 x,интеграл от 1 x 2,интеграл от 1 до 1,интеграл от 1 до 2 x 2 dx,интеграл от 2 x,интеграл от 2 x dx,интеграл от dx,интеграл от dx x,интеграл от dx x 2,интеграл от x,интеграл от x 1,интеграл от x 1 2,интеграл от x 2,интеграл от x 2 1,интеграл от x 2 dx,интеграл от x 2 x dx,интеграл от x 3 x,интеграл от x dx,интеграл от х,интеграл от х 1,интеграл от х dx,интеграл от х в х,интеграл посчитать,интеграл рассчитать,интеграл решение онлайн,интеграл формула,интеграл х,интеграл х 1,интеграл х 1 2,интеграл х по dx,интеграла онлайн,интегралов онлайн,интегралы калькулятор,интегралы калькулятор онлайн с решением,интегралы неопределенные онлайн,интегралы неопределенные онлайн с подробным решением,интегралы онлайн,интегралы онлайн калькулятор,интегралы онлайн калькулятор с подробным решением,интегралы онлайн калькулятор с решением,интегралы онлайн решение,интегралы онлайн решить,интегралы решать онлайн,интегралы решение онлайн,интегралы решить,интегралы решить онлайн,интегралы с решением онлайн,интегралы формула,интегрирование калькулятор онлайн,интегрирование онлайн,интегрирование онлайн калькулятор,интегрирование онлайн с решением,интегрирование тригонометрических функций онлайн калькулятор,інтеграли онлайн калькулятор,как найти первообразную функции онлайн,калькулятор для интегралов,калькулятор интегралов и производных,калькулятор интегралов неопределенных,калькулятор интегралов неопределенных онлайн,калькулятор интегралов онлайн с подробным решением,калькулятор интегралов с решением,калькулятор интегралов с решением онлайн,калькулятор інтегралів,калькулятор неопределенного интеграла,калькулятор неопределенный интеграл,калькулятор неопределенных интегралов,калькулятор неопределенных интегралов онлайн,калькулятор неопределенных интегралов онлайн с подробным решением,калькулятор неопределенных интегралов онлайн с решением,калькулятор неопределенных интегралов с подробным решением онлайн,калькулятор неопределенных интегралов с решением онлайн,калькулятор онлайн вычислить интеграл,калькулятор онлайн интеграла,калькулятор онлайн интегралы,калькулятор онлайн неопределенный интеграл,калькулятор онлайн неопределенный интеграл с подробным решением,калькулятор онлайн неопределенных интегралов,калькулятор онлайн первообразной,калькулятор онлайн первообразных,калькулятор первообразная,калькулятор первообразной,калькулятор первообразных,калькулятор первообразных онлайн,калькулятор производных и интегралов,калькулятор решение интегралов,найдите интегралы,найдите неопределенный интеграл,найдите неопределенный интеграл онлайн,найдите первообразную для функции f x онлайн,найти интеграл,найти интеграл онлайн,найти интеграл онлайн калькулятор с подробным решением,найти интеграл онлайн с подробным решением,найти интегралы,найти интегралы онлайн,найти неопределенный интеграл,найти неопределенный интеграл калькулятор онлайн,найти неопределенный интеграл онлайн,найти неопределенный интеграл онлайн калькулятор,найти общий вид первообразной для функции f x онлайн калькулятор,найти общий вид первообразной для функции онлайн,найти онлайн первообразную с подробным решением,найти первообразную онлайн с подробным решением,найти первообразную функции онлайн,найти первообразную функции онлайн калькулятор,найти первообразную функции онлайн с решением,нахождение интеграла онлайн,нахождение интеграла онлайн с подробным решением,нахождение интегралов онлайн,нахождение неопределенного интеграла онлайн,нахождение первообразной онлайн калькулятор,неопределенные интегралы онлайн,неопределенные интегралы онлайн с подробным решением,неопределенный интеграл калькулятор,неопределенный интеграл калькулятор онлайн,неопределенный интеграл онлайн,неопределенный интеграл онлайн калькулятор,неопределенный интеграл онлайн с подробным решением,неопределенный интеграл онлайн с решением,неопределенный интеграл решение,неопределенный интеграл решить,неопределенный интеграл решить онлайн,неопределенный интеграл с решением онлайн,онлайн взятие интеграла,онлайн вычисление интеграла,онлайн вычисление интегралов,онлайн вычисление интегралов калькулятор,онлайн вычисление первообразной,онлайн интеграл решение,онлайн интегралы с решением,онлайн интегрирование,онлайн интегрирование с решением,онлайн калькулятор интегралов,онлайн калькулятор интегралов неопределенных,онлайн калькулятор интегралов неопределенных с решением,онлайн калькулятор интегралов с подробным решением,онлайн калькулятор интегралов с подробным решением неопределенных,онлайн калькулятор интегралов с решением,онлайн калькулятор найти первообразную,онлайн калькулятор нахождение первообразной,онлайн калькулятор неопределенных интегралов,онлайн калькулятор неопределенных интегралов с подробным решением,онлайн калькулятор неопределенных интегралов с решением,онлайн калькулятор первообразной,онлайн калькулятор первообразных,онлайн калькулятор первообразных с решением,онлайн калькулятор решение интегралов,онлайн найдите неопределенный интеграл,онлайн нахождение интеграла,онлайн нахождение интегралов,онлайн нахождение неопределенного интеграла,онлайн неопределенный интеграл с решением,онлайн расчет интегралов,онлайн решение интеграл,онлайн решение интеграла,онлайн решение интегралов,онлайн решение интегралов с решением,онлайн решение интегральных уравнений,онлайн решение неопределенного интеграла,онлайн решение неопределенных интегралов,онлайн решение первообразных,первообразная онлайн,первообразная онлайн с решением,первообразная функции онлайн,первообразная функции онлайн калькулятор,первообразные онлайн,посчитать интеграл онлайн,рассчитать интеграл,рассчитать интеграл онлайн,расчет интеграла онлайн,решать интегралы онлайн,решать онлайн интегралы,решение интеграл онлайн,решение интеграла онлайн,решение интегралов калькулятор,решение интегралов онлайн,решение интегралов онлайн калькулятор,решение интегралов онлайн с подробным,решение интегралов с решением онлайн,решение интегралы онлайн,решение интегральных уравнений онлайн,решение неопределенного интеграла онлайн,решение неопределенных интегралов онлайн,решение онлайн интеграл,решение онлайн интегралов с решением,решение первообразных онлайн,решить интеграл,решить интеграл неопределенный,решить интеграл онлайн,решить интеграл с решением онлайн,решить интегралы,решить интегралы онлайн,решить неопределенный интеграл,решить онлайн интегралы,решить онлайн неопределенный интеграл,с решением неопределенный интеграл онлайн,считать интегралы онлайн.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 dx интеграл. Просто введите задачу в окошко и нажмите «решить» здесь (например, 1 x 3 интеграл).

Решить задачу 1 dx интеграл вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Метод замены переменной в неопределённом интеграле

• Суть метода замены переменной
• Применяем замену переменной вместе
• Применить замену переменной самостоятельно, а затем посмотреть решение
• Снова применяем замену переменной вместе

Во многих случаях подынтегральное выражение не позволяет сразу же найти интеграл по таблице. Тогда введение новой переменной интегрирования помогает свести нахождение данного интеграла к нахождению табличного интеграла. Такой метод называется методом подстановки или методом замены переменной.

Вводится новая переменная, назовём её t. Например,

• в интеграле можем ввести новую переменную ;
• в интеграле можем ввести новую переменную ;
• в интеграле можем ввести новую переменную .

Далее dx определеяем как дифференциал по переменной t. После этого интеграл можно найти по таблице интегралов. Заменив обратно t на функцию от x, находим данный интеграл окончательно.

Прежде чем перейти к подробным решениям примеров, следует привести теорему, в которой обобщаются перечисленные выше действия.

Теорема.  Пусть функция определена и дифференцируема на некотором промежутке Т и пусть Х – множество значений этой функции, на котором определена функция f(x). Тогда, если на множестве Х функция f(x) имеет первообразную, то на множестве Т справедлива формула

                        (1)

Формула (1) называется формулой замены переменной в неопределённом интеграле.

Метод замены переменной обычно применяется, когда подынтегральное выражение представляет собой независимую переменную, умноженную на многочлен от этой переменной, или на тригонометрическую функцию от этой переменной или на степенную функцию (в том числе корень) от этой переменной.

Надо полагать, вы уже держите перед собой домашние задания и готовы применять к ним приёмы по аналогии с теми, которые мы ниже рассмотрим. При этом не обойтись без преобразований выражений. Для этого потребуется открыть в новых окнах пособия Действия со степенями и корнями и Действия с дробями.

Пример 1.  Найти неопределённый интеграл методом замены переменной:

Решение. Производим замену x − 1 = t; тогда x = t + 1. Отсюда dx = dt. По формуле (1)

(воспользовались табличными интегралами 7, 9 и 10).

Возвращаясь к переменной x, окончательно получаем

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

---

Замечание. При замене переменной в неопределённом интеграле иногда более удобно задавать не х как функцию t, а, наоборот, задавать t как функцию от x.

Заметим, что удачный выбор подстановки обычно представляет известные трудности. Для их преодоления необходимо овладеть техникой дифференцирования и хорошо знать табличные интегралы.

Пример 2.  Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим . Отсюда
.
По формуле (1) и, пользуясь табличными интегралом 13, находим

.

Возвращаясь к переменной x, окончательно получаем

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Если трудно уследить, куда в процессе решения примера 2 делись и , это признак того, что нужно повторить действия со степенями из элементарной (школьной) математики.

Пример 3.  Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда и .

Тогда , в свою очередь .

Заменяем переменную и получаем:

,

где степени при t складываются. Продолжаем преобразования и, пользуясь уже упомянутым табличным интегралом 7, получаем:

Приводим дроби к общему знаменателю и возвращаемся к переменной x.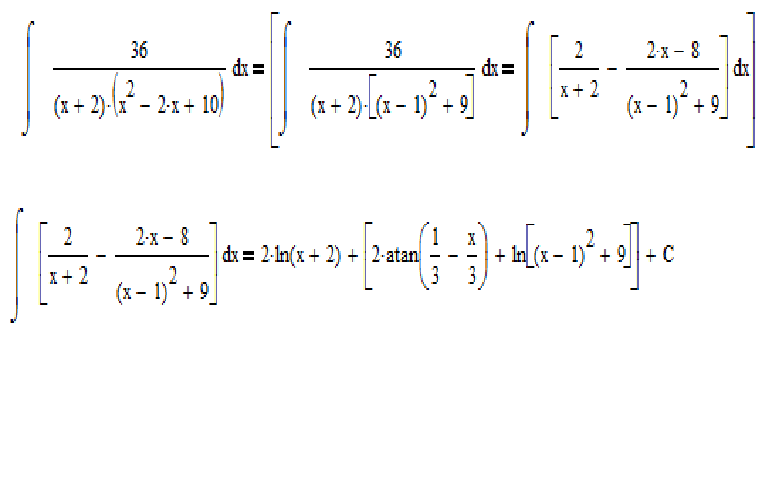 Решаем и получаем ответ:

Нет времени вникать в решение? Можно заказать работу!

Пример 4.  Найти неопределённый интеграл методом замены переменной:

.

Посмотреть правильное решение и ответ.

Пример 5.  Найти неопределённый интеграл методом замены переменной:

.

Посмотреть правильное решение и ответ.

Пример 6.  Найти неопределённый интеграл методом замены переменной:

.

Посмотреть правильное решение и ответ.

Пример 7.  Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда , , .

Тогда

(не забываем о правиле дифференцирования сложной функции).

Заменяем переменную и получаем:

.

Возвращаясь к переменной х, получаем ответ:

.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Пример 8.  Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , откуда , .

Заменяем переменную и получаем:

Подставляя вместо t его выражение через x получаем ответ:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Кому лишь смутно понятно или совсем не понятно, как преобразуются выражения в примере 5, пожалуйста, повторите из курса элементарной (школьной) математики действия с корнями, степенями и дробями!

И если вы ещё не открыли в новых окнах пособия Действия со степенями и корнями и Действия с дробями, то сделайте это сейчас!

Пример 9.  Найти неопределённый интеграл методом замены переменной:

.

Решение. Положим , тогда
.

Заменяем переменную и получаем:

Решение с переменной t получено с использованием формулы 21 из таблицы интегралов.

Подставляя вместо t его выражение через x получаем ответ:

.

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.

Назад

Листать

Вперёд>>>

К началу страницы

Пройти тест по теме Интеграл

Начало темы «Интеграл»

Неопределённый интеграл: основные понятия, свойства, таблица неопределённых интегралов

Найти неопределённый интеграл: начала начал, примеры решений

Продолжение темы «Интеграл»

Интегрирование подведением под знак дифференциала

Метод интегрирования по частям

Интегрирование дробей

Интегрирование рациональных функций и метод неопределённых коэффициентов

Интегрирование некоторых иррациональных функций

Интегрирование тригонометрических функций

Определённый интеграл

Несобственные интегралы

Площадь плоской фигуры с помощью интеграла

Объём тела вращения с помощью интеграла

Вычисление двойных интегралов

Длина дуги кривой с помощью интеграла

Площадь поверхности вращения с помощью интеграла

Определение работы силы с помощью интеграла

Поделиться с друзьями

Решение интегралов.

Рассказываем, как решать интегралы.

Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная дифференцированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:

Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:

Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.

F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной.

Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой.

Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin²+cos²=1
m,n – четные, sin²x=(1-cos2x)/2 и cos²x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg²x=1/cos²x — 1

С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1:
Решить интеграл:

Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.

Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:

Проверим решение(найдем производную):

Пример 2. Решаем интеграл

Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t⁵. t⁵ = x+5 . Получаем.

Но dx нужно тоже заменить на t. x= t⁵ — 5, dx = (t⁵ — 5)’ = 5t⁴. Подставляем:

Интеграл из таблицы. Считаем:

Подставляем в ответ вместо t ,

Решение интеграла:

Пример 3. Решение интеграла:

Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.

В итоге получаем:

Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.

Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию. Программирование одна из дочек математики!

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Виды интегралов и способы их решения. Решение интегралов онлайн

Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций. Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн .

Решить неопределенный интеграл

Онлайн сервис на сайт позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт сайт поможет решить интеграл онлайн и справиться с поставленной задачей. Используя онлайн решение интеграла на сайте сайт, вы всегда получите точный ответ.

Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.

Слово «интеграл» происходит от латинского integralis — целостный. Это название предложил в 17 в. ученик великого Лейбница (и также выдающийся математик) И. Бернулли. А что такое интеграл в современном понимании? Ниже мы постараемся дать всесторонний ответ на этот вопрос.

Исторические предпосылки возникновения понятия интеграла

В начале 17 в. в рассмотрении ведущих ученых находилось большое число физических (прежде всего механических) задач, в которых нужно было исследовать зависимости одних величин от других. Самыми наглядными и насущными проблемами были определение мгновенной скорости неравномерного движения тела в любой момент времени и обратная этой задача нахождения величины пути, пройденного телом за определенный промежуток времени при таком движении. Сегодня мы уже знаем, что такое интеграл от скорости движения — это и есть пройденный путь. Но понимание того, как его вычислять, зная скорость в каждый момент времени, появилось не сразу.

Поначалу из рассмотрения таких зависимостей физических величин, например, пути от скорости, было сформировано математическое понятие функции y = f(x). Исследование свойств различных функций привело к зарождению математического анализа. Ученые активно искали способы изучения свойств различных функций.

Как возникло вычисление интегралов и производных?

После создания Декартом основ аналитической геометрии и появления возможности изображать функциональные зависимости графически в осях декартовой системы координат, перед исследователями встали две крупные новые задачи: как провести касательную к кривой линии в любой ее точке и как найти площадь фигуры, ограниченной сверху этой кривой и прямыми, параллельными осям координат. Неожиданным образом оказалось, что первая из них эквивалентна нахождению мгновенной скорости, а вторая — нахождению пройденного пути. Ведь он при неравномерном движении изображался в декартовых осях координат «расстояние» и «время» некоторой кривой линией.

Гением Лейбница и Ньютона в середине 17 в. были созданы методы, позволившие решать обе эти задачи. Оказалось, что для проведения касательной к кривой в точке нужно найти величину так называемой производной от функции, описывающей эту кривую, в рассматриваемой ее точке, и эта величина оказывается равной скорости изменения функции, т. е. применительно к зависимости «путь от скорости» собственно мгновенной скоростью тела.

Для нахождения же площади, ограниченной кривой линией, следовало вычислить определенный интеграл, который давал ее точную величину. Производная и интеграл — основные понятия дифференциального и интегрального исчисления, являющихся базисом современного матанализа — важнейшего раздела высшей математики.

Площадь под кривой линией

Итак, как же определить ееточную величину? Попробуем раскрыть процесс ее вычисления через интеграл подробно, с самых азов.

Пусть f является непрерывной на отрезке функцией. Рассмотрим кривую у = f(x), изображенную на рисунке ниже. Как найти площадь области, ограниченной кривой), осью х, и линиями х = а и х = b? То есть площадь заштрихованной фигуры на рисунке.

Самый простой случай, когда f является постоянной функцией; то есть, кривая есть горизонтальная линия f(X) = k, где k постоянная и k ≥ 0, как показано на рисунке ниже.

В этом случае область под кривой — всего лишь прямоугольник с высотой k и шириной (b — a), так что площадь определяется как: k · (b — а).

Области некоторых других простых фигур, таких как треугольник, трапеция и полуокружность, даются формулами из планиметрии.

Площадь под любой непрерывной кривой у = f(х) дается определенным интегралом, который записывается так же, как обычный интеграл.

Риманова сумма

Прежде чем погрузиться в подробный ответ на вопрос, что такое интеграл, выделим некоторые основные идеи.

Во-первых, область под кривой делится на некоторое число n вертикальных полос достаточно малой ширины Δx. Далее каждая вертикальная полоса заменяется вертикальным прямоугольником высотой f(х), шириной Δx, и площадью f(х)dx. Следующим шагом является формирование суммы площадей всех этих прямоугольников, называемой Римановой суммой (смотрите рисунки ниже).

Рисуя наши прямоугольники шириной Δx, мы можем брать их высоту, равную значению функции на левом краю каждой полоски, т. е. на кривой будут лежать крайние левые точки их верхних коротких сторон шириной Δx. При этом на участке, где функция растет, и ее кривая является выпуклой, все прямоугольники оказываются ниже этой кривой, т. е. их сумма будет заведомо меньшей точной величины площади под кривой на этом участке (см. рисунок ниже). Такой способ аппроксимации называется левосторонним.

В принципе, можно нарисовать аппроксимирующие прямоугольники таким образом, чтобы на кривой лежали крайние правые точки их верхних коротких сторон шириной Δx. Тогда они будут выше кривой, и приближение площади на этом участке окажется больше ее точной величины, как показано на рисунке ниже. Этот способ носит название правостороннего.

Но мы можем также взять высоту каждого из аппроксимирующих прямоугольников, равной просто некоторому значению функции в произвольной точке x* i внутри соответствующей полоски Δx i (смотри рис. ниже). При этом мы даже можем не брать одинаковую ширину всех полосок.

Составим Риманову сумму:

Переход от Римановой суммы к определенному интегралу

В высшей математике доказывается теорема, которая гласит, что если при неограниченном возрастании числа n аппроксимирующих прямоугольников наибольшая их ширина стремится к нулю, то Риманова сумма A n стремится к некоторому пределу A. Число A — одно и то же при любом способе образования аппроксимирующих прямоугольников и при любом выборе точек x* i .

Наглядное пояснение теоремы дает рисунок ниже.

Из него видно, что, чем уже прямоугольники, тем ближе площадь ступенчатой фигуры к площади под кривой. При числе прямоугольников n→∞ их ширина Δx i →0, а предел A суммы A n численно равен искомой площади. Этот предел и есть определенный интеграл функцииf (х):

Символ интеграла, представляющий собой видоизмененную курсивную литеру S, был введен Лейбницем. Ставить сверху и снизу обозначения интеграла его пределы предложил Ж. Б. Фурье. При этом ясно указывается начальное и конечное значение x.

Геометрическое и механическое истолкование определенного интеграла

Попробуем дать развернутый ответ на вопрос о том, что такое интеграл? Рассмотрим интеграл на отрезке от положительной внутри него функции f(х), причем считаем, что верхний предел больше нижнего a

Если ординаты функции f(х) отрицательны внутри , то абсолютное значение интеграла равно площади между осью абсцисс и графиком y=f(х), сам же интеграл отрицателен.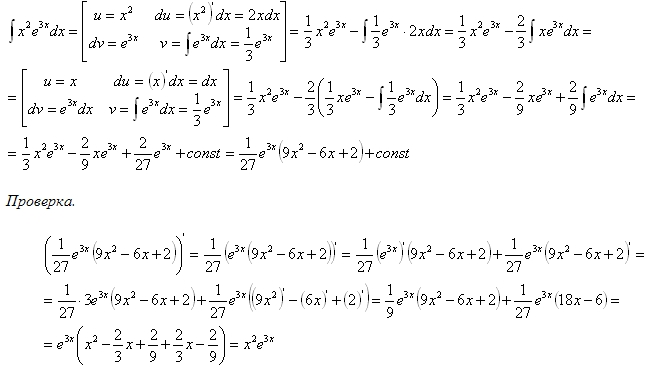

В случае же однократного или неоднократного пересечения графиком y=f(х) оси абсцисс на отрезке , как показано на рисунке ниже, для вычисления интеграла нужно определить разность, в которой уменьшаемое будет равно суммарной площади участков, находящихся над осью абсцисс, а вычитаемое — суммарной площади участков, находящихся под ней.

Так, для функции, показанной на рисунке выше, определенный интеграл от a до b будет равен (S1 + S3) — (S2+S4).

Механическое истолкование определенного интеграла тесно связано с геометрическим. Вернемся к разделу «Риманова сумма» и представим, что приведенный на рисунках график выражает функцию скорости v=f(t) при неравномерном движении материальной точки (ось абсцисс является осью времени). Тогда площадь любого аппроксимирующего прямоугольника шириной Δt, который мы строили при формировании Римановой суммы, будет выражать приближенно путь точки за время Δt, а именно v(t*)Δt.

Полная сумма площадей прямоугольников на отрезке от t 1 =a до t 2 =b выразит приближенно путь s за время t 2 — t 1 , а предел ее, т. е. интеграл (определенный) от a до b функции v = f(t) по dt даст точное значение пути s.

Дифференциал определенного интеграла

Если вернуться к его обозначению, то вполне можно предположить, что a = const, а b является конкретным значением некоторой независимой переменной x. Тогда определенный интеграл с верхним пределом x̃ из конкретного числа превращается в функцию от x̃. Такой интеграл равен площади фигуры под кривой, обозначенной точками aABb на рисунке ниже.

При неподвижной линии aA и подвижной Bb эта площадь становится функцией f(x̃), причем приращения Δx̃ по-прежнему откладываются вдоль оси х, а приращением функции f(x̃) являются приращения площади под кривой.

Предположим, что мы дали переменной x̃ = b некоторое малое приращение Δx̃. Тогда приращение площади фигуры aABb складывается из площади прямоугольника (заштрихован на рисунке) Bb∙Δx̃ и площади фигуры BDC под кривой. Площадь прямоугольника равна Bb∙Δx̃ = f(x̃)Δx̃, т.е она является линейной функцией приращения независимой переменной.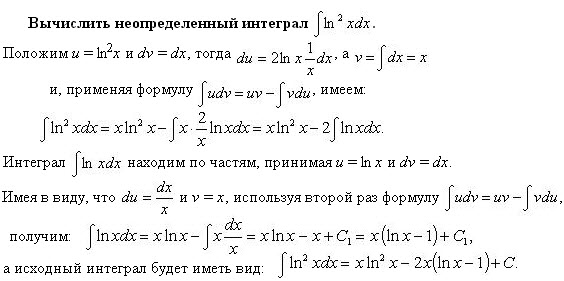 Площадь же фигуры BDC заведомо меньше, чем площадь прямоугольника BDCK = Δx̃∙Δy, и при стремлении Δx̃ →0 она уменьшается еще быстрее него. Значит, f(x̃)Δx̃ = f(x̃)dx̃ есть дифференциал переменной площади aABb, т. е. дифференциал определенного интеграла

Отсюда можно заключить, что вычисление интегралов заключается в разыскании функций по заданным выражениям их дифференциалов. Интегральное исчисление как раз и представляет собой систему способов разыскания таких функций по известным их дифференциалам.

Фундаментальное соотношение интегрального исчисления

Оно связывает отношения между дифференцированием и интегрированием и показывает, что существует операция, обратная дифференцированию функции, — ее интегрирование. Оно также показывает, что если любая функция f(х) непрерывна, то применением к ней этой математической операции можно найти целый ансамбль (совокупность, множество) функций, первообразных для нее (или иначе, найти неопределенный интеграл от нее).

Пусть функция F(x) является обозначением результата интегрирования функции f(х). Соответствие между этими двумя функциями в результате интегрирования второй из них обозначается следующим образом:

Как видно, при символе интеграла отсутствуют пределы интегрирования. Это означает, что из определенного он преобразован в неопределенный интеграл. Слово «неопределенный» означает, что результатом операции интегрирования в данном случае является не одна, а множество функций. Ведь, кроме собственно функции F(x), последним выражениям удовлетворяет и любая функция F(x)+С, где С = const. При этом подразумевается, что постоянный член в ансамбле первообразных можно задавать по произволу.

Следует подчеркнуть, что, если интеграл, определенный от функции, является числом, то неопределенный есть функция, точнее, их множество. Термин «интегрирование» применяется для определения операции разыскания обоих видов интегралов.

Основное правило интегрирования

Оно представляет собой полную противоположность соответствующему правилу для дифференцирования. Как же берутся неопределенные интегралы? Примеры этой процедуры мы рассмотрим на конкретных функциях.

Давайте посмотрим на степенную функцию общего вида:

После того как мы сделали это с каждым слагаемым в выражении интегрируемой функции (если их несколько), мы добавляем постоянную в конце. Напомним, что взятие производной от постоянной величины уничтожает ее, поэтому взятие интеграла от любой функции даст нам восстановление этой постоянной. Мы обозначаем ее С, так как постоянная неизвестна — это может быть любое число! Поэтому мы можем иметь бесконечно много выражений для неопределенного интеграла.

Давайте рассмотрим простые неопределенные интегралы, примеры взятия которых показаны ниже.

Пусть нужно найти интеграл от функции:

f(х) = 4x 2 + 2x — 3.

Начнем с первого слагаемого. Мы смотрим на показатель степени 2 и увеличиваем его на 1, затем делим первый член на результирующий показатель 3. Получаем: 4(x 3) / 3.

Затем мы смотрим на следующий член и делаем то же самое. Так как он имеет показатель степени 1, то результирующий показатель будет 2. Таким образом, мы разделим это слагаемое на 2: 2(x 2) / 2 = x 2 .

Последний член имеет множитель х, но мы просто не видим его. Мы можем представить себе последнее слагаемое как (-3x 0). Это эквивалентно (-3)∙(1). Если мы используем правило интегрирования, мы добавим 1 к показателю, чтобы поднять его до первой степени, а затем разделим последний член на 1. Получим 3x.

Это правило интегрирования работает для всех значений n, кроме n = — 1 (потому что мы не можем разделить на 0).

Мы рассмотрели самые простой пример нахождения интеграла. Вообще же решение интегралов является делом непростым, и в нем хорошим подспорьем является уже накопленный в математике опыт.

Таблицы интегралов

В разделе выше мы видели, что из каждой формулы дифференцирования получается соответствующая формула интегрирования. Поэтому все возможные их варианты уже давно получены и сведены в соответствующие таблицы. Нижеприведенная таблица интегралов содержит формулы интегрирования основных алгебраических функций. Эти формулы нужно знать на память, заучивая их постепенно, по мере их закрепления упражнениями.

Еще одна таблица интегралов содержит основные тригонометрические функции:

Как же вычислить определенный интеграл

Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница

Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.

Рассмотрим некоторые интегралы с подробным решением.

Найдем площадь участка под одной полуволной синусоидой.

Вычислим заштрихованную площадь под гиперболой.

Рассмотрим теперь интегралы с подробным решением, использующим в первом примере свойство аддитивности, а во втором — подстановку промежуточной переменной интегрирования.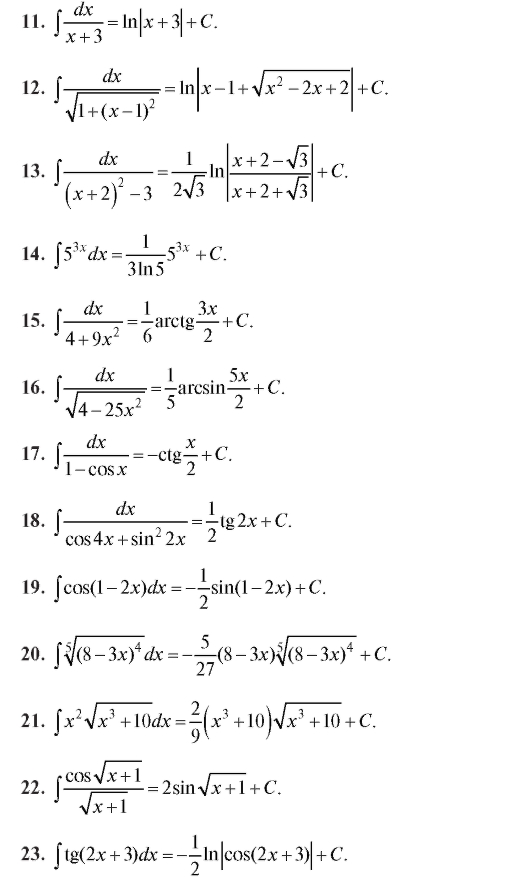 Вычислим определенный интеграл от дробно-рациональной функции:

y=(1+t)/t 3 от t=1 до t=2.

Теперь покажем, как можно упростить взятие интеграла введением промежуточной переменной. Пусть нужно вычислить интеграл от (x+1) 2 .

О несобственных интегралах

Мы говорили об определенном интеграле для конечного промежутка от непрерывной на нем функции f(х). Но ряд конкретных задач приводит к необходимости расширить понятие интеграла на случай, когда пределы (один или оба) равны бесконечности, или при разрывной функции. Например, при вычислении площадей под кривыми, асимптотически приближающимися к осям координат. Для распространения понятия интеграла на этот случай, кроме предельного перехода при вычислении Римановой суммы аппроксимирующих прямоугольников, выполняется еще один. При таком двукратном переходе к пределу получается несобственный интеграл. В противоположность ему все интегралы, о которых говорилось выше, называются собственными.

Определённым интегралом от непрерывной функции f (x ) на конечном отрезке [a , b ] (где ) называется приращение какой-нибудь её первообразной на этом отрезке. (Вообще, понимание заметно облегчится, если повторить тему неопределённого интеграла) При этом употребляется запись

Как видно на графиках внизу (приращение первообразной функции обозначено ), определённый интеграл может быть как положительным, так и отрицательным числом (Вычисляется как разность между значением первообразной в верхнем пределе и её же значением в нижнем пределе, т. е. как F (b ) — F (a )).

Числа a и b называются соответственно нижним и верхним пределами интегрирования, а отрезок [a , b ] – отрезком интегрирования.

Таким образом, если F (x ) – какая-нибудь первообразная функция для f (x ), то, согласно определению,

(38)

Равенство (38) называется формулой Ньютона-Лейбница . Разность F (b ) – F (a ) кратко записывают так:

Поэтому формулу Ньютона-Лейбница будем записывать и так:

(39)

Докажем, что определённый интеграл не зависит от того, какая первообразная подынтегральной функции взята при его вычислении. Пусть F (x ) и Ф(х ) – произвольные первообразные подынтегральной функции. Так как это первообразные одной и той же функции, то они отличаются на постоянное слагаемое: Ф(х ) = F (x ) + C . Поэтому

Тем самым установлено, что на отрезке [a , b ] приращения всех первообразных функции f (x ) совпадают.

Таким образом, для вычисления определённого интеграла необходимо найти любую первообразную подынтегральной функции, т.е. сначала следует найти неопределённый интеграл. Постоянная С из последующих вычислений исключается. Затем применяется формула Ньютона-Лейбница: в первообразную функцию подставляется значение верхнего предела b , далее — значение нижнего предела a и вычисляется разность F(b) — F(a) . Полученное число и будет определённым интегралом. .

При a = b по определению принимается

Пример 1.

Решение. Сначала найдём неопределённый интеграл:

Применяя формулу Ньютона-Лейбница к первообразной

(при С = 0), получим

Однако при вычислении определённого интеграла лучше не находить отдельно первообразную, а сразу записывать интеграл в виде (39).

Пример 2. Вычислить определённый интеграл

Решение. Используя формулу

Свойства определённого интеграла

Теорема 2. Величина определённого интеграла не зависит от обозначения переменной интегрирования , т.е.

(40)

Пусть F (x ) – первообразная для f (x ). Для f (t ) первообразной служит та же функция F (t ), в которой лишь иначе обозначена независимая переменная. Следовательно,

На основании формулы (39) последнее равенство означает равенство интегралов

Теорема 3. Постоянный множитель можно выносить за знак определённого интеграла , т.е.

(41)

Теорема 4. Определённый интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме определённых интегралов от этих функций , т.е.

(42)

Теорема 5. Если отрезок интегрирования разбит на части, то определённый интеграл по всему отрезку равен сумме определённых интегралов по его частям , т. е. если

(43)

Теорема 6. При перестановке пределов интегрирования абсолютная величина определённого интеграла не меняется, а изменяется лишь его знак , т.е.

(44)

Теорема 7 (теорема о среднем). Определённый интеграл равен произведению длины отрезка интегрирования на значение подынтегральной функции в некоторой точке внутри его , т.е.

(45)

Теорема 8. Если верхний предел интегрирования больше нижнего и подынтегральная функция неотрицательна (положительна), то и определённый интеграл неотрицателен (положителен), т.е. если

Теорема 9. Если верхний предел интегрирования больше нижнего и функции и непрерывны, то неравенство

можно почленно интегрировать , т.е.

(46)

Свойства определённого интеграла позволяют упрощать непосредственное вычисление интегралов.

Пример 5. Вычислить определённый интеграл

Используя теоремы 4 и 3, а при нахождении первообразных – табличные интегралы (7) и (6), получим

Определённый интеграл с переменным верхним пределом

Пусть f (x ) – непрерывная на отрезке [a , b ] функция, а F (x ) – её первообразная. Рассмотрим определённый интеграл

(47)

а через t обозначена переменная интегрирования, чтобы не путать её с верхней границей. При изменении х меняется и опредёленный интеграл (47), т.е. он является функцией верхнего предела интегрирования х , которую обозначим через Ф (х ), т.е.

(48)

Докажем, что функция Ф (х ) является первообразной для f (x ) = f (t ). Действительно, дифференцируя Ф (х ), получим

так как F (x ) – первообразная для f (x ), а F (a ) – постояная величина.

Функция Ф (х ) – одна из бесконечного множества первообразных для f (x ), а именно та, которая при x = a обращается в нуль. Это утверждение получается, если в равенстве (48) положить x = a и воспользоваться теоремой 1 предыдущего параграфа.

Вычисление определённых интегралов методом интегрирования по частям и методом замены переменной

где, по определению, F (x ) – первообразная для f (x ). Если в подынтегральном выражении произвести замену переменной

то в соответствии с формулой (16) можно записать

В этом выражении

первообразная функция для

В самом деле, её производная, согласно правилу дифференцирования сложной функции , равна

Пусть α и β – значения переменной t , при которых функция

принимает соответственно значения a и b , т.е.

Но, согласно формуле Ньютона-Лейбница, разность F (b ) – F (a ) есть

Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!

Решение неопределённых интегралов

Это онлайн сервис в один шаг :

Решение определённых интегралов

Это онлайн сервис в один шаг :

• Ввести подинтегральное выражение (подинтегральную функцию)
• Ввести нижний предел для интеграла
• Ввести верхний предел для интеграла

Решение двойных интегралов

• Ввести подинтегральное выражение (подинтегральную функцию)

Решение несобственных интегралов

• Ввести подинтегральное выражение (подинтегральную функцию)
• Введите верхнюю область интегрирования (или + бесконечность)
• Ввести нижнюю область интегрирования (или — бесконечность)

Решение тройных интегралов

• Ввести подинтегральное выражение (подинтегральную функцию)
• Ввести нижний и верхний пределы для первой области интегрирования
• Ввести нижний и верхний предел для второй области интегрирования
• Ввести нижний и верхний предел для третьей области интегрирования

Данный сервис позволяет проверить свои вычисления на правильность

Возможности

• Поддержка всех возможных математических функций: синус, косинус, экспонента, тангенс, котангенс, корень квадратный и кубический, степени, показательные и другие.
• Есть примеры для ввода, как для неопределённых интегралов, так и для несобственных и определённых.
• Исправляет ошибки в ведённых вами выражениях и предлагает свои варианты для ввода.
• Численное решение для определённых и несобственных интегралов (в том числе для двойных и тройных интегралов).
• Поддержка комплексных чисел, а также различных параметров (вы можете указывать в подинтегральном выражении не только переменную интегрирования, но и другие переменные-параметры)

Интегральное исчисление.

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке , если в любой точке этого отрезка верно равенство:

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F 1 (x) = F 2 (x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

2.

3.

4.

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Интеграл		Значение	Интеграл		Значение
		lnsinx+ C
		ln

Методы интегрирования.

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования
можно сделать вывод, что искомый интеграл равен
, где С – некоторое постоянное число. Однако, с другой стороны
. Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл
, но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Доказательство : Продифференцируем предлагаемое равенство:

По рассмотренному выше свойству №2 неопределенного интеграла:

f (x ) dx = f [  (t )]  (t ) dt

что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Пример. Найти неопределенный интеграл
.

Сделаем замену t = sinx , dt = cosxdt .

Пример.

Замена
Получаем:

Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:

или
;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Интегрирование элементарных дробей.

Определение: Элементарными называются дроби следующих четырех типов:

I.
III.

II.
IV.

m, n – натуральные числа (m  2, n  2) и b 2 – 4ac

Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Рассмотрим применение указанной выше формулы на примерах.

Пример.

Вообще говоря, если у трехчлена ax 2 + bx + c выражение b 2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.

Пример .

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.

Сначала рассмотрим частный случай при М = 0, N = 1.

Тогда интеграл вида
можно путем выделения в знаменателе полного квадрата представить в виде
. Сделаем следующее преобразование:

Второй интеграл, входящий в это равенство, будем брать по частям.

Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл
.

Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u 2 + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n , а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.

Пример :

Интегрирование рациональных функций.

Интегрирование рациональных дробей.

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.

Теорема: Если
— правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P (x ) = (x — a )  …(x — b )  (x 2 + px + q )  …(x 2 + rx + s )  ), то эта дробь может быть разложена на элементарные по следующей схеме:

где A i , B i , M i , N i , R i , S i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A i , B i , M i , N i , R i , S i применяют так называемый метод неопределенных коэффициентов , суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

Применение этого метода рассмотрим на конкретном примере.

Пример.

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x — 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

3x 3 – 4x 2 – 17x + 6 x — 3

3x 3 – 9x 2 3x 2 + 5x — 2

Таким образом 3x 3 – 4x 2 – 17x + 6 = (x – 3)(3x 2 + 5x – 2) = (x – 3)(x + 2)(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений . Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

=

Пример.

Найдем неопределенные коэффициенты:

Тогда значение заданного интеграла:

Интегрирование некоторых тригонометрических

функций.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида
.

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример.

Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Пример.

Интеграл вида
если

функция R cosx .

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx .

Функция
может содержать cosx только в четных степенях, а, следовательно, может быть преобразована в рациональную функцию относительно sinx.

Пример.

Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида
если

функция R является нечетной относительно sinx .

По аналогии с рассмотренным выше случаем делается подстановка t = cosx .

Пример.

Интеграл вида

функция R четная относительно sinx и cosx .

Для преобразования функции R в рациональную используется подстановка

t = tgx.

Пример.

Интеграл произведения синусов и косинусов

различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

Пример.

Пример.

Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

Пример.

Пример.

Иногда применяются некоторые нестандартные приемы.

Пример.

Интегрирование некоторых иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида
где n — натуральное число.

С помощью подстановки
функция рационализируется.

Пример.

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Проиллюстрируем это на примере.

Пример.

Интегрирование биноминальных дифференциалов.

Интегральный калькулятор: интеграция с Wolfram|Alpha

О, о! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

WolframAlpha

Решение интегралов с помощью Wolfram|Alpha

x sin

x2

dx

Исчисление и суммирование

• 3 9 0029
• 0025

больше, чем онлайн -интеграл

WOLFRAR | Alpha Alpha Anturetivation и Solider Solver

.

неправильные интегралы. Он также показывает графики, альтернативные формы и другую важную информацию для улучшения вашей математической интуиции.

Узнать больше о:

• Интегралы » 92 sin y dx dy, x=0 to 1, y=0 to pi

• Посмотреть другие примеры »

Доступ к средствам мгновенного обучения

Получите мгновенную обратную связь и рекомендации с помощью пошаговых решений и Генератора проблем Wolfram

Узнайте больше о:

• Пошаговые решения »
• Генератор задач Wolfram »

Что такое интегралы?

Интегрирование — важный инструмент в исчислении, который может дать первообразную или представить площадь под кривой.

Неопределенный интеграл от , обозначенный , определяется как первообразная от . Другими словами, производная от . Поскольку производная константы равна 0, неопределенные интегралы определяются только с точностью до произвольной константы. Например, поскольку производная от . Определенный интеграл от до , обозначаемый , определяется как площадь со знаком между и осью, от до .

Оба типа интегралов связаны между собой основной теоремой исчисления. Это утверждает, что если непрерывно на и является его непрерывным неопределенным интегралом, то . Это означает . Иногда требуется приближение к определенному интегралу. Обычный способ сделать это — поместить тонкие прямоугольники под кривую и сложить подписанные области вместе. Wolfram|Alpha может решать широкий спектр интегралов

Как Wolfram|Alpha вычисляет интегралы

Wolfram|Alpha вычисляет интегралы иначе, чем люди. Он вызывает функцию Integrate из Mathematica, которая представляет собой огромное количество математических и вычислительных исследований. Integrate не вычисляет интегралы так, как это делают люди. Вместо этого он использует мощные общие алгоритмы, которые часто включают очень сложную математику. Есть несколько подходов, которые он чаще всего использует. Один включает в себя разработку общей формы для интеграла, затем дифференцирование этой формы и решение уравнений для соответствия неопределенным символическим параметрам. Даже для довольно простых подынтегральных выражений уравнения, сгенерированные таким образом, могут быть очень сложными, и для их решения потребуются мощные алгебраические вычислительные возможности Mathematica. Другой подход, который Mathematica использует при вычислении интегралов, состоит в том, чтобы преобразовать их в обобщенные гипергеометрические функции, а затем использовать наборы соотношений для этих весьма общих математических функций.

Хотя эти мощные алгоритмы дают Wolfram|Alpha возможность очень быстро вычислять интегралы и обрабатывать широкий спектр специальных функций, важно также понимать, как человек будет интегрировать. В результате Wolfram|Alpha также имеет алгоритмы для пошаговой интеграции. В них используются совершенно разные методы интегрирования, которые имитируют то, как люди подходят к интегралу. Это включает интегрирование подстановкой, интегрирование по частям, тригонометрическую подстановку и интегрирование по неполным дробям.

Калькулятор неопределенных интегралов + онлайн-решатель с бесплатными шагами

Калькулятор неопределенных интегралов — это онлайн-калькулятор, который используется для вычисления неопределенных интегралов различных функций f(x) по отношению к различным переменным. Калькулятор неопределенных интегралов обеспечивает быстрое и точное решение.

Калькулятор неопределенных интегралов — самый эффективный онлайн-калькулятор, потому что он мгновенно выдает результаты, не занимая много времени на обработку. Он также предоставляет подробное решение, чтобы пользователь мог сразу понять концепцию.

Калькулятор неопределенных интегралов также очень прост в использовании, так как позволяет пользователю удобно перемещаться по интерфейсу. Он также обслуживает одну из самых фундаментальных концепций исчисления.

Что такое калькулятор неопределенных интегралов?

Калькулятор неопределенных интегралов — это бесплатный онлайн-калькулятор, который используется для решения неопределенных интегралов относительно определенной переменной. Этот калькулятор может иметь дело со всеми видами функций и обеспечивает быстрые результаты.

Калькулятор неопределенных интегралов используется только для вычисления неопределенных интегралов. Неопределенные интегралы являются ключевым понятием в исчислении, поскольку это интегралы, которые не ограничены какими-либо указанными пределами.

Решение этих неопределенных интегралов всегда дает функцию f(x) вместе с константой c. Общая формула, которую использует калькулятор неопределенных интегралов , приведена ниже:

\[ \int f(x) dx = F(x) + c \]

Где $c$ — константа, полученная после вычисления неопределенного интеграла.

Вручную неопределенные интегралы решаются с помощью различных методов, таких как метод подстановки, метод интегрирования по частям и т. д., но Калькулятор неопределенных интегралов упрощает эту работу, представляя решение за несколько секунд.

Лучшая особенность Калькулятора неопределенных интегралов заключается в том, что он позволяет пользователям вводить любые функции, будь то сложный полином или тригонометрическая функция.

Как пользоваться калькулятором неопределенных интегралов?

Вы можете использовать калькулятор неопределенных интегралов , непосредственно введя функцию, которую нужно интегрировать. Он довольно прост в использовании благодаря простому интерфейсу, который также довольно удобен для пользователя. Интерфейс калькулятора неопределенных интегралов состоит из 2 простых полей ввода, которые предлагают пользователю ввести входные значения.

Первое поле ввода калькулятора неопределенных интегралов помечен «Интегрировать» , что предлагает пользователю ввести функцию, которую он хочет интегрировать. Другими словами, функция f(x) входит в это первое поле ввода.

Второе поле ввода Калькулятора неопределенных интегралов имеет заголовок «относительно» , что позволяет пользователю вводить переменную. Эта переменная является переменной, с которой интегрируется функция.

После двух полей ввода последняя заметная метка из Калькулятор неопределенных интегралов — это кнопка с надписью Вычислить . После того, как пользователь добавил входные данные, все, что ему нужно сделать, это нажать на эту кнопку, чтобы получить желаемое решение.

Для подробного понимания работы Калькулятора неопределенных интегралов ознакомьтесь с пошаговым руководством, приведенным ниже:

Шаг 1

интегралов, первым шагом является анализ данной функции и переменной. Нет ограничений на тип функции или переменной. Вы можете выбрать любую функцию f(x) для вычисления неопределенного интеграла.

Шаг 2

После того, как вы проанализировали свою функцию f(x), следующим шагом будет ввод входных данных. Во-первых, перейдите к первому полю ввода с заголовком «Интеграция» и введите свою функцию f(x) в это поле ввода.

Шаг 3

После заполнения первого поля ввода перейдите ко второму полю ввода. Этот ввод имеет заголовок «Относительно» и введите свою переменную в это поле ввода. Именно по этой переменной интегрируется функция f(x).

Шаг 4

Теперь, когда оба поля ввода заполнены, последний шаг — нажать кнопку с надписью «Рассчитать».  При этом Калькулятор неопределенных интегралов начнет обработку и представит решение через несколько секунд.

Вывод калькулятора неопределенных интегралов

После того, как калькулятор закончил свою обработку, он представляет результат. Результат, представленный Калькулятором неопределенных интегралов состоит из решения неопределенного интеграла вместе с входной интерпретацией неопределенного интеграла с функцией f(x) и переменной.

Как работает калькулятор неопределенных интегралов?

Калькулятор неопределенных интегралов работает путем вычисления неопределенных интегралов для функций f(x). Работа этого калькулятора основана на одной из самых важных концепций исчисления, которая решает неопределенные интегралы.

Чтобы получить четкое представление о работе Калькулятора неопределенных интегралов, давайте кратко повторим предыдущие темы, чтобы укрепить наше понимание работы.

Что такое неопределенные интегралы?

Неопределенные интегралы — это интегралы, вычисляемые без указания пределов. Другими словами, эти интегралы не ограничены ни верхними, ни нижними пределами.

Так как интегрирование является процессом, обратным дифференцированию, то интегрируемая функция является производной, и ее интегрирование даст исходную функцию f(x).

Решение неопределенных интегралов, помимо получения исходной функции f(x), также дает постоянное значение, называемое c. Этот постоянный член с служит основным дифференцирующим фактором между определенными и неопределенными интегралами.

Это потому, что определенные интегралы всегда дают определенный ответ, поскольку эти интегралы ограничены пределами. Тогда как неопределенные интегралы не заключены в пределы, поэтому они дают неопределенный ответ, который представляется как константа интегрирования c.

Примеры решенных задач

Чтобы еще больше улучшить ваше понимание работы калькулятора неопределенных интегралов, ниже приведены несколько примеров.

Пример 1

Для следующей функции вычислите неопределенный интеграл: 9{\frac{2}{3}} \]

При анализе функция f(x) оказывается простой полиномиальной функцией. Так как функция выражается через переменную x, значит, мы будем интегрировать эту функцию f(x) по x.

Следующим шагом является заполнение полей ввода. У нас уже есть функция f(x), поэтому просто вставьте эту функцию f(x) в первое поле ввода. Затем введите переменную во второе поле ввода. Переменная также указана, и это x.

После ввода двух входных значений просто перейдите к кнопке с надписью «Рассчитать» и нажмите на нее. Калькулятор неопределенных интегралов начнет обработку решения. 9{x} \]

Поскольку нет ограничений на тип функции, используемой в качестве входных данных для калькулятора неопределенных интегралов, следовательно, эта функция f(x) идеально подходит.

Эта функция f(x) будет нашим первым входом и войдет в первое поле ввода с заголовком «Интегрировать».

Следующим шагом является заполнение второго поля ввода, которое необходимо заполнить переменной. При анализе функции становится очевидным, что единственная правдоподобная переменная, которую можно использовать для интеграции этой функции, — это x, поэтому вставьте x во второе поле ввода с меткой «В отношении». 9{х}$.

Пример 3

Вычислите неопределенный интеграл для следующей тригонометрической функции:

 f(x) = sin(2x) 

Решение

Сначала давайте проанализируем нашу функцию f(x). Очевидно, что функция f(x) является тригонометрической функцией. Функция приведена ниже:

f(x) = sin(2x)

Далее, для переменной для интегрирования. При анализе функции f(x), поскольку функция выражается через x, пусть переменная интегрирования будет x.

Теперь, когда у нас есть и функция, и переменная, введите их в первый и второй ввод соответственно.

После вставки входных значений нажмите кнопку с надписью «Рассчитать». Калькулятор выдаст следующее решение:

\[ \int sin(2x) dx = -\frac{1}{2} cos(2x) + константа \]

Список математических калькуляторов

Интегральный калькулятор | Лучшая онлайн-интеграция по частям Калькулятор

Введение в интегральный калькулятор

Наш расширенный интегральный калькулятор — это наиболее полное интегральное решение в Интернете, с помощью которого вы можете выполнять множество операций интеграции. Вам нужно ввести функцию, переменную и границы, и все готово.

Калькулятор интегрирования с шагами позволяет изучить принципы расчета интегралов, не тратя слишком много времени. Вы можете вычислить интеграл, используя интегральный калькулятор с шагами, легко онлайн.

Точно так же вы можете найти калькулятор двойного интеграла на этом сайте. Калькулятор двойного интеграла показывает вам графики, графики, шаги и визуальное представление, что помогает вам изучить расширенные концепции двойного интегрирования.

Есть много других полезных калькуляторов, которые можно использовать для получения выгоды. Точно так же вы можете определить объем тела вращения с помощью калькулятора метода шайбы и определить поперечные сечения тела вращения с помощью калькулятора метода диска.

Как решить Интеграция?

Чтобы найти определенный интеграл, вы должны сначала понять, что определенные интегралы имеют начальную и конечную точки, также известные как пределы или интервалы, представленные как (a,b) и расположенные сверху и снизу интеграла.

Мы можем обобщить интегралы на основе функций и областей, через которые выполняется интегрирование. Калькулятор интегрирования по частям с шагами помогает вычислять интегралы в цифровом виде.

Например, линейный интеграл выражается функциями двух или более переменных с заменой интервала интегрирования кривой, соединяющей две точки на интервале.

С другой стороны, есть поверхностный интеграл, где символ заменяет кривую в трехмерном пространстве. 93$$

вычисление границ: 4

-3,4

-12

С другой стороны, неопределенный интеграл отличается от определенного из-за отсутствия у первого определенных пределов.

Неопределенный интеграл, таким образом, вычисляется по формуле:

$$\int f(x)dx$$

Вышеприведенный решатель интегрирования может вычислять неопределенный интеграл и определенный интеграл, но если вы хотите вычислить только неопределенный интеграл, найдите лучший Онлайн-калькулятор неопределенного интеграла.

Связанный: Найдите этот полезный блог, чтобы узнать об определенном интеграле и неопределенном интеграле

Как вычислить неправильный интеграл?

Одна из причин, по которой определенный интеграл становится несобственным, заключается в том, что один или оба предела достигают бесконечности. Калькулятор интегрального исчисления можно использовать для вычисления неправильных интегралов.

Этот интеграл затем решается путем превращения его в проблему пределов, где c случается приближаться к бесконечности или к отрицательной бесконечности. 9c$$

$$\lim_{c\to \infty} [-\frac {1}{c}] -(-\frac{1}{1})]$$

0+1

1

Поскольку ответ на несобственный интеграл конечен, мы считаем его сходящимся.

Если вы хотите вычислить только определенные интегралы, используйте этот лучший пошаговый онлайн-калькулятор определенных интегралов.

Связанный: Используйте калькулятор метода оболочки с шагами, чтобы легко найти объем тела вращения онлайн.

Как рассчитать непрерывную интеграцию?

Основная теорема исчисления устанавливает четкую связь между интегральным и дифференциальным исчислением. Наш интегральный калькулятор с шагами способен вычислить непрерывное интегрирование.

Если f(x) непрерывна для интервала a и b при заданной переменной x и G(x) является функцией в таком смысле, что dG/dx = f(x) для всех значений x в (a,b)

Пусть f непрерывна на интервале ‘y’. Выберите точку p в y, тогда функция f(x) будет определена как:

Пусть F(x) будет следующим 9c f(t)dt$$

Для вашего удобства и углубленного изучения множественных интегралов мы предлагаем один из самых быстрых калькуляторов тройных интегралов. Этот инструмент, несомненно, поможет вам вычислить определенные и неопределенные тройные интегралы онлайн, сделав несколько кликов.

Связанный: Понимание интегрирования неполной дробью за 5 минут!

Что такое интегральный калькулятор?

В течение многих лет существовал только один способ вычислить интегралы — вычисление вручную. В наши дни у нас есть много онлайн-калькуляторов интеграции, чтобы легко рассчитать стоимость интеграции. Большинство студентов обычно имеют прочные теоретические представления об исчислении. Таким образом, вычисление интегралов или производных на самом деле не проблема, когда у нас есть такие калькуляторы, как калькулятор интегрирования или калькулятор производных.

Однако это проблема, когда дело доходит до домашних заданий, когда ученики обычно получают массу задач, требующих решения интегралов. Для получения справки, пожалуйста, прочитайте статью, в которой говорится об интеграции, ее важности и различных методах.

Было бы неразумно повторно вычислять интегралы вручную. Калькулятор определенных интегралов удобен для решения сложных задач интегрирования. Он бесплатный и простой в использовании, и вы получаете ответ почти мгновенно, так как вы можете легко найти интегральный калькулятор с пошаговыми инструкциями в Интернете.

Также используйте другие полезные математические калькуляторы, которые важны для общих процессов интеграции. Подобно калькулятору преобразования Лапласа, вы можете преобразовать интеграл данной производной функции, а калькулятор преобразования Фурье позволяет преобразовать функцию времени в частоту.

Как найти лучший калькулятор интеграции?

В Интернете доступно множество интегральных калькуляторов, например, calculated, symbolab, wolframalpha и другие.

Однако наш интегральный калькулятор объема лучше, быстрее, обладает большей функциональностью и является лучшим калькулятором интеграции с пошаговыми инструкциями, доступными в Интернете. Узнайте о преимуществах использования нашего интегрального онлайн-калькулятора.

Когда вы вводите функцию, переменную, верхнюю и нижнюю границы пределов, наш интегральный решатель вычисляет интеграл и отображает все необходимые шаги, чтобы дать пользователю лучшее понимание вычисления интегрирования.

Вы также можете рассчитать интеграцию по вертикали и интеграцию по горизонтали в области кривых с помощью нашего интегрального онлайн-калькулятора с ограничениями.

Это еще не все. Наш интегральный решатель также отображает антипроизводные вычисления для пользователей, которые могут быть заинтересованы в математической концепции и шагах, связанных с интегрированием.

Кроме того, этот калькулятор интеграции по частям поставляется с визуализацией расчета с помощью интуитивно понятных графиков.

Связанный: Как найти объем тела вращения

Как использовать интегральный калькулятор с шагами?

Пользоваться калькулятором интегрирования по частям легко и быстро.

Выполните следующие шаги:

Шаг 1: Введите функцию

Для вычисления интегралов у вас должна быть правильная функция. Вам нужно ввести свою функцию в функциональную строку калькулятора интеграции. Существует также список «пример загрузки». Вы можете щелкнуть этот список, чтобы загрузить пример уравнения для пошагового расчета интегралов.

Шаг 2: Выберите переменную

Для вычисления интегралов можно использовать три переменные. Этими переменными являются x, y и z. Роль этих трех переменных отличается друг от друга, и все они по-разному влияют на общий результат. Вы можете выбрать переменные как x, y и z из раздела переменных.

Шаг 3: Дайте значение верхней границы

Верхней границей является значение, которое помогает нам суммировать интеграл при его максимальном значении. Верхняя граница обозначается как U, и ее определение имеет решающее значение в процессе интегрирования. Вы можете ввести верхнюю границу своего лимита в разделе верхней границы калькулятора верхней границы.

Шаг 4: Введите значение нижней границы

Нижняя граница — это наименьшее значение, которое мы установили для начала интегрирования. Чтобы получить точные результаты интегрирования, наименьшее значение интервала обозначается буквой L. Чтобы получить точные результаты интегрирования. Вам необходимо ввести фактическую сумму вашего нижнего лимита в разделе нижней границы калькулятора верхней и нижней границ.

После выполнения всех вышеперечисленных шагов Нажмите кнопку «GO».

Сразу после нажатия на кнопку заработает наш интегральный калькулятор. Калькулятор интегрирования по частям покажет вам антипроизводную, интегральные шаги, дерево разбора и график вашего результата. Все эти функции и функции делают его лучшим калькулятором линейного интеграла для вычисления интеграла сложных задач интеграции.

По мере того, как вы вводите данные, под входными данными будет отображаться визуальное уравнение, где вы можете визуализировать, как ваши входные данные будут выглядеть в уравнении.

Часто задаваемые вопросы

Как вычислять интегралы?

Интегралы бывают двух типов: определенные и неопределенные. Вы можете решить их оба путем интеграции. Отличие состоит в том, что в определенных интегралах нужно ставить предельные значения после интегрирования, тогда как в неопределённых интегралах предельные значения ставить не нужно. 93 (1-х) дх \;=\; \left( 3 — \frac{9}{2} \right) \;-\; \влево( -4 -2 \вправо) \;=\; \frac{21}{2} $$

Итак, площадь под данной кривой равна 21/2. Мы можем убедиться в этом, оценив интегральный калькулятор для перекрестной проверки вашего ответа.

Калькулятор интеграла — отличный ресурс для вычислений такого типа, позволяющий сэкономить ваше время.

Чему равен интеграл от 1/x?

Интеграл 1/x is,

$$ \int \frac{1}{x} dx \;=\; ln(x) + c$$

Получайте удовольствие от вычисления интегралов с интегральным онлайн-калькулятором!

∫ Интегральный калькулятор онлайн — с шагами

 

Наверное, никто не станет спорить, что решать математические задачи иногда бывает сложно. Особенно когда речь идет об интегральных уравнениях. Если у вас когда-нибудь возникнут трудности с ними, вы можете использовать этот калькулятор, который предлагает пошаговое решение. Пользоваться онлайн-калькулятором интегралов очень просто, достаточно ввести уравнение, которое необходимо решить. Кроме того, вы можете использовать кнопку по умолчанию, чтобы не тратить время зря. Легко найти ошибки в своих расчетах, когда вы видите каждый шаг процесса. Воспользуйтесь дополнительными опциями калькулятора, если вас не полностью устраивают результаты. Не нужно плакать и нервничать из-за математической задачи. Просто поищите альтернативные решения, такие как этот онлайн-инструмент.

Типы интегралов

Пример:

Определенный интеграл функции f (x) на отрезке [a; б] — предел целых сумм при стремлении диаметра разбиения к нулю, если оно существует независимо от разбиения и выбора точек внутри элементарных отрезков.

Пример:

Собственные и несобственные интегралы

Собственный интеграл – это определенный интеграл, ограниченный как расширенной функцией, так и областью интегрирования.

Пример:

Несобственный интеграл — определенный интеграл, который является неограниченной или расширенной функцией, или областью интегрирования, или и тем, и другим вместе на любом отрезке Пределом интеграла и называется несобственный интеграл первого рода функции а к и

Пособие содержит основы теории некоторых интегралов. Приведены примеры решения типовых задач. Представлено большое количество задач для самостоятельного решения, в том числе варианты индивидуальной расчетной задачи, содержащей ситуационные (прикладные) задачи.
Пособие предназначено для студентов бакалавриата, изучающих дифференциальное и интегральное исчисление функции одной переменной в рамках учебной программы.
    Учебно-методическое пособие предназначено для студентов биомедицинского факультета для оказания помощи в освоении учебного материала, а теоретическая часть учебного материала может рассматриваться как конспект лекций. В работе даны определения основных понятий и формулировки теорем, рабочие формулы и математические выражения, даны практические рекомендации по разбору примеров с целью облегчения усвоения материала и выполнения курсового расчетного задания.

Калькулятор определенных интегралов

Понятие конкретного интеграла и процедура вычисления — интегрирования встречаются в самых разнообразных задачах физики, химии, техники, математической биологии, теории вероятностей и математической статистики. Необходимость использования некоторого интеграла приводит к задаче вычисления площади криволинейной области, длины дуги, объема и массы тела с переменной плотностью, пути, пройденного движущимся телом, работы переменной силы, потенциал электрического поля и многое другое.
      Общим для этого типа задач является подход к решению задачи: большое можно представить как сумму малых, площадь плоской области можно представить как сумму площадей прямоугольников, в которые область мысленно делится, объем как сумма объемов частей, масса тела как сумма масс частей и т. д. .
      Математика обобщает прикладные задачи, заменяя физические, геометрические величины абстрактными математическими понятиями (функцией, размахом или областью интегрирования), исследует условия интегрируемости и дает практические рекомендации по использованию того или иного интеграла.
       Теория некоторого интеграла составляет составную часть раздела математического анализа — интегрального исчисления функции одной переменной.
Вы можете изменить направление. Результатом будет отрицательное выражение исходной функции:

. Если вы рассматриваете целочисленный интервал, который начинается и заканчивается в одном и том же месте, результатом будет 0:

. Вы можете сложить вместе два соседних интервала:

 

Историческая справка

История понятия интеграла тесно связана с проблемами нахождения квадратур, когда задачами квадратуры той или иной плоской фигуры математики Древней Греции и Рима называли задачи по вычислительным областям. Латинское слово «квадратура» переводится как «придание

квадратной формы. Необходимость специального термина объясняется тем, что в древности

действительных чисел, поэтому математики оперировали их геометрическими аналогами или скалярными величинами. Тогда задача нахождения площадей были сформулированы как задача «квадратуры круга»: построить квадрат, изометричный этой окружности.Ученым, предвидевшим понятие интеграла, был древнегреческий ученый Евдокс Книдский, живший около 408-355 гг. до н.э.Он дал полное доказательство теоремы об объемах пирамид, теоремы о том, что площади двух кругов относятся как квадраты их радиусов.Для доказательства он применил метод «исчерпания», который нашел свое применение в трудах его последователей Вслед за Евдоксом методом «исчерпания» и его вариантами вычисления объемов и площадей пользовался античный ученый Архимед.Удачно развивая свои идеи рецессоров, он определил длину окружности, площадь круга, объем и поверхность мяча. Он показал, что определение объема шара, эллипсоида, гиперболоида и параболоида вращения сводится к определению объема цилиндра. Архимед предвосхитил многие идеи интегральных методов, но прошло более полутора тысяч лет, прежде чем они получили четкое математическое оформление и превратились в интегральное исчисление.

 

Основные понятия и теория интегрального и дифференциального исчисления, связанные с операциями дифференцирования и интегрирования, а также их приложения к решению прикладных задач. Теория была разработана в конце 17 века и основывалась на идеях, сформулированных европейским ученым И. Кеплером. Он в 1615 году нашел формулы для расчета объема бочки и для объемов самых разнообразных тел вращения.

 

Для каждого из тел Кеплеру приходилось создавать новые, часто очень хитроумными методами, которые были крайне неудобны. Попытки найти общие, а главное простые методы решения подобных задач и привели к появлению интегрального исчисления, теорию которого И. Кеплер в

разработал в своем сочинении «Новая астрономия», опубликованном в 1609 году.

С помощью этих формул он производит вычисление, эквивалентное вычислению некоторого интеграла:

В 1615 году он написал сочинение «Стереометрия винных бочек, », где правильно рассчитали ряд площадей, например, площадь фигуры, ограниченной эллипсом и объемами, при этом тело было разрезано на бесконечно тонкие пластины. Эти исследования были продолжены итальянскими математиками Б. Кавальери и Э. Торричелли. В 17 веке многие открытия связаны с интегральным исчислением. Так, П. Фарм в 1629 г.

Я рассмотрел задачу возведения в квадрат любой кривой года, нашел формулу их вычисления и на этой основе решил ряд задач по нахождению центров тяжести. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования. И. Барроу,

учитель Ньютона, вплотную подошел к пониманию связи интегрирования и дифференцирования. Большое значение имели работы английских ученых по представлению функций в виде степенных рядов.

Немецкий ученый Г. Лейбниц одновременно с английским ученым И. Ньютоном разработал в 80-х годах 17 века основные принципы дифференциального и интегрального исчисления. Теория набрала силу после того, как Лейбниц и Ньютон доказали, что дифференцирование и интегрирование — взаимно обратные операции. Это свойство хорошо знал Ньютон, но только Лейбниц видел здесь ту замечательную возможность, которая открывает применение символического метода.

Интеграл Ньютона или «беглый» предстал, прежде всего, как неопределенный, т. е. как первообраз. Понятие интеграла у Лейбница выступало, напротив, прежде всего в виде определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, по которым разбивается та или иная величина. Введение понятия интеграла и его обозначений Г. Лейбницем относится к осени 1675 г. Знак интеграла был опубликован в статье Лейбница в 1686 г. Термин «интеграл» впервые в печати был использован Швейцарский ученый Ж. Бернулли в 169 г.0. Затем

вошло в обиход и выражение «интегральное исчисление», до этого Лейбниц говорил о «суммирующем исчислении». Вычисление интегралов производили Г. Лейбниц и его ученики, первыми из которых были братья Якоб и Иоганн Бернулли. Они свели вычисление к операции, обратной операции дифференцирования

, т. е. к нахождению первообразных. Постоянная интеграция в печати появилась в статье Лейбница в 1694 году.

Проблема:

Решение:

Вот краткое и простое объяснение природы интегралов для лучшего понимания подобных математических задач.

Интеграл является результатом непрерывного суммирования бесконечно большого числа бесконечно малых членов. Интегрирование функции принимает бесконечно малые приращения ее аргументов и вычисляет бесконечную сумму приращений функции на этих участках. В геометрическом смысле интеграл от двумерной функции в некотором сечении удобно представлять как площадь фигуры, замкнутой между графиком этой функции, осью X и прямыми, соответствующими выбранный интервал перпендикулярен ему.

Пример: Интегрирование функции Y = X² на интервале от X = 2 до X = 3. Для этого нужно вычислить первообразную интегрируемой функции и взять за концы разность ее значений интервала.
X³/3 в точке X=3 занимает 9, а в точке X=2 имеем 8/3. Следовательно, значение нашего интеграла равно 9 — 8/3 = 19/3 ≈ 6,33.

Интегральный калькулятор отзывы покупателей

Час идти до зачета и я не понял 🙁 …

Добавлены примеры решения интегралов. Спасибо за комментарий.

Спасибо за статью, в учебниках такая чушь написана! Мол, вот, напиши сюда и все понятно, вот тебе все решение, без объяснений! По крайней мере, теперь я понимаю, что все такие интегралы, т. е. суть понята. А стол очень хороший, полный.

Тут все понятно, нужно посидеть и подумать. А попробуйте решать задачи по физике с интегралами… В частности теоретические основы электротехники, там можно про излучение и оптику загнуть вообще молчу :)))) (

Большое человеческое Спасибо.. Учебники не понятные и все понятно написано доступным языком.

спасибо большое оч помогло пока читал не понял что это такое и как решать=)

примеры решения интегралов добавил. статья немного расширена.

Спасибо за статью, такую ​​чушь в учебниках пишут! Типа, пиши сюда soE, тут все понятно, вот тебе и все решение, без объяснений! теперь я хотя бы понял, что такое интегралы вообще, т.е. понял суть. А стол очень хороший, полный. 93). Интегрируемая функция та же. Интеграл в таком виде вычислять не надо — просто выпишите.

Пишу по просьбе моей подруги, настоящее имя которой не указываю по ее просьбе пусть будет условно Лиза. У Лизы дела с пространственным воображением плохи (и не только), поэтому, столкнувшись с темой «Геометрические приложения одного интеграла» в своем университете, Лиза конкретно загрузилась, в смысле, загрустила, потому что даже не заплакала . В связи с описанной выше ситуацией у меня вопрос: в какой книге в наиболее доступной форме изложена тема «Геометрические приложения одного интеграла»?
Заранее спасибо за исчерпывающий ответ.

Каков метод сравнения для определения сходимости несобственных интегралов?

Какие физические задачи сводятся к вычислению определенных или неправильных интегралов?

У вас есть инструкция по использованию интегрального калькулятора?

Большое спасибо! Буду рекомендовать другим продолжать пользоваться вашими сайтами

Этот калькулятор спас мою задницу на экзамене 🙂

Последнее обновление: четверг, 10 сентября 2020 г., 15:58

Интегральный калькулятор | Лучший интегральный калькулятор

Определение интегрального калькулятора

Интегральный калькулятор представляет собой математический инструмент, который позволяет легко вычислять интегралы . Интегральный онлайн-калькулятор обеспечивает быстрый и надежный способ решения различных интегральных задач. онлайн-калькулятор интеграции и его процесс отличается от обратного производный калькулятор, поскольку эти два являются основными понятиями исчисления.

Что такое интеграция?

Интегрирование находит дифференциальное уравнение математических интегралов. Интегральная функция дифференцирует и вычисляет площадь под кривой графика.

Определение интеграла помогает найти площадь, центральную точку, объем и т. д. Онлайн-калькулятор интегрирования определение интеграла для нахождения площади под кривой следующим образом:

Где

F(x) — функция, а

А — площадь под кривой.

Что такое Integrand в калькуляторе интеграции?

Интегранд является интегралом уравнения или формулы интегрирования, она обозначается как функция f(x). В калькуляторе интеграции вам нужно будет ввести значение, чтобы оно работало правильно.

Как интегральный калькулятор взаимодействует с интегральной записью?

Для интегрального уравнения

∫ 2x dx

∫ — символ интеграла, а 2x — функция, которую мы хотим интегрировать.

В этом интегральном уравнении dx является дифференциалом переменной x. Он подчеркивает, что переменная интеграции равна x. dx показывает направление вдоль оси x, а dy показывает направление вдоль оси y.

Интегральные символы и интегральные правила используются калькулятором интегралов для быстрого получения результатов.

Как вычислить интеграл?

Мы можем вычислить функцию за несколько простых шагов. Сначала разделите площадь на срезы и сложите ширину этих срезов с Δx. Тогда ответ будет не точен. (см. рис. 1)

Если сделать Δx много меньшей ширины и сложить все эти маленькие кусочки, то точность ответа станет лучше. (см. рисунок 2)

Если ширина срезов приближается к нулю, то ответ приближается к истинному или фактическому результату. Итак,

Теперь мы говорим, что dx означает, что срезы Δx приближаются к нулю по ширине.

Обратите внимание, что интеграл является обратной производной

Вычисляет ли калькулятор интегралов определенный интеграл и неопределенный интеграл?

Этот онлайн-калькулятор интегрирования позволит вам вычислять определенные интегралы и неопределенные интегралы. Вам просто нужно указать значения в поле ввода. Определенный интеграл имеет как начальное значение, так и конечное значение. Интеграл исчисления функции f(x) представляет собой площадь под кривой от x = a до x = b.

Неопределенный интеграл не имеет верхнего предела и нижнего предела функции f(x). Неопределенный интеграл также известен как первообразная.

Узнайте, как найти предел функциональности здесь.

Как вычислить двойные интегралы?

Одной из трудностей при вычислении двойных интегралов является определение пределов интегрирования. Пределы интегрирования в порядке dxdydxdy необходимы для определения пределов интегрирования для эквивалентного интегрального порядка dydxdydx.

Сложность вычисления двойных интегралов заключается в определении пределов интегрирования. Пределы интегрирования в порядке dxdydxdy определяют пределы интегрирования для целочисленного порядка dydxdydx.

Предоставляет ли интегральный калькулятор шаги?

Наш калькулятор интегрального исчисления предоставляет вам шаги, чтобы вы могли увидеть, как был рассчитан ваш запрос. Вы можете еще больше расширить свои знания и понимание, просматривая пошаговый ответ.

Этот интегральный решатель очень эффективен для сложных задач интеграции, поскольку он обеспечивает быстрый ответ на сложные проблемы интеграции и решения.

Используйте калькулятор площади сектора, чтобы еще больше укрепить свои математические понятия, связанные с вычислением площади.

Как найти лучший интегральный калькулятор?

Расчетный имеет лучший калькулятор частных интегралов с точки зрения точности, скорости и результатов. Калькуляторные методы интегрального исчисления могут быть разными, но методы и концепции остаются теми же. Вы можете выполнить поиск по запросу calculateed или найти наш интегральный онлайн-калькулятор в Google.

Как использовать интегральный калькулятор с шагами?

Для базовых примеров интеграции и решений очень эффективен калькулятор линейного интеграла. Калькулятор интеграции по частям прост и удобен в использовании. Все, что вам нужно сделать, это выполнить следующие шаги:

Шаг #1: Заполните интегральное уравнение, которое вы хотите решить.

Шаг №2: Выберите переменную как X или Y.

Шаг №3: Введите значение верхней границы.

Шаг №4: Введите значение нижней границы.

Шаг № 5: Нажмите кнопку «РАССЧИТАТЬ».

После того, как вы выполните указанные выше шаги и нажмете кнопку расчета, онлайн-калькулятор интеграции с шагами немедленно решит интеграл по частям. Вы увидите результаты антипроизводной, интегральных шагов, дерева синтаксического анализа и график результата.

Вы также можете заполнить примеры интегралов для решения интегралов для практики. Мы надеемся, что вы найдете полезную информацию об интегралах и их вычислениях.

Пожалуйста, оставьте свой ценный отзыв ниже. Удачи вам в обучении и расчетах. Ваше здоровье! 92 + x + 1}dx}$ это из предыдущих задач)

Как это выглядит? Сделал ли я что-то серьезно неправильное (я не совсем уверен в части дробей)? Любые предложения о том, как я мог бы получить ответ быстрее или эффективнее?

неопределенные интегралы

$\endgroup$

1

$\begingroup$

Я думаю, что мы могли бы сделать это проще, не используя комплексные числа.

No related posts.