Решение неравенств онлайн с параметром: Решение неравенств любого вида | Онлайн калькулятор

Содержание

Уравнения и неравенства с параметрами. 11 класс

Похожие презентации:

Уравнения и неравенства с параметрами

Дробно–линейные уравнения и неравенства с параметрами

Целое уравнение с параметром

Уравнения и неравенства с параметрами. Часть 1

Решение уравнений и неравенств, содержащих переменную под знаком модуля

Уравнения и неравенства. 11 класс

Уравнения и неравенства с двумя переменными, содержащие параметр

Неравенства. Линейные неравенства. Квадратные неравенства

Решение неравенств методом интервалов

Линейные неравенства. Квадратные неравенства

Под уравнением с параметром, обычно принято понимать,
уравнение вида f(x;a)=0, где х – переменная, относительно которой
надо решить уравнение, а – произвольное действительное число,
параметр.
Трудностей при решении уравнений с параметрами довольно
много, так как в зависимости от параметра уравнение может принимать
совершенно разный вид.

Так, при одном значении параметра уравнение может не иметь
решений, при другом бесконечно много решений, при третьем значении
решаться одним способом, при четвертом совершенно другим. Мы
постараемся разобрать основные принципы, которыми следует
руководствоваться при решении уравнений.
Пример. Решить относительно х:
а) 3а(а-3)х = а-3
б) 3а(а-3)х > а-3
Решение.
а) Нам с вами дано обычное линейное уравнение, решается
которое довольно просто, число в правой части уравнения делим на
коэффициент при х в левой части уравнения.
В правой части уравнения число равняется а-3.
В левой части уравнения коэффициент при х равен 3а(а-3).
Тогда решение в общем виде будет
, но параметр а
может принимать любые значения. Мы прекрасно знаем, что на ноль
делить нельзя, тогда 3а(а-3)≠0, что означает а≠0 и а≠3.
То есть мы получили, при а=0 и а=3 – решений нет, так как на
ноль делить нельзя.
При всех остальных значениях параметра а,

б) Нам так же дано обычное линейное неравенство.

В этом
случае нам стоит учесть еще одно условие. В зависимости от знака
коэффициента при х, мы меняем, либо не меняем знак неравенства, при
делении на этот коэффициент.
В этот раз рассмотрим случаи:
1. a=0 2. a=3 3. а<0 4. 0<a<3
5. a>3
1. a=0 В этом случае неравенство принимает вид 0·х>-3, которое
выполняется при любых х.
2. a=3 В этом случае неравенство принимает вид 0·х>0, которое
не имеет решений.
3. а<0 Коэффициент 3а(а-3) положителен, значит, при делении на
этот коэффициент, знак неравенства остается прежним, тогда решением
в этом случае будет
4. 0<a<3 В этом случае, коэффициент отрицателен, тогда нам
следует знак неравенства сменить на противоположный,
5. a>3 Коэффициент 3а(а-3) положителен, значит, при делении на
этот коэффициент, знак неравенства остается прежним, тогда решением
в этом случае будет
. Пункты 3 и 5 можно объединить в один при
записи в ответ.
Ответ: а) Уравнение не имеет решений при а=0 и а=3.

При всех
других а решением уравнения будет
б) При а=0, неравенство выполняется при любых х.
Если а=3, то решений нет.
Если а<0 и a>3,
Если 0<a<3,
Пример. Решить уравнение:
Решение.
При решении квадратных уравнений с параметром, как правило,
следует рассматривать два случая:
1. коэффициент при старшей степени равен нулю.
2. коэффициент при старшей степени не равен нулю.
Рассмотрим первый случай. При а=2, наше уравнение принимает
вид обычного линейного уравнения:
Перейдем ко второму случаю, найдем дискриминант нашего

уравнения:
Дальше следует рассуждать о знаке дискриминанта.
а) При D<0, корней уравнения нет. В нашем случае, при а<-1 –
решений нет.
б) При D=0, один корень. В нашем случае, при а=-1 – одно
решение. Найдем это решение
в) При D>0, два корня уравнения. В нашем случае, при а>-1 –
два решения.
Ответ:
При а=2, х=-0,5. При a<-1 – решений нет.
При а=-1, х=0.

При а>-1,
Пример. Решить уравнение:
Решение. Начнем с обычного действия, возведем обе части
уравнения в квадрат.
Найдем дискриминант данного уравнения.
Перейдем к рассмотрению трех возможных случаев:
Осталось выполнить проверку полученных корней, но проверка
таких корней, представляет собой довольно таки сложную операцию.
Давайте построим два графика функции и найдем их точки пересечения.
Рассмотрим три случая для значений параметра а:
а. а=0 б. a<0 в. a>0
а. При а=0, графики выглядят следующим образом
Графики пересекаются в
одной точке А(0;0), значит
уравнение имеет одно
решение х=0.
б. При a<0, график корня квадратного сместится вправо на а
единиц, а график линейной функции сместится на а единиц вниз. Как
видно из схематичного рисунка, наши графики не могут пересечься,
значит, корней нет.
в. При a>0, графики функций пересекаются в одной точке. Выше
мы получили два возможных корня уравнения, нам нужно выбрать один
из этих корней удовлетворяющий графику ниже.

Мы можем заметить, что абсцисса точки пересечения больше
нуля, но меньше чем а/2.
Проверим наши корни
Для уверенности в правильности решения проверим второй
корень.
Ответ: При а=0, х=0.
При а<0, решений нет.
Задачи для самостоятельного решения.
1. Решить относительно х:

а) 5а(а-4)х = а-4
б) 5а(а-4)х < а-4
2. Решить уравнение:
3. Решить уравнение:

English Русский Правила

Тригонометрические неравенства с параметром с решением примеров

п.1. Примеры

Пример 1. Решите неравенства:

a) \(sinax\gt\frac12\) \begin{gather*} \frac\pi6+2\pi k\lt ax\lt\frac{5\pi}{6}+2\pi k \end{gather*} При \(a=0\) решений нет.
При \(a\lt 0:\ \frac{\pi}{6a}+\frac{2\pi k}{a}\gt x\gt \frac{5\pi}{6a}+\frac{2\pi k}{a}\)
При \(a\gt 0:\ \frac{\pi}{6a}+\frac{2\pi k}{a}\lt x\lt \frac{5\pi}{6a}+\frac{2\pi k}{a}\)

Ответ:
При \(a=0\) решений нет, \(x\in\varnothing\)
При \(a\lt 0,\ x\in\left(\frac{5\pi}{6a}+\frac{2\pi k}{a};\ \frac{\pi}{6a}+\frac{2\pi k}{a}\right). \)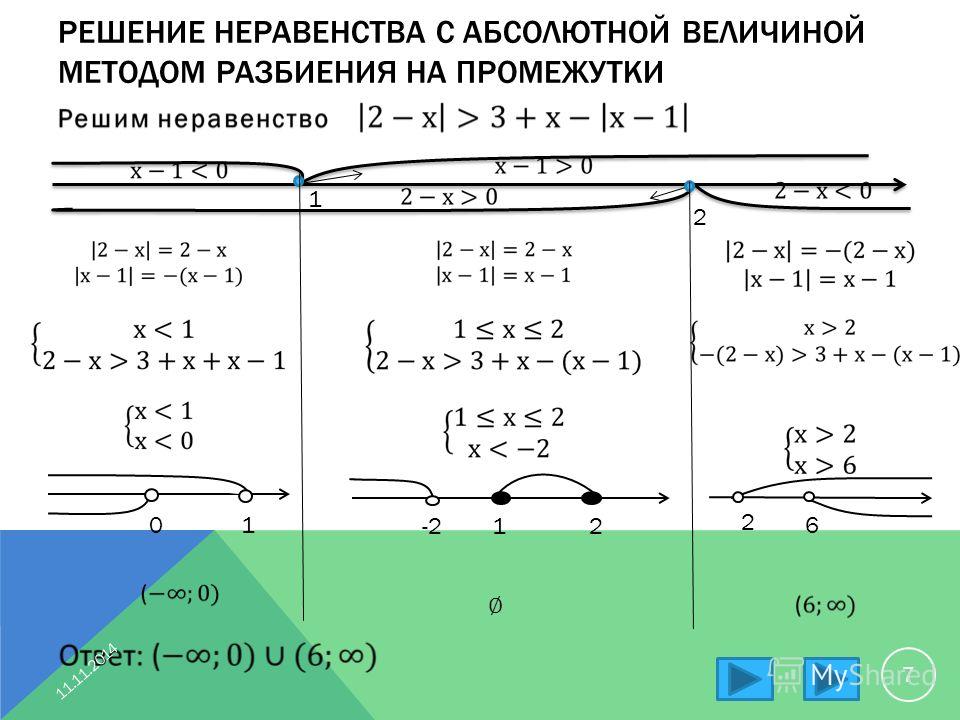
При \(a\gt 0,\ x\in\left(\frac{\pi}{6a}+\frac{2\pi k}{a};\ \frac{5\pi}{6a}+\frac{2\pi k}{a}\right)\)

б) \(tg(ax+3)\geq 5\)
\(arctg5+\pi k\leq ax+3\lt\frac\pi2+\pi k\Rightarrow arctg5 -3+\pi k\leq ax\lt \frac\pi2-3+\pi k\)

При \(a=0\) необходимо, чтобы: \begin{gather*} \begin{cases} arctg5-3+\pi k\leq 0\\ \frac\pi2-3+\pi k\gt 0 \end{cases} \Rightarrow \begin{cases} k\leq \frac{3-arctg5}{\pi}\lt 0,52\\ k\gt\frac3\pi-\frac12\gt 0,44 \end{cases} \Rightarrow 0,44\lt k\lt 0,52 \end{gather*} Т.к. \(k\) — целое, решений нет.
При \(a\lt 0:\ \frac{arctg5-3}{a}+\frac{\pi k}{a}\geq x\gt \frac{\frac\pi2-3}{a}+\frac{\pi k}{a}\)
При \(a\gt 0:\ \frac{arctg5-3}{a}+\frac{\pi k}{a}\leq x\lt \frac{\frac\pi2-3}{a}+\frac{\pi k}{a}\)
Ответ:
При \(a=0\) решений нет, \(x\in\varnothing\)
При \(a\lt 0,\ x\in\left.\left(\frac{\frac\pi2-3}{a}+\frac{\pi k}{a};\ \frac{arctg5-3}{a}+\frac{\pi k}{a}\right.\right]\)
При \(a\gt 0,\ x\in\left.\left[\frac{arctg5-3}{a}+\frac{\pi k}{a};\ \frac{\frac\pi2-3}{a}+\frac{\pi k}{a}\right.

2+7}=\frac78,\ x=\pi k \end{gather*} Откуда: \(a\gt\frac78\)

Ответ: \(a\in\left(\frac78;+\infty\right)\)

Пример 3. Найдите \(a\), при которых система имеет единственное решение:
a) \begin{gather*} \begin{cases} (tgx-1)(x+a)=0\\ |x|\lt 1 \end{cases} \end{gather*} Решаем уравнение: \begin{gather*} (tgx-1)(x+a)=0\Rightarrow \left[ \begin{array}{l l} tgx=1\\ x=-a \end{array} \right. \Rightarrow \left[ \begin{array}{l l} x=\frac\pi4+\pi k\\ x=-a \end{array} \right. \end{gather*} Пусть единственным решением будет \(x=\frac\pi4+\pi k\). Тогда, учитывая \(|x|\lt 1\), исключаем второе решение: \begin{gather*} \begin{cases} x=\frac\pi4+\pi k\\ |x|\lt 1\\ |-a|\geq 1 \end{cases} \Rightarrow \begin{cases} x=\frac\pi4\\ |a|\geq 1 \end{cases} \end{gather*} Также, решения совпадают, если: \begin{gather*} a=-\frac\pi4:\ \begin{cases} tgx=1\\ x=\frac\pi4\\ |x|\gt 1 \end{cases} \Rightarrow x=\frac\pi4 \end{gather*} При других \(a\) решений будет два.
Ответ: \(a\in\left.\left(-\infty;-1\right.

2-5a-2=0\Rightarrow (3a+1)(a-2)=0 \Rightarrow \left[ \begin{array}{l l} a=-\frac13\\ a=2 \end{array} \right. \end{gather*}

При \(a=-\frac13\) вершина \(x_0=\frac13.\)
Единственное решение \(\left(\frac13,\ \pi-arccos\frac35\right)\)

При \(a=2\) вершина \(x_0=-2.\)
Единственное решение \(\left(-2,\ \pi-arccos\frac35\right)\)

При других значениях \(a\) парабола либо поднимается выше уровня 5, и тогда система не имеет решений; либо опускается ниже уровня 5, и тогда система имеет бесконечное множество решений.

Ответ: \(a=-\frac13\), единственное решение \(\left(\frac13,\ \pi-arccos\frac35\right)\)
\(a=2\), eдинственное решение \(\left(-2,\ \pi-arccos\frac35\right)\)

Неравенства типа Ляпунова для краевых задач второго порядка с параметром

На этой странице проблемы со значением параметра. Неравенства обобщают некоторые ранние результаты в литературе.

1. Введение

До сих пор интегральные неравенства привлекали внимание многих исследователей в связи с их широким применением при исследовании качественных и количественных свойств, таких как существование в целом, ограниченность и устойчивость дифференциальных и интегральных уравнений (см. [1–26] и ссылки в них). Среди этих неравенств важным видом является неравенство типа Ляпунова, которое первоначально было представлено Ляпуновым в [27] следующим образом.

Если есть решение удовлетворяющих и для , то и впоследствии по Винтнеру [28] как где .

Вслед за эпохальной работой Ляпунова появилось множество ссылок, посвященных неравенству типа Ляпунова и его обобщениям, которые широко используются в различных задачах, таких как асимптотическая теория, неосцилляция и задачи на собственные значения дифференциальных уравнений и разностных уравнений (см. [29] –41] и ссылки в нем).

Например, в 2003 г. Ян [29] получил следующий результат для полулинейного уравнения второго порядка: где такие, что , для и .

Теорема 1. (см. [29]). Предположим, что краевая задача (4) имеет решение ; тогда имеет место следующее неравенство: где .
В 2012 г. Tiryaki et al. В [34] установлено неравенство для краевой задачи вида где и . Их результат таков.

Теорема 2. (см. [34]). Предположим, что краевая задача (6) имеет решение ; тогда имеет место следующее неравенство: где , , и .

В 2015 г. Agarwal et al. В [36] установлено неравенство типа Ляпунова для вынужденной краевой задачи второго порядка вида: в субполулинейном и суперполулинейном случаях, где и интегрируемы на с на . Их результат таков.

Теорема 3. (см. [36]). Пусть , , — последовательные нули нетривиального решения первой части уравнения (8), тогда имеет место неравенство, где и .

Агарвал и Озбеклер [36] также установили неравенство типа Ляпунова для вынужденной краевой задачи второго порядка со смешанными нелинейностями: где . Результат следующий.

Теорема 4. (см. [36]). Предположим, что , , – последовательные нули нетривиального решения первой части уравнения (10), тогда имеет место неравенство, где и .

Находим, что в [36] авторы изучали случай уравнения (10). Будет интересно доказать неравенства типа Ляпунова для уравнения (10) или другого уравнения, когда α и γ имеют другое соотношение. Руководствуясь [36], в настоящей работе установим неравенство типа Ляпунова для нелинейной краевой задачи второго порядка вида где такое, что , , при , , и – вещественный параметр, а с краевым условием (13) , где такие, что , , для , , и является действительным параметром. Наши результаты расширяют и дополняют результаты работы [29]., 36].

2. Основные результаты

Лемма 1. Если u является дифференциальным на [a, b] удовлетворяющим и для , то

Доказательство. Так как u является дифференциалом на [ a , b ] удовлетворяющим , то имеем So, Следовательно, (15) выполняется.

Лемма 2. (см. [13]). Пусть и будет дано. Тогда для каждого выполняется .

Теорема 5. Пусть u есть решение уравнения (12), удовлетворяющее граничным условиям (13). Тогда где .

Доказательство. Умножая (12) на и интегрируя по , получаем: Интегрируя по частям до первого интеграла в левой части (20) и из (13), имеем Тогда получаем, т. е. используя неравенство Гёльдера с индексов ,с , получаем, что т. е., наоборот, из леммы 1 получаем Тогда из (23), (26) и (27) получаем Для первого интеграла в правой части (28 ), из неравенства (18) в лемме 2 при , , и для следует, что В силу (28) и (29) получаем Из леммы 1 имеем Ввиду (30) и (31) получаем, что Поскольку (действительно, если , имеем для В силу условия (13) получаем для , что противоречит , ), деля обе части (32) на , получаем, что также приводит к (19). Доказательство завершено.
Если взять и в неравенстве (19), то получим следующий результат.

Следствие 1. Пусть u есть решение уравнения, удовлетворяющее граничному условию (13). Тогда где .

Теорема 6. Пусть u есть решение уравнения (14), удовлетворяющее граничному условию (13). Тогда где .

Доказательство. Умножая (14) на и интегрируя по выходам. Используя интегрирование по частям к первому и второму интегралам в левой части (37) и из (13), имеем, т. е. Используя неравенство Гёльдера (24) при , получаем, что, т. е. из (26), (39), (41) и леммы 1, получаем Для правой части (42) неравенство (18) в лемме 2 с , , и следует, что Из (27), (42) и (43) имеем Таким образом , разделив обе части (29) на , получим, что также приводит к (36). Доказательство завершено.

Замечание 1. Отметим, что при , и (5) можно получить из теорем 5 и 6 соответственно.
Если взять и в неравенстве (36), то получим следующий результат.

Следствие 2. Пусть u есть решение уравнения, удовлетворяющее граничному условию (13). Тогда где .

Теорема 7. Пусть u — решение уравнения (14), удовлетворяющее граничному условию (13). Тогда, где , и .

Доказательство. Из доказательства теоремы 6 имеем (39). В силу (39) и леммы 1 получаем. Используя неравенство Гёльдера (24) с соответственно, получаем, что Таким образом, из (49), (51) и (52) имеем Для правой части (53) неравенство (18) в лемме 2 при , , и следует, что Из (53) и (54) имеем Таким образом, разделив обе части (55) на , получим, что также приводит к (48). Доказательство завершено.

Замечание 2. Отметим, что при , и классический результат (3) можно получить из теорем 5–7 соответственно.
Если взять и в неравенстве (48), то получим следующий результат.

Следствие 3. Пусть u — решение уравнения (46), удовлетворяющее граничному условию (13). Тогда, где , и .

Доступность данных

Данные не использовались для поддержки этого исследования.

Конфликт интересов

Автор заявляет об отсутствии конфликта интересов в связи с публикацией данной статьи.

Благодарности

Это исследование было поддержано Фондом естественных наук провинции Шаньдун (Китай) (№ ZR2018MA018) и Национальными фондами естественных наук Китая (№ 11671227 и 61873144).

Ссылки

Х. Д. Лю, «О некоторых нелинейных интегральных неравенствах типа Вольтерра-Фредгольма с запаздыванием во временных масштабах и их приложениях», Journal of Inequalities and Applications , vol. 2018, с. 211, 2018.
Просмотр:
Сайт издателя | Google Scholar
Д. Л. Чжао, С. Л. Юань и Х. Д. Лю, «Стохастическая динамика хемостата замедленного действия с шумами Леви», International Journal of Biomathematics , vol. 12, нет. 5, ID статьи 1950056, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Лю, Ф. Менг и П. Лю, «Колебания и асимптотический анализ нового обобщенного уравнения Эмдена-Фаулера», Прикладная математика и вычисления , том. 219, нет. 5, стр. 2739–2748, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
HD Liu и CQ Ma, «Критерии колебаний для динамических уравнений с нейтральным запаздыванием второго порядка с нелинейностями, заданными интегралами Римана-Стилтьеса», Abstract and Applied Analysis , vol. 2013 г., идентификатор статьи 530457, 9 страниц, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Э. Тунч и Х. Д. Лю, «Колебательное поведение для затухающего дифференциального уравнения второго порядка с нелинейностями, включая интегралы Римана-Стилтьеса», Электронный журнал дифференциальных уравнений , том. 2018, нет. 54, 2018.
Просмотр по адресу:
Google Scholar
Х. Д. Лю и Ф. В. Мэн, «Существование положительных периодических решений для системы хищник-жертва функциональной реакции типа IV Холлинга с взаимными помехами и импульсными эффектами», Дискретная динамика в природе и обществе , том. 2015 г., идентификатор статьи 138984, 12 страниц, 2015 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
Д. Чжао и Х. Лю, «Сосуществование в модели хемостата двух видов с марковскими переключениями», Applied Mathematics Letters , vol. 94, стр. 266–271, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю и Ф. В. Менг, «Некоторые новые обобщенные неравенства дискретных дробных сумм типа Вольтерра-Фредгольма и их приложения», Journal of Inequalities and Applications , vol. 2016, нет. 1, с. 213, 2016.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю и К. К. Инь, «Некоторые обобщенные динамические интегральные неравенства типа Вольтерра-Фредгольма с двумя независимыми переменными в парах шкалы времени», Advances in Difference Equations , vol. 2020, нет. 1, с. 31, 2020.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Гу и Ф. Менг, «Некоторые новые нелинейные динамические интегральные неравенства типа Вольтерра-Фредгольма во временных масштабах», Прикладная математика и вычисления , том. 245, стр. 235–242, 2014.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю и Ф. В. Мэн, «Нелинейные запаздывающие интегральные неравенства во временных масштабах и их приложения», Journal of Mathematical Inequalities , vol. 12, нет. 1, стр. 219–234, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Б. Чжан, Дж. С. Чжуан, Х. Д. Лю, Дж. Д. Цао и Ю. Х. Ся, «Главная-ведомая синхронизация класса нечетких нейронных сетей Такаги-Сугено дробного порядка», Успехи в разностных уравнениях , vol. 2018, с. 473, 2018.
Посмотреть по адресу:
Сайт издателя | Google Scholar
HD Liu, CY Li, and FC Shen, «Класс новых нелинейных динамических интегральных неравенств, содержащих интегрирование на бесконечном интервале во временных масштабах», Advances in Difference Equations , vol. 2019, с. 311, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю и К. К. Ма, «Критерии колебаний динамических уравнений с запаздыванием четного порядка с нелинейностями, заданными интегралами Римана-Стилтьеса», Реферативный и прикладной анализ , том. 2014 г., идентификатор статьи 395381, 8 страниц, 2014 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Чжао, «Исследование на пороге стохастической модели эпидемии SIR и ее расширений», Communications in Nonlinear Science and Numerical Simulation , vol. 38, стр. 172–177, 2016.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю, «Класс запаздывающих интегральных неравенств типа Вольтерра-Фредгольма на шкалах времени и их приложения», Журнал неравенств и приложений , том. 2017, с. 293, 2017.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Л. Чжао, С. Л. Юань и Х. Д. Лю, «Случайное периодическое решение для стохастической модели эпидемии SIS с постоянным размером населения», Advances in Difference Equations , vol. 2018 г., идентификатор статьи 64, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю и Ф. В. Менг, «Критерии интервальных колебаний для нелинейных вынужденных дифференциальных уравнений второго порядка с переменным показателем», Успехи в разностных уравнениях , vol. 2016 г., идентификатор статьи 291, 2016 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Д. Чен, К. И. Коу и Ю. Х. Ся, «Линейные динамические уравнения с кватернионными значениями во временных масштабах», Journal of Applied Analysis and Computation , vol. 8, стр. 172–201, 2018.
Посмотреть по адресу:
Google Scholar
Х. Д. Лю, «Некоторые новые интегральные неравенства со смешанными нелинейностями для разрывных функций», Успехи в разностных уравнениях , vol. 2018 г., идентификатор статьи 22, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ф. Мэн и Дж. Шао, «Некоторые новые динамические интегральные неравенства типа Вольтерра-Фредгольма во временных масштабах», Applied Mathematics and Computation , vol. 223, стр. 444–451, 2013.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю, «Некоторые новые полулинейные интегральные неравенства во временных масштабах и приложениях», Дискретная динамика в природе и обществе , том. 2019 г., идентификатор статьи 9860302, 9 страниц, 2019 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ю. Ся, Л. Чен, К. И. Коу и Д. О’Реган, «Гельдеровость теоремы Гробмана-Хартмана для динамических уравнений в цепочках мер», Бюллетень Малазийского общества математических наук , об. 41, нет. 3, стр. 1153–1180, 2018.
Посмотреть по адресу:
Сайт издателя | Академия Google
Х. Д. Лю и Ф. В. Мэн, «Некоторые новые нелинейные интегральные неравенства со слабо сингулярным ядром и их приложения к FDE», Journal of Inequalities and Applications , vol. 2015, с. 209, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
HD Liu и PC Liu, «Критерии колебаний для некоторых новых обобщенных динамических уравнений Эмдена-Фаулера во временных масштабах», Abstract and Applied Analysis , vol. 2013 г., статья ID 962590, 16 страниц, 2013 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
HD Liu, «Полулинейные интегральные неравенства типа Вольтерра-Фредгольма на шкалах времени и их приложения», Journal of Applied Analysis and Computation , vol. 10, нет. 2020. Т. 1. С. 234–248.3)», Annales de la Faculté des Sciences de Toulouse , vol. 2, стр. 27–247, 1907.
Посмотреть по адресу:
Google Scholar
А. Винтнер, «Об отсутствии сопряженных точек», American Journal of Mathematics , vol. 73, нет. 2, стр. 368–380, 1951.
Посмотреть по адресу:
Сайт издателя | Google Scholar
XJ Yang, «О неравенствах типа Ляпунова», Applied Mathematics and Computation , vol. 134, нет. 2-3, стр. 293–300, 2003.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. П. Пинаско, «Нижние оценки собственных значений одномерного p-лапласиана», Abstract and Applied Analysis , vol. 2004, нет. 2, стр. 147–153, 2004 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
C.-F. Ли, К.-К. Да, К.-Х. Хонг и Р. П. Агарвал, «Неравенства Ляпунова и Виртингера», Applied Mathematics Letters , vol. 17, нет. 7, стр. 847–853, 2004.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Машиев Р. А., Алисой Г., Ограс С. Неравенства Ляпунова, Опиала и Бисека для одномерных уравнений p(t)-лапласиана, Applied Mathematics and Computation , vol. 216, нет. 12, стр. 3459–3467, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ван Ю. Неравенства типа Ляпунова для некоторых дифференциальных уравнений высших порядков с антипериодическими краевыми условиями, Письма по прикладной математике , том. 25, нет. 12, стр. 2375–2380, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Тиряки, Д. Чакмак и М. Ф. Актас, «Неравенства типа Ляпунова для определенного класса нелинейных систем», Computers & Mathematics with Applications , vol. 64, нет. 1, стр. 1804–1811, 2012.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Лю Х. Д. Неравенства типа Ляпунова для некоторых полулинейных дифференциальных уравнений высокого порядка, Журнал математических неравенств , том. 13, нет. 4, стр. 1159–1170, 2019.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. П. Агарвал и А. Озбеклер, «Несоосность через неравенства типа Ляпунова и Валле-Пуссена для вынужденных дифференциальных уравнений», Applied Mathematics and Computation , vol. 265, стр. 456–468, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Лю Х. Д., Неравенства типа Ляпунова для некоторых разностных уравнений высокого порядка со смешанными нелинейностями, Успехи в разностных уравнениях , vol. 2018 г., идентификатор статьи 229, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
X.-H. Тан и М. Чжан, «Неравенства Ляпунова и устойчивость для линейных гамильтоновых систем», Journal of Differential Equations , vol. 252, нет. 1, стр. 358–381, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Чжан К. М., Тан X. Х. Неравенства типа Ляпунова для квазилинейных разностных систем, стр. 9.0019 Дискретная динамика в природе и обществе , том. 2012 г., идентификатор статьи 860598, 16 страниц, 2012 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Х. Д. Лю, «Улучшение неравенства Ляпунова для некоторых дифференциальных уравнений более высокого порядка», Journal of Inequalities and Applications , vol. 2018 г., идентификатор статьи 215, 2018 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Джлели и Б. Самет, «О неравенствах типа Ляпунова для -лапласовских систем», Журнал неравенств и приложений , том. 2017 г., идентификатор статьи 100, 2017 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar

Copyright

Copyright © 2020 Haidong Liu. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Как построить график неравенств с одной переменной на TI-84 Plus

Автор: Джефф МакКалла и К.С. Эдвардс и

Обновлено: 26 марта 2016 г. Графический калькулятор для чайников, 3-е издание

Обзор книги Купить на Amazon

Ваш калькулятор TI-84 Plus не предназначен для построения графиков неравенств на числовой прямой, но его можно использовать для выполнения этой задачи. Причина, по которой ваш калькулятор может выполнять задачу, для которой он не предназначен, заключается в булевой логике, которую ваш калькулятор использует для оценки утверждений.

Возможно, вы помните, что ваш калькулятор использует истинные значения: 1 = Истина и 0 = Ложь.

Когда вы вводите такое утверждение, как 1 – X > 3 , ваш калькулятор вычисляет, где утверждение верно, и возвращает 1, а где утверждение ложно, возвращает значение 0. Почему бы не использовать это в своих интересах в графическая среда?

Выполните следующие действия, чтобы построить на калькуляторе неравенство с одной переменной (как если бы вы построили график на числовой прямой):

Нажмите [Y=] и введите полное неравенство.
См. первый экран.
Нажмите [2nd][MATH], чтобы ввести неравенство из меню Test.
Нажмите [ZOOM][6], чтобы построить график неравенства с одной переменной.
См. второй экран. Когда y -значение графика равно 1, неравенство верно. Когда y -значение графика равно 0, неравенство неверно.
Ваш график выглядит как числовая линия. Числовая линия находится чуть выше 9.0019 x -ось точно так же, как мои ученики любят рисовать числовую линию в своей домашней работе. Чего только не хватает? Точка x = –2 открыта или закрыта? См. следующий шаг для метода проверки значения истинности при x = –2.
Нажмите [TRACE] и введите значение x, которое вы хотите проверить.
См. третий экран. Ввод –2 дает y -значение 0 (что означает ложь). Вы можете с уверенностью заключить, что точка открыта в x = –2, а решение неравенства x < –2.
Нажмите [2nd][GRAPH] для отображения таблицы. Это действительно интересный способ взглянуть на значения истинности (1 и 0), которые возвращаются для введенного вами неравенства.

Этот метод работает и для составных неравенств. Единственным недостатком является то, что может быть сложно определить точное значение, с которого начинается график.

Шаги для ввода сложных неравенств точно такие же, как и для ввода неравенств с одной переменной. На первом экране для Y 9 вводится неравенство «или».0643 1 и неравенство «и» для Y ₂ . Y ₁ отображается на втором экране, а Y ₂ — на третьем.

Вставьте «и» или «или» в меню «Логика» и нажмите

.
Эта статья взята из книги:
TI-84 Plus CE Graphing Calculator For Dummies, 3rd Edition,
Об авторе книги:
Джефф МакКалла — учитель математики в Епископальной школе Святой Марии в Мемфисе. , ТН. Он стал соучредителем группы суперпользователей TI-Nspire и получил Президентскую премию за выдающиеся достижения в области преподавания естественных наук и математики.
No related posts.