Решение неравенств с модулем онлайн: Решение неравенств с модулем онлайн · Как пользоваться Контрольная Работа РУ

Неравенства с модулем

Существует несколько способов решения неравенств, содержащих модуль. Рассмотрим некоторые из них.

1) Решение неравенства с помощью геометрического свойства модуля.

Напомню, что такое геометрическое свойство модуля: модуль числа x – это расстояние от начала координат до точки с координатой x.

В ходе решения неравенств этим способом может возникнуть 2 случая:

1. |x| ≤ b, тогда картинка решения выглядит так:

И неравенство с модулем очевидно сводится к системе двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

2. |x| ≥ b, тогда картинка решения выглядит так:

И неравенство с модулем очевидно сводится к совокупности двух неравенств. Тут знак может быть и строгим, в этом случае точки на картинке будут «выколотыми».

Пример 1.

Решить неравенство |4 – |x|| ≥ 3.

Решение.

Данное неравенство равносильно следующей совокупности:

[4 – |x| ≤ -3
[4 – |x| ≥ 3.

Хочу напомнить принципиальное отличие понятия совокупности от понятия системы. Когда мы ставим знак системы « { », мы подразумеваем, что выполняются и первое и второе неравенства одновременно, то есть мы ищем общие решения двух неравенств. Когда мы ставим знак совокупности « [ », мы подразумеваем, что выполняется или первое неравенство, или второе, то есть мы ищем те значения неизвестного x, которые являются решением либо первого, либо второго неравенства.

Теперь решаем систему.

[-|x| ≤ -7
[-|x| ≥ -1,
[|x| ≥ 7
[|x| ≤ 1.

Решаем отдельно первое неравенство:

[x ≥ 7
[x ≤ -7.

Решаем отдельно второе неравенство:

{x ≥ -1
{x ≤ 1.

Мы получили совокупность, состоящую из подсовокупности и системы. Решением исходного неравенства будут все x, которые удовлетворяют хотя бы одному неравенству из совокупности и каждому из неравенств системы.

Ответ: x € (-∞; -7] U [-1;1] U [7; +∞]

Пример 2.

Решить неравенство ||x+2| – 3| ≤ 2.

Решение.

Данное неравенство равносильно следующей системе.

{|x + 2| – 3 ≥ -2
{|x + 2| – 3 ≤ 2,
{|x + 2| ≥ 1
{|x + 2| ≤ 5.

Решим отдельно первое неравенство системы. Оно эквивалентно следующей совокупности:

[x + 2 ≥ 1
[x + 2 ≤ -1,
[x ≥ -1
[x ≤ -3.

Решим отдельно второе неравенство системы. Оно эквивалентно следующей системе:

{x + 2 ≤ 5
{x + 2 ≥ -5,
{x ≤ 3
{x ≥ -7.

Мы получили систему, состоящую из подсистемы и совокупности. Решением исходного неравенства будут все x, которые являются одновременно решением совокупности и решением подсистемы.

Ответ: х € [-7; -3] U [-1; 3].

2) Решение неравенств, используя определение модуля.

Напомню для начала определение модуля.

|a| = a, если a ≥ 0 и |a| = -a, если a < 0.

Например, |34| = 34, |-21| = -(-21) = 21.

Пример 1.

Решить неравенство 3|x – 1| ≤ x + 3.

Решение.

Используя определение модуля получим две системы:

{x – 1 ≥ 0
{3(x – 1) ≤ x + 3

и

{x – 1 < 0
{-3(x – 1) ≤ x + 3.

Решая первую вторую системы в отдельности, получим:

{x ≥ 1
{x ≤ 3,

{x < 1
{x ≥ 0.

Решением исходного неравенства будут все решения первой системы и все решения второй системы.

Ответ: x € [0; 3].

3) Решение неравенств методом возведения в квадрат.

Пример 1.

Решить неравенство |x² – 1| < | x² – x + 1|.

Решение.

Возведем обе части неравенства в квадрат. Замечу, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева и справа стоят модули, поэтому мы можем это сделать.

(|x² – 1|)² < (|x² – x + 1|)².

Теперь воспользуемся следующим свойством модуля: (|x|)² = x².

(x² – 1)² < (x² – x + 1)²,

(x² – 1)² – (x² – x + 1)

2 < 0.

Дальше лучше всего воспользоваться формулой разности квадратов. Можно, конечно и возводить в квадрат левую и правую скобку, но это займет гораздо больше времени.

(x² – 1 – x² + x – 1)( x² – 1 + x² – x + 1) < 0,

(x – 2)(2x² – x) < 0,

x(x – 2)(2x – 1) < 0.

Решаем методом интервалов.

Ответ: x € (-∞; 0) U (1/2; 2)

4) Решение неравенств методом замены переменных.

Пример.

Решить неравенство (2x + 3)² – |2x + 3| ≤ 30.

Решение.

Заметим, что (2x + 3)² = (|2x + 3|)². Тогда получим неравенство

(|2x + 3|)² – |2x + 3| ≤ 30.

Сделаем замену y = |2x + 3|.

Перепишем наше неравенство с учетом замены.

y² – y ≤ 30,

y² – y – 30 ≤ 0.

Разложим квадратный трехчлен, стоящий слева, на множители.

D = 121,

y1 = (1 + 11) / 2,

y2 = (1 – 11) / 2,

y1 = 6,

y2 = -5.

(y – 6)(y + 5) ≤ 0.

Решим методом интервалов и получим:

-5 ≤ y ≤ 6.

Вернемся к замене:

-5 ≤ |2x + 3| ≤ 6.

Данное двойное неравенство равносильно системе неравенств:

{|2x + 3| ≤ 6
{|2x + 3| ≥ -5.

Решим каждое из неравенств в отдельности.

Первое равносильно системе

{2x + 3 ≤ 6
{2x + 3 ≥ -6.

Решим ее.

{x ≤ 1. 5
{x ≥ -4.5.

Второе неравенство очевидно выполняется для всех x, так как модуль по определению число положительное. Так как решение системы – это все x, которые удовлетворяют одновременно и первому и второму неравенству системы, то решением исходной системы будет решение ее первого двойного неравенства (ведь второе верно для всех x).

Ответ: x € [-4,5; 1,5].

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Примеры решений неравенств с модулем с ответами

Алгоритм решения неравенств с модулем

Теорема

Неравенства с модулем – это неравенства, содержащее неизвестные под знаком модуля.

При решении неравенств с модулем используется определение модуля числа.

Определение модуля числа.

   

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решений неравенств с модулем

Пример 1

Задача

Решить неравенство:

   

Решение

   

При

   

   

   

Отсюда или

Ответ

Пример 2

Задача

Решить неравенство:

   

Решение

Решить неравенство:

   

   

   

Ответ

Пример 3

Задача

Решить неравенство:

   

Решение

   

   

   

   

Решением системы является

Решением системы является

Окончательно

Ответ

Пример 4

Задача

Решить неравенство:

   

Решение

При

   

   

– решений нет

   

   

Ответ

Пример 5

Задача

Решить неравенство:

   

Решение

   

   

   

   

   

   

   

Ответ

   

Пример 6

Задача

Решить неравенство:

   

Решение

   

   

   

   

   

Ответ

Пример 7

Задача

Решить неравенство:

   

Решение

   

   

   

   

   

Ответ

   

Пример 8

Задача

Решить неравенство:

   

Решение

   

Неравенство является квадратным относительно

   

   

   

   

   

Ответ

   

Пример 9

Задача

Решить неравенство:

   

Решение

   

   

   

   

   

   

Ответ

   

Пример 10

Задача

Решить неравенство:

   

Решение

   

   

   

   

   

   

   

Ответ

   

Средняя оценка 5 / 5.

Количество оценок: 1

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

12813

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Решение линейных неравенств / Форматирование ответов

Простые примеры, сложные примеры

Purplemath

Вероятно, недавно вы научились решать линейные уравнения с одной переменной. Вы научились перемещать все термины, содержащие переменную, вместе на одну сторону знака «равно», а все свободные числа — на другую сторону знака «равно». Затем, объединив одинаковые члены, вы разделили на то, что было умножено на переменную.

Содержание продолжается ниже

MathHelp.com

Решение неравенств

Решение линейных неравенств почти точно такое же, как решение линейных уравнений. Но там, где решениями линейных уравнений являются единичные значения, решениями линейных неравенств являются бесконечные интервалы.

Вместо, скажем, решения « x  = 2″ для линейного уравнения, у вас будет решение, скажем, « x  ≤ 2″ для линейного неравенства. И хотя это решение «меньше или равно» имеет граничное значение (то есть конкретную краевую точку решения)

x  = 2, само решение содержит бесконечно много точек, представляющих собой каждое действительное число слева от 2.

• Решите x + 3 < 0

Если бы мне дали решить линейное уравнение » x  + 3 = 0″, я бы точно знал, как поступить: я бы вычел 3 из обеих частей, получив переменную сам по себе.

Я могу сделать то же самое здесь:

Тогда мое решение:

x < −3

---

Как оформляются решения?

Решения линейных неравенств с одной переменной можно форматировать любым из четырех способов.

• Обозначение неравенства: x  < −3
• Установить обозначение: { x | x < −3}
• Обозначение интервала: (−∞, −3)
• Графика: штриховка (утолщение) числовой линии

В упражнении, которое я сделал выше, мое решение было отформатировано в виде неравенства, так называемого, потому что решение было записано как неравенство. Это, вероятно, самая простая из нотаций решения и наиболее естественная в использовании, но есть еще три нотации, с которыми вам может понадобиться ознакомиться.

Решение в «обозначении набора» записывает решение в виде набора точек. Приведенное выше решение будет записано в системе обозначений как:

{ x | х — действительное число, x < −3}

… что произносится как «множество всех x -значений, таких, что x является действительным числом, а x меньше минус трех».

Упрощенная форма этого обозначения будет примерно такой:

{ x | x < −3}

… что произносится как «все x , такие что x меньше минус три». Вы могли бы даже увидеть решения с обозначением множества, указанные как решение неравенства, но это неравенство будет заключено в фигурные скобки, чтобы сказать, что решение представляет собой набор точек: { x  < −3}.

«Обозначение интервала» записывает решение в виде интервала (т. е. в виде сечения или длины вдоль числовой прямой). Приведенное выше решение x  < −3 будет записано как:

(−∞, −3)

… что произносится как «интервал от отрицательной бесконечности до минус трех», или просто «минус бесконечность до минус трех».

Обозначение интервала может быть легче писать, чем произносить, из-за неоднозначности относительно того, включены ли конечные точки в интервал. (Примечание: бесконечность *никогда* не включается в качестве конечной точки; это не «точка», которую можно «достичь».) Для обозначения, например, решения неравенства « x  ≤ -3″, интервал будет записан как:

(-∞ ≤ -3]

… что произносится как «минус бесконечность от до (не просто «до») минус три» или «от минус бесконечности до минус трех включительно», что означает, что -3 должно быть включено в решение. Правая скобка в интервальной форме решения x  < -3 указывает на то, что -3 не было включено; -скобка в интервальной форме x  ≤ −3 указывает, что она включена.

Последняя форма обозначения решения на самом деле является скорее иллюстрацией. Вы можете быть направлены на «график» решения. Это означает, что вы должны провести числовую прямую, а затем выделить часть, которая входит в решение неравенства. Во-первых, вы должны отметить край интервала решения, в нашем примере это точка -3. Поскольку −3 не включено в решение (поскольку это неравенство «меньше чем», а не неравенство «меньше или равно»), вы должны отметить эту точку открытой точкой или открытой скобкой, указывающей в направлении остальной части интервала решения:

…или:

Затем нужно заштриховать в соответствующую сторону:

…или:

Зачем закрашивать влево? Потому что им нужны все значения, которые на меньше −3, и эти значения находятся слева от граничной точки. Если бы им нужны были точки «больше чем», я бы заштриховал их вправо.

---

Всего мы рассмотрели четыре способа, с парой вариантов, для обозначения решения приведенного выше неравенства:

• обозначение неравенства:
  • записано: x < −3
  • разговорный: x меньше минус три
• установить обозначение:
  • написано:
    1. { х | x — действительное число, x < −3} или
       
    2. { х | x < −3} или просто { x  < −3}
  • говорил:
    1. множество всех x , такое что x является действительным числом, а x меньше минус трех
    2. все x такие, что x меньше минус три
9Обозначение интервала 0025:
• написано: (-∞, -3)
• произносится: интервал от минус бесконечности до минус трех
• графическое обозначение:
  • написано (с открытой точкой или скобками):
  • произносится: минус бесконечность до минус три

---

Обозначения немного отличаются, когда неравенство относится к типу «или равно», поэтому я перечислю их все для следующего примера:

Если бы мне дали уравнение « x  − 4 = 0″, я бы решил его, прибавив четыре к каждой стороне. Я могу сделать то же самое с неравенством здесь:

Тогда мой ответ:

x ≥ 4

---

Как и прежде, это решение (а именно, x ≥ 4) может быть представлено любым из четырех следующих способов: 3 90 :

• письменный: x ≥ 4
• разговорный: x больше или равно четырем

установить обозначение:

• написано:
  1. { х | x — действительное число, x ≥ 4} или
     
  2. { х | x ≥ 4} или просто { x  ≥ 4}
• говорил:
  1. множество всех x , такое что x является действительным числом, а x больше или равно четырем
  2. все x такие, что x больше или равно четырем

Обозначение интервала

:

• написано: [4, ∞)
• произносится: интервал от четырех до положительной бесконечности включительно

графическое обозначение:

• пишется (с помощью закрытой точки или скобки):
• разговорный: от четырех до плюс бесконечности включительно

Когда вы строите график решения, квадратные скобки идут вместе со скобками, а закрытые (то есть заполненные) точки идут с открытыми точками.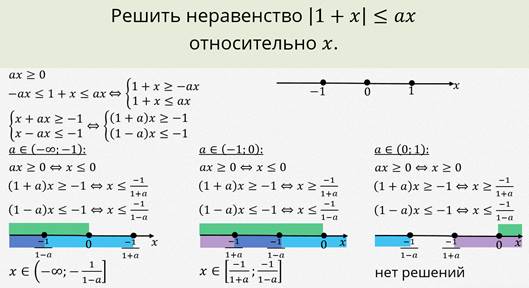

Если (далее) у вас есть неравенство, в котором обе конечные точки являются действительными числами (то есть ни одна конечная точка не является −∞ или +∞), и одна конечная точка включена, а другая нет, вы захотите использовать совпадающие символы: одна скобка и одна квадратная скобка или одна открытая и одна закрытая точки. Не смешивайте символы. Я не знаю, что это было бы неправильно само по себе, но это наверняка будет раздражать оценщика.

В то время как ваш текущий учебник может требовать, чтобы вы знали только один или два из вышеуказанных форматов для ваших ответов, эта тема неравенства имеет тенденцию возникать в других контекстах в других книгах для других курсов. Поскольку позже вам может понадобиться понять другие форматы, убедитесь, что вы знаете их все сейчас. Однако до конца этого урока я буду использовать только обозначение неравенства.

Мне больше нравится.

---

Кстати, в вашем учебнике может также быть «проверка на предмет того, является ли значение решением». Это означает, что они дадут вам неравенство вместе с числом, и они ожидают, что вы подставите число в неравенство и посмотрите, работает ли число. Например:

• Является ли 2 решением уравнения x  ≤ 5?

Ну и ладно! Из курс два меньше пяти! Но они хотят, чтобы я «показал» это. Хорошо:

x ≤ 5

(2) ≤ 5

Да, 2 — это решение.

С другой стороны:

• Является ли 2 решением x  > 5?

Ну и ладно! Из , конечно, два *не* больше пяти! Но они хотят, чтобы я «показал» это. Хорошо:

x > 5

(2) > < 5

Нет, 2 *не* решение.

Конечно, существует бесконечно много других точек, которые являются (или не являются) решениями любого заданного неравенства. Таким образом, вы не увидите много такого рода упражнений.

---

URL: https://www.purplemath.com/modules/ineqlin.htm

Page 2Page 3

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании записи неравенства в запись интервала. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Преобразовать в интервальную нотацию», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и перейдите на следующую страницу.)

Пожалуйста, примите «предпочтительные» файлы cookie, чтобы включить этот виджет.

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

Решение проблем неравенства в образовании — онлайн-курс

Поисковый запрос

Извините, этот курс в настоящее время не запущен. Просмотрите другие курсы по политике и обществу.

4.7 (87 отзывов)

Узнайте, как технологии могут помочь решить проблему неравенства и дать возможность будущим поколениям полностью раскрыть свой потенциал с помощью образования.

6,969  записаны на этот курс

Другие курсы, которые могут вам понравиться

Этот курс сейчас не проводится. Мы можем отправить вам электронное письмо, когда он снова начнется, или проверить другие курсы, которые могут вам понравиться.

Определите, как технологии можно использовать для решения проблемы неравенства в образовании

В этом курсе вы узнаете, как технологии определяют и переопределяют способы нашего обучения, и раскроете возможности, которые технологии предоставляют для решения проблемы неравенства в образовании.

Каким будет будущее образования?

Вместе с вдохновляющими наставниками, которые увлечены изменением будущего образования, в том числе с рэпером Леди Лешерр и футуристом Джесси Хиршем, вы обдумаете свой собственный путь обучения и начнете понимать, насколько важными будут цифровые обучающие сети для будущих поколений.

Вы познакомитесь с человеческим опытом обучения, а также поймете, как технологии превратили обучение во все более социальный и интерактивный опыт.

Познакомившись с концепцией радикального переосмысления, вы обнаружите различные практики, меняющие способ обучения.

Узнайте о разрыве неравенства

Вместе с наставником и педагогом Нобл Келли вы узнаете о разрыве неравенства.

Вы узнаете о роли школ в современном обществе и обдумаете, как может выглядеть будущее образования с технологической точки зрения.

Откройте для себя привилегии в сфере образования с амбассадором курса леди Лешерр

Когда вы дойдете до конца курса, вы услышите информацию об образовании и привилегиях в связи с движением Black Lives Matter от основного докладчика, рэпера и певицы Леди Лешерр.

На последнем этапе курса вам будет предложено разработать коммерческое предложение, услугу или продукт, отвечающие на вопрос: Как технологии могут помочь решить проблему неравенства в образовании?

Обучение на этом курсе

На каждом этапе курса вы можете встречаться с другими учащимися, делиться своими идеями и участвовать в активных дискуссиях в комментариях.

Чего ты добьешься?

К концу курса вы сможете.