Решение задач по логике – онлайн примеры и образцы с ответами
Логика изучает абстрактное мышление как средство постижения мира, исследует формы и законы, по которым мир отражается в процессе мышления. Логика является философской дисциплиной и связана с теорией познания. Логика является философской дисциплиной и связана с теорией познания, поскольку процесс восприятия мира полностью изучается философией, а логика изучает лишь один из аспектов когнитивного мышления.
Логика происходит от греческого слова «логос», что означает «мысль», «слово», «причина» или «закономерность». Это слово используется, во-первых, для обозначения набора правил, которым должен следовать процесс мышления, и, во-вторых, для обозначения науки о правилах рассуждения и формах, в которых они осуществляются. Изучение мышления. Но мышление изучается не только логикой, но и различными другими науками, такими как психология, кибернетика, педагогика и т.д., каждая из которых изучает тот или иной аспект мышления.
Законы логики объективны и действуют независимо от воли или желания человека. Они имеют универсальный характер, заключающийся в том, что во все исторические периоды люди мыслят по одним и тем же законам. Законы, изучаемые в формальной логике, — это закон тождества, закон непротиворечия, закон достаточного основания и закон исключенной трети.
Если у вас нет времени на выполнение заданий по логике, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.
Ответы на вопросы по заказу заданий по логике:
Сколько стоит помощь?
- Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.
Какой срок выполнения?
- Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней.
 Мы всегда стараемся выполнять любые работы и задания раньше срока.
Мы всегда стараемся выполнять любые работы и задания раньше срока.
Если требуется доработка, это бесплатно?
- Доработка бесплатна. Срок выполнения от 1 до 2 дней.
Могу ли я не платить, если меня не устроит стоимость?
- Оценка стоимости бесплатна.
Каким способом можно оплатить?
- Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.
Какие у вас гарантии?
- Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.
В какое время я вам могу написать и прислать задание на выполнение?
- Присылайте в любое время! Я стараюсь быть всегда онлайн.
Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Логика«, если у вас есть желание и много свободного времени!
Содержание:
- Ответы на вопросы по заказу заданий по логике:
- Логические операции над высказываниями
- Конъюнкция (логическое умножение)
- Дизъюнкция (логическое сложение)
- Импликация
- Эквиваленция
- Задача 1
- Решение:
- Задача 2
- Решение:
- Задача 3
- Решение:
- Задача 4
- Решение:
- Задача 5
- Решение:
- Задача 6
- Решение:
- Задача 7
- Решение:
- Задача 8
- Решение:
- Задача 9
- Решение:
- Задача 10
- Решение:
Основным (неопределяемым) понятием математической логики является понятие «простого высказывания». Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».
Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».
Приведем примеры высказываний.
- 1) Новгород стоит на Волхове.
- 2) Париж — столица Англии.
- 3) Карась не рыба.
- 4) Число 6 делится на 2 и на 3.
- 5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.
Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны. Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием. Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).
Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то…», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась — рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Так, высказывание 3) получается из простого высказывания «Карась — рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: истинное значение высказывания — буквой или цифрой 1, а ложное значение — буквой или цифрой 0. Если высказывание а истинно, то будем писать а если ложно, то
Если высказывание а истинно, то будем писать а если ложно, то
Возможно, вас также заинтересует эта ссылка:
Контрольная работа по логике заказать |
Логические операции над высказываниями
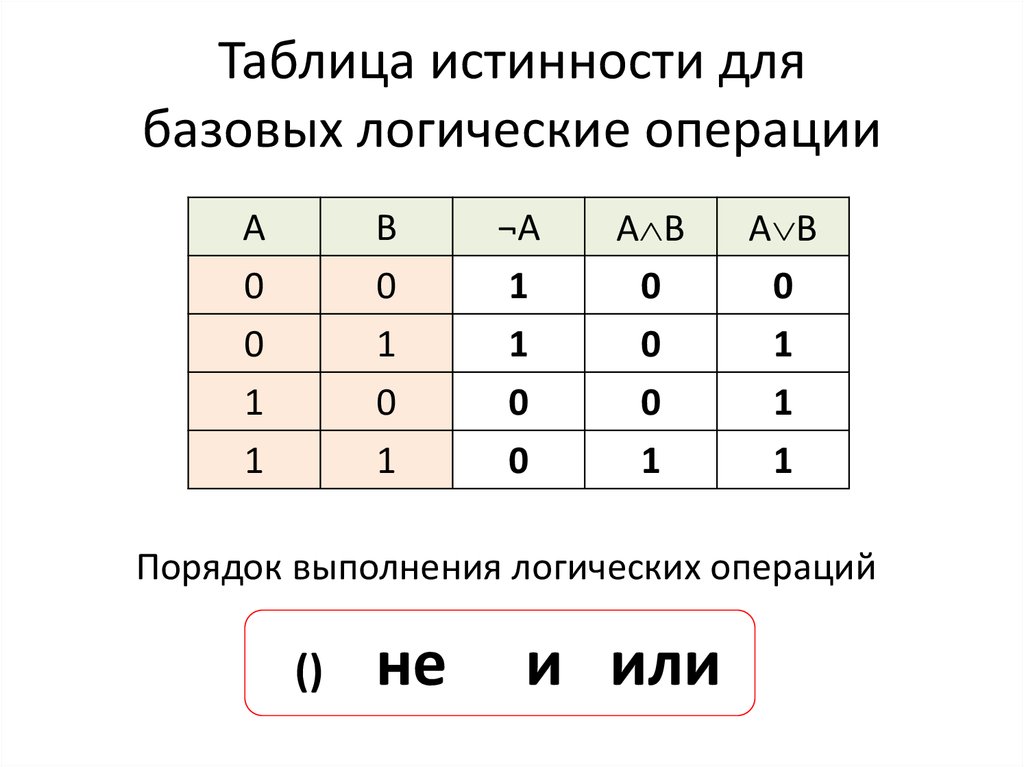
1. Отрицание. Отрицанием высказывания называется новое высказывание, которое является истинным, если высказывание ложно, и ложным, если высказывание истинно. Отрицание высказывания обозначается и читается «не » или «неверно, что ». Логические значения высказывания можно описать с помощью таблицы
Таблицы такого вида принято называть таблицами истинности. Пусть высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание которое называется двойным отрицанием высказывания . Ясно, что логические значения высказываний и совпадают. Например, для высказывания «Река Волхов вытекает из озера Ильмень» отрицанием будет высказывание «Неверно, что река Волхов вытекает из озера Ильмень» или «Река Волхов не вытекает из озера Ильмень», а двойным отрицанием будет высказывание «Неверно, что река Волхов не вытекает из озера Ильмень»
Возможно, вас также заинтересует эта ссылка:
Помощь по логике онлайн |
Конъюнкция (логическое умножение)
Конъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если оба высказывания истинны, и ложным, если хотя бы одно из них ложно. Конъюнкция высказываний обозначается символом или читается Высказывания называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:
Конъюнкция высказываний обозначается символом или читается Высказывания называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:
Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний. Из определения операции конъюнкции и отрицания ясно, что высказывание всегда ложно.
Возможно, вас также заинтересует эта ссылка:
Курсовая работа по логике заказать готовую онлайн |
Дизъюнкция (логическое сложение)
Дизъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Дизъюнкция высказываний обозначается символом читается Высказывания называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
Дизъюнкция высказываний обозначается символом читается Высказывания называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
Например, высказывание «В треугольнике угол или угол острый» истинно, так как обязательно истинно хотя бы одно из высказываний: «В треугольнике угол острый», «В треугольнике угол острый». В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле. Из определения операции дизъюнкции и отрицания ясно, что высказывание всегда истинно.
Возможно, вас также заинтересует эта ссылка:
РГР по логике расчетно графическая работа |
Импликация
Импликацией двух высказываний называется новое высказывание, которое считается ложным, если истинно, а — ложно, и истинным во всех остальных случаях. Импликация высказываний обозначается символом читается «если то » или «из следует ». Высказывание называют условием или посылкой, высказывание — следствием или заключением, высказывание — следованием или импликацией.
Импликация высказываний обозначается символом читается «если то » или «из следует ». Высказывание называют условием или посылкой, высказывание — следствием или заключением, высказывание — следованием или импликацией.
Логические значения операции импликации описываются следующей таблицей истинности:
Например, высказывание «Если число 12 делится на 6, то оно делится на 3», очевидно, истинно, так как здесь истинна посылка «Число 12 делится на 6» и истинно заключение «Число 12 делится на 3». Употребление слов «если то …» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание ложно, то высказывание «Если , то » вообще не имеет смысла. Кроме того, строя предложение вида «если , то » в обыденной речи, мы всегда подразумеваем, что предложение вытекает из предложения . Употребление слов «если …, то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается. Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если , то ».
Возможно, вас также заинтересует эта ссылка:
Задачи по логике с решением |
Эквиваленция
Эквиваленцей (или эквивалентностью) двух высказываний называется новое высказывание, которое считается истинным, когда оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний обозначается символом , читается «для того, чтобы , необходимо и достаточно, чтобы » или « тогда и только тогда, когда ». Высказывания называются членами эквиваленции.
Задача 1
Существуют ли три таких высказывания чтобы одновременно выполнялись для них следующие условия:
Решение:
Из первого условия, по определению дизъюнкции, следует, что и т. е. Тогда второе данное условие, по определению импликации, влечет Отсюда Следовательно, что противоречит третьему данному условию. Значит, трех высказываний удовлетворяющих данным условиям, не существует.
е. Тогда второе данное условие, по определению импликации, влечет Отсюда Следовательно, что противоречит третьему данному условию. Значит, трех высказываний удовлетворяющих данным условиям, не существует.
Задача 2
Следующие составные высказывания расчлените на простые и запишите символически, введя буквенные обозначения для простых их составляющих: а) Если число делится на 2 и не делится на 3, то оно не делится на 6. б) Произведение трех чисел равно нулю тогда и только тогда, когда одно из них равно нулю. в) Если производная функции в точке равна нулю и вторая производная этой функции в той же точке отрицательна, то данная точка есть точка локального максимума функции. г) Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии их пересечения. д) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и прямые и не параллельны (утверждение ), то прямая перпендикулярна всякой прямой лежащей в плоскости (утверждение ). е) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и неперпендикулярна некоторой прямой лежащей в этой же плоскости (утверждение ), то прямые и параллельны ( — утверждение ). ж) Если две прямые и лежащие в плоскости , непараллельны (утверждение ) и прямая неперпендикулярна некоторой прямой лежащей в плоскости (утверждение ), то неперпендикулярна одной из прямых или (утверждение ). з) Если какие-либо два из трех векторов коллинеарны, то их смешанное произведение равно нулю и) Логарифм некоторого положительного числа будет положительным, если основание логарифма и логарифмируемое число будут больше 1 или если основание логарифма и логарифмируемое число будут заключены между 0 и 1. к) Если в параллелограмме не все углы прямые или не все стороны равны между собой, то этот параллелограмм не прямоугольник или не ромб. л) Если в треугольнике любая его медиана не является высотой и биссектрисой, то этот треугольник не равнобедренный и не равносторонний.
е) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и неперпендикулярна некоторой прямой лежащей в этой же плоскости (утверждение ), то прямые и параллельны ( — утверждение ). ж) Если две прямые и лежащие в плоскости , непараллельны (утверждение ) и прямая неперпендикулярна некоторой прямой лежащей в плоскости (утверждение ), то неперпендикулярна одной из прямых или (утверждение ). з) Если какие-либо два из трех векторов коллинеарны, то их смешанное произведение равно нулю и) Логарифм некоторого положительного числа будет положительным, если основание логарифма и логарифмируемое число будут больше 1 или если основание логарифма и логарифмируемое число будут заключены между 0 и 1. к) Если в параллелограмме не все углы прямые или не все стороны равны между собой, то этот параллелограмм не прямоугольник или не ромб. л) Если в треугольнике любая его медиана не является высотой и биссектрисой, то этот треугольник не равнобедренный и не равносторонний.
Решение:
Выделим и следующим образом обозначим простейшие составляющие высказывания: А: «В треугольнике некоторая его медиана является высотой»; В: «В треугольнике некоторая его медиана является биссектрисой»; С: «Этот треугольник равнобедренный»; D: «Этот треугольник равносторонний». Тогда данное высказывание символически записывается так: будут формулами. Далее, формулами будут выражения Наконец выражение представляющее собой данную последовательность, также является формулой.
Задача 3
В следующей последовательности символов всевозможными способами расставьте скобки так, чтобы получилась формула:
Решение:
л) Вот эти формулы (внешние скобки опущены):
Задача 4
Составьте таблицы истинности для следующих формул и укажите, какие из формул являются выполнимыми, какие — опровержимыми, какие — тождественно истинными (тавтологиями), какие — тождественно ложными (противоречиями):
Решение:
Пользуясь определениями логических связок (операций над высказываниями), составим таблицу истинности данной формулы (логические значения этой формулы записаны в последнем столбце таблицы, где сама формула обозначена
Из построенной таблицы истинности видно, что данная формула выполнима, так как если, например, вместо пропозициональной переменной вставить в формулу ложное высказывание, а вместо — истинное, то вся формула превратится в истинное высказывание. Но эта формула является также и опровержимой, поскольку если, например, вместо пропозициональной переменной вставить в формулу истинное высказывание, а вместо переменной — ложное, то вся формула превратится в ложное высказывание. Следовательно, формула не является ни тавтологией, ни тождественно ложной формулой.
Но эта формула является также и опровержимой, поскольку если, например, вместо пропозициональной переменной вставить в формулу истинное высказывание, а вместо переменной — ложное, то вся формула превратится в ложное высказывание. Следовательно, формула не является ни тавтологией, ни тождественно ложной формулой.
Возможно, вас также заинтересует эта ссылка:
- Решение задач
Задача 5
Докажите, что следующие формулы выполнимы, не составляя для них таблиц истинности, а указав какие-нибудь значения входящих в них пропозициональных переменных, при которых эти формулы обращаются в истинные высказывания:
Решение:
л) Заключение второй импликации есть, очевидно, тождественно ложная формула. Поэтому если посылка второй импликации превратится при некоторой подстановке в ложное высказывание, то эта импликация станет истинным высказыванием и, следовательно, вся данная импликация превратится в истинное высказывание независимо от того, в какое высказывание обратится посылка всей данной импликации.
Посылка второй импликации обращается в ложное высказывание, когда вместо переменных и подставляются ложные высказывания.
Итак, данная формула выполнима, поскольку она обращается в истинное высказывание, если вместо и подставить ложные высказывания, а вместо — произвольное высказывание (его истинностное значение в данном случае не повлияет на истинностное значение всего высказывания).
Задача 6
Выясните, справедливы ли следующие утверждения (если утверждение несправедливо, то постарайтесь определить, обе его части «тогда» и «только тогда» не выполняются или только одна): а) тогда и только тогда, когда б) тогда и только тогда, когда в) тогда и только тогда, когда г) тогда и только тогда, когда д) тогда и только тогда, когда е) тогда и только тогда, когда ж) тогда и только тогда, когда з) тогда и только тогда, когда и) тогда и только тогда, когда к) тогда и только тогда, когда л) тогда и только тогда, когда м) тогда и только тогда, когда
Решение:
л) Данное утверждение в полном объеме несправедливо: неверна его часть «тогда» (необходимость). Для подтверждения этого нужно указать такие конкретные формулы и чтобы по меньшей мере одна из них не была тавтологией, а формула тавтологией была бы. Вот пример таких формул: Ни одна из них не является тавтологией, но формула — тавтология. Еще пример: Проверьте, что этот пример действительно опровергает необходимость данного утверждения. Приведите самостоятельно аналогичный пример. Рассмотрим теперь часть «только тогда» (достаточность) данного утверждения. Оказывается, она верна. В самом деле, предположим, что и Это означает, что для любых высказываний высказывания будут истинными. Следовательно, для любых высказываний истинным будет и высказывание А это означает, что формула является тавтологией, т.е. м) Покажем, что данное утверждение справедливо. Необходимость. Пусть Следовательно, формула тождественно ложна. Но тогда, ввиду определения дизъюнкции, тождественно ложны обе формулы и А раз так, то отрицание каждой из этих формул будет всегда принимать лишь истинные значения, т.
Для подтверждения этого нужно указать такие конкретные формулы и чтобы по меньшей мере одна из них не была тавтологией, а формула тавтологией была бы. Вот пример таких формул: Ни одна из них не является тавтологией, но формула — тавтология. Еще пример: Проверьте, что этот пример действительно опровергает необходимость данного утверждения. Приведите самостоятельно аналогичный пример. Рассмотрим теперь часть «только тогда» (достаточность) данного утверждения. Оказывается, она верна. В самом деле, предположим, что и Это означает, что для любых высказываний высказывания будут истинными. Следовательно, для любых высказываний истинным будет и высказывание А это означает, что формула является тавтологией, т.е. м) Покажем, что данное утверждение справедливо. Необходимость. Пусть Следовательно, формула тождественно ложна. Но тогда, ввиду определения дизъюнкции, тождественно ложны обе формулы и А раз так, то отрицание каждой из этих формул будет всегда принимать лишь истинные значения, т. е. Докажите достаточность самостоятельно: убедитесь, что каждый логический шаг, сделанный при доказательстве необходимости, может быть проделан в обратном направлении.
е. Докажите достаточность самостоятельно: убедитесь, что каждый логический шаг, сделанный при доказательстве необходимости, может быть проделан в обратном направлении.
Задача 7
Докажите, что справедливы следующие логические следования, руководствуясь определением этого понятия: Выясните, будут ли верны обратные следования, т.е. будет ли формула, стоящая слева, логическим следствием формулы, стоящей справа.
Решение:
л) (Изучите сначала ход решения задачи 1.35, м.) Составим таблицу истинности для формул и участвующих в отношении следования:
Последовательный просмотр по строкам столбцов () и () показывает, что как только в какой-либо строке столбца () появляется 1, так сейчас же в этой строке и в столбце () обнаруживается 1. Значит, требуемое логическое следование действительно выполняется (алгоритм см. в Учебнике, с. 55). Обратное же следование неверно, поскольку, например, в первой же строке (т.е. при ) формула принимает значение 1 (столбец ()), а формула тем не менее принимает значение 0 (столбец ()).
Задача 8
Следующие формулы преобразуйте равносильным образом так, чтобы отрицание было отнесено только к пропозициональным переменным и не стояло перед скобками:
Решение:
л) Проделаем требуемые равносильные преобразования:
Задача 9
Каждую из формул предыдущей задачи преобразуйте равносильным образом так, чтобы она содержала только логические связки
Решение:
л) Воспользуемся результатом равносильных преобразований данной формулы, выполненных в предыдущей задаче, и продолжим преобразования для решения данной задачи:
Задача 10
Для каждой из следующих систем высказываний найдите логически эквивалентную ей, но более простую систему высказываний, если известно, что в данной системе по меньшей мере одно высказывание истинно:
Решение:
л) По меньшей мере одно из высказываний данной совокупности будет истинным тогда и только тогда, когда истинна дизъюнкция всех этих высказываний. Поэтому, составив дизъюнкцию из данных высказываний и приведя ее с помощью равносильных преобразований к дизъюнкции более простого вида, можно получить более простую систему высказываний, эквивалентную данной. В нашем случае имеем следующую дизъюнкцию, которую затем упрощаем: Следовательно, по меньшей мере одно высказывание из данной системы будет истинным тогда и только тогда, когда будет истинным одно из высказываний или Поэтому данная система трех высказываний логически эквивалентна более простой системе из двух высказываний
Поэтому, составив дизъюнкцию из данных высказываний и приведя ее с помощью равносильных преобразований к дизъюнкции более простого вида, можно получить более простую систему высказываний, эквивалентную данной. В нашем случае имеем следующую дизъюнкцию, которую затем упрощаем: Следовательно, по меньшей мере одно высказывание из данной системы будет истинным тогда и только тогда, когда будет истинным одно из высказываний или Поэтому данная система трех высказываний логически эквивалентна более простой системе из двух высказываний
Возможно, вас также заинтересует эта ссылка:
Заказать работу по логике помощь в учёбе |
|
Каталог Поиск книг Электронные приложения Авторизация Подписка на рассылку Стихи о нас Богатство Трудности эти уже превратились в смыслы. Тивикова С.К., зав. каф. начального образования НИРО Обратная связь Отправить сообщение с сайта Партнёры |
Глава 1. Информация и информационные процессы Информация. Информационная грамотность и информационная культура Подходы к измерению информации Информационные связи в системах различной природы Обработка информации Передача и хранение информации Тест 1 Глава 2. История развития ВТ Основополагающие принципы устройства ЭВМ Программное обеспечение компьютера Файловая система компьютера Тест 2 Глава 3. Представление информации в компьютере Представление чисел в позиционных СС Перевод чисел из одной системы счисления в другую Арифметические операции в позиционных системах счисления Представление чисел в компьютере Кодирование текстовой информации Кодирование графической информации Кодирование звуковой информации Тест 3 Глава 4. Элементы теории множеств и алгебры логики Некоторые сведения из теории множеств Алгебра логики Таблицы истинности Преобразование логических выражений Элементы схемотехники Логические задачи и способы их решения Тест 4 Глава 5. Текстовые документы Объекты компьютерной графики Компьютерные презентации Тест 5 |
Калькулятор логической алгебры — онлайн-калькулятор логической алгебры
Булева алгебра — это раздел математики, который имеет дело с операциями над логическими значениями и включает двоичные переменные.
Что такое калькулятор булевой алгебры?
«Калькулятор булевой алгебры» — это онлайн-инструмент, который помогает вычислять таблицы истинности для заданных входных данных. Онлайн-калькулятор булевой алгебры Калькулятор поможет вам преобразовать расчет таблиц истинности для заданных входных данных за несколько секунд.
Как пользоваться калькулятором булевой алгебры?
Выполните следующие шаги, которые помогут вам использовать калькулятор.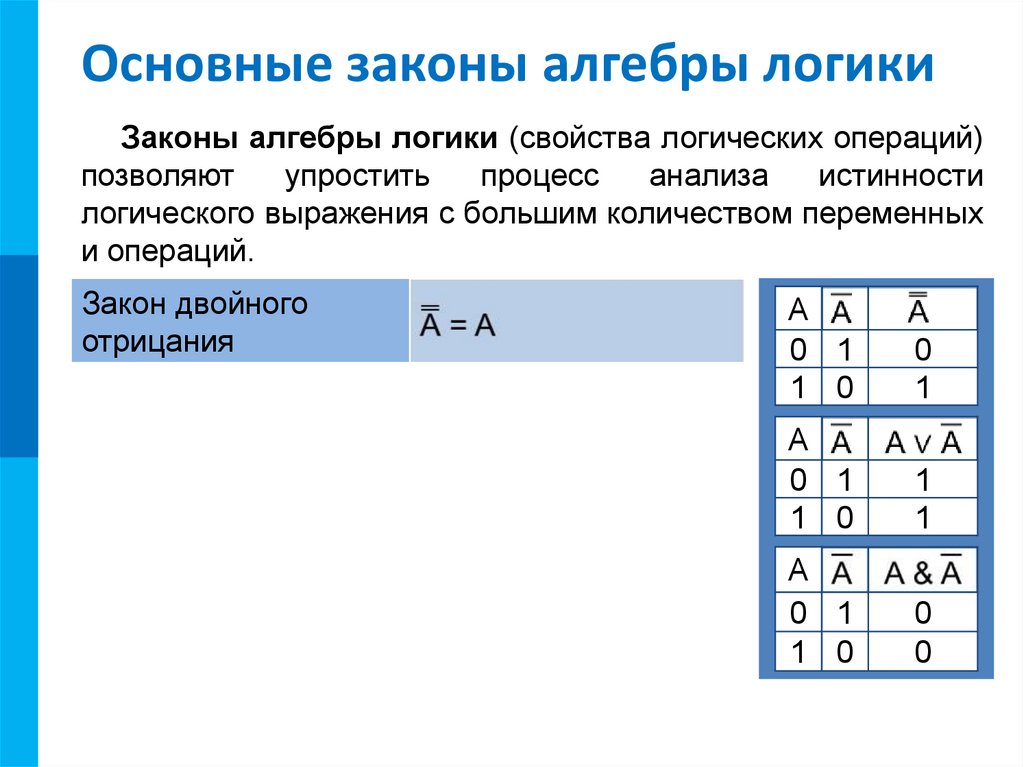
- Шаг 1 . Выберите логическую алгебру из раскрывающегося списка.
- Шаг 2 : Нажмите кнопку « Показать «, чтобы найти таблицы истинности для ввода.
- Шаг 3 : Нажмите кнопку « Сбросить «, чтобы очистить поле и выбрать новую логическую алгебру.
Как найти булеву алгебру?
Булевы переменные представлены в виде двоичных чисел для представления истинности, т. е. 1 = истина и 0 = ложь. Элементарная алгебра имеет дело с числовыми операциями, тогда как булева алгебра имеет дело с логистическими операциями. Существуют различные типы логических вентилей, например вентили И, ИЛИ и ИЛИ-НЕ.
Соединение или вентиль И: Рассмотрите утверждение «p и q», обозначенное p∧q
- Правило 1 : Если «p» и «q» оба утверждения истинны, то «p и q (p∧q )» также является верным утверждением.
- Правило 2 : Если «p» равно False, а «q» равно True, то «p and q (p∧q)» равно False.
 Чтобы «p и q» были истинными, нам нужно, чтобы оба утверждения были истинными. Поскольку одно ложно, «p и q» ложны.
Чтобы «p и q» были истинными, нам нужно, чтобы оба утверждения были истинными. Поскольку одно ложно, «p и q» ложны. - Правило 3 : Если «p» равно True, а «q» – False, то «p and q (p∧q)» – False. Чтобы «p и q» были истинными, нам нужно, чтобы оба утверждения были истинными. Поскольку одно ложно, «p и q» ложны.
- Правило 4 : Если оба утверждения ложны, то «p и q» ложны.
Дизъюнкция или вентиль ИЛИ: Рассмотрим утверждение «p ИЛИ q»
- Правило 1 : Если оба утверждения истинны, то «p или q» также является истинным утверждением.
- Правило 2 : Если «p» равно False, а «q» равно True, то «p or q» равно True. Так как один Истинно.
- Правило 3 : Если «p» – Истина, а q – Ложь, тогда p или q – Истина. Так как один Истинно.
- Правило 4 : Если оба утверждения ложны, то «p или q» ложны.
XOR gate: Рассмотрите утверждение «p XOR q»
- Правило 1 : Если оба утверждения истинны, то «p xor q» ложно.

- Правило 2 : Если «p» равно False, а «q» равно True, то «p xor q» равно True.
- Правило 3 : Если «p» равно True, а «q» – False , тогда p xor q – True.
- Правило 4 : Если оба утверждения ложны, то «p xor q» ложно.
Ворота ИЛИ-НЕ: Рассмотрите утверждение «p ИЛИ q»
- Правило 1 : Если оба утверждения истинны, то «p и q» является ложным утверждением.
- Правило 2 : Если «p» равно False, а «q» равно True, то утверждение «p or q» является False.
- Правило 3 : Если «p» равно True, а «q» – False , то «p, ни q» является ложным утверждением.
- Правило 4 : Если оба утверждения ложны, то «p, ни q» является истинным утверждением.
Отрицание или ворота НЕ: Отрицание — это утверждение, представленное символом ¬p, поэтому оно будет иметь истинностное значение, противоположное p. Если p равно True, то ¬p равно False. Если p равно False, то ¬p равно True.
Если p равно True, то ¬p равно False. Если p равно False, то ¬p равно True.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Забронировать бесплатный пробный урок
Решено Пример:Найдите возможные таблицы истинности для p ∧ q
Решение:Пусть p и q — утверждения. Здесь 1 означает «Истина», а 0 — «Ложь».
P Q P ∧ Q
1 0 0
0 1 0
1 1 1
0 0 0
Аналогично, вы можете попробовать калькулятор, чтобы найти таблицы правды для:
- P ∧ q стр
- п в кв ¬кв
Рабочие листы по математике и визуальная программа
Как решать выражения булевой алгебры?
Булева алгебра происходит от алгебры, которая является одним из основных разделов математики. Существует так много разделов математики, таких как исчисление, арифметика, алгебра, геометрия, численный анализ и т. д., которые в дальнейшем разбиваются на различные категории. Эти ответвления используются почти во всех областях и имеют разные методы решения связанных с ними проблем.
Существует так много разделов математики, таких как исчисление, арифметика, алгебра, геометрия, численный анализ и т. д., которые в дальнейшем разбиваются на различные категории. Эти ответвления используются почти во всех областях и имеют разные методы решения связанных с ними проблем.
Чтобы обсудить булеву алгебру, мы просто рассмотрим ее основную ветвь, то есть алгебру. Существует пять различных типов алгебры:
- Абстрактная алгебра
Этот тип алгебры используется для решения понятий, касающихся множеств, бинарных операций, ассоциативности, элементов идентичности и обратных элементов.
- Высшая алгебра
Эта ветка поможет вам решить задачи, связанные с уравнениями с неравенствами, коническими сечениями, полиномиальными уравнениями, последовательностями и рядами, матрицами, квадратичными функциями с неравенствами, рациональными выражениями и т. д.
- Элементарная алгебра
Охватывает понятия, включая оценку выражений и уравнений, переменных, свойства неравенств и равенств и т. д.
д.
- Линейная алгебра уравнения и матрицы и разложение матриц рассматриваются в этой ветви.
- Коммуникативная алгебра
- НЕ Операция
- ИЛИ Операция
- И Операция
- И Право
- OR Law
- Закон инверсии
- Ассоциативный закон
- Распределительное право
- Коммутативное право
Эта отрасль изучает алгебраическую теорию чисел, алгебраическую геометрию и т. д.
Определение булевой алгебрыБулева алгебра имеет дело с операциями над логическими значениями, а значения ее переменных являются только значениями истинности, т. е. истина и ложь . Обычно это обозначается 1 и 0. Булева алгебра также называется логической алгеброй или бинарной алгеброй и существует в основной ветви абстрактной алгебры.
Операции, выполняемые над булевой алгебройНиже приведены основные операции, которые выполняются над булевой алгеброй:
Не операции также называются отрицанием и представляются как ¬ или !
или операция известна как дизъюнкция и представлена как ∨ или I
, где
и операция также определяется как соединение и представлен как ∧ или &&
∧ или && ∧ OR && ∧ OR && OR && 9004 ∧ OR && OR && 9000 3 OR. алгебраические операции
алгебраические операции Операции булевой алгебры могут быть представлены диаграммой Венна путем затенения перекрывающихся областей.
Диаграмма Венна, представляющая конъюнкции, дизъюнкции и отрицания, выглядит следующим образом:
Булевы выражения:Булевы выражения — это логические операторы, которые записываются с помощью логических операторов.
Например:
X OR Y
A AND B
(Здесь ИЛИ и И — логические операторы)
Таблица истинности:Таблица истинности содержит все возможные логические значения логических переменных и их комбинации.
| A | B | A ∨ B | A ∧ B |
| True (1) | True (1) | True (1) | True (1 ) |
| Верно (1) | Ложно (0) | Верно (1) | Ложно (0) |
| Ложно (0) | Верно (1) 292 Верно (1)0293 | True (1) | False (0) |
| False (0) | False (0) | False (0) | False (0) |
| A | — A |
| TRUE (1) | FALSE (0) |
| ЛОЖЬ (0) | TRUE (1) |
 которые используются для решения булевых алгебраических выражений:
которые используются для решения булевых алгебраических выражений:х . 0 = 0
х . 1 = х
х . х = х
х . x՟ = 0
x + 0 = x
x + 1 = 1
x + x = x
x + x՟ = 1
x + x̿ = 1
(Это означает, что результатом двойной инверсии переменной является исходная переменная.)
(х.у) . г = х . (y . z)
(x + y) + z = x + (y + z)
x . (y.z) = (x.y) + (x.z)
x + (y.z) = (x + y) . (x.z)
x . у = у . x
у = у . x
x + y = y + x
Решение выражений булевой алгебры по закону Де Моргана:Наиболее часто используемые теоремы для решения булевой алгебры — это законы Де Моргана. Они бывают двух типов: первый закон де Моргана и второй закон де Моргана.
Первый закон Де Моргана: ( x . y)’ = x’ + y’
Он гласит, что сумма их индивидуальных дополнений переменных равна дополнению произведения переменных.
Таблица истинности для проверки первого закона Де Моргана:
| x | y | x’ | y’ | (x . y)’ | x’ + y’ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 |
 у’
у’ Он утверждает, что дополнение суммы переменных равно произведению их отдельных дополнений или наоборот.
Truth table to verify De Morgan Second Law:
| x | y | x’ | y’ | (x . y)’ | x ‘ + у’ |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
Boolean algebra expressions can be written in different forms and their result can be generated with truth tables by с помощью калькулятора булевой алгебры.

 Мы всегда стараемся выполнять любые работы и задания раньше срока.
Мы всегда стараемся выполнять любые работы и задания раньше срока.
 Компьютер и его программное обеспечение
Компьютер и его программное обеспечение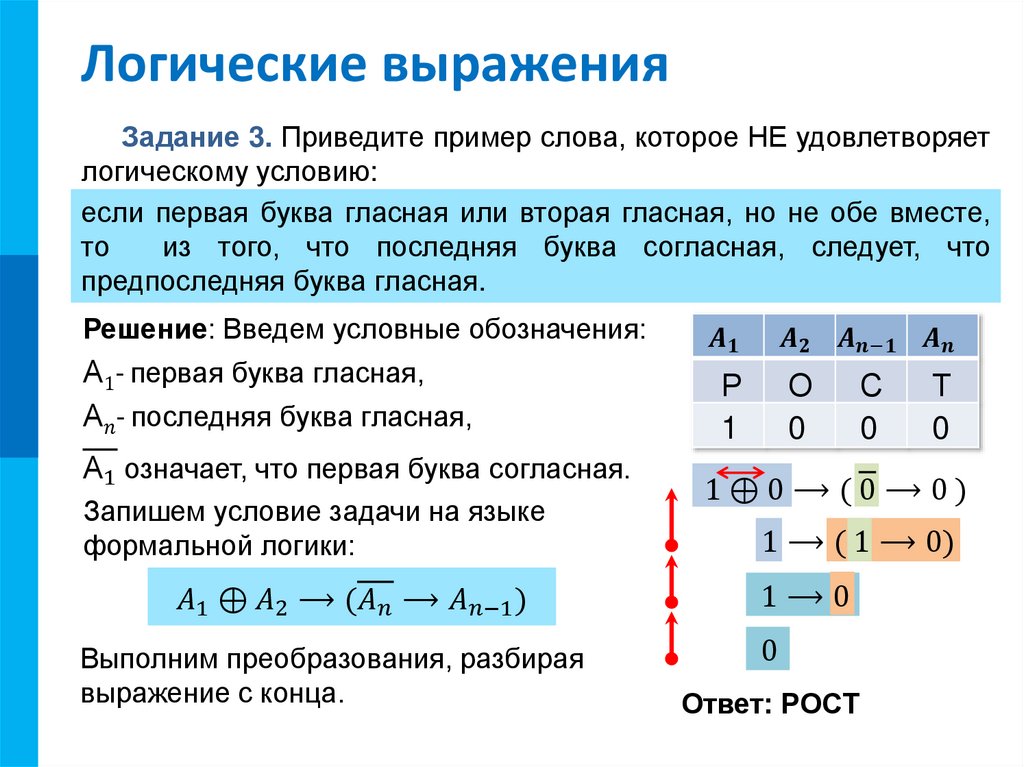 Современные технологии создания и обработки информационных объектов
Современные технологии создания и обработки информационных объектов Чтобы «p и q» были истинными, нам нужно, чтобы оба утверждения были истинными. Поскольку одно ложно, «p и q» ложны.
Чтобы «p и q» были истинными, нам нужно, чтобы оба утверждения были истинными. Поскольку одно ложно, «p и q» ложны.