Решение онлайн неравенств с решением: Решение логарифмических неравенств онлайн · Как пользоваться Контрольная Работа РУ

Решение неравенств онлайн со сложными дробно-рациональными дробями

Решение неравенств онлайн со сложными дробно-рациональными дробями

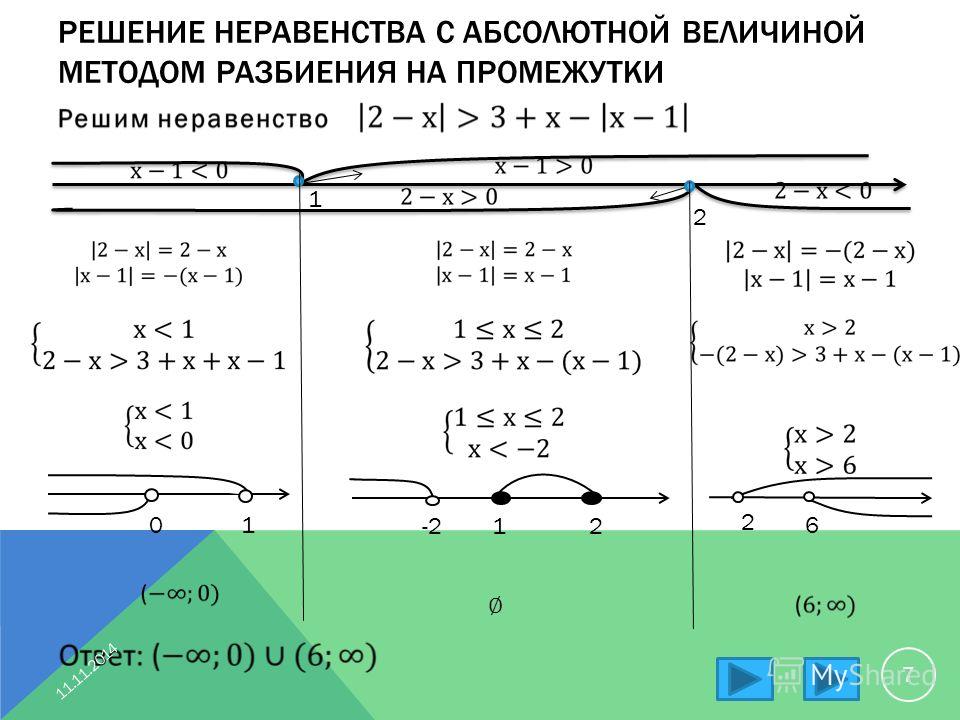
Решение неравенств со сложными  дробно-рациональными дробями Вначале необходимо определить область допустимых значений. Знаменатель дроби не может равняться 0. Поэтому не может равняться нулю и каждый из множителей, входящих в знаменатель. Поэтому запишем такую систему уравнений Решаем неравенство методом интервалов.Решаем вспомогательные уравнения. Уравнение 1 Теперь решение исходного уравнения разбивается на отдельные случаи. Случай 1.1 Перенесем известные величины в правую часть уравнения. Итак,ответ этого случая: . Случай 1.2 Перенесем известные величины в правую часть уравнения. Итак, ответ этого случая: . Ответ этого уравнения: . Уравнение 2 Находим дискриминант. Дискриминант равен нулю, значит,  уравнение имеет один корень. Воспользуемся формулой корней квадратного уравнения. Ответ этого уравнения: Уравнение 3 Перенесем известные величины в правую часть уравнения. Ответ этого уравнения: Отметим найденные критические точки и соответствующие им интервалы на числовой прямой. Теперь чтобы продолжить это неравенство онлайн надо провести расчет знаков. Случай 1 Удобно взять вот такое значение из этого интервала Итак, этот случай удовлетворяет неравенству. Случай 2: . Посчитаем, какого знака будет неравенство, если взять число из этого интервала Итак, этот случай не удовлетворяет неравенству. Случай: Выберем из этого интервала значение Итак, этот случай удовлетворяет неравенству.

Случай 4: . В это случае легко просчитать знаки Итак, этот случай удовлетворяет неравенству. Случай : . Пусть Итак, этот случай не удовлетворяет неравенству. Случай 6: Для определения знака на последнем промежутке возьмем вот такое целое значение x Итак, этот случай удовлетворяет неравенству. Полученное решение отметим на рисунке. При решении неравенства онлайн указываем окончательный ответ:

PHP

Алгебраические преобразования, уравнения, неравенства

Другое

Логарифмические, показательные уравнения , неравенства

Начала анализа

Планиметрия

Прогрессии

Стереометрия

Текстовые задачи

Тригонометрия

Числа и выражения

Онлайн калькулятор: Уравнивание химических реакций

УчебаХимия

Калькулятор для уравнивания, или балансирования химических реакций.

Калькулятор ниже предназначен для уравнивания химических реакций.

Как известно, существует несколько методов уравнивания химических реакций:

• Метод подбора коэффициентов
• Математический метод
• Метод Гарсиа
• Метод электронного баланса
• Метод электронно-ионного баланса (метод полуреакций)

Последние два применяются для окислительно-восстановительных реакций

Данный калькулятор использует математический метод — как правило, в случае сложных химических уравнений он достаточно трудоемок для ручных вычислений, но зато прекрасно работает, если все за вас рассчитывает компьютер.

Математический метод основан на законе сохранения массы. Закон сохранения массы гласит, что количество вещества каждого элемента до реакции равняется количеству вещества каждого элемента после реакции. Таким образом, левая и правая части химического уравнения должны иметь одинаковое количество атомов того или иного элемента. Это дает возможность балансировать уравнения любых реакций (в том числе и окислительно-восстановительных). Для этого необходимо записать уравнение реакции в общем виде, на основе материального баланса (равенства масс определенного химического элемента в исходных и полученных веществах) составить систему математических уравнений и решить ее.

Рассмотрим этот метод на примере:

Пусть дана химическая реакция:

Обозначим неизвестные коэффициенты:

Составим уравнения числа атомов каждого элемента, участвующего в химической реакции:
Для Fe:
Для Cl:
Для Na:
Для P:
Для O:

Запишем их в виде общей системы:

В данном случае имеем пять уравнений для четырех неизвестных, причем пятое можно получить умножением четвертого на четыре, так что его можно смело отбросить.

Перепишем эту систему линейных алгебраических уравнений в виде матрицы:

Эту систему можно решить методом Гаусса. Собственно, не всегда будет так везти, что число уравнений будет совпадать с числом неизвестных. Однако прелесть метода Гаусса в том, что он как раз и позволяет решать системы с любым числом уравнений и неизвестных. Специально для этого был написан калькулятор Решение системы линейных уравнений методом Гаусса с нахождением общего решения, который и используется при уравнивании химических реакций.

То есть калькулятор ниже разбирает формулу реакции, составляет СЛАУ и передает калькулятору по ссылке выше, решающему СЛАУ методом Гаусса. Решение потом используется для отображения сбалансированного уравнения.

Химические элементы следует писать так, как они написаны в таблице Менделеева, т. е. учитывать большие и маленькие буквы (Na3PO4 — правильно, na3po4 — неправильно).

Уравнение химической реакции

Уравнение химической реакции

Сбалансированное уравнение

 

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Решение неоднородной системы линейных алгебраических уравнений матричным методом
• • Решение системы линейных алгебраических уравнений методом Гаусса с сохранением дробей
• • Метод секущих
• • Метод итераций (метод последовательных приближений)
• • Метод бисекции
• • Раздел: Химия ( 14 калькуляторов )

 #наука #химия баланс балансирование математический метод реакция уравнение Химия

 PLANETCALC, Уравнивание химических реакций

Timur2020-11-03 14:19:33

Решение линейных неравенств (Алгебра 1, Линейные неравенства) – Mathplanet

График линейного неравенства с одной переменной представляет собой числовую прямую. Используйте открытый кружок для < и > и закрытый кружок для ≤ и ≥.

График для x > -3

График для x ≥ 2

Неравенства, имеющие одно и то же решение, называются эквивалентными. Есть свойства неравенства, а есть свойства равенства. Все приведенные ниже свойства верны и для неравенств с участием ≥ и ≤.

Свойство сложения неравенства гласит, что добавление одного и того же числа к каждой части неравенства дает эквивалентное неравенство

$$If \: x>y,\: then\: x+z>y+z$$

$$If\: x

Свойство вычитания неравенства говорит нам, что вычитание одного и того же числа из обеих частей неравенства дает эквивалентное неравенство.

$$If \: x>y,\: then\: x-z>y-z$$

$$If\: x

Свойство умножения неравенства говорит нам, что умножение обеих частей неравенства с положительным числом дает эквивалентное неравенство.

$$Если \: x>y \: и\: z>0,\: то\: xz>yz$$

$$If\: x0,\: then\: xz

Умножение в каждой части неравенства с отрицательным числом, с другой стороны, не дает эквивалентного неравенства, если мы также не изменяем направление символа неравенства

$$Если \: x>y \: и\: z<0,\: то\: xz

$$Если\: xyz$$

То же самое относится и к свойству деления неравенства.

Деление обеих частей неравенства на положительное число дает эквивалентное неравенство.

$$If \: x>y \: and\: z>0,\: then\: \frac{x}{z}>\frac{y}{z}$$

$$If\: x0,\: then\: \frac{x}{z}<\frac{y}{z}$$

И деление в обе стороны неравенства с отрицательным числом дает эквивалентное неравенство, если символ неравенства перевернуть.

$$If \: x>y \: and\: z<0,\: then\: \frac{x}{z}<\frac{y}{z}$$

$$If\: x\frac{y}{z}$$

при решении многошаговых уравнений. Возьмите одну вещь за раз, желательно, начиная с изоляции переменной от констант. При решении многошаговых неравенств важно не забывать менять знак неравенства при умножении или делении отрицательных чисел.

---

Пример

Решить неравенство

$$-2\left ( x+3 \right )<10$$

$$-2x-6<10$$

$$-2x-6 \, {\color{green}{ +\, 6}<10\, {\color{green} {+\, 6}}$$

$$-2x<16$$

$$\frac {-2x}{{\color{green}{-2}}}\: {\color{blue} {>}}\: \frac{16}{{\color{green} {- 2}}}$ $

$$x>-8$$

---

Решить линейное неравенство

$$ -2\left (x+2 \right ) > 4 — x$$

Калькулятор неравенства — Примеры, Калькулятор неравенства онлайн

Калькулятор неравенства помогает рассчитать значение переменной в соответствии с заданным неравенством. Неравенство — это отношение, которое сравнивает два числа или алгебраические выражения. В отличие от уравнений математические выражения в неравенствах не равны.

Что такое калькулятор неравенства?

Калькулятор неравенства — это онлайн-инструмент, который помогает вычислить значения переменной для заданного неравенства. В неравенстве два выражения связаны друг с другом с помощью знаков «больше», «меньше» или «равно». Чтобы использовать это неравенство калькулятор введите значения в поля ввода.

Калькулятор неравенства

Как пользоваться калькулятором неравенства?

Чтобы найти значение переменной для данного неравенства с помощью онлайн-калькулятора неравенства, выполните следующие шаги:

• Шаг 1: Перейдите к онлайн-калькулятору неравенства Cuemath.
• Шаг 2: Введите неравенство в поле ввода калькулятора неравенства.
• Шаг 3: Нажмите кнопку «Решить» , чтобы вычислить значение переменной для заданного неравенства.
• Шаг 4:
  Нажмите кнопку «Сброс», чтобы очистить поля и ввести новые значения.

Как работает калькулятор неравенства?

Математические выражения, в которых обе стороны не равны, называются неравенствами . Если между двумя алгебраическими выражениями стоит знак «равно», это означает, что эти две величины равны. Однако, когда необходимо сравнить две неравные величины, используются неравенства. Ниже приведены шаги для решения неравенства.

1. Если в неравенстве есть дроби, умножьте все члены на знаменатель этой дроби.
2. Сдвиньте все члены с переменными (здесь x) в одну сторону неравенства (скажем, в левую часть или L.H.S).
3. Сдвиг всех постоянных членов в другую сторону или в правую сторону (вправо).
4. Решите LHS, используя арифметические операции.
5. Далее, решите правую сторону, чтобы получить одно слагаемое. Если переменная на LHS не имеет коэффициента, это будет решением неравенства.
6. Если переменная имеет коэффициент, разделите правую шкалу на это значение, чтобы получить ответ.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Решенные примеры на калькуляторе неравенства

Пример 1:

Решить данное неравенство 2x + 5 > 11 и проверить его с помощью калькулятора неравенства?

Решение :

Дано: Уравнение 2x + 5 > 11

Объедините одинаковые члены с каждой стороны неравенства, т. е. переменные и константы

2x > 11 — 5

Пример 2:

Решить данное неравенство 2x — 6 < 12x + 14 и проверить его с помощью калькулятора неравенств?

Решение :

Дано: Уравнение 2x — 6 < 12x + 14

Объедините одинаковые члены с каждой стороны неравенства, т.