примеры решения производных
Производная функции является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.
Таблица производных и правила дифференцирования
Основные ссылки — таблица производных, правила дифференцирования и примеры решений (10 шт).
ПримерЗадание. Найти производную функции
Решение. Так как производная суммы равна сумме производных, то
Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
Ответ.
Больше примеров решений →
Производные сложных функций
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание.Найти производную функции
Решение. По правилу дифференцирования сложной функции:
В свою очередь производная также берется по правилу дифференцирования сложной функции:
Ответ.
Больше примеров решений →
Применение дифференциала в приближенных вычислениях
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Геометрический смысл производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Механический смысл производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Точка движется по закону .
Чему равна скорость в момент времени ?
Точка движется по закону .
Чему равна скорость в момент времени ?
Решение. Найдем скорость точки как первую производную от перемещения:
В момент времени скорость равна
Ответ.
Больше примеров решений →
Уравнение касательной, нормали и угол между прямыми
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Записать уравнение касательной к графику функции в точке
Решение. Найдем значение функции в заданной точке:
Найдем производную заданной функции по правилу дифференцирования произведения:
Вычислим её значение в заданной точке
Используя формулу
запишем уравнение касательной:
Ответ. Уравнение касательной:
Больше примеров решений →
Производные высших порядков
Основные ссылки — теоретический материал и
примеры решений (10 шт).
Задание. Найти производную второго порядка от функции
Решение. Находим первую производную как производную сложной функции:
Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель — — есть сложной функцией:
Ответ.
Больше примеров решений →
Механическое смысл второй производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
Пример Задание. Уравнение движения материальной точки вдоль оси имеет вид (м). Найти ускорение точки в момент времени c.Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:
Первая производная
(м/с)
вторая производная
(м/с2)
В момент времени c
(м/с2)
Ответ. (м/с2)
(м/с2)
Больше примеров решений →
Дифференциалы высших порядков
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти дифференциал третьего порядка функции
Решение. По формуле
Найдем третью производную заданной функции:
Тогда
Ответ.
Больше примеров решений →
Производная функции, заданной неявно
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Производная функции, заданной параметрически
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Логарифмическое дифференцирование
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти производную функции
Найти производную функции
Решение. Применим логарифмическое дифференцирование:
Тогда, продифференцировав левую и правую часть, будем иметь:
Отсюда получаем, что
Ответ.
Больше примеров решений →
Формулы Маклорена и Тейлора
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Вы поняли, как решать? Нет?
Помощь с решением
Решение производных
Для того чтобы понять определение производной рассмотрим следующий график функции.
Рис.1. Пример функции и ее производной.
Глядя на рисунок можно увидеть места, где функция растет быстрее, а где убывает. Например, с точки a до точки b график поднимается стремительнее, чем с точки b до точки c.
Например, с точки a до точки b график поднимается стремительнее, чем с точки b до точки c.
Если перенести точки с графика функции на новую систему координат таким образом, чтобы точки возрастания располагались выше по оси x, а точки убывания ниже оси x (соблюдая масштаб) и соединить эти точки, то получится новый график новой функции (нижний график на рис. 1). Данная функция и есть производная от основной функции. Данный график есть не что иное, как показатель скорости изменения функции. Другими словами, производная – показатель скорости изменения функции. На практике производные применяются для определения скорости изменения каких-нибудь процессов: физических, химических, экономических и т.д.
Если говорить более сложным языком, то производная – это предел, к которому стремится отношение приращения x к приращению y. В общем виде производная функция выглядит и определяется следующим образом:
Процесс вычисления производной функции называется дифференцированием. 2+6x-72
2+6x-72
Решение сложных производных
На практике с решением производных сложных функций приходится сталкиваться значительно чаще, чем с простыми.
Правило определения производной сложной функции выглядит следующим образом:
(a(b))’=a’(b)*b’, где a-внешняя функция, b-внутренняя функция.
Рассмотрим пример
Необходимо найти производную функции F(x)=sin(3x-5)
Найти производную данной функции, воспользовавшись таблицей простых (элементарных) функций, не получится, так как под sin находится целое выражение, т.е. функция состоит из двух функций a=sin(x)(внешняя функция) и b=3x-5 (внутренняя функция).
Воспользуемся правилом определения производной сложной функции и получим:
F’(x)=(sin(3x-5))’=cos(3x-5)*(3x-5)’=3cos(3x-5).
заметка: деревянные окна (http://www.woodlan.ru/) и Продвижение товара и услуг в интернете недорого от частного специалиста подробнее на http://seoshnig.ru.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Пример 1. Найти производную функции
Найти производную функции
y = cos 2x
Решение. Воcпользовавшись формулой для производной сложной функции y = cos (kx + b) в случае, когда k = 2, b = 0, получим
(cos 2x)’ = – 2sin 2x .
Замечание. Очень часто школьники, а также и студенты, при решении примера 1 пишут:
(cos 2x)’ = – sin 2x .
Это ошибка !!!
Перепишем верный ответ еще раз:
(cos 2x)’ = – 2sin 2x .
Приведем также верные ответы в похожих примерах:
Пример 2. Найти производную функции
y = sin3x
Решение. Воcпользовавшись формулой для производной сложной функции y = ( f (x)) c в случае, когда f (x) = sin x , а c = 3, получим
Ответ:
Пример 3. Найти производную функции
Найти производную функции
y = (3x – 7)5 .
Решение. Воcпользовавшись формулой для производной сложной функции y = (kx + b)c в случае, когда k = 3, b = – 7, а c = 5, получим
y’ = 15(3x – 7)4 .
Ответ:
Пример 4 . Найти производную функции
Решение. Поскольку
,
то исходную функцию можно переписать в виде
Воcпользовавшись формулой для производной сложной функции y = ( f (x)) c в случае, когда
,
а c = 8, получим
Ответ:
Пример 5 . Найти производную функции
Решение. Воcпользовавшись правилом 5 для вычисления производной частного двух функций и формулой для производной сложной функции y = arccos (kx + b) в случае, когда k = 3, b = 0, получим
Воcпользовавшись правилом 5 для вычисления производной частного двух функций и формулой для производной сложной функции y = arccos (kx + b) в случае, когда k = 3, b = 0, получим
Ответ:
.Пример 6. Найти производную функции
Решение. Воcпользовавшись правилом 4 для вычисления производной произведения двух функций, формулой для производной сложной функции y = arctg (kx + b) в случае, когда k = 5, b = 0, и формулой для производной сложной функции y = akx + b в случае, когда a = 3, k = 2, b = 0, получим
Ответ:
Пример 7 . Найти производную функции
Решение. Поскольку
то, воcпользовавшись формулой для производной сложной функции y = e f (x) в случае, когда , и формулой для производной сложной функции y = (kx + b)c в случае, когда с = – 1, k = 7, b = – 1, получим
Ответ:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Производная дроби — доказательство — примеры
Формула производной дроби
Пусть функции и определены в некоторой окрестности точки и имеют в точке производные. И пусть . Тогда их частное имеет в точке производную, которая определяется по формуле:
(1) .
Доказательство
Введем обозначения:
;
.
Здесь и являются функциями от переменных и . Но для простоты записи мы будем опускать обозначения их аргументов.
Далее замечаем, что
;
.
По условию функции и имеют производные в точке , которые являются следующими пределами:
;
.
Из существования производных следует, что функции и непрерывны в точке . Поэтому
;
.
Рассмотрим функцию y от переменной x, которая является дробью из функций и :
.
Рассмотрим приращение этой функции в точке :
.
Умножим на :
.
Отсюда
.
Теперь находим производную:
.
Итак,
.
Формула доказана.
Вместо переменной можно использовать любую другую переменную. Обозначим ее как x. Тогда если существуют производные и , причем , то производная дроби, составленной двух функций, определяется по формуле:
.
Или в более короткой записи
(1) .
Доказательство вторым способом
Примеры
Здесь мы рассмотрим простые примеры вычисления производной дроби, применяя формулу производной частного (1). Заметим, что в более сложных случаях, находить производную дроби проще с помощью логарифмической производной.
Пример 1
Найдите производную дроби
,
где , , , – постоянные.
Решение
Применим правило дифференцирования суммы функций:
.
Производная постоянной
.
Из таблицы производных находим:
.
Тогда
;
.
Заменим на и на :
.
Теперь находим производную дроби по формуле
.
.
Ответ
.
Пример 2
Найти производную функции от переменной x
.
Решение
Применяем правила дифференцирования, как в предыдущем примере.
;
.
Применяем правило дифференцирования дроби
.
.
Раскрываем скобки.
.
Ответ
.
Пример 3
Найти производную дроби
.
Решение
Из таблицы производных находим:
.
Применяем правила дифференцирования суммы и постоянной.
;
.
Применяем формулу для производной дроби:
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано: Изменено:
Производная | ЕГЭ по математике (профильной)
Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:
$f'(x_0)={lim}↙{△x→0}{△f(x_0)}/{△x}$
Дифференцированием называют операцию нахождения производной.
Решение:
1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции
$v(t) = x'(t) = 1,5·2t -3 = 3t -3$
2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:
$3t-3 = 12$
$3t = 15$
$t = 5$
Ответ: $5$
Геометрический смысл производной
Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.
$k = tgα$
Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:
$f'(x_0) = k$
Следовательно, можем составить общее равенство:
$f'(x_0) = k = tgα$
На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.
На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.
На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.
На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.
Решение:
Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$
Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.
Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)
$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$
$f'(x_0) = tg ВАС = 0,25$
Ответ: $0,25$
Производная так же применяется для нахождения промежутков возрастания и убывания функции:
Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.
Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.
На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.
В ответ запишите количество данных точек.
Решение:
Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.
В выделенных интервалах находятся точки $х_2, х_4$. 6, {x, 3}]
6, {x, 3}]
| Out[1]= |
Или несколько раз запишем символ штриха:
| In[2]:= | ⨯Sin''[x] |
| Out[2]= |
Также, как и в предыдущих разделах, формулы математического анализа доступны через естественную форму ввода:
| In[1]:= | Xproduct rule formula |
| Out[1]= |
Справочная информация: Математический анализ »
Hands–on Start to
Wolfram Mathematica »
Полная документация »
Demonstrations Project »
2 \ right) + \ dfrac {d} {dx} (\ cos x) = \,… $Правило продукта для производных
\ begin {align *}
\ dfrac {d} {dx} (fg) & = \ left (\ dfrac {d} {dx} f \ right) g + f \ left (\ dfrac {d} {dx} g \ right) \\ [8px]
& = \ Big [\ text {(производное от 1-го)} \ times \ text {(2-е)} \ Big] + \ Big [\ text {(1-е)} \ times \ text {(производное от 2-го )}\Большой]
\ end {align *}
IV.
 2} \\ [8px]
& = \ dfrac {{\ Big [\ text {(производная от числителя)} \ times \ text {(знаменатель)} \ Big] — \ Big [\ text {(числитель)} \ times \ text {(производная от знаменателя )}} \ Big]} {\ text {все делится на [знаменатель, в квадрате]}}
2} \\ [8px]
& = \ dfrac {{\ Big [\ text {(производная от числителя)} \ times \ text {(знаменатель)} \ Big] — \ Big [\ text {(числитель)} \ times \ text {(производная от знаменателя )}} \ Big]} {\ text {все делится на [знаменатель, в квадрате]}} \ end {align *}
Многие студенты помнят правило частного, думая о числителе как о «привет», а о демонинаторе — как «Lo», производная как «d», а затем пение
«lo d-hi minus hi d-lo over lo-lo»
[свернуть]
6.Производные продукты и коэффициенты
М. Борна
ПРАВИЛО ПРОДУКТА
Если u и v — две функции x , то производная от произведения uv дается как …
`(d (uv)) / (dx) = u (dv) / (dx) + v (du) / dx`
На словах это можно запомнить как:
«Производная произведения двух функций — это первое, умноженное на производное второго, плюс второе, умноженное на производное первого.
«
Откуда взялась эта формула? Как и все встречающиеся нам формулы дифференцирования, она основана на производных от первых принципов.
Пример 1
Если у нас есть такой товар, как
y = (2 x 2 + 6 x ) (2 x 3 + 5 x 2 )
мы можем найти производную, не умножая выражение справа.2) `(в главе« Дифференциация трансцендентных функций ».) Это выражение нельзя умножить почленно, поэтому нам нужен метод, чтобы дифференцировать произведения таких функций.
Примечание
Мы можем написать правило продукта разными способами:
`(d (uv)) / (dx) = uv’ + vu’`
ИЛИ
`(d (fg)) / (dx)` `= f (x) d / (dx) g (x) + g (x) d / (dx) f (x)`… и т. Д.
ЧИТАТЕЛЬНОЕ ПРАВИЛО
(частное — это всего лишь дробь. 2) `
2) `
3.5 Производные тригонометрических функций — Исчисление Том 1
Цели обучения
- Найдите производные функции синуса и косинуса.
- Найдите производные стандартных тригонометрических функций.
- Вычислить производные синуса и косинуса высшего порядка.
Одним из наиболее важных типов движения в физике является простое гармоническое движение, которое связано с такими системами, как объект с массой, колеблющейся на пружине.Простое гармоническое движение можно описать с помощью функций синуса или косинуса. В этом разделе мы расширяем наши знания о формулах производных, чтобы включить производные этих и других тригонометрических функций. Мы начинаем с производных функций синуса и косинуса, а затем используем их для получения формул для производных остальных четырех тригонометрических функций. Возможность вычислять производные функций синуса и косинуса позволит нам найти скорость и ускорение простого гармонического движения.
Найдите производную от
Решение
Нахождение производной функции, содержащей
Найдите производную от.
Решение
Применяя правило частного, получаем
.Упрощая, получаем
Найдите производную от.
Решение
Приложение к скорости
Частица движется вдоль оси координат таким образом, что ее положение во времени определяется выражением для.В какое время частица находится в состоянии покоя?
Частица движется по координатной оси. Его положение в данный момент определяется формулой for. В какое время частица находится в состоянии покоя?
Решение
Поскольку оставшиеся четыре тригонометрические функции могут быть выражены как частные, включающие синус, косинус или и то, и другое, мы можем использовать правило частного, чтобы найти формулы для их производных.
Производная касательной функции
Найдите производную от.
Найдите производную от.
Решение
Производные остальных тригонометрических функций могут быть получены с помощью аналогичных методов. Мы приводим эти формулы в следующей теореме.
Нахождение уравнения касательной
Найдите уравнение прямой, касательной к графику at.
Нахождение производной тригонометрических функций
Найдите производную от.
Решение
Найдите наклон касательной к графику в.
Решение
Ключевые концепции
- Мы можем найти производные от и, используя определение производной и предельные формулы, найденные ранее. Результаты а также .
- С помощью этих двух формул мы можем определить производные всех шести основных тригонометрических функций.
Найдите для данных функций следующие упражнения.
1.
Решение
2.
3.
Решение
4.
5.
Решение
6.
7.
Решение
8.
9.
Решение
10.
Для следующих упражнений найдите уравнение касательной к каждой из заданных функций при указанных значениях.Затем используйте калькулятор, чтобы построить график функции и касательной, чтобы убедиться, что уравнение для касательной линии правильное.
12. [Т]
14. [Т]
15. [Т]
[show-answer q = ”780193 ″] Показать решение [/ show-answer]
[hidden-answer a =” 780193 ″]
16. [Т]
Найдите для данных функций следующие упражнения.
17.
Решение
18.
19.
Решение
20.
21.
Решение
22.
23. Найдите все значения на графике, где касательная линия является горизонтальной.
Решение
, где — целое число
24. Найдите все значения на графике, где касательная линия имеет наклон 2.
26. [T] Масса на пружине подпрыгивает вверх и вниз в простом гармоническом движении, моделируемом функцией где измеряется в дюймах и измеряется в секундах. Найдите скорость, с которой пружина колеблется в точке s.
Решение
30. [T] Количество осадков в месяц в Фениксе, штат Аризона, может быть приблизительно равно, где — количество месяцев, прошедших с января. Найдите и воспользуйтесь калькулятором, чтобы определить интервалы, в которые количество осадков уменьшается.
Найдите и воспользуйтесь калькулятором, чтобы определить интервалы, в которые количество осадков уменьшается.
Для следующих упражнений используйте правило частного, чтобы вывести данные уравнения.
31.
32.
33.
34. Используйте определение производной и идентичность
, чтобы доказать это.
Для следующих упражнений найдите требуемую производную высшего порядка для заданных функций.
35. из
[show-answer q = ”501872 ″] Показать решение [/ show-answer][hidden-answer a = ”501872 ″]
36. из
38. из
производная | Определение и факты
Производная , в математике, скорость изменения функции по отношению к переменной. Производные имеют фундаментальное значение для решения задач в области исчисления и дифференциальных уравнений. Как правило, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы получить скорость изменения некоторой интересующей переменной, включить эту информацию в какое-либо дифференциальное уравнение и использовать методы интегрирования для получения функции, которую можно использовать для прогнозирования поведения исходной система в различных условиях.
Как правило, ученые наблюдают за изменяющимися системами (динамическими системами), чтобы получить скорость изменения некоторой интересующей переменной, включить эту информацию в какое-либо дифференциальное уравнение и использовать методы интегрирования для получения функции, которую можно использовать для прогнозирования поведения исходной система в различных условиях.
Британская викторина
Определите: математические термины
Вот ваша миссия, если вы решите принять ее: Определите следующие математические термины до того, как истечет время.
Геометрически производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке.Фактически, его расчет происходит из формулы наклона прямой линии, за исключением того, что для кривых необходимо использовать процесс ограничения. Наклон часто выражается как «подъем» по сравнению с «пробегом» или, в декартовых терминах, отношение изменения y к изменению x . Для прямой, показанной на рисунке, формула наклона имеет вид ( y 1 — y 0 ) / ( x 1 — x 0 ). Другой способ выразить эту формулу: [ f ( x 0 + h ) — f ( x 0 )] / h , если h используется для x 1 — x 0 и f ( x ) для y .Это изменение в обозначениях полезно для перехода от идеи наклона прямой к более общей концепции производной функции.
Наклон часто выражается как «подъем» по сравнению с «пробегом» или, в декартовых терминах, отношение изменения y к изменению x . Для прямой, показанной на рисунке, формула наклона имеет вид ( y 1 — y 0 ) / ( x 1 — x 0 ). Другой способ выразить эту формулу: [ f ( x 0 + h ) — f ( x 0 )] / h , если h используется для x 1 — x 0 и f ( x ) для y .Это изменение в обозначениях полезно для перехода от идеи наклона прямой к более общей концепции производной функции.
Две точки, например ( x 0 , y 0 ) и ( x 1 , y 1 ), определяют наклон прямой линия.
Encyclopædia Britannica, Inc.
Для кривой это соотношение зависит от того, где выбраны точки, что отражает тот факт, что кривые не имеют постоянного наклона.Чтобы найти наклон в желаемой точке, выбор второй точки, необходимой для расчета отношения, представляет собой трудность, потому что, как правило, отношение будет представлять только средний наклон между точками, а не фактический наклон в любой точке ( см. рисунок ). Чтобы обойти эту трудность, используется процесс ограничения, при котором вторая точка не фиксируется, а задается переменной, например h в соотношении для прямой линии выше. Нахождение предела в этом случае — это процесс нахождения числа, к которому отношение приближается, когда h приближается к 0, так что предельное отношение будет представлять фактический наклон в данной точке.Некоторые манипуляции нужно проделать с частным [ f ( x 0 + h ) — f ( x 0 )] / h , чтобы его можно было переписать в виде в котором предел h приближается к 0, можно увидеть более прямо. Рассмотрим, например, параболу x 2 . При нахождении производной x 2 , когда x равно 2, частное составляет [(2 + h ) 2 — 2 2 ] / h .При расширении числителя частное становится (4 + 4 h + h 2 -4) / h = (4 h + h 2 ) / h . И числитель, и знаменатель по-прежнему приближаются к 0, но если h на самом деле не ноль, а только очень близко к нему, тогда h можно разделить, давая 4 + h , что легко увидеть, что приближается к 4 как h. приближается к 0.
Рассмотрим, например, параболу x 2 . При нахождении производной x 2 , когда x равно 2, частное составляет [(2 + h ) 2 — 2 2 ] / h .При расширении числителя частное становится (4 + 4 h + h 2 -4) / h = (4 h + h 2 ) / h . И числитель, и знаменатель по-прежнему приближаются к 0, но если h на самом деле не ноль, а только очень близко к нему, тогда h можно разделить, давая 4 + h , что легко увидеть, что приближается к 4 как h. приближается к 0.
Можно определить наклон или мгновенную скорость изменения кривой в определенной точке ( x 0 , f ( x 0 )). соблюдая предел средней скорости изменения, когда вторая точка ( x 0 + h , f ( x 0 + h )) приближается к исходной точке.
Подводя итог, производная от f ( x ) при x 0 , записывается как f ′ ( x 0 ), ( d f / d x ) ( x 0 ) или D f ( x 0 ), определяется, как если бы этот предел существует.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасДифференциация — i.е., вычисление производной — редко требует использования базового определения, но вместо этого может быть выполнено посредством знания трех основных производных, использования четырех правил работы и знания того, как манипулировать функциями.
Производные и задачи по физике
Упражнение 1
Уравнение прямолинейного движения: d (t) = t³ — 27t. В какой момент скорость равна нулю? Кроме того, какое ускорение сейчас?
Лучшие доступные репетиторы по математике
Первый урок бесплатноУпражнение 2
Какова скорость, с которой движется транспортное средство в соответствии с уравнением d (t) = 2 — 3t² на пятой секунде пути? В этой интуиции пространство измеряется в метрах, а время — в секундах.
Упражнение 3
Из-за плохих условий окружающей среды миллионная колония бактерий не размножается в течение первых двух месяцев исследования. Функция, которая представляет популяцию колонии в течение всего исследования (время представлено в месяцах), задается следующим образом:
1. Убедитесь, что численность населения является непрерывной функцией времени.
2. Рассчитайте среднюю скорость изменения совокупности в интервале [0, 2] и [0, 4].
3.Вычислите мгновенную скорость изменения при t = 4.
Упражнение 4
Рост бактериальной популяции представлен функцией p (t) = 5,000 + 1,000t², где t — время, измеряемое в часах. Определить:
1. Средняя скорость роста.
2. Мгновенная скорость роста.
3. Мгновенный темп роста при t 0 = 10 часов.
Упражнение 5
Уравнение кругового движения: φ (t) = ½t². Каковы угловая скорость и ускорение на семисекундной отметке?
Упражнение 6
Человек находится в 2000 м от основания башни и запускает ракету в направлении этой же башни. Когда ракета взлетает, изменение угла между траекторией полета и землей представляется как Φ (t) в зависимости от времени. Зная, что Φ ‘(t) = / 3, определите:
Когда ракета взлетает, изменение угла между траекторией полета и землей представляется как Φ (t) в зависимости от времени. Зная, что Φ ‘(t) = / 3, определите:
1. Высота ракеты при Φ = Π / 3 радиан.
2. Скорость ракеты при Φ = / 3 радиан?
Упражнение 7
Газ закачивается в сферический резервуар со скоростью 6 м³ / мин. Если давление остается постоянным, с какой скоростью изменяется размер радиуса при диаметре 120 см?
Решение упражнения 1
Уравнение прямолинейного движения: d (t) = t³ — 27t.В какой момент скорость равна нулю? Кроме того, какое ускорение сейчас?
v (t) = d′t) = 3t² — 27 3t² — 27 = 0t = ± 3
a (t) = d ′ ‘(t) = 6ta (−3) = −18a (3) = 18
Решение упражнения 2
Какую скорость движется транспортное средство в соответствии с уравнением d (t) = 2 — 3t² на пятой секунде пути? В этой интуиции пространство измеряется в метрах, а время — в секундах.
Решение упражнения 3
Из-за плохих условий окружающей среды колония из миллиона бактерий не воспроизводится в течение первых двух месяцев исследования. Функция, которая представляет популяцию колонии в течение всего исследования (время представлено в месяцах), задается следующим образом:
Функция, которая представляет популяцию колонии в течение всего исследования (время представлено в месяцах), задается следующим образом:
1. Убедитесь, что численность населения является непрерывной функцией времени.
2. Рассчитайте среднюю скорость изменения совокупности в интервале [0, 2] и [0, 4].
3. Рассчитайте мгновенную скорость изменения при t = 4.
Решение упражнения 4
Рост бактериальной популяции представлен функцией p (t) = 5,000 + 1,000t², где t — время, измеряемое в часах. Определить:
1. Средняя скорость роста.
2. Мгновенная скорость роста.
3. Мгновенная скорость роста при t 0 = 10 часов.
Решение упражнения 5
Уравнение кругового движения: φ (t) = ½t². Каковы угловая скорость и ускорение на семисекундной отметке?
ω (t) = φ ′ (t) = t ω = 7
α (t) = φ ′ ′ (t) = 1 α = 1
Решение упражнения 6
Человек на высоте 2000 м от основания башни и запускает ракету в направлении этой же башни. Когда ракета взлетает, изменение угла между траекторией полета и землей представляется как Φ (t) в зависимости от времени.Зная, что Φ ‘(t) = / 3, определите:
Когда ракета взлетает, изменение угла между траекторией полета и землей представляется как Φ (t) в зависимости от времени.Зная, что Φ ‘(t) = / 3, определите:
1. Высота ракеты при Φ = Π / 3 радиан.
2. Скорость ракеты при Φ = Π / 3 радиан?
Решение упражнения 7
Газ подается в сферический резервуар со скоростью 6 м³ / мин. Если давление остается постоянным, с какой скоростью изменяется размер радиуса при диаметре 120 см?
Дискретные аппроксимации решений и производных сингулярно возмущенного параболического уравнения конвекции – диффузии
Аннотация
В данной статье мы рассматриваем сеточные аппроксимации краевой задачи на отрезке для сингулярно возмущенное параболическое уравнение конвекции – диффузии; используются классические конечно-разностные аппроксимации на кусочно-однородных сетках, сгущающихся в окрестности пограничного слоя. Необходимо найти численные приближения как к решению, так и к его производным (первого порядка) с ошибками, слабо зависящими от параметра возмущения ε . Ошибки аппроксимации решений и производных исследуются в метрике ρ , которая подходит для захвата сингулярных решений задач с пограничными слоями. В этой метрике ошибки решения и его производной ( ∂ / ∂t ) u ( x , t ) определяются абсолютными ошибками, а ошибка производной ( ∂ / ∂x ) u ( x , t ) определяется относительной ошибкой (по отношению к мажорантной функции для этой производной) в пограничном слое и абсолютной ошибкой за его пределами.В классе сеток, размер ячеек которых в пограничном слое не уменьшается при удалении от границы, показано, что не существует сеток, на которых схема сходится равномерно ε -метрике ρ . Устанавливаются условия, накладываемые на параметры кусочно-однородных сеток, при которых схемы сходятся в метрике ρ почти ε -равномерно, то есть со скоростью O (ε − νN − 1 + N0−1), где ν > 0 может быть сколь угодно малым; N и N 0 определяют количество узлов сетки в x и t , соответственно.
Необходимо найти численные приближения как к решению, так и к его производным (первого порядка) с ошибками, слабо зависящими от параметра возмущения ε . Ошибки аппроксимации решений и производных исследуются в метрике ρ , которая подходит для захвата сингулярных решений задач с пограничными слоями. В этой метрике ошибки решения и его производной ( ∂ / ∂t ) u ( x , t ) определяются абсолютными ошибками, а ошибка производной ( ∂ / ∂x ) u ( x , t ) определяется относительной ошибкой (по отношению к мажорантной функции для этой производной) в пограничном слое и абсолютной ошибкой за его пределами.В классе сеток, размер ячеек которых в пограничном слое не уменьшается при удалении от границы, показано, что не существует сеток, на которых схема сходится равномерно ε -метрике ρ . Устанавливаются условия, накладываемые на параметры кусочно-однородных сеток, при которых схемы сходятся в метрике ρ почти ε -равномерно, то есть со скоростью O (ε − νN − 1 + N0−1), где ν > 0 может быть сколь угодно малым; N и N 0 определяют количество узлов сетки в x и t , соответственно.
Ключевые слова
Сингулярно возмущенное параболическое уравнение
Конвекция – диффузия
Конечно-разностные методы
Кусочно-однородные сетки
Параметрическая однородная сходимость
Аппроксимация производных
Нормы Резюме
Рекомендуемые статьи 0Copyright © 2003 Elsevier BV Все права защищены.
Рекомендуемые статьи
Ссылки на статьи
Уровень 1 Обучение Соответствие RG146
Обзор курса
Вы уже действующий советник и хотите стать совместимым в области знаний ASIC RG146 Derivatives?
Kaplan Professional, ведущий национальный провайдер образования в области финансовых услуг, предлагает решение Kaplan Tier 1 RG 146 Compliance Solution для существующих консультантов, которые хотят дать общие или личные советы в области знаний специалистов по деривативам.
Этот курс знакомит существующих консультантов с концепциями деривативов применительно к розничным клиентам. Также рассматриваются принципы, лежащие в основе основ, регулирования и рисков, связанных с отраслью производных финансовых инструментов. Существующим консультантам, возможно, потребуется выполнить дополнительные нормативные требования или требования лицензиата, прежде чем давать конкретные рекомендации в этих областях.
Также рассматриваются принципы, лежащие в основе основ, регулирования и рисков, связанных с отраслью производных финансовых инструментов. Существующим консультантам, возможно, потребуется выполнить дополнительные нормативные требования или требования лицензиата, прежде чем давать конкретные рекомендации в этих областях.
Существующие консультанты научатся анализировать и оценивать деривативы, а также получат понимание документации и налоговых требований при работе с портфелями розничных клиентов.
Существующие консультанты могут выбрать вариант изучения общего или личного совета для этого курса.
Общий вариант консультации: после успешного завершения этого варианта существующие консультанты будут соответствовать образовательным требованиям ASIC Regulatory Guide 146 (RG146) для предоставления общих рекомендаций по деривативам для розничных клиентов.
Вариант личного совета — Больше не открыт для новых участников : После успешного завершения этого варианта существующие консультанты будут соответствовать образовательным требованиям Руководства по регулированию ASIC 146 (RG146) для предоставления личных консультаций по производным финансовым инструментам розничным клиентам.
Единицы компетенции присуждаются только существующим консультантам, которые выполнили вариант личного совета по этому предмету. См. Схему темы «Производные инструменты уровня 1 — Персональные консультации», чтобы ознакомиться с соответствующей единицей компетенции.
Пожалуйста, обратитесь к теме для получения дополнительной информации.
Сборы
Решение соответствия уровня 1 — производные
Персональный совет: 315 долларов (без НДС) Больше не открыт для новых зачислений.
Общие консультации: 270 долларов США (без НДС)
Чтобы узнать о дополнительных сборах, связанных с обучением, нажмите здесь
Продолжительность
Общая консультация:
Физические лица всего:
- 12 недель на выполнение требований к обучению и оценке производных финансовых инструментов уровня 1 — Общие рекомендации с момента их первоначальной активации.
- Дополнительные четыре (4) недели для повторной подачи заявки — если человек достигает конца своего первоначального периода зачисления и считается еще не компетентным для сдачи экзамена, ему будут предоставлены дополнительные 4 недель, при условии, что человек попытался пройти всю оценку задачи на начальном этапе зачисления.
 Плата за это продление не взимается.
Плата за это продление не взимается.
Таким образом, если человек завершает обучение и оценку и предоставляется время повторной подачи по каждому предмету, продолжительность составит 16 недель.
Персональный совет: больше не открыт для новых зачислений.
Физические лица всего:
- 12 недель на выполнение требований к обучению и оценке для предмета «Производные инструменты уровня 1 — персональный совет» с момента их первоначальной активации.
- Дополнительные четыре (4) недели повторной подачи заявки — если человек достигает конца своего первоначального периода зачисления и считается еще не компетентным в одной или нескольких задачах, то ему будут предоставлены дополнительные 4 недель, при условии, что человек попытался все оценочные задания в течение начального периода зачисления.
Таким образом, если человек завершает обучение и оценку и предоставляется время повторной подачи по каждому предмету, продолжительность составит 16 недель.
Объем обучения по этому курсу может составлять до 10 часов в неделю. Объем обучения — это часы, которые человек может рассчитывать потратить на выполнение своей курсовой работы и оценок.
В дополнение к количеству обучения, лицам, которые плохо знакомы с отраслью или профессионально-техническим обучением, может потребоваться до 5 часов в неделю, известных как часы без учителя.Эти дополнительные часы предназначены для изучения навыков или дальнейших исследований. Например, человеку, не работающему в отрасли, потребуется больше времени, чтобы просмотреть отраслевые веб-сайты, которые обычно используются при обучении соответствию на рабочем месте.
Лица, работающие в промышленности, могут иметь возможность выполнить требования курса в более короткие сроки или за меньшее количество часов в неделю.
При формальном продлении и повторном зачислении взимается дополнительная плата за обучение. Пожалуйста, ознакомьтесь с таблицей оплаты за профессиональное образование, которую можно найти здесь.
Пожалуйста, ознакомьтесь также с нашими Правилами и условиями регистрации в профессиональном образовании и обучении (VET) здесь или в нашем Справочнике для студентов здесь, чтобы получить важную информацию о:
- Сроки активации и завершения темы
- Расширения
- Повторная регистрация субъектов
Требования к поступающим
Требования к образованиюС 1 января 2019 года новые требования FASEA к профессиональным стандартам для финансовых консультантов постепенно заменят минимальные стандарты обучения, указанные в Регламенте 146 Лицензирование: обучение консультантов по финансовым продуктам (RG 146).
RG 146 будет по-прежнему применяться к финансовым консультантам, уполномоченным их лицензиатом финансовых услуг Австралии (AFS) в качестве «существующего поставщика», до тех пор, пока к ним не будут применяться новые требования.
RG 146 также будет по-прежнему применяться к консультантам, которые не являются «соответствующими поставщиками услуг» —
- то есть те, кто дает только общие советы,
- лица, предоставляющие консультации по финансовым продуктам уровня 2 или менее
- и тех, кто дает только советы относительно схемы разделения времени.

ASIC пересмотрит и обновит свои рекомендации для консультантов, которые не являются соответствующими поставщиками.
RG 146 не будет применяться к новым участникам отрасли, стремящимся стать соответствующим поставщиком услуг с 1 января 2019 года, или существующим консультантам, предоставляющим личные консультации с 1 января 2024 года. Они должны будут соответствовать новым требованиям профессиональных стандартов FASEA.
Общий совет:
Существующие консультанты, заполняющие деривативы уровня 1 — общие рекомендации, должны будут иметь общие знания.
Персональный совет: Больше не открыт для новых зачислений.
Существующие консультанты, заполняющие деривативы уровня 1 — личный совет, должны обладать необходимыми квалификационными единицами и иметь общие знания уровня 1. Если существующие консультанты не соответствуют требованиям для поступления, они должны заполнить DFP1 «Основы финансового планирования».
Необходимые единицы:
- FNSCUS505 Определение требований и ожиданий клиентов
- FNSCUS506 Запишите и выполните инструкции клиента.
Физические лица должны быть в возрасте 18 лет или старше, чтобы записаться на этот предмет.
Этот курс требует, чтобы вы прочитали исчерпывающие учебные пособия для учащихся, выполнили ряд письменных оценок, предприняли независимые исследования и время от времени участвовали в онлайн-форумах и обсуждениях. Кроме того, способ доставки основан на широком использовании письменного общения.
Если у вас есть какие-либо сомнения относительно наличия у вас языковых навыков, грамотности и навыков счета для прохождения программы Kaplan Professional, мы рекомендуем вам поговорить с нашей службой поддержки студентов по телефону 1300 662 203 или по электронной почте @ kaplan.edu.au.
Рекомендуемые браузеры
Вы можете получить доступ к KapLearn с помощью любого из указанных ниже браузеров, но лучше всего он работает в последних версиях:
- Firefox 3 или более поздней версии
- Chrome 4 или новее
- Safari 3 или новее
- Internet Explorer
Возможно, вам будет полезно установить на вашем компьютере несколько браузеров. Если у вас возникли проблемы при использовании системы онлайн-обучения Kaplan, попробуйте использовать другой браузер.
Если у вас возникли проблемы при использовании системы онлайн-обучения Kaplan, попробуйте использовать другой браузер.
Настройки и поддержка браузера
Для максимального удобства пользователей в системе онлайн-обучения Kaplan выберите следующие настройки браузера:
- включить куки
- включить JavaScript
- не блокировать всплывающие окна
Приложение для записи звука
Вам нужно будет использовать бесплатное или платное приложение для записи звука на телефоне, планшете или компьютере, чтобы записать и отправить свое устное задание. Большинство устройств поставляются со встроенным бесплатным приложением для записи звука и голоса.Дополнительная информация должна быть доступна в руководстве к вашему устройству или на веб-сайте производителя устройства. Ниже приведены справочные ссылки для некоторых популярных устройств.
Для успешного завершения этой квалификации людям потребуются базовые навыки работы с компьютером. Это может включать:
Это может включать:
- сохранение и редактирование документов Microsoft Office
- поиск, доступ и поиск в Интернете
- загрузка и сохранение документов с веб-сайтов
- загрузка документов через веб-сайты
- создание аудиозаписи с помощью смартфона, планшета или компьютера
- участвуют в онлайн-обсуждениях
Информация о зачислении
Вы можете записаться на этот курс в любое время и начать обучение сразу после регистрации.*
Чтобы зарегистрироваться онлайн, выполните следующие действия:
- В раскрывающемся списке «Категория» выберите Финансовые услуги — Уровень 1
- В раскрывающемся списке «Искать по» выберите тему
- Если вы просто нажмете кнопку поиска, отобразятся все предметы уровня 1, и вы сможете записаться на несколько предметов
или
- Вы можете найти конкретный предмет, на который вы хотите записаться, введя название предмета и нажав поиск.

Доставка
Этот курс проводится онлайн с помощью системы управления обучением Kaplan KapLearn.
Вы получите данные для входа в KapLearn после регистрации. Когда вы входите в KapLearn, вы получаете доступ к предметным заметкам, оценкам, дополнительным учебным материалам, таким как СМИ, тематические исследования, практические занятия и ваш онлайн-наставник.
Оценки доступны и отправляются через KapLearn.
Корпоративным клиентам следует связаться с нашим представителем по корпоративным решениям по телефону
1300 728 505, чтобы обсудить варианты личного общения и способы адаптации нашего обучения к потребностям вашего бизнеса.
Признание предшествующего обучения
Физические лица могут иметь возможность получить Признание предшествующего обучения (RPL) по предмету награды Kaplan на основе их предыдущего обучения и / или опыта работы. Для этого люди должны представить доказательства, подтверждающие, что они уже выполнили требования субъекта с помощью этих других средств.
Доказательства могут принимать различные формы, такие как информация об утвержденном исследовании, информация об опыте работы, сертификаты, стенограммы или другие учетные данные.
Чтобы узнать, имеете ли вы право на RPL, перейдите на нашу страницу «Перевод кредитов и признание предшествующего обучения» (RPL).
* Если вы ранее не изучали общие знания, убедитесь, что вы записались на этот предмет, поскольку он является предварительным условием для областей знаний уровня 1.
Оценка
Оценки по каждому предмету перечислены ниже. Единицы компетенции оцениваются совместно по темам внутри предметов, как указано в «Единицах компетенции».
| Предмет | Оценка | Детали оценки |
|---|---|---|
| Производные инструменты уровня 1 — Общие рекомендации | 1 Экзамен | Экзамен по открытой книге с множественным выбором под наблюдением, три (3) попытки.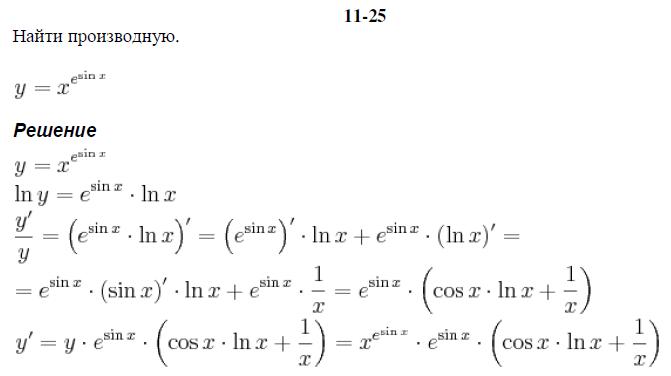 |
| Производные финансовые инструменты Уровня 1 — Персональные консультации | 1 Экзамен | Контрольный экзамен по открытой книге с множественным выбором, четыре (4) попытки. |
| 1 Письменное и устное задание | Письменное и устное задание — две (2) попытки • Письменное — подготовка серии рекомендаций по продукту и стратегии для ряда тематических исследований в соответствии с законодательными и передовыми практическими рекомендациями. • Устная — ролевая игра Устная оценка — аудиозапись. В рамках требований курса людям необходимо будет найти волонтера, который поможет им с их ролевой игрой в устном задании. |
Физические лица могут попытаться сдать экзамен и / или представить свои письменные и устные задания в любое время, если они считают, что они достаточно подготовлены. По мере приближения сроков сдачи экзаменов люди будут получать электронные письма с личными напоминаниями.
Для получения персональной консультации, лица должны считаться компетентными по всем пунктам оценивания, включая демонстрацию компетентности по всем вопросам экзамена, чтобы получить их квалификацию или курс.
Чтобы узнать больше о том, чего ожидать при выполнении устного задания с использованием аудио, щелкните здесь.
Лица, завершившие предмет «Личный совет», получат справку о достижении.
Экзамены Каплана
Вы можете сдать экзамен под присмотром на рабочем месте или в офисе Kaplan Professional.
Щелкните здесь, чтобы узнать время и место проведения экзаменов в офисе Kaplan Professional.
Политики
Студенческие политики
Лица, записывающиеся на курс Kaplan Professional, обязаны соблюдать наши опубликованные политики, в том числе политику, устанавливающую наши правила оценки.Физические лица могут ознакомиться с этими правилами здесь. Политика также помогает людям, когда их учебная программа идет не так, как запланировано, и им требуется дополнительная поддержка.

 «
« Плата за это продление не взимается.
Плата за это продление не взимается.
