Решение логарифмических неравенств
Множество решений представляет собой числовой интервал \(\ (-4 ; 1) \), на котором левая часть последнего неравенства отрицательна (есть знак минус). Принимая во внимание ДВУ, мы получаем решение данного неравенства: \(\ x \in(-1 ; 1) \)
\(\ x \in(-1 ; 1) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Квадратные неравенства и их решение Бесконечная убывающая геометрическая прогрессия и ее формулы Формула n-го члена геометрической прогрессии Формула n-го члена арифметической прогрессии
Узнать цену работы
Узнай цену
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПринимаю Политику конфиденциальности
Подпишись на рассылку, чтобы не пропустить информацию об акциях
Логарифмические неравенства.
 2{(x+1)}+10≤11 \lg{(x+1)}\)
2{(x+1)}+10≤11 \lg{(x+1)}\)
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
Примеры:
|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)\({(x+1)}\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства. 2-24≥-x\) невозможен.
2-24≥-x\) невозможен.
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\) |
Выпишем ОДЗ. |
|
|
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\) |
ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами. |
|
|
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\) |
Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) |
|
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\) |
Мы привели неравенство к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем. |
|
|
\(\frac{3x-2}{2x-3}\)\(≥\) \(3\) |
Переносим \(3\) и приводим к общему знаменателю, пользуясь свойствами дробей. |
|
|
\(\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\) |
Раскрываем скобки, приводим подобные слагаемые. |
|
|
\(\frac{-3x+7}{2x-3}\)\(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
|
\(\frac{3x-7}{2x-3}\)\(≤\) \(0\) |
Далее выносим \(3\) из числителя и \(2\) из знаменателя. |
|
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\) |
|
|
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
|
Записываем окончательный ответ. |
Раскладываем левую часть неравенства на множители. |
|
\(D=1+8=9\) |
Решаем неравенство методом интервалов. |
|
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену. |
|
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
|
Запишем ответ. |
Ответ: \((0; \frac{1}{3})∪(9;∞)\)
Смотрите также:
Показательные неравенства
11 класс. Алгебра. Показательная и логарифмическая функции.
 Логарифмические уравнения и неравенства. — Решение логарифмических неравенств.Комментарии преподавателя
Логарифмические уравнения и неравенства. — Решение логарифмических неравенств.Комментарии преподавателяРешение логарифмических неравенств
Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т.е. функции вида (). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.
Вспомним основные свойства логарифмической функции.
Рис. 1. График логарифмической функции при различных основаниях
Функция монотонна на всей своей области определения. При монотонно возрастает, т.е. большему значению аргумента соответствует большее значение функции, . При монотонно убывает, т.е. большему значению аргумента соответствует меньшее значение функции,, .
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
Рассмотрим решение логарифмического неравенства, когда основание логарифма .
То есть знак неравенства сохраняется.
При этом необходимо не забыть про ОДЗ, т.к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:
Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел получаем систему неравенств, которая соответствует исходному неравенству:
Пример 1 – решить неравенство:
Согласно методике решения простейших логарифмичеких неравенств, первым действием необходимо уравнять основания логарифмов, в данном случае представить правую часть в виде логарифма с требуемым основанием:
Получаем неравенство:
Поскольку основание логарифма больше единицы, в эквивалентной системе знак неравенства сохранится:
Преобразуем:
Ответ:
Пример 2 – решить неравенство:
Учтем ОДЗ:
ОДЗ:
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
Нам известно, что число Пи больше единицы (). Поэтому в эквивалентном неравенстве знак исходного неравенства сохраняется:
Поэтому в эквивалентном неравенстве знак исходного неравенства сохраняется:
Преобразуем полученное неравенство:
Корни квадратного уравнения, стоящего в левой части, согласно теореме Виета . Имеем параболу, ветви которой направлены вверх. Интересующие нас значения находятся между корней уравнения:
Ответ с учетом ОДЗ:
Сведение к простейшему логарифмическому неравенству часто осуществляется с помощью замены переменных.
Пример 3 – решить неравенство:
Приведем второй член к основанию 5:
Получили неравенство:
Очевидна замена:
Имеем:
Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: . Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями.
Вернемся к исходным переменным:
Преобразуем согласно определению логарифма:
Ответ:
Пример 4 – решить неравенство:
Учтем ОДЗ:
ОДЗ:
Согласно свойству логарифма преобразуем в левой части сумму логарифмов с одинаковым основанием в логарифм произведения:
Преобразуем правую часть в логарифм с требуемым основанием:
Имеем неравенство:
Основание логарифма больше единицы, получаем эквивалентное неравенство с тем же знаком:
Преобразуем:
Согласно теореме Виета корни квадратного уравнения, стоящего в левой части: . Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями:
Имеем параболу, ветви которой направлены вверх. Интересующие нас решения находятся в интервале между корнями:
Ответ с учетом ОДЗ:
Итак, мы рассмотрели решение различных типовых логарифмических неравенств.
Решение логарифмических неравенств (продолжение) 1. Введение
Пусть а – некоторое фиксированное число, при чем , а – основание логарифма. Логарифмическая функция монотонно возрастает. Тогда нам известно эквивалентное решение логарифмического неравенства:
Теперь пусть . Логарифмическая функция монотонно убывает:
Рассмотрим случай, когда основание логарифма зависит от х . Тогда нужно рассмотреть два случая:
Наша цель состоит в том, чтобы упростить полученную громоздкую совокупность.
Напомним важный опорный факт:
Нам потребуются следующие выражения:
Теперь нам проще решить следующую задачу.
Дано:
Доказать:
Доказательство:
Мы определили, что заданное неравенство эквивалентно следующей совокупности:
Преобразуем:
Согласно опорному факту, полученная совокупность эквивалентна системе:
Что и требовалось доказать.
Пример 1 – решить неравенство:
Уравняем основания логарифмов, в данном случае представим число в правой части как логарифм с требуемым основанием:
Имеем неравенство:
Решим неравенство двумя способами.
Способ 1:
Проиллюстрируем решение:
Рис. 1. Иллюстрация к решению примера 1
Ответ:
Составим эквивалентную систему:
Проиллюстрируем решение дробно-рационального неравенства:
Рис. 2. Интервалы знакопостоянства
Получаем решение системы:
Ответ:
Теперь рассмотрим решение нестрогого логарифмического неравенства , где
Заданному неравенству эквивалентна система:
Пример 2 – решить неравенство:
Решаем с помощью эквивалентной системы (второй способ). Уравняем основания логарифмов, в данном случае представим число в правой части как логарифм с требуемым основанием:
Уравняем основания логарифмов, в данном случае представим число в правой части как логарифм с требуемым основанием:
Имеем неравенство:
Составим эквивалентную систему:
Покажем решение первого неравенства методом интервалов:
Рис. 3. Иллюстрация решения примера 2
Учитывая ОДЗ, имеем ответ:
Итак, мы рассмотрели решение логарифмических неравенств повыщенной сложности.
ИСТОЧНИК
http://interneturok.ru/ru/school/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/reshenie-logarifmicheskih-neravenstv
http://interneturok.ru/ru/school/algebra/11-klass/pokazatelnaya-i-logarifmicheskaya-funktsii/reshenie-logarifmicheskih-neravenstv-prodolzhenie
http://www.youtube.com/watch?v=fgzG30EqVys
http://ege-ok.ru/2012/02/10/reshenie-logarifmicheskih-neravenstv
https://downloader. disk.yandex.ru/disk/197fa925c280a3c019e8f0b97c7065779aec80a75626f3c3c7877370509af9a4/56a1139b/gl1wdmatkHwr1IvHwfPzjlCbLxx51K2AXTrKx-khOfQ1WIGwVJDIxTfxWZJp9W23tYCJlb2c61QroEWHqjfeTQ%3D%3D?uid=0&filename=%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&disposition=attachment&hash=Ev/JAxs9FONy74%2BMIKGz214ILPNlyMZo/xnQbixz5Z8%3D%3A/%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&limit=0&content_type=application%2Fpdf&fsize=18366111&hid=c9e0cd334be9f7c6de02c1f2d04edf87&media_type=document&tknv=v2
disk.yandex.ru/disk/197fa925c280a3c019e8f0b97c7065779aec80a75626f3c3c7877370509af9a4/56a1139b/gl1wdmatkHwr1IvHwfPzjlCbLxx51K2AXTrKx-khOfQ1WIGwVJDIxTfxWZJp9W23tYCJlb2c61QroEWHqjfeTQ%3D%3D?uid=0&filename=%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&disposition=attachment&hash=Ev/JAxs9FONy74%2BMIKGz214ILPNlyMZo/xnQbixz5Z8%3D%3A/%D0%9C%D0%BE%D1%80%D0%B4%D0%BA%D0%BE%D0%B2%D0%B8%D1%87-%D0%90.%D0%93.-%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0-%D0%B8-%D0%BD%D0%B0%D1%87%D0%B0%D0%BB%D0%B0-%D0%B0%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7%D0%B0.11-%D0%BA%D0%BB%D0%B0%D1%81%D1%81-%D0%A7%D0%B0%D1%81%D1%82%D1%8C-1.pdf&limit=0&content_type=application%2Fpdf&fsize=18366111&hid=c9e0cd334be9f7c6de02c1f2d04edf87&media_type=document&tknv=v2
https://downloader. disk.yandex.ru/disk/4938274f13bc98046e8564063df40fcafe9fb762422d9929dbb48ce183e5bb38/56a2c71d/Odg6yN9ywrwT2cixdZsfiEDSD3e5Q69ddvKnYg8qBWJsyC7BArEtdQC84mMkIOZdV9PU-YKS3p_HWw0BvEuyHA%3D%3D?uid=0&filename=670.pdf&disposition=attachment&hash=aSLGLZV5IlrmNFQ9dfVZbUu5Mq4FVeCO/Cz5EcxDQsk%3D&limit=0&content_type=application%2Fpdf&fsize=5808072&hid=b5d4f65d7105982fb54709be551438ae&media_type=document&tknv=v2
disk.yandex.ru/disk/4938274f13bc98046e8564063df40fcafe9fb762422d9929dbb48ce183e5bb38/56a2c71d/Odg6yN9ywrwT2cixdZsfiEDSD3e5Q69ddvKnYg8qBWJsyC7BArEtdQC84mMkIOZdV9PU-YKS3p_HWw0BvEuyHA%3D%3D?uid=0&filename=670.pdf&disposition=attachment&hash=aSLGLZV5IlrmNFQ9dfVZbUu5Mq4FVeCO/Cz5EcxDQsk%3D&limit=0&content_type=application%2Fpdf&fsize=5808072&hid=b5d4f65d7105982fb54709be551438ae&media_type=document&tknv=v2
http://ov1098.jimdo.com/учащимся/11-класс-тесты/
логарифмических неравенств | Brilliant Math & Science Wiki
Содержание
- Введение
- Логарифмические неравенства — одно и то же основание
- Логарифмические неравенства — основание меньше 1
- Логарифмические неравенства — аналогичное основание
- Логарифмические неравенства — другое основание
- Логарифмические неравенства — несколько терминов
- Логарифмические неравенства — решение задач
- Смотрите также
Ключом к работе с логарифмическими неравенствами является следующий факт:
Если a>1a>1a>1 и x>yx>yx>y, то logax>logay\log_ax>\log_aylogax>logay.
В противном случае, если 0
Конечно, основание логарифма не может быть 1 или неположительным. Что еще более важно, верно и обратное:
Если a>1a>1a>1 и logax>logay\log_ax>\log_aylogax>logay, то x>yx>yx>y. В противном случае, если 0
Говоря более формально, логарифмическая функция f(x)=logaxf(x)=\log_a xf(x)=logax равна монотонно возрастающей (\big((увеличение xxx всегда увеличивает f(x) )f(x)\big)f(x)) для a>1a>1a>1 и монотонно убывающих (\big((увеличение xxx всегда уменьшает f(x))f(x)\big)f( x)) для 0 К счастью, оба этих факта интуитивно понятны: когда основание больше 1, сторона с большим аргументом будет больше, и наоборот, когда основание меньше 1. Например, без всякого Зная факты, формализованные выше, можно было бы интуитивно ожидать, что log2100\log_2100log2100 будет больше, чем log295\log_295log295. Также важно иметь в виду следующий факт: Аргумент логарифма должен быть положительным! Таким образом, также необходимо учитывать любые неравенства, вытекающие из положительности аргументов; например, неравенство, включающее термин log2(2x−3)\log_2 (2x-3)log2(2x−3), немедленно требует x>32x>\frac{3}{2}x>23. Когда обе части неравенства имеют одну и ту же основу, ключевые факты из введения могут быть применены напрямую. Например, Какие значения xxx удовлетворяют следующему неравенству: log2(2x+3)>log2(3x)?\log_2(2x+3)>\log_2(3x)?log2(2x+3)>log2(3x)? Поскольку основание равно 2, что больше 1, тот факт, что log2(2x+3)>log2(3x)\log_2(2x+3)>\log_2(3x)log2(2x+ 3)>log2(3x) означает, что 2x+3>3x2x+3>3x2x+3>3x. Вычитание 2x2x2x с обеих сторон дает 3>x3>x3>x. Кроме того, аргументы обоих логарифмов должны быть положительными, поэтому дополнительно 3x>03x>03x>0 и 2x+3>02x+3>02x+3>0. Истинно, только если n≤10 n \leq 10 n≤10
Ложь всегда
Верно, только если n≤100 n \leq 100 n≤100
Всегда верно Верно или неверно? Для всех натуральных чисел n≥2n \geq 2n≥2, log10(n−1)+log10(n+1)<2log10n. \log_{10} (n-1) + \log_{10} (n+1) < 2 \log_{10} n.log10(n−1)+log10(n+1)<2log10n. 1log4(x+1x+2)<1log4(x+3) \dfrac{1}{\log_{4}\left(\dfrac{x+1}{x+2}\right)} Если диапазон xxx, который удовлетворяет равенство выше равно (a,∞)(a,\infty)(a,∞), найдите значение aaa. Эта же концепция может быть применена к большим «стекам» логарифмов: Какие значения xxx удовлетворяют следующему неравенству: log2(log3(4x+1))>log2(log3(2x+3))?\log_2\big(\log_3(4x+1)\big)>\log_2\big( \log_3(2x+3)\big)?log2(log3(4x+1))>log2(log3(2x+3))? Поскольку основание равно 2, что больше 1, данное неравенство подразумевает log3(4x+1)>log3(2x+3)\log_3(4x+1) > \log_3(2x+3) log3(4x+1)>log3(2x+3). Кроме того, аргументы всех логарифмов должны быть положительными, но это действительно так, когда xxx больше 1. Следовательно, набор решений равен x>1x>1x>1. □_\квадрат□
9{ 2 }+4x+а) }. 1+log5(x2+1)≥log5(ax2+4x+a). Если диапазон значений aaa может быть выражен в виде (A,B], (A,B],(A,B], то найти значение A+B. A + B. A+B В случае, когда основание меньше 1, предыдущая интуиция существенно меняется на противоположную: теперь больше сторона имеет меньший показатель Какие значения xxx удовлетворяют следующему неравенству: log12(3x)>log12(2x+3)?\log_{\frac{1}{2}}(3x)>\log_{\frac{1}{2}}(2x+3) ?log21(3x)>log21(2x+3)? Поскольку основание равно 12\frac{1}{2}21, что меньше 1, из данного неравенства следует 3x<2x+33x<2x+33x<2x+3. Тогда х<3х<3х<3. Кроме того, аргумент каждого логарифма должен быть положительным, поэтому 3x>03x>03x>0 и 2x+3>02x+3>02x+3>0. Найдите xxx. x∈(43,1722) x\in \left(\frac { 4 }{ 3 } ,\frac { 17 }{ 22 } \right ) x∈(34,2217)
x∈(43,−1722) x\in \left(\frac {4}{3},-\frac{17}{22} \right) x∈(34,−2217)
x∈(−43,1722) x\in \left(-\frac { 4 }{ 3 } ,\frac { 17 }{ 22 } \right ) x∈(−34,2217)
x∈(−43,−1722) x\in \left(-\frac { 4 }{ 3 } ,-\frac { 17 }{ 22 } \right ) x∈(−34,−2217) 9{ 2 }+8x+8\big) } >2 log3x+5(9×2+8x+8)>2 Решите приведенное выше неравенство для x x x. Та же концепция может применяться, когда имеется несколько терминов: Какие значения xxx удовлетворяют следующему неравенству: log2(x)>log2(3)+log4(25)+log8(343)?\log_2(x)>\log_2(3)+\log_4(25)+\log_8( 343)?log2(x)>log2(3)+log4(25)+log8(343)? Запись всех логарифмов по основанию 2 дает log2(x)>log2(3)+log2(5)+log2(7)⇒log2(x)>log2(105),\begin{выровнено}
\log_2(x)&>\log_2(3)+\log_2(5)+\log_2(7)\\
\стрелка вправо \log_2(x)&>\log_2(105),
\end{выровнено}log2(x)⇒log2(x)>log2(3)+log2(5)+log2(7)>log2(105), , значит х>105х>105х>105. Когда основания разные и не связаны общей основой (как в предыдущем разделе), становится необходимым использование формулы смены основания. Например, Какие значения xxx удовлетворяют следующему неравенству: log7(x+5)>log5(x+5)? \log_7(x+5)>\log_5(x+5)?log7(x+5)>log5(x+5)? При замене основания неравенство дает log(x+5)log7>log(x+5)log5.\frac{\log(x+5)}{\log 7}>\frac{\log(x+5) }{\log 5}.log7log(x+5)>log5log(x+5). Это верно только тогда, когда log(x+5)\log(x+5)log(x+5) отрицательно, что означает, что log(x+5)<0 ⟹ x+5<1 ⟹ x<−4,\log(x+5)<0 \подразумевается x+5<1 \подразумевается x<-4,log(x+5) )<0⟹x+5<1⟹x<−4, , и поскольку x+5x+5x+5 должно быть положительным, x>−5x>-5x>−5, а окончательный набор решений равен −5 2 Если log0,3(x−1) Таким образом, либо log2(x)>2 ⟹ log2(x)>log24 ⟹ x>4\log_2(x)>2 \имплицитно \log_2(x)>\log_24 \имплицитно x>4log2 (x)>2⟹log2(x)>log24⟹x>4 или log2(x)<−3 ⟹ log2(x) Таким образом, набор решений равен 0 Сколько натуральных решений могут удовлетворять указанному выше неравенству? В случае цепочки неравенств обычно целесообразно рассматривать каждое неравенство отдельно, а затем объединять результаты. Например, Какие значения xxx удовлетворяют следующему неравенству: log12(x+2)<−2 Первое неравенство имеет вид log12(x+2)<−2\log_{\frac{1}{2}}(x+2)<-2log21(x+2)<−2, или log 12(x+2) Второе неравенство: −2 Таким образом, 2 Имейте в виду, что основание логарифма может быть меньше 1, что связано с равенством logab=−log1ab,\large \log_ab = -\log_{\frac{1}{a} }b,logab=−loga1b, , так что не забывайте об этом регистре! Решить неравенство logx+42(log22x−13+x)<0.\log_{\frac{x+4}{2}}\left(\log_{2}\frac{2x-1}{3+ x}\right)<0.log2x+4(log23+x2x−1)<0. Во-первых, основание должно быть положительным и не равным 1, поэтому сразу x>−4x>-4x>−4 и x≠−2x \neq -2x=−2. Теперь рассмотрим два случая: Случай 1. 0 В этом случае необходимо, чтобы log22x−13+x>1\log_2\frac{2x-1}{3+x}>1log23+x2x−1>1 или 2x−13+x >2\frac{2x-1}{3+x}>23+x2x−1>2, поэтому 2x−13+x−2=−73+x>0\frac{2x-1}{3+x }-2=\frac{-7}{3+x}>03+x2x−1−2=3+x−7>0. Следовательно, 3+x3+x3+x отрицательно, или x<−3x<-3x<−3. Таким образом, все xxx такие, что −4 Помните, что эта стратегия вычитания двух сторон, а не умножения, позволяет избежать работы с делами, связанной с умножением, поскольку больше нет необходимости учитывать последствия отрицательного значения умноженного количества. Случай 2. x+42>1 ⟺ x>−2\frac{x+4}{2}>1 \iff x>-22x+4>1⟺x>−2 В этом случае необходимо, чтобы log22x−13+x<1\log_2\frac{2x-1}{3+x}<1log23+x2x−1<1, или 2x−13+x <2\frac{2x-1}{3+x}<23+x2x−1<2, поэтому 2x−13+x−2=−73+x<0\frac{2x-1}{3+x }-2=\frac{-7}{3+x}<03+x2x−1−2=3+x−7<0. Это всегда верно, поскольку x>−2x>-2x>−2, поэтому любое значение x>−2x>-2x>−2 будет работать. Однако помните, что только x>12 или −4 Следовательно, набор решений равен x>12, −4 Типичная стратегия решения проблем заключается в использовании формулы замены основания, чтобы все логарифмы имели одинаковое основание. Это значительно упрощает применение других неравенств, таких как AM-GM. Покажите, что logn(n+1)>logn+1(n+2)\log_n(n+1)>\log_{n+1}(n+2)logn(n+1)>logn+ 1(n+2) для всех целых чисел n≥2n \geq 2n≥2. Произведения логарифмов — важный признак использования AM-GM, поскольку с суммой логарифмов очень легко иметь дело. В частности, logn+log(n+2)2≥lognlog(n+2) ⟹ log(n(n+2))2≥lognlog(n+2).\frac{\ log n + \ log (n + 2)} {2} \ geq \ sqrt {\ log n \ log (n + 2)} \ подразумевает \ frac {\ log \ big (n (n + 2) \ big)} { 2} \geq \sqrt{\log n\log(n+2)}.2logn+log(n+2)≥lognlog(n+2)⟹2log(n(n+2))≥lognlog( п+2). 92>\log n\log(n+2),(log(n+1))2>lognlog(n+2), , доказывающее исходное неравенство. □_\квадрат□ Процитировать как: Логарифмические неравенства. Brilliant. В разделе 6.3 мы решали уравнения и неравенства, включающие экспоненциальные функции, используя одну из двух основных стратегий. Теперь мы обратим наше внимание на уравнения и неравенства, включающие логарифмические функции, и неудивительно, что есть две основные стратегии на выбор. Например, предположим, что мы хотим решить \(\log_{2}(x) = \log_{2}(5)\). Как минимум, пример 6.4.1 демонстрирует важность проверки на наличие посторонних решений 2 при решении уравнений с логарифмами. Несмотря на то, что мы проверили наши ответы графически, посторонние решения легко обнаружить — любое предполагаемое решение, которое приводит к отрицательному числу внутри логарифма, должно быть отброшено. Как и в случае с уравнениями в примере 6.3.1, многое можно узнать, проверив все ответы в примере 6.4.1 аналитически. Мы оставляем это читателю и обращаем наше внимание на неравенства с логарифмическими функциями. котором который его которого он ему он показал, мы пересматриваем понятие pH, впервые использованное в упражнении 77 в разделе 6.1. 9{-1}(x)\) и проверьте свой ответ графически с помощью калькулятора. Решение Сначала запишем \(y=f(x)\), затем поменяем местами \(x\) и \(y\) и найдем \(y\). \[\begin{array}{rclr} y & = & f(x) & \\ y & = & \dfrac{\log(x)}{1-\log(x)} & \\[8pt ] x & = & \dfrac{\log(y)}{1-\log(y)} & \mbox{Поменять местами $x$ и $y$.}\\[8pt] x\left(1-\log (y)\right) & = & \log(y) & \\ x — x\log(y) & = & \log(y) & \\ x & = & x \log(y) + \log( y) & \\ x & = & (x+1) \log(y) & \\ \dfrac{x}{x+1} & = & \log(y) & \\ y & = & 10^{ \frac{x}{x+1}} & \mbox{Перепишите как показательное уравнение. 1 Однако они представляют одно и то же семейство комплексных чисел. На этом мы останавливаемся и отсылаем читателя к хорошему курсу по комплексным переменным. 2 Напомним, что постороннее решение – это полученный аналитически ответ, не удовлетворяющий исходному уравнению. 3 Обратитесь к странице 4 для обсуждения того, что это означает. Эта страница под названием 6.4: Логарифмические уравнения и неравенства распространяется под лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Карлом Стицем и Джеффом Зегером с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу. от Frezelle Чтобы решить логарифмическое уравнение, перепишите уравнение в экспоненциальной форме и найдите переменную. Пример 1: Найдите x в уравнении Ln ( x )=8. Решение: и примерный ответ Проверить. Вы можете проверить свой ответ двумя способами. Вы можете построить график функции Ln ( x )-8 и посмотреть, где она пересекает ось x. Если вы правы, график должен пересечь ось X в ответе, который вы получили алгебраически. Пример 2. Найдите x в уравнении 7 Log (3 x )=15. Решение: теперь можно записать как это точный ответ и приблизительный ответ. Проверка. Вы можете проверить свой ответ двумя способами: построить график функции или подставить значение x в исходное уравнение. Если вы выберете графическое изображение, пересечение по оси x должно совпадать с полученным вами ответом ( ). Пример 3. Найдите x в уравнении Другой способ взглянуть на уравнение на шаге 3 — понять, что если Ln ( a ) = Ln ( b ), то a должно быть равно b. В случае этой проблемы, то Проверить: Вы можете проверить свой ответ, построив график функции и определить, равен ли x-пересечение также 9. Если это так, вы правильно решили задачу. Посмотрите, как решать логарифмические неравенства: Ресурсы: /watch?v=7J4cIyko2uI https://www.
 Первый является более строгим, так как x>0x>0x>0, поэтому окончательный набор решений равен 0
Первый является более строгим, так как x>0x>0x>0, поэтому окончательный набор решений равен 0 Отсюда также следует, что 4x+1>2x+34x+1>2x+34x+1>2x+3 или что 2x>2 ⟹ x>12x>2 \ подразумевает x>12x>2⟹x>1. Следовательно, xxx должно быть больше 1.
Отсюда также следует, что 4x+1>2x+34x+1>2x+34x+1>2x+3 или что 2x>2 ⟹ x>12x>2 \ подразумевает x>12x>2⟹x>1. Следовательно, xxx должно быть больше 1.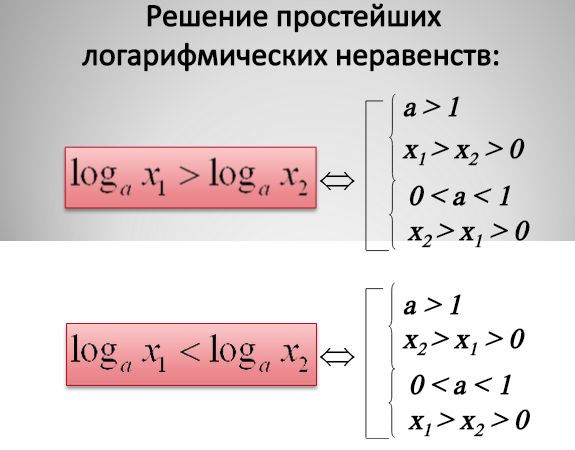 {2} + 1}\right) > 0 log0.2log6(x2+1×2−x)> 0
{2} + 1}\right) > 0 log0.2log6(x2+1×2−x)> 0 Попробуйте Fun с неравенствами-1 и Fun с неравенствами-3.
 Все xxx больше 105 удовлетворяют исходному неравенству. □_\квадрат□
Все xxx больше 105 удовлетворяют исходному неравенству. □_\квадрат□ y<-3.y<−3.
y<-3.y<−3.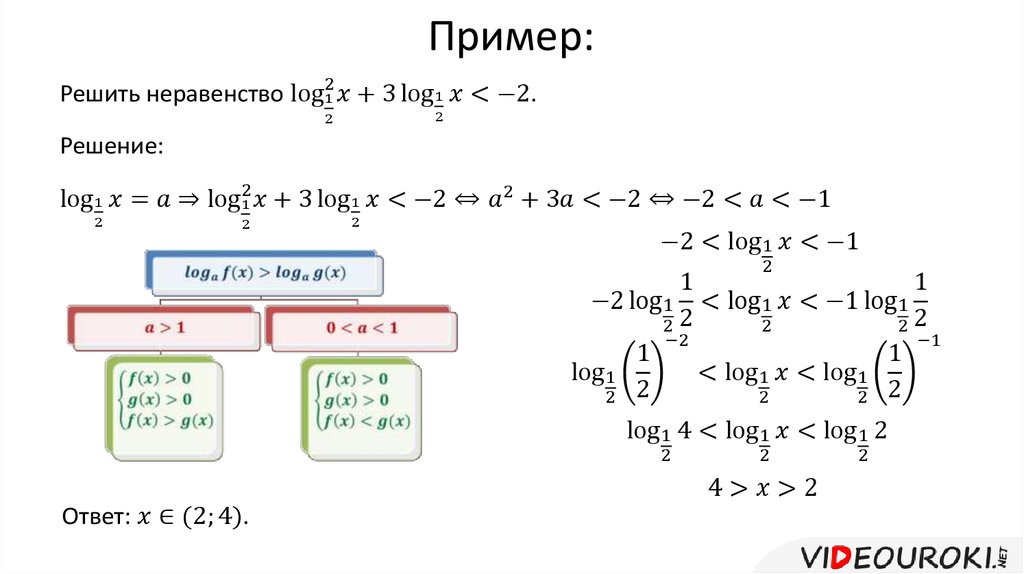 Точно так же аргумент log22x−13+x\log_2\frac{2x-1}{3+x}log23+x2x−1 должен быть положительным, поэтому 2x−1x+3>0 ⟹ x>12 или x<−3\frac{2x-1}{x+3}>0 \ подразумевает x>\frac12 \text{ или } x<-3x+32x−1>0⟹x>21 или x<−3 . Таким образом, единственными возможными значениями xxx являются x>12 или −4
Точно так же аргумент log22x−13+x\log_2\frac{2x-1}{3+x}log23+x2x−1 должен быть положительным, поэтому 2x−1x+3>0 ⟹ x>12 или x<−3\frac{2x-1}{x+3}>0 \ подразумевает x>\frac12 \text{ или } x<-3x+32x−1>0⟹x>21 или x<−3 . Таким образом, единственными возможными значениями xxx являются x>12 или −4
 92>\лог п\лог(п+2).
\end{выровнено}logn(n+1)>logn+1(n+2)⟺lognlog(n+1)>log(n+1)log(n+2)⟺(log(n +1))2>lognlog(n+2).
92>\лог п\лог(п+2).
\end{выровнено}logn(n+1)>logn+1(n+2)⟺lognlog(n+1)>log(n+1)log(n+2)⟺(log(n +1))2>lognlog(n+2). org .
Извлекаются из
https://brilliant.org/wiki/логарифмические-неравенства/
org .
Извлекаются из
https://brilliant.org/wiki/логарифмические-неравенства/ 6.4: Логарифмические уравнения и неравенства
 2-7x-4=0\). Решая, находим \(x = -\frac{1}{2}\) и \(x=4\). Построив график, находим \(y = f(x) = \frac{\ln(1-2x)}{\ln(7)}\) и \(y=g(x) = 1 — \frac{\ln (3-x)}{\ln(7)}\) пересекаются только в точке \(x=-\frac{1}{2}\). Проверка \(x=4\) в исходном уравнении дает \(\log_{7}(-7) = 1 — \log_{7}(-1)\), что является явным нарушением предметной области. 9{3} = \frac{x+3}{6-x}\nonumber\] Это сводится к линейному уравнению \(8(6-x) = x+3\), которое дает нам \(x = 5\ ). Когда мы рисуем \(f(x) = \frac{\ln(x+3)}{\ln(2)}\) и \(g(x) = \frac{\ln(6-x)}{ \ln(2)} + 3\), мы находим, что они пересекаются в точке \(x=5\).
2-7x-4=0\). Решая, находим \(x = -\frac{1}{2}\) и \(x=4\). Построив график, находим \(y = f(x) = \frac{\ln(1-2x)}{\ln(7)}\) и \(y=g(x) = 1 — \frac{\ln (3-x)}{\ln(7)}\) пересекаются только в точке \(x=-\frac{1}{2}\). Проверка \(x=4\) в исходном уравнении дает \(\log_{7}(-7) = 1 — \log_{7}(-1)\), что является явным нарушением предметной области. 9{3} = \frac{x+3}{6-x}\nonumber\] Это сводится к линейному уравнению \(8(6-x) = x+3\), которое дает нам \(x = 5\ ). Когда мы рисуем \(f(x) = \frac{\ln(x+3)}{\ln(2)}\) и \(g(x) = \frac{\ln(6-x)}{ \ln(2)} + 3\), мы находим, что они пересекаются в точке \(x=5\). Используя квадратичную формулу, мы получаем \(x = 1 \pm \sqrt{3}\). Графики \(f(x) = 1 + \frac{2\ln(x+1)}{\ln(4)}\) и \(g(x) = \frac{2 \ln(x)}{ \ln(2)}\), мы видим, что графики пересекаются только в точке \(x = 1 + \sqrt{3} \приблизительно 2,732\). Решение \(x = 1 — \sqrt{3} < 0\), что означает, что при подстановке в исходное уравнение член \(2 \log_{2}\left(1 - \sqrt{3}\right) \) не определено.
Используя квадратичную формулу, мы получаем \(x = 1 \pm \sqrt{3}\). Графики \(f(x) = 1 + \frac{2\ln(x+1)}{\ln(4)}\) и \(g(x) = \frac{2 \ln(x)}{ \ln(2)}\), мы видим, что графики пересекаются только в точке \(x = 1 + \sqrt{3} \приблизительно 2,732\). Решение \(x = 1 — \sqrt{3} < 0\), что означает, что при подстановке в исходное уравнение член \(2 \log_{2}\left(1 - \sqrt{3}\right) \) не определено. {1}\), что допускает \(x = 9\). Мы выбираем тестовые значения \(x\) так, чтобы \(x+1\) было степенью \(10\), и мы получаем \(-1 < -0,9 < 0 < \sqrt{10} -1 < 9 < 99\). Наша диаграмма знаков дает решение \((-1,0] \cup [9, \infty)\). Калькулятор указывает, что график \(y= f(x) = x \log(x+1)\) находится выше \(y=g(x) = x\) на интервалах решения, и графики пересекаются в \ (х=0\) и \(х=9\).
{1}\), что допускает \(x = 9\). Мы выбираем тестовые значения \(x\) так, чтобы \(x+1\) было степенью \(10\), и мы получаем \(-1 < -0,9 < 0 < \sqrt{10} -1 < 9 < 99\). Наша диаграмма знаков дает решение \((-1,0] \cup [9, \infty)\). Калькулятор указывает, что график \(y= f(x) = x \log(x+1)\) находится выше \(y=g(x) = x\) на интервалах решения, и графики пересекаются в \ (х=0\) и \(х=9\). }\\ \end{массив}\nonumber\] 9{-12}}\справа) = 150\)
}\\ \end{массив}\nonumber\] 9{-12}}\справа) = 150\) (См. упражнение 77 в разделе 6.1.) 9{-1}\) равно \((-\infty, \infty)\), и его диапазон совпадает с доменом \(f\), а именно \((-1, 1)\).
(См. упражнение 77 в разделе 6.1.) 9{-1}\) равно \((-\infty, \infty)\), и его диапазон совпадает с доменом \(f\), а именно \((-1, 1)\). Ссылка
 stitz-zeager.com/latex-source-code.html
stitz-zeager.com/latex-source-code.html РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ – Math-Yahoo!

Вы также можете проверить свой ответ, подставив значение x в исходное уравнение и определить, равна ли левая часть правой части. Например, если Ln (2980,95798704)=8, вы правы. Так и есть, и вы правы.  Если основание не указано, это означает, что основание логарифма равно 10. Напомним также, что логарифмы являются показателями степени, поэтому показатель степени . Уравнение
Если основание не указано, это означает, что основание логарифма равно 10. Напомним также, что логарифмы являются показателями степени, поэтому показатель степени . Уравнение
Если вы выберете замену, значение левой части исходного уравнения должно равняться значению правой части уравнения после того, как вы вычислите значение каждой стороны на основе вашего ответа на x.  Если мы потребуем, чтобы x был любым действительным числом, большим 3, все три термина будут действительными. Если все три условия верны, то уравнение верно.
Если мы потребуем, чтобы x был любым действительным числом, большим 3, все три термина будут действительными. Если все три условия верны, то уравнение верно. 
Вы также можете проверить свой ответ, подставив 9 вместо x в левой и правой частях исходного уравнения. Если после подстановки левая часть уравнения имеет то же значение, что и правая часть уравнения, вы правильно решили задачу. 

 {-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).
{-1}\) \(=\log\) \(_\frac{1}{3}\) \(3\).

 2-t-2>0\)
2-t-2>0\) 
 В противном случае, если 0
В противном случае, если 0