Решение систем по формуле крамера: Онлайн калькулятор. Решение систем линейных уравнений. Метод Крамера

Решение системы по формулам Крамера

Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!

Рассмотрим систему уравнений 

На первом шаге вычислим определитель   , его называют главным определителем системы. Если  , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать Метод Гауса.

Если  , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:  и 

На практике вышеуказанные определители также могут обозначаться латинской буквой  .

Корни уравнения находим по формулам: , 

Пример 7

Решить систему линейных уравнений 

В подобных случаях и приходят на помощь формулы Крамера.

, значит, система имеет единственное решение.

;

; 

Ответ:  ,  .

Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения     в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.

Пример 8 Решить систему по формулам Крамера.  Ответ представить в обыкновенных неправильных дробях. Сделать проверку.

Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

Находим главный определитель системы:

Если  , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса.

Если  , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя: ,  , 

И, наконец, ответ рассчитывается по формулам: ,  , 

Пример 9 Решить систему по формулам Крамера.

  

Решение: Решим систему по формулам Крамера. , значит, система имеет единственное решение.

Ответ:  .

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц. Таким образом, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарные преобразования используются в методе Гаусса для приведения матрицы к треугольному или ступенчатому виду.

Элементарными преобразованиями строк называют:

• перестановка местами любых двух строк матрицы;

• умножение любой строки матрицы на константу  ,  ;

• прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

В некоторых курсах линейной алгебры перестановка местами двух строк матрицы не вносятся в определение элементарных преобразований так как перестановку местами любых двух строк матрицы можно получить используя умножение любой строки матрицы на константу  ,   и прибавление к любой строке матрицы другой строки, умноженной на константу  ,  .

Аналогично определяются элементарные преобразования столбцов.

Элементарные преобразования обратимы.

Обозначение   указывает на то, что матрица   может быть получена из   путём элементарных преобразований (или наоборот).

Ме́тод Га́усса^[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные

^[2].

Решить систему уравнений методом Гаусса:

                                                      x +  y — 3z = 2,

                                                    3x — 2y +  z = — 1,

                                                    2x +  y — 2z = 0.

Решение. Выпишем расширенную матрицу данной системы

и произведем следующие элементарные преобразования над ее строками:

а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

 ~  ;

б) третью строку умножим на (-5) и прибавим к ней вторую:

.

В результате всех этих преобразований данная система приводится к треугольному виду:

                                                    x + y — 3z = 2,

                                                    -5y + 10z = -7,

                                                           — 10z = 13.

Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим  x = — 0,7.

Решение систем алгебраических уравнений методом Крамера

Метод Крамера.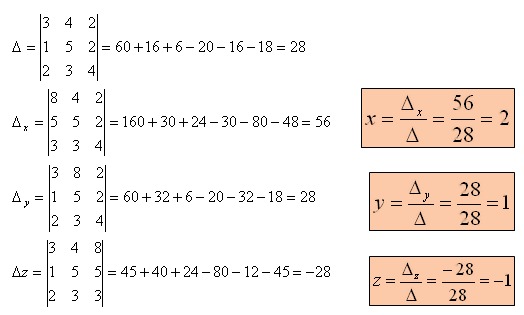

Метод Крамера применяется  для решения систем линейных алгебраических уравнений (СЛАУ), в которых число  неизвестных переменных равно числу  уравнений и определитель основной матрицы отличен от нуля. В этой статье мы разберем как по методу Крамера  находятся неизвестные 

переменные и получим формулы. После этого  перейдем к примерам и подробно опишем решение систем линейных алгебраических уравнений методом Крамера.

При изучении материала  Вам может быть полезна статья вычисление определителя матрицы, свойства определителя.

Навигация по странице.

• Метод Крамера — вывод формул.
• Алгоритм решения систем линейных алгебраических уравнений методом Крамера.
• Примеры решения систем линейных алгебраических уравнений методом Крамера.

Метод Крамера — вывод формул.

Пусть нам требуется  решить систему линейных уравнений  вида 
 
где x₁, x₂, …, x_n – неизвестные переменные, a_{i j} , i = 1, 2, …, n, j = 1, 2, …, n – числовые коэффициенты, b₁, b₂, …, b_n — свободные члены.

Решением СЛАУ называется такой набор значений x₁, x₂, …, x_n при которых все уравнения системы обращаются в тождества.

В матричном виде эта система может быть записана как A ⋅ X = B, где   — основная матрица системы, ее элементами являются коэффициенты при неизвестных переменных,   — матрица – столбец свободных членов, а   — матрица – столбец неизвестных переменных. После нахождения неизвестных переменных x₁, x₂, …, x_n, матрица   становится решением системы уравнений и равенство A ⋅ X = B обращается в тождество  .

Будем считать, что  матрица А – невырожденная, то есть, ее определитель отличен от нуля. В этом случае система линейных алгебраических уравнений имеет единственное решение, которое может быть найдено методом Крамера. (Методы решения систем при  разобраны в разделе решение систем линейных алгебраических уравнений).

Метод Крамера основывается на двух свойствах определителя матрицы:

1. Определитель квадратной матрицы   равен сумме произведений элементов какой-либо строки (столбца) на их алгебраические дополнения: 
   
2. Сумма произведений элементов какой-либо строки (столбца) квадратной матрицы на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю: 
   

Итак, приступим  к нахождению неизвестной переменной x₁. Для этого умножим обе части первого уравнения системы на А_{1 1} , обе части второго уравнения – на А_{2 1} , и так далее, обе части n-ого уравнения – на А_{n 1} (то есть, уравнения системы умножаем на соответствующие алгебраические дополнения первого столбца матрицы А): 

Сложим все левые  части уравнения системы, сгруппировав слагаемые при неизвестных 

переменных x₁, x₂, …, x_n, и приравняем эту сумму к сумме всех правых частей уравнений: 

Если обратиться к озвученным ранее свойствам  определителя, то имеем 
  
и предыдущее равенство примет вид 
  
откуда 

Аналогично находим x₂. Для этого умножаем обе части уравнений системы на алгебраические дополнения второго столбца матрицы А: 

Складываем все  уравнения системы, группируем слагаемые  при неизвестных переменных x₁, x₂, …, x_n и применяем свойства определителя: 

Откуда 
.

Аналогично находятся  оставшиеся неизвестные переменные.

Если обозначить 
 
  
 
то получаем формулы для нахождения неизвестных переменных по методу Крамера  .

Замечание.

Если система  линейных алгебраических уравнений  однородная, то есть  , то она имеет лишь тривиальное решение   (при  ). Действительно, при нулевых свободных членах все определители   будут равны нулю, так как будут содержать столбец нулевых элементов. Следовательно, формулы   дадут  .

К началу страницы

Алгоритм  решения систем линейных алгебраических уравнений методом Крамера.

Запишем алгоритм решения систем линейных алгебраических уравнений методом Крамера.

1. Вычисляем определитель основной матрицы системы   и убеждаемся, что он отличен от нуля.
2. Находим определители 
     
   которые являются определителями матриц, полученных из матрицы А заменой k-ого столбца (k = 1, 2, …, n) на столбец свободных членов.
3. Вычисляем искомые неизвестные переменные x₁, x₂, …, x_n по формулам  .
4. Выполняем проверку результатов, подставляя x₁, x₂, …, x_n в исходную СЛАУ. Все уравнения системы должны обратиться в тождества. Можно также вычислить произведение матриц A ⋅ X, если в результате получилась матрица, равная B, то решение системы найдено верно. В противном случае в ходе решения была допущена ошибка.

К началу страницы

Примеры решения систем линейных алгебраических уравнений методом Крамера.

Разберем решения  нескольких примеров.

Пример.

Найдите решение  неоднородной системы линейных алгебраических уравнений методом Крамера  .

Решение.

Основная матрица  системы имеет вид  . Вычислим ее определитель по формуле  : 

Так как определитель основной матрицы системы отличен  от нуля, то СЛАУ имеет единственное решение, и оно может быть найдено  методом Крамера. Запишем определители   и  . Заменяем первый столбец основной матрицы системы на столбец свободных членов, и получаем определитель  . Аналогично заменяем второй столбец основной матрицы на столбец свободных членов, и получаем .

Вычисляем эти определители: 

Находим неизвестные  переменные x₁ и x₂ по формулам  : 

Выполним проверку. Подставим полученные значения x₁ и x₂ в исходную систему уравнений: 

Оба уравнения системы  обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Некоторые элементы основной матрицы СЛАУ могут быть равны нулю. В этом случае в уравнениях системы будут отсутствовать  соответствующие неизвестные переменные. Разберем пример.

Пример.

Найдите решение  системы линейных уравнений методом  Крамера  .

Решение.

Перепишем систему  в виде  , чтобы стало видно основную матрицу системы  . Найдем ее определитель по формуле 

Имеем 

Определитель основной матрицы отличен от нуля, следовательно, система линейных уравнений имеет  единственное решение. Найдем его методом  Крамера. Вычислим определители  : 

Таким образом, 

Ответ:

.

Обозначения неизвестных  переменных в уравнениях системы  могут отличаться от x₁, x₂, …, x_n. Это не влияет на процесс решения. А вот порядок следования неизвестных переменных в уравнениях системы очень важен при составлении основной матрицы и необходимых определителей метода Крамера. Поясним этот момент на примере.

Пример.

Используя метод  Крамера, найдите решение системы  трех линейных алгебраических уравнений  с тремя неизвестными  .

Решение.

В данном примере  неизвестные переменные имеют другое обозначение (x, y и z вместоx₁, x₂ и x₃). Это не влияет на ход решения, но будьте внимательны с обозначениями переменных. В качестве основной матрицы системы НЕЛЬЗЯ брать  . Необходимо сначала упорядочить неизвестные переменные во всех уравнениях системы. Для этого перепишем систему уравнений как  . Теперь основную матрицу системы хорошо видно  . Вычислим ее определитель: 

Определитель основной матрицы отличен от нуля, следовательно, система уравнений имеет единственное решение. Найдем его методом Крамера. Запишем определители   (обратите внимание на обозначения) и вычислим их: 

Осталось найти  неизвестные переменные по формулам  : 

Выполним проверку. Для этого умножим основную матрицу  на полученное решение   (при необходимости смотрите раздел операции над матрицами): 

В результате получили столбец свободных членов исходной системы уравнений, поэтому решение  найдено верно.

Ответ:

x = 0, y = -2, z = 3.

Пример.

Решите методом  Крамера систему линейных уравнений  , гдеa и b – некоторые действительные числа.

Решение.

Вычислим определитель основной матрицы системы: 

Определитель отличен  от нуля, следовательно, можно применить  метод Крамера. 

Находим неизвестные  переменные 

Рекомендуем проверить  полученные результаты.

Ответ:

.

Пример.

Найдите решение  системы уравнений   методом Крамера,   — некоторое действительное число.

Решение.

Вычислим определитель основной матрицы системы:  . Область значений выражения   есть интервал  , поэтому   при любых действительных значениях  . Следовательно, система уравнений имеет единственное решение, которое может быть найдено методом Крамера. Вычисляем   и  : 

Таким образом,  .

Выполним проверку: 

Уравнения системы  обращаются в тождества, следовательно, решение найдено верно.

Ответ:

.

Пример.

Решите систему  линейных алгебраических уравнений  методом Крамера  .

Решение.

Вычислим определитель основной матрицы системы уравнений: 

Определитель основной матрицы равен нулю, следовательно, метод Крамера не подходит для  решения такой системы уравнений.

Пример.

Методом Крамера  найдите решение СЛАУ  .

Решение.

Эта система однородная, так как все свободные члены  равны нулю. Определитель основной матрицы отличен от нуля  , поэтому ее единственным решением является x₁ = 0, x₂ = 0. О таких СЛАУ мы уже упоминали вышев замечании.

Ответ:

x₁ = 0, x₂ = 0.

Пример.

Найдите решение  системы четырех линейных алгебраических уравнений   содержащую четыре неизвестных переменных.

Решение.

Сразу скажем, что  не будем подробно описывать вычисление определителей матриц, так как  это выходит за рамки данной статьи.

Вычислим определитель основной матрицы системы, разложив его по элементам второй строки: 

Определитель основной матрицы системы отличен от нуля, поэтому можно воспользоваться  методом Крамера для решения  системы.

Найдем  : 
  
аналогично вычисляются 

Таким образом, 

Ответ:

.

К началу страницы

Подведем  итог.

Метод Крамера позволяет  находить решение систем линейных алгебраических уравнений, если определитель основной матрицы отличен от нуля. По сути метод сводится к вычислению определителей  матриц порядка n на n и применению соответствующих формул для нахождения неизвестных переменных.

Если число уравнений  в системе велико (больше трех), то целесообразно искать решениеметодом Гаусса.

Как решать системы уравнений по правилу Крамера (практика)

В этом посте мы объясняем, что такое правило Крамера, и, кроме того, вы найдете примеры и упражнения для систем уравнений, решаемых по правилу Крамера.

Содержание

Формула правила Крамера

Правило Крамера — это формула, используемая для решения систем линейных уравнений с использованием определителей. Давайте посмотрим, как использовать правило Крамера:

Дана система линейных уравнений:

Пусть A — квадратная матрица с коэффициентами при неизвестных:

Правило Крамера утверждает, что решение системы уравнений можно вычислить следующим образом:

Обратите внимание, что определители числителей подобны определитель матрицы A, но заменив столбец каждой неизвестной на столбец констант. А определитель знаменателя дроби всегда является определителем матрицы А.

Поэтому метод Крамера используется для решения систем линейных уравнений. Но есть много других способов решения системы уравнений, например метод исключения Гаусса.

Ниже вы можете увидеть пример решения системы линейных уравнений по правилу Крамера.

Пример правила Крамера

• Решите следующую систему из 3-х уравнений с 3-мя неизвестными по правилу Крамера:

Сначала составим матрицу А с коэффициентами при неизвестных:

3 900 Правило Крамера для решения системы уравнений. Для этого сначала нужно найти определитель матрицы A:

Чтобы вычислить неизвестное x по правилу Крамера, заменим первый столбец определителя A столбцом констант и разделим его на определитель A:

Чтобы найти неизвестное y по правилу Крамера, заменяем второй столбец определителя А столбцом констант и делим его на определитель А:

И, наконец, для вычисления переменной z по правилу Крамера меняем местами третий столбец определителя А с столбец констант и разделить его на определитель матрицы A: 9

Задача 1 решение

Сначала мы строим матрицу A с коэффициентами переменных:

Теперь мы используем правило Крамера для решения системы уравнений. Таким образом, мы оцениваем определитель матрицы A:

Чтобы вычислить неизвестный x по правилу Крамера, заменим первый столбец определителя A на столбец констант и разделим его на определитель A:

И найдем значение неизвестного y , заменим второй столбец определителя A на столбец констант и разделим его на определитель матрицы A:

Таким образом, решение системы уравнений:

 

Задача 2

Найдите решение следующей системы трех уравнений с 3 неизвестными по правилу Крамера:

См. решение

Матрица А – это матрица со всеми коэффициентами при переменных:

Вычислим определитель матрицы A для применения правила Крамера:

Чтобы вычислить неизвестный x методом Крамера, мы заменяем первый столбец определителя A на столбец констант и делим его на определитель A:

Во-вторых, чтобы найти неизвестный y методом Крамера, заменим второй столбец определителя A столбцом констант и разделим его на определитель A:

И, наконец, для вычисления z с помощью По правилу Крамера, меняем третий столбец определителя А на столбец констант и делим его на определитель А:

Таким образом, решение системы уравнений:

 

Задача 3

Решите следующую систему линейных уравнений, применяя правило Крамера:

См. решение

Сначала найдем матрицу A системы:

Теперь используем правило Крамера для решения системы. Сначала возьмем определитель матрицы A:

. Чтобы вычислить неизвестное x по правилу Крамера, заменим первый столбец определителя A на столбец констант и разделим его на определитель A:

Чтобы найти неизвестное y по правилу Крамера, мы заменяем второй столбец определителя A столбцом констант и делим его на определитель A:

Чтобы вычислить неизвестное z по правилу Крамера, заменяем третий столбец определителя A столбцом констант и делим его на определитель A:

Таким образом, решение системы линейных уравнений:

 

Правило Крамера

Сложно решить систему линейных уравнений, хотя у нас есть некоторые методы для решения этих задач.

Метод Гаусса — один из них, но сейчас мы изучим правило или метод Крамера.

Это правило можно использовать только в том случае, если решаемая система уравнений удовлетворяет двум условиям:

1. В системе столько уравнений, сколько неизвестных.
2. Определитель матрицы коэффициентов не равен нулю.

Теперь мы увидим процедуру, которой нужно следовать, чтобы использовать правило Крамера. Возьмем систему, удовлетворяющую двум необходимым условиям: $$$\left\{ \begin{array}{c} x+y+z=1 \\ x-2y+3z=2 \\ x-z=5 \end{array} \right.$$$ Первым делом нужно будет переписать систему с помощью матрицы коэффициентов и вычислить ее определитель, чтобы убедиться, что он не равен нулю: $$$\begin{pmatrix} 1 & 1 & 1 \\ 1 & -2 & 3 \\ 1 & 0 & 1\end{pmatrix}$$$ И определитель $$$\Delta=\left| \begin{matrix} 1 & 1 & 1\\ 1 & -2 & 3 \\ 1 & 0 & 1 \end{matrix} \right|=2$$$ (действительно и отлично от нуля).

Определим теперь определители $$\Delta_i$$, полученные заменой столбца $$i$$ матрицы коэффициентов столбцом постоянных членов. Вычислим эти определители:

$$\Delta_1=\left| \begin{matrix} 1 & 1 & 1\\ 2 & -2 & 3 \\ 5 & 0 & 1 \end{matrix} \right|=21, \ \ $$ $$\Delta_2=\left| \begin{matrix} 1 & 1 & 1\\ 1 & 2 & 3 \\ 1 & 5 & 1 \end{matrix} \right|=8, \ \ $$ $$\Delta_3=\left| \begin{matrix} 1 & 1 & 1\\ 1 & -2 & 2 \\ 1 & 0 & 5 \end{matrix} \right|=-11$$

Правило Крамера гласит, что решением системы уравнений является $$x_i=\dfrac{\Delta_i}{\Delta}$$.

В этом случае $$x_1=\dfrac{21}{2}$$, $$x_2=\dfrac{-8}{2}$$, $$x_3=\dfrac{-11}{ 2}$$.

После первого примера мы теперь установим общие шаги для любой системы уравнений. $$$\left\{ \begin{array}{c} a_{11}x_1+a_{12}x_2+a_{13}x_3+\ldots+a_{1n}x_n=b_1 \\ a_{21}x_1+ a_{22}x_2+a_{23}x_3+\ldots+a_{2n}x_n=b_2 \\ a_{31}x_1+a_{32}x_2+a_{33}x_3+\ldots+a_{3n}x_n=b_3 \\ \ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots \\ a_{m1}x_1+a_{m2}x_2+a_{m3}x_3+\ldots+a_{mn}x_n=b_m \end{ массив} \right.$$$

1) Проверить, что система удовлетворяет двум условиям: равное количество неизвестных и уравнений $$(n=m)$$ и ненулевой определитель матрицы коэффициентов $$(\Delta\neq0)$$

2) Вычислить определитель матрицы коэффициентов $$$\Delta=\left| \begin{matrix} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} &\ldots & a_{2n} \\ \ldots & \ldots & \ ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & a_{mm} \end{matrix} \right|$$$

3) Определители $$\Delta_i$$ вычисляются путем замены столбца $$i$$ столбцом постоянных членов:

$$\Delta_1=\left| \begin{matrix} b_1 & a_{12} & \ldots & a_{1n} \\ b_2 & a_{22} &\ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ b_m & a_{m2} & \ldots & a_{mm} \end{matrix} \right| \\$$, $$\Delta_2=\left| \begin{matrix} a_{11} & b_1 & \ldots & a_{1n} \\ a_{21} & b_2 &\ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & b_m & \ldots & a_{mm} \end{matrix} \right| \ \ $$, $$\ldots$$, $$\Delta_n=\left| \begin{matrix} a_{11} & a_{12} & \ldots & b_1 \\ a_{21} & a_{22} &\ldots & b_2 \\ \ldots & \ldots & \ldots & \ldots \\ a_{m1} & a_{m2} & \ldots & b_m \end{matrix} \right|$$

4) Решения $$$x_i=\dfrac{\Delta_i}{\Delta}$$$

Если в системе с $$m$$ уравнениями и $$n$$ неизвестными все постоянные члены равны нулю, то говорят, что она является однородным.