Решение системы уравнений с тремя неизвестными: Решить систему из 3-х уравнений с 3-мя неизвестными онлайн / Калькуляторы

Содержание

Методы решения систем линейных уравнений с двумя неизвестными

Веселова Наталья Павловна, учитель математики

Разделы: Математика, Химия

Оборудование: кодоскоп, кодопозитивы.

Цели урока:

Систематизация и повторение знаний по теме “Азотная кислота” через решение задач.
Повторение методов решения систем линейных уравнений с двумя переменными.
Умение применять на практике полученные знания.
Развитие интереса к предмету.

“…одна из важнейших задач математики – помощь другим наукам”
Морделл Л.

При решении некоторых задач по химии используются математические методы. Рассмотрим несколько задач, для решения которых необходимо уметь решать системы уравнений с двумя переменными.

Задача 1: 5 г хлорида магния получено при обработке 6,5 граммов смеси оксида и бромида магния соляной кислотой. Определить состав смеси.

Объяснение начинает учитель химии.

Дано:

m(MgO+MgBr₂)= 6,5 г
m(MgCl₂)= 5г
M(MgO)= 40 г/моль
M(MgBr₂)= 184г/моль
M(MgCl₂)= 95 г

(1) 40г/моль – 95 г/моль
х г – А г
А= 2,4х
(2)184 г/моль — 95 г/моль
у г – В г
В = 0,5 у

m(MgO)-?
m(MgBr₂)-?

Составим уравнения

А + В = 6,5 г; х + у = 5

Подставим значения А и В. Решим уравнения в системе:

Объяснение продолжает учитель математики.

Вопрос. Какие методы решения систем уравнений вы знаете?

Метод подстановки
Метод сложения
Графический метод

Решим систему методом сложения

Математическую часть задачи решает 1 ученик у доски.

Задача 2: Имеется раствор, содержащий одновременно соляную и азотную кислоты. Определить массу каждой из кислот, если при нейтрализации 7 г. этого раствора расходуется 47,25 г. 20% раствора КOH.

Химическую часть задачи разбирает у доски один ученик.

Дано:

w(КОН)=20% m_р-р(KOH)= 47,25 г m(HCl + HNO₃)= 7 г	M(KOH) = 56 г/моль M(HNO₃) = 63 г/моль M(HCL) = 35,5 г/моль 1) 35,5 г/моль – 56 г/моль х г. – А г. A = 1, 53 х 2) 63 г/моль – 56 г/моль у = В г. В = 0,89 у
m(HCl) – ? m(HNO₃) – ?

20% раствор – это 20 г вещества в 100 г. раствора

20 г – 100 г

х г – 47,25 г

х = 9б, 45 г – масса КОН

Составим систему уравнений.

Систему уравнений класс решает самостоятельно:

I вариант – методом подстановки;
II вариант – графическим методом.

а) Решение методом подстановки:

10,71 – 1,53у +0,89у = 9,45

– 0,64 у = -1,26

б) графический метод:

1		2
x	y	x	y
6,2	0	7	0
3,3	5	4	3

Сравниваются полученные результаты по вариантам. Проверяется правильность решения с помощью кодоскопа.

Ответ: НСl – 5 г; HNO₃ – 2 г.

Третью задачу класс решает самостоятельно, сами выбирают метод решения системы. По ходу решения ребята сравнивают результаты с результатами на экране.

Задача 3: 7,5 грамма смеси цинка и железа обработали соляной кислотой, при этом выделилось 2,78 л водорода. Определите состав смеси в граммах.

Дано:

V(H₂) = 2, 78 л
m(Zn + Fe) = 7,5

M(Zn) = 65 г/моль
M(Fe) = 56 г/моль
1) 65 г/моль – 22, 4 л
х – А л
А = 0,34 х
2) 56 г/моль – 22,4 л
у – В л
В = 0,4 у

m(Zn) – ?
m(Fe) – ?

Решение методом подстановки:

0,34(7,5 – у) + 0,4 у = 2,78

2,55 – 0,34 у + 0,4 у = 2,78

0,06 у = 0, 23

б) Решение методом сложения:

1		2
x	y	x	y
8,2	0	7,5	0
2,3	5	2,5	5

Ответ: Zn – 3,7 г; Fe – 3,8 г.

Домашнее задание

Задача: При взаимодействии нитрата серебра и 2,66 г смеси хлорида натрия и хлорида калия получено 5,74 г хлорида серебра. Сколько хлорида натрия и хлорида калия содержалось в смеси (в граммах)?

Подведение итогов урока

Математические методы используются при решении задач с практическим содержанием. Это могут быть задачи по физике, химии, расчет биополей по биологии и т.д. Надо только правильно составить уравнения, решения которых с математической точки зрения достаточно просты.

23.03.2005

9.2: Системы линейных уравнений — три переменные

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 1384

OpenStax
OpenStax

Цели обучения

Решать системы из трех уравнений с тремя переменными.
Найдите несовместимые системы уравнений, содержащие три переменные.

Выразите решение системы зависимых уравнений, содержащей три переменные.

Джон получил наследство в размере $$12,000$, которое он разделил на три части и вложил тремя способами: в фонд денежного рынка с выплатой $3\%$ годовых процентов; в муниципальных облигациях с выплатой $4\%$ годовых; и во взаимных фондах, выплачивающих $7\%$ годовых. Джон вложил в муниципальные фонды $$4000$ больше, чем в муниципальные облигации. Он заработал $$670$ в виде процентов за первый год. Сколько Джон инвестировал в каждый тип фонда?

Рисунок $\PageIndex{1}$: (кредит: «Elembis», Wikimedia Commons)

Понимание правильного подхода к постановке задач, подобных этой, делает поиск решения проблемой следуя шаблону. В этом разделе мы решим эту и подобные задачи с тремя уравнениями и тремя переменными. При этом используются методы, аналогичные тем, которые используются для решения систем двух уравнений с двумя переменными.

Однако поиск решений систем из трех уравнений требует большей организованности и некоторой визуальной гимнастики.

Решение систем трех уравнений с тремя переменными

Для решения систем уравнений с тремя переменными, известных как системы «три на три», мы будем использовать основной инструмент, который называется методом исключения Гаусса, названным в честь плодовитого немецкого математика. Карл Фридрих Гаусс. Хотя нет определенного порядка, в котором должны выполняться операции, существуют конкретные рекомендации относительно того, какие типы движений можно выполнять. Мы можем пронумеровать уравнения, чтобы отслеживать шаги, которые мы применяем. Цель состоит в том, чтобы исключить одну переменную за раз, чтобы получить верхнетреугольную форму, идеальную форму для системы три на три, поскольку она позволяет найти решение с помощью прямой обратной подстановки $(x,y,z)$ , которую мы называем упорядоченной тройкой. Система в верхнем треугольном виде выглядит следующим образом:

\[\begin{align*} Ax+By+Cz &= D \nonumber \\[4pt] Ey+Fz &= G \nonumber \\[4pt] Hz &= K \nonumber \end{align*} \nonumber\]

Третье уравнение можно решить относительно $z$, а затем выполнить обратную подстановку, чтобы найти $y$ и $x$. Чтобы записать систему в верхнем треугольном виде, мы можем выполнить следующие операции:

Поменять местами любые два уравнения.
Умножить обе части уравнения на ненулевую константу.
Добавить ненулевое кратное одного уравнения к другому уравнению.

Решение множества для системы три на три представляет собой упорядоченную тройку ${(x,y,z)}$. Графически упорядоченная тройка определяет точку пересечения трех плоскостей в пространстве. Вы можете визуализировать такое пересечение, представив себе любой угол в прямоугольной комнате. Угол определяется тремя плоскостями: двумя примыкающими стенами и полом (или потолком). Любая точка, где встречаются две стены и пол, представляет собой пересечение трех плоскостей.

КОЛИЧЕСТВО ВОЗМОЖНЫХ РЕШЕНИЙ

На рисунке $\PageIndex{2}$ и рисунке $\PageIndex{3}$ показаны возможные сценарии решения для систем три на три.

Системы, имеющие единственное решение, это те, которые после исключения дают множество решений, состоящее из упорядоченной тройки ${(x,y,z)}$. Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
Системы, имеющие бесконечное число решений, — это те, которые после исключения приводят к всегда истинному выражению, например $0=0$. Графически бесконечное количество решений представляет собой линию или совпадающую плоскость, которая служит пересечением трех плоскостей в пространстве.
Системы, не имеющие решения, это те, которые после исключения приводят к утверждению, являющемуся противоречием, например $3=0$. Графически система без решения изображается тремя плоскостями, не имеющими общих точек.

Рисунок $\PageIndex{2}$: (a) Три плоскости пересекаются в одной точке, представляя систему три на три с единственным решением. (b) Три плоскости пересекаются по прямой, представляя систему три на три с бесконечными решениями.

Рисунок $\PageIndex{3}$: Все три рисунка представляют системы три на три без решения. а) Три плоскости пересекаются друг с другом, но не в одной точке. (b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. в) Все три плоскости параллельны, поэтому точек пересечения нет.

Пример $\PageIndex{1}$: определение того, является ли упорядоченная тройка решением системы

Определить, является ли упорядоченная тройка $(3,−2,1)$ решением системы.

\[\begin{align*} x+y+z &= 2 \nonumber \\[4pt] 6x−4y+5z &= 31 \nonumber \\[4pt] 5x+2y+2z &= 13 \nonumber \end{align*} \nonumber\]

Решение

Мы проверим каждое уравнение, подставив значения упорядоченной тройки вместо $x,y$ и $z$.

\[\begin{array}{rrr} { \text{} \nonumber \\[4pt] x+y+z=2 \nonumber \\[4pt] (3)+(−2)+(1) =2 \номер \\[4pt] \text{True}} & {6x−4y+5z=31 \неномер \\[4pt] 6(3)−4(−2)+5(1)=31 \неномер \\[4pt] 18+8+5=31 \не число \\[4pt] \text{True} } & { 5x+2y+2z = 13 \не число \\[4pt] 5(3)+2(−2 )+2(1)=13 \не число \\[4pt] 15−4+2=13 \не число \\[4pt] \text{True}} \end{массив}\]

Упорядоченная тройка $(3,−2,1)$ действительно является решением системы.

Как: Дана линейная система из трех уравнений, решить для трех неизвестных

Выберите любую пару уравнений и решите для одной переменной.
Выберите другую пару уравнений и решите для той же переменной.
Вы создали систему двух уравнений с двумя неизвестными. Решите полученную систему два на два.
Обратно подставьте известные переменные в любое из исходных уравнений и найдите отсутствующую переменную.

Пример $\PageIndex{2}$: Решение системы из трех уравнений с тремя переменными методом исключения

Найдите решение следующей системы:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] −x+3y−z=−6 \; &(2) \номер \\[4pt] 2x−5y+5z=17 \; &(3) \nonumber \end{align} \nonumber\]

Решение

Всегда будет несколько вариантов, с чего начать, но наиболее очевидным первым шагом здесь является устранение $x$ с помощью складывая уравнения (1) и (2).

\[\begin{align} x−2y+3z=9 \; \; &(1) \nonumber \\[4pt] \underline{−x+3y−z=−6 }\; \; &(2) \nonumber \\[4pt] y+2z=3 \;\; &(3) \nonumber \end{align} \nonumber\]

Второй шаг – умножение уравнения (1) на $−2$ и добавление результата к уравнению (3). Эти два шага устранят переменную $x$.

\[\begin{align} −2x+4y−6z=−18\; &(1) \;\;\;\; \text{ умножить на }−2 \nonumber \\[4pt] \underline{2x−5y+5z=17} \; & (3) \nonumber \\[4pt]−y−z=−1 \; &(5) \nonumber \end{align} \nonumber\]

В уравнениях (4) и (5) мы создали новую систему два на два. Мы можем найти $z$, добавив два уравнения.

\[\begin{align} y+2z=3 \; &(4) \nonumber \\[4pt] \underline{−y−z=−1} \; & (5) \номер \\[4pt] z=2 \; & (6) \nonumber \end{align} \nonumber\]

Выбирая по одному уравнению из каждой новой системы, получаем верхнетреугольную форму:

\[\begin{align} x−2y+3z=9 \; &(1) \nonumber \\[4pt] y+2z =3 \; &(4) \номер \\[4pt] z=2 \; &(6) \nonumber \end{align} \nonumber\]

Затем мы снова подставляем $z=2$ в уравнение (4) и находим $y$.

\[\begin{align} y+2(2) &=3 \nonumber \\[4pt] y+4 &= 3 \nonumber \\[4pt] y &= −1 \nonumber \end{align} \nonumber\]

Наконец, мы можем обратно подставить $z=2$ и $y=−1$ в уравнение (1).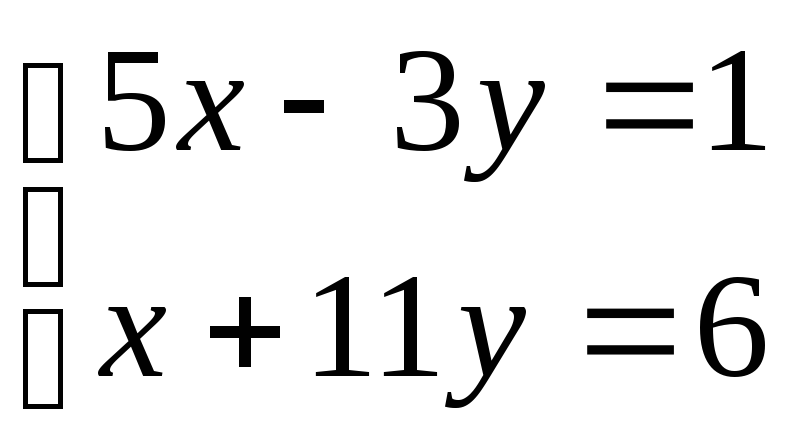 Это даст решение для $x$.

\[\begin{align} x−2(−1)+3(2) &= 9 \nonumber \\[4pt] x+2+6 &=9 \nonumber \\[4pt] x &= 1 \nonumber \end{align} \nonumber\]

Решением является упорядоченная тройка $(1,−1,2)$. См. рисунок $\PageIndex{4}$.

Рисунок $\PageIndex{4}$

Пример $\PageIndex{3}$: решение реальной задачи с использованием системы трех уравнений с тремя переменными

В проблема, поставленная в начале раздела, Джон вложил свое наследство $$12,000$ в три разных фонда: часть в фонд денежного рынка, выплачивающий $3\%$ годовых процентов; участие в муниципальных облигациях с выплатой $4\%$ ежегодно; а остальное в паевые инвестиционные фонды с выплатой $7\%$ ежегодно. Джон вложил в паевые инвестиционные фонды на 4000 долларов больше, чем в муниципальные облигации. Общая сумма процентов, полученных за один год, составила $$670$. Сколько он инвестировал в каждый тип фонда?

Решение

Чтобы решить эту задачу, мы используем всю предоставленную информацию и составим три уравнения. Во-первых, мы назначаем переменную каждой из трех сумм инвестиций:

\[\begin{align} x &= \text{сумма, инвестированная в фонд денежного рынка} \nonumber \\[4pt] y &= \text{ сумма, вложенная в муниципальные облигации} \nonumber \\[4pt] z &= \text{сумма, вложенная в паевые инвестиционные фонды} \nonumber \end{align} \nonumber\]

Первое уравнение показывает, что сумма трех основных сумм составляет $$12 000$.

\[x+y+z=12,000 \nonnumber\]

Составим второе уравнение на основе информации о том, что Джон вложил $$4,000$ в паевые инвестиционные фонды больше, чем он вложил в муниципальные облигации.

\[z=y+4,000 \nonnumber\]

Третье уравнение показывает, что общая сумма процентов, полученных от каждого фонда, равна $670$$.

\[0,03x+0,04y+0,07z=670 \нечисло\]

Затем мы записываем три уравнения в виде системы.

\[\begin{align} x+y+z &=12 000 \не число \\[4pt] −y+z &= 4 000 \не число \\[4pt] 0,03x+0,04y+0,07z &= 670 \ не номер \end{align} \nonumber\]

Чтобы упростить вычисления, мы можем умножить третье уравнение на $100$. Таким образом,

\[\begin{align} x+y+z &=12,000 \; &(1) \nonumber \\[4pt] −y+z &= 4000 \; &(2) \nonumber \\[4pt] 3x+4y+7z &= 67 000 \; &(3) \nonumber \end{align} \nonumber\]

Шаг 1. Поменяйте местами уравнение (2) и уравнение (3) так, чтобы два уравнения с тремя переменными совпали.

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] 3x+4y+7z &= 67 000 \nonumber \\[4pt] −y+z &= 4 000 \nonumber \end {выравнивание} \ноннумеро\]

Шаг 2. Умножьте уравнение (1) на $−3$ и добавьте к уравнению (2). Запишите результат в виде строки 2.

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] y+4z &= 31 000 \nonumber \\[4pt] −y+z &= 4,000 \nonumber \end{align} \nonumber\]

Шаг 3. Добавьте уравнение (2) к уравнению (3) и запишите результат как уравнение (3).

\[\begin{align} x+y+z &= 12 000 \nonumber \\[4pt] y+4z &= 31 000 \nonumber \\[4pt] 5z &= 35 000 \nonumber \end{align} \nonumber \]

Шаг 4. Найдите $z$ в уравнении (3). Подставьте обратно это значение в уравнение (2) и найдите $y$. Затем подставьте обратно значения для $z$ и $y$ в уравнение (1) и решите для $x$.

\[\begin{align} 5z &= 35,000 \не число \\[4pt] z &= 7,000 \не число \\[4pt] \ не число \\[4pt] y+4(7,000) &= 31,000 \не число \ \[4pt] y &=3,000 \nonumber \\[4pt] \nonumber \\[4pt] x+3,000+7,000 &= 12,000 \nonumber \\[4pt] x &= 2,000 \nonumber \end{align} \nonumber \]

Джон вложил $2000$$ в фонд денежного рынка, $3000$$ в муниципальные облигации и $7000$$ в паевые инвестиционные фонды.

Упражнение $\PageIndex{1}$

Решите систему уравнений с тремя переменными.

\[\begin{align} 2x+y−2z &= −1 \nonumber \\[4pt] 3x−3y−z &= 5 \nonumber \\[4pt] x−2y+3z &= 6 \nonumber \end{align} \nonumber\]

Ответ: $(1,−1,1)$

Выявление несовместных систем уравнений с тремя переменными

Так же, как и с системами уравнений с двумя переменными, мы можем столкнуться с противоречивой системой уравнений с тремя переменными, а это означает, что она не имеет решения, удовлетворяющего всем трем уравнениям. Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном и том же месте. Процесс исключения приведет к ложному утверждению, такому как $3=7$ или какому-либо другому противоречию.

Пример $\PageIndex{4}$: Решение противоречивой системы из трех уравнений с тремя переменными

Решите следующую систему.

\[\begin{align} x−3y+z &=4 \label{4.1}\\[4pt] −x+2y−5z &=3 \label{4.2} \\[4pt] 5x−13y+ 13z &=8 \label{4.3} \end{align} \nonumber\]

Решение

Глядя на коэффициенты $x$, мы видим, что мы можем исключить $x$, добавив Уравнение \ref{4.1} к уравнению \ref{4.2}.

\[\begin{align} x−3y+z = 4 &(1) \nonumber \\[4pt] \underline{−x+2y−5z=3} & (2) \nonumber \\[4pt] −y−4z =7 & (4) \nonumber \end{align} \nonumber\]

Затем мы умножаем уравнение (1) на $−5$ и добавляем его к уравнению (3).

\[\begin{align} −5x+15y−5z =−20 & (1) \;\;\;\;\; \text{умножается на }−5 \nonumber \\[4pt] \underline{5x−13y+13z=8} &(3) \nonumber \\[4pt] 2y+8z=−12 &(5) \nonumber \ end{align} \nonumber\]

Затем мы умножаем уравнение (4) на 2 и добавляем его к уравнению (5).

\[\begin{align} −2y−8z=14 & (4) \;\;\;\;\; \text{умножить на }2 \nonumber \\[4pt] \underline{2y+8z=−12} & (5) \nonumber \\[4pt] 0=2 & \nonumber \end{align} \nonumber\]

Итоговое уравнение $0=2$ является противоречием, поэтому делаем вывод, что система уравнений несовместна и, следовательно, не имеет решения.

Анализ

В этой системе каждая плоскость пересекает две другие, но не в одном и том же месте. Следовательно, система несовместима.

Упражнение $\PageIndex{2}$

Решите систему трех уравнений с тремя переменными.

\[\begin{align} x+y+z &= 2 \nonumber \\[4pt] y−3z &=1 \nonumber \\[4pt] 2x+y+5z &=0 \nonumber \end{ выровнять} \номер\]

Ответить: Нет решения.

Выражение решения системы зависимых уравнений с тремя переменными

Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений. То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может быть результатом нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на прямой, имеющей бесконечные решения. Или два уравнения могут быть одинаковыми и пересекать третье по прямой.

Пример $\PageIndex{5}$: Поиск решения зависимой системы уравнений

Найдите решение заданной системы трех уравнений с тремя переменными.

\[\begin{align} 2x+y−3z &= 0 &(1) \nonumber \\[4pt] 4x+2y−6z &=0 &(2) \nonumber \\[4pt] x−y +z &= 0 &(3) \nonumber \end{align} \nonumber\]

Решение

Во-первых, мы можем умножить уравнение (1) на $−2$ и добавить его к уравнению (2 ).

\[\begin{align} −4x−2y+6z = 0 & (1) \;\;\;\;\; \text{умножается на }−2 \nonumber \\[4pt] \underline{4x+2y−6z=0} & (2) \nonumber \\[4pt] 0=0& \nonumber \end{align} \nonumber\ ]

Нам не нужно продолжать. В результате мы получаем тождество $0=0$, которое говорит нам, что эта система имеет бесконечное число решений. Есть и другие способы начать решать эту систему, например, умножить уравнение (3) на $−2$ и добавить его к уравнению (1). Затем мы выполняем те же шаги, что и выше, и находим тот же результат, $0=0$.

Когда система зависима, мы можем найти общие выражения для решений. Складывая уравнения (1) и (3), имеем

\[\begin{align} 2x+y−3z &= 0 \nonumber \\[4pt]x−y+z &= 0 \nonumber \\[4pt] 3x−2z &= 0 \nonumber \end{align } \nonumber\]

Затем мы решаем полученное уравнение относительно $z$.

\[\begin{align} 3x−2z &= 0 \nonumber \\[4pt] z &= \dfrac{3}{2}x \nonumber \end{align} \nonumber\]

подставьте выражение для $z$ в одно из уравнений и найдите $y$.

\[\begin{align} 2x+y−3 (\dfrac{3}{2}x) &= 0 \nonumber \\[4pt] 2x+y−\dfrac{9}{2}x &= 0 \nonumber \\[4pt] y &= \dfrac{9}{2}x−2x \nonumber \\[4pt] y &=\dfrac{5}{2}x \nonumber \end{align} \nonumber\]

Таким образом, общее решение: $\left(x,\dfrac{5}{2}x,\dfrac{3}{2}x\right)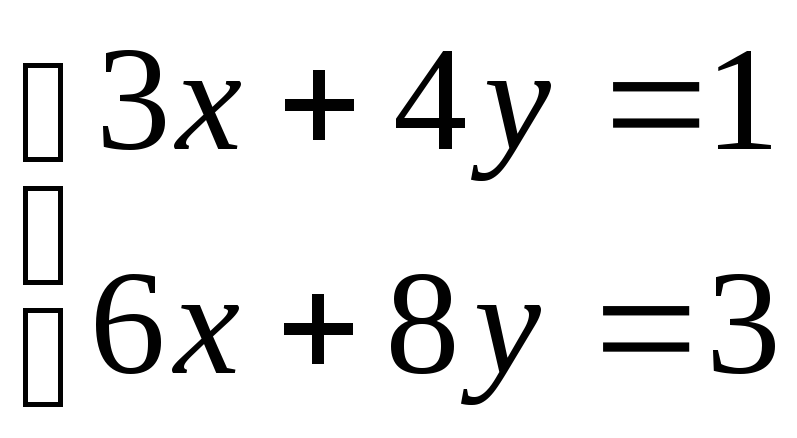$. В этом решении $x$ может быть любым вещественным числом. Значения $y$ и $z$ зависят от значения, выбранного для $x$.

Анализ

Как показано на рисунке $\PageIndex{5}$, две плоскости одинаковы и пересекают третью плоскость по прямой. Набор решений бесконечен, так как все точки вдоль линии пересечения будут удовлетворять всем трем уравнениям.

Рисунок $\PageIndex{5}$

Вопросы и ответы: Всегда ли общее решение для зависимой системы должно быть записано в терминах $x$?

Нет, общее решение можно записать в терминах любой из переменных, но обычно его записывают в терминах $x$ и, при необходимости, $x$ и $y$.

Упражнение $\PageIndex{3}$:

Решите следующую систему.

\[\begin{align} x+y+z &= 7 \nonumber \\[4pt] 3x−2y−z &= 4 \nonumber \\[4pt] x+6y+5z &= 24 \nonumber \ конец {выравнивание} \nonumber\]

Ответить: Бесконечное число решений вида $(x,4x−11,−5x+18)$.

Медиа

Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами уравнений с тремя переменными.

Пример 1: Система трех уравнений с тремя неизвестными с использованием исключения
пр. 2: Система трех уравнений с тремя неизвестными с использованием исключения

Набор решений — это упорядоченная тройка {(x,y,z)}, представляющая собой пересечение трех плоскостей в пространстве. См. пример $\PageIndex{1}$.
Систему из трех уравнений с тремя переменными можно решить, используя ряд шагов, которые заставляют исключить переменную. Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. См. пример $\PageIndex{2}$.
Системы трех уравнений с тремя переменными полезны для решения многих различных типов реальных задач. См. пример $\PageIndex{3}$.
Система уравнений с тремя переменными несовместна, если не существует решения. После выполнения операций исключения получается противоречие. См. пример $\PageIndex{4}$.
Противоречивые системы уравнений с тремя переменными могут быть результатом трех параллельных плоскостей, двух параллельных плоскостей и одной пересекающейся плоскости или трех плоскостей, которые пересекают две другие, но не в одном и том же месте.
Система уравнений с тремя переменными является зависимой, если она имеет бесконечное число решений. После выполнения операций исключения результатом является тождество. См. пример $\PageIndex{5}$.
Системы уравнений с тремя переменными, которые являются зависимыми, могут быть получены из трех одинаковых плоскостей, трех плоскостей, пересекающихся по прямой, или двух одинаковых плоскостей, пересекающих третью по прямой.

Авторы

Эта страница под названием 9. 2: Системы линейных уравнений — три переменные распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Наверх

Была ли эта статья полезной?

Тип изделия
Раздел или Страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать страницу TOC
нет
Включено
да
Теги
1. источник@https://openstax. org/details/books/precalculus
2. система линейных уравнений
3. три переменные

5.4 Решение для трех переменных – промежуточная алгебра

Глава 5: Системы уравнений

Когда даны три переменные, вы получаете уравнение для плоскости или плоской поверхности, похожей на лист бумаги. Некоторые из возможных решений пересечений этих уравнений можно визуализировать ниже.

При решении систем уравнений с тремя переменными используйте стратегии, используемые при решении систем двух уравнений. Один из рекомендуемых методов состоит в том, чтобы исключить одну переменную в начале, превратив таким образом систему из трех уравнений с тремя неизвестными в два уравнения с двумя неизвестными. Стандартный метод работы с тремя или более уравнениями заключается в использовании вычитания и/или сложения.

Найдите пересечение или решение следующей системы уравнений: [латекс]3x+2y-z=-1, -2x-2y+3z=5,[/латекс] и [латекс]5x+2y-z=3 .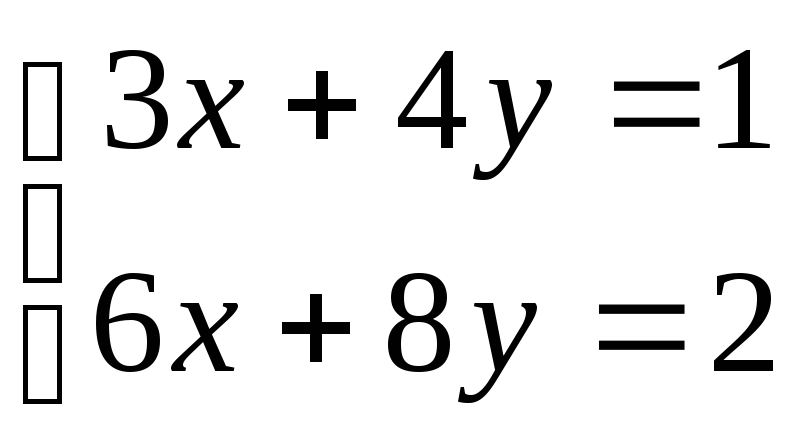 [/латекс]

Как и в случае с набором из двух уравнений, сначала выровняйте уравнения, чтобы выбрать переменную, которую мы хотим исключить:

[латекс]\left\{ \begin{array}{rrrrrrr} 3x&+&2y&-&z&= &-1 \\ -2x&-&2y&+&3z&=&5 \\ 5x&+&2y&-&z&=&3 \end{array} \right.[/latex]

В этих уравнениях проще всего исключить [latex]y [/latex]-переменная. Для этого сложите первое и второе уравнения вместе, а затем сложите вместе второе и третье уравнения:

[латекс]\begin{array}{rr} \begin{array}{rrrrrrrr} &3x&+&2y&-&z&=&-1 \\ +&-2x&-&2y&+&3z&=&5 \\ \hline &&&x&+&2z&= &4 \end{array} &\hspace{0.25in} \begin{array}{rrrrrrrr} &-2x&-&2y&+&3z&=&5 \\ +&5x&+&2y&-&z&=&3 \\ \hline &&&3x&+&2z&=&8 \ end{array} \end{array}[/latex]

Теперь у вас осталось [latex]x+2z=4[/latex] и [latex]3x + 2z = 8.[/latex] Теперь мы решаем как это было сделано ранее с набором из двух уравнений:

[латекс]\влево\{ \begin{array}{rrrrr} x&+&2z&=&4 \\ 3x&+&2z&=&8 \end{массив}\right.[/latex]

Умножение верхнего или нижнего уравнение на -1, чтобы исключить [latex]z[/latex]-переменную.

[латекс]\begin{array}{rrrrrrr} &(x&+&2z&=&4)&(-1) \\ &3x&+&2z&=&8& \\ \\ &-x&-&2z&=&-4& \\ +&3x& +&2z&=&8& \\ \hline &&&\dfrac{2x}{2}&=&\dfrac{4}{2}& \\ \\ &&&x&=&2& \end{array}[/latex]

Затем найдите [latex]z[/latex], используя одно из [latex]x+2z=4[/latex] или [latex]3x+2z=8[/latex] и решение [latex]x= 2 .[/latex] [latex]x+2z=4[/latex] кажется самым простым в работе.

[латекс]\begin{array}{rrrrr} x&+&2z&=&4 \\ 2&+&2z&=&4 \\ -2&&&&-2 \\ \hline &&\dfrac{2z}{2}&=&\dfrac{ 2}{2} \\ \\ &&z&=&1 \end{array}[/latex]

Наконец, найдите [latex]y[/latex], используя одно из трех исходных уравнений:

[латекс]\begin{array}{rrrrrrr} 3x&+&2y&-&z&=&-1 \\ 3(2)&+&2y&-&(1)&=&-1 \\ 6&+&2y&-&1&=& -1 \\ &&5&+&2y&=&-1 \\ &&-5&&&=&-5 \\ \hline &&&&\dfrac{2y}{2}&=&\dfrac{-6}{2} \\ \\ &&&&y& =&-3 \end{array}[/latex]

Эти плоскости пересекаются в точках [latex]x = 2,[/latex] [latex]y = -3,[/latex] и [latex]z = 1[/latex], или координата [latex](2, -3, 1).[/latex]

Иногда вам дают набор из трех уравнений с отсутствующими переменными. Для решения этих систем уравнений требуется чуть больше размышлений, чем для решения предыдущих задач.

Найдите пересечение или решение следующей системы уравнений: [латекс]x+2y-z=0, 3x-2y=-2,[/latex] и [латекс]y+z=3.[/latex]

Сначала выстроим уравнения, чтобы выбрать переменную, которую мы хотим исключить:

[латекс]\left\{ \begin{array}{rrrrrrr} x&+&2y&-&z&=&0 \\ 3x&-&2y&&&=&- 2 \\ &&y&+&z&=&3 \end{массив}\right.[/latex]

В этом примере добавление первого и последнего уравнений исключает переменную [latex]z,[/latex] без необходимости изменять какое-либо из уравнений:

[latex]\begin{array}{rrrrrrrr} &x&+&2y&- &z&=&0 \\ +&&&y&+&z&=&3 \\ \hline &&&x&+&3y&=&3 \\ \end{array}[/latex]

Теперь осталось два уравнения:

[латекс]\left\{ \begin{array}{rrrrr} 3x&-&2y&=&-2 \\ x&+&3y&=&3 \end{array}\right.[/latex]

Сначала умножьте нижнее уравнение на −3, затем добавьте его к верхнему уравнению, чтобы исключить переменную [латекс]x[/латекс]:

[латекс]\begin{array}{rrrrrrr} &(x&+&3y& =&3)&(-3) \\ \\ &3x&-&2y&=&-2& \\ +&-3x&-&9y&=&-9& \\ \hline &&&-11y&=&-11& \\ &&&y&=&1& \\ \ end{array}[/latex]

Теперь выберите одно из двух оставшихся уравнений, [latex]3x-2y=-2[/latex] или [latex]x+3y=3,[/latex], чтобы найти переменную [latex]x. [/latex] Выбор [latex]x+3y= 3,[/latex] оставляет:

[латекс]\begin{array}{rrrrr} x&+&3(1)&=&3 \\ x&+&3&=&3 \\ &-&3&=&-3 \\ \hline &&x&=&0 \end{array} [/latex]

Наконец, чтобы найти третью переменную, используйте одно из трех исходных уравнений: [latex]x+2y-z=0, 3x-2y=-2,[/latex] или [latex]y+ z=3.[/latex] Выбор [latex]y + z = 3,[/latex] дает:

[latex]\begin{array}{rrrrr} (1)&+&z&=&3 \\ &&z&=&2 \end{array}[/latex]

Эти плоскости пересекаются в точках [latex]x = 0, y = 1,[/latex] и [latex]z = 2,[/latex] или координате [latex] (0, 1, 2).[/латекс]

Решите каждую из следующих систем уравнений.

[латекс]\left\{ \begin{array}{rrrrrrr} a&-&b&+&2c&=&2 \\ 2a&+&b&-&c&=&2 \\ a&+&b&+&c&=&3 \end{array}\right. [/латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} 2a&+&3b&-&c&=&12 \\ 3a&+&4b&+&c&=&19 \\ a&-&2b&+&c&=&-3 \end{array}\right .[/латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} 3x&+&y&-&z&=&7 \\ x&+&3y&-&z&=&5 \\ x&+&y&+&2z&=&3 \end{array}\right. [ /латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&4 \\ x&+&2y&+&3z&=&10 \\ x&-&y&+&4z&=&20 \end{array}\right.[ /латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} x&+&2y&-&z&=&0 \\ 2x&-&y&+&z&=&15 \\ 3x&-&2y&-&4z&=&-5 \end{array}\right .[/латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} x&-&y&+&2z&=&-3 \\ x&+&2y&+&3z&=&4 \\ 2x&+&y&+&z&=&-3 \end{array} \право.[/латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&6 \\ 2x&-&y&-&z&=&-3 \\ x&-&2y&+&3z&=&6 \end{array}\right .[/латекс]
[латекс]\text{сложно:} \left\{ \begin{array}{rrrrrrr} x&+&y&-&z&=&0 \\ x&+&2y&-&4z&=&0 \\ 2x&+&y&+&z&=&0 \end{ массив}\право.[/латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} x&+&y&+&z&=&2 \\ 2x&-&y&+&3z&=&9\\ &&y&-&z&=&-3 \end{массив}\right.[/latex]
[латекс]\left\{ \begin{array}{rrrrrrr} 6x&-&y&-&2z&=&-1 \\ 4x&&&+&z&=&3 \\ -2x&+&3y&&&=&5 \end{array}\right.[/ латекс]
[латекс]\left\{ \begin{array}{rrrrrrr} &&y&+&z&=&5 \\ 2x&-&3y&+&z&=&-1 \\ x&&&-&z&=&-2 \end{array}\right.
No related posts.

Решение системы уравнений с тремя неизвестными: Решить систему из 3-х уравнений с 3-мя неизвестными онлайн / Калькуляторы

Методы решения систем линейных уравнений с двумя неизвестными

9.2: Системы линейных уравнений — три переменные

Цели обучения

Решение систем трех уравнений с тремя переменными

КОЛИЧЕСТВО ВОЗМОЖНЫХ РЕШЕНИЙ

Пример \(\PageIndex{1}\): определение того, является ли упорядоченная тройка решением системы

Как: Дана линейная система из трех уравнений, решить для трех неизвестных

Пример \(\PageIndex{2}\): Решение системы из трех уравнений с тремя переменными методом исключения

Пример \(\PageIndex{3}\): решение реальной задачи с использованием системы трех уравнений с тремя переменными

Упражнение \(\PageIndex{1}\)

Выявление несовместных систем уравнений с тремя переменными

Пример \(\PageIndex{4}\): Решение противоречивой системы из трех уравнений с тремя переменными

Упражнение \(\PageIndex{2}\)

Выражение решения системы зависимых уравнений с тремя переменными

Пример \(\PageIndex{5}\): Поиск решения зависимой системы уравнений

Вопросы и ответы: Всегда ли общее решение для зависимой системы должно быть записано в терминах \(x\)?

Упражнение \(\PageIndex{3}\):

Медиа

Авторы

5.4 Решение для трех переменных – промежуточная алгебра

Добавить комментарий Отменить ответ