Решение сокращение дробей онлайн: Сокращение дробей онлайн | umath.ru

Калькулятор дробей онлайн с решением

Понятие “дробь” слышал и встречал каждый человек, хотя бы потому что их проходят в школе на уроках математики. Однако не многие запоминают эту важную арифметическую тему, которая вполне может пригодиться в дальнейшей жизни. Настало время вспомнить, что же из себя представляют дроби и как с ними работать.

Что такое дроби?

Появились дроби еще во время первых цивилизаций, когда людям приходилось разделять между собой различные ресурсы и имущество. Таким образом, дроби (они же доли) были крайне полезны для понимания рыночной системы и экономики тех лет. На сегодняшний день дроби все так же актуальны, и именно поэтому рекомендуется внимательнее изучать эту тему на школьных уроках математики.

Дробью в арифметике называют число, которое складывается из одной или многих дробных единиц. Простыми словами, дробь – это определенное число, которое складывается из нескольких долей (равных частей).

Записывают простые дроби с помощью двух натуральных чисел. Одно из них помещают над горизонтальной короткой чертой, а другое – под ней. Иногда используется вертикальная косая линия. Например, 1\7. Линия называется чертой дроби.

Число, которое помещают над чертой дроби, называется числителем. Другое число, записываемое под чертой дроби, зовется знаменателем.

Виды дробей

Есть несколько видов дробей, каждый из которых имеет свои особенности и пути решения. Рассмотрим каждый из них.

Правильная дробь

Правильной дробью называется та, где числитель представляет собой число, которое меньше числа знаменателя.

Данная дробь (3\4) является правильной, потому что числитель (3) меньше знаменателя (4).

Неправильная дробь

Неправильной дробью именуют ту дробь, где числитель либо выступает равным знаменателю, либо превышает его по значению.

Пример: 4\3

Данная дробь является неправильной, так как числитель (4) превосходит по значению знаменатель (3).

Смешанная дробь

Смешанная дробь обычно представляет собой сочетание натурального числа и обыкновенной дроби. При этом натуральное число именуется целой частью дроби, а обыкновенная дробь – дробной.

Например, 2 целых 3\7.

Сократимая и несократимая

В случае, если делимое и знаменатель дроби можно поделить на какое-либо число, кроме единицы, она называется сократимой.

В случае, когда делимое и знаменатель дроби нельзя поделить на какое-то число, кроме единицы, дробь называется несократимой.

Имеем дроби 3\5 и 3\9.

Числа 3 и 5 являются взаимно простыми, что свидетельствует о том, что их нельзя поделить на одно и то же число.

Тем временем во второй дроби оба числа (и числитель, и знаменатель) возможно поделить на 3. Значит, дробь представляется сократимой.

Десятичная дробь

Когда знаменатель дроби включает в себя число, кратное десяти, то дробь считается десятичной.

Десятичные дроби записываются не так, как простые. Обычно они записываются при помощи двух натуральных чисел, отделенных друг от друга запятой.

Например, 3\10 = 0,3

Что умеет калькулятор дробей?

Современные калькуляторы дробей способны производить практически какие угодно математические действия и расчеты, связанные с дробями. Калькулятор дробей поможет с детальным решением задач, а также закрепит ваши знания по теме и прочее.

Калькулятор дробей онлайн без проблем справляется как с обыкновенными дробями, так и с десятичными или смешанными (содержащие целые числа).

Решение задач, содержащих дроби, часто пригождается ученикам, студентам, аспирантам и даже инженерам. Это освобождает свободное время, экономит энергию и силы на более важные дела.

Наш дробный калькулятор позволяет пользователям совершать такие действия, как:

• Деление;
• Умножение;
• Вычитание и сложение дробей.

При необходимости можно использовать и дополнительные функции калькулятора, не связанные напрямую с дробями.

Преимущество подобного калькулятора состоит в его мобильности. Вы можете использовать его на телефоне или компьютере, так что для него не нужно будет освобождать место или носить с собой.

Некоторые преподаватели позволяют своим студентам пользоваться на занятиях подобными калькуляторами для решения задач с дробями.

Это помогает лучше запоминать алгоритм действий, укреплять свои знания о дробях и регулярно их использовать.

Полезно это приспособление будет и для учеников средней школы. При помощи онлайн калькулятора можно проверять ранее самостоятельно решенные задачи. Это необходимо, для того чтобы ребенок смог сделать работу над ошибками и проанализировать свою работу.

Сложение дробей

Сложением принято именовать одно из арифметических действий, результатом которого выступает совершенно новое число.

Если вы имеете дроби с равными делителями, которые требуется сложить, то лучше всего сделать это так:

Для получения суммы двух дробей с одинаковыми знаменателями, следует просто сложить между собой делимые, а знаменатель оставить прежним.

Например:

Имеем дроби 3\5 и 4\5. Складываем числители 3 и 4, получаем дробь 7\5.

Если вы имеете дроби с разными знаменателями, которые необходимо сложить, то лучше всего сделать это так:

• Ищем наименьший общий знаменатель;
• Используем для осуществления задачи предыдущее правило.

Рассмотрим это немного подробнее. Сначала нужно найти меньшее общее кратное. Это поможет определить единый делитель.

Для этого можно перемножить делимое и делитель на один и тот же множитель. После этого действия делитель будет равен наименьшему общему кратному. После этого следует перейти к сложению.

Как сложить смешанные числа? Существует несколько вариантов решения такой задачи.

• Во-первых, можно сложить по отдельности целые и дробные части.
• Во-вторых, можно сначала перевести обычные дроби в неправильные. И только после этого начать складывать дроби.
• Иногда возникает необходимость привести дроби к общему знаменателю.
• После этого неправильную дробь можно снова перевести в смешанную.

Вычитание дробей

Как совершить вычитание дробей, когда они имеют одинаковые знаменатели? Сделать это на самом деле достаточно просто: следует из первого числителя отнять делимое второй дроби. Знаменатель, как и в примере сложения, остается прежним, так как менять его нет необходимости.

Что делать, если знаменатели разные? В таком случае необходимо привести дроби к общему знаменателю и тогда по вышеупомянутому правилу производить вычитание.

Такие же дела обстоят и с натуральными числами. Из натурального числа делают неправильную дробь, после чего приводят к одинаковому знаменателю и производят вычитание.

Умножение дробей

Умножение дробей – это еще одно популярное арифметическое действие, требуемое для решения различных задач.

Чтобы умножить простые дроби, необходимо числитель одной умножить на числитель другой, а знаменатель одной перемножить со знаменателем другой.

Умножение смешанных дробей с простыми или между собой производится так же. Сначала из смешанных дробей делают неправильные, а затем перемножают числители и знаменатели.

Деление дробей

Делением называют действие в арифметике, которое позволяет узнать, какое количество раз одно число возможно вместить в другом числе. вдобавок деление можно наименовать действием, противоположным умножению.

Как разделить обыкновенную дробь на вторую обыкновенную дробь?

Для решения необходимо совершить некоторый перечень действий:

• Числитель одной дроби умножаем на знаменатель другой дроби. Результат умножения записываем в качестве числителя новой дроби.
• Знаменатель первой умножаем на числитель второй, итоговое решение помещаем на место знаменателя в получившейся дроби.

Разобраться в таких сложных на первый взгляд правилах всегда можно либо при помощи примеров, либо при помощи работы с онлайн калькулятором для дробей.

Имеем дроби 3\4 и 5\6. Необходимо умножить 3 на 6 и 4 на 5. Ответ: 18/20=9/10

Как разделить дробь на натуральное целое число?

Процесс решения такой задачи состоит из нескольких последовательных действий:

• Из целого числа нужно сделать неправильную дробь, где числитель будет равен этому же натуральному числу. В качестве знаменателя часто указывают единицу.
• Затем производят деление по упомянутому выше правилу.

Имеем натуральное число 2 и дробь 1\2. Натуральное число преобразуем в 2\1. Делим 2\1 на 1\2. Ответ: 4/1=4.

Как делить дробь на смешанное число?

Процесс решения такой задачи состоит из нескольких последовательных действий:

• Первым делом необходимо сделать из смешанной дроби дробь неправильного типа;
• Теперь простую и неправильную дробь делим по упомянутым ранее правилам.

Вопрос-ответ о дробях

Каковы ключевые свойства дробей?

• При умножении числителя и знаменателя на одно и то же число, получается дробь, равная предыдущей.
• При делении числителя и знаменателя на одно и то же число, получается дробь, которая равна предыдущей.

Какую дробь можно считать несократимой?

Несократимой именуют дробь, где как числитель, так и знаменатель представляют собой простые числа.

Как определить общий знаменатель дробей?

Общим знаменателем дробей именуют общее кратное этих делителей.

Что представляют собой сокращение дроби?

Сокращением дроби именуют деление делимого и знаменателя на их общий делитель.

Как сделать из обычной дроби десятичную?

Чтобы перевести обычную дробь в дробь десятичного типа, необходимо разделить её числитель на знаменатель.

Онлайн калькулятор сокращения алгебраических дробей с подробным решением позволяет сократить дробь и перевести неправильную дробь в правильную дробь. Сокращение алгебраических дробей

Работая с дробями, многие ученики допускают одни и те же ошибки. А все потому, что они забывают элементарные правила арифметики . Сегодня мы повторим эти правила на конкретных задачах, которые я даю на своих занятиях.

Вот задача, которую я предлагаю каждому, кто готовится к ЕГЭ по математике:

Задача. Морская свинья ест 150 грамм корма в день. Но она выросла и стала есть на 20% больше. Сколько грамм корма теперь ест свинья?

Неправильное решение. Это задача на проценты, которая сводится к уравнению:

Многие (очень многие) сокращают число 100 в числителе и знаменателе дроби:

Вот такую ошибку допустила моя ученица прямо в день написания этой статьи. Красным отмечены числа, которые были сокращены.

Излишне говорить, что ответ получился неправильный. Судите сами: свинья ела 150 грамм, а стала есть 3150 грамм. Увеличение не на 20%, а в 21 раз, т.е. на 2000%.

Чтобы не допускать подобных недоразумений, помните основное правило:

Сокращать можно только множители. Слагаемые сокращать нельзя!

Таким образом, правильное решение предыдущей задачи выглядит так:

Красным отмечены цифры, которые сокращаются в числителе и знаменателе. Как видите, в числителе стоит произведение, знаменателе — обыкновенное число. Поэтому сокращение вполне законно.

Работа с пропорциями

Еще одно проблемное место — пропорции . Особенно когда переменная стоит с обеих сторон. Например:

Задача. Решите уравнение:

Неправильное решение — у некоторых буквально руки чешутся сократить все на m :

Сокращаемые переменные показаны красным. Получается выражение 1/4 = 1/5 — полный бред, эти числа никогда не равны.

А теперь — правильное решение. По существу, это обыкновенное

линейное уравнение . Решается либо переносом всех элементов в одну сторону, либо по основному свойству пропорции:

Многие читатели возразят: «Где ошибка в первом решении?» Что ж, давайте разбираться. Вспомним правило работы с уравнениями:

Любое уравнение можно делить и умножать на любое число, отличное от нуля .

Просекли фишку? Можно делить только на числа, отличные от нуля . В частности, можно делить на переменную m , только если m != 0. А что делать, если все-таки m = 0? Подставим и проверим:

Получили верное числовое равенство, т.е. m = 0 — корень уравнения. Для остальных m != 0 получаем выражение вида 1/4 = 1/5, что, естественно, неверно. Таким образом, не существует корней, отличных от нуля.

Выводы: собираем все вместе

Итак, для решения дробно-рациональных уравнений помните три правила:

1. Сокращать можно только множители. Слагаемые — нельзя. Поэтому учитесь раскладывать числитель и знаменатель на множители;
2. Основное свойство пропорции: произведение крайних элементов равно произведению средних;
3. Уравнения можно умножать и делить только на числа k , отличные от нуля. Случай k = 0 надо проверять отдельно.

Помните эти правила и не допускайте ошибок.

Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Yandex.RTB R-A-339285-1

Что такое «сокращение дробей»

Сократить дробь

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

К примеру, возьмем обыкновенную дробь 6 24 и сократим ее. Разделим числитель и знаменатель на 2 , в результате чего получим 6 24 = 6 ÷ 2 24 ÷ 2 = 3 12 .

В этом примере мы сократили исходную дробь на 2 .

Приведение дробей к несократимому виду

В предыдущем примере мы сократили дробь 6 24 на 2 , в результате чего получили дробь 3 12 . Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

a b = a ÷ Н О Д (a , b) b ÷ Н О Д (a , b)

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

Вернемся к дроби 6 24 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6 . Сократим дробь:

6 24 = 6 ÷ 6 24 ÷ 6 = 1 4

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

1. Найти НОД числителя и знаменателя.
2. Разделить числитель и знаменатель на их НОД.

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Дана дробь 182 195 . Сократим ее.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

195 = 182 · 1 + 13 182 = 13 · 14 Н О Д (182 , 195) = 13

Разделим числитель и знаменатель на 13 . Получим:

182 195 = 182 ÷ 13 195 ÷ 13 = 14 15

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Дана дробь 360 2940 . Сократим ее.

Для этого представим исходную дробь в виде:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

Сократим дробь 2000 4400 .

Сразу видно, что числитель и знаменатель имеют общий множитель 100 . Сокращаем дробь на 100 и получаем:

2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44

20 44 = 20 ÷ 2 44 ÷ 2 = 10 22

Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:

10 22 = 10 ÷ 2 22 ÷ 2 = 5 11

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.

Yandex.RTB R-A-339285-1

Смысл сокращения алгебраической дроби

В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.

Сокращение алгебраической дроби представляет собой аналогичное действие.

Определение 1

Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.

К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х, и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 .

Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.

Все ли алгебраические дроби подлежат сокращению?

Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .

С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.

В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .

В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х, или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.

Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.

Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.

Правило сокращения алгебраических дробей

Правило сокращения алгебраических дробей состоит из двух последовательных действий:

• нахождение общих множителей числителя и знаменателя;
• в случае нахождения таковых осуществление непосредственно действия сокращения дроби.

Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.

Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .

Характерные примеры

Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:

5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ;

Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).

К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105

Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105

(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105

По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.

Пример 1

Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение.

Решение

Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6

Однако, более рациональным способом будет запись решения в виде выражения со степенями:

27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .

Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6

Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).

Пример 2

Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.

Решение

Возможно сократить дробь таким образом:

2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2

Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК (5 , 10) = 10 . Тогда получим:

2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .

Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2

Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

Пример 3

Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить.

Решение

Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49)

Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:

2 · b 2 · (a 2 + 14 · a + 49) b 3 · (a 2 — 49) = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7)

Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · (a + 7) . Произведем сокращение:

2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b

Краткое решение без пояснений запишем как цепочку равенств:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · (a 2 + 14 a + 49) b 3 · (a 2 — 49) = = 2 · b 2 · (a + 7) 2 b 3 · (a — 7) · (a + 7) = 2 · (a + 7) b · (a — 7) = 2 · a + 14 a · b — 7 · b

Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .

Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.

Пример 4

Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.

Решение

На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:

1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2

Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:

x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10

Теперь становится виден общий множитель, осуществляем сокращение:

2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x

Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x .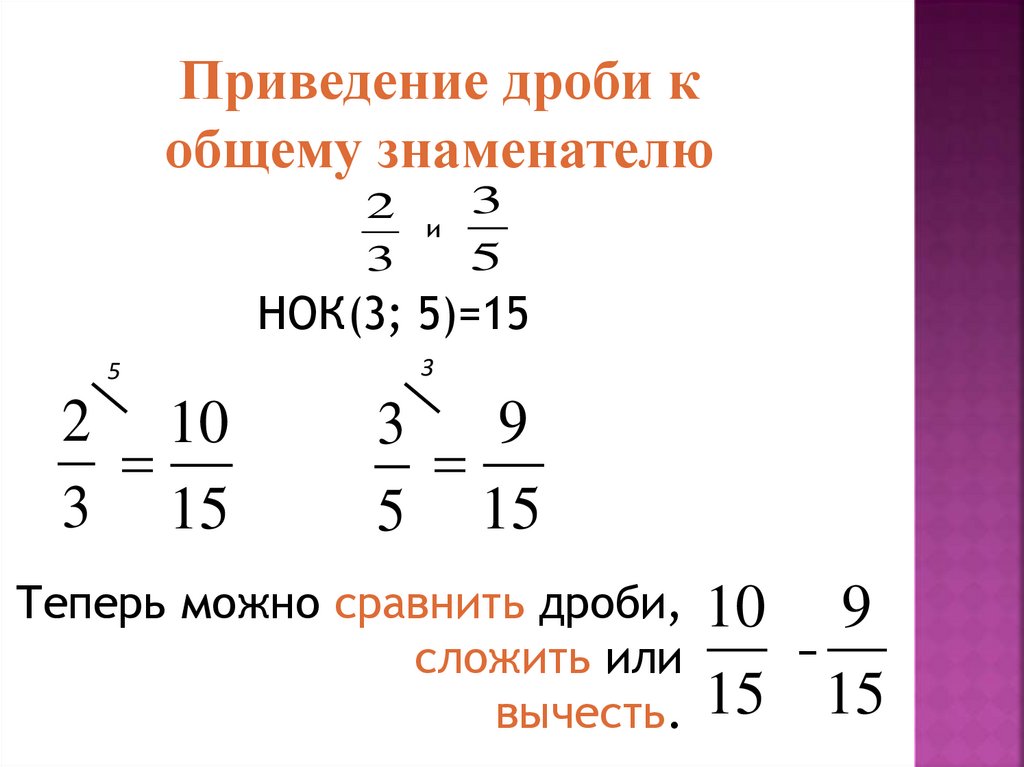

Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

На первый взгляд алгебраические дроби кажутся очень сложными, и неподготовленный учащийся может подумать, что с ними невозможно ничего сделать. Нагромождение переменных, чисел и даже степеней навевает страх. Тем не менее, для сокращения обычных (например, 15/25) и алгебраических дробей используются одни и те же правила.

Шаги

Сокращение дробей

Ознакомьтесь с действиями с простыми дробями. Операции с обычными и алгебраическими дробями аналогичны. К примеру, возьмем дробь 15/35. Чтобы упростить эту дробь, следует найти общий делитель . Оба числа делятся на пять, поэтому мы можем выделить 5 в числителе и знаменателе:

15

→

5 * 3

35 → 5 * 7

Теперь можно сократить общие множители , то есть вычеркнуть 5 в числителе и знаменателе. В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяются точно так же, как и в обычных. В предыдущем примере мы смогли легко выделить 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x – 5. Найдем общий множитель. В данном случае это будет 5, так как оба члена (15x и -5) делятся на 5. Как и ранее, выделим общий множитель и перенесем его влево .

15x – 5 = 5 * (3x – 1)

Чтобы проверить, все ли правильно, достаточно умножить на 5 стоящее в скобках выражение — в результате получатся те же числа, что были сначала. Сложные члены можно выделять точно так же, как и простые. Для алгебраических дробей применимы те же принципы, что и для обычных. Это наиболее простой способ сократить дробь. Рассмотрим следующую дробь:

(x+2)(x-3)

(x+2)(x+10)

Отметим, что и в числителе (сверху), и в знаменателе (снизу) присутствует член (x+2), поэтому его можно сократить так же, как общий множитель 5 в дроби 15/35:

(x+2) (x-3)

→

(x-3)

(x+2) (x+10) → (x+10)

В результате получаем упрощенное выражение: (x-3)/(x+10)

Сокращение алгебраических дробей

Найдите общий множитель в числителе, то есть в верхней части дроби. При сокращении алгебраической дроби первым делом следует упростить обе ее части. Начните с числителя и постарайтесь разложить его на как можно большее число множителей. Рассмотрим в данном разделе следующую дробь:

9x-3

15x+6

Начнем с числителя: 9x – 3. Для 9x и -3 общим множителем является число 3. Вынесем 3 за скобки, как это делается с обычными числами: 3 * (3x-1). В результате данного преобразования получится следующая дробь:

3(3x-1)

15x+6

Найдите общий множитель в числителе. Продолжим выполнение приведенного выше примера и выпишем знаменатель: 15x+6. Как и раньше, найдем, на какое число делятся обе части. И в этом случае общим множителем является 3, так что можно записать: 3 * (5x +2). Перепишем дробь в следующем виде:

3(3x-1)

3(5x+2)

Сократите одинаковые члены. На этом шаге можно упростить дробь. Сократите одинаковые члены в числителе и знаменателе. В нашем примере это число 3.

3 (3x-1)

→

(3x-1)

3 (5x+2) → (5x+2)

Определите, что дробь имеет простейший вид. Дробь полностью упрощена в том случае, когда в числителе и знаменателе не осталось общих множителей. Учтите, что нельзя сокращать те члены, которые стоят внутри скобок — в приведенном примере нет возможности выделить x из 3x и 5x, поскольку полными членами являются (3x -1) и (5x + 2). Таким образом, дробь не поддается дальнейшему упрощению, и окончательный ответ выглядит следующим образом:

(3x-1) (5x+2)

Потренируйтесь сокращать дроби самостоятельно. Лучший способ усвоить метод заключается в самостоятельном решении задач. Под примерами приведены правильные ответы.

4(x+2)(x-13)

(4x+8)

Ответ: (x=13)

2x 2 -x

5x

Ответ: (2x-1)/5

Специальные приемы

Вынесите отрицательный знак за пределы дроби. Предположим, дана следующая дробь:

3(x-4)

5(4-x)

Заметьте, что (x-4) и (4-x) “почти” идентичны, но их нельзя сократить сразу, поскольку они “перевернуты”. Тем не менее, (x — 4) можно записать как -1 * (4 — x), подобно тому как (4 + 2x) можно переписать в виде 2 * (2 + x). Это называется “переменой знака”.

-1 * 3(4-x)

5(4-x)

Теперь можно сократить одинаковые члены (4-x):

-1 * 3 (4-x)

5 (4-x)

Итак, получаем окончательный ответ: -3/5 . Научитесь распознавать разницу квадратов. Разница квадратов — это когда квадрат одного числа вычитается из квадрата другого числа, как в выражении (a 2 — b 2). Разницу полных квадратов всегда можно разложить на две части — сумму и разницу соответствующих квадратных корней. Тогда выражение примет следующий вид:

A 2 — b 2 = (a+b)(a-b)

Этот прием очень полезен при поиске общих членов в алгебраических дробях.

• Проверьте, правильно ли вы разложили то или иное выражение на множители. Для этого перемножьте множители — в результате должно получиться то же самое выражение.
• Чтобы полностью упростить дробь, всегда выделяйте наибольшие множители.

Калькулятора онлайн выполняет сокращение алгебраических дробей в соответствии с правилом сокращения дробей: замена исходной дроби равной дробью, но с меньшими числителем и знаменателем, т.е. одновременное деление числителя и знаменателя дроби на их общий наибольший общий делитель (НОД). Также калькулятор выводит подробное решение, которое поможет понять последовательность выполнения сокращения.

Дано:

Решение:

Выполнение сокращения дробей

проверка возможности выполнения сокращения алгебраической дроби

1) Определение наибольшего общего делителя (НОД) числителя и знаменателя дроби

определение наибольшего общего делителя (НОД) числителя и знаменателя алгебраической дроби

2) Сокращение числителя и знаменателя дроби

сокращение числителя и знаменателя алгебраической дроби

3) Выделение целой части дроби

выделение целой части алгебраической дроби

4) Перевод алгебраической дроби в десятичную дробь

перевод алгебраической дроби в десятичную дробь

Помощь на развитие проекта сайт

Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Порядок действий при сокращении алгебраической дроби калькулятором онлайн:

1. Чтобы выполнить сокращение алгебраической дроби введите в соответствующие поля значения числителя, знаменателя дроби. Если дробь смешанная, то также заполните поле, соответствующее целой части дроби. Если дробь простая, то оставьте поле целой части пустым.
2. Чтобы задать отрицательную дробь, поставьте знак минус в целой части дроби.
3. В зависимости от задаваемой алгебраической дроби автоматически выполняется следующая последовательность действий:

• определение наибольшего общего делителя (НОД) числителя и знаменателя дроби ;
• сокращение числителя и знаменателя дроби на НОД ;
• выделение целой части дроби , если числитель итоговой дроби больше знаменателя.
• перевод итоговой алгебраической дроби в десятичную дробь с округлением до сотых.

В результате сокращения может получиться неправильная дробь. В этом случае у итоговой неправильной дроби будет выделена целая часть и итоговая дробь будет переведена в правильную дробь.

II. Для справки:

Дробь — число, состоящее из одной или нескольких частей (долей) единицы. Обыкновенная дробь (простая дробь) записывается в виде двух чисел (числитель дроби и знаменатель дроби), разделенных горизонтальной чертой (дробной чертой), обозначающей знак деления. числитель дроби — число, стоящее над дробной чертой. Числитель показывает, сколько долей взяли у целого. знаменатель дроби — число, стоящее под дробной чертой. Знаменатель показывает, на сколько равных долей разделено целое. простая дробь — дробь, не имеющая целой части. Простая дробь может быть правильной или неправильной. правильная дробь — дробь, у которой числитель меньше знаменателя, поэтому правильная дробь всегда меньше единицы. Пример правильных дроби: 8/7, 11/19, 16/17. неправильная дробь — дробь, у которой числитель больше или равен знаменателю, поэтому неправильная дробь всегда больше единицы или равна ей. Пример неправильных дроби: 7/6, 8/7, 13/13. смешанная дробь — число, в состав которого входит целое число и правильная дробь, и обозначает сумму этого целого числа и правильной дроби. Любая смешанная дробь может быть преобразована в неправильную простую дробь. Пример смешанных дробей: 1¼, 2½, 4¾.

III. Примечание:

1. Блок исходных данных выделен желтым цветом , блок промежуточных вычислений выделен голубым цветом , блок решения выделен зеленым цветом .
2. Для сложения, вычитания, умножения и деления обыкновенных или смешанных дробей воспользуйтесь онлайн калькулятором дробей с подробным решением.

Упроститель дробей | Шаги по уменьшению дроби до наименьшего члена

Бесплатный онлайн-калькулятор Fraction Simplifier легко определяет сокращенную форму дроби. Введите значения числителя и знаменателя дроби и нажмите кнопку расчета, чтобы использовать упрощенную дробь в качестве вывода в кратчайшие сроки.

---

Калькулятор упрощенных дробей: Вы можете использовать удобный инструмент для упрощения дробей, чтобы получить значение упрощенной дроби. Здесь мы даем подробные ручные шаги для расчета сокращенных дробей. Также знайте решенные примеры вопросов на упрощение дробей.

---

Как упростить дроби?

Это простые шаги, чтобы найти значение уменьшенной дроби.

• Возьмите любую дробь со значениями числителя и знаменателя.
• Найдите множители числителя и знаменателя.
• После этого рассчитайте GCF значений.
• Разделить дробь на общий делитель, т.е. GCF
• Наконец, вы получаете простейшую форму дроби.

---

Примеры вопросов по сокращению дробей

Вопрос 1:

Найдите простейшую форму дроби 1225/520?

Решение:

Дана дробь 1225/520

Чтобы привести дробь к наименьшему члену, вы должны разделить и числитель, и знаменатель на GCF.

GCF 1225, 520 равно 5

Разделите дробь на 5, т.е. (1225÷5)/(520÷5)

= 245/104

Следовательно, сокращенная форма дроби 1225/520 равна 245/104.

Вопрос 2:

Упростить дробь 1008/36?

Решение:

Данная дробь равна 1008/36

Чтобы сократить дробь до наименьшего члена, вы должны разделить и числитель, и знаменатель на GCF.

GCF 1008 и 36 равно 36

Разделите дробь на 36, т.е. (1008÷36)/(36÷36)

= 26/1

Следовательно, упрощенная дробь равна 26/1 или 26.

---

Simplifying Fractions Examples

Simplify 67/21

Simplify 3/58

Simplify 62/28

Simplify 79/90

Simplify 69/20

Упростить 58/11

Упростить 57/51

Упрощение 19/44

Упростить 41/6

Упростить 30/27

18. Упрощенная 89918

30/27

9001

./53

Simplify 49/11

Simplify 88/37

Simplify 17/63

Simplify 19/14

Simplify 21/44

Simplify 13/77

Simplify 13/88

Simplify 44/85

Simplify 85/5

Simplify 39/51

Simplify 30/81

Simplify 41/19

Simplify 83/65

Simplify 77/70

Simplify 82/19

Simplify 25/53

Simplify 8/53

Simplify 40/42

Упростить 80/73

Упростить 46/27

Упростить 1/44

Упростить 22/50

Упрощение 83/15

9003

.0019

Simplify 17/68

Simplify 14/37

Simplify 56/52

Simplify 61/33

Simplify 58/74

Simplify 3/30

Упростить 37/48

Упростить 20/61

Упрощение 10/37

Упрощение 7/53

Упростить 27/74

59. 37459. 37445. 37445.

5 9003

0019

Упростить 58/55

Упростить 75/19

Упрощение 52/14

---

FAQS на фракциях.

Самый простой способ упростить дроби — использовать наш бесплатный калькулятор дробей. Он просто принимает дробные значения и выдает упрощенную дробь в секундах.

---

2. Что такое 4/8 в простейшей форме?

4 — общий множитель 4 и 8. Итак, делим 4/8 на 4.

(4÷4)/(8÷4) = 1/2.

---

3. Какова цель упрощения дробей?

В общем, мы упрощаем дроби, так как их легко читать, писать, запоминать и легко использовать в простейших значениях дробей в математических расчетах.

---

4. Как уменьшить дробь?

Чтобы представить дробь в ее наименьшем члене, мы должны вычислить наибольший общий делитель верхней и нижней части дроби. Позже разделите дробь на GCF, чтобы получить результирующую дробь.

---

Как привести дробь к наименьшему члену

Обновлено: 13 июля 2021 г.

Базовая математика и предварительная алгебра: все в одном для чайников (+ викторины по главам онлайн)

Исследуйте книгу Buy On Amazon

Даже если дроби выглядят по-разному, на самом деле они могут представлять одну и ту же сумму; другими словами, одна из дробей будет иметь уменьшенные члены по сравнению с другой. Возможно, вам придется уменьшить члены дробей, чтобы работать с ними в уравнении.

Приведение дробей к наименьшему виду требует деления. Но поскольку вы не всегда можете делить, сокращение требует некоторой ловкости.

Здесь вы узнаете формальный способ сокращения дробей, который работает во всех случаях. Затем вы научитесь более неформальному способу, который сможете использовать, когда вам будет более комфортно.

Метод 1: формальное сокращение дробей

Сокращение дробей формальным способом зависит от понимания того, как разбить число на его простые множители.

Вот как уменьшить дробь:

1. Разложите числитель (верхнее число) и знаменатель (нижнее число) на простые множители.

   Например, предположим, что вы хотите уменьшить дробь 12/30. Разложите числа 12 и 30 на их простые множители:

   .

2. Вычеркните любые общие факторы.

   В этом примере вы вычеркиваете 2 и 3, потому что они являются общими множителями, то есть они появляются и в числителе, и в знаменателе:

3. Умножьте оставшиеся числа, чтобы получить уменьшенные числитель и знаменатель.

   Это показывает, что дробь 12/30 сводится к 2/5:

В качестве другого примера, вот как вы уменьшаете дробь 32/100:

На этот раз вычеркните две двойки сверху и снизу как общие множители. Остальные двойки сверху и 5 снизу не являются общими факторами. Таким образом, дробь 32/100 сводится к 8/25.

Метод 2: неформальное сокращение дробей

Вот более простой способ сокращения дробей после того, как вы освоитесь с концепцией:

1. Если числитель (верхнее число) и знаменатель (нижнее число) делятся на 2, то есть если они оба четные, разделите оба на 2.

   Например, предположим, что вы хотите уменьшить дробь 24/60. И числитель, и знаменатель четные, поэтому разделите их на 2:

2. Повторяйте шаг 1 до тех пор, пока числитель или знаменатель (или оба) не перестанут делиться на 2.

   В полученной дроби оба числа по-прежнему четные, поэтому повторите первый шаг еще раз:

3. Повторите шаг 1, используя число 3, затем 5, а затем 7, продолжая проверять простые числа, пока не убедитесь, что числитель и знаменатель не имеют общих делителей.

   Теперь и числитель, и знаменатель делятся на 3, поэтому разделите оба на 3:

   Ни числитель, ни знаменатель не делятся на 3, поэтому этот шаг завершен.

   No related posts.