Решение уравнений с тремя неизвестными: Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с. Учебник для средних общеобразовательных школ СССР в 50-60-е годы. Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым. Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений. Оглавление ГЛАВА ПЕРВАЯ АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ. § 2. Алгебраические выражения. § 3. Допустимые значения букв. § 4. Порядок действий. § 5. Основные законы сложения и умножения. § 6. Краткие исторические сведения. ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА. § 7. Положительные и отрицательные числа. § 8. Числовая ось. § 9. Противоположные числа. § 10. Абсолютная величина числа. § 11. Сравнение рациональных чисел. § 12. Сложение рациональных чисел. § 13. Сложение нескольких чисел. § 14. Законы сложения. § 15. Вычитание рациональных чисел. § 16. Алгебраическая сумма. § 17. Умножение. § 18. Умножение нескольких чисел. § 19. Законы умножения. § 20. Деление. § 21. Свойства деления. § 22. Возведение в степень. § 23. Порядок выполнения действий. § 24. Уравнения. § 25. Решение задач с помощью уравнений. § 26. Графики. § 27. Краткие исторические сведения. (Из истории отрицательных чисел.) ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ. 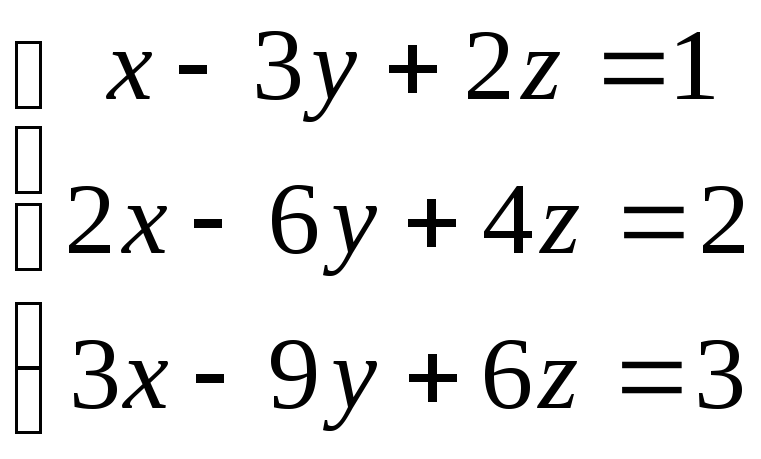§ 28. Одночлен и многочлен. § 29. Тождества и тождественные преобразования. § 30. Коэффициент. § 31. Расположенные многочлены. § 32. Приведение подобных членов. § 33. Сложение одночленов и многочленов. § 34. Противоположные многочлены. § 35. Вычитание одночленов и многочленов § 36. Умножение одночленов. § 37. Умножение многочлена на одночлен. § 38. Умножение многочленов. § 39. Умножение расположенных многочленов. § 40. Возведение одночленов в степень. § 41. Формулы сокращённого умножения. § 42. Общие замечания о делении целых алгебраических выражений. § 43. Деление одночленов. § 44. Деление многочлена на одночлен § 45. Примеры решения уравнений. ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ. § 47. Равносильные уравнения. § 48. Два основных свойства уравнений. § 49. Уравнения, содержащие неизвестное в обеих частях. § 50. Уравнение первой степени с одним неизвестным. § 51. Общие указания к решению уравнений. § 52. Решение задач с помощью уравнений. § 53. Краткие исторические сведения. (Из истории уравнений.) ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ. § 54. Понятие о разложении на множители. § 55. Вынесение за скобки общего множителя. § 56. Способ группировки. § 57. Применение формул сокращённого умножения. § 58. Применение нескольких способов. § 59. Деление многочленов при помощи разложения на множители. ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ. § 60. Понятие об алгебраической дроби. § 61. Основное свойство дроби и сокращение дробей. § 62. Перемена знака у членов дроби. § 63. Целая отрицательная и нулевая степени числа. § 64. Приведение дробей к общему знаменателю. § 65. Сложение дробей. § 66. Вычитание дробей. § 67. Умножение дробей. § 68. Деление дробей. § 69. Возведение дроби в натуральную степень. § 70. Дробные уравнения. § 71. Примеры решения уравнений с буквенными коэффициентами. ГЛАВА СЕДЬМАЯ. КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ. § 72. Координаты точки на плоскости. § 73. Прямо пропорциональная зависимость. § 74. График прямо пропорциональной зависимости. § 75. Линейная зависимость. § 76. Обратно пропорциональная зависимость. ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ. § 77. Уравнение первой степени с двумя неизвестными. § 78. Система двух уравнений первой степени с двумя неизвестными. § 79. Равносильные системы. § 80. Решение систем уравнений. § 81. Графическое решение системы двух уравнений. § 82. Решение задач. § 83. Уравнение с тремя неизвестными. § 84. Система трёх уравнений с тремя неизвестными. ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА. § 85. Равномерные и неравномерные шкалы. § 86. Устройство счётной (логарифмической) линейки. § 87. Основная шкала. § 88. Умножение и деление с помощью счётной линейки. ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ. § 89. Построение графика зависимости y = x^2 § 90. (1/3) § 130. Примеры графического решения уравнений и систем уравнений.

II. Система трех линейных уравнений с тремя неизвестными

Система трех линейных уравнений с тремя неизвестными имеет вид

     (7)

Определитель

     (8)

составленный из коэффициентов при неизвестных, называется определителем системы.

1. Если определитель системы , то система (7) имеет решение, и притом единственное. Это решение находится по формулам

     (9)

Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

Определители, стоящие в числителях дробей (9), будем обозначать соответственно через D_x, D_y, D_z.

2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей D_x, D_y и D_z не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если D = 0 и все определители, стоящие в числителях дробей (9), — D_x, D_y, D_z — равны нулю, т. е. если

D = D_x = D_y = D_z = 0,

но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.

4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей D_x, D_y, D_z не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.

5. Если в определителях D, D_x, D_y, D_z все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.

Линейными операциями над векторам называются операции сложения векторов и умножения вектора на число.

Системы координат на плоскости и в пространстве

Прямолинейной системой координат на плоскости называется сово­купность двух числовых осей с общим началом. Если масштабы на осях равны и оси перпендикулярны, то система координат называется прямоугольной декартовой. Обычно используется правая прямоугольная декартова система координат. Любая точка на плоскости однозначно определяется парой своих координат, и наоборот: любая пара действительных чисел задает единственную точку на плоскости. ² —

Векторы и линейные операции над ними _ _

Вектором называется направленный отрезок. Обозначаются векторы тремя способами: а, или а, или АВ. Два вектора равны, если их длины равны и они однонаправленны. Три вектора а Ь и с в пространстве назы­ваются компланарными, если они параллельны одной плоскости. Координаты вектора равны разности координат конца и начала. Сумма и разность векторов определяются по правилу треугольника:

Произведением вектора а на число λ называется вектор, длина которо­го равна |λ||а|; он однонаправлен с исходным, если λ>0, и противоположно направлен, если λ<0. Из определения суммы следуют правило параллелограмма для суммы двух векторов и правило многоугольника для суммы нескольких векторов:

Если даны координаты векторов, то координаты суммы равны сумме ко­ординат, координаты разности равны разности координат, а координаты про­изведения вектора на число равны произведению координат на это число.

Геометрические примеры трех уравнений с тремя неизвестными

Одно уравнение с тремя неизвестными можно интерпретировать геометрически в трехмерном пространстве. Уравнение

\begin{уравнение*} Топор+By+Cz=D \end{уравнение*}

имеет решения, образующие плоскость, если хотя бы одно из \(A, B, C\) не равно нулю. Если мы посмотрим на систему таких линейных уравнений, то множество решений — это множество всех точек, лежащих во всех соответствующих плоскостях.

Пример 2.7.1. Три плоскости пересекаются в одной точке.

Рассмотрим систему линейных уравнений

\begin{уравнение*} \начать{массив}{rl} х+у+г \amp= 2\\ х+2у+г\амп=3\\ х+2y-3z \amp=2 \конец{массив} \end{уравнение*}

Расширенная матрица

\begin{уравнение*} \begin{bmatrix} 1\amp1\amp1\amp2\\ 1\amp2\amp1\amp3\\ 1\amp2\amp-3\amp2 \end{bmatrix} \end{уравнение*}

, у которого сокращенная форма эшелона строк равна

.

\begin{уравнение*} \begin{bmatrix} 1\amp0\amp0\amp\frac34\\ 0\amp1\amp0\amp1\\ 0\amp0\amp1\amp\frac14 \end{bmatrix} \end{уравнение*}

Это означает, что существует единственное решение: \((x,y,z)=(\frac34,1,\frac14)\text{. }\) Вот три плоскости, соответствующие трем уравнениям:

Рисунок 2.7.2. Три плоскости, пересекающиеся в одной точке

Пример 2.7.3. Три плоскости пересекаются по одной прямой.

Рассмотрим систему линейных уравнений

\begin{уравнение*} \начать{массив}{rl} х+у-г \amp= 3\\ х+у+г\усилитель=1\\ 2x+2y \amp=4 \конец{массив} \end{уравнение*}

Расширенная матрица равна

\begin{уравнение*} \begin{bmatrix} 1\amp1\amp-1\amp3\\ 1\amp1\amp1\amp1\\ 2\amp2\amp0\amp4 \end{bmatrix} \end{уравнение*}

, у которого сокращенная форма эшелона строк равна

.

\begin{уравнение*} \begin{bmatrix} 1\amp1\amp0\amp2\\ 0\amp0\amp1\amp-1\\ 0\amp0\amp0\amp0 \end{bmatrix} \end{уравнение*}

Это означает \(y=t\text{,}\) \(x=2-t\) и \(z=-1\), так что \((x,y,z)=(2-t, t,-1)\) является решением для любого действительного числа \(t\text{.}\)

Рисунок 2.7.4. Три плоскости пересекаются по прямой

Пример 2.7.5. Три пересекающиеся плоскости без решений.

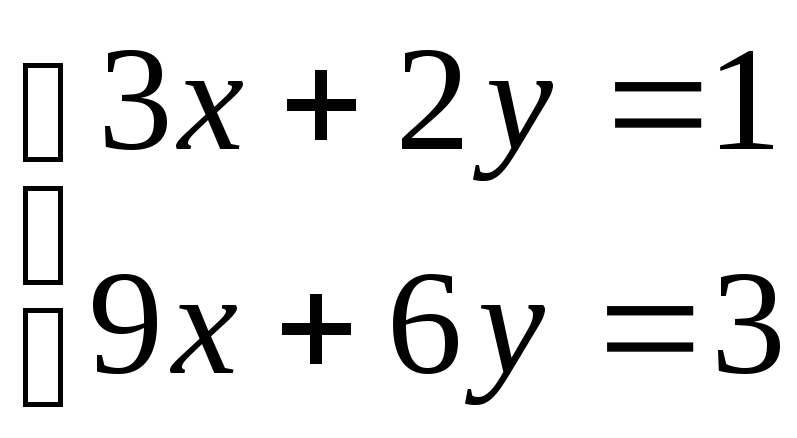
Рассмотрим систему линейных уравнений

\begin{уравнение*} \начать{массив}{rl} 2x-y+z \amp= 1\\ х+у+г\усилитель=2\\ 4x+y+3z \amp=3 \конец{массив} \end{уравнение*}

Расширенная матрица

\begin{уравнение*} \begin{bmatrix} 2\amp-1\amp1\amp1\\ 1\amp1\amp1\amp2\\ 4\amp1\amp3\amp3 \end{bmatrix} \end{уравнение*}

, у которого сокращенная форма эшелона строк равна

.

\begin{уравнение*} \begin{bmatrix} 1\amp0\amp\frac23\amp0\\ 0\amp1\amp\frac13\amp0\\ 0\amp0\amp0\amp1 \end{bmatrix} \end{уравнение*}

Последняя строка указывает на отсутствие решения.

Рисунок 2.7.6. Три попарно пересекающиеся плоскости без общей точки

Пример 2.7.7. Три непересекающиеся плоскости без решений.

Рассмотрим систему линейных уравнений

\begin{уравнение*} \begin{array}{rl} 2x-y+z \amp= 1\\ 2x-y+z \amp= 2\\ 2x-y+z \amp=3 \конец{массив} \end{уравнение*}

Расширенная матрица

\begin{уравнение*} \begin{bmatrix} 2\amp-1\amp1\amp1\\ 2\amp-1\amp1\amp2\\ 2\amp-1\amp1\amp3 \end{bmatrix} \end{уравнение*}

, у которого сокращенная форма эшелона строк равна

.

\begin{уравнение*} \begin{bmatrix} 1\amp -\frac12\amp\frac12\amp0\\ 0\amp0\amp0\amp1\\ 0\amp0\amp0\amp0\\ \end{bmatrix} \end{уравнение*}

Средняя строка указывает на отсутствие решения.

Рисунок 2.7.8. Три параллельные плоскости

Глава 2.6: Системы линейных уравнений: три переменные – предварительное исчисление

Цели обучения

В этом разделе вы:

• Решите системы из трех уравнений с тремя переменными.
• Найдите несовместимые системы уравнений, содержащие три переменные.
• Выразите решение системы зависимых уравнений с тремя переменными.

Рисунок 1. (кредит: «Элембис», Wikimedia Commons)

Джон получил наследство в размере 12 000 долларов, которое он разделил на три части и вложил тремя способами: в фонд денежного рынка с выплатой 3% годовых; в муниципальных облигациях с выплатой 4% годовых; и во взаимных фондах, выплачивающих 7% годовых. Джон вложил в муниципальные фонды на 4000 долларов больше, чем в муниципальные облигации. В первый год он заработал 670 долларов в виде процентов. Сколько Джон инвестировал в каждый тип фонда?

Понимание правильного подхода к постановке проблем, подобных этой, делает поиск решения вопросом следования образцу. В этом разделе мы решим эту и подобные задачи с тремя уравнениями и тремя переменными. При этом используются методы, аналогичные тем, которые используются для решения систем двух уравнений с двумя переменными. Однако поиск решений систем из трех уравнений требует большей организованности и некоторой визуальной гимнастики.

Решение систем трех уравнений с тремя переменными

Для решения систем уравнений с тремя переменными, известных как системы «три на три», мы будем использовать основной инструмент, который называется методом исключения Гаусса, названным в честь плодовитого немецкого математика Карла Фридриха Гаусса. Хотя нет определенного порядка, в котором должны выполняться операции, существуют конкретные рекомендации относительно того, какие типы движений можно выполнять. Мы можем пронумеровать уравнения, чтобы отслеживать шаги, которые мы применяем. Цель состоит в том, чтобы исключить одну переменную за раз, чтобы получить верхнетреугольную форму, идеальную форму для системы три на три, потому что она позволяет с помощью прямой обратной подстановки найти решение, которое мы называем упорядоченной тройкой. Система в верхнем треугольном виде выглядит следующим образом:

 

Третье уравнение можно решить, а затем выполнить обратную подстановку, чтобы найти и Чтобы записать систему в верхнем треугольном виде, мы можем выполнить следующие операции:

1. Поменять местами любые два уравнения.
2. Умножить обе части уравнения на ненулевую константу.
3. Добавить ненулевое кратное одного уравнения к другому уравнению.

Набор решений для системы три на три представляет собой упорядоченную тройку Графически упорядоченная тройка определяет точку пересечения трех плоскостей в пространстве. Вы можете визуализировать такое пересечение, представив себе любой угол в прямоугольной комнате. Угол определяется тремя плоскостями: двумя примыкающими стенами и полом (или потолком). Любая точка, где встречаются две стены и пол, представляет собой пересечение трех плоскостей.

Количество возможных решений

(Рисунок) и (Рисунок) иллюстрируют возможные сценарии решения для систем три на три.

• Системы, имеющие единственное решение, это те, которые после исключения приводят к набору решений, состоящему из упорядоченной тройки. Графически упорядоченная тройка определяет точку, являющуюся пересечением трех плоскостей в пространстве.
• Системы с бесконечным числом решений — это те, которые после исключения приводят к выражению, которое всегда истинно, например: Графически бесконечное число решений представляет собой линию или совпадающую плоскость, служащую пересечением трех плоскостей в пространстве. .
• Системы, не имеющие решения, это те, которые после исключения приводят к утверждению, являющемуся противоречием, например: Графически система без решения представлена ​​тремя плоскостями, не имеющими общих точек.

Рис. 2. (a) Три плоскости пересекаются в одной точке, представляя систему три на три с единственным решением. (b) Три плоскости пересекаются по прямой, представляя систему три на три с бесконечными решениями. Рисунок 3. Все три рисунка представляют системы три на три без решения. а) Три плоскости пересекаются друг с другом, но не в одной точке. (b) Две плоскости параллельны и пересекаются с третьей плоскостью, но не друг с другом. в) Все три плоскости параллельны, поэтому точек пересечения нет.

Определение того, является ли упорядоченная тройка решением системы

Определить, является ли упорядоченная тройка решением системы.

Показать решение

Мы проверим каждое уравнение, подставив значения упорядоченной тройки вместо и

Заказанное тройное действительно является решением системы.

How To

Дана линейная система из трех уравнений, найдите три неизвестных.

1. Выберите любую пару уравнений и решите одну переменную.
2. Выберите другую пару уравнений и решите для той же переменной.
3. Вы создали систему двух уравнений с двумя неизвестными. Решите полученную систему два на два.
4. Обратно подставьте известные переменные в любое из исходных уравнений и найдите отсутствующую переменную.

Решение системы трех уравнений с тремя переменными методом исключения

Найдите решение следующей системы:

Показать решение

Всегда будет несколько вариантов, с чего начать, но наиболее очевидным первым шагом здесь является исключение складывая уравнения (1) и (2).

Вторым шагом является умножение уравнения (1) на и добавление результата к уравнению (3). Эти два шага устранят переменную

.

В уравнениях (4) и (5) мы создали новую систему два на два. Мы можем решить, сложив два уравнения.

Выбирая из каждой новой системы по одному уравнению, получаем верхнетреугольную форму:

Далее, мы делаем обратную подстановку в уравнение (4) и находим

Наконец, мы можем подставить и обратно в уравнение (1). Это даст решение для

Раствор упорядоченной тройки См. (рисунок).

Рисунок 4.

Решение реальной задачи с использованием системы трех уравнений с тремя переменными рыночный фонд, выплачивающий 3% годовых; участие в муниципальных облигациях с выплатой 4% годовых; а остальное в паевые инвестиционные фонды с выплатой 7% годовых. Джон вложил в паевые инвестиционные фонды на 4000 долларов больше, чем в муниципальные облигации. Общая сумма процентов, заработанных за один год, составила 670 долларов. Сколько он инвестировал в каждый тип фонда?

Показать решение

Чтобы решить эту задачу, мы используем всю предоставленную информацию и составим три уравнения. Сначала мы назначаем переменную каждой из трех сумм инвестиций:

.

Первое уравнение показывает, что сумма трех основных сумм составляет 12 000 долларов.

Составим второе уравнение на основании информации о том, что Джон вложил в паевые инвестиционные фонды на 4000 долларов больше, чем в муниципальные облигации.

Третье уравнение показывает, что общая сумма процентов, полученных от каждого фонда, равна 670 долларов.

Затем мы записываем три уравнения в виде системы.

Чтобы упростить вычисления, мы можем умножить третье уравнение на 100. Таким образом,

Шаг 1. Поменяйте местами уравнение (2) и уравнение (3) так, чтобы два уравнения с тремя переменными совпали.

Шаг 2. Умножьте уравнение (1) на и добавьте к уравнению (2). Запишите результат как строку 2.

Шаг 3. Добавьте уравнение (2) к уравнению (3) и запишите результат в виде уравнения (3).

Шаг 4. Решить уравнение (3). Подставьте обратно это значение в уравнение (2) и решите для Затем подставьте обратно значения для и в уравнение (1) и решите для

Джон вложил 2000 долларов в фонд денежного рынка, 3000 долларов в муниципальные облигации и 7000 долларов во взаимные фонды.

Попробуйте

Решите систему уравнений с тремя переменными.

Показать раствор

Идентификация несовместных систем уравнений с тремя переменными

Так же, как и с системами уравнений с двумя переменными, мы можем столкнуться с несовместной системой уравнений с тремя переменными, что означает, что она не имеет решения, удовлетворяющего всем трем уравнениям. Уравнения могут представлять три параллельные плоскости, две параллельные плоскости и одну пересекающуюся плоскость или три плоскости, которые пересекают две другие, но не в одном и том же месте. Процесс исключения приведет к ложному утверждению, например, или к какому-либо другому противоречию.

Решение несовместимой системы трех уравнений с тремя переменными

Решите следующую систему.

Показать решение

Глядя на коэффициенты мы видим, что мы можем исключить, добавив уравнение (1) к уравнению (2).

Далее умножаем уравнение (1) на и добавляем к уравнению (3).

Затем мы умножаем уравнение (4) на 2 и добавляем его к уравнению (5).

Итоговое уравнение является противоречием, поэтому делаем вывод, что система уравнений несовместна и, следовательно, не имеет решения.

Анализ

В этой системе каждая плоскость пересекает две другие, но не в одном и том же месте. Следовательно, система несовместима.

Попробуйте

Решите систему из трех уравнений с тремя переменными.

Показать решение

Нет решения.

Выражение решения системы зависимых уравнений с тремя переменными

Из работы с системами уравнений с двумя переменными мы знаем, что зависимая система уравнений имеет бесконечное число решений. То же верно и для зависимых систем уравнений с тремя переменными. Бесконечное количество решений может быть результатом нескольких ситуаций. Три плоскости могут быть одинаковыми, так что решение одного уравнения будет решением двух других уравнений. Все три уравнения могут быть разными, но они пересекаются на прямой, имеющей бесконечные решения. Или два уравнения могут быть одинаковыми и пересекать третье по прямой.

Найти решение зависимой системы уравнений

Найти решение данной системы трех уравнений с тремя переменными.

Показать решение

Во-первых, мы можем умножить уравнение (1) на и добавить его к уравнению (2).

Нам не нужно продолжать дальше. В результате мы получаем тождество, которое говорит нам, что эта система имеет бесконечное число решений. Есть и другие способы начать решать эту систему, например, умножить уравнение (3) на и добавить его к уравнению (1). Затем мы выполняем те же шаги, что и выше, и находим тот же результат,

Когда система зависима, мы можем найти общие выражения для решений. Складывая уравнения (1) и (3), имеем

Затем мы решаем полученное уравнение для

Подставляем обратно выражение для в одно из уравнений и находим

Таким образом, общее решение В этом решении может быть любое действительное число. Значения и зависят от значения, выбранного для

Анализ

Как показано на (Рисунок), две плоскости одинаковы и пересекают третью плоскость по прямой. Набор решений бесконечен, так как все точки вдоль линии пересечения будут удовлетворять всем трем уравнениям.

Рисунок 5.

Всегда ли общее решение для зависимой системы должно быть записано в терминах

Нет, вы можете записать общее решение в терминах любой из переменных, но обычно запишите его через x и, если необходимо, и

Попробуйте

Решите следующую систему.

Показать решение

Бесконечное число решений вида

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами уравнений с тремя переменными.

• Пример 1: Система трех уравнений с тремя неизвестными с использованием исключения
• пр. 2: Система трех уравнений с тремя неизвестными с использованием исключения

Ключевые понятия

• Набор решений — это упорядоченная тройка, представляющая собой пересечение трех плоскостей в пространстве. См. (Рисунок).
• Систему из трех уравнений с тремя переменными можно решить, используя серию шагов, которые заставляют исключить переменную. Шаги включают изменение порядка уравнений, умножение обеих частей уравнения на ненулевую константу и добавление ненулевого кратного одного уравнения к другому уравнению. См. (Рисунок).
• Системы трех уравнений с тремя переменными полезны для решения многих различных типов реальных задач. См. (Рисунок).
• Система уравнений с тремя переменными несовместна, если не существует решения. После выполнения операций исключения получается противоречие. См. (Рисунок).
• Противоречивые системы уравнений с тремя переменными могут быть результатом трех параллельных плоскостей, двух параллельных плоскостей и одной пересекающейся плоскости или трех плоскостей, которые пересекают две другие, но не в одном и том же месте.
• Система уравнений с тремя переменными является зависимой, если она имеет бесконечное число решений. После выполнения операций исключения результатом является тождество. См. (Рисунок).
• Системы уравнений с тремя переменными, которые являются зависимыми, могут быть результатом трех одинаковых плоскостей, трех плоскостей, пересекающихся по прямой, или двух одинаковых плоскостей, пересекающих третью по прямой.

Раздел Упражнения

Вербальные

1. Может ли линейная система из трех уравнений иметь ровно два решения? Объясните, почему или почему нет

Показать решение

Нет, решений может быть только одно, ноль или бесконечно много.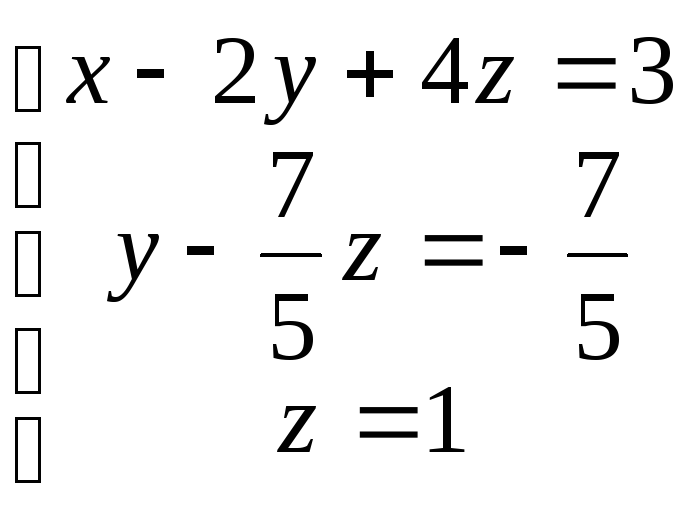

 

2. Если данная упорядоченная тройка решает систему уравнений, то единственно ли это решение? Если да, объясните почему. Если нет, приведите пример, когда он не уникален.

3. Если данная упорядоченная тройка не решает систему уравнений, то решения нет? Если да, объясните почему. Если нет, приведите пример.

Показать решение

Не обязательно. Решений может быть ноль, одно или бесконечно много. Например, не является решением приведенной ниже системы, но это не значит, что она не имеет решения.

 

4. Можно ли решить систему методом сложения только одним способом?

5. Можете ли вы объяснить, может ли быть только один метод решения линейной системы уравнений? Если да, приведите пример такой системы уравнений. Если нет, объясните почему.

Показать решение

Любую систему уравнений можно решить графически, подстановкой и сложением. Однако системы из трех уравнений становятся очень сложными для графического решения, поэтому другие методы обычно предпочтительнее.

Алгебраический

В следующих упражнениях определите, является ли данная упорядоченная тройка решением системы уравнений.

 

6. и

 

7. и

 

Показать раствор

№

 

8. и

 

9. и

 

Показать решение

Да

 

10. и

 

В следующих упражнениях решите каждую систему путем замены.

 

11.

 

Показать решение

 

12.

 

13.

 

Показать решение

 

14.

 

15.

 

Показать решение

 

16.

 

В следующих упражнениях решите каждую систему методом исключения Гаусса.

 

17.

 

Показать решение

 

18.

 

19.

 

Показать решение

 

20.

 

21.

 

Показать решение

22.

23.

SHOW SOLICE

NOR SOGLETIONS существует

24.

25.

Показать решение

26.

27.

Показать решение

 

28.

 

29.

 

Показать решение

 

30.

 

31.

 

Показать решение

 

32.

 

33.

Показать решение

34.

 

35.

 

Показать решение

 

36.

 

37.

 

Показать решение

 

38.

 

39.

 

Показать решение

 

40.

 

41.

 

Показать решение

 

42.

 

43.

Показать решение

 

 

44.

 

45.

 

Показать решение

Extensions

Для следующих упражнений решите систему для и

 

46.

 

47.

 

Показать решение

 

48.

 

49.

 

Показать решение

 

50.

Реальные приложения

51. Сумма трех четных чисел дает 108. Меньшее число в два раза больше, а среднее число
больше. Какие три числа?

Показать решение

24, 36, 48

 

52. Три числа в сумме дают 147. Наименьшее число составляет половину среднего числа, которое составляет половину наибольшего числа. Какие три числа?

 

53. На воссоединении семьи присутствовали только кровные родственники, в том числе дети, родители, бабушки и дедушки. Всего было 400 человек. Родителей было вдвое больше, чем бабушек и дедушек, и на 50 детей больше, чем родителей. Сколько детей, родителей, бабушек и дедушек было на мероприятии?

Show Solution

70 бабушек и дедушек, 140 родителей, 190 детей

 

54. В приюте для животных содержится 350 животных, включая кошек, собак и кроликов. Если количество кроликов на 5 меньше половины количества кошек, а кошек на 20 больше, чем собак, то сколько каждого животного находится в приюте?

 

55. Ваша соседка по комнате Сара предложила купить продукты для вас и другой вашей соседки по комнате. Общий счет составил 82 доллара. Она забыла сохранить отдельные чеки, но помнила, что ваши продукты были на 0,05 доллара дешевле, чем половина ее продуктов, и что продукты вашего соседа по комнате были на 2,10 доллара дороже, чем ваши продукты. Сколько стоила каждая ваша доля продуктов?

Показать решение

Ваша доля составила 19,95 долларов, доля Сары — 40 долларов, а доля другой вашей соседки по комнате — 22,05 доллара.

 

56. Ваш сосед по комнате Джон предложил купить предметы домашнего обихода для вас и другого вашего соседа по комнате. Вы живете недалеко от границы трех штатов, в каждом из которых свой налог с продаж. Общая сумма потраченных денег составила 100,75 долларов. Ваши товары были куплены с налогом 5%, товары Джона — с налогом 8%, а товары вашего третьего соседа по комнате — с налогом с продаж 9%. Общая сумма денег, потраченных без учета налогов, составляет 9 долларов.3.50. Если ваши запасы до налогообложения были на 1 доллар больше, чем половина запасов вашего третьего соседа по комнате до уплаты налогов, сколько каждый из вас потратил? Дайте ответ как с налогами, так и без них.

 

57. Три сотрудника работают на одного работодателя. Их рабочие места — менеджер склада, офис-менеджер и водитель грузовика. Сумма годовой заработной платы заведующего складом и офис-менеджера составляет 82 000 долларов США. Офис-менеджер ежегодно зарабатывает на 4000 долларов больше, чем водитель грузовика. Годовая зарплата заведующего складом и водителя грузовика составляет 78 000 долларов. Какова годовая заработная плата каждого из сотрудников?

Показать решение

Существует бесконечно много решений; нам нужно больше информации

 

58. На карнавале в конце дня были сняты чеки на сумму 2 914,25 долларов. Стоимость детского билета составляла 20,50 долларов, взрослого билета — 29,75 долларов, а билета для пенсионеров — 15,25 долларов. Пожилых людей было в два раза больше, чем взрослых, и на 20 детей больше, чем пожилых людей. Сколько билетов для детей, взрослых и пенсионеров было продано?

 

59. Билеты на концерт местной группы распроданы. Они продали все 1175 билетов на общую сумму 28 112,50 долларов. Билеты стоили 20 долларов для студентов, 22,50 долларов для детей и 29 долларов для взрослых. Если группа продала в два раза больше билетов для взрослых, чем для детей, сколько билетов каждого типа было продано?

Show Solution

500 учащихся, 225 детей и 450 взрослых

 

60. В сумке у ребенка 325 монет стоимостью 19,50 долларов. Было три типа монет: пенни, пятаки и десять центов. Если в мешке было столько же пятицентовых монет, сколько и десятицентовиков, то сколько монет каждого типа было в мешке?

 

61. В прошлом году в автосалоне Haven’s Pond для определенной модели BMW, Jeep и Toyota можно было купить все три автомобиля на общую сумму 140 000 долларов. В этом году из-за инфляции те же автомобили будут стоить 151 830 долларов. Стоимость BMW выросла на 8%, Jeep — на 5%, Toyota — на 12%. Если цена прошлогоднего джипа была на 7000 долларов меньше, чем цена прошлогоднего BMW, какова была цена каждой из трех машин в прошлом году?

Show Solution

BMW стоил 49 долларов636 долларов, джип — 42 636 долларов, а Toyota — 47 727 долларов.

 

62. Недавний выпускник колледжа воспользовался своим бизнес-образованием и инвестировал в три инвестиции сразу после выпуска. Он вложил 80 500 долларов в три счета: один с выплатой 4% простых процентов, другой с выплатой 90 142 простых процентов и третий с выплатой простых процентов. Он заработал 2670 долларов процентов в конце одного года. Если сумма денег, вложенных на второй счет, в четыре раза превышала сумму, вложенную в третий счет, сколько было вложено на каждый счет?

 

63. Вы унаследовали один миллион долларов. Вы инвестируете все это в три счета на один год. На первый счет начисляются 3% годовых, на второй счет начисляются 4% годовых, а на третий счет начисляются 2% годовых. Через год вы заработаете 34 000 долларов в виде процентов. Если вы инвестируете в четыре раза больше денег на счет, который приносит 3% по сравнению с 2%, сколько вы инвестируете в каждый счет?

Показать решение

400 000 долларов на счете с выплатой 3% годовых, 500 000 долларов США на счете с выплатой 4 процентов годовых и 100 000 долларов США на счете с выплатой 2 процентов годовых.

 

64. Вы унаследовали сто тысяч долларов. Вы инвестируете все это в три счета на один год. На первый счет начисляются 4% годовых, на второй счет начисляются 3% годовых, а на третий счет начисляются 2% годовых. Через год вы заработаете 3650 долларов в виде процентов. Если вы инвестируете в пять раз больше денег на счет, который приносит 4% по сравнению с 3%, сколько вы инвестируете в каждый счет?

 

65. В тройку лидеров по потреблению нефти в определенный год входят США, Япония и Китай. В миллионах баррелей в день три ведущие страны потребляли 390,8% потребляемой в мире нефти. Соединенные Штаты потребляют на 0,7% больше, чем в четыре раза превышает потребление Китая. Соединенные Штаты потребляли на 5% больше, чем в три раза больше, чем Япония. Какой процент мирового потребления нефти приходится на США, Японию и Китай? ^[1]

Показать решение

США потребляли 26,3 %, Япония — 7,1 %, а Китай — 6,4 % мировой нефти.

 

66. В тройку лидеров по добыче нефти в том же году входят Саудовская Аравия, США и Россия. В миллионах баррелей в день тройка ведущих стран производила 31,4% добываемой в мире нефти. На Саудовскую Аравию и США вместе взятые приходится 22,1% мировой добычи, а Саудовская Аравия добывала на 2% больше нефти, чем Россия. Какой процент мировой добычи нефти приходится на Саудовскую Аравию, США и Россию? ^[2]

 

67. Тремя крупнейшими источниками импорта нефти для США в том же году были Саудовская Аравия, Мексика и Канада. На долю трех ведущих стран пришлось 47% импорта нефти. Соединенные Штаты импортировали из Саудовской Аравии на 1,8% больше, чем из Мексики, и на 1,7% больше из Саудовской Аравии, чем из Канады. Какой процент импорта нефти в США приходится на эти три страны? ^[3]

Показать решение

Саудовская Аравия импортировала 16,8%, Канада импортировала 15,1% и Мексика 15,0%

 

68. Тремя крупнейшими производителями нефти в США в определенный год являются Мексиканский залив, Техас и Аляска. На эти три региона приходилось 64% добычи нефти в США. Мексиканский залив и Техас вместе взятые дают 47% добычи нефти. Техас произвел на 3% больше, чем Аляска. Какой процент добычи нефти в США приходится на эти регионы? ^[4]

 

69. В свое время в США 398 видов животных находились в списке исчезающих видов. Лучшие группы были млекопитающими, птицами и рыбами, которые составляли 55% исчезающих видов. На птиц приходилось на 0,7% больше, чем на рыб, а на рыб приходилось на 1,5% больше, чем на млекопитающих. Какой процент исчезающих видов приходится на млекопитающих, птиц и рыб?

Show Solution

19,3% птиц, 18,6% рыб и 17,1% млекопитающих

 

70. Потребление мяса в США можно разделить на три категории: красное мясо, птица и рыба. Если рыба составляет на 4% меньше, чем четверть потребления птицы, а потребление красного мяса на 18,2% выше, чем потребление птицы, каковы проценты потребления мяса? ^[5]

Глоссарий

набор решений

множество всех упорядоченных пар или троек, удовлетворяющих всем уравнениям в системе уравнений

---

1. «Запасы, добыча и потребление нефти в 2001 г.», по состоянию на 6 апреля 2014 г., http://scaruffi.com/politics/oil.html. ↵
2. «Запасы, добыча и потребление нефти в 2001 г.», по состоянию на 6 апреля 2014 г., http://scaruffi.com/politics/oil.html. ↵
3. «Запасы, добыча и потребление нефти в 2001 г.», по состоянию на 6 апреля 2014 г., http://scaruffi.com/politics/oil.

   No related posts.