Решение уравнений 3-й и 4-й степеней
Цели:
- Систематизировать и обобщить знания и умения по теме: Решения уравнений третьей и четвертой степени.
- Углубить знания, выполнив ряд заданий, часть из которых не знакома или по своему типу, или способу решения.
- Формирование интереса к математике через изучение новых глав математики, воспитание графической культуры через построение графиков уравнений.
Тип урока: комбинированный.
Оборудование: графопроектор.
Наглядность: таблица «Теорема Виета».
Ход урока
1. Устный счет
Вопросы:
а) Чему равен остаток от деления многочлена рn (х) = аnхn + аn-1хn-1 + … + а1х1 + a0на двучлен х-а?
б) Сколько корней может иметь кубическое уравнение?
в) С помощью чего мы решаем уравнение третьей и четвертой степени?
г) Если b четное число в квадратном уравнение, то чему равен Д и х1;х2
2. Самостоятельная работа (в группах)
Составить уравнение, если известны корни (ответы к заданиям закодированы) Используется «Теорема Виета»
3 |
2 |
-4 |
8 |
-18 |
7 |
1 |
-1 |
-10 |
-5 |
ы |
п |
ф |
р |
й |
л |
0 |
н |
и |
ь |
1 группа
Корни: х1 = 1; х2 = -2; х3 = -3; х4 = 6
Составить уравнение:
— b=1 -2-3+6=2; b=-2
с=-2-3+6+6-12-18= -23; с= -23
d=6-12+36-18=12; d= -12
е=1(-2)(-3)6=36
х4 — 2 х3 — 23х2 — 12 х + 36 = 0 (это уравнение решает потом 2 группа на доске)
Решение. Целые корни ищем среди делителей числа 36.
р = ±1;±2;±3;±4;±6…
р4(1)=1-2-23-12+36=0 Число 1 удовлетворяет уравнению, следовательно, =1 корень уравнения. По схеме Горнера
|
1 |
-2 |
-23 |
-12 |
36 |
1 |
1 |
-1 |
-24 |
-36 |
0 |
-2 |
1 |
-3 |
-18 |
0 |
|
р3(x) = х3 -х2 -24x -36
р3(-2) = -8 -4 +48 -36=0, х2=-2
р2(x) = х2 -3х -18=0
х3=-3, х4=6
Ответ: 1;-2;-3;6 сумма корней 2 (П)
2 группа
Корни: х1 = -1; х2 = х3 =2; х4 =5
Составить уравнение:
— b=-1+2+2+5-8; b= -8
с=2(-1)+4+10-2-5+10=15; с=15
-d=-4-10+20-10= -4; d=4
е=2(-1)2*5=-20;е=-20
-8+15+4х-20=0 (это уравнение решает на доске 3 группа)
р = ±1;±2;±4;±5;±10;±20.
|
1 |
-8 |
15 |
4 |
-20 |
-1 |
1 |
-9 |
24 |
-20 |
0 |
2 |
1 |
-7 |
10 |
0 |
|
р4(1)=1-8+15+4-20=-8
р4(-1)=1+8+15-4-20=0
р3(x) = х3 -9х2 +24x -20
р3(2) = 8 -36+48 -20=0
р2(x) = х2 -7х +10=0 х1=2; х2=5
Ответ: -1;2;2;5 сумма корней 8(Р)
3 группа
Корни: х1 = -1; х2 =1; х3 =-2; х4 =3
Составить уравнение:
-в=-1+1-2+3=1;в=-1
с=-1+2-3-2+3-6=-7;с=-7
-d=2+6-3-6=-1; d=1
е=-1*1*(-2)*3=6
х4 — х3 — 7х2 + х + 6 = 0 (это уравнение решает потом на доске 4 группа)
Решение. Целые корни ищем среди делителей числа 6.
р = ±1;±2;±3;±6
|
1 |
-1 |
-7 |
1 |
6 |
1 |
1 |
0 |
-7 |
-6 |
0 |
1 |
1 |
-1 |
-6 |
0 |
р4(1)=1-1-7+1+6=0
р3(x) = х3 — 7x -6
р3(-1) = -1+7-6=0
р2(x) = х2 -х -6=0; х1=-2; х2=3
Ответ:-1;1;-2;3 Сумма корней 1(О)
4 группа
Корни: х1 = -2; х2 =-2; х3 =-3; х4 =-3
Составить уравнение:
-b=-2-2-3+3=-4; b=4
с=4+6-6+6-6-9=-5; с=-5
-d=-12+12+18+18=36; d=-36
е=-2*(-2)*(-3)*3=-36;е=-36
х4 + 4х3 – 5х2 – 36х -36 = 0 (это уравнение решает потом 5 группа на доске)
Решение. Целые корни ищем среди делителей числа -36
р = ±1;±2;±3…
|
1 |
4 |
-5 |
-36 |
-36 |
-2 |
1 |
2 |
-9 |
-18 |
0 |
-2 |
1 |
0 |
-9 |
0 |
|
р(1)= 1 + 4-5-36-36 = -72
р4 (-2) = 16 -32 -20 + 72 -36 = 0
р3(х) = х3+2х2-9х-18 = 0
р3(-2)= -8 + 8 + 18-18 = 0
р2(х) = х2 -9 = 0; x=±3
Ответ: -2; -2; -3; 3 Сумма корней-4 (Ф)
5 группа
Корни: х1= -1; х2 =-2; х3 =-3; х4 =-4
Составить уравнение
-b=-10;b=10
с=35
-d= -50; d=50
е=24
х4+ 10х3 + 35х2 + 50х + 24 = 0 (это уравнение решает потом 6группа на доске)
Решение. Целые корни ищем среди делителей числа 24.
р = ±1;±2;±3
|
1 |
10 |
35 |
50 |
24 |
-1 |
1 |
9 |
26 |
24 |
0 |
-2 |
1 |
7 |
12 |
0 |
|
p4 (1)≠0
р4 (-1) = 1 -10 + 35 -50 + 24 = 0
р3(х) = x-3 + 9х2 + 26x+ 24 = 0
p3(-2) = -8 + 36-52 + 24 = О
р2(х) = x2 + 7x+ 12 = 0
Д=49-48=1
Ответ:-1;-2;-3;-4 сумма-10 (И)
6 группа
Корни: х1 = 1; х2 = 1; х3 = -3; х4 = 8
Составить уравнение
-b=1+1-3+8=7;b=-7
с=1 -3+8-3+8-24= -13
-d=-3-24+8-24= -43; d=43
е= -24
х4 — 7х3— 13х2 + 43x — 24 = 0 (это уравнение решает потом 1 группа на доске)
Решение. Целые корни ищем среди делителей числа -24.
|
1 |
-7 |
-13 |
43 |
-24 |
1 |
1 |
-6 |
-19 |
24 |
0 |
1 |
1 |
-5 |
-24 |
0 |
|
р = +1;±2;±3
р4(1)=1-7-13+43-24=0
р3(1)=1-6-19+24=0
р2(x)= х2 -5x — 24 = 0
х3=-3, х4=8
Ответ: 1;1;-3;8 сумма 7 (Л)
3. Решение уравнений с параметром
1. Решить уравнение х3 + 3х2 + mх — 15 = 0; если один из корней равен (-1)
Ответ записать в порядке возрастания
Решение:
|
1 |
3 |
-13 |
-15 |
-1 |
1 |
2 |
-15 |
0 |
R=Р3(-1)=-1+3-m-15=0
-m- 13=0
m=-13
х3 + 3х2 -13х — 15 = 0; -1+3+13-15=0
По условию х1 = — 1; Д=1+15=16
Р2(х) = х2+2х-15 = 0
х2=-1-4 = -5;
х3=-1 + 4 = 3;
Ответ:- 1;-5; 3
В порядке возрастания: -5;-1;3. ( Ь Н Ы)
2. Найти все корни многочлена х3 — 3х2 + ах — 2а + 6, если остатки от его деления на двучлены х-1 и х +2 равны.
Решение: R=Р3(1) = Р3(-2)
Р3(1) = 1-3 + а- 2а + 6 = 4-а
Р3(-2) = -8-12-2а-2а + 6 = -14-4а
4-a=-14-a
3a=-18
a=-6
x3 -Зх2 -6х + 12 + 6 = х3 -Зх2 -6х + 18
x2(x-3)-6(x-3) = 0
(х-3)(х2-6) = 0
Произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю, а другой при этом имеет смысл.
х1=3 или х2 — 6 = 0
;
Ответ: -; ; 3 (Произведение 18) (Й)
4. Домашнее задание
1. Решить уравнение х3 — (2а + 1)х2 + (а2 + а)х — (а2 — а) = 0 , где а — параметр.
Решение:
Подбором находим х1 = 1 корень, а — любое число.
Р3 (1)=1-2а-1+ а2+а-а2 =0
|
1 |
-2а-1 |
а²+а |
-а²+а |
1 |
1 |
-2а |
а²-а |
0 |
Р2(х) = х2 -2ах+(а2 – а)=0
Р2(х) = 0;Д = а2 -а2 +а = а, Д >0
1)если а<0, то корней нет
2) а>0, х2 = а — √а; х3 = а + √а
3) а=0, х2 -0*х2 +0 = 0; х2 =0; х4=0
Ответ:
а<0; х=1
а=0; х=0; х=1
а>0; х=1; х=а ± √а
2. Составить уравнение
1 группа. Корни: -4; -2; 1; 7;
2 группа. Корни: -3; -2; 1; 2;
3 группа. Корни: -1; 2; 6; 10;
4 группа. Корни: -3; 2; 2; 5;
5 группа. Корни: -5; -2; 2; 4;
6 группа. Корни: -8; -2; 6; 7.
urok.1sept.ru
Как решать уравнение третьей степени 🚩 Математика
Автор КакПросто!
Уравнения третьей степени еще называют кубическими уравнениями. Это уравнения, в которых старшей степенью при переменной x является куб (3).
Статьи по теме:
Инструкция
Кубическое уравнение в общем виде выглядит так: ax³ + bx² + cx + d = 0, a не равно 0; a, b, c, d — вещественные числа. Универсальным методом решения уравнения третьей степени является метод Кардано. Для начала приводим уравнение к виду y³ + py + q = 0. Для этого производим замену переменной x на y — b/3a. Подстановку замены смотрите на рисунке. Для раскрытия скобок используются две формулы сокращенного умножения: (a-b)³ = a³ — 3a²b + 3ab² — b³ и (a-b)² = a² — 2ab + b². Затем приводим подобные слагаемые и группируем по степеням переменной y.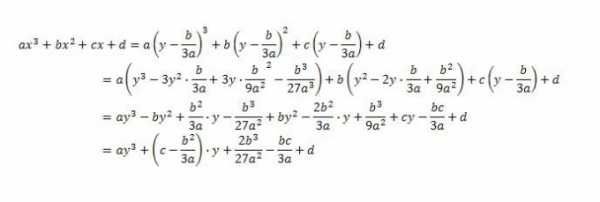
Теперь, чтобы получить при y³ единичный коэффициент, делим все уравнение на a. Тогда получим следующие формулы для коэффициентов p и q в уравнении y³ + py + q = 0.
Затем вычисляем специальные величины: Q, α, β, которые позволят вычислить корни уравнения с y.
Тогда три корня уравнения y³ + py + q = 0 вычисляются по формулам на рисунке.
Если Q > 0, то уравнение y³ + py + q = 0 имеет только один вещественный корень y1 = α + β (и два комплексных, вычислите их по соответствующим формулам, если необходимо).Если Q = 0, то все корни вещественны и по крайней мере два из них совпадают, при этом α = β и корни равны: y1 = 2α, y2 = y3 = -α.
Если Q
После нахождения y1, y2 и y3 подставьте их в замену x = y — b/3a и найдите корни первоначального уравнения.
Полезный совет
Если удается подобрать один из корней кубического уравнения x1, то можно кубический многочлен разделить на (x — x1) и решать получившееся квадратное уравнение.
Источники:
- Метод решения кубического уравнения
- уравнение 3 степени
Совет полезен?
Распечатать
Как решать уравнение третьей степени
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
§7. Уравнения третьей степени.
Уравнение третьей
степени x3+ax2+bx+c=0 (1)
подстановкойx=y–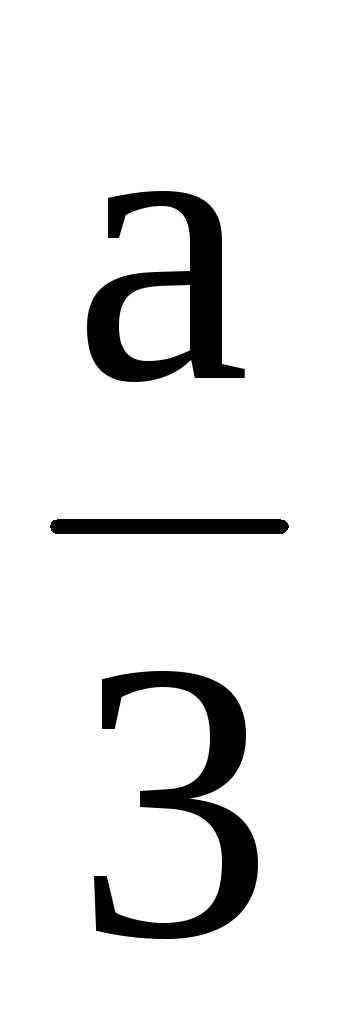 приводится кприведенному кубическому
уравнению y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=, (3)
гдеu=
приводится кприведенному кубическому
уравнению y3+py+q=0. (2)
Корни
такого уравнения можно найти по формулам
Кардано:y=u+v=, (3)
гдеu=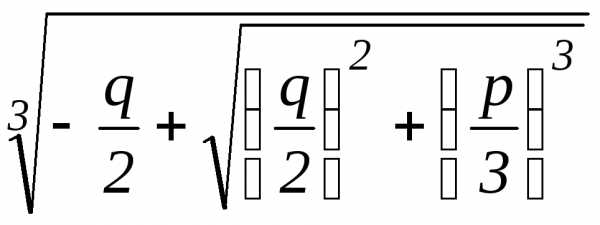 ,v=
,v=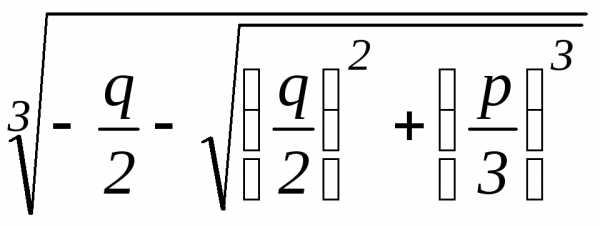 и
они связаны соотношениемuv=
и
они связаны соотношениемuv=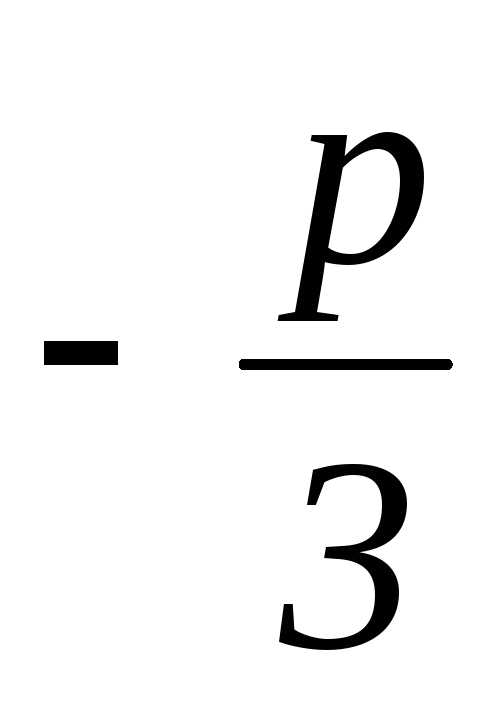 . (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u
. (4)
С
учётом (4) формулу Кардано (3) можно
использовать и в таком виде:y=u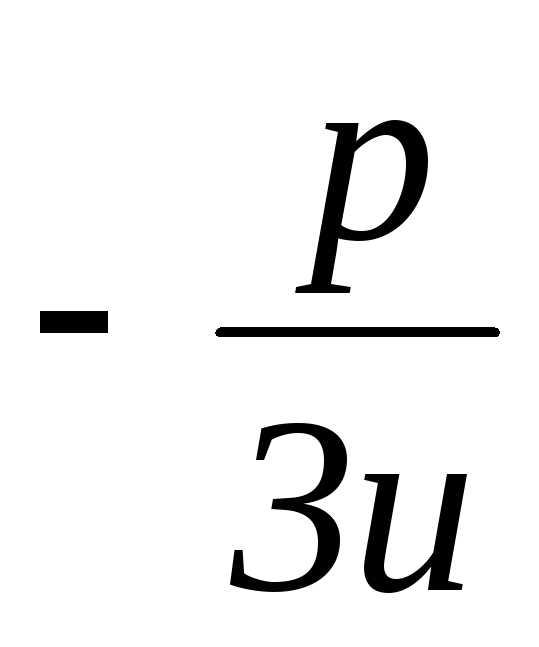 ,
гдеu=
,
гдеu=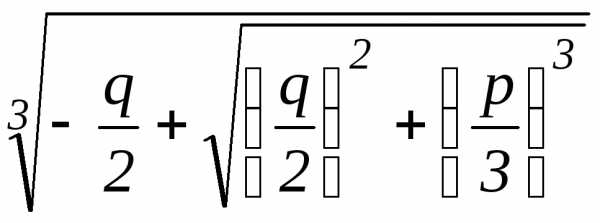 . (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
. (5)
Здесь
можно брать любое (одно из двух) значение
квадратного корня; три значения
кубического корня дают три корня
приведенного уравнения (2). Заметим, чтоu0,
еслиp0;
еслиp=0, то никакая
специальная формула не нужна (имеемдвучленное уравнение).
Чтобы не запоминать
формулу, можно пользоваться методом
решения, по сути повторяющим вывод
формул Кардано. Чтобы найти корни
уравнения (2) (считаем р0),
пологаяy=u+v,
подставляем его в уравнение: (u+v)3+p(u+v)+q=0.
Раскрыв
скобки, и перегруппировав члены,
получим:
(u3+v3+q)+(
3uv+p)(u+v)=0.
Для
уничтожения второго слагаемого подберёмu, vтак, чтобы 3uv+p=0
илиuv=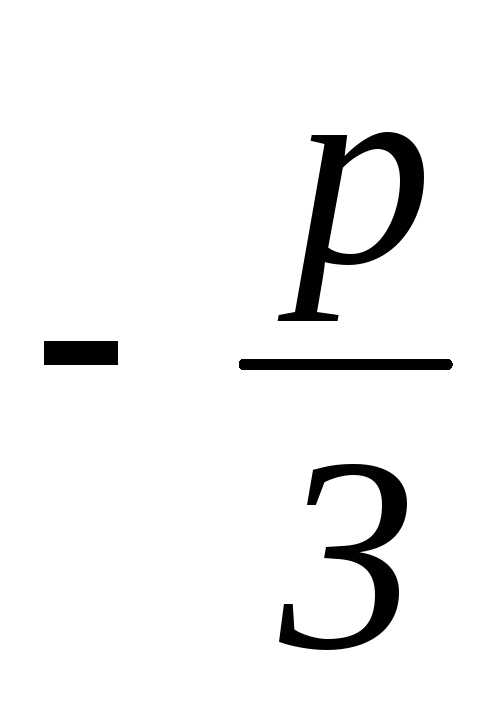 .
Тогда уравнение (2) приводится к системе
уравнений:
.
Тогда уравнение (2) приводится к системе
уравнений:

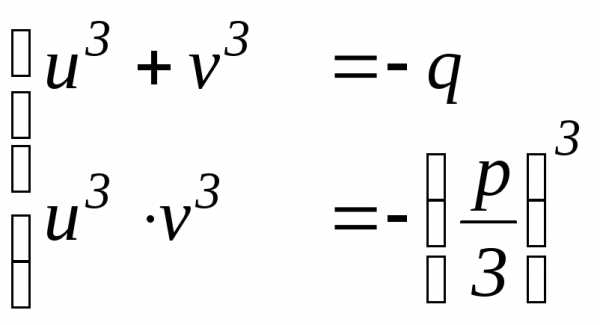 Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz
Замечаем,
чтоu3,v3– корни квадратного уравненияz2+qz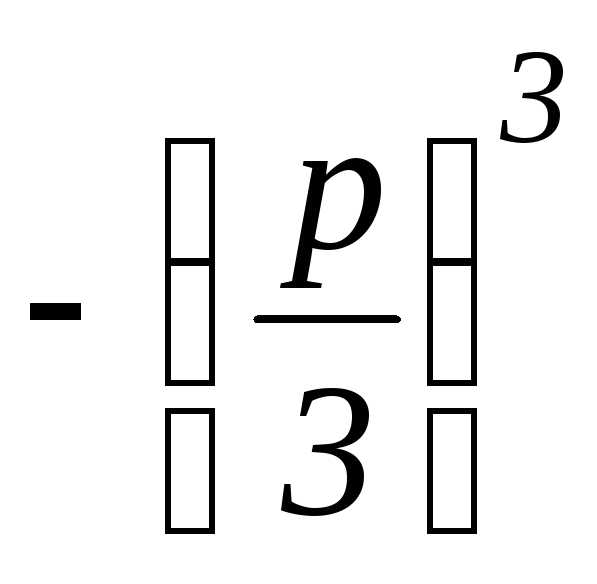 =0.
=0.
Затем, выбираем
один (любой) корень z1этого квадратного уравнения. Берём
в качествеu1одно (любое) значение кубического корня
изz1и вычисляем
корни кубического уравнения (1) по
следующей схеме: u1, v1=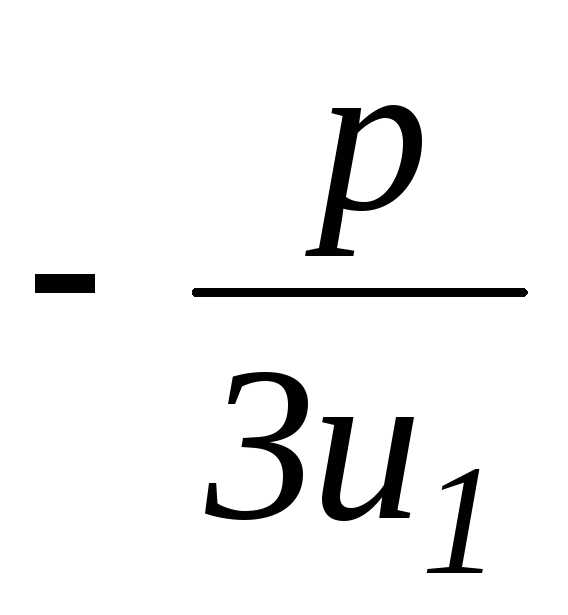 ,y1=u1+v1,x1=y1–
,y1=u1+v1,x1=y1–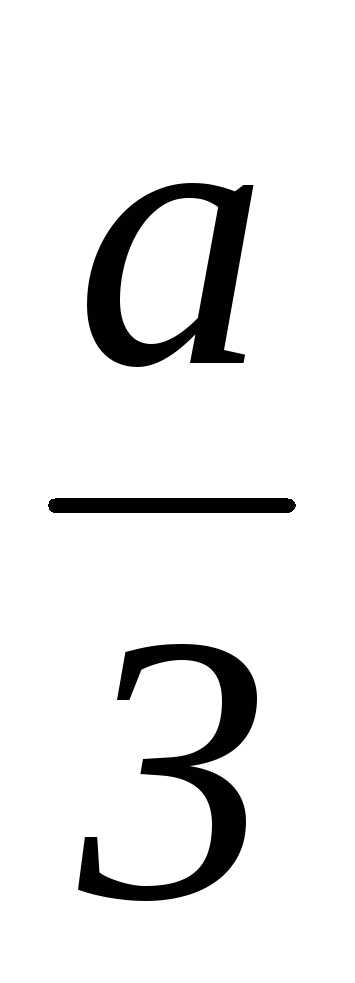 ;u2= u11, v2= v12,y2=u2+v2,x2=y2–
;u2= u11, v2= v12,y2=u2+v2,x2=y2–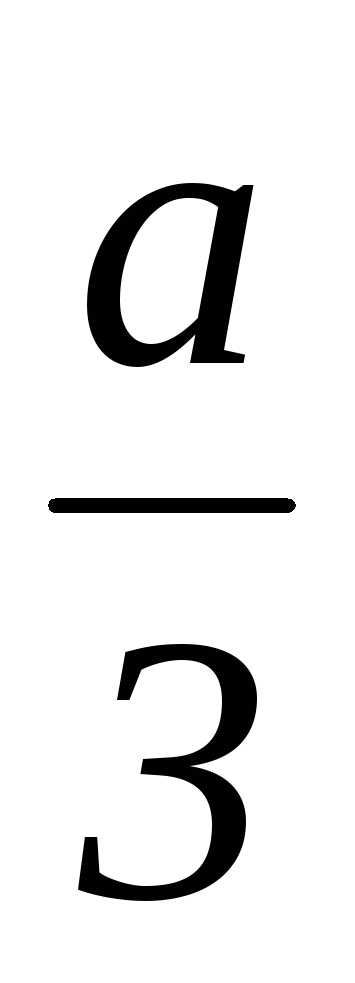 ;u3= u12, v3= v11,y3=u3+v3,x3=y3–
;u3= u12, v3= v11,y3=u3+v3,x3=y3–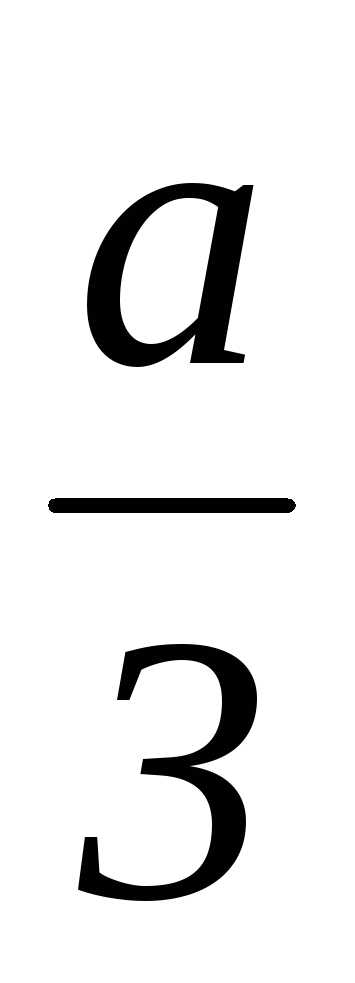 ;
где1,2=
;
где1,2=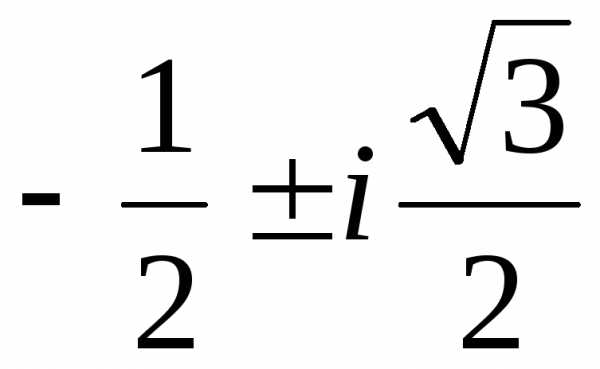 невещественные кубические корни из
единицы. Заметим, что2=(1)2=
невещественные кубические корни из
единицы. Заметим, что2=(1)2=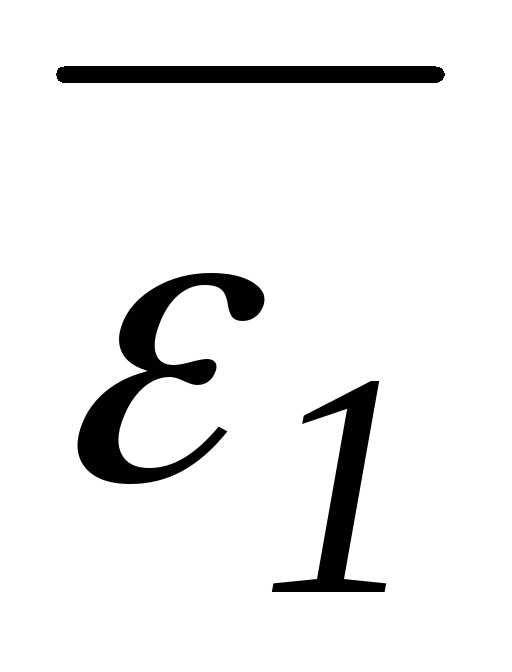 и1=(2)2=
и1=(2)2=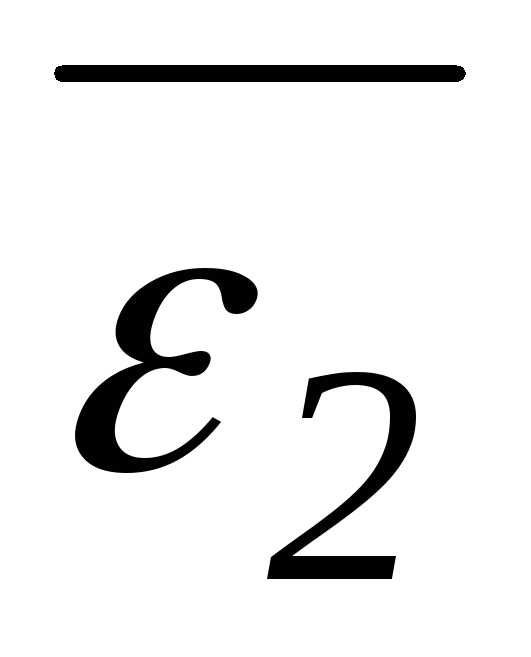 ,
это позволяет варьировать нахождениеu2, v2, u3, v3.
,
это позволяет варьировать нахождениеu2, v2, u3, v3.
При исследовании уравнений третьей степени используют теорему:
Теорема. Пустьx3+px+q=0
неполное кубическое уравнение с
действительными коэффициентами.
Обозначим
∆=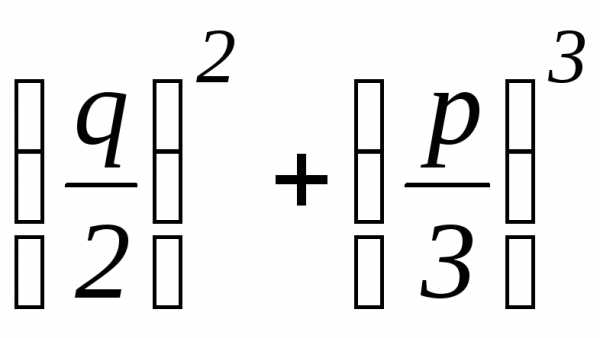 .
.
Если ∆>0, то уравнение имеет один действительный и два мнимых сопряжённых корня.
Если ∆=0, то корни уравнения действительны и хотя бы один из них кратный.
Если ∆<0, то все корни действительны и различны.
Если не все
коэффициенты уравнения (2) действительны,
то для упрощения вычислений можно
вычислить ∆. Если ∆=0 (p0,q0),
тогда уравнение (2) имеет два равных
корняy2=y3, и в этом случае корни уравнения (2)
можно найти, не прибегая к извлечению
корней второй и третьей степени, а
именноy1=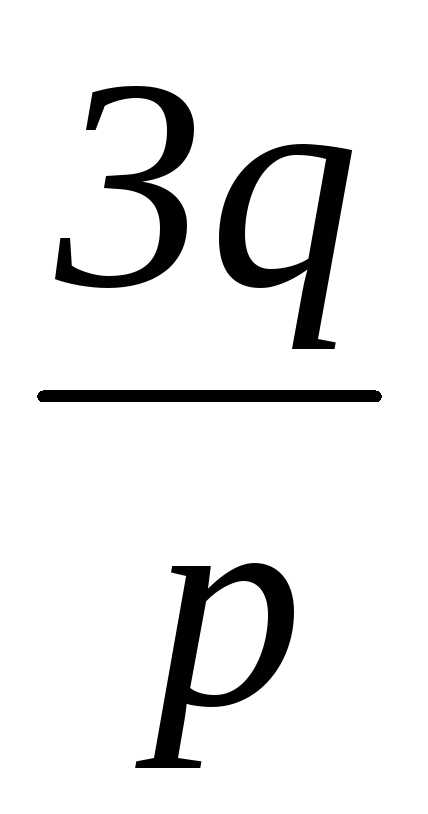 ; y2=y3=
; y2=y3=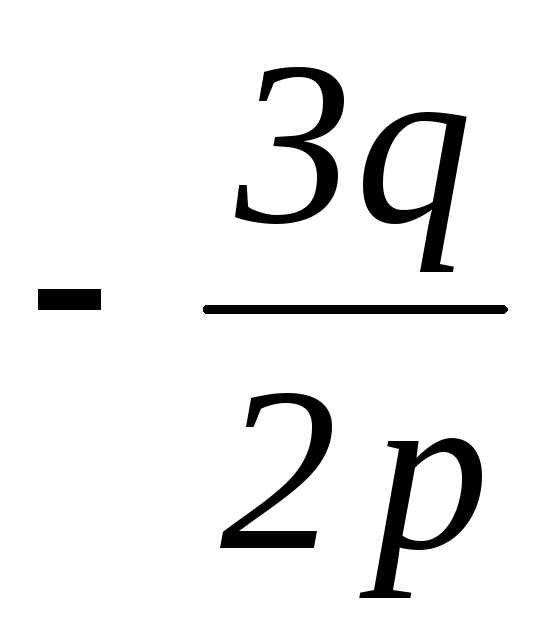 . (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
. (6)
Если
же ∆0, то уравнение
(2) имеет три различных корня, для
нахождения которых, используют один
из вышеописанных способов.
Пример 1. Решить уравнение:
x3–6x+9=0.
Решение.Уравнение
приведенное (отсутствует член сx2).
Используем модифицированную формулу
Кардано (5):
∆=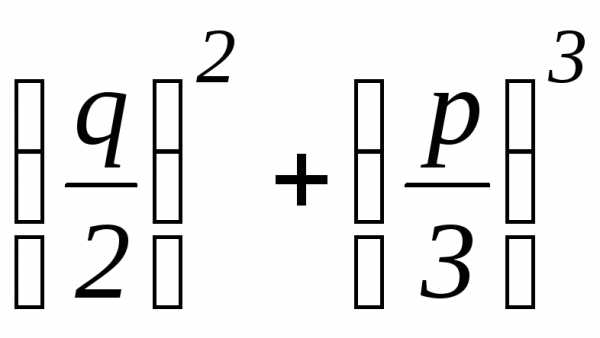 =
=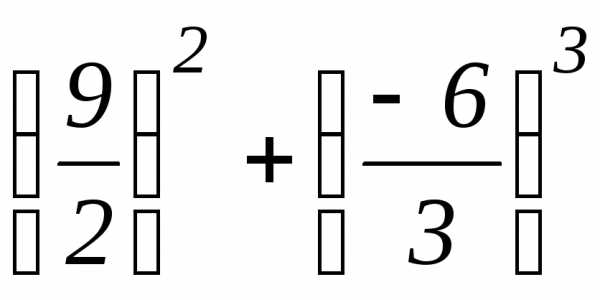 =
=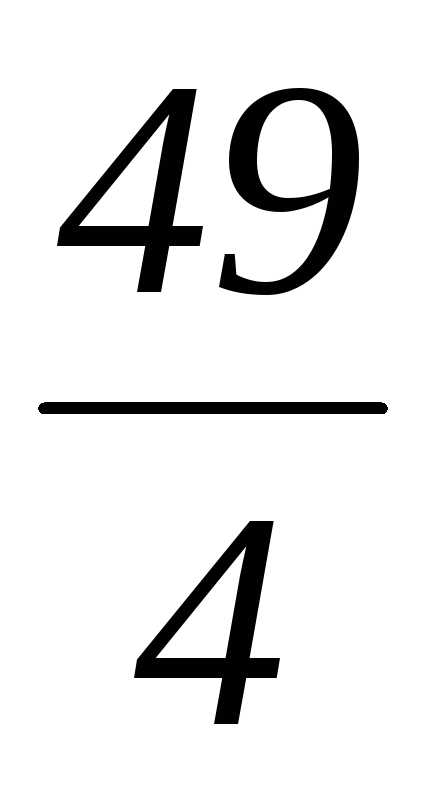 >0.
>0.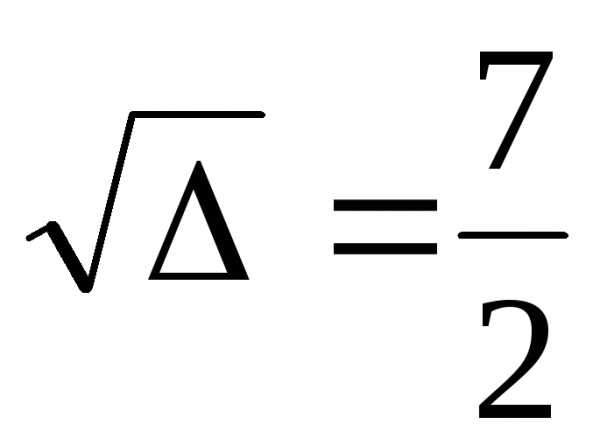 (берём
только одно значение квадратного
корня). Тогдаu=
(берём
только одно значение квадратного
корня). Тогдаu=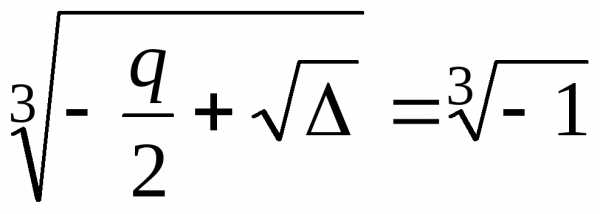 .
Одно
из значений
.
Одно
из значений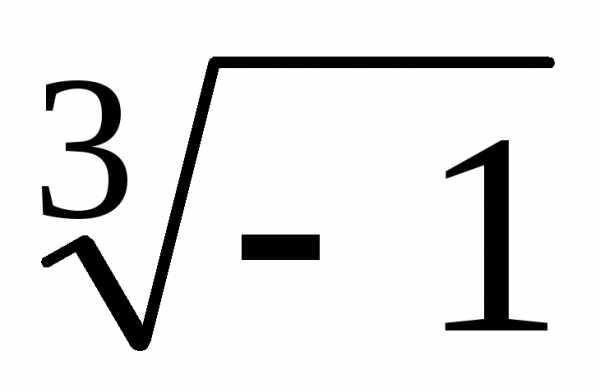 естьu1=–1, ещё
два значения получим, умножаяu1на1,2 – кубические корни из единицы. Итак, u1=–1
, x1=
u1–
естьu1=–1, ещё
два значения получим, умножаяu1на1,2 – кубические корни из единицы. Итак, u1=–1
, x1=
u1–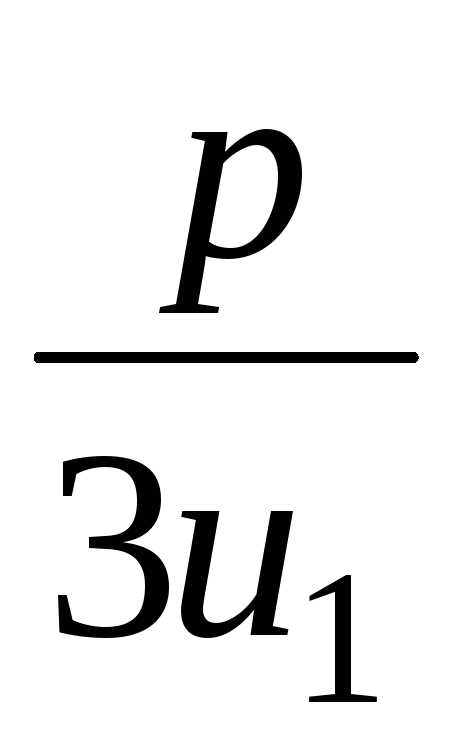 =–1–
=–1–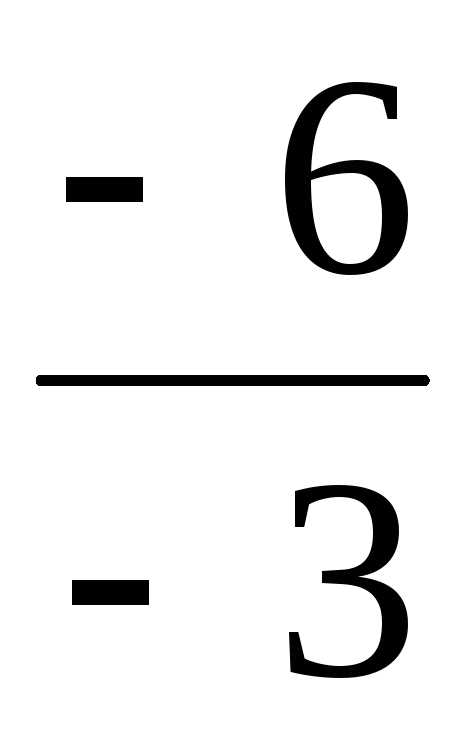 =–3; u2= u11=–1, x2=
u2–
=–3; u2= u11=–1, x2=
u2–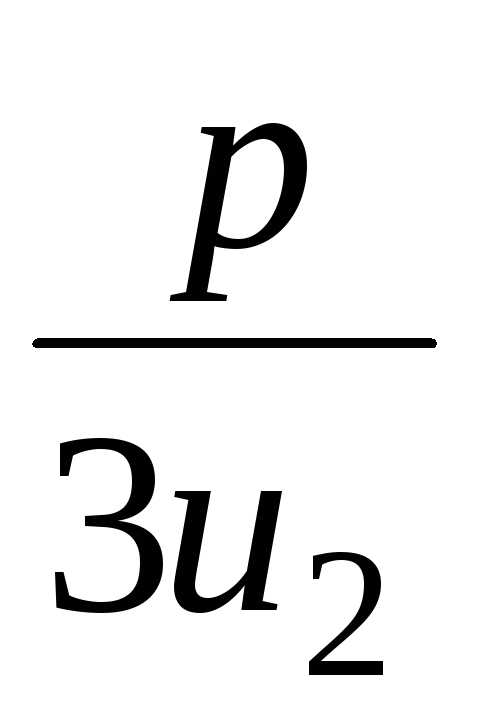 =–1+
=–1+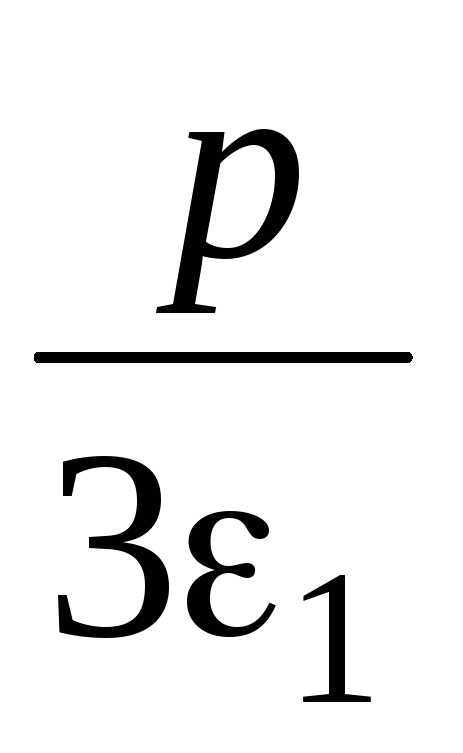 =–1–2/1= =–1–22=.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=
=–1–2/1= =–1–22=.
Так
как коэффициенты данного уравнения
действительны и ∆>0, тоx3=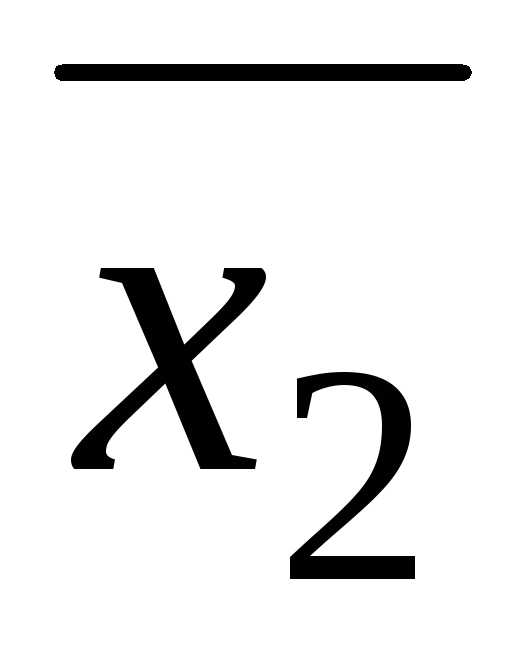 (x3не нужно
вычислять по формуле).
(x3не нужно
вычислять по формуле).
Ответ:x1=–3, x2,3=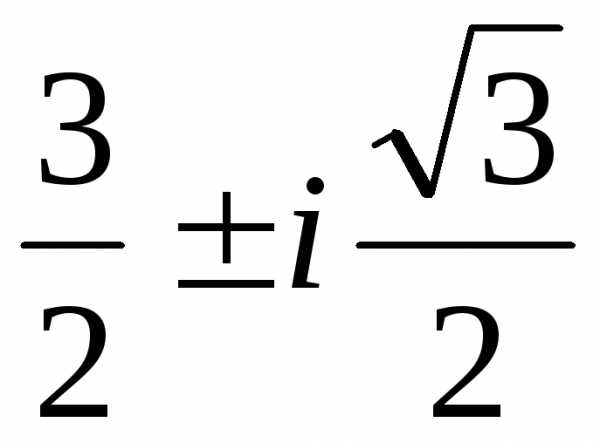 .
.
Пример 2. Решить уравнение:x3+9x2+18x+28=0.
Решение.
Сделаем подстановкуx=y–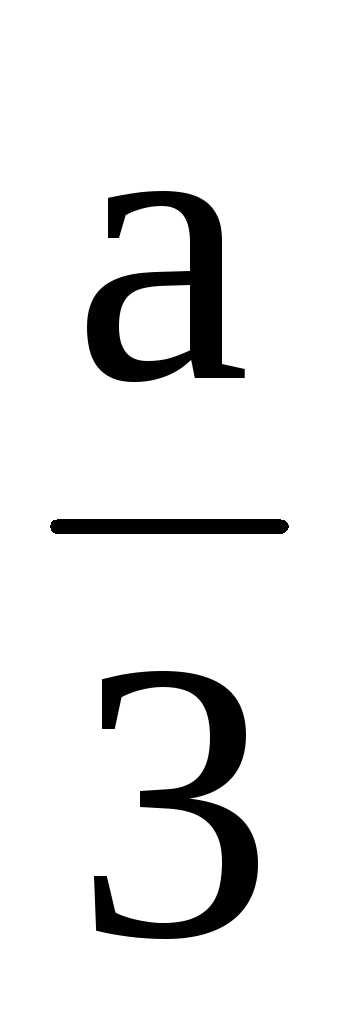 =y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v: (u+v)3–9(u+v)+28=0, (u3+v3+28)+(3uv–9)(u+v)=0.
Откуда
=y–3.
Получим уравнениеy3–9y+28=0.
Полагаемy=u+v: (u+v)3–9(u+v)+28=0, (u3+v3+28)+(3uv–9)(u+v)=0.
Откуда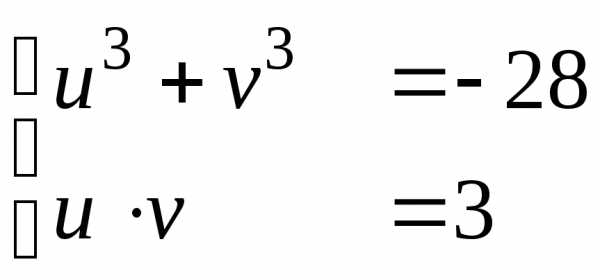 ,
или
,
или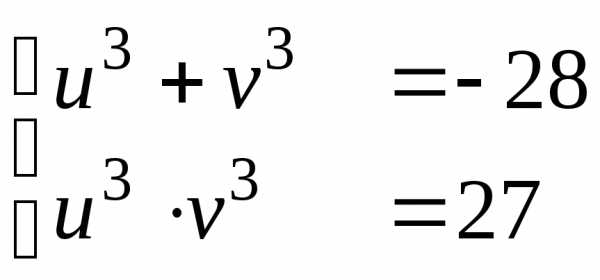 ,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
,
гдеu3,v3– корни квадратного уравненияz2+28z+27=0.
Один из корней
последнего уравнения z1=–1,
тогдаu1=–1, v1=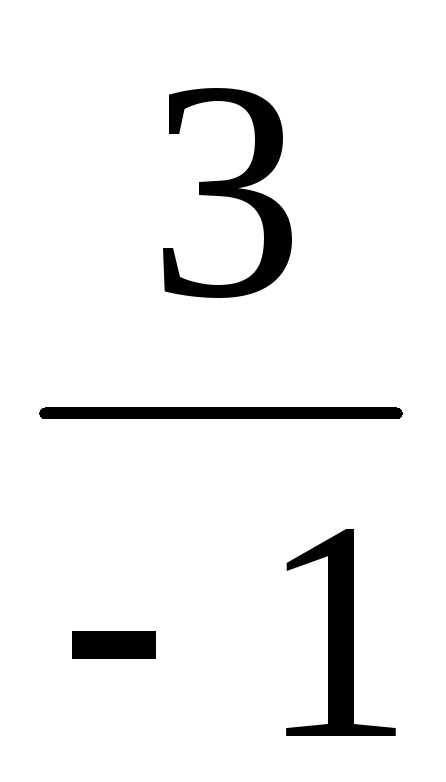 =–3,y1=–4,x1=–7;u2= u11=
=–3,y1=–4,x1=–7;u2= u11=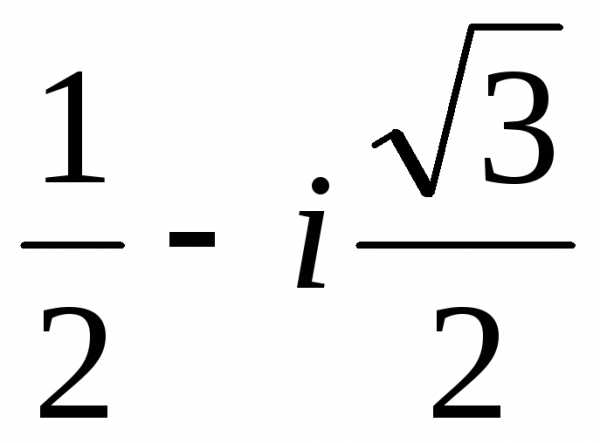 ,v2= v12=
,v2= v12=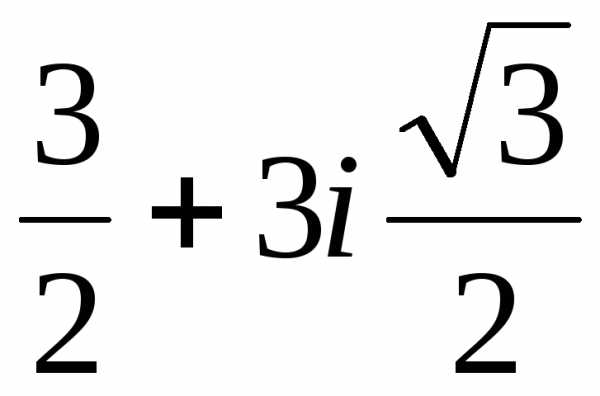 ,y2=
,y2=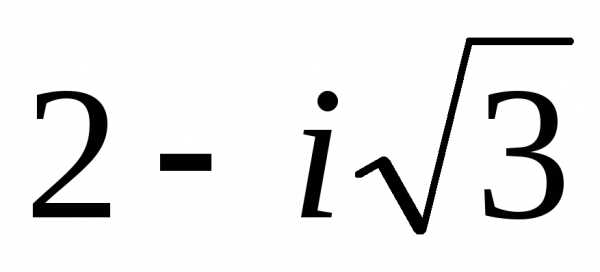 ,x2=
,x2=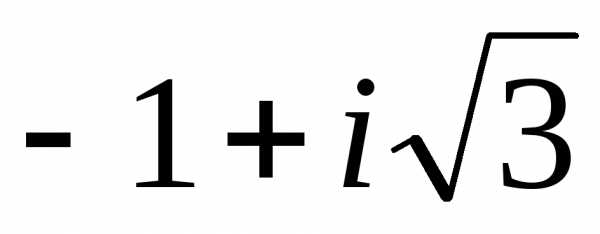 ; Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=
; Поскольку коэффициенты уравнения
действительны и ∆>0, тоx3=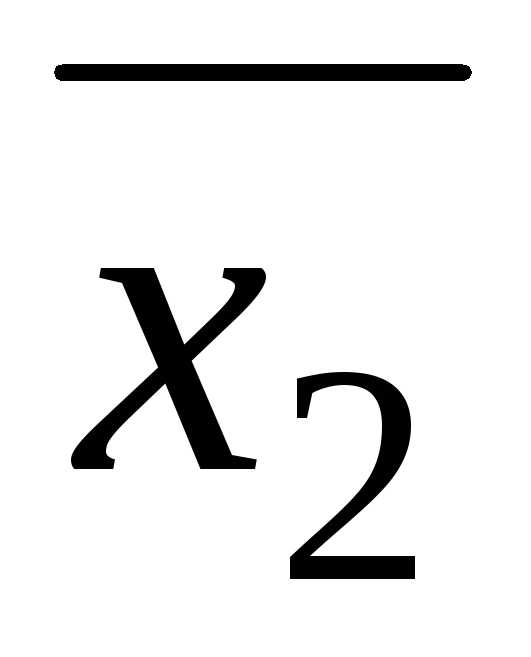 .
.
Ответ: x1=–7, x2,3=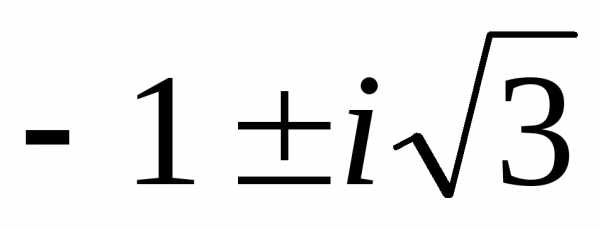 .
.
Пример 3. Решить уравнение:x3+3x–2i=0.
Решение. Данное
уравнение приведенное, и не все его
коэффициенты действительны, поэтому
вычислим ∆.
∆=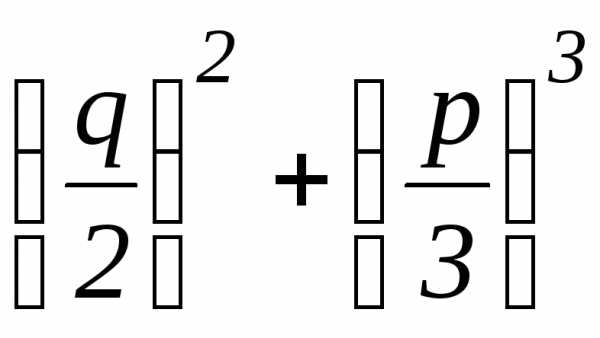 =
=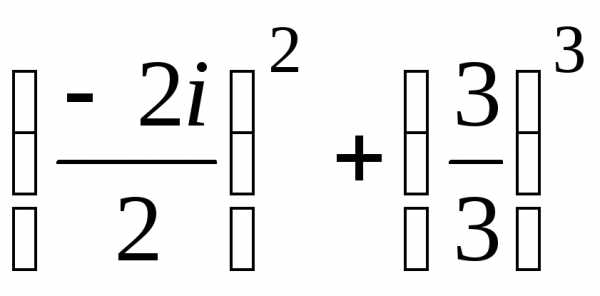 =–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1=
=–1+1=0
Таким
образом корни уравнения можно вычислить
по формулам (6).x1=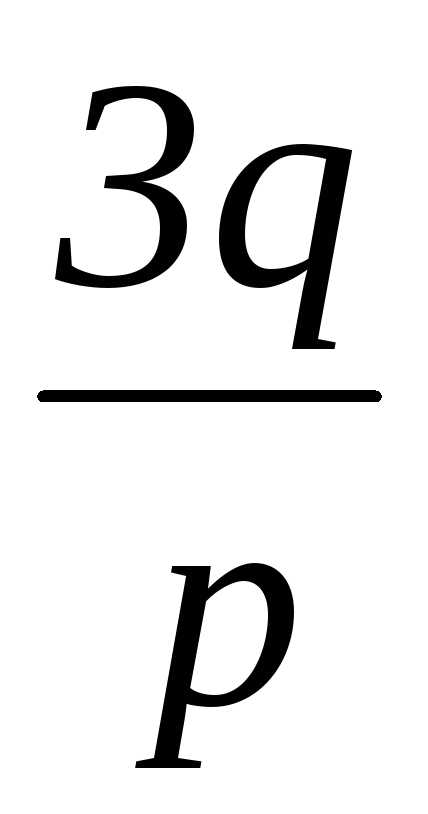 =
=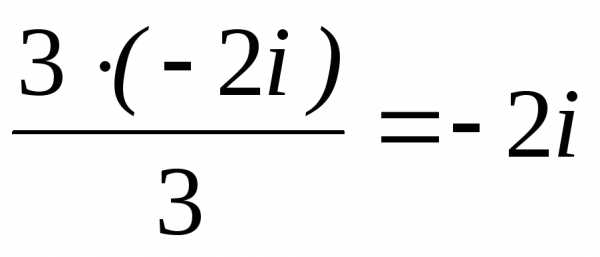 ; x2=x3=
; x2=x3=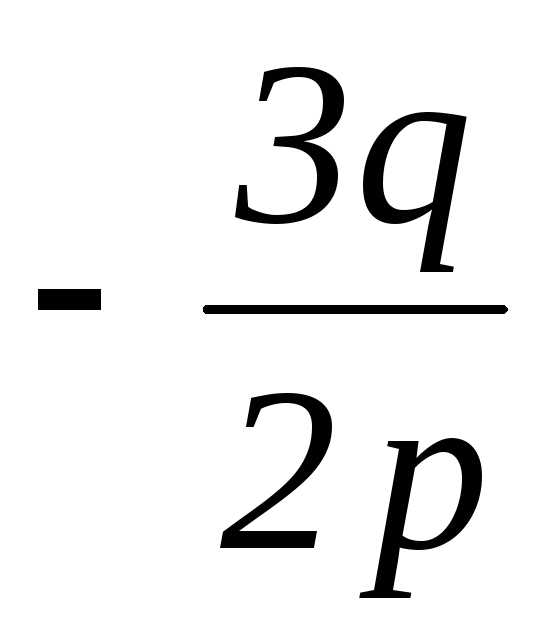 =
=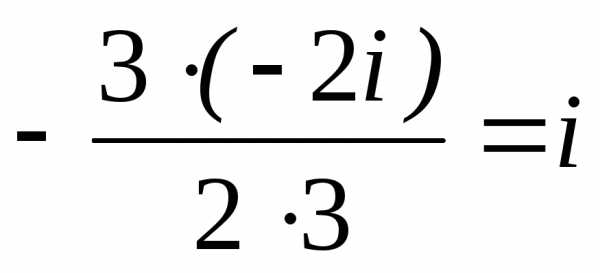 .
.
Ответ: x1=–2i, x2,3=i.
Пример 4. Решить уравнение:x3–3abx+ a3+b3=0
Решение.
Пологаяx=u+v,
получим
(u+v)3–3ab(u+v)+
a3+b3=0
или (u3+v3+ a3+b3)+(3uv–3ab)(u+v)=0.
ОткудаОдно
из решений последней системы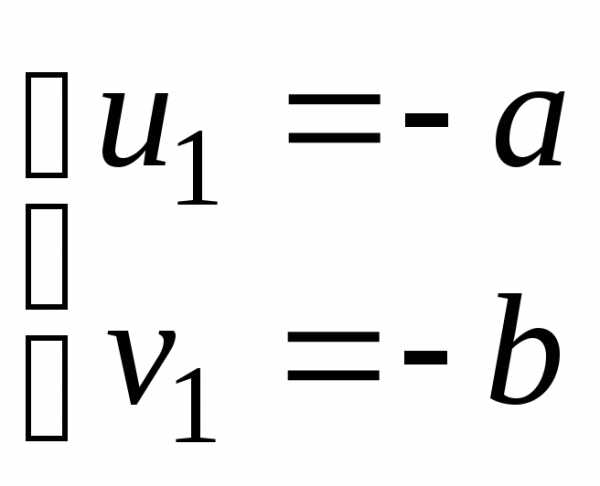
Тогда u1=–a, v1=–b, x1=–a–b; u2= u11=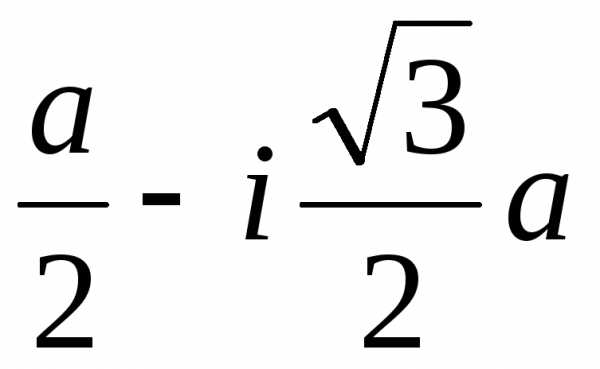 , v2= v12=
, v2= v12=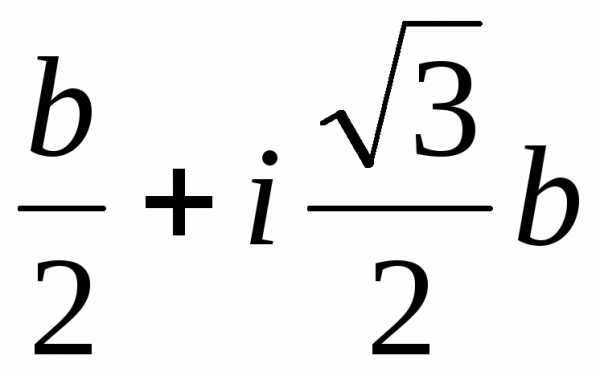 , x2=
, x2=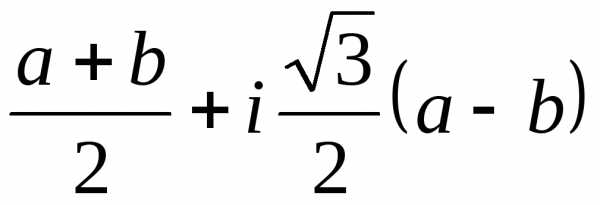 .
.
Ответ: x1=–a–b, x2,3=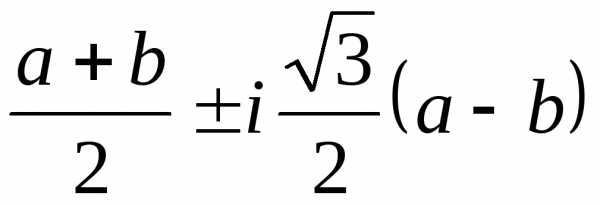 .
.
Замечание: При выписывании ответа воспользовались тем, что при вещественныхa,bне надо вычислять x3. Но если выписанное значениеx3есть корень уравнения при (любых) вещественныхa иb, то ясно, чтоx3 будет корнем при любыхa,b.
Для самостоятельного решения.
Решить уравнения:
x3+6x2–12x+32=0
x3+9x2–18x+44=0
x3–3x2–6x+36=0
x3–12x2+24x–40=0
x3–6ix+4(1–i)=0
x3+(3–3i
 )x–9=0
)x–9=0x3+3ax+1–a3=0
Ответы:
(–8;
 )
)(–11;
 )
)(–3;
 )
)(10;
 )
)(2+2i; –1–i; –1–i)
(i
 ;
; 

(a–1;
studfiles.net

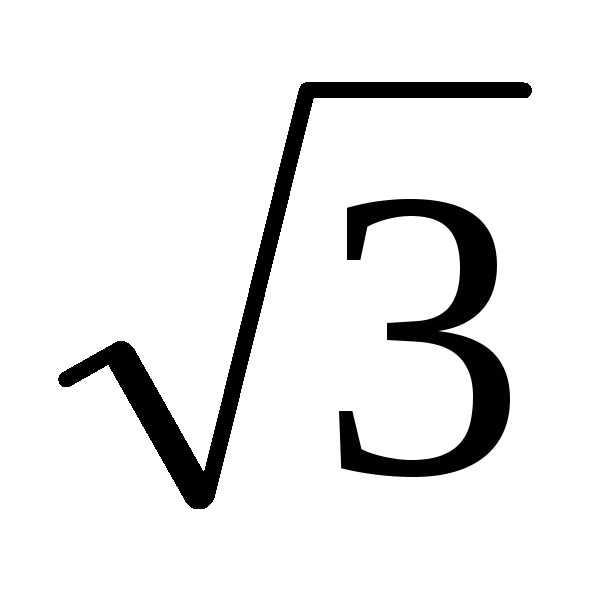 )x–9=0
)x–9=0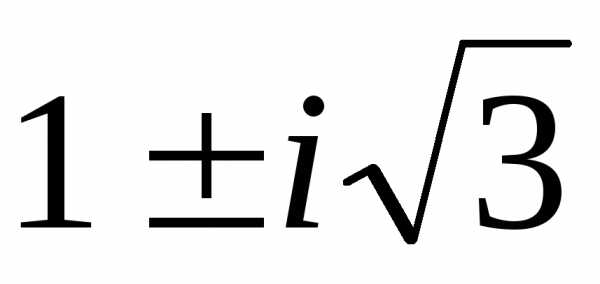 )
)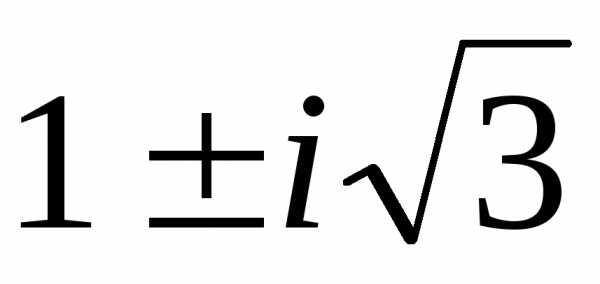 )
) )
)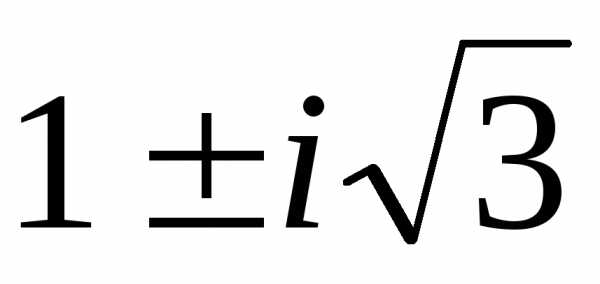 )
) ;
;