49. Показательные уравнения, показательно-степенные уравнения
Показательным уравнением называется уравнение, которое содержит неизвестную величину в показателе степени при постоянном основании A (A > 0).
Типы показательных уравнений и способы их решения
Всюду далее F(X), G(X) – некоторые выражения с неизвестной величиной X.
I тип: уравнение вида
где (6.2)
Имеет решение, если B > 0. Его решают логарифмированием по основанию A:
Тогда
(6.3)
Решение уравнения (6.3) производят соответственно типу этого уравнения.
II тип: Уравнение вида
где (6.4)
По свойству равенства степеней равносильно уравнению
Последнее уравнение решают в зависимости от его типа.
III тип: уравнение вида
(6.5)
Где F – некоторое выражение относительно
Производят замену переменной и решают уравнение F(

Если – корни уравнения, то после возвращения к старой переменной решение уравнения (6.5) сводится к решению равносильной ему совокупности уравнений
IV тип: уравнения, решаемые графическим методом.
Для таких уравнений строят соответствующие графики для левой и правой частей уравнения. Определяют, для каких значений X графики имеют общую ординату. Используют также иные функциональные свойства, в частности, монотонность функции (возрастание, убывание).
Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).
Типы показательно-степенных уравнений
И способы их решения
Всюду далее F(X), G(X), H(X) – Некоторые выражения с неизвестной X, F(X) > 0.
I тип: уравнение вида
(6. 6)
6)
Решение уравнения (6.6) на ОДЗ сводится к решению совокупности
II тип: уравнение вида
(6.7)
Решение уравнения (6.7) на ОДЗ сводится к решению совокупности
Пример 1. Решить уравнение
Решение. 1-й способ. Имеем уравнение I типа (формула (6.2)). Решаем логарифмированием по основанию 3. Получаем:
т. е.
Приходим к линейному уравнению
Откуда
2-й способ. Преобразуем правую часть при помощи основного логарифмического тождества:
Получили уравнение II типа (формула (6.4)), которое решаем по свойству равенства степеней:
Пришли к ответу:
Пример 2. Решить уравнение
Решение. Выполним необходимые преобразования, сведем показательные выражения к одному и тому же основанию 3:
По свойству степеней:
Получаем ответ: Х = 0.
Пример 3. Решить уравнение
Решение. Преобразуем уравнение
Преобразуем уравнение
Имеем квадратное уравнение относительно 2Х. Решаем при помощи замены Получаем:
Корнями последнего уравнения являются значения
Возвращаясь к неизвестной X, имеем совокупность:
Первое уравнение совокупности решений не имеет. Решаем второе уравнение:
т. е.
Получили ответ: Х = 3.
Пример 4. Решить уравнение
Решение. Выполним необходимые преобразования:
Имеем однородное уравнение. Разделим обе части уравнения на 92Х (92Х ¹ 0). Получим:
Т. е. получили квадратное уравнение относительно Вводим замену Тогда
Откуда
Возвращаемся к старой переменной:
Получили ответ:
Пример 5. Решить уравнение
Решение. 1-й способ. Подбором убеждаемся, что Х = 2– корень уравнения. Функции (т. е. ) и монотонно возрастают (рис. 6.12). Они имеют единственную общую точку.
Рис. 6.12
2-й способ. Разделим обе части уравнения на 2Х. Получим:
или
Заменим Получим
При Х = 2 получим основное тригонометрическое тождество, т. е. Х = 2 является корнем исходного уравнения.
Получили ответ: Х = 2.
Пример 6. Решить уравнение
Решение. ОДЗ: X = 2, 3, …, N, … .
Перепишем уравнение в виде
Разделим обе части уравнения на (так как ). Получим:
Вводим замену
Получаем квадратное уравнение откуда
Возвращаемся к старой переменной:
Но ни один из корней не подходит по ОДЗ. Следовательно, уравнение корней не имеет.
Пример 7. Решить уравнение
Решение. ОДЗ: X ¹ 2.
Решением является совокупность
Корень X = 2 не подходит по ОДЗ.
Получили ответ: X = 1, X = 3.
| < Предыдущая | Следующая > |
|---|
Как решать показательно-степенные уравнения
- Альфашкола
- Статьи
- Как решать показательно-степенные уравнения
Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).
Типы показательно-степенных уравнений и методы их решения
Всюду далее F(X), G(X), H(X) – Некоторые выражения с неизвестной X, F(X) > 0.
Автор — Дмитрий Айстраханов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Ольга Викторовна Пятаева
Репетитор по математике
Стаж (лет)
Образование:
Ташкентский ордена Дружбы народов гос. педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 5-9 класса.
Ирина Владимировна Никитина
Репетитор по математике
Стаж (лет)
Образование:
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-6 классов. Я люблю математику за то, что математика- царица точных наук. Она не
только интересна и «красива», она еще и полезна, как для других наук, так и в
быту. Стараюсь прививать и поддерживать интерес детей к предмету.
Я люблю математику за то, что математика- царица точных наук. Она не
только интересна и «красива», она еще и полезна, как для других наук, так и в
быту. Стараюсь прививать и поддерживать интерес детей к предмету.
Оксана Александровна Латтеган
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-7 классов. Применяю различные методы работы, учитываю индивидуальные особенности учащихся, делаю упор на повышение уровня качества знаний. Работаю на результат — чтобы ученики поняли и усвоили. С удовольствием провожу занятия , в каждом ученике вижу личность, помогаю понять и полюбить математику.
Применяю различные методы работы, учитываю индивидуальные особенности учащихся, делаю упор на повышение уровня качества знаний. Работаю на результат — чтобы ученики поняли и усвоили. С удовольствием провожу занятия , в каждом ученике вижу личность, помогаю понять и полюбить математику.
Похожие статьи
- Площадь прямоугольной пирамиды
- Площадь произвольного четырехугольника
- Как решать логарифмические уравнения
- НИУ ВШЭ: Логистика и Управление целями поставок
- ПМФ (МФТИ)
- ЕГЭ по математике, базовый уровень. Планиметрия. Прямоугольный треугольник (вариант 4)
- Как вести себя, если ребенок получает двойки?
- Что вредит нашему сну, как создать комфортную обстановку для расслабления и что такое парасомнии.

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Уравнения высших степеней
|
Титул || Оглавленеие ||Уравнения содержащие знак модуля || Уравнения высших степеней || Тригонометрические уравнения || Показательные уравнения || Показательно-степенные уравнения || Страничка автора || |
Методы решения уравнений высших степеней
- Решение уравнений с помощью деления в столбик
- Возвратные уравнения и к ним сводящиеся
· Возвратные уравнения четной степени
· Возвратные уравнения нечетной степени
- Уравнения вида, где
- Замена переменных по явным признакам
- В следующих уравнениях используется “идея однородности”
· Пример №1
· Пример №2
· Пример №3
- Уравнения вида, где
- В уравнениях вида и в уравнениях к ним сводящимся
- В уравнениях вида
- Выделение полного квадрата
- Решение уравнений с помощью формулы
- Уравнения вида и к ним сводящиеся
- Решение уравнений относительно коэффициентов
- Метод разложения на простейшие дроби
I) Решение уравнений с помощью деления в столбик
Очевидно — корень уравнения
Очевидно — корень уравнения
Ответ: -5;2;3;4
II) Возвратные уравнения и к ним сводящиеся
Уравнение называется возвратным,
если в нем коэффициенты равноудаленные от концов совпадают, т. е. , ,
е. , ,
1) Возвратные уравнения четной степени.
т.к. — не является корнем уравнения, то разделим обе части уравнения на .
Введем замену.
Пусть , , получим
;
Вернемся к замене.
или
корней нет
Ответ:
2) Возвратные уравнения нечетной степени
Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1
Очевидно — корень уравнения.
или
т.к — не является корнем уравнения, то разделим обе части
уравнения на
Введем замену.
Пусть , , , получим
или или
корней нет
Ответ: , ,
II) Уравнения вида, где
решаются как
возвратные.
IV) Замена переменных по явным признакам
V) В следующих уравнениях используется “идея однородности”
Пример №1
Введем замену.
Пусть , , тогда
1) если , тогда , тогда
решений нет
2) Разделим обе части уравнения на , получим
Решим последнее уравнение, как квадратное относительно , получим
;
;
Вернемся к замене.
или
корней нет
Ответ:
Пример №2
Пусть , , тогда
Найдем
Составим систему:
Решая систему подстановкой, получим
или
корней нет ;
Ответ: ;
Пример №3
— не является корнем уравнения
Разделим обе части уравнения на , получим
Введем замену.
Пусть , тогда
;
или
; ;
Ответ: ; ; ;
VI) Уравнения вида, где
эффективно решать перемножением и , а затем делать замену.
VII) В уравнениях вида
и в уравнениях к ним сводящимся
в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.
(1)
(2)
При переходе область определения
уравнения сузилась на . Проверим, является ли корнем уравнения. Не
является.
Проверим, является ли корнем уравнения. Не
является.
Введем замену.
Пусть , , тогда
;
или
Ответ: ;
VIII) В уравнениях вида
обе части уравнения делятся на
— не является корнем уравнения. Разделим на , получим
Введем замену.
Пусть ; , тогда
;
или
Ответ: ;
IX) Выделение полного квадрата
Введем замену.
Пусть , тогда
;
Вернемся к замене.
или
корней нет
Ответ:
X) Решение уравнений с помощью формулы
или
корней нет
XI) Уравнения вида и к ним сводящиеся
решаются при помощи замены
Введем замену.
Пусть , тогда
или корней нет
;
Вернемся к замене.
или
Ответ: ;
XII) Решение уравнений относительно коэффициентов
или
; — посторонний корень
корней нет
Ответ: ;
XIII) Метод разложения на простейшие дроби
Ответ:
|
|| Титул || Оглавленеие ||Уравнения содержащие знак модуля || Уравнения высших степеней || Тригонометрические уравнения || Показательные уравнения || Показательно-степенные уравнения || Страничка автора || |
© Gussnick corp. 2009 Н.В. Гусятников [email protected]
2009 Н.В. Гусятников [email protected]
Уравнения высших степеней. Степенные или показательные уравнения Уравнение 5 степени
На канал на youtube нашего сайта сайт, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a a … a=a n
1. a 0 = 1 (a ≠ 0)
3. a n a m = a n + m
4. (a n) m = a nm
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2 х = 2 3
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2 х = 2 3
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
3 3х — 9 х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n) m = a nm .
3 3х = (3 2) х+8
Получим 9 х+8 =(3 2) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10 4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n) m = a nm .
4 х = (2 2) х = 2 2х
И еще используем одну формулу a n a m = a n + m:
2 2х+4 = 2 2х 2 4
Добавляем в уравнение:
2 2х 2 4 — 10 2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2:
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2) х = 3 2х
Получаем уравнение:
3 2х — 12 3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены . Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t 1 = 9
t 2 = 3
Возвращаемся к переменной x .
Берем t 1:
t 1 = 9 = 3 х
Стало быть,
3 х = 9
3 х = 3 2
х 1 = 2
Один корень нашли. Ищем второй, из t 2:
t 2 = 3 = 3 х
3 х = 3 1
х 2 = 1
Ответ: х 1 = 2; х 2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу
Судя по началу публикации, которое мы здесь опустим, текст писал Юрий Игнатьевич. И написано хорошо, и проблематика злободневная, вот только так называть Россию, как это делает Мухин…
Как бы кто ни относился к антинародной власти, Россия выше неё и не заслуживает оскорблений. Даже от талантливого разоблачителя лжи американского агенства НАСА.
*
Обращение к тов. Мухину Ю.И.
Уважаемый Юрий Игнатьевич! Я знаю, что вы посещаете эти страницы. Поэтому обращаюсь к вам напрямую.
Мы все ценим ваш подвижнический труд на ниве разоблачения лжи Запада, лжи Америки, лжи псевдоучёных, лжи либералов. Мы с удовольствием и пользой для себя и общества задумываемся над серьёзными темами, которые вы нам время от времени подбрасываете, будь то меритократия или метафизика, любовь к отечественной истории или восстановление справедливости.
Однако ваши определения нашей общей с вами Родины вызывают недоумение и сильно огорчают.
Впрочем, посудите сами: как бы вы охарактеризовали человека, который стал оскорблять свою заболевшую и от этого временно переставшую работать мать?
А ведь Россия, как бы она ни именовалась, и какой бы хорошей или отвратительной ни была власть, — Россия это наша Родина. Родина-мать. За неё наши деды проливали кровь и клали свои жизни.
Поэтому ставить её в один ряд с властью — это опускать духовное возвышенное на уровень материального, да ещё и низкого. Т.е. вы проводите сравнение совершенно различных категорий. Вещь, недопустимая для любого вменяемого человека.
Прошу вас, уважаемый тов. Мухин, серьёзно задуматься над этим.
**
…А с уравнениями (я этого и не знал) положение таково. Как найти корни квадратного уравнения догадались ещё в древнем Египте .
Как найти корни кубического уравнения и уравнения четвёртой степени, нашли в шестнадцатом веке, а вот найти корни уравнения пятой степени до 2016 года не могли. А пытались далеко не простые люди.
А пытались далеко не простые люди.
В шестнадцатом веке найти корни уравнения пятой степени пытался основоположник символической алгебры Франсуа Виет, в девятнадцатом веке это пытался сделать основатель современной высшей алгебры французский математик Эварист Галуа, после него найти корни уравнений пятой степени пробовал норвежский математик Нильс Хенрик Абель, который, в конце концов, сдался и доказал невозможность решения уравнения пятой степени в общем виде.
Читаем в Википедии о заслугах Абеля: «Абель закончил блестящее исследование древней проблемы: доказал невозможность решить в общем виде (в радикалах) уравнение 5-й степени…
В алгебре Абель нашёл необходимое условие для того, чтобы корень уравнения выражался «в радикалах» через коэффициенты этого уравнения. Достаточное условие вскоре открыл Галуа, чьи достижения опирались на труды Абеля.
Абель привёл конкретные примеры уравнения 5-й степени, чьи корни нельзя выразить в радикалах, и тем самым в значительной степени закрыл древнюю проблему».
Как видите, если теорему Пуанкаре доказать пытались всё время и Перельман оказался удачливее остальных математиков, то после Абеля за уравнения пятой степени математики и не брались.
А в 2014 году математик из Томска Сергей Зайков , о котором по фото можно судить, что он уже в годах, а по данным из статьи о нём, что он выпускник факультета прикладной математики и кибернетики Томского государственного университета, в ходе своей работы получил уравнения пятой степени. Тупик? Да, тупик! Но Сергей Зайков взялся его проломить.
И в 2016 году он нашёл способы решений уравнений пятой степени в общем виде! Сделал то, невозможность чего доказали математики Галуа и Абель.
Я попытался найти сведения о Сергее Зайкове в Википедии, но хрен вам! О математике Сергее Зайкове и о нахождении им решения уравнений пятой степени сведений нет!
Пикантность делу придаёт и то, что для математиков существует аналог Нобелевской премии — Абелевская премия (Нобель запретил давать премию математикам и теперь её дают за математические испражнения, называя их «физикой
»).
Эта математическая премия в честь того самого Абеля, который доказал невозможность того, что сделал Зайков . Однако, самовыдвижение на эту премию не допускается. А Зайков математик-одиночка и нет никаких организаций, которые могли бы предложить его кандидатуру на соискание этой премии.
Правда у нас есть Академия наук, но ведь там академики сидят не для развития математики, а «бабло пилить». Кому там нужен этот Зайков?
Ну а для новостных агентств Зайков — это вам не Перельман! Посему открытие Зайкова для СМИ — это не сенсация.
Вот то, что Порошенко дверью ошибся — это да! Это настоящая сенсация!
Томский математик решил проблему, которую не могли решить двести лет
С появлением алгебры ее основной задачей считалось решение алгебраических уравнений. Решение уравнения второй степени было известно еще в Вавилоне и Древнем Египте. Мы проходим такие уравнения в школе. Помните уравнение x2 + ax + b = 0, и дискриминант?
Сергей Зайков с книгой
Решение алгебраических уравнений третьей и четвертой степени было найдено в шестнадцатом веке. Но решить уравнение пятой степени не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени стало возможным потому, что их можно свести к уравнениям, ранее уже решенным. Уравнение третьей степени можно свести к уравнению второй степени, а уравнение четвертой — к уравнению третьей. Но уравнение пятой степени сводится к уравнению шестой, т. е. более сложному, поэтому традиционные методы решения не применимы.
Но решить уравнение пятой степени не удалось. Причину нашел Лагранж. Он показал, что решение уравнений третьей и четвертой степени стало возможным потому, что их можно свести к уравнениям, ранее уже решенным. Уравнение третьей степени можно свести к уравнению второй степени, а уравнение четвертой — к уравнению третьей. Но уравнение пятой степени сводится к уравнению шестой, т. е. более сложному, поэтому традиционные методы решения не применимы.
Вопрос о решении уравнения пятой степени сдвинулся с места лишь двести лет назад, когда Абель доказал, что не все уравнения пятой степени можно решить в радикалах, т. е. в квадратных, кубических и иных корнях, известных нам по школе. А Галуа вскоре, т. е. двести лет назад, нашел критерий, позволяющий определить, какие уравнения пятой степени можно решить в радикалах, а какие нет. Он заключается в том, что группа Галуа, разрешимых в радикалах уравнения пятой степени, должна быть либо циклической или метациклической. Но Галуа не нашел способ решения в радикалах тех уравнений пятой степени, которые разрешимы в радикалах. Теория Галуа очень известна, о ней написано много книг.
Теория Галуа очень известна, о ней написано много книг.
До сих пор находились лишь частные решения для разрешимых в радикалах уравнений пятой степени. И только в этом году томский математик Сергей Зайков решил задачу, которую не могли решить двести лет. Опубликовал книгу «Как решаются в радикалах алгебраические уравнения пятой степени», в которой указал способ решения для любых уравнений пятой степени, которые разрешимы в радикалах. Зайков — выпускник факультета прикладной математики и кибернетики Томского государственного университета. Нам удалось взять у него интервью.
— Сергей, почему Вы стали решать эту задачу?
— Мне нужно было решение уравнения пятой степени для решения задачи из другого раздела математики. Я начал выяснять, как его найти, и узнал, что не все из них решаются в радикалах. Тогда я попытался найти в научной литературе способ решения тех уравнений, которые разрешимы в радикалах, но нашел лишь критерий, по которому можно определить, какие разрешимы, а какие нет. Я не алгебраист, но, разумеется, как выпускник ФПМК, умею применять и алгебраические методы. Поэтому я с 2014 г. всерьез начал искать решение и нашел его сам.
Я не алгебраист, но, разумеется, как выпускник ФПМК, умею применять и алгебраические методы. Поэтому я с 2014 г. всерьез начал искать решение и нашел его сам.
Способ был найден мной два года назад, я подготовил книгу, в которой был описан не только он, но и способы решения некоторых уравнений степеней больше пятой. Но у меня не было денег для ее издания. В этом году я решил, что проще опубликовать лишь часть этой работы, и взял только ее половину, посвященную способу решения уравнения пятой степени в радикалах.
Я поставил своей целью публикацию что-то вроде руководства по решению этой задачи, понятной для математиков, которым необходимо решить конкретное уравнение. Поэтому упростил ее, убрав множество длинных формул и значительную часть теории, урезав более чем наполовину, оставив только необходимое. Поэтому у меня получилось что-то вроде книжки «для чайников», по которой математики, не знакомые с теорией Галуа, могут решить нужное им уравнение.
— За это большое спасибо Владиславу Бересневу, с которым мы знакомы много лет. Он проспонсировал издание книги.
Он проспонсировал издание книги.
— Возможно ли получение Вами какой-либо премии по математике за решение этой задачи? Например, Вы упоминали Абеля. А ведь есть Абелевская премия по математике, которую считают аналогом нобелевской?
— Полностью исключить такую возможность нельзя. Но и надеяться на это не стоит.
Например, заявки на кандидатов на Абелевскую премию 2019 г. подаются до 15 сентября. Причем самовыдвижение не допускается. А я математик-одиночка. Нет никаких организаций или известных математиков, которые предложат мою кандидатуру. Поэтому она не будет рассматриваться независимо от того, заслуживает ли моя работа этой премии, и насколько соответствует духу этой премии вручение ее тем, кто продолжает работы Абеля. Но даже в случае, если она будет представлена, все зависит еще и от уровня работ других кандидатов.
Книга рассчитана на тех, кто не знаком с теорией Галуа. Основы теории Галуа даются только в той части, в которой они необходимы для решения уравнения, детально описан способ решения, показаны приемы, упрощающие решение. Значительная часть книги посвящена примеру решения конкретного уравнения. Рецензентами книги являются доктор технических наук Геннадий Петрович Агибалов и доктор физ. мат. наук, профессор Петр Андреевич Крылов.
Значительная часть книги посвящена примеру решения конкретного уравнения. Рецензентами книги являются доктор технических наук Геннадий Петрович Агибалов и доктор физ. мат. наук, профессор Петр Андреевич Крылов.
ПОДГОТОВИЛА АНАСТАСИЯ СКИРНЕВСКАЯ
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x:
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · (a n) n — 1 · x + a 0 · (a n) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 (x) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 (x) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 (x) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде (x — x 1) (x — x 2) · P n — 2 (x) = 0 .Здесь P n — 2 (x) будет частным от деления P n — 1 (x) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m (x) = 0 . Здесь P n — m (x) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m (x) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Пример 1
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на (х — 1) в столбик:
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 (- 1) 3 + 2 · (- 1) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на (х + 1) в столбик:
Получаем, что
x 4 + x 3 + 2 x 2 — x — 3 = (x — 1) (x 3 + 2 x 2 + 4 x + 3) = = (x — 1) (x + 1) (x 2 + x + 3)
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1:
1 2 + (- 1) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 (- 3) 2 + (- 3) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Пример 2
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 (- 1) 4 — (- 1) 3 — 5 · (- 1) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
В итоге мы получим x — 2 (x 3 + x 2 — 3 x — 6) = 0 .
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2:
В итоге получим (x — 2) 2 · (x 2 + 3 x + 3) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ : x = — 3 2 ± i 3 2 .
Пример 3
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x:
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
В XVI веке математики почти случайно натолкнулись на комплексные числа (см. Главу 11). К XVIII веку комплексные числа считались расширением области действительных чисел, но работа с ними все еще приводила к ошибке четности, как в труде Леонарда Э своем великом труде по теории чисел «Арифметические исследования» (1801) избегал использования так называемых «мнимых чисел». Как мне кажется, самая важная часть этой работы — первое доказательство фундаментальной теоремы алгебры. Гаусс понял, насколько важной была эта теорема, создав за последующие годы несколько дополнительных доказательств. В 1849 году он переделал первый вариант, на сей раз использовав комплексные числа. Пользуясь современными терминами, можно сказать, что для любого конечного многочленного уравнения с действительными или комплексными коэффициентами все его корни будут действительными или комплексными числами. Таким образом, мы получаем отрицательный ответ на давний вопрос о том, требует ли решение полиномиальных уравнений высокого порядка создания чисел более высокого порядка, чем комплексные.
Пользуясь современными терминами, можно сказать, что для любого конечного многочленного уравнения с действительными или комплексными коэффициентами все его корни будут действительными или комплексными числами. Таким образом, мы получаем отрицательный ответ на давний вопрос о том, требует ли решение полиномиальных уравнений высокого порядка создания чисел более высокого порядка, чем комплексные.
Одной из самых тернистых проблем алгебры того времени был вопрос, разрешим ли алгебраическими методами, то есть с помощью конечного числа алгебраических шагов, полиномиал пятого порядка — квинтик. Сейчас в школе учат формулу решения квадратных уравнений, а с XVI века известны аналогичные методы для решения уравнений третьей и четвертой степени (Глава 11). Но для квинтиков не было найдено ни одного метода. Может показаться, что фундаментальная теорема алгебры содержит перспективу положительного ответа, но на самом деле она просто гарантирует, что решения существуют, в ней ничего не говорится о существовании формул, дающих точные решения (к тому времени уже существовали приблизительные числовые и графические методы). И вот появились два математических гения с трагической судьбой.
И вот появились два математических гения с трагической судьбой.
Нильс Хенрик Абель (1802–1829) родился в большой бедной семье, жившей в маленькой деревушке в Норвегии — стране, разоренной долгими годами войны с Англией и Швецией. Учитель, доброжелательно настроенный к мальчику, давал ему частные уроки, но после смерти отца, в восемнадцать лет, несмотря на юный возраст и хрупкое здоровье, Абель вынужден был содержать семью. В 1824 году он издал научную статью, в которой заявил, что квинтик не разрешим алгебраическими средствами, как, впрочем, и любой полиномиал более высокого порядка. Абель полагал, что эта статья послужит ему пропуском в научный мир, и послал ее Гауссу в университет Геттингена. К сожалению, Гаусс так и не собрался разрезать страницы ножом (в те дни этим приходилось заниматься любому читателю) и не прочитал статью. В 1826 году норвежское правительство наконец выделило Абелю средства для поездки по Европе. Опасаясь, что личное общение с Гауссом не доставит ему большой радости, математик решил не посещать Геттинген и вместо этого поехал в Берлин. Там он подружился с Августом Леопольдом Крелле (1780–1855), математиком, архитектором и инженером, консультировавшим прусское министерство образования по вопросам математики. Крелл собирался основать «Журнал чистой и прикладной математики». Так Абель получил возможность распространить свой труд и много печатался, особенно в ранних номерах «Журнала», который сразу же стал считаться очень престижным и авторитетным научным изданием. Норвежец напечатал там расширенную версию своего доказательства, что квинтик неразрешим алгебраическими методами. А затем уехал в Париж. Эта поездка очень огорчила Абеля, потому что он практически не получил так необходимой ему поддержки французских математиков. Он сблизился с Огюстеном Луи Коши (1789–1857), который в то время был главным светилом математического анализа, но имел очень сложный характер. Как выразился сам Абель, «Коши безумен, и с этим ничего нельзя поделать, хотя в настоящее время он — единственный, кто на что-то способен в математике». Если пытаться искать оправдания проявлениям неуважения и пренебрежения, исходившим от Гаусса и Коши, можно сказать, что квинтик достиг определенной славы и привлекал внимание как уважаемых математиков, так и оригиналов.
Там он подружился с Августом Леопольдом Крелле (1780–1855), математиком, архитектором и инженером, консультировавшим прусское министерство образования по вопросам математики. Крелл собирался основать «Журнал чистой и прикладной математики». Так Абель получил возможность распространить свой труд и много печатался, особенно в ранних номерах «Журнала», который сразу же стал считаться очень престижным и авторитетным научным изданием. Норвежец напечатал там расширенную версию своего доказательства, что квинтик неразрешим алгебраическими методами. А затем уехал в Париж. Эта поездка очень огорчила Абеля, потому что он практически не получил так необходимой ему поддержки французских математиков. Он сблизился с Огюстеном Луи Коши (1789–1857), который в то время был главным светилом математического анализа, но имел очень сложный характер. Как выразился сам Абель, «Коши безумен, и с этим ничего нельзя поделать, хотя в настоящее время он — единственный, кто на что-то способен в математике». Если пытаться искать оправдания проявлениям неуважения и пренебрежения, исходившим от Гаусса и Коши, можно сказать, что квинтик достиг определенной славы и привлекал внимание как уважаемых математиков, так и оригиналов. Абель возвратился в Норвегию, где все сильнее страдал от туберкулеза. Он продолжал посылать свои работы Крелле, но в 1829 году умер, не зная о том, насколько упрочилась его репутация в научном мире. Через два дня после смерти на адрес Абеля пришло предложение занять научную должность в Берлине.
Абель возвратился в Норвегию, где все сильнее страдал от туберкулеза. Он продолжал посылать свои работы Крелле, но в 1829 году умер, не зная о том, насколько упрочилась его репутация в научном мире. Через два дня после смерти на адрес Абеля пришло предложение занять научную должность в Берлине.
Абель показал, что любой полиномиал выше четвертого порядка не может быть решен с помощью радикалов, вроде корней квадратных, кубических или более высокого порядка. Однако явные условия, при которых в особых случаях эти полиномиалы могли быть решены, и метод их решения сформулировал Галуа. Эварист Галуа (1811–1832) прожил короткую и богатую событиями жизнь. Он был невероятно одаренным математиком. Галуа был неумолим к тем, кого считал менее талантливым, чем он сам, и при этом терпеть не мог социальную несправедливость. Он не выказывал никаких способностей к математике до тех пор, пока не прочитал труд Лежандра «Начала геометрии» (изданная в 1794 году, эта книга в течение последующих ста лет была основным учебником). Затем он буквально проглотил остальные труды Лежандра и, позднее, Абеля. Его энтузиазм, уверенность в себе и нетерпимость привели к поистине ужасным последствиям в его отношениях с преподавателями и экзаменаторами. Галуа принял участие в конкурсе на поступление в Политехническую школу — колыбель французской математики, но из-за неподготовленности провалил экзамен. Некоторое время после знакомства с новым преподавателем, который признал его дарование, ему удавалось держать свой нрав под контролем. В марте 1829 года Галуа издал свою первую статью о непрерывных дробях, которую считал своей самой значительной работой. Он послал сообщение о своих открытиях в Академию наук, и Коши обещал представить их, но забыл. Более того, он просто потерял рукопись.
Затем он буквально проглотил остальные труды Лежандра и, позднее, Абеля. Его энтузиазм, уверенность в себе и нетерпимость привели к поистине ужасным последствиям в его отношениях с преподавателями и экзаменаторами. Галуа принял участие в конкурсе на поступление в Политехническую школу — колыбель французской математики, но из-за неподготовленности провалил экзамен. Некоторое время после знакомства с новым преподавателем, который признал его дарование, ему удавалось держать свой нрав под контролем. В марте 1829 года Галуа издал свою первую статью о непрерывных дробях, которую считал своей самой значительной работой. Он послал сообщение о своих открытиях в Академию наук, и Коши обещал представить их, но забыл. Более того, он просто потерял рукопись.
Второй провал Галуа при поступлении в Политехническую школу вошел в математический фольклор. Он настолько привык постоянно держать в голове сложные математические идеи, что его привели в бешенство мелочные придирки экзаменаторов. Поскольку экзаменаторы с трудом понимали его объяснения, он бросил тряпку для стирания с доски в лицо одному из них. Вскоре после этого умер его отец, покончивший с собой в результате церковных интриг. На его похоронах практически вспыхнул бунт. В феврале 1830 года Галуа написал следующие три статьи, послав их в Академию наук на соискание гран-при по математике. Жозеф Фурье, в то время бывший секретарем академии, умер, так и не прочитав их, и после его смерти статей среди его бумаг не нашли. Такой поток разочарований свалил бы любого. Галуа восстал против власть имущих, потому что чувствовал: они не признавали его достоинств и погубили его отца. Он с головой окунулся в политику, став ярым республиканцем, — не самое мудрое решение во Франции 1830 года. В последней отчаянной попытке он послал научную статью знаменитому французскому физику и математику Симеону Дени Пуассону (1781–1840), который в ответе потребовал дополнительных доказательств.
Вскоре после этого умер его отец, покончивший с собой в результате церковных интриг. На его похоронах практически вспыхнул бунт. В феврале 1830 года Галуа написал следующие три статьи, послав их в Академию наук на соискание гран-при по математике. Жозеф Фурье, в то время бывший секретарем академии, умер, так и не прочитав их, и после его смерти статей среди его бумаг не нашли. Такой поток разочарований свалил бы любого. Галуа восстал против власть имущих, потому что чувствовал: они не признавали его достоинств и погубили его отца. Он с головой окунулся в политику, став ярым республиканцем, — не самое мудрое решение во Франции 1830 года. В последней отчаянной попытке он послал научную статью знаменитому французскому физику и математику Симеону Дени Пуассону (1781–1840), который в ответе потребовал дополнительных доказательств.
Это стало последней каплей. В 1831 году Галуа был дважды арестован — в первый раз за то, что якобы призывал к убийству короля Луи Филиппа, а затем ради того, чтобы его защитить, — власти опасались республиканского бунта! На сей раз он был приговорен к шестимесячному заключению по сфабрикованному обвинению в незаконном ношении формы расформированного артиллерийского батальона, в который он поступил. Освобожденный под честное слово, он занялся делом, которое вызывало у него такое же отвращение, как и все остальное в жизни. В письмах к преданному другу Шевалье чувствуется его разочарование. 29 мая 1832 года он принял вызов на дуэль, причины которой до конца не выяснены. «Я пал жертвой бесчестной кокетки. Моя жизнь гаснет в жалкой ссоре», — пишет он в «Письме всем республиканцам». Самая известная работа Галуа была набросана в ночь перед роковым поединком. На полях рассыпаны жалобы: «У меня больше нет времени, у меня больше нет времени». Он вынужден был оставить другим подробное изложение промежуточных шагов, которые были несущественны для понимания основной идеи. Ему необходимо было выплеснуть на бумагу основу своих открытий — истоки того, что ныне называют теоремой Галуа. Он закончил свое завещание, попросив Шевалье «обратиться к Якоби и Гауссу с просьбой публично высказать свое мнение не относительно правильности, а относительно важности этих теорем». Ранним утром Галуа отправился на встречу со своим соперником.
Освобожденный под честное слово, он занялся делом, которое вызывало у него такое же отвращение, как и все остальное в жизни. В письмах к преданному другу Шевалье чувствуется его разочарование. 29 мая 1832 года он принял вызов на дуэль, причины которой до конца не выяснены. «Я пал жертвой бесчестной кокетки. Моя жизнь гаснет в жалкой ссоре», — пишет он в «Письме всем республиканцам». Самая известная работа Галуа была набросана в ночь перед роковым поединком. На полях рассыпаны жалобы: «У меня больше нет времени, у меня больше нет времени». Он вынужден был оставить другим подробное изложение промежуточных шагов, которые были несущественны для понимания основной идеи. Ему необходимо было выплеснуть на бумагу основу своих открытий — истоки того, что ныне называют теоремой Галуа. Он закончил свое завещание, попросив Шевалье «обратиться к Якоби и Гауссу с просьбой публично высказать свое мнение не относительно правильности, а относительно важности этих теорем». Ранним утром Галуа отправился на встречу со своим соперником. Они должны были стреляться с расстояния в 25 шагов. Галуа был ранен и умер в больнице на следующее утро. Ему было всего двадцать лет.
Они должны были стреляться с расстояния в 25 шагов. Галуа был ранен и умер в больнице на следующее утро. Ему было всего двадцать лет.
Галуа опирался на работы Лагранжа и Коши, однако он разработал более общий метод. Это было крайне важное достижение в области решения квинтиков. Ученый уделял меньше внимания исходным уравнениям или графической интерпретации, а больше думал о природе самих корней. Для упрощения Галуа рассматривал только так называемые неприводимые квинтики, то есть те, которые не могли быть разложены на множители в виде полиномиалов более низкого порядка (как мы сказали, для любых полиномиальных уравнений до четвертого порядка есть формулы нахождения их корней). Вообще неприводимый многочлен с рациональными коэффициентами — это полиномиал, который не может быть разложен на более простые многочлены, имеющие рациональные коэффициенты. Например, (x 5 — 1) может быть разложен на множители (х-1)(x 4 + х 3 + х 2 + х + 1), тогда как (x 5 — 2) неприводим. Цель Галуа состояла в том, чтобы определить условия, при которых все решения общего неприводимого многочленного уравнения могут быть найдены в терминах радикалов.
Цель Галуа состояла в том, чтобы определить условия, при которых все решения общего неприводимого многочленного уравнения могут быть найдены в терминах радикалов.
Ключ к решению заключается в том, что корни любого неприводимого алгебраического уравнения не независимы, они могут быть выражены один через другой. Эти соотношения были формализованы в группу всех возможных перестановок, так называемую группу симметрии корней — для квинтика эта группа содержит 5! = 5 х 4 х 3 х 2 х 1 = 120 элементов. Математические алгоритмы теории Галуа очень сложны, и, скорее всего, отчасти именно вследствие этого их поначалу понимали с большим трудом. Но после того как уровень абстракции позволил перейти от алгебраических решений уравнений к алгебраической структуре связанных с ними групп, Галуа смог предсказать разрешимость уравнения на основании свойств таких групп. Более того, его теория также обеспечила метод, которым можно было найти сами эти корни. Что касается квинтиков, то математик Жозеф Лиувилль (1809–1882), который в 1846 году издал большую часть работ Галуа в своем «Журнале чистой и прикладной математики», отметил, что молодой ученый доказал «красивую теорему», и для того, «чтобы неприводимое уравнение исходной степени было разрешимо в терминах радикалов, необходимо и достаточно, чтобы все его корни были рациональными функциями любых двух из них». Поскольку для квинтика это невозможно, он не может быть решен с помощью радикалов.
Поскольку для квинтика это невозможно, он не может быть решен с помощью радикалов.
За три года математический мир потерял две самые яркие новые звезды. Последовали взаимные обвинения и переоценка ценностей, и Абель и Галуа добились заслуженного признания, но лишь посмертно. В 1829 году Карл Якоби через Лежандра узнал о «потерянной» рукописи Абеля, и в 1830 году разразился дипломатический скандал, когда норвежский консул в Париже потребовал отыскать статью своего соотечественника. В конце концов Коши нашел статью, но лишь затем, чтобы ее снова потеряли в редакции академии! В том же году Абелю был присужден Гран-при по математике (совместно с Якоби) — но он был уже мертв. В 1841 году была издана его биография. В 1846 году Лиувилль отредактировал некоторые из рукописей Галуа для публикации и во введении выразил сожаление, что первоначально академия отвергла работу Галуа из-за ее сложности, — «действительно, необходима ясность изложения, когда автор уводит читателя с избитого пути на неизведанные дикие территории». Он продолжает: «Галуа больше нет! Не будем впадать в бесполезный критицизм. Давайте отбросим недостатки и посмотрим на достоинства!» Плоды краткой жизни Галуа умещаются всего на шестидесяти страницах. Редактор математического журнала для кандидатов в Эколь Нормаль и Политехническую школу прокомментировал дело Галуа следующим образом: «Соискатель с высоким интеллектом был отсеян экзаменатором с более низким уровнем мышления. Barbarus hic ego sum, quia non intelligor illis ».
Он продолжает: «Галуа больше нет! Не будем впадать в бесполезный критицизм. Давайте отбросим недостатки и посмотрим на достоинства!» Плоды краткой жизни Галуа умещаются всего на шестидесяти страницах. Редактор математического журнала для кандидатов в Эколь Нормаль и Политехническую школу прокомментировал дело Галуа следующим образом: «Соискатель с высоким интеллектом был отсеян экзаменатором с более низким уровнем мышления. Barbarus hic ego sum, quia non intelligor illis ».
Прежде всего, вторая страница этой работы не обременена именами, фамилиями, описаниями положения в обществе, титулами и элегиями в честь некоего скупого принца, кошелек которого будет открыт с помощью этих фимиамов — с угрозой закрыть его, когда восхваления закончатся. Вы не увидите здесь почтительных восхвалений, написанных буквами втрое большими, чем сам текст, обращенных к тем, кто обладает высоким положением в науке, некоему мудрому покровителю — нечто обязательное (я бы сказал, неизбежное) для кого-то в возрасте двадцати лет, кто хочет что-то написать. Я не говорю здесь никому, что я обязан их совету и поддержке всем хорошим, что есть в моей работе. Я не говорю этого потому, что это было бы ложью. Если бы мне пришлось упомянуть кого-либо из великих в обществе или в науке (в настоящее время различие между этими двумя классами людей практически незаметно), клянусь, это не было бы знаком благодарности. Я обязан им тем, что я издал первые из этих двух статей столь поздно, и тем, что написал все это в тюрьме — в месте, которое вряд ли можно считать подходящим для научных размышлений, и я часто поражаюсь своей сдержанности и способности держать рот на замке по отношению к тупым и злобным зоилам. Мне кажется, я могу использовать слово «зоилы» без опасения быть обвиненным в неблагопристойности, поскольку именно так я именую моих оппонентов. Я не собираюсь писать здесь о том, как и почему я был отправлен в тюрьму, но я должен сказать, что мои рукописи чаще всего просто терялись в папках господ членов академии, хотя, по правде говоря, я не могу представить себе подобной неосмотрительности со стороны людей, на совести которых смерть Абеля.
Я не говорю здесь никому, что я обязан их совету и поддержке всем хорошим, что есть в моей работе. Я не говорю этого потому, что это было бы ложью. Если бы мне пришлось упомянуть кого-либо из великих в обществе или в науке (в настоящее время различие между этими двумя классами людей практически незаметно), клянусь, это не было бы знаком благодарности. Я обязан им тем, что я издал первые из этих двух статей столь поздно, и тем, что написал все это в тюрьме — в месте, которое вряд ли можно считать подходящим для научных размышлений, и я часто поражаюсь своей сдержанности и способности держать рот на замке по отношению к тупым и злобным зоилам. Мне кажется, я могу использовать слово «зоилы» без опасения быть обвиненным в неблагопристойности, поскольку именно так я именую моих оппонентов. Я не собираюсь писать здесь о том, как и почему я был отправлен в тюрьму, но я должен сказать, что мои рукописи чаще всего просто терялись в папках господ членов академии, хотя, по правде говоря, я не могу представить себе подобной неосмотрительности со стороны людей, на совести которых смерть Абеля. На мой взгляд, любой хотел бы, чтобы его сравнивали с этим блестящим математиком. Достаточно сказать, что моя статья по теории уравнений была направлена в Академию наук в феврале 1830 года, что извлечения из нее были посланы в феврале 1829 года, и при этом ничего из этого не было напечатано, и даже рукопись оказалось невозможно возвратить.
На мой взгляд, любой хотел бы, чтобы его сравнивали с этим блестящим математиком. Достаточно сказать, что моя статья по теории уравнений была направлена в Академию наук в феврале 1830 года, что извлечения из нее были посланы в феврале 1829 года, и при этом ничего из этого не было напечатано, и даже рукопись оказалось невозможно возвратить.
Галуа, неопубликованное предисловие, 1832 год
Класс: 9
Основные цели:
- Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n > 3).
- Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его решения.
Формы, методы и педагогические приемы, которые используются учителем на уроке:
- Лекционно-семинарская система обучения (лекции – объяснение нового
материала, семинары – решение задач).

- Информационно-коммуникационные технологии (фронтальный опрос, устная работа с классом).
- Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на развитие математического аппарата и мыслительных способностей каждого конкретного ученика.
- Печатный материал – индивидуальный краткий конспект урока (основные понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
План урока:
- Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить содержательные рамки урока. - Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам - Изучение новой темы (лекция). Цель этапа: сформулировать основные методы решения уравнений высших степеней (n > 3)
- Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на уроке.
- Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
Конспект урока
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений из теории. Учащиеся формулируют основные определения и дают формулировки необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного уравнения с одной переменной.
- Понятие равносильности уравнений, уравнения-следствия (понятие посторонних корней), переход не по следствию (случай потери корней).
- Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n -й степени.
 Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение.
Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение. - Переход к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители.
- Понятие многочлена n -й степени от x . Теорема Безу. Следствия из теоремы Безу. Теоремы о корнях (Z -корни и Q -корни) целого рационального уравнения с целыми коэффициентами (соответственно приведенного и неприведенного).
- Схема Горнера.
3. Изучение новой темы.
Будем рассматривать целое рациональное уравнение n -й степени
стандартного вида с одной неизвестной переменной x: P n (x) = 0
, где P n (x) = a n x n + a n-1 x n-1
+ a 1 x + a 0 – многочлен n -й степени от x , a n ≠ 0
. Если a n
= 1 то такое уравнение называют приведенным целым рациональным уравнением n -й степени. Рассмотрим такие уравнения при различных значениях n и перечислим основные методы их решения.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Метод группировки.
Пример: x 3 – 4x 2 – x + 4 = 0 (x – 4)(x 2 – 1) = 0 x 1 = 4 , x 2 = 1, x 3 = -1.
Возвратное кубическое уравнение вида ax 3 + bx 2 + bx + a = 0. Решаем, объединяя члены с одинаковыми коэффициентами.
Пример: x 3 – 5x 2 – 5x + 1 = 0 (x + 1)(x 2 – 6x + 1) = 0 x 1 = -1, x 2 = 3 + 2, x 3 = 3 – 2.
Подбор Z-корней на основании теоремы.
Схема Горнера. При применении этого метода необходимо сделать акцент на том, что
перебор в данном случае конечный, и корни мы подбираем по определенному
алгоритму в соответствии с теоремой о Z -корнях приведенного целого
рационального уравнения с целыми коэффициентами.
Пример: x 3 – 9x 2 + 23x – 15 = 0. Уравнение приведенное. Выпишем делители свободного члена {+ 1; + 3; + 5; + 15}. Применим схему Горнера:
| x 3 | x 2 | x 1 | x 0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1 – 9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15 – 15 = 0 | 1 – корень |
| x 2 | x 1 | x 0 |
Получаем
(x – 1)(x 2 – 8x + 15) = 0 x 1 = 1, x 2 = 3, x 3 = 5.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. При применении этого метода необходимо сделать акцент на том, что перебор в данном случае конечный и корни мы подбираем по определенному алгоритму в соответствии с теоремой о Q -корнях неприведенного целого рационального уравнения с целыми коэффициентами.
Пример: 9x 3 + 27x 2 – x – 3 = 0. Уравнение неприведенное. Выпишем делители свободного члена {+ 1; + 3}. Выпишем делители коэффициента при старшей степени неизвестного. {+ 1; + 3; + 9} Следовательно, корни будем искать среди значений {+ 1; + ; + ; + 3}. Применим схему Горнера:
| x 3 | x 2 | x 1 | x 0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 x 9 + 27 = 36 | 1 x 36 – 1 = 35 | 1 x 35 – 3 = 32 ≠ 0 | 1 – не корень |
| -1 | 9 | -1 x 9 + 27 = 18 | -1 x 18 – 1 = -19 | -1 x (-19) – 3 = 16 ≠ 0 | -1 – не корень |
| 9 | x 9 + 27 = 30 | x 30 – 1 = 9 | x 9 – 3 = 0 | корень | |
| x 2 | x 1 | x 0 |
Получаем
(x –
)(9x 2
+ 30x + 9) = 0 x 1 =
, x 2 = —
, x 3 = -3.
Для удобства подсчета при подборе Q-корней бывает удобно сделать замену переменной, перейти к приведенному уравнению и подбирать Z-корни .
.
.
Формула Кардано. Существует универсальный метод решения кубических уравнений – это формула Кардано. Эту формулу связывают с именами итальянских математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Метод группировки.
Пример: x 4 + 2x 3 + 5x 2
+ 4x – 12 = 0
(x 4 + 2x 3) + (5x 2 + 10x )
– (6x + 12) = 0
(x + 2)(x 3 + 5x – 6) = 0
(x + 2)(x – 1)(x 2 + x + 6) = 0 x 1 = -2, x 2 = 1.
Метод замены переменной.
- Биквадратное уравнение вида ax 4 + bx 2 + с = 0 .
Пример: x 4 + 5x 2 – 36 = 0. Замена y = x 2 . Отсюда y 1 = 4, y 2 = -9. Поэтому x 1,2 = + 2 .
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax 4 + bx 3 + cx 2 + kbx + k 2 a = 0 .
Пример 3. Замена общего вида (вытекает из вида конкретного
уравнения).
Замена общего вида (вытекает из вида конкретного
уравнения).
n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней n = 3.
Формула общего вида. Существует универсальный метод решения уравнений четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565). Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени
имеет корень x = -1 и после разложения его на множители получаем, что
один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное
уравнение четной степени (его степень на единицу меньше, чем степень исходного
уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x
= φ содержит и корень вида
.
Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.
Любое возвратное уравнение четной степени вместе с корнем вида x
= φ содержит и корень вида
.
Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой степени (это показали итальянский математик Паоло Руффини (1765–1822) и норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это показал французский математик Эварист Галуа (1811–1832)).
- Напомним еще раз, что на практике возможно использование комбинации перечисленных выше методов. Удобно переходить к совокупности уравнений более низких степеней путем разложения исходного уравнения на множители .
- За рамками нашего сегодняшнего обсуждения остались широко используемые на практике графические методы решения уравнений и методы приближенного решения уравнений высших степеней.
- Бывают ситуации, когда у уравнения нет R-корней.
 Тогда решение
сводится к тому, чтобы показать, что уравнение корней не имеет. Для
доказательства анализируем поведение рассматриваемых функций на промежутках
монотонности. Пример: уравнение x 8 – x 3
+ 1 = 0 не имеет корней.
Тогда решение
сводится к тому, чтобы показать, что уравнение корней не имеет. Для
доказательства анализируем поведение рассматриваемых функций на промежутках
монотонности. Пример: уравнение x 8 – x 3
+ 1 = 0 не имеет корней. - Использование свойства монотонности функций . Бывают ситуации, когда использование различных свойств функций позволяет упростить поставленную задачу.
Пример 1: уравнение x 5 + 3x – 4 = 0 имеет один корень x = 1. По свойству монотонности анализируемых функций других корней нет.
Пример 2: уравнение x 4 + (x – 1) 4 = 97 имеет корни x 1 = -2 и x 2 = 3. Проанализировав поведение соответствующих функций на промежутках монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений
высших степеней (для n > 3).
Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В
зависимости от вида уравнения мы должны будем научиться определять, какой способ
решения в данном случае является наиболее эффективным, а также правильно
применять выбранный метод.
В
зависимости от вида уравнения мы должны будем научиться определять, какой способ
решения в данном случае является наиболее эффективным, а также правильно
применять выбранный метод.
5. Домашнее задание.
: п.7, стр. 164–174, №№ 33–36, 39–44, 46,47.
: №№ 9.1–9.4, 9.6–9.8, 9.12, 9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
- Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность
подбора Z -корней и Q -корней уравнений при помощи достаточно
простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются
различными стандартными типами замены переменных, которые позволяют существенно
упрощать вид задачи. Особый интерес обычно вызывают графические методы решения.
В этом случае дополнительно можно разобрать задачи на графический метод решения
уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени;
проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом
соответствующего графика. Ниже приведен список книг, в которых можно найти
дополнительную информацию по данной тематике.
Ниже приведен список книг, в которых можно найти
дополнительную информацию по данной тематике.
Список литературы:
- Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с углубленным изучением математики” – М., Просвещение, 2007 – 367 с.
- Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение, 2008 – 192 с.
- Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055 с.
- Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9 классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с.
- Звавич Л.И. и др. “Алгебра и начала анализа. 8–11 кл. Пособие для школ и классов с углубленным изучением математики” – М., Дрофа, 1999 – 352 с.
- Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н. “Задания по математике для подготовки к письменному экзамену в 9 классе” –
М.
 , Просвещение, 2007 – 112 с.
, Просвещение, 2007 – 112 с. - Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с.
- Иванов А.А., Иванов А.П. “Тематические тесты для систематизации знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с.
- Иванов А.П. “Тесты и контрольные работы по математике. Учебное пособие”. – М., Физматкнига, 2008 – 304 с.
- Лейбсон К.Л. “Сборник практических заданий по математике. Часть 2–9 класс” – М., МЦНМО, 2009 – 184 с.
- Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с углубленным изучением математики.” – М., Просвещение, 2006 – 224 с.
- Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник” – М., Мнемозина, 2006 – 296 с.
- Савин А.П. “Энциклопедический словарь юного математика” – М.,
Педагогика, 1985 – 352 с.

- Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 – 95 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 1–4” – М., Первое сентября, 2006 – 88 с.
- Чулков П.В. “Уравнения и неравенства в школьном курсе математик. Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
3.1.9. Показательные и логарифмические уравнения
Глава 3. Решение уравнений и неравенств
3.1.
3.1.9.
Показательные уравнения
Уравнения вида af (x) = b, a > 0, a ≠ 1, b > 0
По определению логарифма из основного логарифмического тождества получаем, что
Если f (x) − алгебраическая функция, то и это уравнение будет алгебраическое, которое можно решить с помощью стандартных методов (так как
− это конкретное число, такое же, как и 5, π,
и т. п.).
п.).
Уравнения вида
Такие уравнения решаются в два этапа:
a) С помощью замены это уравнение сводится к уравнению F (t) = 0, у которого ищутся все его положительные корни (пусть таких корней ровно n штук).
b) Для каждого решается уравнение типа рассмотренного выше:
Эти два типа показательных уравнений являются основными, к ним сводятся все остальные методы.
Пример 1
Решите уравнение
Показать решение
Уравнения вида af (x) = ag (x), a > 0, a ≠ 1
В силу свойств монотонности показательной функции это уравнение равносильно уравнению f (x) = g (x).
Пример 2
Решите уравнение
Показать решение
Пример 3
Решите уравнение
Показать решение
Уравнения вида af (x) = bg (x), a > 0, a ≠ 1, b > 0, b ≠ 1
|
Модель 3.3. Решение показательных уравнений |
При решении таких уравнений применяется стандартный приём. Прологарифмируем обе его части по любому основанию. В нашем случае удобно логарифмировать по основанию a (или b), то есть по основанию показательной функции, входящей в уравнение:
А это уравнение уже можно решать стандартными алгебраическими способами, если f (x) и g (x) – алгебраические выражения.
Пример 4
Решите уравнение
Показать решение
Замечание. Рассмотренный приём перехода от уравнения af (x) = bg (x) к уравнению f (x) = g (x) loga b или, в общем случае, переход от уравнения
| F (x) = G (x) | (1) |
| loga F (x) = logb G (x) (a > 0, a ≠ 0) | (2) |
Заметим, что переход (1) → (2) в общем случае нарушает равносильность, так как логарифм существует только у неотрицательного числа.
Например, логарифмирование обеих частей уравнения x = x3, которое имеет вид (1), приводит нас к неравносильному уравнению lg x = lg x3 (область определения сузилась). Действительно,
Действительно,
Таким образом, произошла потеря корней исходного уравнения. Как видно, логарифмирование не является «безобидной» операцией, но в процессе решения уравнения типа af (x) = bg (x) эти неприятности не возникают, так как обе его части положительны.
Логарифмические уравнения
Уравнения вида loga f (x) = b, a > 0, a ≠ 1
Здесь предполагается, что f (x) − функция, уравнения с которой мы уже умеем решать. По определению логарифма из основного логарифмического тождества получаем, что f (x) = ab. Это уравнение можно решать любыми доступными методами, поскольку ab – это число.
Уравнения вида
Совершенно аналогично показательным уравнениям, уравнения такого типа решаются в два этапа.
-
С помощью замены это уравнение сводится к уравнению F (x) = 0, у которого ищутся все его корни (пусть таких корней ровно n штук).
-
Для каждого решается уравнение типа рассмотренного выше:
Понятно, что совершенно не обязательно уравнение будет иметь рассмотренный вид. А значит, в процессе преобразований логарифмических уравнений следует стремиться к тому, чтобы привести все входящие в уравнение логарифмы к одному основанию. При этом необходимо помнить об области определения рассматриваемых выражений, стараясь, чтобы при преобразовании она не уменьшалась, − те корни, которые, возможно, будут приобретены, можно будет отсеять проверкой.
Пример 5
Решите уравнение
Показать решение
Пример 6
Решите уравнение
Показать решение
Уравнения вида loga f (x) = loga g (x), a > 0, a ≠ 1
|
Модель 3. |
ОДЗ данного уравнения:
В силу монотонности логарифмической функции, каждое своё значение она принимает ровно один раз. Следовательно, в ОДЗ имеем:
Полная система равносильности выглядит так:
Из двух последних систем выбирается та, которая проще (это зависит от конкретного вида функций f (x) и g (x)). На практике, как правило, проще решить уравнение f (x) = g (x) и проверить для его корней положительность одной из функций: f (x) > 0 или g (x) > 0, так как из равенства одной из этих функций следует положительность и другой.
Рассмотренный переход от уравнения loga f (x) = loga g (x) к уравнению f (x) = g (x) называется потенцированием.
Заметим, что потенцирование не является равносильным преобразованием. Область определения уравнения при потенцировании расширяется, так как второе уравнение определено при всех x, для которых определены функции f (x) и g (x), а первое − только при тех x, для которых f (x) > 0 и g (x) > 0.
Пример 7
Решите уравнение
Показать решение
Пример 8
Решите уравнение
Показать решение
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
||||||||
|
||||||||
|
|
||||||||
Показательно-степенные неравенства 11 класс онлайн-подготовка на Ростелеком Лицей
1. Свойства показательной функции, простейшие примеры
Показательно-степенные неравенства – это такие показательные неравенства, в которых основание является переменной величиной.
Начнем с небольшого повторения. Мы изучили свойства показательной функции и отметили, что показательная функция монотонна, причем может как возрастать, так и убывать.
Мы научились решать простейшие показательные уравнения и неравенства. Их решение основано на монотонности показательной функции:
Их решение основано на монотонности показательной функции:
Заметим, что в данном случае основание степени а – это конкретное число, не зависящее от х.
Рассмотрим примеры для степеней с постоянным основанием.
Пример 1 – решить уравнение:
Согласно методике решения простейших показательных уравнений, необходимо уравнять основания степеней, после этого приравнять показатели:
Пример 2 – решить неравенство:
Согласно методике решения простейших показательных неравенств при основании, большем единицы, необходимо уравнять основания степеней, после этого сравнить показатели, оставив знак неравенства без изменений:
Пример 3 – решить неравенство:
Согласно методике решения простейших показательных неравенств при основании, меньшем единицы, необходимо уравнять основания степеней, после этого сравнить показатели, изменив знак неравенства на противоположный:
2.
 Решение показательно-степенного неравенства первым способом, пример
Решение показательно-степенного неравенства первым способом, пример
Все остальные более сложные показательные уравнения и неравенства сводятся к простейшим и решаются на основании вышеописанных методик.
Теперь рассмотрим случаи, когда основание степени – переменная величина, то есть а зависит от х:
Нам предстоит решать неравенства вида:
Необходимо рассматривать два случая:
Обратим внимание, что нужно еще рассмотреть третий случай:
Пример 4 – решить неравенство:
Функция, стоящая в левой части, называется показательно-степенной функцией, данная функция определена тогда, когда основание больше нуля.
Уравняем основания степеней:
Рассматриваем два случая:
Ответ:
3. Второй способ решения показательно-степенных неравенств
Рассмотрим другой способ решения показательно-степенного неравенства:
Имеем систему:
Распишем ее:
Напомним важный опорный факт:
На основании опорного факта можно переписать систему так:
При решении показательно-степенных неравенств первым способом необходимо решать две системы и объединять решения. При решении вторым способом нужно решить только одну систему, причем неравенство уже разложено на множители, т. е. удобно применить метод интервалов.
При решении вторым способом нужно решить только одну систему, причем неравенство уже разложено на множители, т. е. удобно применить метод интервалов.
4. Решение примеров
Пример 5 – решить неравенство:
Уравняем основания степеней:
Пользуемся вторым способом:
Покажем решение первого неравенства методом интервалов:
Рис. 1. Решение неравенства
Добавим к решению второе неравенство:
Рис. 2. Иллюстрация к примеру 5
Очевиден ответ:
Пример 6:
Приведем к одинаковому основанию:
Решим первым способом:
Ответ:
Решим заданное неравенство вторым способом:
Проиллюстрируем решение:
Рис. 3. Иллюстрация к примеру 6
Ответ:
Очевидно, что второй способ более легкий в применении. Решим с его помощью следующее неравенство.
Пример 7:
Приведем к одинаковому основанию:
Составим систему:
Несложно заметить в первом неравенстве формулу разности квадратов, распишем:
При первые две скобки первого неравенства положительны, имеем право их отбросить, получаем:
Ответ:
Итак, мы рассмотрели решение показательно-степенных неравенств. Далее перейдем к изучению логарифмов.
Далее перейдем к изучению логарифмов.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интерне
- Mathematics-repetition.com (Источник).
- Matematika-10.blogspot.com (Источник).
- Matematika.uznateshe.ru (Источник).
Домашнее задание
1. Решить неравенства:
а) ; б) ;
в); г) ;
2. Решить неравенства:
Формула мощности
в физике, уравнение и примеры | Что такое уравнение мощности? — Видео и стенограмма урока
Научные курсы / Физика 111: Физика I Курс / Понимание работы, энергии и мощности Глава
Корали Неттлз, Мэтью Бергстрессер- Автор Корали Неттлз
Корали преподает физику в университете и обучает старшеклассников и студентов колледжей по STEM с 2012 года.
Посмотреть биографию Она имеет степень бакалавра наук и докторскую степень по физике Университета Ньюкасла. Она работала в университетах и школах трех разных стран.
Она имеет степень бакалавра наук и докторскую степень по физике Университета Ньюкасла. Она работала в университетах и школах трех разных стран. - Инструктор Мэтью Бергстрессер
Мэтью имеет степень магистра гуманитарных наук в области физического образования. Он преподавал химию и физику в средней школе в течение 14 лет.
Посмотреть биографию
Понять, что такое уравнение мощности. Узнайте, как найти мощность в физике, используя формулы мощности. Попрактикуйтесь на примерах расчета мощности в физике. Обновлено: 28.10.2021
Содержание
- Определение мощности в физике
- Примеры мощности в физике
- Краткое содержание урока
Создайте учетную запись, чтобы разблокировать этот урок
ПоказатьОпределение мощности в физике
Слово мощность — это то, что люди слышат каждый день во многих ситуациях. Но что такое мощность в физике? В физике мощность определяется как количество энергии, использованной или переданной за определенный промежуток времени. При приложении силы для перемещения объекта над объектом совершается работа. О власти можно думать в ряде различных ситуаций. Некоторые ситуации, когда можно рассчитать мощность, — это вождение автомобиля, бегущий человек и лошадь, тянущая телегу.
При приложении силы для перемещения объекта над объектом совершается работа. О власти можно думать в ряде различных ситуаций. Некоторые ситуации, когда можно рассчитать мощность, — это вождение автомобиля, бегущий человек и лошадь, тянущая телегу.
Рассмотрим пример: человек прикладывает силу горизонтально, чтобы переместить ящик на некоторое расстояние, как показано на диаграмме. Человек работает над ящиком, который зависит от величины силы и расстояния, на которое перемещается ящик.
В этом случае мощность представляет собой изменение работы в течение некоторого времени. Единица работы — джоуль (Дж), единица времени — секунды. Поэтому единицей мощности является джоуль в секунду, который известен как 9.0031 Вт (Вт). Итак, если человек в приведенном выше примере применяет ту же силу и перемещается на то же расстояние, но делает это за половину времени, сила удваивается. Если это займет у них вдвое больше времени, мощность уменьшится вдвое. Иными словами, то, что имеет более высокую номинальную мощность, использует или передает энергию за более короткий промежуток времени.
Если это займет у них вдвое больше времени, мощность уменьшится вдвое. Иными словами, то, что имеет более высокую номинальную мощность, использует или передает энергию за более короткий промежуток времени.
Какое уравнение для мощности?
Определение мощности приведено выше как работа, совершаемая в единицу времени. Но каково уравнение мощности? Есть несколько уравнений, которые можно использовать для расчета мощности. Первый из них называется 9.0031 уравнение рабочего времени и определяется как
{экв}P = Вт/т {/экв}
работа, выполненная за некоторое время, заданное {eq}t {/eq}. Это уравнение показывает, что чем быстрее можно выполнить работу, тем выше будет выходная мощность. Работу можно рассчитать, используя силу и расстояние в соответствии с формулой
{eq}W = Fd {/eq}
Предполагая, что сила и расстояние имеют одинаковое направление. Подставляя это в уравнение для мощности, получаем
{eq}P=Fd/t {/eq}
Это уравнение можно упростить, зная, что расстояние, деленное на время, является скоростью, при условии, что скорость постоянна. Это означает, что уравнение может быть записано как
Это означает, что уравнение может быть записано как
{eq}P=Fv {/eq}
Это известно как уравнение силы-скорости . Любое из этих уравнений можно использовать для расчета мощности в зависимости от известных значений. Также можно использовать уравнения вместе для решения различных задач.
Определение мощности и формулы
Сколько путей вы знаете, чтобы добраться от вашего дома до ближайшего продуктового магазина? Если один маршрут по какой-то причине заблокирован, то другой путь может привести вас туда, куда вам нужно. Эта аналогия применима к физике в том смысле, что несколько уравнений равны одному и тому же. Например, мощность можно рассчитать двумя разными способами. Давайте пройдемся по двум формулам мощности и поработаем с некоторыми примерами, используя эти формулы.
Мощность
Мощность — скорость использования энергии. Автомобильные двигатели работают, что позволяет автомобилю двигаться по дороге. Чем быстрее машина может выполнять работу, тем выше мощность. Автомобили с более высокой мощностью могут двигаться очень быстро. Первое уравнение для мощности — это работа, деленная на время, как вы можете видеть ниже.
Автомобили с более высокой мощностью могут двигаться очень быстро. Первое уравнение для мощности — это работа, деленная на время, как вы можете видеть ниже.
Единицей работы является джоуль, а время измеряется в секундах. Джоуль в секунду называется ваттом (или Вт), который является единицей измерения мощности. Работа — это точечный продукт силы и перемещения, который представлен как:
Если предположить, что сила и перемещение направлены в одном направлении, θ будет равно 0, что сводит уравнение к простому произведению силы и смещения. Подставив это в исходное уравнение мощности, мы получим:
Мы можем использовать это уравнение в другом направлении, точно так же, как мы можем пойти разными путями в продуктовый магазин, превратив перемещение во времени в скорость. Который, как вы можете видеть ниже, равен:
Который, как вы можете видеть ниже, равен:
Однако при использовании уравнения Fv есть одна загвоздка, заключающаяся в том, что скорость должна быть постоянной. Теперь, когда мы рассмотрели два уравнения для мощности, давайте воспользуемся ими для решения некоторых физических задач, связанных с мощностью.
Произошла ошибка при загрузке этого видео.
Попробуйте обновить страницу или обратитесь в службу поддержки.
Вы должны cСоздать учетную запись, чтобы продолжить просмотр
Зарегистрируйтесь, чтобы просмотреть этот урок
Вы студент или преподаватель?
Создайте свою учетную запись, чтобы продолжить просмотр
Как участник вы также получите неограниченный доступ к
уроки математики, английского языка, науки, истории и многое другое. Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Кроме того, получите практические тесты, викторины и индивидуальное обучение, которые помогут вам
преуспеть.
Получите неограниченный доступ к более чем 84 000 уроков.
Попробуй это сейчас
Настройка занимает всего несколько минут, и вы можете отменить ее в любое время.
Уже зарегистрированы? Войдите здесь для доступ
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня. Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Назад
Далее: Линейный импульс: определение, уравнение и примеры
пройти викторину Смотреть следующий урок
Повтор
Просто отмечаюсь.
 Вы все еще смотрите? Да! Продолжай играть.
Вы все еще смотрите? Да! Продолжай играть.Ваш следующий урок будет играть в 10 секунд
- 0:00 Определение мощности и формулы
- 1:46 Силовые сценарии
- 5:00 Итоги урока
Сохранять Сохранять Сохранять
Хронология
Автовоспроизведение
Автовоспроизведение
Скорость
Скорость
Примеры мощности в физике
Чтобы лучше понять мощность, полезно увидеть несколько примеров мощности в физике. Мощность можно рассчитать несколькими способами и использовать для расчета других величин, таких как скорость. Несколько примеров показаны ниже.
Мощность можно рассчитать несколькими способами и использовать для расчета других величин, таких как скорость. Несколько примеров показаны ниже.
Пример 1. Использование формулы мощности в физике
Вот пример использования формулы мощности. Рассмотрим приведенный выше пример, когда человек применяет силу для перемещения ящика. Человек прикладывает силу 7 Н и перемещает ящик на 3 м. Это занимает у человека 9 секунд. В чем сила человека?
Первым шагом является расчет работы. Это можно рассчитать по формуле
{экв}W = Fd {/экв}
Подстановка известных значений дает
{экв}W = (7N)(3m) {/экв}
Итак, работа { экв}W = 21 Дж {/экв}. Следующим шагом является расчет мощности в соответствии с уравнением рабочего времени для мощности, которое равно 9.0003
{eq}P = Вт/т {/eq}
Следовательно, мощность равна
{eq}P = 21 Дж/9 с {/eq}
Мощность человека составляет {eq}2,3 Вт {/ экв}.
Пример 2. Как найти степень в физике
Рассмотрим другой пример. Лифт может поднять человека и несколько ящиков общей массой 500 кг на второй этаж здания. Если лифт имеет номинальную мощность 1500 Вт, с какой скоростью он может перемещать человека и ящики?
Лифт может поднять человека и несколько ящиков общей массой 500 кг на второй этаж здания. Если лифт имеет номинальную мощность 1500 Вт, с какой скоростью он может перемещать человека и ящики?
F в числителе — это вес ящика (мг), а d в числителе — расстояние, на которое ящик был перемещен (ч). Это меняет наше уравнение на:
Это меняет наше уравнение на:
Подставляя эти значения, мы получаем ответ:
Это номинальная мощность робота в данном сценарии. Если бы он мог поднять эту массу на полку быстрее, его номинальная мощность была бы выше. Давайте посмотрим на другой пример.
Пример 2
Подсказка: мощность другого робота составляет 1000 Вт. Какую силу нужно приложить к массе 500 кг, чтобы сдвинуть ее со скоростью 3 м/с?
Решение: Поскольку этот сценарий включает в себя скорость и силу, мы будем использовать:
Решая для F , получаем:
Подстановка значения приводит к силе, прилагаемой роботом, которая составляет:
У нас есть еще один сценарий для работы. Давайте приступим!
Давайте приступим!
Пример 3
Подсказка: Спортсмен весом 65 кг участвует в соревнованиях. В одном случае он может использовать силу своей руки, чтобы поднять груз весом 25 кг на 0,5 метра за 0,3 секунды. Во втором случае он должен подняться по вертикальной веревке только руками. Как быстро он сможет подняться по веревке?
Решение: В этом сценарии нам нужно установить оба уравнения мощности равными друг другу и найти время. Первые шаги выглядят так:
Здесь:
- мА масса спортсмена
- vup скорость спортсмена, поднимающегося по канату
- mw масса гири
- hwl высота поднятия веса
- tl это время, необходимое для подъема веса
- g ускорение свободного падения
Мы можем отменить g с обеих сторон и найти vup , что даст:
Результат подстановки значений:
Другими словами, спортсмен поднялся по канату со скоростью 0,64 м/с.
Краткое содержание урока
Мощность — скорость использования энергии, единица измерения — джоуль в секунду или ватт (обозначается как Вт). Есть два уравнения для мощности с участием движущихся объектов.
Скорость в первом уравнении должна быть постоянной, чтобы ее можно было использовать. Использование каждого уравнения по отдельности или вместе позволяет нам решать множество физических задач, связанных с мощностью.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Определение мощности и формулы
Сколько путей вы знаете, чтобы добраться от вашего дома до ближайшего продуктового магазина? Если один маршрут по какой-то причине заблокирован, то другой путь может привести вас туда, куда вам нужно. Эта аналогия применима к физике в том смысле, что несколько уравнений равны одному и тому же. Например, мощность можно рассчитать двумя разными способами. Давайте пройдемся по двум формулам мощности и поработаем с некоторыми примерами, используя эти формулы.
Например, мощность можно рассчитать двумя разными способами. Давайте пройдемся по двум формулам мощности и поработаем с некоторыми примерами, используя эти формулы.
Мощность
Мощность — скорость использования энергии. Автомобильные двигатели работают, что позволяет автомобилю двигаться по дороге. Чем быстрее машина может выполнять работу, тем выше мощность. Автомобили с более высокой мощностью могут двигаться очень быстро. Первое уравнение для мощности — это работа, деленная на время, как вы можете видеть ниже.
Единицей работы является джоуль, а время измеряется в секундах. Джоуль в секунду называется ваттом (или Вт), который является единицей измерения мощности. Работа — это точечный продукт силы и перемещения, который представлен как:
Если предположить, что сила и перемещение направлены в одном направлении, θ будет равно 0, что сводит уравнение к простому произведению силы и смещения. Подставив это в исходное уравнение мощности, мы получим:
Подставив это в исходное уравнение мощности, мы получим:
Мы можем использовать это уравнение в другом направлении, точно так же, как мы можем пойти разными путями в продуктовый магазин, превратив перемещение во времени в скорость. Который, как вы можете видеть ниже, равен:
Однако при использовании уравнения Fv есть одна загвоздка, заключающаяся в том, что скорость должна быть постоянной. Теперь, когда мы рассмотрели два уравнения для мощности, давайте воспользуемся ими для решения некоторых физических задач, связанных с мощностью.
Power Scenarios
Пример 1
Вот наш первый пример, и вот наша подсказка:
Подсказка: Робот должен переместить 1000-килограммовый ящик с земли на полку на высоте 3 метра над полом. Робот может сделать это за 4 секунды. Какова номинальная мощность робота?
Робот может сделать это за 4 секунды. Какова номинальная мощность робота?
Вот наше решение:
Решение: Поскольку мы должны рассчитать мощность робота, нам нужно уравнение мощности. Поскольку у нас есть масса ящика, расстояние, на которое ящик был перемещен, и время, затраченное на его перемещение, мы будем использовать:
| . |
F в числителе — это вес ящика (мг), а d в числителе — расстояние, на которое ящик был перемещен (ч). Это меняет наше уравнение на:
Подставляя эти значения, мы получаем ответ:
Это номинальная мощность робота в данном сценарии. Если бы он мог поднять эту массу на полку быстрее, его номинальная мощность была бы выше. Давайте посмотрим на другой пример.
Пример 2
Подсказка: мощность другого робота составляет 1000 Вт. Какую силу нужно приложить к массе 500 кг, чтобы сдвинуть ее со скоростью 3 м/с?
Какую силу нужно приложить к массе 500 кг, чтобы сдвинуть ее со скоростью 3 м/с?
Решение: Так как этот сценарий включает в себя скорость и силу, мы будем использовать:
Решая для F , получаем:
Подстановка значения дает силу, приложенную роботом, а именно:
У нас есть еще один сценарий для работы. Давайте приступим!
Пример 3
Подсказка: Спортсмен весом 65 кг участвует в соревновании. В одном случае он может использовать силу своей руки, чтобы поднять груз весом 25 кг на 0,5 метра за 0,3 секунды. Во втором случае он должен подняться по вертикальной веревке только руками. Как быстро он сможет подняться по веревке?
Решение: В этом сценарии нам нужно установить оба уравнения мощности равными друг другу и найти время. Первые шаги выглядят так:
Первые шаги выглядят так:
Здесь:
- мА масса спортсмена
- vup скорость спортсмена, поднимающегося по канату
- mw масса гири
- hwl высота поднятия груза
- tl это время, необходимое для подъема веса
- g ускорение свободного падения
Мы можем отменить g с обеих сторон и найти vup , что даст:
Результат подстановки значений:
Другими словами, спортсмен поднялся по канату со скоростью 0,64 м/с.
Сводка урока
Мощность — это скорость использования энергии, а единица измерения — джоуль в секунду или ватт (обозначается как Вт). Есть два уравнения для мощности с участием движущихся объектов.
Скорость в первом уравнении должна быть постоянной, чтобы ее можно было использовать. Использование каждого уравнения по отдельности или вместе позволяет нам решать множество физических задач, связанных с мощностью.
Использование каждого уравнения по отдельности или вместе позволяет нам решать множество физических задач, связанных с мощностью.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свой аккаунт
Как рассчитать мощность в физике?
Мощность можно рассчитать двумя основными способами. Во-первых, разделить проделанную работу на время, затраченное на нее. Во-вторых, умножить силу на скорость.
Какова формула мощности в ваттах?
Формула мощности в ваттах определяется работой и временем. Формула P = W/t, где W — работа, выполненная за некоторое время t.
Формула мощности — уравнения с примерами
Большинству вещей вокруг нас для эффективной работы требуется определенная мощность. Здесь слово мощность используется для обозначения всего, что обеспечивает необходимую силу или энергию для правильной работы. Например, многие устройства, такие как мобильные телефоны, компьютеры, вентиляторы и т. Д., Работают от электричества, и если мы не зарядим аккумулятор нашего телефона, он выключится. Точно так же, если в доме нет электричества, вентилятор не может работать. Следовательно, электричество является источником энергии для таких устройств. Кроме того, эта сила может быть и в какой-то другой форме, например, в виде физических или человеческих ресурсов.
Здесь слово мощность используется для обозначения всего, что обеспечивает необходимую силу или энергию для правильной работы. Например, многие устройства, такие как мобильные телефоны, компьютеры, вентиляторы и т. Д., Работают от электричества, и если мы не зарядим аккумулятор нашего телефона, он выключится. Точно так же, если в доме нет электричества, вентилятор не может работать. Следовательно, электричество является источником энергии для таких устройств. Кроме того, эта сила может быть и в какой-то другой форме, например, в виде физических или человеческих ресурсов.
Преимущества формулы мощности
Формула мощности служит многим целям, например:
Формула мощности помогает определить работу, выполняемую конкретным объектом или человеком в определенное время.
Помогает определить, какой объект более эффективен, а какой менее эффективен.
 Например, если x и y выполняют одну и ту же задачу и x выполняет ее за 4 часа, а y выполняет ту же задачу за 6 часов. Это означает, что «х» более эффективен, чем «у». Это просто потому, что у x больше мощности, чем у.
Например, если x и y выполняют одну и ту же задачу и x выполняет ее за 4 часа, а y выполняет ту же задачу за 6 часов. Это означает, что «х» более эффективен, чем «у». Это просто потому, что у x больше мощности, чем у.Из приведенного примера также можно понять, как мощность может помочь в определении количества выполненной работы и в какое время она была совершена. И, зная об эффективности работы кого-то или чего-то, мы также можем сделать некоторые правильные выводы и решения в отношении того же самого.
Краткий обзор формул мощности.
Проще говоря, мощность чего угодно можно получить, разделив работу, которую выполнил объект, на время, затраченное объектом на выполнение этой работы. Это общая идея власти, есть много случаев, когда формула власти меняется.
Существует одна формула силы, называемая «законом Ома», названная в честь ученого, который дал эту формулу.
 Формула выглядит так: P = VI, и она приведена в главе книги, посвященной электричеству. В формуле P = VI, p обозначает мощность, V обозначает разность потенциалов, а I обозначает ток.
Формула выглядит так: P = VI, и она приведена в главе книги, посвященной электричеству. В формуле P = VI, p обозначает мощность, V обозначает разность потенциалов, а I обозначает ток.Закон Ома также имеет вариант, который выглядит как P = r × l2 или V2/R, это формула для электрической мощности. Здесь R — сопротивление, V — разность потенциалов, а l — ток.
Есть еще одна формула, которая называется уравнением механической мощности, или просто уравнением мощности. Формула P = E/t, где P означает мощность, E означает энергию, а t означает время в секундах. Эта формула гласит, что мощность – это потребление энергии в единицу времени.
Есть много других формул мощности, которые вы можете легко найти в PDF-файле, который Vedantu предоставляет бесплатно.
Если мы посмотрим вокруг себя, мы обнаружим несколько вещей, которые требуют энергии для запуска или работы. Эта сила может быть чем угодно в виде электричества, физических, человеческих ресурсов и т. д. Основная повестка дня остается прежней: способность выполнять работу в определенное время.
Эта сила может быть чем угодно в виде электричества, физических, человеческих ресурсов и т. д. Основная повестка дня остается прежней: способность выполнять работу в определенное время.
Формулу пороха можно определить как работу, выполненную любым конкретным объектом или источником за заданное время.
Предположим, что два человека A и B выполняют одну и ту же задачу, но A закончил ее раньше B, тогда что это значит?
Это просто означает, что A более эффективен, чем B, и эффективность прямо пропорциональна мощности, поэтому мы можем сказать, что A эффективнее, чем B. Это именно то, что представляет собой мощность, она определяется как работа, выполненная телом в данное время.
Мощность = Работа, выполненная объектом или телом / Общее затраченное время.
Формула мощности различается в соответствии с требуемыми формулировками, например, она может быть разной для силовых объектов, а также может отличаться для электронных устройств.
Формула мощности для различных отношений и единиц измерения:
P = VI
Эта формула мощности взята из главы об электричестве. Формула дана великим ученым по имени Ом, и эта формула названа в его честь и также известна как закон Ома.
Утверждается, что мощность прямо пропорциональна разности потенциалов проводника. Здесь P обозначает мощность, V обозначает разность потенциалов, а I обозначает ток. Единицей СИ является ватт. Единицей измерения V является вольт, а для I — столбец.
Формула электрической мощности
P = R × I2 или V2 / R: Эти формулы являются вариантом закона Ома. Здесь R обозначает сопротивление, V обозначает разность потенциалов, а I обозначает ток.
В нем указано, что мощность прямо пропорциональна квадрату разности потенциалов и обратно пропорциональна сопротивлению проводника.
Уравнение мощности
P = E/t: Эту формулу также называют уравнением механической мощности. Здесь E обозначает энергию в джоулях, а t обозначает время в секундах.
Здесь E обозначает энергию в джоулях, а t обозначает время в секундах.
Эта формула гласит, что потребление энергии в единицу времени называется мощностью.
P = w/t
Это самая распространенная и основная формула силы, о которой мы узнали очень рано. Эта формула получена из теоремы работы-энергии.
В нем говорится, что работа, совершаемая в единицу времени, называется мощностью. Здесь W обозначает работу в джоулях, а t обозначает время в секундах.
P = F × s/t
В этой формуле F обозначает силу, приложенную к объекту, s обозначает перемещение объекта, а t обозначает общее время.
В нем говорится, что общее время, затрачиваемое объектом на перемещение из одного места в другое при приложении к нему внешней силы, называется мощностью.
Формула силы различна для разных полей, как указано выше, но смысл ее остается практически одинаковым для всех.
NCERT Тематические решения для всех классов
Вывод некоторых формул мощности:2 × R
Или,
P = V × V / R
P = V2 / R. (отсюда доказано)
Здесь
P = Сила объекта или тела.
В = Разность потенциалов между двумя концами проводника.
I = ток, протекающий по цепи.
R = сопротивление провода.
Формула мощности
P = F × s/t
Как мы знаем,
Мощность = работа за время
P = w/t
Работа = сила (F) × перемещение (с)0003
P = F × s/t
Здесь
P = мощность.
F = Сила, приложенная к телу.
Вт = работа, совершаемая телом.
t = общее время.
с = полное перемещение тела.
Преимущества формулы мощности — уравнения с примерами.
В предмете науки уравнения играют жизненно важную роль, и поэтому уравнения должны пониматься лучше. Потому что только запоминание уравнений не поможет учащимся лучше понять концепцию электричества.
Со стороны примеров служит иллюстрацией уравнений. То есть с помощью примеров уравнения можно понять на более глубоком уровне.
Как рассчитать электрическую мощность и энергию
Электрическая мощность – это скорость выполнения работы. (См. также: Что такое работа, энергия и мощность?) Электроэнергия — это скорость, с которой электричество работает или дает энергию. Единицей мощности в СИ является ватт, один джоуль в секунду.
Электроэнергия обычно вырабатывается электрическими генераторами, но также может обеспечиваться электрическими батареями. Электроэнергия обычно продается электрическими компаниями в киловатт-часах (3,6 МДж), что представляет собой произведение мощности в киловаттах на время работы в часах. Электроэнергетические компании измеряют мощность с помощью счетчика электроэнергии, который ведет учет электроэнергии, поставленной потребителю.
Электроэнергия обычно продается электрическими компаниями в киловатт-часах (3,6 МДж), что представляет собой произведение мощности в киловаттах на время работы в часах. Электроэнергетические компании измеряют мощность с помощью счетчика электроэнергии, который ведет учет электроэнергии, поставленной потребителю.
Определение и уравнения для мощности
Электрическая мощность — это скорость выполнения работы, измеряемая в ваттах и обозначаемая буквой P. Термин «ваттность» используется для обозначения «электрической мощности в ваттах». Электрическая мощность в ваттах, производимая электрическим током I, состоящим из заряда Q кулонов, каждые t секунд, проходящего через разность электрических потенциалов (напряжений) V, равна:
P = работа, совершаемая в единицу времени = VQ/t = (В)(I) или мощность = напряжение x ток или вольты x ампер
где: Q — электрический заряд в кулонах, t — время в секундах, I — электрический ток в амперах, а V — электрический потенциал или напряжение в вольтах
Электрическая энергия
Электрическая энергия = мощность x время. Общее количество потребляемой электроэнергии зависит от общей мощности, используемой всеми вашими электрическими устройствами, и общего времени их использования в вашем доме.
Общее количество потребляемой электроэнергии зависит от общей мощности, используемой всеми вашими электрическими устройствами, и общего времени их использования в вашем доме.
Электрическая энергия измеряется в киловатт-часах
Энергия = мощность x время или киловатт-часы = киловатты x часы
Один киловатт-час равен 1000 ваттам мощности, используемой в течение одного часа.
Как рассчитать стоимость электроэнергии
Из Con Ed Bill — «Мы измеряем вашу электроэнергию тем, сколько киловатт-часов ((кВтч) вы используете. Один киловатт-час зажжет 100-ваттную лампочку в течение 10 часов». «В 2015 году среднегодовое потребление электроэнергии бытовым потребителем коммунальных услуг в США составило 10 812 киловатт-часов (кВтч), в среднем 901 кВтч в месяц . В Луизиане было самое высокое годовое потребление электроэнергии — 15 435 кВтч на одного бытового потребителя, а на Гавайях — 6166 кВтч на одного бытового потребителя». -кондиционер на 10 часов подряд?0003
-кондиционер на 10 часов подряд?0003
ДАННЫЕ ИЗ СЧЕТА NYC CON ED 2017
Очень многое нужно для понимания того, за что вы платите. Существует не только стоимость топлива, но и стоимость доставки, сборы за различные услуги и налоги.
Чтобы объяснить это, мы используем реальный счет Con Ed за небольшую квартиру в Нью-Йорке с помощью Con Edison.
ВАШИ ПЛАТЫ ЗА ЭЛЕКТРИЧЕСТВО
От Con Edison:
Электроэнергия, которую вы использовали в течение этого 30-дневного расчетного периода с 03 января 2013 г. по 02 февраля 2017 г.
Мы измеряем вашу электроэнергию по тому, сколько киловатт-часов (кВтч) вы используете.
Один киловатт-час зажжет 100-ваттную лампочку в течение 10 часов.
February 02,17 actual reading 95175 kWh
Jan 03 , 17 actual reading 94838 kWh
Your electricity use was therefore 337 kWh
YOUR SUPPLY /CHARGES — were 337 kWh @0.
 5282c/kwh (это плата за электроэнергию, поставляемую вам Con Ed = 18,83 долл. США
5282c/kwh (это плата за электроэнергию, поставляемую вам Con Ed = 18,83 долл. США Плата за функции продавца — плата, связанная с получением кредита на электроэнергию и деятельностью, связанной со сбором = 1,41 долл. США
GRT и другие налоги = 0,48 долл. США
Общая плата за поставку = 20,52 долл. США
центов за кВт/ч, что составляет 6 центов.ОПЛАТА ДОСТАВКИ
Базовая плата за обслуживание 16,38 долл. США
Это изменение базовой инфраструктуры системы и услуг, связанных с клиентами, включая учет клиентов, снятие показаний счетчиков и техническое обслуживание счетчиков.
Доставка 337 кВтч @11,0208 центов/кВтч = $37,14
Это плата за обслуживание системы, через которую Con ed поставляет вам электроэнергию.
Изменение системной выгоды из расчета 0,6706 центов/кВтч = 2,26 доллара США
Это возмещает расходы, связанные с деятельностью в области экологически чистой энергии, проводимой New York STate Energy Research Associate введено государством
GRT and other surcharges $2. 87
87
Total delivery charges $69.5
YOUR SALES TAX @4.5000% collected on behalf of NY State = $3.58
YOUR TOTAL ELECTRICITY CHARGES IS $63.15
ОБРАЗЕЦ ВОПРОСА:
Какова плата за поставку для работы холодильника мощностью 600 Вт в течение 24 часов (во время использования) по цене 0,06 цента/кВтч? Примечание. Холодильники не работают непрерывно.
Решение: Энергия = Мощность x Время = 600 Вт x 24 часа = 14,4 кВтч x 0,06 цента/кВтч = 864 цента = 8,64 $
Проверьте свои Понимание: 1.
Какое из этих утверждений неверно
а) мощность можно выразить как работу, совершаемую в единицу времени
б) Энергия может быть выражена как мощность x время
c) Единицами измерения мощности являются киловатты в час 9. 0534
d) Мощность может быть описана в единицах Вольт x Ампер = Ватт
0534
d) Мощность может быть описана в единицах Вольт x Ампер = Ватт
2.
В 2015 году среднее потребление электроэнергии составило около 90 175 90 534.
а) 1901 кВтч в месяц
б) 10 081 кВтч в месяц
в) 337 кВтч в месяц
г) 901 кВтч в месяц
3.
Сколько энергии потребляет фен мощностью 1000 Вт, который используется в течение 10 минут подряд ?
а) 1000 ватт х 10 минут = 10 кВтч
б) 1000 Вт/10 мин = 100 кВт/ч
в) 1000 Вт x 10 минут = 100 000 кВтч
г) ничего из вышеперечисленного
4. Какова стоимость использования фена мощностью 1000 Вт в течение 10 минут подряд при стоимости 6 центов/кВтч
а) 6 центов
б) 60 центов
в) $6
г) ничего из вышеперечисленного
5. Какова будет стоимость доставки того же фена при стоимости доставки 11 центов/кВтч
Какова будет стоимость доставки того же фена при стоимости доставки 11 центов/кВтч
а) 1,10 доллара
б) 11 центов
в)
1,10 доллара США
Функция POWER в Excel (формула, примеры)
В математике у нас были показатели степени, степени для заданного основного числа. В Excel у нас есть аналогичная встроенная функция, известная как функция СТЕПЕНЬ, которая используется для вычисления мощности данного числа или основания. Чтобы использовать эту функцию, мы можем использовать ключевое слово =POWER( в ячейке и указать два аргумента, один как число, а другой как мощность.
Например, предположим, что основание 4 возведено в степень 3, т. е. 4 куба. =4*4*4 = 64.
СТЕПЕНЬ в Excel — это математическая/тригонометрическая функция, которая вычисляет и возвращает результат возведения числа в степень. Функция POWER Excel принимает два аргумента: основание (любое действительное число) и показатель степени (степень , означающая, сколько раз данное число будет умножено само на себя) . Например, 5, умноженное на степень 2, равно 5 х 5.
Например, 5, умноженное на степень 2, равно 5 х 5.
Содержание
- Степень в Excel
- Формула функции СТЕПЕНЬ
- Объяснение функции СТЕПЕНЬ в Excel
- Как использовать функцию СТЕПЕНЬ в Excel
- МОЩНОСТЬ в Excel, пример № 3
- МОЩНОСТЬ в Excel, пример № 4
- Рекомендуемые статьи
Формула функции МОЩНОСТЬ
Объяснение функции МОЩНОСТЬ в Excel
Функция СТЕПЕНЬ в Excel принимает оба аргумента как числовое значение. Следовательно, передаваемые аргументы имеют целочисленный тип, где число является базовым числом, а СТЕПЕНЬ — показателем степени. Оба аргумента являются обязательными и необязательными.
Мы можем использовать функцию СТЕПЕНЬ в Excel разными способами, например, для математических операций. Например, мы можем использовать уравнение функции СТЕПЕНЬ для вычисления реляционных алгебраических функций.
Как использовать функцию POWER в Excel
92 (=POWER(10,2)Теперь, выбрав значения x и y из диапазона B4:K5, выберите график (в этом примере мы выбрали график рассеяния с плавными линиями) из «Вставить
Таким образом, мы получаем линейный экспоненциальный график для заданного уравнения функции СТЕПЕНЬ. 0, где x неизвестен, а a, b и c — коэффициенты.Решение этого уравнения функции СТЕПЕНЬ дает корни уравнения, которые являются значениями x.
0, где x неизвестен, а a, b и c — коэффициенты.Решение этого уравнения функции СТЕПЕНЬ дает корни уравнения, которые являются значениями x.
Корни квадратного уравнения функции СТЕПЕНИ вычисляются по следующей математической формуле:
- x = (-b+ (b 2 -4ac) 1/2 )/2a
- x = (-b+ (b 2 -4ac) b- (b 2 -4ac) 1/2 )/2a
b2-4ac называется дискриминантом и описывает число корней уравнения квадратичной функции POWER.
Теперь у нас есть список уравнений квадратичной функции СТЕПЕНИ, приведенный в столбце A. Но сначала нам нужно найти корни уравнений. 92.
У нас есть пять квадратичных уравнений функции СТЕПЕНЬ, и мы будем решать их, используя формулу с помощью функции СТЕПЕНЬ в Excel, чтобы найти корни.
В первом уравнении функции СТЕПЕНЬ a=4, b=56 и c = -96. Если мы решим их математически, используя приведенную выше формулу, мы получим корни -15,5 и 1,5.
Чтобы реализовать это в формуле Excel, мы будем использовать функцию POWER в Excel, и формула будет:
- = ((-56+POWER(POWER(56,2)-(4*4*(-9)3)),1/2)))/(2*4) даст первый корень и
- = ((-56-СТЕПЕНЬ(СТЕПЕНЬ(56,2)-(4*4*(-93) ),1/2)))/(2*4) даст второй корень уравнения
Итак, полная формула будет,
=»Корни уравнений»&» «&(( -56+МОЩНОСТЬ(МОЩНОСТЬ(56,2)-(4*4*(-93)),1/2)))/(2*4)&” , “&((-56-МОЩНОСТЬ(МОЩНОСТЬ(56) ,2)-(4*4*(-93)),1/2)))/(2*4)
Формулы объединяются строкой «Корни уравнения».
Используя ту же формулу для других уравнений функции СТЕПЕНЬ, мы имеем:
Вывод:
СТЕПЕНЬ в Excel Пример №3
Итак, мы можем использовать функцию СТЕПЕНЬ в Excel для различных математических расчетов.
Предположим, нам нужно определить сложный процент. Сложный процент. Сложный процент — это процент, начисляемый на сумму основной суммы и общего процента, начисленного на нее до сих пор.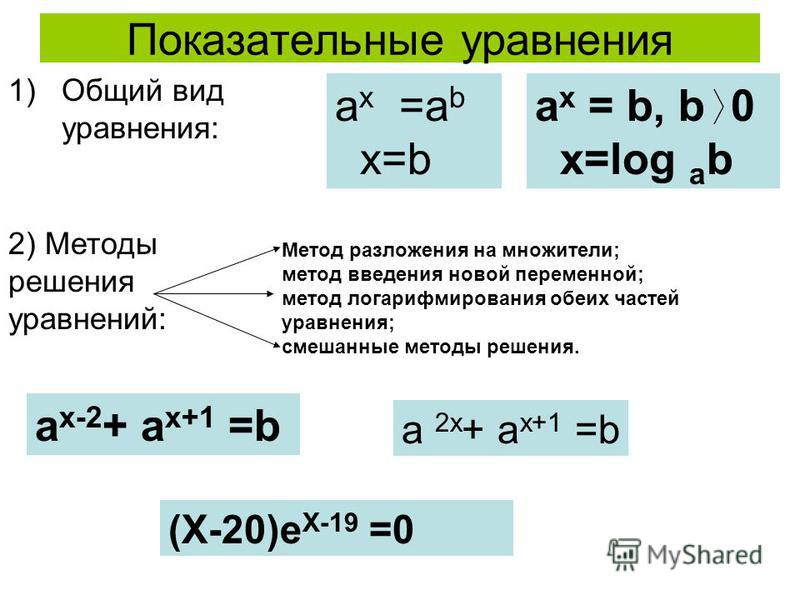 Он играет решающую роль в получении более высокой прибыли от инвестиций. Подробнее, для которых формула:
Он играет решающую роль в получении более высокой прибыли от инвестиций. Подробнее, для которых формула:
Сумма = Основная сумма (1 + r/n) nt
- Где r — процентная ставка, n — количество начислений процентов в год, а t — время.
- Если сумма в размере 4000 долларов США депонирована на счет (сберегательный) с процентной ставкой 5% годовых, ежемесячно начисляемой на сложные проценты, стоимость инвестиции через 5 лет может быть рассчитана с использованием приведенной выше формулы сложных процентов.
- Когда основная сумма = 4000 долларов США, ставка = 5/100, т. е. 0,05, n = 12 (ежемесячное начисление сложных процентов), время = 5 лет.
У нас есть формула, использующая формулу сложных процентов и реализующая ее в формуле Excel с помощью функции POWER.
=B2*(POWER((1+(B3/B5)),(B4*B5)))
Таким образом, баланс инвестиций через 5 лет составляет 5 133,43 доллара США.
СИЛА в Excel Пример № 4
Согласно закону тяготения Ньютона, два тела на расстоянии r от их центра тяжести притягиваются друг к другу во Вселенной в соответствии с формулой гравитационной СИЛА Excel.
F = (G*M*m)/r 2
Когда F — величина гравитационной силы, G называется гравитационной постоянной, M — масса первого тела, m — масса второго второго тела, а r — расстояние между телами от их центра тяжести. 930 будет представлено как 1,98*степень (10,30), аналогично другим значениям.
Так как значение, полученное как сила, является большим числом, Excel выразил его научной записьюExcel выразил ее научной записьюВ Excel научная запись — это особый стиль записи чисел в научной и экспоненциальной формах. Экспоненциальная запись помогает компактно отображать значения, позволяя нам сравнивать и использовать их в расчетах.Подробнее. Чтобы преобразовать его в дробь, измените формат на дробь.
Вывод:
Итак, Солнце притягивает Землю с силой 3522
83107
0000 Ньютон.

Рекомендуемые статьи
Эта статья представляет собой руководство по функции POWER в Excel. Здесь мы обсуждаем формулу POWER в Excel и способы использования функции POWER Excel, а также примеры Excel и загружаемые шаблоны Excel. Вы также можете посмотреть на эти полезные функции в Excel: –
- Excel против AccessExcel против. AccessExcel и Access — два самых мощных инструмента Microsoft для анализа данных и создания отчетов, но между ними есть существенные различия. Excel — более старый продукт Microsoft, тогда как Access — самый продвинутый и сложный продукт Microsoft. В Excel очень легко создавать информационные панели и формулы, тогда как в Access очень легко создавать базы данных и соединения.Подробнее
- GetPivotData в Excel
- НЕ Функция
19.4 Электроэнергия | Техасский шлюз
Цели обученияПрактические задачиПроверьте свое понимание
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Дать определение электрической мощности и описать уравнение электрической мощности
- Расчет электрической мощности в цепях резисторов последовательно, параллельно и комплексно
Энергия у многих ассоциируется с электричеством. Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи являются наглядными примерами электроснабжения. Мы также используем электроэнергию, чтобы заводить автомобили, компьютеры или освещать дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность – это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это значит, но и какие факторы определяют электрическую мощность.
Для начала давайте подумаем об лампочках, которые часто характеризуются номинальной мощностью в ваттах. Сравним лампочку мощностью 25 Вт с лампочкой мощностью 60 Вт (см. рис. 19.23). Хотя оба работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходная мощность электрической цепи определяется не напряжением, а чем-то иным.
Лампы накаливания, такие как две, показанные на рис. 19.23, по существу представляют собой резисторы, которые нагреваются, когда через них проходит ток, и нагреваются настолько, что излучают видимый и невидимый свет. Таким образом, две лампочки на фотографии можно рассматривать как два разных резистора. В простой цепи, такой как лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, как и напряжение, должен определять мощность.
Рис. 19.23 Слева — лампочка мощностью 25 Вт, справа — лампочка мощностью 60 Вт. Почему их выходная мощность различна, несмотря на то, что они работают на одном и том же напряжении?
Формулу мощности можно найти с помощью размерного анализа. Рассмотрим единицы мощности. В системе СИ мощность выражается в ваттах (Вт), что представляет собой энергию в единицу времени, или Дж/с
19,47 Вт=Джс.Вт=Джс.
Вспомним теперь, что напряжение — это потенциальная энергия на единицу заряда, а это означает, что единицы напряжения составляют Дж/Кл
19. 48В=JC.V=JC.
48В=JC.V=JC.
Мы можем переписать это уравнение как J=V×CJ=V×C и подставить его в уравнение для ватт, чтобы получить
W=Js=V×Cs=V×Cs.W=Js=V×Cs=V ×Сс.
Но кулон в секунду (Кл/с) — это электрический ток, который мы можем видеть из определения электрического тока, I=ΔQΔtI=ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или
Р=IV. Р=IV.
Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .
Например, рассмотрим схему на рис. 19.24. По закону Ома ток, протекающий через цепь, равен
19,49I=VR=12 В100 Ом=0,12 A.I=VR=12 В100 Ом=0,12 А. VI=(12 В)(0,12 А)=1,4 Вт.P=VI=(12 В)(0,12 А)=1,4 Вт.
Куда уходит эта мощность? В этой схеме мощность идет в основном на нагрев резистора в этой цепи.
Рис. 19.24 Простая схема, потребляющая электроэнергию.
При расчете мощности в цепи на рис. 19.24 мы использовали сопротивление и закон Ома для определения силы тока. Закон Ома дает ток: I=V/RI=V/R, который мы можем подставить в уравнение для электрической мощности, чтобы получить
P=IV=(VR)V=V2RP.P=IV=(VR)V= В2Р.
Мощность определяется только напряжением и сопротивлением.
Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности только через ток и сопротивление. Если мы запишем закон Ома как V=IRV=IR и используйте это, чтобы устранить В в уравнении P=IVP=IV получаем
P=IV=I(IR)=I2R.P=IV=I(IR)=I2R.
Мощность определяется только током и сопротивлением.
Таким образом, комбинируя закон Ома с уравнением P=IVP=IV для электрической мощности, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — наоборот, конденсаторы либо хранят электроэнергию, либо отдают ее обратно в цепь.
Обратите внимание, что в выражения для электрической мощности входят только сопротивление (а не емкость или что-то еще), ток и напряжение. Это означает, что физической характеристикой цепи, которая определяет, сколько мощности она рассеивает, является ее сопротивление. Любые конденсаторы в цепи не рассеивают электроэнергию — наоборот, конденсаторы либо хранят электроэнергию, либо отдают ее обратно в цепь.
Чтобы понять, как связаны между собой напряжение, сопротивление, ток и мощность, рассмотрите рис. 19.25, на котором показано колесо формулы . Величины в центральной четверти окружности равны количествам в соответствующей внешней четверти окружности. Например, чтобы выразить потенциал V через мощность и ток, мы видим из круга формул, что V=P/IV=P/I.
Рис. 19.25 Колесо формул показывает, как соотносятся вольты, сопротивление, ток и мощность. Количества во внутренних четвертях кругов равны количествам в соответствующих внешних четвертях кругов.
Рабочий пример
Найдите сопротивление лампочки
Типичная старая лампочка накаливания имела мощность 60 Вт. Если предположить, что на лампочку подается напряжение 120 В, какова сила тока через лампочку?
СТРАТЕГИЯ
Нам известны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P=IVP=IV, чтобы найти ток I , протекающий через лампочку.
Решение
Решение P=IVP=IV для тока и подстановка заданных значений напряжения и мощности дает
19,51P=IVI=PV=60 W120 V=0,50 A.P=IVI=PV=60 W120 V=0,50 A.
Таким образом, через лампочку проходит полампера, когда на нее подается напряжение 120 В.
Обсуждение
Это значительный ток. Напомним, что бытовая электроэнергия является переменным, а не постоянным током, поэтому 120 В, подаваемые из бытовых розеток, представляют собой переменную, а не постоянную мощность. 120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.
120 В — это фактически усредненная по времени мощность, выдаваемая такими розетками. Таким образом, средний ток, проходящий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.
Пример работы
Грелки для ботинок
Чтобы согреть ботинки в холодные дни, вы решили вшить в стельку ботинок схему с несколькими резисторами. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите питать их от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны оказывать на каждую стельку?
СТРАТЕГИЯ
Мы знаем желаемую мощность и напряжение (18 В, потому что у нас есть две 9-вольтовые батареи, соединенные последовательно), поэтому мы можем использовать уравнение P=V2/RP=V2/R, чтобы найти необходимое сопротивление .
Решение
Решая P=V2/RP=V2/R для сопротивления и подставляя данные напряжения и мощности, мы получаем
19,52P=V2RR=V2P=(18 V)210 W=32 Ω. P=V2RR =V2P=(18 В)210 Вт=32 Ом.
P=V2RR =V2P=(18 В)210 Вт=32 Ом.
Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.Ом.
Обсуждение
Давайте посмотрим, какой ток будет проходить через эту цепь. У нас есть напряжение 18 В, приложенное к сопротивлению 32 Ом, поэтому закон Ома дает0003
Все аккумуляторы имеют этикетки, на которых указано, сколько заряда они могут обеспечить (в пересчете на ток, умноженный на время). Типичная щелочная батарея 9 В может обеспечить заряд 565 мА⋅чмА⋅ч. (таким образом, две батареи 9 В обеспечивают 1130 мА⋅чмА⋅ч), поэтому эта система отопления будет работать в течение времени
19,54t=1130×10−3 A⋅ч0,56 A=2,0 ч.t=1130×10−3 А⋅ч0,56 А=2,0 ч.
Рабочий пример
Мощность через ветвь цепи
Сопротивление каждого резистора в схеме ниже составляет 30 Ом. Какая мощность рассеивается на средней ветви цепи?
СТРАТЕГИЯ
Средняя ветвь схемы содержит последовательно соединенные резисторы R3 и R5R3 и R5. Напряжение на этой ветви равно 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем, используя P=V2/RP=V2/R, найдем мощность, рассеиваемую в ветви.
Напряжение на этой ветви равно 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем, используя P=V2/RP=V2/R, найдем мощность, рассеиваемую в ветви.
Решение
Эквивалентное сопротивление равно Rmiddle=R3+R5=30 Ω+30 Ω=60 ΩRmiddle=R3+R5=30 Ω+30 Ω=60 Ω. Мощность, рассеиваемая средней ветвью цепи, составляет
19,55Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.Pmiddle=V2Rmiddle=(12 В)260 Ом=2,4 Вт.
Обсуждение
Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, выдаваемой батареей. Во-первых, эквивалентное сопротивление левой ветви равно
19,56Rleft=11/R1+1/R2+R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом. Rleft=11/R1+1/R2 +R4=11/30 Ом+1/30 Ом+30 Ом=45 Ом.
Мощность через левую ветвь
19,57Pleft=V2Rleft=(12 В)245 Ом=3,2Вт.Pleft=V2Rleft=(12 В)245 Ом=3,2 Вт. эквивалентное сопротивление равно Rright=R6=30 ΩRright=R6=30 Ω. Мощность через правую ветвь равна
19,58Pright=V2Rright=(12 В)230 Ом=4,8Вт. Pright=V2Rright=(12 В)230 Ом=4,8 Вт
Pright=V2Rright=(12 В)230 Ом=4,8 Вт
Полная мощность, рассеиваемая цепью, представляет собой сумму мощностей, рассеиваемых в каждой ветви .
19.59P=Pleft+Pmiddle+Pright=2.4 W+3.2 W+4.8 W=10.4 WP=Pleft+Pmiddle+Pright=2.4 W+3.2 W+4.8 W=10.4 Вт
Мощность батареи составляет
19.60P=IV.P=IV.
, где I — общий ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить я . Ответвления вносят токи
19,61Ileft=VRleft=12 V45 Ω=0,2667 AImiddle=VRmiddle=12 V60 Ω=0,20 AIright=VRright=12 V30 Ω=0,40 AIleft=VRleft=12 V45 Ω=0,40 A.Ileft=VRleft=12 V05 6Ω=6Ω 12 V60 Ω=0,20 AIright=VRright=12 V30 Ω=0,40 A. =0,2667 A+0,20 A+0,40 A=0,87 A.
и мощность, обеспечиваемая аккумулятором, равна
19,63P=IV=(0,87 A)(12 В)=10,4 W.P=IV=(0,87 A)(12 В)=10,4 Вт.
Это та же мощность, которая рассеивается на резисторах цепи, что показывает сохранение энергии в этой цепи.
Практические задания
Какова формула для мощности, рассеиваемой на резисторе?
- Формула мощности, рассеиваемой на резисторе: P=IV.P=IV.
- Формула мощности, рассеиваемой на резисторе: P=VI.P=VI.
- Формула мощности, рассеиваемой на резисторе: P = IV .
- Формула для мощности, рассеиваемой на резисторе: P = I 2 В .
Какова формула для мощности, рассеиваемой резистором, при заданном его сопротивлении и напряжении на нем?
- Формула для мощности, рассеиваемой на резисторе: P=RV2P=RV2
- Формула мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула для мощности, рассеиваемой на резисторе: P=V2RP=V2R
- Формула для мощности, рассеиваемой на резисторе: P=I2RP=I2R
Проверьте свое понимание
Упражнение 8
Какие элементы схемы рассеивают мощность?
- конденсаторы
- катушки индуктивности
- идеальные переключатели
- резисторы
Упражнение 9
Объясните словами уравнение для мощности, рассеиваемой на данном сопротивлении.
- Электрическая мощность пропорциональна току через резистор, умноженному на квадрат напряжения на резисторе.
- Электрическая мощность пропорциональна квадрату тока через резистор, умноженному на напряжение на резисторе.
- Электрическая мощность пропорциональна току через резистор, деленному на напряжение на резисторе.
- Электрическая мощность пропорциональна току через резистор, умноженному на напряжение на резисторе.
- Печать
- Поделиться
Вывод уравнения мгновенной мощности
Ключевые выводы
Понять, что такое мгновенная мощность.

Узнайте, как выводится уравнение мгновенной мощности в цепях постоянного и переменного тока.
Исследуйте разницу между мгновенной мощностью и средней мощностью.
Что такое мгновенная мощность?
В физике мощность определяется количеством энергии, переданной за определенный период времени. Между тем, мгновенная мощность относится к мощности, потребляемой в конкретный момент времени. Мгновенная мощность является важным показателем в электронике. Это позволяет разработчику прогнозировать способность компонентов справляться с энергопотреблением. Это также позволяет разработать модуль питания, способный обеспечить необходимую мощность в любой конкретный момент использования.
Мощность в электронике часто выражается как произведение напряжения и силы тока. Поэтому мгновенная мощность в электронике — это измерение обоих параметров в конкретный момент времени. Получение уравнения мгновенной мощности зависит от типа схемы, с которой вы работаете. Не существует универсальной формулы, которая работает для всех цепей.
Получение уравнения мгновенной мощности зависит от типа схемы, с которой вы работаете. Не существует универсальной формулы, которая работает для всех цепей.
Ниже приведена формула мощности. Это будет описывать такие вещи, как механическая мощность, коэффициент мощности в электронике, полная мощность и общая электрическая энергия. Ваш расчет мощности должен быть как можно более точным в наш век повышения энергоэффективности, и поэтому вы должны быть уверены, что у вас не только есть правильное уравнение энергии, но и что вы начинаете с правильного распределения ампер, мгновенного напряжения и потенциальной энергии, чтобы получить реальную мощность вашего устройства.
Это будет описывать такие вещи, как механическая мощность, коэффициент мощности в электронике, полная мощность и общая электрическая энергия. Ваш расчет мощности должен быть как можно более точным в наш век повышения энергоэффективности, и поэтому вы должны быть уверены, что у вас не только есть правильное уравнение энергии, но и что вы начинаете с правильного распределения ампер, мгновенного напряжения и потенциальной энергии, чтобы получить реальную мощность вашего устройства.
Как вывести уравнение мгновенной мощности
Выражение мгновенной мощности в цепи постоянного тока.
Уравнение мгновенной мощности полезно при анализе цепи постоянного тока. Он обеспечивает точное представление о том, сколько энергии подается на нагрузку в любой момент времени. Знание мгновенной мощности позволяет реализовать надлежащие стратегии управления тепловым режимом.
Причина, по которой не существует универсального уравнения для мгновенной мощности, заключается в том, что электроника питается от источника постоянного или переменного тока. Рассмотрим простую замкнутую цепь, состоящую из источника постоянного тока и резистора. Он будет иметь стабильный, ровный уровень напряжения, что приводит к одинаково постоянному току.
Рассмотрим простую замкнутую цепь, состоящую из источника постоянного тока и резистора. Он будет иметь стабильный, ровный уровень напряжения, что приводит к одинаково постоянному току.
Для цепи постоянного тока уравнение мгновенной мощности довольно простое и представлено следующим уравнением:
P = V x I.
Уравнение мгновенной мощности для цепи постоянного тока также может быть выражено следующим образом:
Однако расчет уравнения мгновенной мощности для цепи переменного тока не так прост. В цепи переменного тока уровень напряжения не является постоянной величиной. Вместо этого и напряжение, и ток представляют собой изменяющиеся во времени синусоидальные волны.
Таким образом, уравнение мгновенной мощности для цепи переменного тока выражается следующим образом:
Первая составляющая (VI cosθ) представляет среднюю мощность, а вторая составляющая указывает изменяющуюся во времени характеристику уравнения.
Мгновенная мощность в сравнении со средней мощностью
Средняя мощность является лучшим представлением потребляемой мощности в цепи переменного тока.
Как бы полезно это ни было для цепей постоянного тока, уравнение мгновенной мощности совершенно бессмысленно для цепи переменного тока. Это потому, что значение всегда меняется в зависимости от времени. Тот факт, что вы рассчитали 1 Вт при T = 0,5 с, не означает, что отдаваемая мощность будет такой же при T = 0,7 с.
Другими словами, мгновенное значение мощности не даст точного представления о том, сколько энергии вырабатывается и потребляется в цепи переменного тока. Для практических целей вам понадобится среднее значение мощности, которое лучше отражает мощность, рассеиваемую в цепи переменного тока.
Средняя мощность определяется по формуле:
И V, и I являются среднеквадратичными (RMS) значениями напряжения и тока. θ представляет фазовый угол между напряжением и током. Средняя мощность не только дает более точную картину количества энергии, потребляемой в цепи, но и ее легче включить в расчеты.
θ представляет фазовый угол между напряжением и током. Средняя мощность не только дает более точную картину количества энергии, потребляемой в цепи, но и ее легче включить в расчеты.
В то время как электрические цепи на самом деле не слишком часто имеют дело со скоростью, понимание силы, действующей за вашим двигателем и вашими PDN, имеет важное значение для принципов проектирования электроэнергии. Используйте правильную формулу мощности, чтобы найти правильную энергию в вашей системе электроснабжения, чтобы обеспечить поддержание напряжения, и вы не остались в неведении относительно таких вещей, как падение напряжения, активная мощность, смещение или выходная мощность. Ваша электрическая цепь для ваших продуктов заслуживает наилучших смоделированных шансов на достижение их пиковой мощности, когда и как вам это нужно.
Теперь, когда вы знаете, как выводится уравнение мгновенной мощности для различных типов цепей, вы захотите построить их с помощью сложного программного обеспечения для проектирования и анализа печатных плат.




 Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение.
Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение.
 , Просвещение, 2007 – 112 с.
, Просвещение, 2007 – 112 с.
 1.
Решение логарифмических уравнений
1.
Решение логарифмических уравнений
 Автозапчасти в наличии
Автозапчасти в наличии Она имеет степень бакалавра наук и докторскую степень по физике Университета Ньюкасла. Она работала в университетах и школах трех разных стран.
Она имеет степень бакалавра наук и докторскую степень по физике Университета Ньюкасла. Она работала в университетах и школах трех разных стран.
 Эти уравнения можно использовать для решения задач, связанных с мощностью. Примеры, представленные в этом уроке, показывают, как можно рассчитать мощность в таких ситуациях, как перемещение тяжелых предметов по горизонтали и вертикали. Они также показали, как мощность связана с работой, силой и скоростью.
Эти уравнения можно использовать для решения задач, связанных с мощностью. Примеры, представленные в этом уроке, показывают, как можно рассчитать мощность в таких ситуациях, как перемещение тяжелых предметов по горизонтали и вертикали. Они также показали, как мощность связана с работой, силой и скоростью. Например, если x и y выполняют одну и ту же задачу и x выполняет ее за 4 часа, а y выполняет ту же задачу за 6 часов. Это означает, что «х» более эффективен, чем «у». Это просто потому, что у x больше мощности, чем у.
Например, если x и y выполняют одну и ту же задачу и x выполняет ее за 4 часа, а y выполняет ту же задачу за 6 часов. Это означает, что «х» более эффективен, чем «у». Это просто потому, что у x больше мощности, чем у. Формула выглядит так: P = VI, и она приведена в главе книги, посвященной электричеству. В формуле P = VI, p обозначает мощность, V обозначает разность потенциалов, а I обозначает ток.
Формула выглядит так: P = VI, и она приведена в главе книги, посвященной электричеству. В формуле P = VI, p обозначает мощность, V обозначает разность потенциалов, а I обозначает ток.