Решение задач логических онлайн: Математическая логика · oнлайн с подробным объяснением

Решение задач по логике – онлайн примеры и образцы с ответами

Логика изучает абстрактное мышление как средство постижения мира, исследует формы и законы, по которым мир отражается в процессе мышления. Логика является философской дисциплиной и связана с теорией познания. Логика является философской дисциплиной и связана с теорией познания, поскольку процесс восприятия мира полностью изучается философией, а логика изучает лишь один из аспектов когнитивного мышления.

Логика происходит от греческого слова «логос», что означает «мысль», «слово», «причина» или «закономерность». Это слово используется, во-первых, для обозначения набора правил, которым должен следовать процесс мышления, и, во-вторых, для обозначения науки о правилах рассуждения и формах, в которых они осуществляются. Изучение мышления. Но мышление изучается не только логикой, но и различными другими науками, такими как психология, кибернетика, педагогика и т.д., каждая из которых изучает тот или иной аспект мышления.

Законы логики объективны и действуют независимо от воли или желания человека. Они имеют универсальный характер, заключающийся в том, что во все исторические периоды люди мыслят по одним и тем же законам. Законы, изучаемые в формальной логике, — это закон тождества, закон непротиворечия, закон достаточного основания и закон исключенной трети.

Если у вас нет времени на выполнение заданий по логике, вы всегда можете попросить меня, пришлите задания мне в whatsapp, и я вам помогу онлайн или в срок от 1 до 3 дней.

Ответы на вопросы по заказу заданий по логике:

Сколько стоит помощь?

• Цена зависит от объёма, сложности и срочности. Присылайте любые задания по любым предметам — я изучу и оценю.

Какой срок выполнения?

• Мне и моей команде под силу выполнить как срочный заказ, так и сложный заказ. Стандартный срок выполнения – от 1 до 3 дней. Мы всегда стараемся выполнять любые работы и задания раньше срока.

Если требуется доработка, это бесплатно?

• Доработка бесплатна. Срок выполнения от 1 до 2 дней.

Могу ли я не платить, если меня не устроит стоимость?

• Оценка стоимости бесплатна.

Каким способом можно оплатить?

• Можно оплатить любым способом: картой Visa / MasterCard, с баланса мобильного, google pay, apple pay, qiwi и т.д.

Какие у вас гарантии?

• Если работу не зачли, и мы не смогли её исправить – верну полную стоимость заказа.

В какое время я вам могу написать и прислать задание на выполнение?

• Присылайте в любое время! Я стараюсь быть всегда онлайн.

Ниже размещён теоретический и практический материал, который вам поможет разобраться в предмете «Логика«, если у вас есть желание и много свободного времени!

Содержание:

1. Ответы на вопросы по заказу заданий по логике:
2. Логические операции над высказываниями
3. Конъюнкция (логическое умножение)
4. Дизъюнкция (логическое сложение)
5. Импликация
6. Эквиваленция
7. Задача 1
8. Решение:
9. Задача 2
10. Решение:
11. Задача 3
12. Решение:
13. Задача 4
14. Решение:
15. Задача 5
16. Решение:
17. Задача 6
18. Решение:
19. Задача 7
20. Решение:
21. Задача 8
22. Решение:
23. Задача 9
24. Решение:
25. Задача 10
26. Решение:

Основным (неопределяемым) понятием математической логики является понятие «простого высказывания».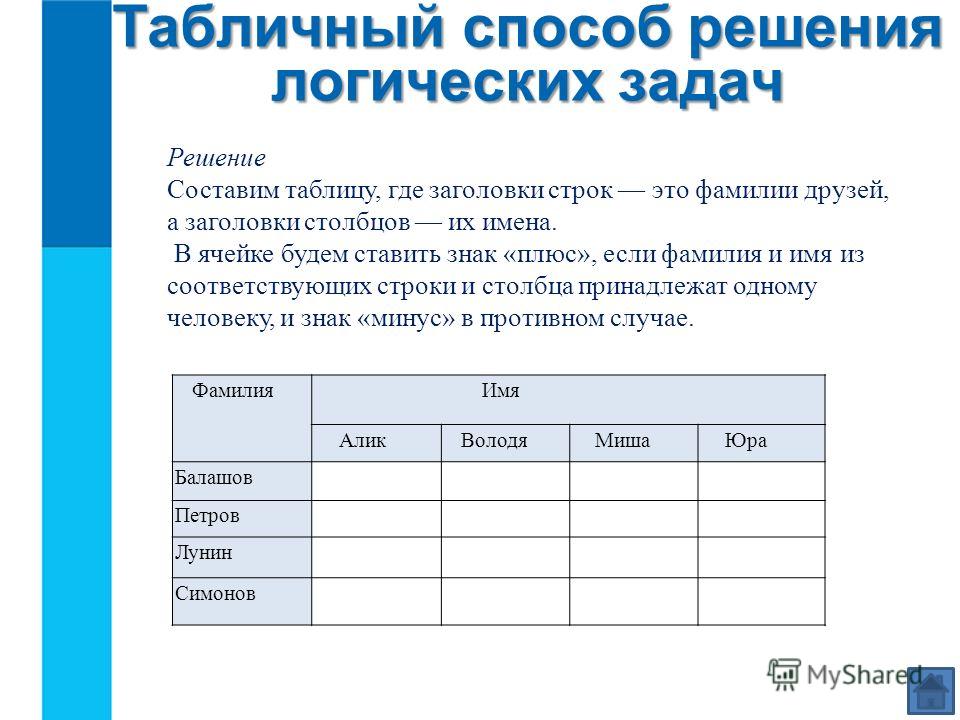 Под высказыванием обычно понимают всякое повествовательное предложение, утверждающее что-либо о чем-либо, и при этом мы можем сказать, истинно оно или ложно в данных условиях места и времени. Логическими значениями высказываний являются «истина» и «ложь».

Приведем примеры высказываний.

• 1) Новгород стоит на Волхове.
• 2) Париж — столица Англии.
• 3) Карась не рыба.
• 4) Число 6 делится на 2 и на 3.
• 5) Если юноша окончил среднюю школу, то он получает аттестат зрелости.

Высказывания 1), 4), 5) истинны, а высказывания 2) и 3) ложны. Очевидно, предложение «Да здравствуют наши спортсмены!» не является высказыванием. Высказывание, представляющее собой одно утверждение, принято называть простым или элементарным. Примерами элементарных высказываний могут служить высказывания 1) и 2).

Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если …, то…», «тогда и только тогда», принято называть сложными или составными. Так, высказывание 3) получается из простого высказывания «Карась — рыба» с помощью отрицания «не», высказывание 4) образовано из элементарных высказываний «Число 6 делится на 2», «Число 6 делится на 3», соединенных союзом «и». Высказывание 5) получается из простых высказываний «Юноша окончил среднюю школу», «Юноша получает аттестат зрелости» с помощью грамматической связки «если …, то …». Аналогично сложные высказывания могут быть получены из простых высказываний с помощью грамматических связок «или», «тогда и только тогда». В алгебре логики все высказывания рассматриваются только с точки зрения их логического значения, а от их житейского содержания отвлекаются. Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.

В дальнейшем будем элементарные высказывания обозначать малыми буквами латинского алфавита: истинное значение высказывания — буквой или цифрой 1, а ложное значение — буквой или цифрой 0. Если высказывание а истинно, то будем писать а если ложно, то

Возможно, вас также заинтересует эта ссылка:

Контрольная работа по логике заказать

Логические операции над высказываниями

1. Отрицание. Отрицанием высказывания называется новое высказывание, которое является истинным, если высказывание ложно, и ложным, если высказывание истинно. Отрицание высказывания обозначается и читается «не » или «неверно, что ». Логические значения высказывания можно описать с помощью таблицы

Таблицы такого вида принято называть таблицами истинности. Пусть высказывание. Так как также является высказыванием, то можно образовать отрицание высказывания , то есть высказывание которое называется двойным отрицанием высказывания . Ясно, что логические значения высказываний и совпадают. Например, для высказывания «Река Волхов вытекает из озера Ильмень» отрицанием будет высказывание «Неверно, что река Волхов вытекает из озера Ильмень» или «Река Волхов не вытекает из озера Ильмень», а двойным отрицанием будет высказывание «Неверно, что река Волхов не вытекает из озера Ильмень»

Возможно, вас также заинтересует эта ссылка:

Помощь по логике онлайн

Конъюнкция (логическое умножение)

Конъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если оба высказывания истинны, и ложным, если хотя бы одно из них ложно. Конъюнкция высказываний обозначается символом или читается Высказывания называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:

Например, для высказываний «6 делится на 2», «6 делится на 3» их конъюнкцией будет высказывание «6 делится на 2 и 6 делится на 3», которое, очевидно, истинно.

Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний. Из определения операции конъюнкции и отрицания ясно, что высказывание всегда ложно.

Возможно, вас также заинтересует эта ссылка:

Курсовая работа по логике заказать готовую онлайн

Дизъюнкция (логическое сложение)

Дизъюнкцией двух высказываний называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Дизъюнкция высказываний обозначается символом читается Высказывания называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:

Например, высказывание «В треугольнике угол или угол острый» истинно, так как обязательно истинно хотя бы одно из высказываний: «В треугольнике угол острый», «В треугольнике угол острый». В повседневной речи союз «или» употребляется в различном смысле: исключающем и не исключающем. В алгебре логики союз «или» всегда употребляется в не исключающем смысле. Из определения операции дизъюнкции и отрицания ясно, что высказывание всегда истинно.

Возможно, вас также заинтересует эта ссылка:

РГР по логике расчетно графическая работа

Импликация

Импликацией двух высказываний называется новое высказывание, которое считается ложным, если истинно, а — ложно, и истинным во всех остальных случаях. Импликация высказываний обозначается символом читается «если то » или «из следует ». Высказывание называют условием или посылкой, высказывание — следствием или заключением, высказывание — следованием или импликацией.

Логические значения операции импликации описываются следующей таблицей истинности:

Например, высказывание «Если число 12 делится на 6, то оно делится на 3», очевидно, истинно, так как здесь истинна посылка «Число 12 делится на 6» и истинно заключение «Число 12 делится на 3». Употребление слов «если то …» в алгебре логики отличается от употребления их в обыденной речи, где мы, как правило, считаем, что, если высказывание ложно, то высказывание «Если , то » вообще не имеет смысла. Кроме того, строя предложение вида «если , то » в обыденной речи, мы всегда подразумеваем, что предложение вытекает из предложения . Употребление слов «если …, то …» в математической логике не требует этого, поскольку в ней смысл высказываний не рассматривается. Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «Если , то ».

Если при этом известно, что истинно и доказана истинность импликации то мы вправе сделать вывод об истинности заключения .

Возможно, вас также заинтересует эта ссылка:

Задачи по логике с решением

Эквиваленция

Эквиваленцей (или эквивалентностью) двух высказываний называется новое высказывание, которое считается истинным, когда оба высказывания либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний обозначается символом , читается «для того, чтобы , необходимо и достаточно, чтобы » или « тогда и только тогда, когда ». Высказывания называются членами эквиваленции.

Задача 1

Существуют ли три таких высказывания чтобы одновременно выполнялись для них следующие условия:

• Решение:

Из первого условия, по определению дизъюнкции, следует, что и т.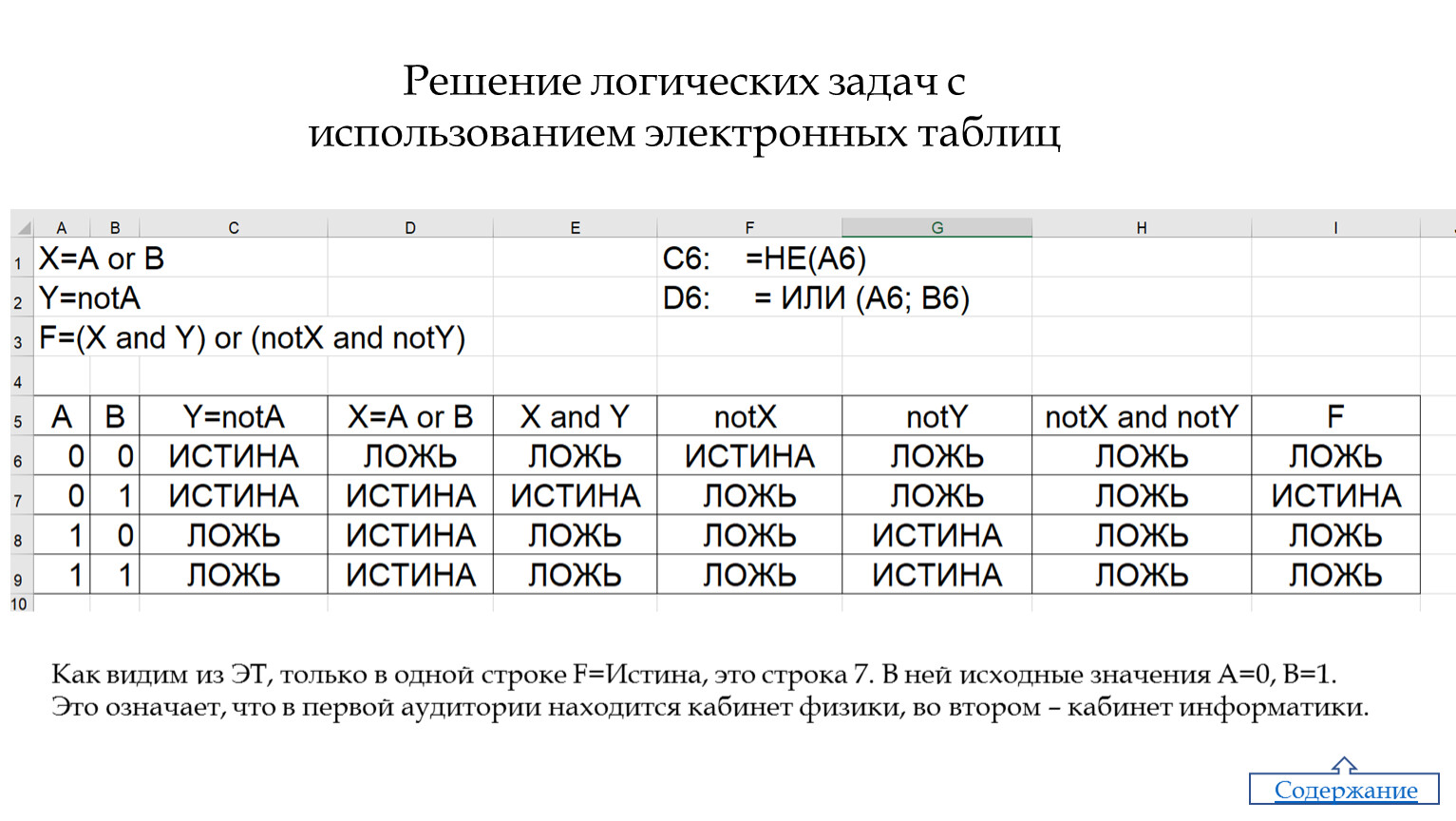 е. Тогда второе данное условие, по определению импликации, влечет Отсюда Следовательно, что противоречит третьему данному условию. Значит, трех высказываний удовлетворяющих данным условиям, не существует.

Задача 2

Следующие составные высказывания расчлените на простые и запишите символически, введя буквенные обозначения для простых их составляющих: а) Если число делится на 2 и не делится на 3, то оно не делится на 6. б) Произведение трех чисел равно нулю тогда и только тогда, когда одно из них равно нулю. в) Если производная функции в точке равна нулю и вторая производная этой функции в той же точке отрицательна, то данная точка есть точка локального максимума функции. г) Если прямая параллельна каждой из двух пересекающихся плоскостей, то она параллельна и линии их пересечения. д) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и прямые и не параллельны (утверждение ), то прямая перпендикулярна всякой прямой лежащей в плоскости (утверждение ).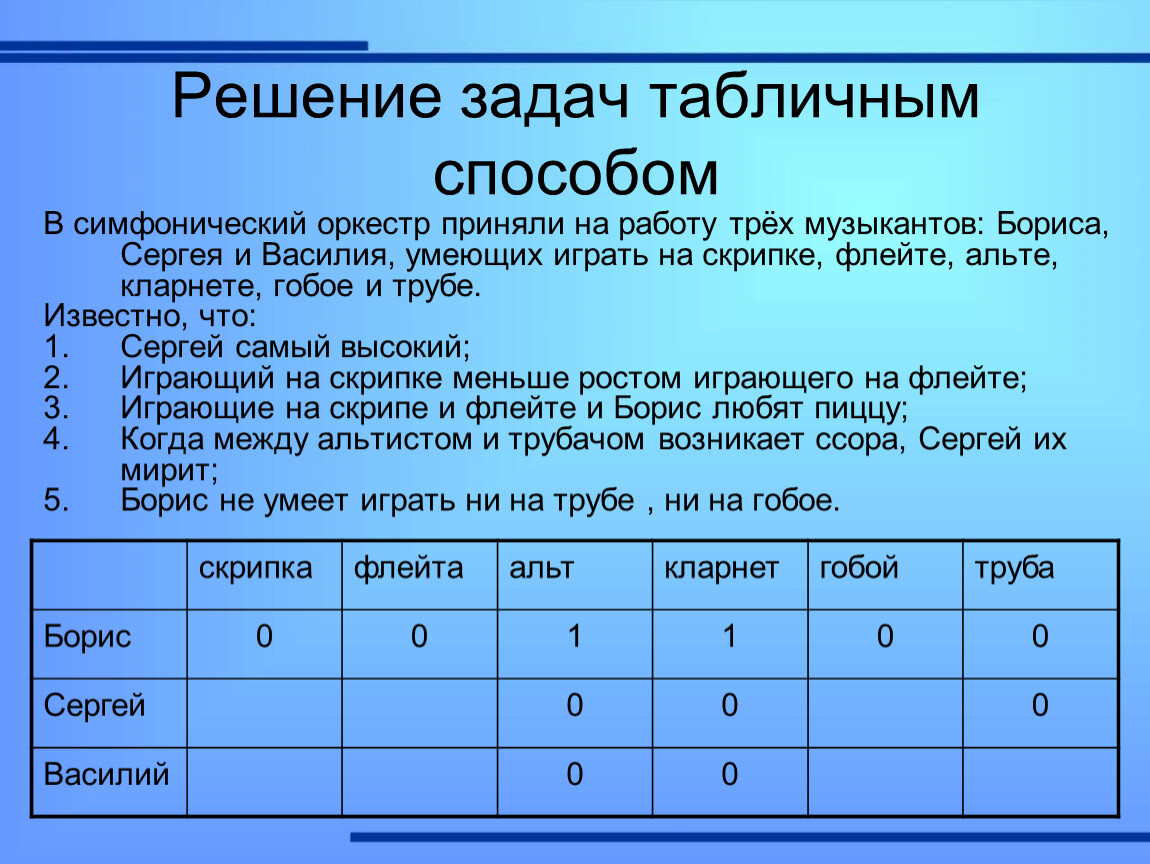

е) Если прямая перпендикулярна двум прямым и лежащим в плоскости (утверждение ), и неперпендикулярна некоторой прямой лежащей в этой же плоскости (утверждение ), то прямые и параллельны ( — утверждение ). ж) Если две прямые и лежащие в плоскости , непараллельны (утверждение ) и прямая неперпендикулярна некоторой прямой лежащей в плоскости (утверждение ), то неперпендикулярна одной из прямых или (утверждение ). з) Если какие-либо два из трех векторов коллинеарны, то их смешанное произведение равно нулю и) Логарифм некоторого положительного числа будет положительным, если основание логарифма и логарифмируемое число будут больше 1 или если основание логарифма и логарифмируемое число будут заключены между 0 и 1. к) Если в параллелограмме не все углы прямые или не все стороны равны между собой, то этот параллелограмм не прямоугольник или не ромб. л) Если в треугольнике любая его медиана не является высотой и биссектрисой, то этот треугольник не равнобедренный и не равносторонний.

• Решение:

Выделим и следующим образом обозначим простейшие составляющие высказывания: А: «В треугольнике некоторая его медиана является высотой»; В: «В треугольнике некоторая его медиана является биссектрисой»; С: «Этот треугольник равнобедренный»; D: «Этот треугольник равносторонний». Тогда данное высказывание символически записывается так: будут формулами. Далее, формулами будут выражения Наконец выражение представляющее собой данную последовательность, также является формулой.

Задача 3

В следующей последовательности символов всевозможными способами расставьте скобки так, чтобы получилась формула:

• Решение:

л) Вот эти формулы (внешние скобки опущены):

Задача 4

Составьте таблицы истинности для следующих формул и укажите, какие из формул являются выполнимыми, какие — опровержимыми, какие — тождественно истинными (тавтологиями), какие — тождественно ложными (противоречиями):

• Решение:

Пользуясь определениями логических связок (операций над высказываниями), составим таблицу истинности данной формулы (логические значения этой формулы записаны в последнем столбце таблицы, где сама формула обозначена

Из построенной таблицы истинности видно, что данная формула выполнима, так как если, например, вместо пропозициональной переменной вставить в формулу ложное высказывание, а вместо — истинное, то вся формула превратится в истинное высказывание. Но эта формула является также и опровержимой, поскольку если, например, вместо пропозициональной переменной вставить в формулу истинное высказывание, а вместо переменной — ложное, то вся формула превратится в ложное высказывание. Следовательно, формула не является ни тавтологией, ни тождественно ложной формулой.

Возможно, вас также заинтересует эта ссылка:

• Решение задач

Задача 5

Докажите, что следующие формулы выполнимы, не составляя для них таблиц истинности, а указав какие-нибудь значения входящих в них пропозициональных переменных, при которых эти формулы обращаются в истинные высказывания:

• Решение:

л) Заключение второй импликации есть, очевидно, тождественно ложная формула. Поэтому если посылка второй импликации превратится при некоторой подстановке в ложное высказывание, то эта импликация станет истинным высказыванием и, следовательно, вся данная импликация превратится в истинное высказывание независимо от того, в какое высказывание обратится посылка всей данной импликации.

Посылка второй импликации обращается в ложное высказывание, когда вместо переменных и подставляются ложные высказывания.

Итак, данная формула выполнима, поскольку она обращается в истинное высказывание, если вместо и подставить ложные высказывания, а вместо — произвольное высказывание (его истинностное значение в данном случае не повлияет на истинностное значение всего высказывания).

Задача 6

Выясните, справедливы ли следующие утверждения (если утверждение несправедливо, то постарайтесь определить, обе его части «тогда» и «только тогда» не выполняются или только одна): а) тогда и только тогда, когда б) тогда и только тогда, когда в) тогда и только тогда, когда г) тогда и только тогда, когда д) тогда и только тогда, когда е) тогда и только тогда, когда ж) тогда и только тогда, когда з) тогда и только тогда, когда и) тогда и только тогда, когда к) тогда и только тогда, когда л) тогда и только тогда, когда м) тогда и только тогда, когда

• Решение:

л) Данное утверждение в полном объеме несправедливо: неверна его часть «тогда» (необходимость). Для подтверждения этого нужно указать такие конкретные формулы и чтобы по меньшей мере одна из них не была тавтологией, а формула тавтологией была бы. Вот пример таких формул: Ни одна из них не является тавтологией, но формула — тавтология. Еще пример: Проверьте, что этот пример действительно опровергает необходимость данного утверждения. Приведите самостоятельно аналогичный пример. Рассмотрим теперь часть «только тогда» (достаточность) данного утверждения. Оказывается, она верна. В самом деле, предположим, что и Это означает, что для любых высказываний высказывания будут истинными. Следовательно, для любых высказываний истинным будет и высказывание А это означает, что формула является тавтологией, т.е. м) Покажем, что данное утверждение справедливо. Необходимость. Пусть Следовательно, формула тождественно ложна. Но тогда, ввиду определения дизъюнкции, тождественно ложны обе формулы и А раз так, то отрицание каждой из этих формул будет всегда принимать лишь истинные значения, т. е. Докажите достаточность самостоятельно: убедитесь, что каждый логический шаг, сделанный при доказательстве необходимости, может быть проделан в обратном направлении.

Задача 7

Докажите, что справедливы следующие логические следования, руководствуясь определением этого понятия: Выясните, будут ли верны обратные следования, т.е. будет ли формула, стоящая слева, логическим следствием формулы, стоящей справа.

• Решение:

л) (Изучите сначала ход решения задачи 1.35, м.) Составим таблицу истинности для формул и участвующих в отношении следования:

Последовательный просмотр по строкам столбцов () и () показывает, что как только в какой-либо строке столбца () появляется 1, так сейчас же в этой строке и в столбце () обнаруживается 1. Значит, требуемое логическое следование действительно выполняется (алгоритм см. в Учебнике, с. 55). Обратное же следование неверно, поскольку, например, в первой же строке (т.е. при ) формула принимает значение 1 (столбец ()), а формула тем не менее принимает значение 0 (столбец ()).

Задача 8

Следующие формулы преобразуйте равносильным образом так, чтобы отрицание было отнесено только к пропозициональным переменным и не стояло перед скобками:

• Решение:

л) Проделаем требуемые равносильные преобразования:

Задача 9

Каждую из формул предыдущей задачи преобразуйте равносильным образом так, чтобы она содержала только логические связки

• Решение:

л) Воспользуемся результатом равносильных преобразований данной формулы, выполненных в предыдущей задаче, и продолжим преобразования для решения данной задачи:

Задача 10

Для каждой из следующих систем высказываний найдите логически эквивалентную ей, но более простую систему высказываний, если известно, что в данной системе по меньшей мере одно высказывание истинно:

• Решение:

л) По меньшей мере одно из высказываний данной совокупности будет истинным тогда и только тогда, когда истинна дизъюнкция всех этих высказываний. Поэтому, составив дизъюнкцию из данных высказываний и приведя ее с помощью равносильных преобразований к дизъюнкции более простого вида, можно получить более простую систему высказываний, эквивалентную данной. В нашем случае имеем следующую дизъюнкцию, которую затем упрощаем: Следовательно, по меньшей мере одно высказывание из данной системы будет истинным тогда и только тогда, когда будет истинным одно из высказываний или Поэтому данная система трех высказываний логически эквивалентна более простой системе из двух высказываний

Возможно, вас также заинтересует эта ссылка:

Заказать работу по логике помощь в учёбе

Логические задачи • Arzamas

У вас отключено выполнение сценариев Javascript. Измените, пожалуйста, настройки браузера.

Детская комната ArzamasМатериалы

Материалы

Arzamas для занятий со школьниками! Подборка материалов для учителей и родителей

Всё, чем можно заняться на онлайн-уроке или просто так

Мультфильмы — победители фестивалей. Часть 2

Сказки, притчи, эксперименты и абсурд

Путеводитель по Ясной Поляне

Любимая скамейка Льва Толстого, теплица, конюшня и другие места музея-усадьбы писателя, которые стоит посмотреть с детьми

Детские стихи обэриутов

Хармс, Введенский, Заболоцкий и Владимиров о котах, тиграх, рыбаках и мальчиках по имени Петя

Мигранты: как бороться за свои права с помощью музыки

Хип-хоп, карнавал, говорящие барабаны и другие неочевидные способы

Старые пластинки: сказки народов мира

Слушаем и разбираем японские, итальянские, скандинавские и русские сказки

Видео: командир МКС спрашивает ученого о космосе

Лекция на высоте 400 километров

Как снять фильм

Фильм ужасов, комедия и мелодрама в домашних условиях

Самые необычные техники анимации

VR, мультфильмы из солнечных зайчиков, киселя и специй

Поиграйте на ударных инструментах мира

Узнайте, как устроены гонг, маримба и барабан, и соберите свой оркестр

Как поставить спектакль

Театр теней, читка и другие варианты домашнего спектакля для детей

Советские ребусы

Разгадайте детские ребусы 1920–70-х годов

22 мультфильма для самых маленьких

Что смотреть, если вам нет шести

От «Дикой собаки динго» до «Тимура и его команды»

Что нужно знать о главных советских книгах для детей и подростков

Путеводитель по детской поэзии ХХ века

От Агнии Барто до Михаила Яснова: детские стихи на русском языке

10 книг художников

Страницы из кальки — миланский туман, а переплет — граница между реальностью и фантазией

Как выбрать современную детскую книжку

«Как „Пеппи“, только про любовь»: объясняем новые книги через старые

Словесные игры

«Шляпа», «телеграммы», «МПС» и другие старые и новые игры

Игры из классических книг

Во что играют герои произведений Набокова, Линдгрен и Милна

Пластилиновая анимация: российская школа

От «Пластилиновой вороны» до пластилиновой «Сосиски»

Мультфильмы — победители фестивалей

«Смелая мама», «Мой странный дедушка», «Очень одинокий петух» и другие

Нон-фикшн для детей

Как бьется сердце кита, что внутри ракеты и кто играет на диджериду — 60 книг о мире вокруг

Путеводитель по зарубежной популярной музыке

200 артистов, 20 жанров и 1000 песен, которые помогут разобраться в музыке 1950–2000-х

Мультфильмы по стихотворениям

Стихи Чуковского, Хармса, Гиппиус и Яснова в российской анимации

Домашние игры

Театр теней, поделки и бумажные куклы из детских книг и журналов XIX–XX веков

Книжки для самых маленьких

Современная литература от 0 до 5: читать, разглядывать, учиться

Кукольная анимация: российская школа

«Влюбчивая ворона», «Чертенок № 13», «Лёля и Минька» и другие старые и новые мультфильмы

Умные раскраски

Музеи и библиотеки предлагают разрисовать свои коллекции

Репринты и переиздания детских книг

Любимые сказки, повести и журналы прошлого века, которые снова можно купить

Что можно услышать в классической музыке

Шаги по льду, голос кукушки и звуки ночного леса в великих композициях XVIII–XX веков

Советские познавательные мультфильмы

Архимед, динозавры, Антарктида и космос — научно‑популярные мультфильмы в СССР

Логические задачи

Разрешите спор мудрецов, сделайте из рубашки птицу и правильно посчитайте котят

Современные детские рассказы

Лучшие короткие истории про бабушек, котов, шпионов и рыцарей

Как устроены русские колыбельные

Объясняем, чем страшен волчок и почему нельзя ложиться на краю. Бонус: 5 колыбельных группы «Наадя»

Музыкальные сказки

Как Чайковский, Римский-Корсаков и Прокофьев работают с сюжетами детских сказок

Армянская школа анимации

Самые бунтарские мультфильмы Советского Союза

Коллекция мультфильмов Дины Годер

Программный директор Большого фестиваля мультфильмов советует, что посмотреть с ребенком

Мультфильмы про искусство

Как рассказать детям о Пикассо, Поллоке и Татлине с помощью анимации

40 загадок обо всем на свете

Что жжет без огня и у кого в носу решето: загадки из «Чижа», «Ежа» и книг Маршака и Чуковского

Дворовые игры

«Светофор», «Штандер», «Колечко» и другие игры для большой компании

Стихи, которые интересно учить наизусть

Что выбрать, если задали выучить стихотворение про маму, Новый год или осень

Старые аудиоспектакли для детей

«Оле-Лукойе», «Серая Шейка», «Золушка» и другие интересные советские записи

Мультфильмы с классической музыкой

Как анимация работает с музыкой Чайковского, Верди и Гласса

Как устроены детские считалки

«Энэ, бэнэ, раба, квэнтэр, мантэр, жаба»: что всё это значит

Разрешите спор мудрецов, сделайте из рубашки птицу и правильно посчитайте котят — Arzamas вместе с проектом «Тогда» предлагает подумать над занимательными задачками XX века

Подготовили Илья Старков, Ася Терехова

Детская комната

Шел Кондрат
В Ленинград,
А навстречу — двенадцать ребят.
У каждого по три лукошка,
В каждом лукошке — кошка,
У каждой кошки — двенадцать котят.
У каждого котенка
В зубах по четыре мышонка.
И задумался старый Кондрат:
«Сколько мышат и котят
Ребята несут в Ленинград?»

Ответ

Глупый, глупый Кондрат!
Он один и шагал в Ленинград,
А ребята с лукошками,
С мышами и кошками
Шли навстречу ему —
В Кострому.

Корней Чуковский.
«Ёж», № 1, 1928

Коля нарисовал барабан и на нем букву Е, потом он сказал Зине:

— Напиши на бумаге, что здесь написано.

— Написала, — сказала Зина через две минуты.

— Теперь, — сказал Коля, — попробуй прочесть наоборот — справа налево.

— Прочла, — медленно читая, ответила Зина. И вдруг закричала:

— Смотри, Коля, то же самое получилось!

— Так и должно быть, — сказал Коля. — Это придумал я!

Какие три слова написала Зина? Они читаются одинаково с обеих сторон.

Ответ

Е на барабане

«Чиж», № 3, 1930

У двух шоферов есть брат Андрей, а у Андрея братьев нет. Как же это так?

Ответ

Шоферы — сестры

«Мурзилка», № 5, 1942

Элизабет, Лиззи,
Бэтси и Бэсс
Весною с корзинкой
Отправились в лес.
В гнезде на березе,
Где не было птиц,
Нашли они пять
Розоватых яиц.
Но всем четверым
По яичку досталось,
И все же четыре на месте осталось.

Ответ

Хоть разные
Названы здесь имена
(Элизабет, Лиззи,
Бэтси и Бэсс),
Но так называлась
Девчонка одна.
Она и ходила с корзинкою в лес.

Перевод английской загадки Самуила Маршака.
«Мурзилка», № 1, 1960

Назовите пять дней недели, не повторяя ни понедельника, ни вторника, ни среды, ни четверга, ни пятницы, ни субботы, ни воскресенья.

Ответ

Позавчера, вчера, сегодня, завтра, послезавтра

«Для наших детей», № 6, 1913

Как из рубашки сделать птицу?

Ответ

Из «Сорочка» отнять букву Ч

«Для наших детей», № 6, 1915

Что нужно сделать с земляникой, чтобы в ней можно было жить?

Ответ

Убрать букву И

«Для наших детей», № 6, 1915

Какие три буквы могут исполнить музыкальную пьесу?

Ответ

Три О

«Для наших детей», № 7, 1915

Одного человека спросили:

— Сколько вам лет?

— Порядочно, — ответил он. — Я старше некоторых своих родственников в шестьсот раз.

Может ли это быть?

Ответ

Деду 50 лет, внуку 1 месяц

Нина Вадченко, Наталья Хаткина.
«600 задач на сообразительность. Энциклопедия», 1997

Два молодых казака, оба лихие наездники, часто бились между собой об заклад, кто кого перегонит. Не раз то тот, то другой был победителем, наконец им это надоело.

— Вот что, — сказал Григорий, — давай спорить наоборот. Пусть заклад достанется тому, чей конь придет в назначенное место вторым, а не первым.

— Ладно! — ответил Михаил.

Казаки выехали на своих конях в степь. Зрителей собралось множество: всем хотелось посмотреть такую диковинку. Один старый казак начал считать, хлопая в ладоши:

— Раз!.. Два!.. Три!..

Спорщики, конечно, ни с места. Зрители стали смеяться, судить да рядить и порешили, что так спор невозможен и что спорщики простоят на месте, как говорится, до скончания века. Тут к толпе подошел седой старик, видавший на своем веку разные виды.

— В чем дело? — спрашивает он.

Ему сказали.

— Эге ж! — говорит старик, — вот я им сейчас шепну такое слово, что поскачут как ошпаренные.

И действительно… Подошел старик к казакам, сказал им что-то, и через полминуты казаки уже неслись по степи во всю прыть, стараясь непременно обогнать друг друга, но заклад все же выиграл тот, чья лошадь пришла второй.

Что сказал старик?

Ответ

Старик шепнул казакам: «Пересядьте». Те поняли, мигом пересели каждый на лошадь своего противника, и каждый погнал теперь во всю прыть чужую лошадь, на которой он сидел, чтобы собственная его лошадь пришла второй.

Нина Вадченко, Наталья Хаткина.
«600 задач на сообразительность. Энциклопедия», 1997

Ответьте на вопрос: какие часы показывают верное время только два раза в сутки?

Ответ

Которые стоят

Нина Вадченко, Наталья Хаткина.
«600 задач на сообразительность. Энциклопедия», 1997

Назовите два числа, у которых количество цифр равно количеству букв, составляющих название каждого из этих чисел.

Ответ

Сто = 100; миллион = 1000000

Нина Вадченко, Наталья Хаткина.
«600 задач на сообразительность. Энциклопедия», 1997

Три неких древних мудреца вступили в спор: кто из троих более мудр? Спор помог решить случайный прохожий, предложивший им испытание на сообразительность.

— Вы видите у меня, — сказал он, — пять колпаков: три черных и два белых. Закройте глаза!

С этими словами он надел каждому по черному колпаку, а два белых спрятал в мешки.

— Можете открыть глаза, — сказал прохожий.

— Кто угадает, какого цвета колпак украшает его голову, тот вправе считать себя самым мудрым.

Долго сидели мудрецы, глядя друг на друга… Наконец один воскликнул:

— На мне черный!

Как он догадался?

Ответ

Мудрец рассуждал так: «Я вижу перед собой два колпака. Предположим, что на мне белый. Тогда второй мудрец, видя перед собой черный и белый колпаки, должен рассуждать так: „Если бы на мне был тоже белый колпак, то третий сразу бы догадался и заявил, что у него черный“. Но он молчит, значит, на мне не белый, а черный. А так как второй не говорит этого, значит, на мне тоже черный».

Нина Вадченко, Наталья Хаткина.
«600 задач на сообразительность. Энциклопедия», 1997

Корнеев, Докшин, Мареев и Скобелев — жители нашего города. Их профессии — пекарь, врач, инженер и милиционер.
Корнеев и Докшин — соседи, и всегда на работу ездят вместе.
Докшин старше Мареева.
Корнеев регулярно обыгрывает Скобелева в пинг-понг.
Пекарь на работу всегда ходит пешком.
Милиционер не живет рядом с врачом.
Инженер и милиционер встречались единственный раз, когда милиционер оштрафовал инженера за нарушение правил дорожного движения.
Милиционер старше врача и инженера.

Определите, кто чем занимается.

Ответ

Здесь уже придется прибегнуть к методу составления «логического квадрата»  Логический квадрат — схема, которая помогает классифицировать суждения и определять логические отношения между ними..

Так как пекарь всегда ходит на работу пешком, а Корнеев и Докшин ездят, можно заключить, что фамилия пекаря — не Корнеев и не Докшин. Отметим этот вывод в квадрате.

Теперь учтем, что милиционер единственный раз встречался с инженером и не является соседом врача. Отсюда следует, что пара соседей «Корнеев + Докшин» не может быть ни парой «милиционер + врач», ни парой «милиционер + инженер». Следовательно, Корнеев и Докшин — врач и инженер. Только пока неизвестно, кто из них врач, а кто инженер. Сделаем соответствующие пометки в квадрате.

Обратим теперь внимание на возрастные данные. С учетом уже сделанных нами выводов и последнего из условий задачи можно сказать, что милиционер старше Корнеева и Докшина. Известно также, что Докшин старше Мареева. Следовательно, Мареев — не милиционер. Значит, милиционер — Скобелев, а Мареев — пекарь.

Пекарь

Врач

Инженер

Милиционер

Корнеев

—

—

Докшин

—

—

Мареев

+

—

—

—

Скобелев

—

—

—

+

Теперь нетрудно сообразить, что партнер милиционера Скобелева по пинг-понгу врач, а не инженер, который единственный раз встречался с милиционером. Итак, Корнеев — врач, а следовательно, Докшин — инженер.

Виктор Болховитинов, Бронислав Колтовой, Игорь Лаговский.
«Твое свободное время», 1970

Четверо друзей: Алексей Иванович, Федор Семенович, Валентин Петрович и Григорий Аркадьевич — были как-то раз со своими детьми в парке культуры и отдыха. Они катались на колесе обозрения. В кабинах колеса оказались вместе: Леня с Алексеем Ивановичем, Андрей с отцом Коли, Тима с отцом Андрея, Федор Семенович с сыном Валентина Петровича, а Валентин Петрович с сыном Алексея Ивановича.

Назовите, кто чей сын и кто с кем катался, если ни один из мальчиков не катался со своим отцом.

Ответ

Выпишем вначале табличку пар «сын — отец». Обозначим в ней для удобства сыновей начальными буквами их имен, а отцов — буквой П с соответствующим индексом.

Л + П_л
А + П_а
Т + П_т
К + П_к

По условию задачи сочетания А + П_к и Т + П_а уже использованы. Вычеркнем их из таблички. Тогда будет ясно, что Леня мог кататься только с папой Тимы. Следователь­но, Алексей Иванович — папа Тимы. А Коля мог кататься только с папой Лени. Поскольку известно, что Валентин Петрович катался с сыном Алексея Ивановича, которого (сына, разумеется), как мы установили, зовут Тима, можно сделать вывод, что Валентин Петрович — отец Андрея (этот вывод опирается на тот факт, что «Тима катался с отцом Андрея»).

Составим теперь табличку пар катающихся, причем отцов будем обозначать их инициалами, а сыновей — буквой С с индексами, соответствую­щими инициалам их отцов.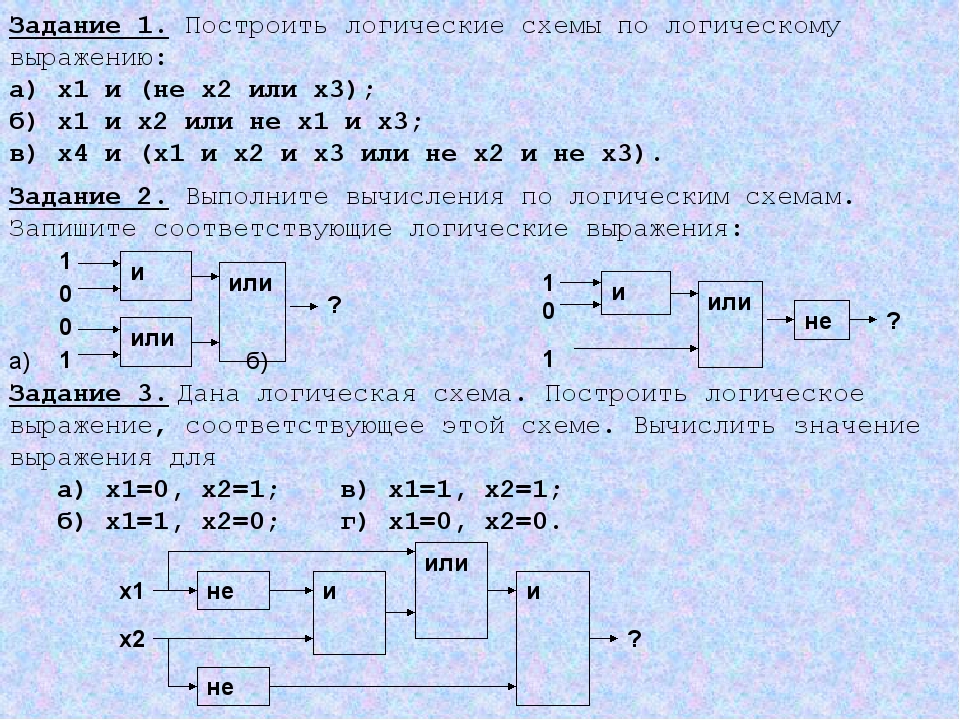 Единственно возможный вариант такой таблички будет выглядеть следующим образом:

Ф. С. — С_В. П.
В. П. — С_А. И.
А. И. — С_Г. А.
Г. А. — С_Ф. С.

Из этой таблички следует, что Леня, с которым катался Алексей Иванович, является сыном Григория Аркадьевича, а сын Федора Семеновича катался с Григорием Аркадьевичем. Заполнив логический квадрат на этой стадии решения, мы увидим, что Коля — сын Федора Семеновича. Итак, Тима — сын Алексея Ивановича, Андрей — сын Валентина Петровича, Леня — сын Григория Аркадьевича, Коля — сын Федора Семеновича.

Теперь ясно и то, кто с кем катался. Леня — с Алексеем Ивановичем, Андрей — с Федором Семеновичем, Тима — с Валентином Петровичем, а Коля — с Григорием Аркадьевичем.

Виктор Болховитинов, Бронислав Колтовой, Игорь Лаговский.
«Твое свободное время», 1970

На столе 3 совершенно одинаковых ящичка. В одном из них лежат 2 черных шарика, в другом — черный и белый, в третьем — 2 белых. На крышках ящичков есть надписи: «2 черных», «2 белых», «черный и белый». Однако известно, что ни одна из этих надписей не соответствует действительности.

Сможете ли вы, вынув наугад шарик (и не заглядывая в ящички), определить, где какие шарики лежат?

Ответ

Нужно вынуть любой шарик из коробки с надписью «черный и белый». Если вынутый шарик белый, значит, и второй должен быть белым. Тогда в ящичке с надписью «2 белых» — 2 черных шарика.

Если же вынутый шарик черный, то и второй должен быть черным. Тогда в коробке с надписью «2 белых» могут быть только черный и белый шарики, а в коробке с надписью «2 черных» — 2 белых шарика.

Виктор Болховитинов, Бронислав Колтовой, Игорь Лаговский.
«Твое свободное время», 1970

В нашем городе обувной магазин закрывается каждый понедельник, хозяйственный — каждый вторник, продовольственный — каждый четверг, а парфюмерный магазин работает только по понедельникам, средам и пятницам. В воскресенье все магазины закрыты.

Однажды подруги Ася, Ира, Клава и Женя отправились за покупками, причем каждая в свой магазин, и притом в один. По дороге они обменивались такими замечаниями.

Ася: «Женя и я хотели пойти вместе еще раньше на этой неделе, но не было такого дня, чтобы мы обе могли сделать наши покупки».

Ира: «Я не хотела идти сегодня, но завтра я уже не смогу купить то, что мне нужно».

Клава: «А я могла бы пойти в магазин и вчера, и позавчера».

Женя: «А я могла бы пойти и вчера, и завтра».

Скажите, кому какой магазин нужен?

Ответ

Заметим вначале, что разговор подруг происходит, как это следует из того, что они все отправились за покупками, либо в среду, либо в пятницу (составьте для нагляд­ности расписание работы магазинов).

Предположим, что разговор подруг происходит в среду. Тогда сразу же можно сказать, что Клава идет в продовольственный магазин (см. расписание). Женя — в обувной, Ира — в парфюмерный, и, следователь­но, Ася — в хозяйственный. Такое распределение магазинов согласуется и со словами Аси.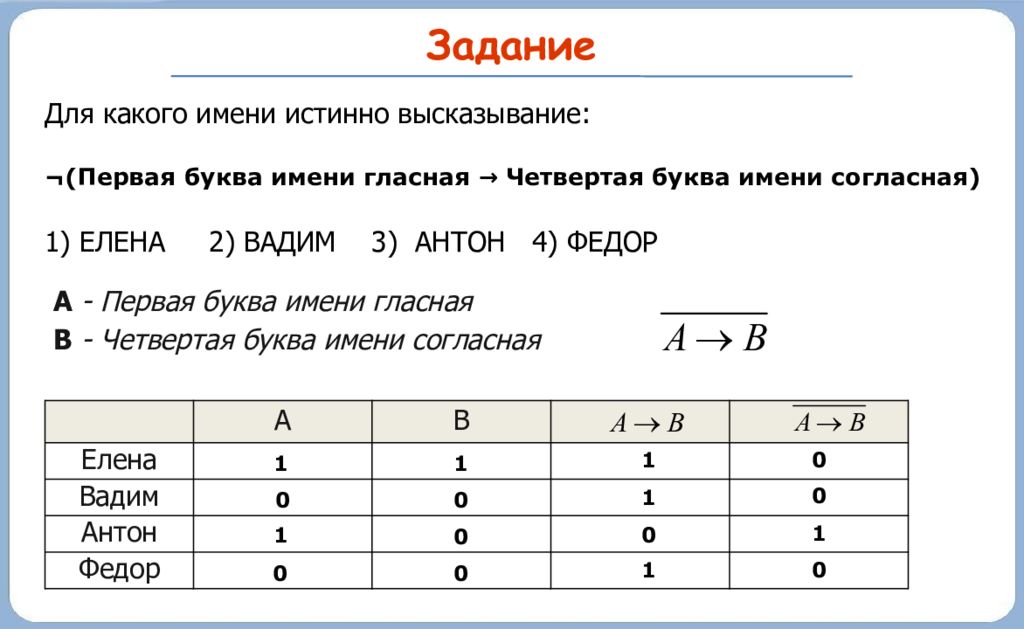
Но, может быть, решение неоднозначное? Посмотрим, что получится, если мы предположим, что разговор подруг происходит в пятницу. Как видно из расписания, в среду работают все магазины, и, следовательно, Женя и Ася могли вместе пойти раньше пятницы каждая в свой магазин. А это противоречит условию. Значит, подруги идут в магазины в среду — и ни в какой другой день. Решение вполне однозначное.  

Виктор Болховитинов, Бронислав Колтовой, Игорь Лаговский.
«Твое свободное время», 1970

Спецпроект

Детская комната Arzamas

Теги

Дети
Развлечения
Игра

ГусьгусьКандидат игрушечных наук

Из чего сделан пластилин? Какое применение ему нашлось в профессиональном спорте? И главное: что делать, если он запутался в волосах? В новом эпизоде детского подкаста продолжаем рассказывать о химии с помощью популярных игрушек

Хотите быть в курсе всего?

Подпишитесь на нашу рассылку, вам понравится. Мы обещаем писать редко и по делу

Курсы

Все курсы

Спецпроекты

О проектеЛицензияПолитика конфиденциальностиОбратная связь

Радио ArzamasГусьгусьСтикеры Arzamas

ОдноклассникиVKYouTubeПодкастыTwitterTelegramRSS

История, литература, искусство в лекциях, шпаргалках, играх и ответах экспертов: новые знания каждый день

© Arzamas 2023. Все права защищены

логических головоломок | Решите головоломку

Выберите размер сетки и диапазон сложности ниже, и головоломка будет инициализирована в соответствии с вашими предпочтениями.

Размер сетки		3×4 Сетка 3×5 Сетка 4×4 Сетка 4×5 Сетка 4×6 Сетка 4×7 Сетка
Диапазон сложности		EasyModerateChallenging

Головоломки с большими размерами сетки и более высокими уровнями сложности будут иметь большее максимальное количество очков. Чтобы увеличить количество очков, выберите больший размер сетки или уровень сложности (или и то, и другое). Окончательные баллы будут начисляться на основе этих факторов, а также общего времени, которое потребовалось вам для решения головоломки.

• Форум
• записей
• Новости

• Том 2 Гималайский альпинизм Разместил: RaRA
  26 мая 2023 г., 8:18
• Почему так много раз по 30 секунд? Разместил: margotbean
  26 мая 2023 г., 00:21
• Почему так много раз по 30 секунд? Разместил: Киберсикоз
  18 мая 2023 г., 8:36
• Почему так много раз по 30 секунд? Разместил: abettle
  16 мая 2023 г., 10:49
• Почему так много раз по 30 секунд? Разместил: NashvilleSCTheBest
  15 мая 2023 г., 11:59
• Почему так много раз по 30 секунд? Разместил: fromalabama
  13 мая 2023 г., 17:10

• Ravenna206 установила новый рекорд в 183 секунды на головоломке № 14284
  1 июня 2023 г. , 9:57
• Ravenna206 установила новый рекорд в 163 секунды на головоломке № 14820
  1 июня 2023 г., 9:51
• блоха установила новый рекорд в 161 секунду на головоломке № 41383
  1 июня 2023 г., 4:45
• блоха установила новый рекорд в 169 секунд на головоломке № 61044
  1 июня 2023 г., 4:32
• kuriosi_t установил новый рекорд в 140 секунд на головоломке № 16342
  1 июня 2023 г., 2:45
• kuriosi_t установил новый рекорд в 123 секунды на головоломке № 16044
  1 июня 2023 г., 1:53

• Новая книга: Детские пазлы с картинками Теперь доступно на Amazon и в крупных книжных магазинах!. ..
  
• Новый сайт: Puzzle Baron Games Игры в слова, пасьянсы, маджонг, судоку и многое другое!…
  
• Пазл Barons Большая книга головоломок Наша новейшая книга теперь доступна для покупки!…
  
• Запуск сайта: Пазлы Наш новейший сайт — собирайте пазлы онлайн!…
  
• Новые печатные сетки Новые головоломки Numbergrid теперь публикуются ежедневно….
  

left

• Наивысший балл

  Зенобия43

  1034567 баллов.

• Наивысший балл

  Серения

  906367 баллов.

• Наивысший балл

  ретепп06

  674551 балл.

вправо

Логические головоломки | Другие наши пазлы

Посмотрите, сможете ли вы заполнить сетку звездами таким образом, чтобы каждая строка, столбец и фигура содержали определенное число, и никакие две звезды никогда не соприкасались, даже по диагонали!

Посетите этот веб-сайт

Найдите комбинацию стрелок, которая однозначно разрешит каждую сетку, не пересекая никакие две стрелки и не оставляя пустых квадратов. Готовы ли вы принять вызов?

Посетите этот веб-сайт

Соедините каждый набор цветных чисел, не пересекая путей и не оставляя пустых квадратов на сетке. У каждой головоломки есть только одно уникальное решение… сможете ли вы его найти?

Посетите этот веб-сайт

Наша новейшая арена для казуальных словесных игр, карточных игр, интеллектуальных игр и многого другого! Играйте в свое удовольствие или войдите в систему, чтобы соревноваться с другими игроками со всего мира!

Посетите этот веб-сайт

Вам дается куча проводов, лампочки и одна батарейка. Ваша задача: подключить все лампочки и провода к аккумулятору, чтобы электрифицировать всю цепь, не создавая петель.

Посетите этот веб-сайт

В этой головоломке вы смотритель парка! Разложите вокруг лагеря определенное количество палаток (по одной на каждое дерево), соблюдая числовые требования, указанные для каждого ряда и столбца.

Посетите этот веб-сайт

Разместите лазеры на сетке так, чтобы каждый пустой квадрат был залит зеленым лазерным светом. Играйте в свое удовольствие или соревнуйтесь с другими зарегистрированными игроками, чтобы попасть в Зал славы Lasergrid!

Посетите этот веб-сайт

Откройте для себя уникальное расположение полимино, которое будет соответствовать заданной сетке. Играйте в свое удовольствие или соревнуйтесь с другими зарегистрированными игроками, чтобы попасть в Зал славы Филломино!

Посетите этот веб-сайт

Неважно, знаете ли вы их как Calcudoku, Mathdoku или KenKen(TM), у нас есть тысячи уникальных головоломок, от самых простых 4×4 до самых сложных 9×9.

Посетите этот веб-сайт

Серия чисел определяет сетку — используйте только логику, чтобы раскрыть скрытые закономерности. Играйте в свое удовольствие или соревнуйтесь с другими игроками за место в Зале славы Numbergrid!

Посетите этот веб-сайт

Думайте об этом как о смеси логической головоломки и поиска слов! Учитывая ряд слов и частично заполненную сетку, ваша задача состоит в том, чтобы поместить каждое слово в сетку так, чтобы использовался каждый квадрат.

Посетите этот веб-сайт

Решите тысячи уникальных пазлов всех размеров и уровней сложности. Играйте в свое удовольствие или зарегистрируйте учетную запись, чтобы соревноваться с другими игроками за место в Зале славы пазлов!

Посетите этот веб-сайт

Своего рода смесь кроссворда и криптограммы, в акростихе вы постепенно откроете скрытую цитату, разгадывая серию подсказок в стиле кроссворда.

Посетите этот веб-сайт

Сможете взломать код? Каждая головоломка представляет собой зашифрованную цитату — ваша задача — использовать распознавание образов, частотный анализ и старый добрый здравый смысл, чтобы раскрыть скрытую цитату.

Посетите этот веб-сайт

Помесь математической головоломки и логической задачи. Введите числа в сетку так, чтобы каждая ячейка была равна сумме соседних, без использования какого-либо числа дважды в одном и том же разделе.

Посетите этот веб-сайт

На квадратной доске из 16 или 25 букв найдите как можно больше допустимых английских слов, комбинируя каждую непрерывную букву. Дополнительные баллы начисляются за редкие и необычные слова!

Посетите этот веб-сайт

Возьмите простой набор подсказок и сопоставьте каждый предмет в четырех разных категориях, используя только чистую логическую дедукцию. Мы предоставляем удобную сетку для каждой головоломки, чтобы помочь вам в вашем пути.

Посетите этот веб-сайт

Зашифрованные буквы известной цитаты представлены в виде ряда столбцов, стоящих над сеткой в ​​​​стиле кроссворда. «Вставьте» каждую букву в сетку, чтобы открыть скрытую цитату!

Посетите этот веб-сайт

Найдите серию связанных слов в сетке букв. На этом сайте вы можете играть в свое удовольствие или соревноваться с другими в играх на время, чтобы попасть в Зал славы Word Search.

Посетите этот веб-сайт

Предпочитаете решать головоломки старомодным способом, с карандашом и бумагой? Тогда попробуйте этот сайт. Кроссворды, акростихи, криптограммы, логические головоломки, судоку и многое другое!

Посетите этот веб-сайт

Решите эти простые кроссворды, даже не читая подсказки! Мы даем вам три буквы для начала — используйте распознавание образов, чтобы заполнить остальную часть сетки.

Посетите этот веб-сайт

Хотите быстро решить кроссворд, но у вас нет времени на всю головоломку? Даются подсказки кроссворда, и каждые 5 секунд открывается новая буква. Сможете ли вы решить ее до того, как истечет время?

Посетите этот веб-сайт

Сможете ли вы открыть спрятанное слово или фразу до того, как палач закончит свою ужасную работу? Здесь доступны тысячи уникальных головоломок с палачами, разделенных на разные категории.

Посетите этот веб-сайт

Более пятидесяти тысяч различных головоломок судоку, от очень простых до невероятно сложных. Подсказки доступны, если вы застряли! Проверьте, сможете ли вы войти в Зал славы судоку.

Посетите этот веб-сайт

Индекс некоторых из лучших и самых популярных сайтов со словесными головоломками в Интернете. Для каждого сайта предусмотрены простые обзоры и рейтинги, а также комментарии пользователей и рейтинги.

Посетите этот веб-сайт

Перетасовывайте каждую двухбуквенную плитку на игровом поле, пока каждая строка и столбец не сформируют правильное слово.

No related posts.