Решение задач онлайн графическим методом: Графический метод решения задач линейного программирования. Решение задач и контрольных работ по линейному программированию онлайн

Решение задач линейного программирования графическим методом

Похожие презентации:

«Методы оптимальных решений» № 1. Задачи линейного программирования и графический метод решения

Решение простейших задач линейного программирования графическим методом

Графическое решение задач линейного программирования

Графическое решение задач линейного программирования

Геометрический метод решения задачи линейного программирования

Задачи и методы оптимального планирования

Решение задач линейного программирования симплекс-методом. Двойственность ЗЛП

Прямая и двойственная задачи и их решение симплекс-методом

Методы оптимальных решений в линейном программировании

Симплекс-метод решения задач линейного программирования

Справочный материал к практике 19 по
дисциплине «Математика» для студентов
направления подготовки
09.03.02 «Информационные системы и
технологии»
Решение задач линейного программирования графическим методом
Составитель:

ст. преподаватель кафедры «Физикоматематические науки» Черемухин А. Д.
Алгоритм решения ЗЛП графическим методом
Пример 1. Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
ограничения выражаются системой неравенств
1. Будем рисовать. Исходя из первых
двух ограничений, работать будем в первом
квадранте. Рисуем схематически
2. Рассмотрим второе ограничение.
Преобразуем его
Нарисуем прямую, соответствующую равенству
Прямая делит плоскость на две полуплоскости.
Неравенство верно только в одной. Выясним, что
Значит, неравенство верно в нижней
полуплоскости (точка (0;0) находится там)
Алгоритм решения ЗЛП графическим методом
Пример 1. Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
ограничения выражаются системой неравенств
2. Итого, после третьего ограничения рисунок выглядит так
3. А после четвертого — так
Алгоритм решения ЗЛП графическим методом
Пример 1. 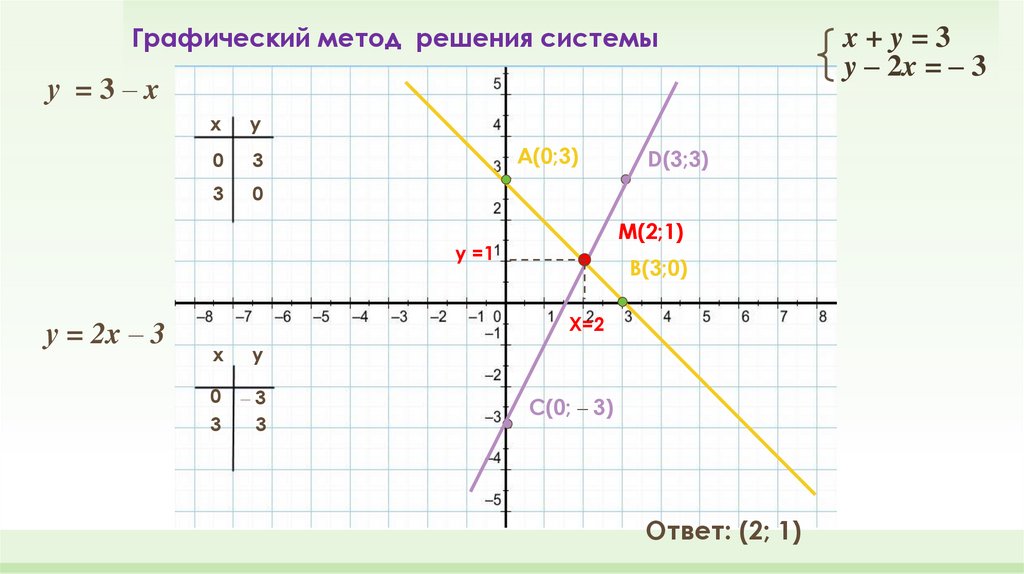Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
ограничения выражаются системой неравенств
Итого, наша система ограничений выглядит так:
Фигура замкнута, значит, решение есть всегда. И оно достигается в вершине этого
многоугольника.
Теперь приравняем целевую функцию к двум значениям – пусть это будет 0 и 10. И
выпишем функцию
И нарисуем обе прямых, соответствующих разным значениям ЦФ
Алгоритм решения ЗЛП графическим методом
Пример 1. Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
ограничения выражаются системой неравенств
3. Рисунок с разными ЦФ
Видно, что чем больше целевое значение функции, тем
прямая целевой функции проходит «выше». Значит, для
достижения максимума прямая должна пройти максимально
высоко – это положение обозначено красным
Соответственно, максимальное значение достигается в
точке I – там, где пересекаются прямые, обозначающие 3 и
4 ограничения.
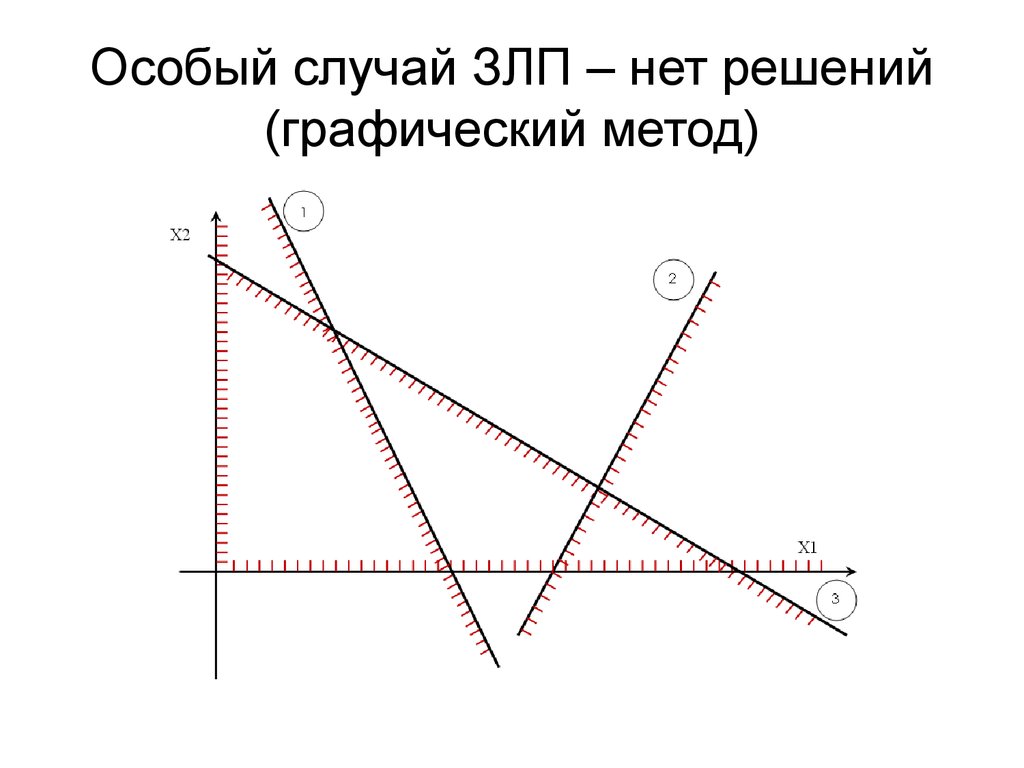
А минимальное значение достигается в точке В – там
прямая максимально низка
Алгоритм решения ЗЛП графическим методом
Пример 1. Решите графически задачу линейного программирования на максимум, если целевая функция Z(X) = 8x+9y, а
ограничения выражаются системой неравенств
4. Найдем координаты точки I
Задача решена
Алгоритм решения ЗЛП графическим методом
Различные исключения:
1. Задача решения не имеет, поскольку система ограничения несовместна (на графике просто нет области,
соответствующей всем ограничениям)
2. Задача имеет бесконечно много решений, если целевая функция совпадет с одной из сторон многоугольника
ограничений
3. Задача не имеет решения ввиду неограниченности системы ограничений (на графике она представляет собой
незамкнутую фигуру, и целевая функция «скользит» неограниченно в бесконечность по одной из сторо)

English     Русский Правила

3.2. Пример использования графического метода

Графический метод решения задач линейного программирования базируется на ее геометрической интерпретации и применяется, как правило, при количестве переменных n = 2 и в отдельных случаях при n = 3 (трехмерное пространство) . Ограниченное использование графического метода обусловлено сложностью построения многогранника решений в трехмерном пространстве (для задач с тремя переменными), а графическое изображение задачи с количеством переменных больше трех вообще невозможно. Однако графический метод позволяет выработать у студентов наглядные представления о линейном программирование и подтвердить справедливость некоторых его теорем. В дальнейшем мы будем рассматривать и решать задачи линейного программирования графическим методом только в двумерном пространстве.

Согласно геометрической интерпретацией задачи линейного программирования каждое i-е ограничение-неравенство определяет полуплоскость с граничной прямой (і = 1, 2, …, т). Если графически изобразить общую часть, или пересечение всех указанных полуплоскостей, то мы получим множество точек, координаты которых удовлетворяют одновременно все ограничения задачи, это множество точек называют многогранником допустимых решений. Условие неотрицательности переменных означает, что область допустимых решений задачи принадлежит первому квадранту системы координат двумерного пространства. Целевая функция геометрически интерпретируется как семья параллельных прямых .

Проиллюстрируем решение задачи линейного программирования графическим методом на примере системы ограничений с двумя переменными.

Пример. Решить графически следующую задачу линейного программирования: найти максимум и минимум целевой функции при ограничениях

Решение

Сначала нам необходимо получить область допустимых решений. Неравенство определяет полуплоскость с граничной прямой. Строим эту прямую (рис. 3.2 , прямая (1)) и определяем полуплоскость допустимых решений. С этой целью в неравенство подставляем координаты какой-то характерной точки, например . Убеждаемся, что эта точка принадлежит выбранной полуплоскости и иллюстрируем этот факт соответствующими направленными стрелками.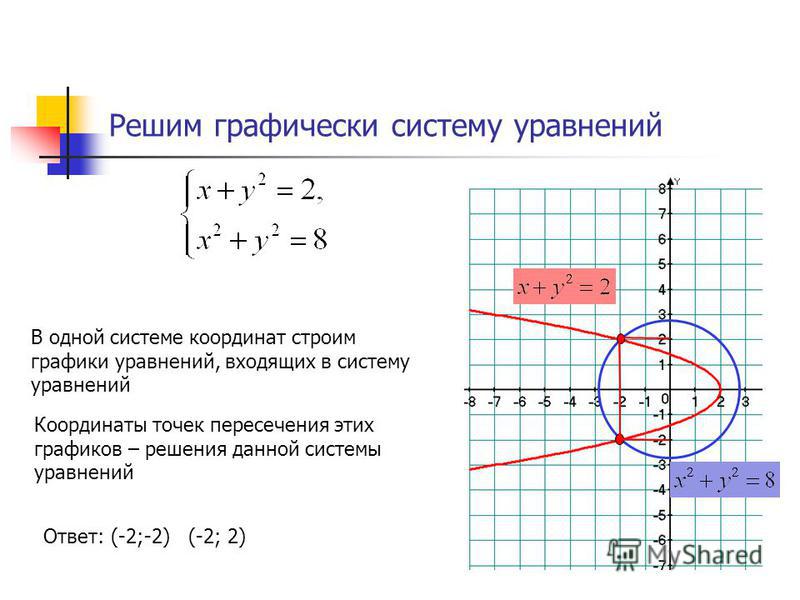 Аналогичным образом строим полуплоскости для остальных неравенств из системы ограничений задачи. В результате пересечения этих полуплоскостей получаем область допустимых решений – многогранник ОABCD.

Вектор нормали (иногда его называют также как радиус-вектор) задает направление роста значений целевой функцииF. Целевая функция определяет семейство параллельных прямых с₁х₁ + с₂х₂ = const, которые называются линиями уровня и каждая из которых соответствует определенному значению целевой функции F. Первая линия уровня проходит через начало координат, при этом F = 0. При увеличении F линии уровня смещаются в направлении вектора, а при уменьшении – в направлении, противоположном вектору . На рис. 3.1 построена прямаяF = 0, которая располагается перпендикулярно вектору нормали .

Рис. 3.2. Графическое представление задачи

Согласно теорем 3 и 4 (см. § 2.4) допустимыми базисными решениями данной задачи являются угловые точки многогранника ОABCD, а по теореме 2 одна (в отдельных случаях – две) из этих точек придает максимального значения целевой функции. В нашем примере максимального значения целевая функция достигнет в точке B, т.е. в вершине многогранника области допустимых решений, которая является наиболее отдаленной от начала координат, если двигаться в направлении вектора .

Координаты точки B находим, решив систему из уравнений прямых № 1 и № 2, на пересечении которых эта точка находится:

Имеем систему двух линейных уравнений с двумя неизвестными, которую можно решить методами Крамера, Гаусса и некоторыми другими.

По методу Крамера решениями этой системы будут значения:

;.

Таким образом оптимальным планом задачи линейного программирования, который обеспечивает максимум целевой функции является точка B (1,54 ; 7,68).

Значение целевой функции в этой точке: .

Минимального значения целевая функция достигает в точке D. Если мы движемся в направлении противоположном вектору нормали , то данная точка является последней вершиной многогранника ОABCD через которую проходит линия уровняF. Прямая (3) пересекает ось 0х1 при х₁ = 2 , следовательно координаты точки D (2 , 0) .

Оптимальным планом задачи линейного программирования, который обеспечивает минимум целевой функции является точка D ( 2 , 0) .

Значение целевой функции в этой точке: .

Графический метод — Industrial Engineer Online

Графический метод — это метод решения задач линейного программирования , который в основном используется для случаев с двумя переменными. Хотя это не очень практично для большого количества переменных, это очень полезно для интерпретации и анализа результатов и чувствительности проблемы.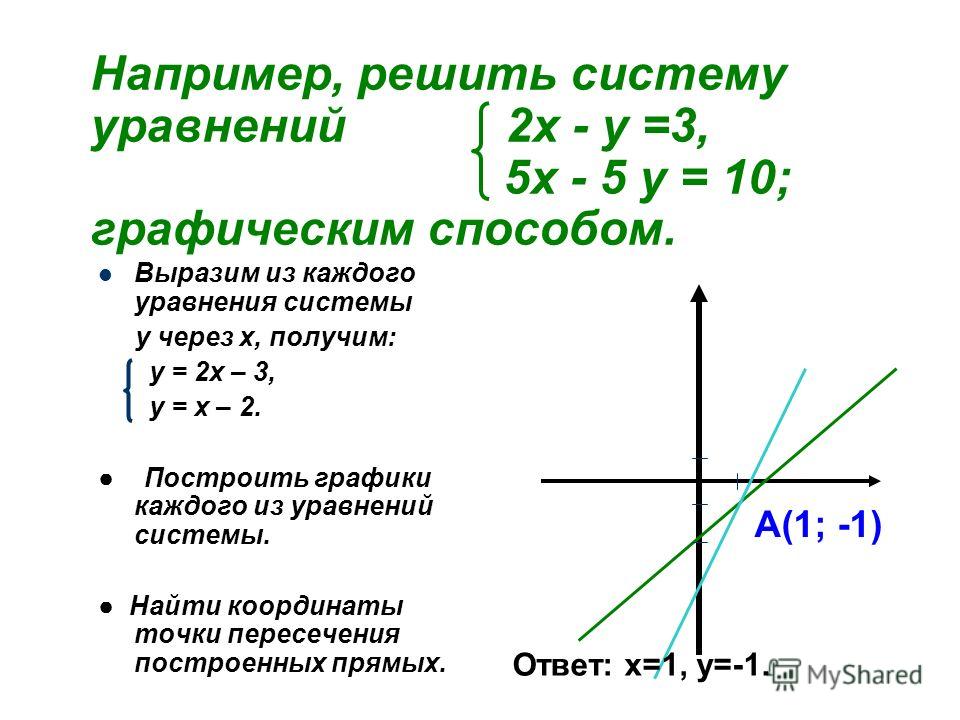 Однако в тех случаях, когда требуется большее количество переменных, можно использовать другие методы, такие как проецирование на плоскость.

Графический метод основан на графическом представлении ограничений модели линейного программирования, что позволяет определить многоугольник решения или допустимую область. Согласно фундаментальной теореме линейного программирования, если существует решение, удовлетворяющее ограничениям модели, оно будет найдено в одной из вершин допустимой области.

Графический метод — это метод, который на протяжении всей истории был предметом споров между разными авторами. Некоторые из них указали, что эта методология содержит определенные допущения или ограничения.

Одно из самых известных предположений состоит в том, что оно не позволяет провести анализ чувствительности в случае одновременного изменения правой части ограничений или коэффициентов целевой функции. Другое предположение состоит в том, что бинарные переменные не могут быть учтены в модели.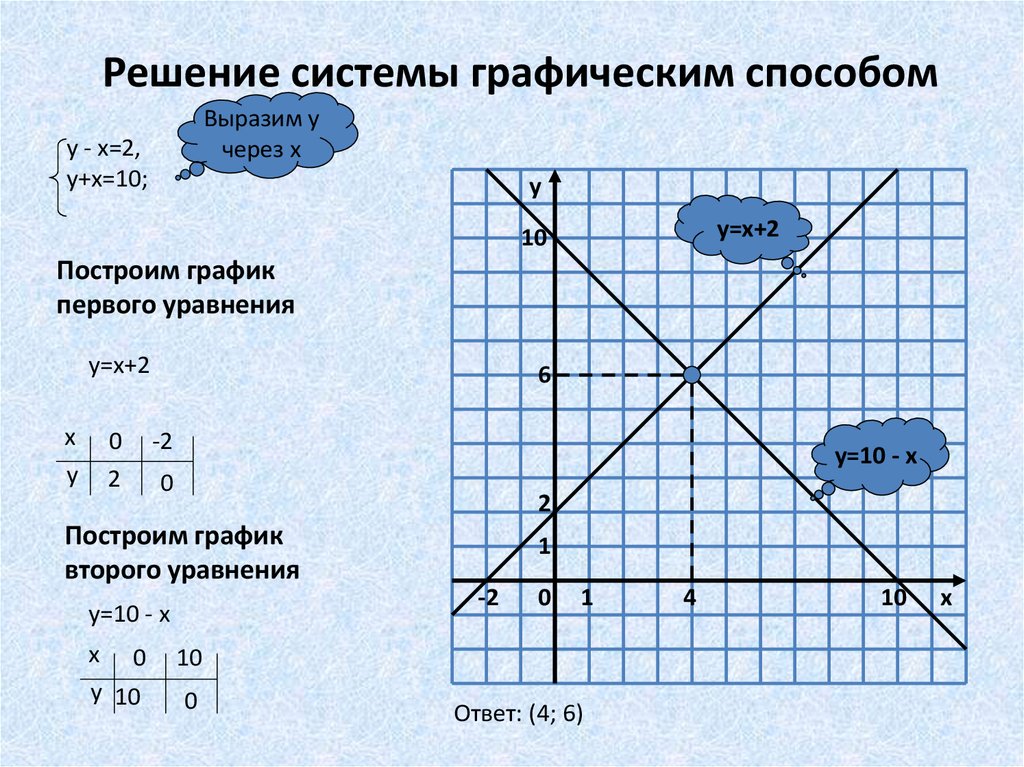

Однако с развитием технологий можно использовать такие инструменты, как GeoGebra, для преодоления этих ограничений и выполнения анализа чувствительности с одновременными изменениями и учетом бинарных переменных в модели. Следовательно, эти предположения больше не действуют в настоящее время.

Предварительные соображения

Необходимо помнить, что графический метод является методом решения, и поэтому предшествующий этап соответствует математическому моделированию.

Задача

Мы будем использовать технически сформулированную задачу, чтобы подойти к каждому из этапов графического метода.

Фабрике Hilados y Tejidos «Salazar» необходимо производить две ткани разного качества: Standard и Premium. Доступно 500 кг нити a, 300 кг нити b и 108 кг нити c. Для получения одного метра ткани Standard в день необходимо 125 граммов а, 150 граммов б и 72 грамма в; для производства одного метра ткани Премиум в день необходимо 200 граммов а, 100 граммов б и 27 граммов в. Ткань Standard продается по цене 4000 долларов за метр, а ткань Premium — по 5000 долларов за метр. Если необходимо получить максимальную прибыль, сколько метров тканей Стандарт и Премиум необходимо произвести?

 

Моделирование линейного программирования

Как упоминалось ранее, основа для использования графического метода соответствует математической модели линейного программирования:

Переменные

x: количество метров стандартной ткани, которое будет производиться в день

y: количество суточного производства ткани Premium

Ограничения

0,12x + 0,2y <= 500 кг нити «а»

0,15x + 0,1y <= 300 кг нити «b»

0,072x + 0,027y <= 108 кг нити «c»

x >= 0 Неотрицательное ограничение

y >= 0 Не- Ограничение отрицательности

Целевая функция

Zmax = 4000x + 5000y (Максимальная общая выручка, указанная в долларах)

---

Решение графическим методом

1: Построение графика ограничений

Процесс поиска допустимого решения начинается с графическое представление ограничений ; каждое из них должно быть представлено таким образом, чтобы ограничить возможные решения модели.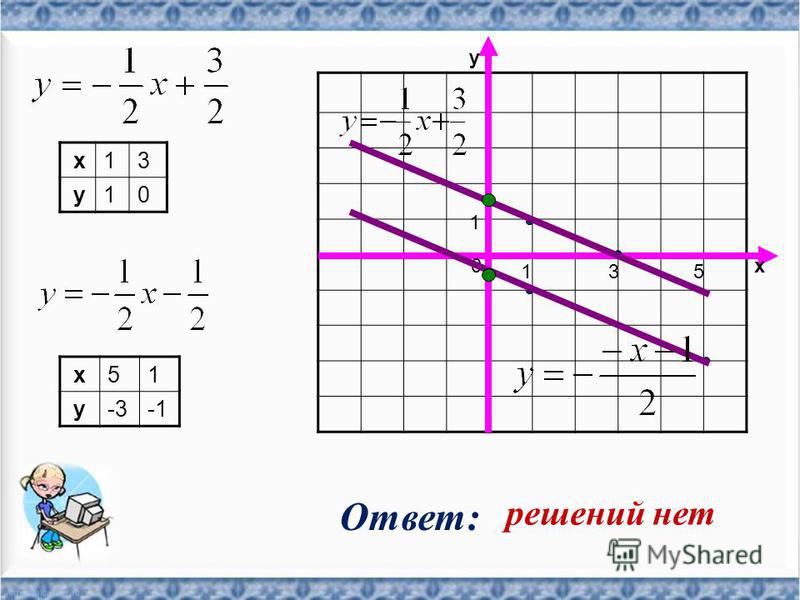

На данный момент мы должны рассмотреть две возможности:

1. Мы выполняем весь процесс вручную
2. Что мы используем графическое программное обеспечение, которое упрощает математические операции

В этом случае мы покажем всю методологию выполнения ручной процедуры, в то же время мы будем использовать графическое программное обеспечение для представления каждого этапа метода.

---

Каждое ограничение соответствует линейной функции, что означает, что оно графически представлено линией на декартовой плоскости. Чтобы провести линию на декартовой плоскости, необходимо знать не менее двух точек функции.

Чтобы начать рисовать ограничения, необходимо установить ограничения равными нулю , чтобы мы могли использовать очистку уравнений для начала табуляции, которая даст нам координаты для рисования каждого из графиков.

Мы устанавливаем ограничения на ноль:

0,12x + 0,2y = 500 (ограничение 1)

0,15x + 0,1y = 300 (ограничение 2)

0,072x + 0,027Y = 108 3)

x = 0                             (Ограничение 4)

y = 0                                         (Ограничение 5)

два: находим координату 1.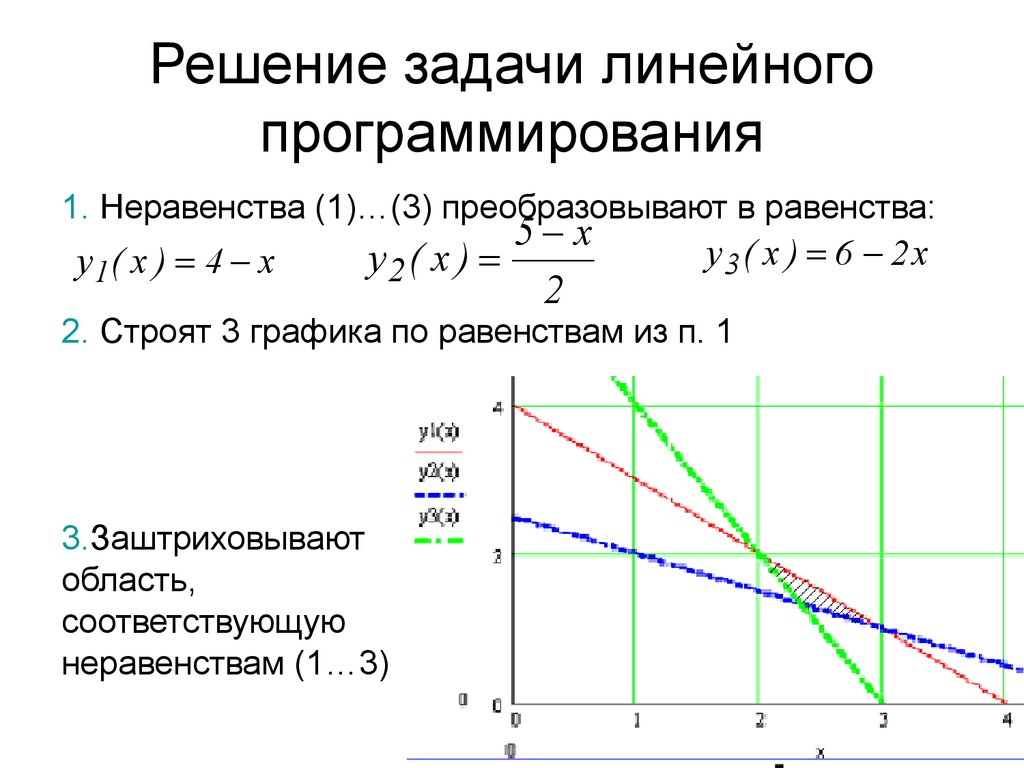 90 Constraint. Чтобы найти координаты, мы обычно устанавливаем одну из переменных в ноль, чтобы вторую было легче очистить.

Например, когда x = 0:

0,12 (0) + 0,2y = 500

0,2y = 500

500/0,2 = Y

2500 = Y

Когда Y = 0:

0,12x. + 0,2(0) = 500

0,12x = 500

x = 500/0,12

x = 4167

Ограничение 1 04 04 04 04	х	г
Первая координата	0	2500
Вторая координата	4167	0

---

Ограничение 2 :

Когда x = 0

0.15 (0) + 0,1y = 300

0.1y = 300

9000 2 0,15. y = 3000

Когда y = 0

0,15x + 0,1 (0) = 300

0,15x = 300

x = 300/0,15

x = 2000

x = 300/0,15

x = 2000

0138 Ограничение 2 х г Первая координата 0 3000 Вторая координата 2000 0

---

Ограничение 3 :

Когда x = 0

0,072x + 0,027Y = 108

0,072 (0) + 0,027Y = 0,027Y = 108

0,072 (0) + 0,07Y = 0,027Y = 108

0,072 (0) + 0,07Y + 0,027Y = 108

0,072 (0) + 0,072x + 0,027Y = 108

9002 0,072 (0).0007

0,027Y = 108

Y = 108/0,027

Y = 4000

Когда Y = 0

0,072x + 0,027 (0) = 108

0,072x = 108

7. /0,072

x = 1500

Ограничение 3	х	г
Первая координата	0	4000
Вторая координата	1500	0

---

Незначальные ограничения:

PASO 2: Найдите область раствора (Polygon Polygon)

После всех ресторанов. или многоугольник решения; что есть не что иное, как область, в которой все точки удовлетворяют всем ограничениям, т. е. допустимы.

Чтобы разграничить допустимую область, необходимо определить смысл ограничений. Здесь я ненадолго останавливаюсь; так как я предпочитаю объяснять это подробно. Каждая линия, представляющая ограничение, делит декартову плоскость на две полуплоскости: по одну и по другую сторону ограничения. Ну, только точки с одной стороны можно считать возможными.

Если мы хотим найти допустимую область, мы должны начать с поиска допустимой стороны каждого из ограничений; это то, что я называю: оценка смысла ограничений.

Давайте рассмотрим пример для первого ограничения:

Оценка направления ограничения 1

Это очень просто, нам просто нужно оценить любую точку на декартовой плоскости, она должна соответствовать одной стороне ограничение. Если ограничение выполнено или нет, мы будем знать его направление.

0,12x + 0,2y <= 500

Желание упростить арифметический процесс является нормальным, и обычно используется точка с координатами (0, 0):

0,12(0) + 0,2(0) <= 500

0 <= 500

Верно!

Поскольку 0 меньше или равно 500 , мы можем утверждать, что по ту сторону ограничения находятся значения, которые ему удовлетворяют.

Зеленая область представляет собой область, в которой расположены все точки, удовлетворяющие ограничению 1.

Когда функция ограничения (прямая на плоскости) проходит через точку (0, 0), вычисление ограничения нецелесообразно. Помните, что необходимо выбрать точку, которая находится на одной стороне ограничения.

Чтобы найти допустимую область, процедуру необходимо повторить для каждого ограничения задачи. Поскольку все ограничения должны быть соблюдены, допустимая область будет результатом пересечения всех допустимых областей каждого ограничения модели.

Заштрихованная область на предыдущем графике соответствует допустимой области.

3: Поиск оптимального решения

Как только будет найдена допустимая область, удовлетворяющая всем ограничениям модели, следующим шагом будет поиск оптимального решения. Важно различать осуществимость и оптимальность.

Оптимальное решение будет зависеть от критерия оптимизации целевой функции и, согласно основной теореме линейного программирования, находится в одной из вершин допустимой области. Технически оптимальное решение находится в вершинах для любого критерия оптимизации: минимальное значение (минимизация) и максимальное значение (максимизация).

Существуют две основные процедуры поиска оптимального решения:

1. Графически
2. Оценка всех вершин (грубая сила)

Графически

Этот метод требует графического представления целевой функции. По крайней мере, дважды.

Необходимо построить график целевой функции и найти направление, в котором она приближается к критерию оптимизации. Как мы это делаем? В каждом случае нам нужны две точки для построения первой линии, представляющей целевую функцию; эти две точки должны давать одно и то же Z. Посмотрим:

Zmax = 4000x + 5000y

Целевая функция (Z1)	4000(х)	5000(у)	я
Первая координата	4000(500)	5000(0)	2000000
Вторая координата	4000(0)	5000(400)	2000000

Ahora, podemos намеренный кон otra представительство de la función objetivo que se acerque aún más al criterio de optimización: Maximizar; es decir, ип Z2 мэр Z1. Веамос:

Объективная функция (Z2)	4000(х)	5000(у)	я
Primera coordenada	4000(1000)	5000(0)	4000000
Сегунда Координада	4000(0)	5000(800)	4000000

Построив графики обеих функций, как Z1, так и Z2, мы получим следующее:

Видно, как целевая функция приближается к критерию оптимизации (увеличивается) при движении вверх. Следующим шагом является поиск последней вершины допустимой области (в данном случае в направлении вверх), где линия, параллельная целевой функции, не пересекает допустимый многоугольник. На этом этапе будет найдено оптимальное решение.

Используйте полосу прокрутки GeoGebra для перемещения целевой функции. Вы увидите, что последняя вершина, в которой целевая функция не пересекает достижимую область, является пересечением ограничений 2 и 3 (вершина C). Эта точка соответствует оптимальному решению.

Чтобы найти значение этой координаты, необходимо решить линейное уравнение 2×2, и можно рассмотреть несколько методов решения, например:

• Метод подстановки
• Метод равенства
• Метод сокращения или исключения
• Метод исключения Гаусса
• Метод исключения Гаусса-Жордана
• Метод определения

Существует множество доступных методов, но одним из наиболее часто используемых является метод сокращения или исключения, который очень прост в применении.

Метод редукции или исключения состоит в уравнивании коэффициентов одной из переменных путем умножения одного или обоих уравнений с учетом того, что эти коэффициенты равны, но с противоположными знаками.

Уравнение 1 0,12x + 0,2y = 500

Уравнение 2 0,15x + 0,1y = 300 Multiplicamos por (-2)

Уравнение 3 (2*(-2)) -0,30x-0 ,2y = -600

Сумма 1 y 3                        -0,18x = -100

Решите для «x” x = -100 / (-0,18)

x = 555,55

Затем мы заменим x = 555,55 на любое из исходных уравнений, чтобы решить «y ».

Уравнение 1 0,12x + 0,2y = 500

Мы заменяем «x» 0,12 (555,55) + 0,2y = 500

Решить для «Y» 66,666 + 0,2y = 500

0,2г = 500 – 66 666

0,2y = 433,334

Y = 433,334 / 0,2

Y = 2166,67

Таким образом, мы получили значения для « x » и « y « x »и« у « x » и « y « x »и« у « .

x: Количество дневных метров ткани Standard, которое будет производиться

y: Количество дневных метров ткани Premium, которое будет производиться

Количество дневных метров ткани Standard, которое будет производиться = 555,55

Количество ежедневно производимых метров ткани Premium = 2166,67

Полученный вклад (путем замены переменных в целевой функции):

Zmax = 4000x + 5000y

Zmax = 4000(555,55) + 5000(2166,67)

Zmax = $13.055.550

Теперь мы можем сравнить результаты с результатами, полученными при решении в Excel, но помните, что метод поиска оптимального решения в графическом методе, который мы используем геометрический и что есть гораздо более сложный, но не менее эффективный способ, которым является метод вершинной итерации. Это состоит в том, чтобы найти все координаты вершин, а затем оценить целевую функцию в каждой координате. Каждая координата дает нам значение в «x» и другое в «y», затем мы заменяем эти значения в целевой функции «4000x + 5000y =?» и оцените результаты, выбрав наибольшее значение.

Решение текстовых задач графическим методом

Задача 1 :

Половина периметра прямоугольного сада, длина которого на 4 м больше его ширины, равна 36 м. Найдите размеры сада.

Решение:

Пусть «x» будет шириной прямоугольного сада

Пусть «y» будет его длиной

y = x + 4  ——— (1)

Половина периметр прямоугольного сада = 36 м

периметр прямоугольника = 2 (L + b)

L + b = 36

y + x = 36

y = 36 — x ——— (2)

Теперь давайте найдем точки пересечения x и y, чтобы построить график.

График 1 ^st строка:

y = x + 4 

x-intercept : положить y = 0 x + 4 = 0 x = -4 (-4, 0)

y — перехват положить x = 0 y = 0 + 4 y = 4 (0, 4)

График 2 ^nd строка :

y = 36 — x

x-intercept : положить y = 0 36 — x = 0 x = 36 (36, 0)

y — перехват поставить x = 0 y = 36 — 0 y = 36 (0, 36)

Две указанные выше линии пересекаются в точке (16, 20). Итак, длина прямоугольного сада 20 м, а ширина прямоугольного сада 16 м.

Задача 2 :

Для заданного линейного уравнения 2 x + 3 y — 8 = 0 напишите другое линейное уравнение с двумя переменными так, чтобы геометрическое представление образованной таким образом пары было:

Решение :

(i) пересекающиеся прямые

Условие пересечения прямых: a₁/a₂ ≠ b₁/b₂.

Согласно приведенному выше условию, мы должны составить уравнение.

 а ₁ = 2          б ₁  = 3            в ₁  = -8

Значения a₂,b₂ и c₂ могут быть любыми реальными значениями, но упрощенные значения a₁/a₂ и b₁/b₂ не должны совпадать.

A ₂ = 3 B ₂ = -3 C ₂ = -16

С. Параллельные прямые

Условие для двух параллельных прямых: a₁/a₂ = b₁/b₂ ≠ c₁/c₂. В соответствии с приведенным выше условием мы должны составить уравнение.

 a ₁  = 2          b ₁  = 3            c ₁  = -8

, если значение a₂, отличное от c₂, равно 4, значение b₂ будет равно 6.