Подробный разбор симплекс-метода / Хабр
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение:
Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
- Делаем замену переменных:
- Если , то
- Если — любой, то , где
Замечание:
Будем нумеровать по номеру неравенства, в которое мы его добавили.
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение:
Точка называется угловой точкой, если представление возможно только при .
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m < n). Разделим переменные на два множества: (n-m) переменные положим равными нулю, а остальные m переменных определяются решением системы исходных уравнений. Если это решение единственно, то тогда ненулевые m переменных называют базисными; нулевые (n-m) переменных – свободными (небазисными), а соответствующие результирующие значения переменных называют базисным решением.
§4. Симплекс-метод
Симплекс-метод позволяет эффективно найти оптимальное решение, избегая простой перебор всех возможных угловых точек. Основной принцип метода: вычисления начинаются с какого-то «стартового» базисного решения, а затем ведется поиск решений, «улучшающих» значение целевой функции.
Необходимые условия для применения симплекс-метода:
- Задача должна иметь каноническую форму.
- У задачи должен быть явно выделенный базис.
Определение:
Явно выделенным базисом будем называть вектора вида:, т.е. только одна координата вектора ненулевая и равна 1.
Замечание: Базисный вектор имеет размерность (m*1), где m – количество уравнений в системе ограничений.
Для удобства вычислений и наглядности обычно пользуются симплекс-таблицами:
- В первой строке указывают «наименование» всех переменных.
- В первом столбце указывают номера базисных переменных, а в последней ячейке – букву Z (это строка функционала).
- В «середине таблицы» указывают коэффициенты матрицы ограничений — aij.
- Последний столбец – вектор правых частей соответствующих уравнений системы ограничений.
- Крайняя правая ячейка – значение целевой функции. На первой итерации ее полагают равной 0.
Замечание:
Базис – переменные, коэффициенты в матрице ограничений при которых образуют базисные вектора.
Замечание: Если ограничения в исходной задаче представлены неравенствами вида ≤, то при приведении задачи к канонической форме, введенные дополнительные переменные образуют начальное базисное решение.
Замечание: Коэффициенты в строке функционала берутся со знаком “-”.
Алгоритм симплекс-метода:
1. Выбираем переменную, которую будем вводить в базис. Это делается в соответствии с указанным ранее принципом: мы должны выбрать переменную, возрастание которой приведет к росту функционала. Выбор происходит по следующему правилу:
- Если задача на минимум – выбираем максимальный положительный элемент в последней строке.
- Если задача на максимум – выбираем минимальный отрицательный.
Такой выбор, действительно, соответствует упомянутому выше принципу: если задача на минимум, то чем большее число вычитаем – тем быстрее убывает функционал; для максимума наоборот – чем большее число добавляем, тем быстрее функционал растет.
Замечание: Хотя мы и берем минимальное отрицательное число в задаче на максимум, этот коэффициент показывает направление роста функционала, т.к. строка функционала в симплекс-таблице взята со знаком “-”. Аналогичная ситуация с минимизацией.
Определение: Столбец симплекс-таблицы, отвечающий выбранному коэффициенту, называется
2. Выбираем переменную, которую будем вводить в базис. Для этого нужно определить, какая из базисных переменных быстрее всего обратится в нуль при росте новой базисной переменной. Алгебраически это делается так:
- Вектор правых частей почленно делится на ведущий столбец
- Среди полученных значений выбирают минимальное положительное (отрицательные и нулевые ответы не рассматривают)
Определение:
Такая строка называется ведущей строкой и отвечает переменной, которую нужно вывести из базиса.
Замечание: Фактически, мы выражаем старые базисные переменные из каждого уравнения системы ограничений через остальные переменные и смотрим, в каком уравнении возрастание новой базисной переменной быстрее всего даст 0. Попадание в такую ситуацию означает, что мы «наткнулись» на новую вершину. Именно поэтому нулевые и отрицательные элементы не рассматриваются, т.к. получение такого результата означает, что выбор такой новой базисной переменной будет уводить нас из области, вне которой решений не существует.
3. Ищем элемент, стоящий на пересечении ведущих строки и столбца.
Определение: Такой элемент называется ведущим элементом.
4. Вместо исключаемой переменной в первом столбце (с названиями базисных переменных) записываем название переменной, которую мы вводим в базис.
5. Далее начинается процесс вычисления нового базисного решения. Он происходит с помощью метода Жордана-Гаусса.
- Новая Ведущая строка = Старая ведущая строка / Ведущий элемент
- Новая строка = Новая строка – Коэффициент строки в ведущем столбце * Новая Ведущая строка
Замечание:
Преобразование такого вида направлено на введение выбранной переменной в базис, т.
6. После этого проверяем условие оптимальности. Если полученное решение неоптимально – повторяем весь процесс снова.
§5. Интерпретация результата работы симплекс-метода
1. Оптимальность
Условие оптимальности полученного решения:
- Если задача на максимум – в строке функционала нет отрицательных коэффициентов (т.е. при любом изменении переменных значение итогового функционала расти не будет).
- Если задача на минимум – в строке функционала нет положительных коэффициентов (т.е. при любом изменении переменных значение итогового функционала уменьшаться не будет).
2. Неограниченность функционала
Однако, стоит отметить, что заданный функционал может не и достигать максимума/минимума в заданной области. Алгебраический признак этого можно сформулировать следующим образом:
При выборе ведущей строки (исключаемой переменной) результат почленного деления вектора правых частей на ведущий столбец содержит только нулевые и отрицательные значения.
Фактически, это значит, что какой бы рост мы не задавали новой базисной переменной, мы никогда не найдем новую вершину. А значит, наша функция не ограничена на множестве допустимых решений.
3. Альтернативные решения
При нахождении оптимального решения возможен еще один вариант – есть альтернативные решения (другая угловая точка, дающая то же самое значение функционала).
Алгебраический признак существования альтернативы:
После достижения оптимального решения имеются нулевые коэффициенты при свободных переменных в строке функционала.
Это значит, что при росте соответствующей переменной с нулевым коэффициентом значение функционала не изменится и новое базисное решение будет также давать оптимум функционала.
Эпилог
Данная статья направлена на более глубокое понимание теоретической части. В замечаниях и пояснениях здесь можно получить ответы на вопросы, которые обычно опускают при изучении этого метода и принимают априори.
Однако, надо понимать, что многие методы численной оптимизации основаны на симплекс-методе (например, метод Гомори, М-Метод) и без фундаментального понимания вряд ли получится сильно продвинуться в дальнейшем изучении и применении всех алгоритмов этого класса.
Чуть позже напишу статью о практической реализации симплекс-метода, а также несколько статей о Методе искусственных переменных (М-Метод), Методе Гомори и Методе ветвей и границ.
Спасибо за внимание!
P.S.
Если уже сейчас Вы мучаетесь с реализацией симплекс-метода, советую почитать книгу А. Таха Введение в исследование операций — там все неплохо разобрано и в теории, и на примерах; а также посмотрите примеры решения задач matburo.ru — это поможет с реализацией в коде.
Симплекс-метод, примеры решения задач
Здесь приведено ручное
(не апплетом) решение двух задач
симплекс-методом (аналогичным решению
апплетом) с подробными объяснениями
для того, чтобы понять алгоритм решения
задач симплекс-методом.
Первая задача
содержит знаки неравенства только »
≤ » (задача с начальным базисом),
вторая может содержить знаки » ≥ «,
» ≤ » или » = » (задача с
искусственным базисом), они решаются
по разному.
1)Симплекс-метод для задачи с начальным базисом (все знаки неравенств-ограничений » ≤ «).
Запишем задачу в канонической форме, т.е. ограничения-неравенства перепишем в виде равенств, добавляя балансовые переменные:
Эта система является системой с базисом (базис s1, s2, s3, каждая из них входит только в одно уравнение системы с коэффициентом 1), x1 и x2 — свободные переменные. Задачи, при решении которых применяется симплекс-метод, должны обладать следующими двумя свойствами: -система ограничений должна быть системой уравнений с базисом; -свободные члены всех уравнений в системе должны быть неотрицательны.
Полученная система
— система с базисом и ее свободные члены
неотрицательны, поэтому можно применить симплекс-метод.
Составим первую симплекс-таблицу
(Итерация 0) для решения задачи на симплекс-метод,
т.е. таблицу коэффициентов целевой
функции и системы уравнений при
соответствующих переменных. Здесь «БП»
означает столбец базисных переменных,
«Решение» — столбец правых частей
уравнений системы. Решение не является
оптимальным, т.к. в z – строке есть
отрицательные коэффициенты.
симплекс-метод итерация 0
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | -6 | 0 | 0 | 0 | 0 | — |
s1 | 2 | 1 | 1 | 0 | 0 | 64 | 64/1=64 |
s2 | 1 | 3 | 0 | 1 | 0 | 72 | 72/3=24 |
s3 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Для улучшения решения
перейдем к следующей итерации симплекс-метода,
получим следующую симплекс-таблицу.
Для этого надо выбрать разрешающий
столбец, т.е.
переменную, которая войдет в базис на
следующей итерации симплекс-метода. Он
выбирается по наибольшему по модулю
отрицательному коэффициенту в z-строке
(в задаче на максимум) – в начальной
итерации симплекс-метода это столбец
x2 (коэффициент -6).
Затем выбирается разрешающая строка, т.е. переменная, которая выйдет из базиса на следующей итерации симплекс-метода. Она выбирается по наименьшему отношению столбца «Решение» к соответствующим положительным элементам разрешающего столбца (столбец «Отношение») – в начальной итерации это строка s3 (коэффициент 20).
Разрешающий элемент находится на пересечении разрешающего
столбца и разрешающей строки, его ячейка
выделена цветом, он равен 1. Следовательно,
на следующей итерации симплекс-метода
переменная x2 заменит в базисе s1.
Заметим, что в z-строке отношение не
ищется, там ставится прочерк » — «.
В случае если есть одинаковые минимальные
отношения, то выбирается любое из них.
Если в разрешающем
столбце все коэффициенты меньше или
равны 0, то решение задачи бесконечно.
Заполним следующую таблицу «Итерация 1». Её мы получим из таблицы «Итерация 0». Цель дальнейших преобразований — превратить разрешающий столбец х2 в единичный (с единицей вместо разрешающего элемента и нулями вместо остальных элементов).
1)Вычисление строки х2 таблицы «Итерация 1». Сначала делим все члены разрешающей строки s3 таблицы «Итерация 0» на разрешающий элемент (он равен 1 в данном случае) этой таблицы, получим строку x2 в таблице «Итерации 1». Т.к. разрешающий элемент в данном случае равен 1, то строка s3 таблицы «Итерация 0» будет совпадать со строкой х2 таблицы «Итерация 1». Строку x2 таблицы «Итерации 1» мы получили 0 1 0 0 1 20, остальные строки таблицы «Итерация 1» будут получены из этой строки и строк таблицы «Итерация 0» следующим образом:
2) Вычисление z-строки
таблицы «Итерация 1».
На месте -6
в первой строке (z-строке) в столбце х2 таблицы «Итерация 0» должен быть 0
в первой строке таблицы «Итерация
1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на 6, получим 0 6
0 0 6 120 и сложим эту строку с первой строкой
(z — строкой) таблицы «Итерация 0» -4
-6
0 0 0 0, получим -4 0
0 0 6 120. В столбце x2 появился ноль
0, цель
достигнута. Элементы разрешающего
столбца х2 выделены красным цветом.
3) Вычисление строки s1 таблицы «Итерация 1». На месте 1 в s1 строке таблицы «Итерация 0» должен быть 0 в таблице «Итерация 1». Для этого все элементы строки х2 таблицы «Итерация 1» 0 1 0 0 1 20 умножим на -1, получим 0 -1 0 0 -1 -20 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 2 1 1 0 0 64, получим строку 2 0 1 0 -1 44. В столбце х2 получен необходимый 0.
4) Вычисление строки
s2 таблицы «Итерация 1». На месте 3
в s2 строке таблицы «Итерация 0» должен
быть 0 в таблице «Итерация 1».
Для
этого все элементы строки х2 таблицы «Итерация 1» 0 1
0 0 1 20 умножим на -3, получим 0 -3
0 0 -3 -60 и сложим эту строку с s1 — строкой таблицы «Итерация 0» 1 3 0
1 0 72, получим строку 1 0
0 1 -3 12. В столбце х2 получен нужный 0. Столбец х2 в таблице «Итерация 1» стал единичным,
он содержит одну 1 и остальные 0.
Строки таблицы «Итерация 1» получаем по следующему правилу:
Новая строка = Старая строка – (Коэффициент разрешающего столбца старой строки)*(Новая разрешающая строка).
Например для z-строки имеем:
Старая z-строка (-4 -6 0 0 0 0) -(-6)*Новая разрешающая строка -(0 -6 0 0 -6 -120) =Новая z-строка (-4 0 0 0 6 120).
Для следующих таблиц пересчет элементов таблицы делается аналогично, поэтому мы его опускаем.
симплекс-метод итерация 1
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | -4 | 0 | 0 | 0 | 6 | 120 | — |
s1 | 2 | 0 | 1 | 0 | -1 | 44 | 44/2=22 |
s2 | 1 | 0 | 0 | 1 | -3 | 12 | 12/1=12 |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | — |
Разрешающий столбец
х1,
разрешающая строка s2,
s2 выходит из базиса, х1 входит в базис.
Совершенно аналогично
получим остальные симплекс-таблицы,
пока не будет получена таблица со всеми
положительными коэффициентами в
z-строке. Это признак оптимальной таблицы.
симплекс-метод итерация 2
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 0 | 4 | -6 | 168 | — |
s1 | 0 | 0 | 1 | -2 | 5 | 20 | 20/5=4 |
x1 | 1 | 0 | 0 | 1 | -3 | 12 | — |
x2 | 0 | 1 | 0 | 0 | 1 | 20 | 20/1=20 |
Разрешающий столбец
s3,
разрешающая строка s1,
s1 выходит из базиса, s3 входит в базис.
симплекс-метод итерация 3
БП | x1 | x2 | s1 | s2 | s3 | Решение | Отношение |
z | 0 | 0 | 6/5 | 8/5 | 0 | 192 | — |
s3 | 0 | 0 | 1/5 | -2/5 | 1 | 4 | — |
x1 | 1 | 0 | 3/5 | -1/5 | 0 | 24 | — |
x2 | 0 | 1 | -1/5 | 2/5 | 0 | 16 | — |
В z-строке все
коэффициенты неотрицательны, следовательно,
получено оптимальное решение x1 = 24, x2 = 16, zmax = 192.
Руководство для начинающих по линейному программированию и симплексному алгоритму | Хенни де Хардер
Ферма с кукурузой. Натюрморт Dall-E 2.Решение широкого круга задач оптимизации
Опубликовано в
·
Чтение через 8 мин.
·
9 января
инструмент. Он находит применение в самых разных областях, включая инженерное дело, финансы и исследования операций. Линейное программирование использовалось для решения таких разнообразных задач, как планирование рейсов авиакомпаний и проектирование производственных процессов. В этом сообщении блога мы рассмотрим основы линейного программирования и то, как его можно использовать для решения практических задач.
Линейное программирование (ЛП) — это метод математической оптимизации. Он используется для поиска оптимального решения задач, связанных с несколькими переменными и ограничениями.
Представляя ограничения и целевую функцию задачи в виде системы линейных уравнений и неравенств, алгоритмы линейного программирования могут систематически искать пространство решений и находить решения, которые максимизируют или минимизируют заданную цель.
Сначала приведу простой пример. Затем мы углубимся в симплекс-алгоритм, который используется в фоновом режиме для быстрого поиска оптимального решения задач LP.
Предположим, у фермера есть 120 акров земли, на которых он выращивает две культуры: пшеницу и кукурузу. Для пшеницы требуется 2 акра земли на тонну, а для кукурузы требуется 1 акр земли на тонну. Фермер хочет максимизировать прибыль от урожая, которая составляет 100 евро с тонны пшеницы и 150 евро с тонны кукурузы. У фермера также есть ограничение в 50 тонн пшеницы и 40 тонн кукурузы, которые можно произвести.
Чтобы решить эту задачу с помощью линейного программирования, нам сначала нужно определить переменные решения, то есть количество пшеницы и кукурузы, которое фермер будет выращивать.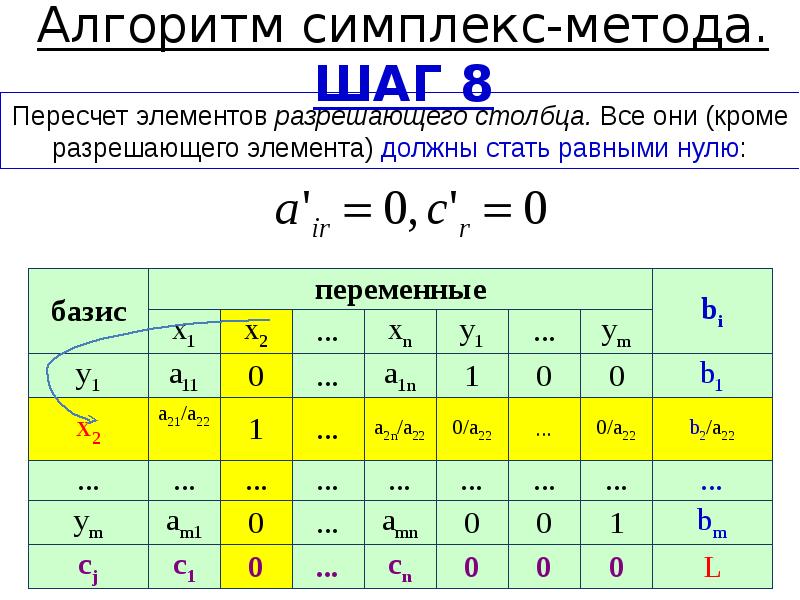
Мы будем использовать переменные w и c для представления количества тонн пшеницы и кукурузы соответственно.
Далее нам нужно написать целевую функцию, которая представляет собой прибыль, которую фермер хочет максимизировать. В этом случае целевая функция:
Затем нам нужно записать ограничения, которые представляют пределы количества пшеницы и кукурузы, которые могут быть произведены. Ограничения:
Первые два ограничения представляют ограничения на общее количество тонн пшеницы и кукурузы, которое может быть произведено. Третье ограничение представляет собой ограничение на общее количество доступной земли.
Чтобы решить эту задачу, мы можем использовать симплекс-алгоритм или другой метод линейного программирования, чтобы найти значения w и c , которые максимизируют целевую функцию с учетом ограничений. В этом случае оптимальным решением будет выращивание 40 тонн пшеницы и 40 тонн кукурузы, что принесет прибыль в размере 10 000 евро.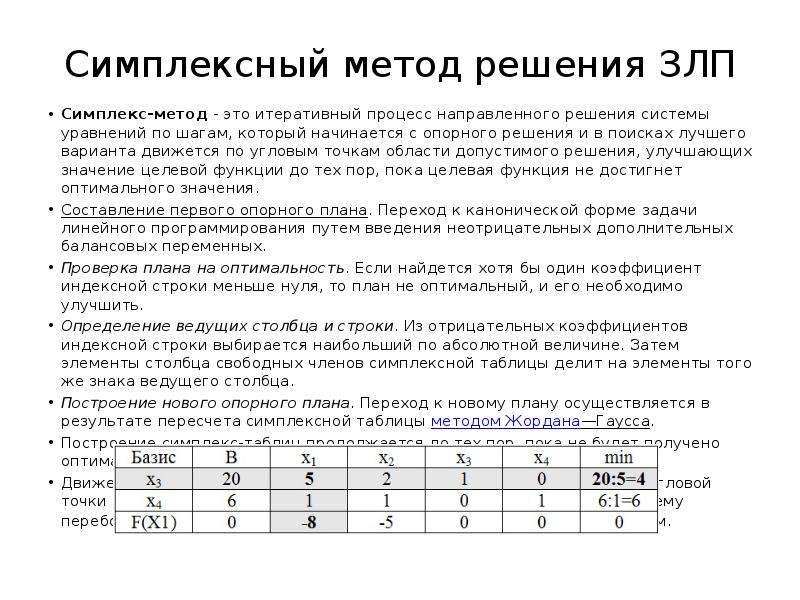
Это простой пример, иллюстрирующий основные этапы решения задачи линейного программирования. На практике линейное программирование используется для решения гораздо более сложных задач с большим количеством переменных и ограничений.
Ниже визуализация проблемы:
Визуализация линейного программирования. Изображение автора.Серая область называется допустимой областью. Каждая точка области содержит допустимое решение. Область ограничена ограничениями.
Фундаментальная теорема линейного программирования утверждает, что максимумы приходятся на углы области. Это важная информация, которую использует симплексный алгоритм.
Симплекс-алгоритм — широко используемый метод решения задач линейного программирования. Он был разработан Джорджем Данцигом в 1947. Интуиция, лежащая в основе алгоритма, состоит в том, чтобы систематически «ходить» из угла в угол в допустимом пространстве области. Когда оптимальное решение найдено, процесс останавливается.
Симплекс-алгоритм — это итеративный процесс, основанный на математических вычислениях и логических рассуждениях для поиска оптимального решения задачи линейного программирования.
Он эффективен и надежен, а также используется в смешанном целочисленном программировании (после ослабления ограничений). Основные шаги симплексного алгоритма следующие:
- Преобразование ограничений задачи линейного программирования в систему линейных уравнений стандартной формы.
- Найдите базовое возможное решение, установив некоторые переменные равными нулю и найдя оставшиеся переменные.
- Протестируйте базовое допустимое решение, чтобы убедиться, что оно оптимально. Если это так, алгоритм завершен. Если нет, алгоритм выбирает переменную для входа в базис и соответствующим образом обновляет базовое допустимое решение.
- Повторяйте шаг 3, пока не будет найдено оптимальное решение.
Давайте пройдемся по шагам один за другим на примере пшеницы и кукурузы.
Шаг 1. Преобразовать ограничения задачи линейного программирования в систему линейных уравнений стандартной формы.
Первый шаг — переписать ограничения и цель в стандартной форме:
Изображение автора.В стандартной форме знаки «меньше чем» заменяются знаками равенства, и к каждому ограничению добавляется резервная переменная (s1, s2, s3). Таким образом, значение меньше чем сохраняется, потому что переменные резерва могут принимать только положительные значения.
Часто для облегчения чтения задачи используется таблица. Таблица — это таблица, в которую мы записываем коэффициенты. Столбец представляет собой переменную, а строка — ограничение. В этом случае нижняя строка содержит коэффициенты цели. Последний столбец содержит значения в правой части уравнений. Мы используем стандартную форму для создания таблицы:
Таблица для задачи о кукурузе и пшенице. Каждое ограничение и цель представлены в строках, а столбцы представляют переменные. Значения являются коэффициентами. Изображение автора. Шаг 2. Найдите базовое допустимое решение, приравняв некоторые переменные к нулю и найдя оставшиеся переменные.
Теперь, когда у нас есть таблица, мы можем использовать ее для поиска базового допустимого решения.
Базовое допустимое решение — это решение, удовлетворяющее всем ограничениям и лежащее в вершине. Мы можем легко обнаружить один из таблицы.
В таблице есть два типа переменных: основных переменных и неосновных переменных . Базовые переменные имеют только одну ненулевую запись, а неосновные переменные имеют более одной ненулевой записи. базис содержит все основные переменные. Если мы посмотрим на текущее состояние таблицы, то в основе лежат переменные резерва с₁ , с₂ и с₃ . Переменные w и c не являются базовыми и равны нулю. Текущее базовое допустимое решение имеет следующие значения: с₁ = 50, с₂ = 40, с₃ = 120, Z = 0, w = 0 и c 900 26 = 0,
Небазовый и основные переменные. Изображение автора.Это решение соответствует следующей угловой точке:
Начальная точка симплексного алгоритма. Изображение автора. Шаг 3. Протестируйте базовое допустимое решение, чтобы убедиться, что оно оптимально.
Если это так, алгоритм завершен. Если нет, алгоритм выбирает переменную для входа в базис и соответствующим образом обновляет базовое допустимое решение.
Проверить, является ли базовое возможное решение оптимальным, можно, взглянув на целевую строку в таблице. Поскольку это задача максимизации, мы можем улучшить ее, удалив отрицательные коэффициенты. Мы больше не сможем улучшаться, если все отрицательные значения исчезнут. В нижнем ряду отрицательные значения, поэтому возможно улучшение, а оптимальное решение пока не найдено.
Теперь нам нужно выбрать переменную для входа в базу. Чтобы выбрать входящую переменную, возьмите наименьший коэффициент в целевом ряду. В нашем случае это -150, что соответствует c. Это вводимая переменная. Затем нам нужно выбрать строку для выполнения исключения Гаусса. Это делается путем деления значений RHS на коэффициенты c .
Итак, в нашем случае мы получили 40/1=40 для второй строки и 120/1=120 для третьей строки. Наименьшее значение — 40, поэтому используется вторая строка. Теперь мы можем стереть таблицу строкой 2, чтобы включить c в базисе:
Новое целевое значение равно 6000, а переменные в базе — c , с₁ и с₃ , равные 40, 50 и 80 соответственно. Мы перешли к новой угловой точке, следующему базовому допустимому решению:
Теперь мы перешли к следующему допустимому решению (нижний правый угол). Изображение автора. Шаг 4. Повторяйте шаг 3, пока не будет найдено оптимальное решение.
Оптимальное решение не найдено, так как в целевой строке таблицы есть отрицательное значение. Итак, давайте повторим шаг 3: вводимая переменная w , потому что она имеет самый низкий коэффициент в целевой строке.
Строка, которую мы должны использовать для исключения Гаусса, — это строка 3, потому что 80/2 < 50/1. После сокращения строки таблица выглядит следующим образом:
Переменные в базе: w , c и s₁ с соответствующими значениями 40, 40 и 10 соответственно. Значение Z (цель) равно 10000. Это как раз оптимальное решение, которое у нас было в начале. В нижней строке нет отрицательных записей, так что это оптимальное решение. Шагов, которые мы сделали:
Шагов, которые мы сделали при решении задачи с симплекс-алгоритмом. Начиная снизу слева, делая два шага, чтобы закончить на оптимальном решении. Изображение автора.Это простой пример того, как работает симплексный алгоритм. Он используется для решения более сложных задач, чем та, которую мы здесь обсуждали.
Линейное программирование — это инструмент, который может помочь отдельным лицам и организациям максимально эффективно использовать свои ресурсы и достигать своих целей.
Независимо от того, являетесь ли вы владельцем бизнеса, пытающимся максимизировать прибыль, исследователем, стремящимся оптимизировать сложный процесс, или студентом, изучающим методы оптимизации, линейное программирование предлагает широкий спектр приложений и возможностей для роста. Поняв принципы линейного программирования и симплекс-алгоритм, вы сможете сделать первый шаг к решению множества задач оптимизации и принятию обоснованных решений, которые могут иметь долгосрочные последствия.
При применении этих методов на практике вам не нужно реализовывать алгоритм, потому что это сделает за вас программное обеспечение для оптимизации.
Симплекс-алгоритм также применяется в смешанном целочисленном программировании, где ослабление ограничений позволяет применить алгоритм. Если вы хотите узнать больше, вы можете прочитать статьи ниже.
Как справиться с проблемами оптимизации?
Простые примеры с решениями и кодом.
по направлению datascience.
com
Эвристика математической оптимизации, которую должен знать каждый специалист по данным
Локальный поиск, генетические алгоритмы и многое другое.
в направлении datascience.com
Симплексный метод: простой способ. Примерный подход к пониманию… | by Vijayasri Iyer
Примерный подход к пониманию метода симплексной оптимизации решить задачи линейного программирования (ЛП). LP занимается поиском оптимального решения линейной функции с учетом некоторых линейных ограничений. Он используется в реальных задачах оптимизации в нескольких областях. Сегодня давайте попробуем понять работу этого алгоритма простым и кратким образом, используя пример, который поможет нам в этом.
Метод- Настройка/преобразование LP в стандартную форму максимизации.
- Настроить начальную симплексную таблицу
- Определить опорную точку
- Найти оптимальную таблицу методом Гаусса-Жордана
- Проверить оптимальность таблицы
- Найти оптимальное решение
Шаг 1: Преобразовать LP в стандартный максимум форма имизации
Учитывайте следующее пример:
Задача максимизации (Примечание: В случае задачи минимизации ее можно преобразовать в задачу двойной максимизации, умножив на -1.
)
В стандартной форме LP все ограничений являются уравнениями и все переменных неотрицательны . Можно выполнить следующие шаги преобразования, чтобы преобразовать все неравенств в ограничения равенства .
- Если ограничение имеет тип (x + y ≤ c), используйте резервную переменную «s» (где «s» неотрицательно), так что x+y+s = c.
2. Если ограничение относится к типу (x + y ≥ c), используйте дополнительную переменную «s» (где «s» неотрицательно), так что х+у-с = с .
Используя этот метод преобразования в нашем примере, мы получаем следующую систему уравнений полученный. Это выглядит примерно так:
Tableau 1.1Шаг 4: Определение опорной точки
В симплексной таблице опорная точка идентифицируется с использованием следующих двух условий
- Сводная колонка выбирается путем определения самой отрицательной записи в нижней строке таблицы.
- Опорная строка определяется путем деления констант (столбец C в таблице) на коэффициенты опорной колонки. Строка, содержащая наименьшее частное, будет основной строкой.
(Подробное объяснение этого метода можно найти здесь.)
В нашем примере столбец «y» является сводным столбцом, поскольку он содержит -40, а сводная строка — R3 (строка 3), поскольку 12/ 2 =6 — наименьший коэффициент в сводном столбце. Следовательно, наш опорный элемент равен 2,9.0005 Таблица 1.2
Шаг 3. Определите оптимальные значения, выполнив операции поворота с использованием метода исключения Гаусса-ЖорданаПосле того, как мы определили элемент поворота, мы выполним метод исключения Гаусса (выполним преобразования строк на R1, R2, R3, R4 ). Мы преобразуем опорный элемент в 1 , а все остальные элементы опорного столбца — в 0. . В этом случае мы будем использовать следующие преобразования строк, чтобы получить результат
9.
0256Наша выходная таблица будет
Tableau 1.3 9 0006 Прежде чем мы приступим к двум следующим Шаги, есть два термина, с которыми вам нужно ознакомиться.Базовая переменная : Обычно говорят, что сводной столбец представляет базовую переменную. Хотя, если говорить проще, базовой переменной является любая переменная в таблице, которая имеет только один ненулевой элемент, т.е. представляет собой единичную матрицу. В таблице 1.3 y, s1, s2 и P являются основными переменными. Для математического определения, пожалуйста, проверьте здесь.
Небазовая переменная : Небазовая переменная, с другой стороны, не представляет единичную матрицу и имеет более одного ненулевого элемента. В таблице 1.3 s3 и x являются неосновными переменными.
Когда нам нужно определить основное допустимое решение, мы установим все неосновные переменные в 0, что даст нам максимальные значения основных переменных.
Установив s3, x = 0, получим y = 6, s1 = 4, s2 = 1, P = 240.
Теперь по симплекс-методу, если в самой нижней строке (т.е. R4) нет отрицательного коэффициента мы можем остановиться здесь. Если нет, то мы повторяем шаги 3 и 4 , пока не удалим все отрицательные члены в нижней строке и не найдем оптимальное решение. В нашей таблице у нас есть -10 в R4, поэтому нам нужно выполнить еще одну итерацию шагов 3 и 4.
Итерация 2
Используя процедуру шага 3, мы идентифицируем нашу новую точку поворота как 1/2 в R2, а столбец «х».
Tableau 1.4Мы будем использовать следующие преобразования строк, чтобы сделать все записи 0 в сводной таблице 1 в столбце «x».
- R2->2R2
- R1->R1–3/2R2
- R3->R3–1/2R2
- R4 ->R4+10R2
Присвоив неосновным переменным значение 0, мы получим x =2, y=5 , s1=1 и P = 260. Следовательно, наши оптимальные значения для x и y равны 2,5. Для тех, кто заинтересован в решении таких задач с использованием графического подхода, пожалуйста, обратитесь сюда.