ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме.  Формула Муавра. Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 34. Сложная функция. 35. Обратная функция. 36.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения).  60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 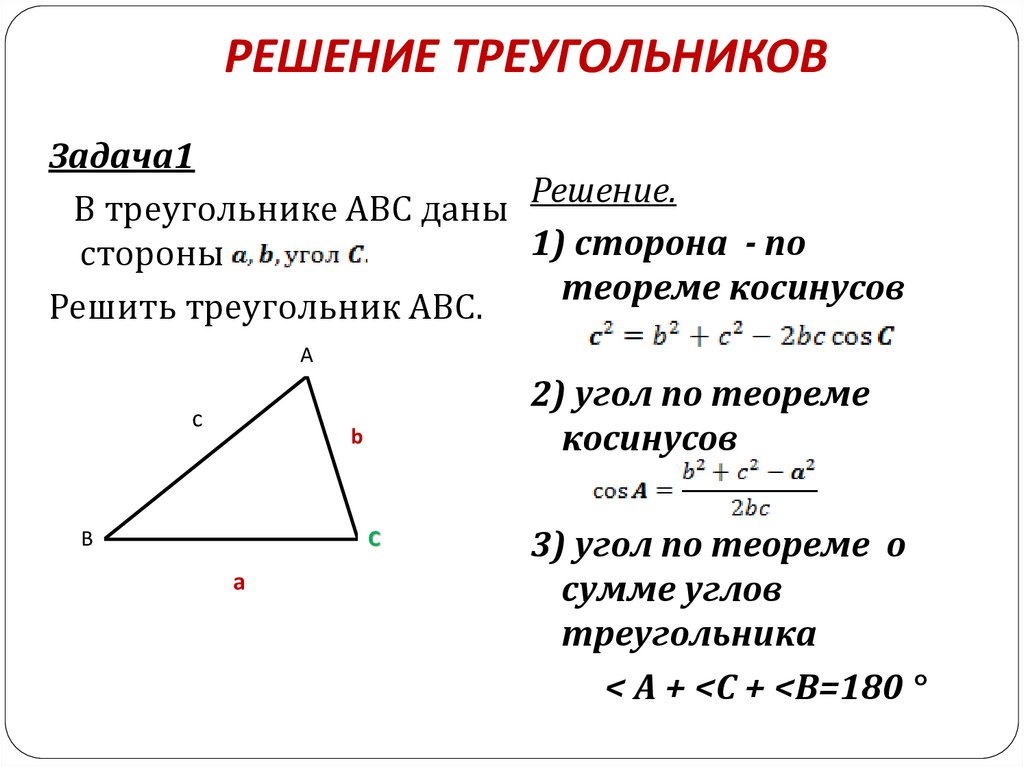 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1.  Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 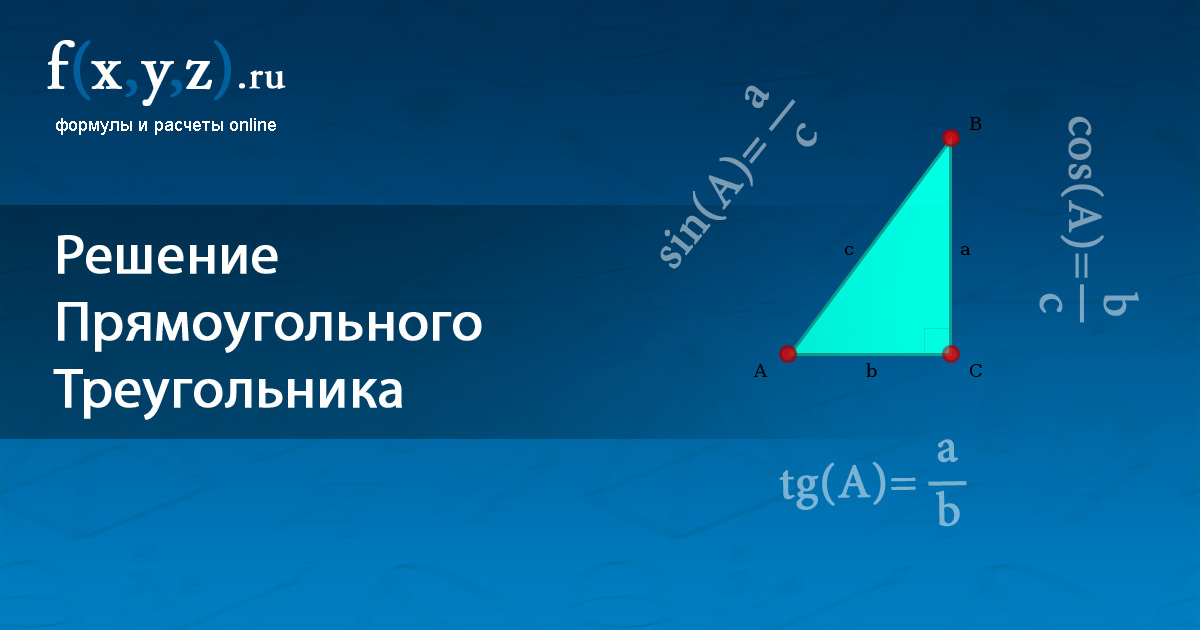 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса.  253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Урок геометрии в 9-м классе по теме: «Решение треугольников»
- Осипкова Валентина Ивановна, учитель технологии
Разделы: Математика
Цель: закрепить знание учащихся теорем синусов и косинусов, научить применять эти теоремы в ходе решения задач.
Оборудование:
- таблицы с изображением треугольников;
- карточки с формулами;
- калькуляторы;
- таблицы Брадиса;
- тест для каждого ученика.

ХОД УРОКА
I. Организация класса. Проверка готовности к уроку. Сообщение темы и цели урока.
II. Повторение изученного материала (или этап разминки)
1. Продолжите:
Квадрат стороны треугольника равен… (теорема косинусов)
2. Заполните пропуски:
3. Продолжите:
Стороны треугольника пропорциональны… (теорема синусов)
4. Заполните пропуски
:
5. Соединить линией части фраз, соответствующие друг другу:
Решение треугольников состоит
— в нахождении неизвестных высот, медиан и биссектрис по известным углам и сторонам треугольника;
— в нахождении неизвестного периметра по известным углам и сторонам треугольника;
— в нахождении неизвестных сторон и углов треугольника по известным его углам и сторонам.
III. Закрепление изученного материала.
1.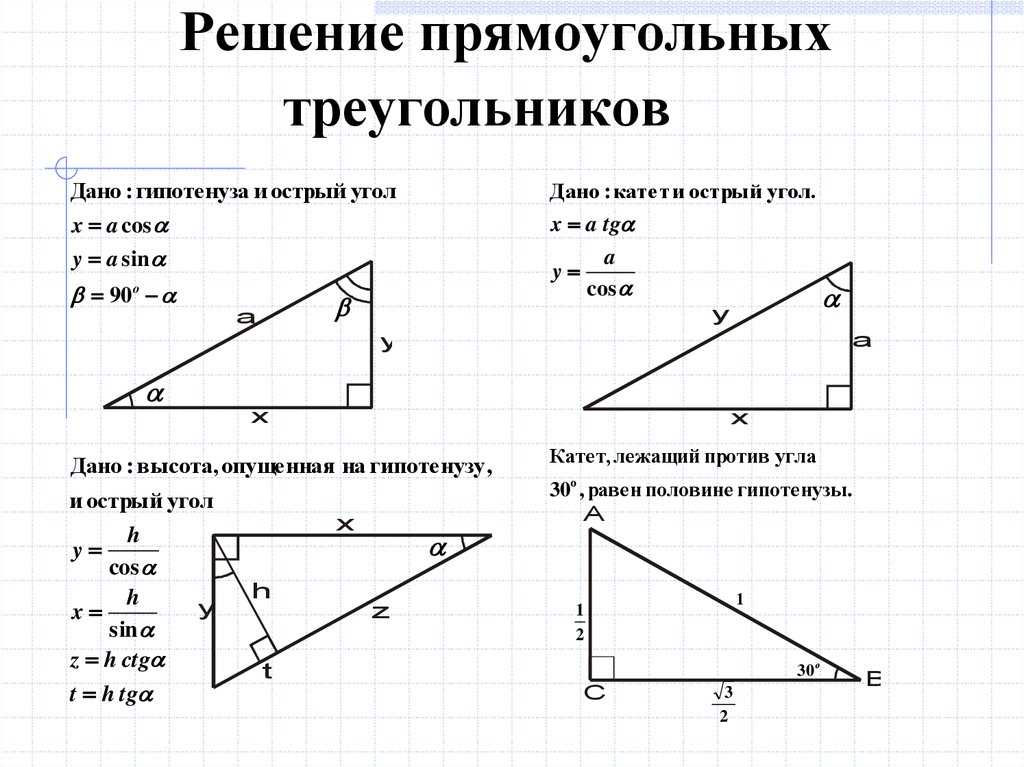 Решение задач по готовым формулам
Решение задач по готовым формулам
Определить формулу, по которой нужно найти данный неизвестный элемент:
карточки с формулами:
2. Решение задач, вытащив одну из карточек:
IV. Промежуточный контроль. Тест для всего класса по вариантам:
Вариант 1.
1. Поставить знак “+” рядом с верным утверждением:
а) Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон;
б) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними;
в) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон, минус произведение этих сторон на косинус угла между ними.
2. Для данного треугольника справедливо равенство…
3. Косинус угла 120° равен…
а) ;
б) -;
в) -;
г) нет правильного ответа.
4. Найти синус 29°30′. Подчеркнуть верный ответ:
а) 0,4919;
б) 0,8707;
в) 0,4924;
г) 0,8701.
5. Чтобы вычислить в треугольнике КМD, нужно знать…
а) КМ, МD, KD;
б) КМ, МD, ;
в) КD, МD, ;
г) нет правильного ответа.
6. Стороны треугольника 5 см и 4 см, а угол между ними равен 30°. Найти третью сторону треугольника.
а)см;
б)см;
в) 5 см;
г) 3 см.
Вариант 2
1. Поставить знак “+” рядом с верным утверждением:
а) Стороны треугольника пропорциональны синусам противолежащих углов;
б) Стороны треугольника обратно пропорциональны синусам противолежащих углов;
в) Стороны треугольника пропорциональны синусам противолежащих углов.
2. Для данного треугольника справедливо равенство…
3. Синус угла 135° равен…
а) ;
б) -;
в) 1;
г) нет правильного ответа.
4. Найти косинус 67°18′. Подчеркнуть верный ответ:
а) 0,3883;
б) 0,9222;
в) 0,9216;
г) 0,3859.
5. В треугольнике АВС известны длина стороны ВС и величина угла С. Чтобы вычислить АВ, нужно знать…
а) АС;
б) ;
в) ;
г) нет правильного ответа.
6. Стороны треугольника 5 см и 3 см, а угол между ними 60°. Найдите третью сторону треугольника.
а) 2 см;
б);
в);
г) 4 см.
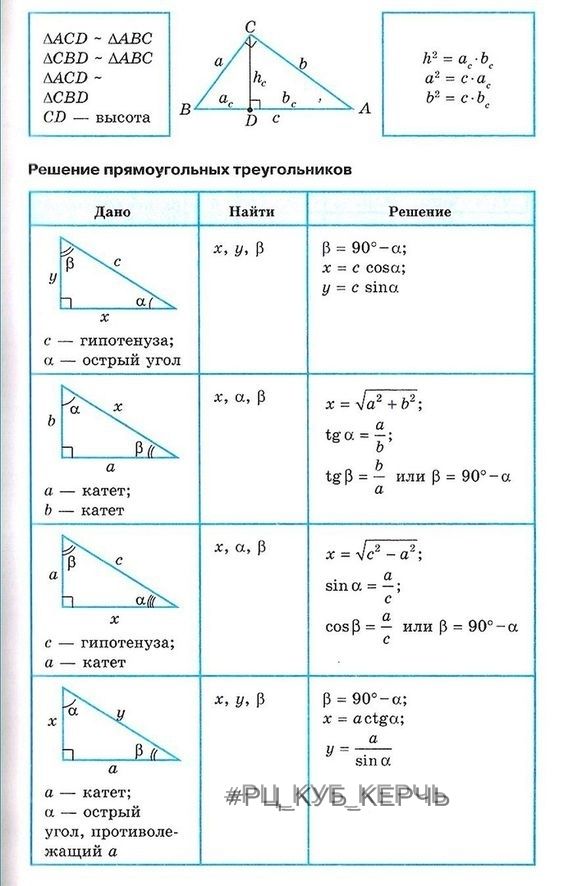
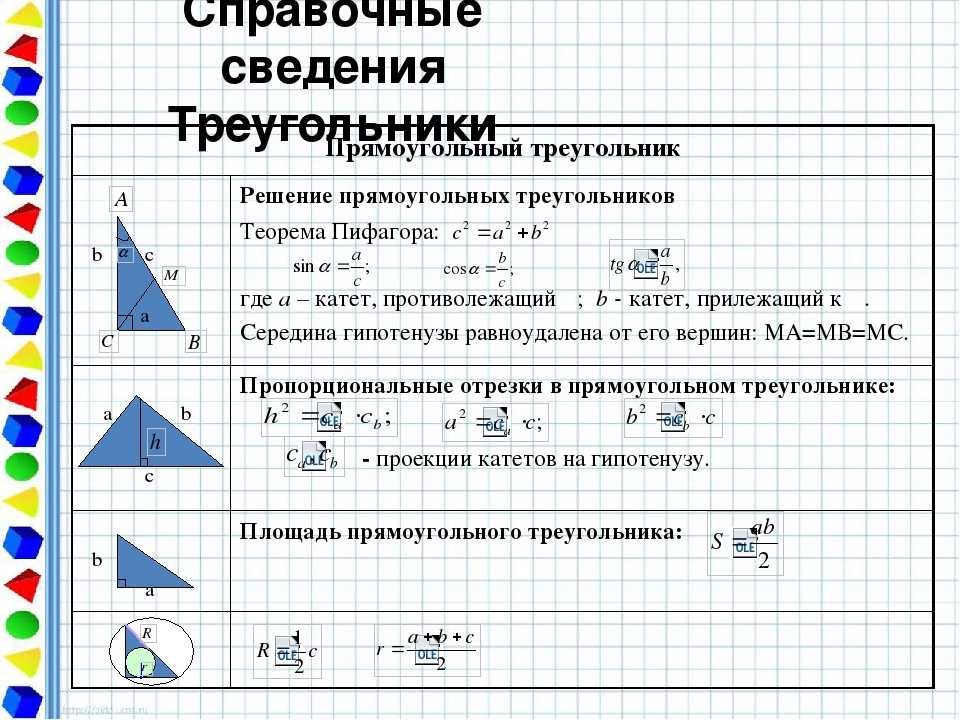
Решение прямоугольных треугольников
Треугольники состоят из трех отрезков. Они встречаются, образуя три угла. Размеры углов и длины сторон связаны друг с другом. Зная размеры (длину) трех из шести частей треугольника (должна быть включена хотя бы одна сторона), можно найти размеры остальных сторон и углов. Если треугольник прямоугольный, вы можете использовать простые тригонометрические отношения, чтобы найти недостающие части. В общем треугольнике (остром или тупоугольном) нужно использовать другие приемы, в том числе закон косинусов и закон синусов. Вы также можете найти площадь треугольника, используя тригонометрические соотношения.
Вы также можете найти площадь треугольника, используя тригонометрические соотношения.Все треугольники состоят из трех сторон и трех углов. Если три угла треугольника помечены ∠ A , ∠ B и ∠ C , то три стороны треугольника должны быть помечены как a , b и c . На рис. 1 показано, как строчные буквы используются для обозначения сторон треугольника, противоположных углам, обозначенным соответствующими прописными буквами. Если известны любые три из этих шести измерений (помимо трех углов), то вы можете вычислить значения трех других измерений. Процесс нахождения пропущенных измерений известен как решение треугольника . Если треугольник прямоугольный, то один из углов равен 90°. Следовательно, вы можете решить прямоугольный треугольник, если вам известны меры двух из трех сторон или если вам известны меры одной стороны и одного из двух других углов.
Рисунок 1
Чертеж для примера 1.
Пример 1 : Решите прямоугольный треугольник, показанный на рисунке (b), если ∠ B = 22°
Поскольку сумма трех углов треугольника должна составлять 180°, ∠ A = 90 ∠ B, таким образом, ∠ A = 68°.
Ниже приведен альтернативный способ решения для сторон a и c:
Это альтернативное решение может быть проще, поскольку в нем нет деления.
Пример 2 : Решите прямоугольный треугольник, показанный на рисунке (b), если b = 8 и a = 13.
Вы можете использовать теорему Пифагора, чтобы найти недостающую сторону, но вместо этого используются тригонометрические отношения. Сначала будут найдены два отсутствующих измерения угла, а затем отсутствующая сторона.
Во многих приложениях определенные углы обозначаются специальными именами. Два из этих специальных имен — , угол подъема и , угол наклона .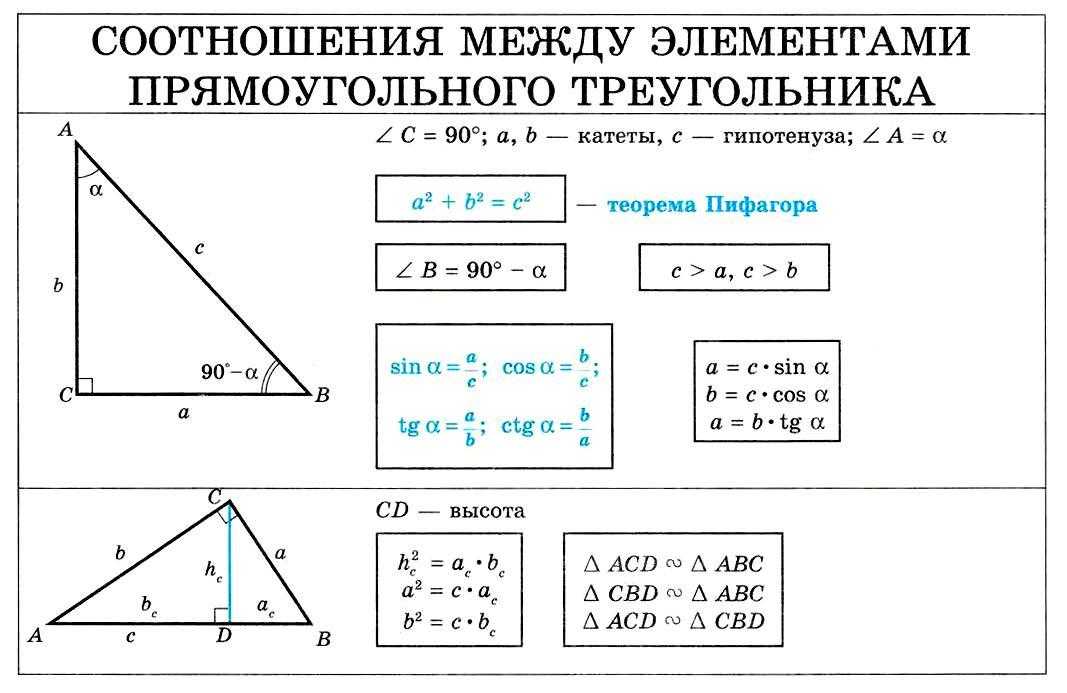 В примерах, показанных на рис. 2, используются эти термины.
В примерах, показанных на рис. 2, используются эти термины.
Пример 3: Большой самолет (самолет A) , летящий на высоте 26 000 футов, видит самолет меньшего размера (самолет B) , летящий на высоте 24 000 футов. Угол депрессии 40°. Каково расстояние прямой видимости ( x ) между двумя плоскостями?
На рисунке 3 показаны условия этой проблемы.
Рисунок 3
Рисунок для примера 3.
Из рисунка 3 можно найти решение, используя синус 40°:
Пример 4: Лестница должна достигать вершины здания. Основание лестницы будет на расстоянии 25 футов от основания здания. Угол подъема от основания лестницы до верха здания составляет 64°. Найдите высоту здания (h) и длину лестницы ( м ).
На рисунке 4 показаны условия этой проблемы.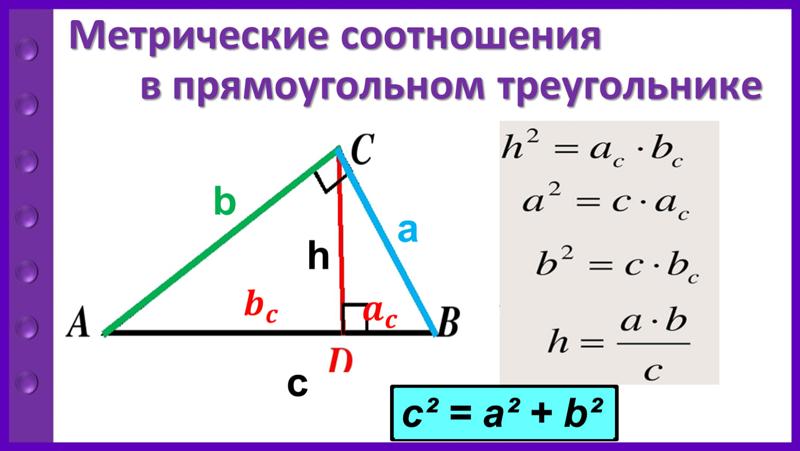
Рисунок 4
Чертеж для примера 4.
Пример 5: Дровосек хочет определить высоту высокого дерева. Он стоит на некотором расстоянии от дерева и определяет, что угол возвышения к вершине дерева равен 40°. Он приближается к дереву на 30′, и теперь угол возвышения составляет 50°. Если глаза дровосека находятся на высоте 5 футов над землей, какой высоты будет дерево?
Рисунок 5 может помочь вам визуализировать проблему.
Рисунок 5
Чертеж для примера 5.
Из маленького прямоугольного треугольника и из большого прямоугольного треугольника очевидны следующие отношения:
Подстановка первого уравнения во второе дает:
Обратите внимание, что к значению x нужно добавить 5 футов, чтобы получить высоту дерева, или 90,06 футов в высоту.
Пример 6: Используя рисунок 6, найдите длины сторон x и y и площадь большого треугольника.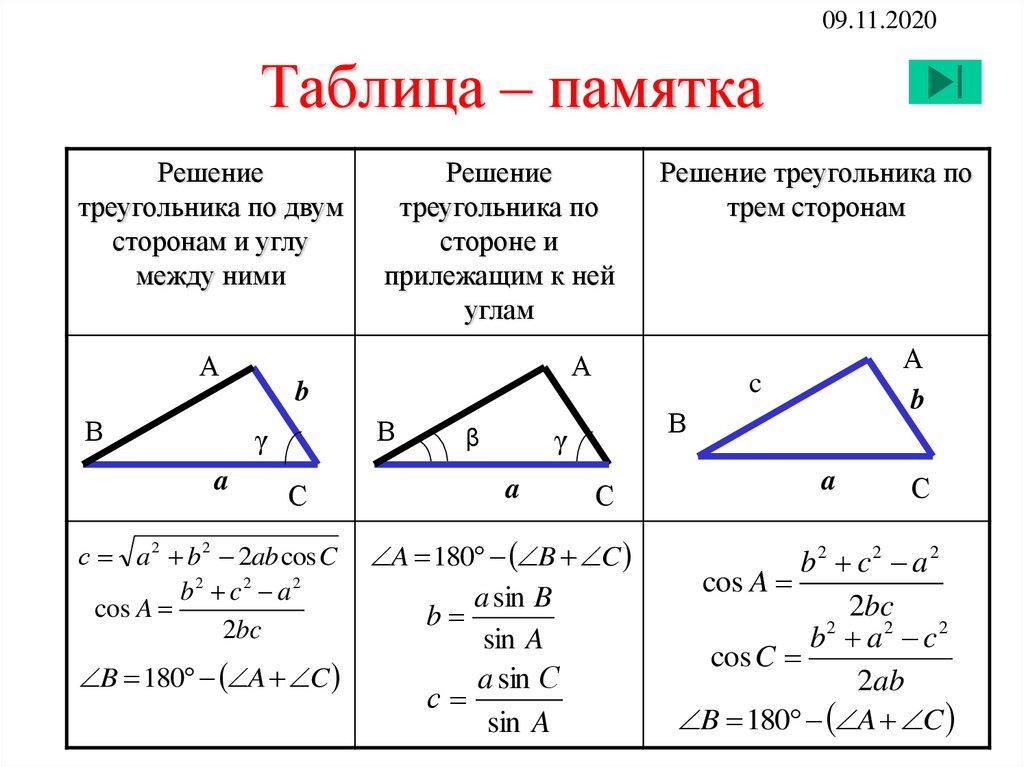
Рисунок 6
Чертеж для примера 6.
Поскольку это равнобедренный треугольник, и равные стороны являются противоположными равными углами, значения x и y совпадают. Если треугольник разделить на два прямоугольных треугольника, основание каждого будет равно 6. Следовательно,
Тригонометрия треугольника: значение, формула и применение
Вы когда-нибудь задумывались, как устроена крыша здания? Или вы задавались вопросом, как измерить высоту дерева, не взбираясь на него? На все эти вопросы можно ответить с помощью тригонометрии треугольника. Находя углы и длины сторон в треугольниках, такие люди, как архитекторы, могут рассчитать уклон крыши.
Что такое определение тригонометрии треугольника?
Во-первых, давайте посмотрим, что такое тригонометрия треугольника.
Тригонометрия треугольника — это раздел математики, изучающий отношения между длинами сторон и углами в треугольнике.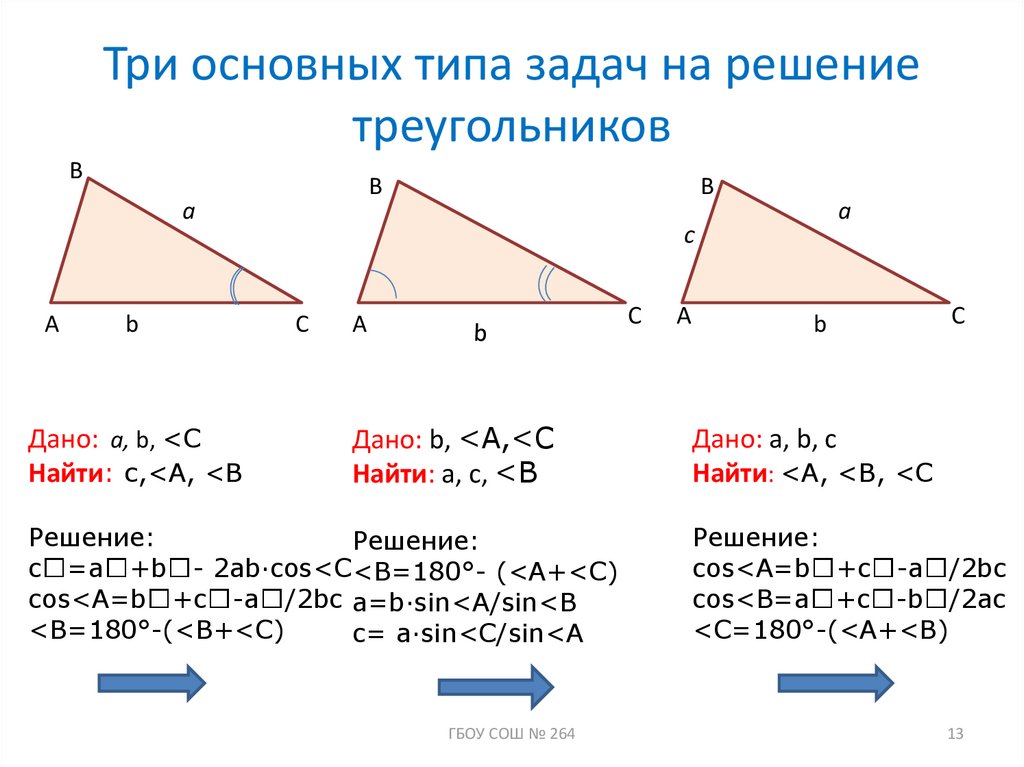
Возможно, вы слышали о тождествах треугольников и тригонометрических тождествах и задавались вопросом, в чем разница.
Тождество треугольника — это правило, верное для всех треугольников. Это включает в себя такие правила, как: 9\circ\), также известный как \(\pi /2\) радианы; и
С другой стороны, тригонометрических тождеств верны ТОЛЬКО для прямоугольных треугольников. К ним относятся такие вещи, как:
- Закон синусов;
- Закон косинусов;
- Теорема Пифагора;
- и многое другое!
Формулы в тригонометрии треугольников
Формулы тригонометрии могут помочь вам найти недостающие длины сторон и недостающие углы в треугольниках. Существуют разные формулы, которые используются в зависимости от того, какую информацию вы получили о треугольнике.
Сначала давайте посмотрим, как вы обычно обозначаете прямоугольный треугольник.
Гипотенуза — это сторона, лежащая против прямого угла. Это всегда сторона с наибольшей длиной в треугольнике.
Выберите угол и дайте ему имя. В этом случае на картинке ниже она называется \(\theta\). Противоположная сторона — это сторона, противоположная углу \(\theta\).
Соседняя сторона — это сторона, примыкающая к углу \(\theta\).
Рис. 1. Маркировка треугольника.
SOHCATOA
В тригонометрии треугольников существуют различные правила (также называемые тригонометрическими тождествами), которым вы можете следовать, чтобы использовать правильные тригонометрические функции. Глядя на прямоугольный треугольник, вы можете пометить каждую сторону, чтобы определить, какую функцию лучше всего использовать. Существует аббревиатура под названием SOHCATOA, которая может помочь вам запомнить, какую функцию использовать.
SOH — S ine equals O pposite over H ypotenuse
CAH — C osine equals A djacent over H ypotenuse
TOA — T Angent равен O pposite над A djacent
SOHCAHTOA применяется только к прямоугольным треугольникам!
Формулы и SOHCATOA
После того, как вы пометили свой треугольник, вы можете определить, какую функцию лучше всего использовать, чтобы получить информацию о прямоугольном треугольнике, а также какую информацию подставить в формулу. Ниже вы можете увидеть шесть основных тригонометрических функций и формулы для каждой из функций:
Ниже вы можете увидеть шесть основных тригонометрических функций и формулы для каждой из функций:
\[ \begin{align} \sin \theta &= \frac {\mbox{противоположный}}{\mbox{гипотенуза}} \\ \cos \theta &= \frac{\mbox{adjacent}}{\ mbox{гипотенуза}}\\ \tan \theta &= \frac {\mbox{напротив}} {\mbox{смежный}} \\ \csc \theta &= \frac{\mbox{гипотенуза}}{\mbox { напротив}}\\ \sec \theta &= \frac {\mbox{гипотенуза}}{\mbox{смежный}} \\ \cot \theta &= \frac{\mbox{смежный}}{\mbox{напротив} }\end{align} \]
Для каждой функции вы можете видеть, что вам нужно ввести информацию из помеченного прямоугольного треугольника, чтобы найти значение функции.
Способ использования формулы можно разбить на этапы:
Шаг 1: Подпишите треугольник.
Шаг 2: Выберите правильную функцию.
Шаг 3: Введите переменные из треугольника и решите, что вам нужно.
Конечно, проще увидеть, как использовать эти вещи на примере.
Найдите значение функции синуса для угла \( \theta\).
Рис. 2. Нахождение угла в треугольнике.
Ответ:
Давайте работать по шагам.
Шаг 1: Обозначьте треугольник. Вам даны гипотенуза и противоположная сторона, так что отметьте их на схеме.
Рис. 3. Треугольник с гипотенузой и противоположными сторонами.
Шаг 2: Выберите правильную функцию.
Когда вам известны противоположность и гипотенуза, у вас есть все необходимое для использования функции синуса.
\[ \sin \theta = \frac{\mbox{напротив}} {\mbox{гипотенуза}} \]
Шаг 3: Введите переменные из треугольника и найдите \(\sin \theta \) .
В этом случае противоположная сторона равна \( 6 \; \text{см}\), а гипотенуза равна \( 8 \; \text{см}\), так что у вас есть
\[ \sin \theta = \ гидроразрыв {6} {8} = \ гидроразрыв {3} {4}. \]
Как насчет площади треугольника?
Площадь треугольников и тригонометрия
Площадь треугольника — это способ рассказать о пространстве внутри трех сторон треугольника.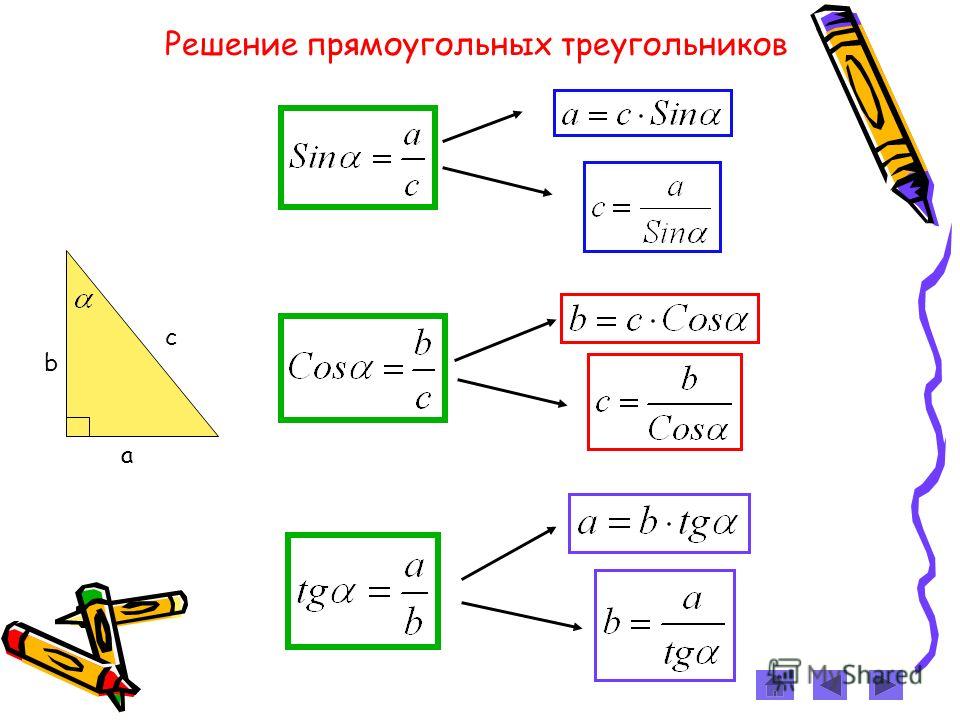 Взгляните на площадь треугольника для получения дополнительной информации и примеров!
Взгляните на площадь треугольника для получения дополнительной информации и примеров!
Применение тригонометрии прямоугольного треугольника
Тригонометрия прямоугольного треугольника может быть применена ко многим различным сценариям реальной жизни. Его можно использовать, чтобы помочь людям понять расстояния. Высоту деревьев или расстояние от вершины утеса до подножия можно измерить с помощью тригонометрии, если вы знаете углы. Эти углы известны как угол возвышения или угол депрессии.
Угол возвышения — это угол от горизонтальной линии до объекта над линией.
Давайте рассмотрим пример.
Предположим, у вас есть дерево, и вы хотите узнать его высоту. От основания дерева вы отступаете на \(100\) футов и с помощью транспортира измеряете угол до вершины дерева от вашего текущего положения, который составляет \(60\) градусов. Насколько высокое дерево?
Ответ:
Вершина дерева находится выше вашего положения, поэтому в этой задаче используется угол возвышения. На самом деле в этом примере угол подъема к вершине дерева составляет \(60\) градусов. Поскольку вам не дали схему, вам нужно будет нарисовать свою собственную и подписать ее.
На самом деле в этом примере угол подъема к вершине дерева составляет \(60\) градусов. Поскольку вам не дали схему, вам нужно будет нарисовать свою собственную и подписать ее.
Рис. 4. Ваше положение относительно дерева.
Шаг 1: Расстояние до дерева составляет \(100\) футов, а угол возвышения составляет \(60\) градусов. Вас просят найти высоту дерева, которое является противоположной стороной. Для удобства дайте этой стороне имя \(h\).
Шаг 2: Выберите правильную функцию.
На картинке выше у вас есть угол и прилежащая сторона, и вас просят найти противоположную сторону. Это касается функции касательной! Помните, что
\[ \tan \theta = \frac{\mbox{напротив}} {\mbox{смежно}}. \]
Шаг 3: Введите переменные из треугольника и найдите \(h\).
Ввод того, что вы знаете,
\[ \tan 45 = \frac{h} {100}. \]
Вы можете использовать свои знания о тригонометрических функциях, чтобы получить
\[ \tan 45 = \frac{\sqrt{3}}{3} ,\]
, так что
\[ \frac{\ sqrt{3}}{3} = \frac{h}{100}\]
и
\[ h = 100 \frac{\sqrt{3}}{3} \, \text{ft}. \]
\]
Это точный ответ. Вас могут попросить узнать приблизительную высоту дерева, поэтому вы можете ввести это в калькулятор, чтобы найти
\[ h \приблизительно 57,7 \, \text{ft}.\]
Как насчет угла депрессия?
Угол углубления — это угол от горизонтальной линии до объекта ниже линии.
Давайте рассмотрим пример.
Вы сегодня занимались скалолазанием! Ваш грузовик припаркован у подножия утеса, примерно в \(200\) ярдах от основания утеса. Это относительно отвесная скала, так что подъем почти вертикальный. Как только вы достигаете вершины утеса, вы оцениваете угол наклона вашего грузовика примерно в \(30\) градусов. Как вы думаете, как далеко вы находитесь?
Ответ:
Шаг 1: Это помогает рисовать! Введите информацию, которую вы знаете, например, что ваш грузовик находится в \(200\) ярдах от основания утеса, а угол наклона составляет около \(30\) градусов. Для удобства назовем высоту обрыва \(h\).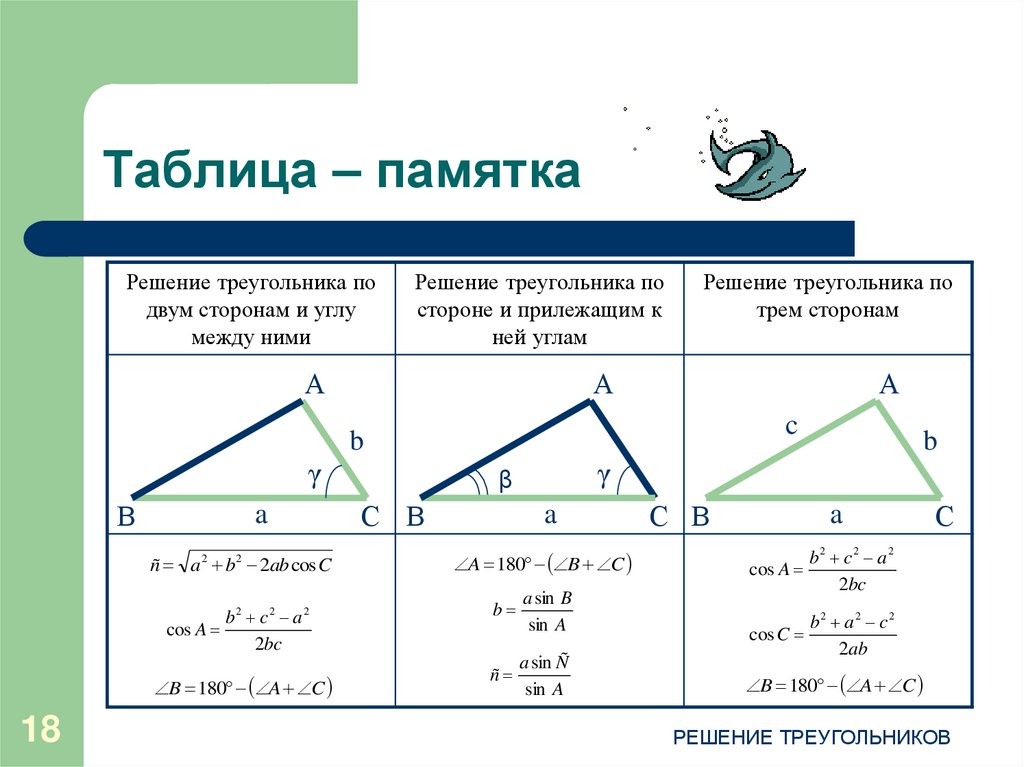
Рис. 5. Треугольник, показывающий вас на вершине утеса и местонахождение вашего грузовика.
Шаг 2: Выберите правильную функцию.
Вы хотите знать, насколько высока скала, другими словами, что такое \(h\)? Если вы посмотрите на расположение угла, у вас есть противоположная сторона \(200\) ярдов, и вы хотите знать соседнюю сторону. Это означает, что вы захотите использовать функцию касательной.
Шаг 3: Введите переменные из треугольника и найдите \(h\).
Используя тот факт, что
\[ \tan \theta = \frac{\mbox{противоположный}} {\mbox{смежный}}, \]
, вы можете ввести информацию, которую вы должны получить
\[ \tan 30 = \frac{200} {ч}. \]
Вы можете использовать свои знания о тригонометрических функциях, чтобы получить
\[ \tan 30 = \frac{\sqrt{3}}{3} ,\]
, так что
\[ \frac{\ sqrt{3}}{3} = \frac{200}{h}\] 92} \\ &= \frac{600\sqrt{3}}{3} \\ &= 200\sqrt{3} \, \text{yd}. \end{align}\]
Это точный ответ.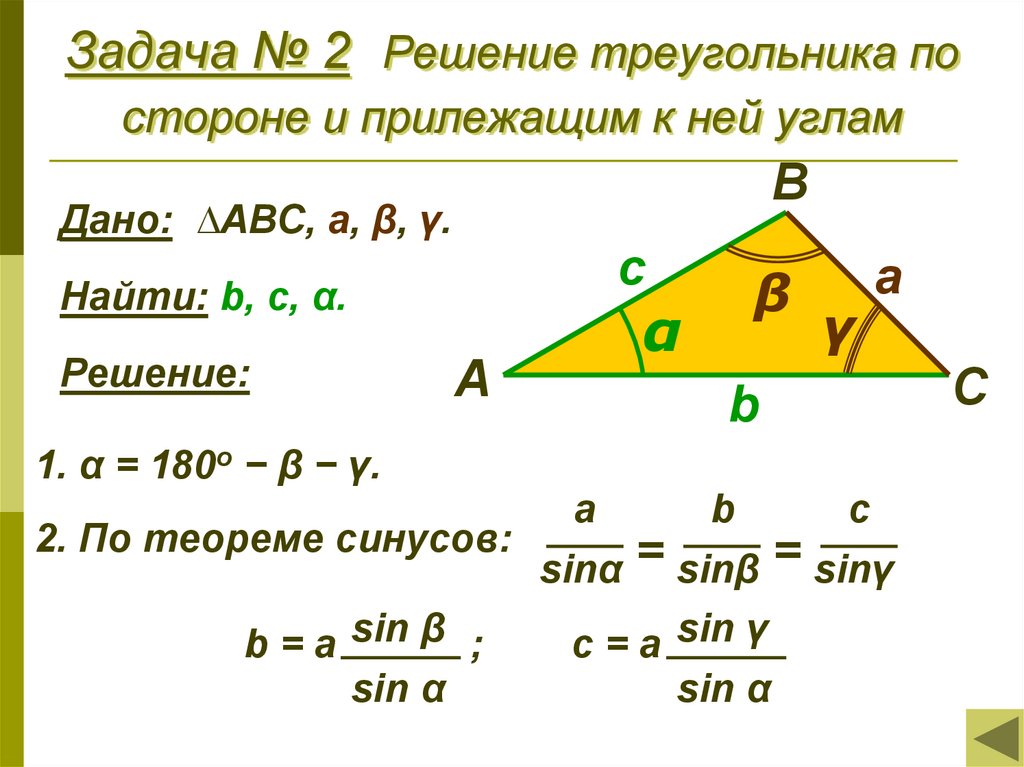 Вас могут попросить определить примерное расстояние, которое, по вашему мнению, вы находитесь, поэтому вы можете ввести его в калькулятор, чтобы найти
Вас могут попросить определить примерное расстояние, которое, по вашему мнению, вы находитесь, поэтому вы можете ввести его в калькулятор, чтобы найти
\[ ч \приблизительно 346 \, \text{yd}.\]
Конечно, есть примеров никогда не бывает много!
Примеры тригонометрии треугольника
Иногда вас попросят найти значения всех шести тригонометрических функций для заданного угла.
Найдите значения шести тригонометрических функций относительно угла \(\theta\).
Рис. 6. Нахождение шести тригонометрических значений угла.
Ответ:
Как обычно, сначала нужно пометить прямоугольный треугольник.
Рис. 7. Треугольник с обозначенными углами и сторонами.
Затем вы можете использовать SOHCHATOA, чтобы найти значения трех тригонометрических функций для угла \(\theta\).
SOH:
\[ \begin{align} \sin \theta &= \frac {\mbox{противоположный}}{\mbox{гипотенуза}} \\ &= \frac{8}{10} \\ & = \фракция{4}{5}. \конец{выравнивание}\]
CAH:
\[\begin{align} \cos \theta &= \frac{\mbox{adjacent}}{\mbox{гипотенуза}}\\ &= \frac{6}{10} \\ & = \frac{3}{5}. \end{align}\]
\end{align}\]
TOA:
\[ \begin{align} \tan \theta &= \frac {\mbox{напротив}} {\mbox{смежно }} \\ &= \frac{8}{6} \\ &= \frac{4}{3}. \end{align} \]
Затем для остальных трех:
Косеканс:
\[ \begin{align} \csc \theta &= \frac{\mbox{гипотенуза}}{\mbox {напротив}} \\ &= \frac{10}{8} \\ &= \frac{5}{4}. \end{выравнивание} \]
Секанс:
\[ \begin{align} \sec \theta &= \frac {\mbox{гипотенуза}}{\mbox{adjacent}} \\ &= \frac{10}{6} \\ & = \фракция{5}{3}. \end{align} \]
Котангенс:
\[ \begin{align} \cot \theta &= \frac{\mbox{adjacent}}{\mbox{opposite}} \\ &= \frac{6 {8} \\ &= \frac{3}{4}. \end{align} \]
Иногда вас попросят найти недостающую сторону.
Найти \(x\).
Рис. 8. Треугольник с данным углом и противоположной стороной.
Ответ:Конечно, шутка в том, чтобы просто нарисовать стрелку к букве \(x\) на картинке! Однако то, что этот вопрос на самом деле просит вас сделать, это найти измерение \(x\) в сантиметрах.
Шаг 1: Подпишите треугольник. Это уже сделано!
Шаг 2: Выберите правильную функцию.
Информация, которая у вас есть, это угол и противоположная сторона, и то, что вы хотите найти, это гипотенуза. Это означает, что вы захотите использовать функцию синуса.
Шаг 3: Введите переменные из треугольника и найдите \(x\).
Используя часть SOH SOHCAHTOA, вы знаете, что
\[\sin \theta = \frac{\mbox{opposite}}{\mbox {гипотенуза}} .\]
Подстановка того, что вы знаете, дает вам
\[\sin 55 = \frac{16}{x} ,\]
, поэтому
\[ x = \frac{ 16}{\sin 55} \, \text{см}. \]
Если вас попросят найти приблизительное значение \(x\) с точностью до двух знаков после запятой, ответ будет таким:
\[ x = 19\circ\), а соседняя сторона имеет длину \(5\, \text{см}\). Таким образом, вы захотите использовать формулу
\[\cos \theta = \frac{\mbox{adjacent}}{\mbox{гипотенуза}}.\]
Подставляя то, что вы знаете,
\[ \cos 50= \frac{5}{x}, \]
поэтому
\[ x = \frac{5}{\cos 50} \, \text{см}.