Алгоритм решения тригонометрических уравнений — Без Сменки
26 мая, 2022
1 мин
Мтмт 📈
Все тригонометрические уравнения очень схожи и решаются по одной схеме.
Отмечаем потенциальное решение на тригонометрической окружности. Вспомни её основные значения!
Затем записываем решение по стандартным формулам с учётом того, что если угол табличный, то вместо аркфункций записываем конкретное значение угла.
❗Заметь, что решение для синуса и косинуса можно записать двумя различными способами, так как у каждого уравнения для синуса и косинуса есть две точки на окружности, каждая из которых повторяется с периодом 2π.
Математика — обязательный для сдачи на ЕГЭ предмет, без которого не получишь аттестат. Это также один из самых сложных экзаменов для выпускников. Рассказываем, как сдать ЕГЭ по математике на 80+ баллов и делимся лучшими ресурсами для подготовки.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите 
Мы обязательно поправим!
Редакция Без Сменки
Честно. Понятно. С душой.
40 подписчиков
+ Подписаться
Редакция Без Сменки
06 июня, 2022
1 мин
Общ 👨👩👧
Правоохранительные органы
К правоохранительным органам РФ принято относить полицию (ОВД), прокуратуру, органы государственной.
..
Редакция Без Сменки
30 июня, 2022
1 мин
Рус 📖
СУФФИКСЫ ПРИЧАСТИЙ
🔸 Если причастие образовано от глагола первого спряжения, то суффиксы причастий — -ущ-, -ющ-, -ем-,…
Редакция Без Сменки
01 июля, 2022
1 мин
Лит 📚
КАК ЦИТИРОВАТЬ ПРОЗУ?
КАК ЦИТИРОВАТЬ ПРОЗУ Не забудь сохранить карточки с правилами цитирования. На ЕГЭ эти знания…
Редакция Без Сменки
07 июня, 2022
1 мин
Англ 🇬🇧
Условные предложения.
Первый тип
☀️ Юзай его, когда говоришь про что-то действительно возможное и осуществимое в настоящем и…
Редакция Без Сменки
10 июня, 2022
1 минБио 🦠
Продолговатый мозг
Головной мозг 🧠 Что вы представили при этой фразе? Что-то «большое шаровидное с бороздами и…
Редакция Без Сменки
20 апреля, 2022
1 мин
Ист 🤴
Февральская революция 1917 года
💥 ПРИЧИНЫ РЕВОЛЮЦИИ:
— участие России в непопулярной среди населения Первой мировой войне;
—.
..
Подпишитесь на еженедельную рассылку полезных материалов про ЕГЭ, высшее образование и вузы и получите скидку на курсы Вебиума
Основные методы решения тригонометрических уравнений
8 800 551-50-78 (бесплатно)
Онлайн подготовка к ЕГЭ-2023 по профильной математике
Подготовьтесь к ЕГЭ на 80+ баллов. Смотрите видео, читайте теорию, занимайтесь на онлайн-тренажерах
1С:Репетитор
8 800 551-50-78
Личный кабинет
1С:Репетитор – подготовка к ЕГЭ по математике
© ООО «1С-Софт» | ЧОУ ДПО «1С-ОБРАЗОВАНИЕ» | 2016–2022
8 800 551-50-78
Связаться с нами:
Главная
Блог
Основные методы решения тригонометрических уравнений
Мы вплотную подошли к решению задачи № 13 варианта КИМ ЕГЭ. Это задание состоит из двух частей — нужно решить тригонометрическое уравнение и выбрать его корни, удовлетворяющие некоторому условию.
За каждую верно решенную часть задачи можно получить один первичный балл.
Постараемся в ходе наших занятий на этой неделе обеспечить себе один первичный балл за задачу №13 — изучим и научимся применять основные методы решения тригонометрических уравнений.
1. Сведение к квадратному уравнению
Начнем мы с самого простого метода, когда тригонометрическое уравнение с помощью замены переменных сводится к квадратному (в общем случае — рациональному) уравнению. Но и здесь есть свои особенности и подводные камни. Посмотрим, как их избежать.
2. Разложение на множители
Нередко при решении тригонометрических уравнений используется такой прием, как разложение на множители. Здесь можно использовать и группировку, и вынесение общего множителя за скобку, и применять формулы сокращенного умножения к формулам тригонометрии.
3. Однородные тригонометрические уравнения
Очень важный тип тригонометрических уравнений — однородные. Что это за уравнения и как их решать, смотрите в видеолекции.
4. Более сложные методы и приемы
Вообще говоря, на этих трех основных методах можно и остановиться — для решения задачи №13 этого вполне достаточно. Но с тригонометрическими уравнениями мы можем встретиться и в других заданиях с развернутым ответом варианта КИМ ЕГЭ, например, в задаче с параметром.
Поэтому для «продвинутых» слушателей нашего курса мы публикуем еще несколько методов решения тригонометрических уравнений.
Следите за обновлениями на сайте и подписывайтесь на наш канал в Ютьюбе и группу Вконтакте!
Календарь занятий
Тема недели
Как найти общее решение тригонометрических уравнений?
от Sastry
Тригонометрические уравнения
Определение:
Уравнение, включающее одно или несколько тригонометрического соотношения неизвестного уклона, называется Тригонометрическим уравнением
. Тригонометрическое уравнение — это тригонометрическое уравнение. тождества. Тождество выполняется для каждого значения неизвестного угла , например, ., cos 2 x = 1 − sin 2 x истинно ∀ x ∈ R, а тригонометрическое уравнение выполняется для некоторых частных значений неизвестного угла.
(1) Корни тригонометрического уравнения: Величина неизвестного угла (переменная величина), удовлетворяющая данному уравнению, называется корнем уравнения, например, .
, cos θ = ½, корень θ = 60° или θ = 300°, потому что уравнение удовлетворяется, если положить θ = 60° или θ = 300°.
(2) Решение тригонометрических уравнений: Значение неизвестного угла, удовлетворяющее тригонометрическому уравнению, называется его решением.
Поскольку все тригонометрические отношения периодические по своей природе, обычно тригонометрическое уравнение имеет более одного решения или бесконечное число решений. Есть в основном три типа решений:
- Частное решение: Конкретное значение неизвестного угла, удовлетворяющее уравнению.
- Основное решение: Наименьшее численное значение неизвестного угла, удовлетворяющего уравнению (численно наименьшее частное решение).
- Общее решение: Полный набор значений неизвестного угла, удовлетворяющих уравнению. Он содержит все частные решения, а также главные решения.
Trigonometrical equations with their general solution
| Trigonometrical equation | General solution | |
| sin θ = 0 | θ = nπ | |
| cos θ = 0 | θ = nπ + п/2 | |
| TAN θ = 0 | θ = nπ | |
| SIN θ = 1 | θ = 2Nπ + π/2 | |
| COS θ = 1 | θ = 2Nπ566995669956699569956699569 | 69919191919191919191919191919191919191919191919191919191919191919191919191919191919199119911991199119911991199119911919191919191919191 гг.θ = nπ + (−1) n α |
| cos θ = cos α | θ = 2nπ ± α | |
| tan θ = tan α | θ = nπ ± α | |
| sin 2 θ = sin 2 α | θ = nπ ± α | |
| tan 2 θ = tan 2 α | θ = nπ ± α | |
| cos 2 θ = cos 2 α | θ = nπ ± α | |
| sin θ = sin α cos θ = cos α | θ = nπ + α | |
| sin θ = sin α tan θ = tan α | θ = nπ + α | |
| Tan θ = tan α Cos. | θ = nπ + α |
αОбщее решение вида a cos θ + b sin θ = c
Метод нахождения главного значения
Предположим, нам нужно найти главное значение sin θ = −½ , удовлетворяющее уравнению .
Поскольку sin θ отрицательный, θ будет находиться в квадранте 3 или 4 .
Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше, чем π. Если мы приблизимся к нему по часовой стрелке, угол будет численно меньше π. В качестве главного значения мы должны взять численно наименьший угол. Итак, по главному значению.
(1) Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол находится в квадранте 3 rd или 4 th , мы должны выбрать направление по часовой стрелке.
(2) Главное значение никогда не бывает численно больше π.
(3) Главное значение всегда лежит в первом круге (т. е. в первом вращении). По приведенным выше критериям θ будет равно −π/6 или −5π/6. Между этими двумя −π/6 имеет наименьшее числовое значение. Следовательно, −π/6 является главным значением θ, удовлетворяющим уравнению sin θ = −½.
Из приведенного выше обсуждения метод нахождения главного значения можно резюмировать следующим образом:
- Сначала начертите тригонометрический круг и отметьте квадрант, в котором может лежать угол.
- Выберите направление против часовой стрелки для квадрантов 1 st и 2 nd и направление по часовой стрелке для квадрантов 3 rd и 4 th .
- Найдите угол первого поворота.
- Выберите угол с наименьшим численным значением. Найденный таким образом угол будет главным значением.
- В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют наименьшему в числовом отношении углу, то в качестве главного значения принято выбирать угол с положительным знаком.
Trigonometric Equations Problems with Solutions
1.
Solution:
2.
Solution:
3.
Solution:
4.
Solution:
5.
Solution:
6.
Solution:
7.
Solution:
8.
Решение:
9.
Решение:
Основные тригонометрические уравнения :
Когда попросили решить 2x — 1 = 0, мы можем легко получить 2x = 1 и x = as отвечать.
Когда нас просят решить 2 sin x – 1 = 0, мы действуем аналогичным образом. Сначала мы рассматриваем sin x как переменную уравнения и решаем, как в первом примере.
2 sin x – 1 = 0
2 sin x = 1
sin x = 1/2
Знаки и квадранты :
значение и определение правильного квадранта (квадрантов) для этого значения.
Рубрики: Математика С тегами: Общее решение, Общее решение вида a cos θ + b sin θ = c, Метод нахождения главного значения, Частное решение, Основное решение, Корни тригонометрического уравнения, Решение тригонометрического уравнения, Тригонометрический Уравнения, тригонометрические уравнения, задачи с решениями, тригонометрические уравнения с их общим решением
Тригонометрические уравнения – формула, решение, шаги решения, примеры
Тригонометрические уравнения включают тригонометрические функции углов в качестве переменных.
Угол θ тригонометрических функций, таких как Sinθ, Cosθ, Tanθ, используется в качестве переменной в тригонометрических уравнениях. Подобно общим полиномиальным уравнениям, тригонометрические уравнения также имеют решения, которые называются главными решениями и общими решениями.
Мы будем использовать тот факт, что период sin x и cos x равен 2π, а период tan x равен π, чтобы найти решения тригонометрических уравнений. Давайте узнаем больше о тригонометрических уравнениях, способах их решения и найдем их решения с помощью нескольких решенных примеров тригонометрических уравнений для лучшего понимания концепции.
| 1. | Что такое тригонометрические уравнения? |
| 2. | Формулы тригонометрических уравнений |
| 3. | Решение тригонометрических уравнений |
| 4. | Шаги для решения тригонометрических уравнений |
5. | Примеры решения тригонометрических уравнений |
| 6. | Часто задаваемые вопросы по тригонометрическим уравнениям |
Что такое тригонометрические уравнения?
Тригонометрические уравнения аналогичны алгебраическим уравнениям и могут быть линейными уравнениями, квадратными уравнениями или полиномиальными уравнениями. В тригонометрических уравнениях тригонометрические отношения Sinθ, Cosθ, Tanθ представлены вместо переменных, как в обычном полиномиальном уравнении. В тригонометрических уравнениях используются следующие тригонометрические отношения: Sinθ, Cosθ или Tanθ.
Линейное уравнение ax + b = 0 может быть записано как уравнение тригонометрии как aSinθ + b = 0, которое также иногда записывается как Sinθ = Sinα. Квадратное уравнение ax 2 + bx + c = 0 в качестве примера тригонометрического уравнения записывается как aCos 2
θ + bCosθ + c = 0. Но в отличие от обычных решений уравнений с числом решений в зависимости от степени переменной, в тригонометрических уравнениях одно и то же значение решения существует для разных значений θ.
Например, мы имеем Sinθ = 1/2 = Sinπ/6 = Sin5π/6 = Sin13π/6 и т. д., поскольку значения функции синуса повторяются через каждые 2π радиан.Ниже приведены некоторые примеры тригонометрических уравнений.
- Sin2x — Sin4x + Sin6x = 0
- 2Cos 2 х + 3Sinx = 0
- Cos4x = Cos2x
- Sin2x + Cosx = 0
- сек 2 2x = 1 — Tan2x
Формулы тригонометрических уравнений
Мы используем некоторые результаты и общие решения основных тригонометрических уравнений для решения других тригонометрических уравнений. Эти результаты таковы:
- Для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1) n
- . Для любых действительных чисел x и y из того, что cos x = cos y, следует x = 2nπ ± y, где n ∈ Z.
- Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.
Теперь мы можем доказать эти результаты, используя тригонометрические формулы.
Докажите, что для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1)
n y, где n ∈ ZДоказательство: Если sin x = sin y, то sin x – sin y = 0
⇒ 2 cos (x + y)/2 sin (x − y)/2 = 0 — [Используя формулу Sin A — Sin B = 2 cos ½ (A + B) sin ½ (A — B)]
⇒ cos (x + y)/2 = 0 или sin (x — y) /2 = 0
⇒ (x + y)/2 = (2n + 1)π /2 или (x − y)/2 = nπ, где n ∈ Z —- [Поскольку sin A = 0 влечет A = nπ и cos A = 0 влечет A = (2n + 1)π/2, где n ∈ Z]
, т. е. x = (2n + 1) π – y или x = 2nπ + y, где n ∈ Z.
Следовательно, x = (2n + 1)π + (–1) 2n + 1 y или x = 2nπ + (–1) 2n y, где n ∈ Z.
Объединяя эти два результата, получаем x = nπ + (–1) n y, где n ∈ Z.
Докажите, что для любых действительных чисел x и y из cos x = cos y следует x = 2nπ ± y, где n ∈ Z.
Доказательство: . Если cos x = cos y, то cos x – cos y = 0
⇒ -2 sin (x + y)/2 sin (x − y)/2 = 0 — [Используя формулу Cos A — Cos B = — 2 sin ½ (A + B) sin ½ (A — B)]
⇒ sin (x + y)/2 = 0 или sin (x − y)/2 = 0
⇒ (x + y)/2 = nπ или (x − y)/2 = nπ, где n ∈ Z —- [Поскольку из sin A = 0 следует A = nπ, где n ∈ Z]
т.
е. x = 2nπ – y или x = 2nπ + y, где n ∈ Z.
Следовательно, x = 2nπ ± y, где n ∈ Z.
Докажите, что если x и y не являются нечетными кратными π/2, то из tan x = tan y следует x = nπ + y, где n ∈ Z.
Доказательство: Если tan x = tan y, тогда тангенс x — тангенс y = 0
⇒ sin x / cos x — sin y / cos y = 0
⇒ (sin x cos y — cos x sin y) / (cos x cos y) = 0
⇒ sin (x — y) / (cos x cos y) = 0 —- [Используя тригонометрическую формулу sin (A — B) = sinA cosB — sinB cosA]
⇒ sin (x — y) = 0
⇒ x — y = nπ, где n ∈ Z — [Поскольку sin A = 0 влечет A = nπ, где n ∈ Z]
⇒ x = nπ + y, где n ∈ Z
Решение тригонометрических уравнений
В отличие от обычных решений алгебраических уравнений с числом решений, основанным на степени переменной, в тригонометрических уравнениях решения бывают двух типов, основанные на различном значении угла тригонометрической функции, для одного и того же решения.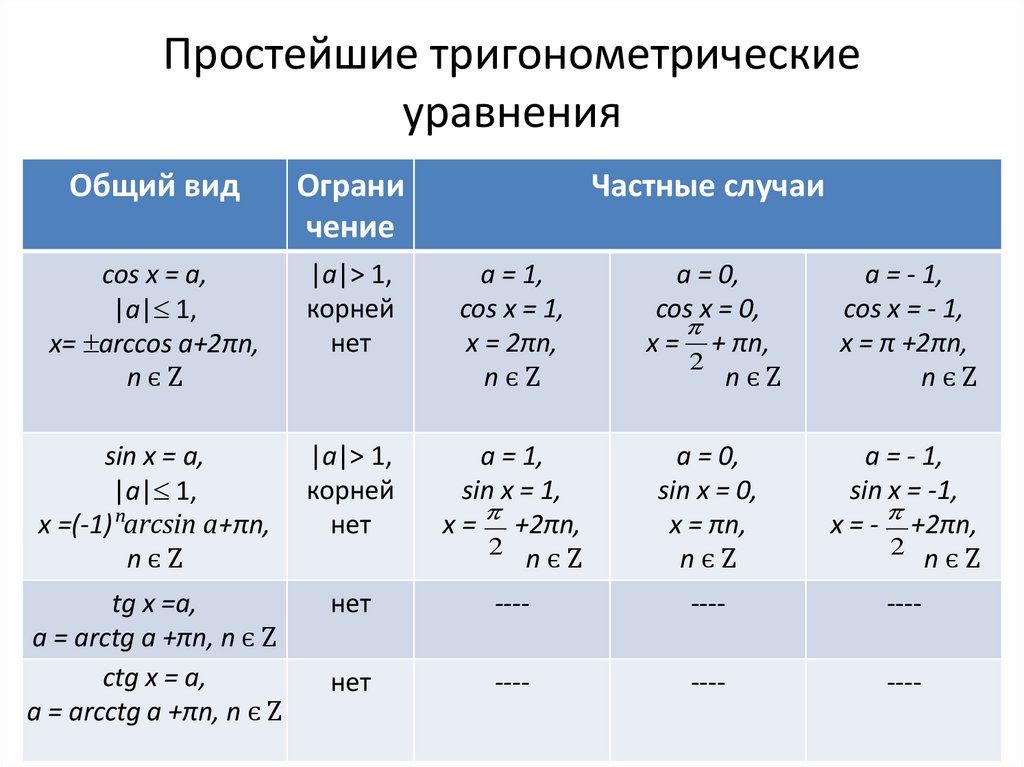
Например, для простого тригонометрического уравнения 2Cosθ — 1 = 0 решение дается выражением Cosθ = 1/2, а значения θ равны π/3, 5π/3, 7π/3, 11π/3 и т. д. поскольку значения функции косинуса повторяются через каждые 2π радиан, а cos x положителен в первом и четвертом квадрантах. У нас есть два типа решений тригонометрических уравнений:
- Основное решение: Начальные значения углов для тригонометрических функций называются главными решениями. Решение Sinx и Cosx повторяется через интервал 2π, а решение Tanx повторяется через интервал π. Решения этих тригонометрических уравнений, для которых x лежит между 0 и 2π, называются главными решениями.
- Общее решение: Значения углов для одного и того же ответа тригонометрической функции называются общим решением тригонометрической функции. Все решения тригонометрических уравнений за пределами 2π объединяются и выражаются в виде общего решения тригонометрических уравнений. Общие решения Sinθ, Cosθ, Tanθ следующие.
- Sinθ = Sinα, и общее решение θ = nπ + (-1) n α, где n ∈ Z
- Cosθ = Cosα, и общее решение θ = 2nπ + α, где n ∈ Z
- Tanθ = Tanα, и общее решение θ = nπ + α, где n ∈ Z
шагов для решения тригонометрических уравнений
Для решения тригонометрического уравнения необходимо выполнить следующие шаги.
- Преобразование данного тригонометрического уравнения в уравнение с одним тригонометрическим отношением (sin, cos, tan)
- Измените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, в простой угол.
- Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.
- Решите тригонометрическое уравнение, аналогичное обычным уравнениям, и найдите значение тригонометрического отношения.
- Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.
Примеры решения тригонометрических уравнений
Пример 1: Найдите главные решения тригонометрического уравнения sin x = √3/2.
Решение: Чтобы найти главные решения sin x = √3/2, мы знаем, что sin π/3 = √3/2 и sin (π — π/3) = √3/2
⇒ sin π/3 = sin 2π/3 = √3/2
Мы можем найти другие значения x такие, что sin x = √3/2, но нам нужно найти только те значения x, что x лежит в [0, 2π], так как главное решение лежит между 0 и 2π.
Таким образом, основными решениями sin x = √3/2 являются x = π/3 и 2π/3.
Пример 2: Найдите решение cos x = 1/2.
Решение: В этом случае мы найдем общее решение cos x = 1/2. Мы знаем, что cos π/3 = 1/2, поэтому имеем
cos x = 1/2
⇒ cos x = cos π/3
⇒ x = 2nπ + (π/3), где n ∈ Z —- [Используя Cosθ = Cosα, и общее решение θ = 2nπ + α, где n ∈ Z]
Таким образом, общее решение cos x = 1/2 равно x = 2nπ + (π/3), где n ∈ Z.
Важные замечания по тригонометрическим уравнениям , sin x = sin y влечет x = nπ + (-1) n y, где n ∈ Z. Похожие темы Часто задаваемые вопросы о тригонометрических уравнениях
Что такое тригонометрические уравнения?
Тригонометрические уравнения аналогичны алгебраическим уравнениям и могут быть линейными уравнениями, квадратными уравнениями или полиномиальными уравнениями. В тригонометрических уравнениях вместо переменных представлены тригонометрические отношения Sinθ, Cosθ, Tanθ.
Что такое формулы трех тригонометрических уравнений?
Три тригонометрических уравнения основаны на трех тригонометрических функциях. Три тригонометрических уравнения: Sinθ = Sinα, Cosθ = Cosα, Tanθ = Tanα. Формулы трех тригонометрических уравнений следующие:
- Для любых действительных чисел x и y из sin x = sin y следует x = nπ + (-1) n y, где n ∈ Z.
- . Для любых действительных чисел x и y из того, что cos x = cos y, следует x = 2nπ ± y, где n ∈ Z.
- Если x и y не являются нечетными кратными π/2, то tan x = tan y влечет x = nπ + y, где n ∈ Z.
Приведите примеры тригонометрических уравнений.
Вот некоторые примеры тригонометрических уравнений:
- Sin2x — Sin4x + Sin6x = 0
- 2Cos 2 х + 3Sinx = 0
- Cos4x = Cos2x
Каковы шаги для решения тригонометрических уравнений?
Следующие шаги помогут решить тригонометрическое уравнение:
- Преобразуйте данное тригонометрическое уравнение в уравнение с одним тригонометрическим соотношением.
- Замените уравнение с тригонометрическим уравнением, имеющим кратные углы или дольные углы, на простое. угол.
- Теперь представим уравнение в виде полиномиального уравнения, квадратного уравнения или линейного уравнения.
- Решите тригонометрическое уравнение, аналогичное обычным уравнениям, и найдите значение тригонометрического отношения.
- Угол тригонометрического отношения или значение тригонометрического отношения представляет собой решение тригонометрического уравнения.
В чем разница между тригонометрическими уравнениями и алгебраическими уравнениями?
Тригонометрическое уравнение и алгебраические уравнения отличаются переменной, используемой в уравнении. В тригонометрическом уравнении переменной является тригонометрическая функция, а в алгебре в качестве переменных берутся алфавиты x, y. И тригонометрические уравнения, и алгебраические уравнения имеют линейные уравнения, квадратные уравнения и полиномиальные уравнения.
В чем разница между тригонометрическими уравнениями и тождествами?
Тригонометрические уравнения похожи на алгебраические уравнения, где от нас требуется найти решение и найти значение переменной. С другой стороны, тригонометрические тождества — это результаты тригонометрии, которые выражают отношения между различными тригонометрическими отношениями.
Что такое главное решение тригонометрических уравнений?
мы знаем, что sin x и cos x повторяются через каждые 2π радиан, а tan x повторяются через каждые π радиан. Решения тригонометрического уравнения, для которых 0 ≤ x < 2π, называются главными решениями.
Как найти общее решение тригонометрического уравнения?
Мы можем найти общее решение тригонометрических уравнений, используя следующие три результата:
- Для любых действительных чисел x и y, sin x = sin y, подразумевает x = nπ + (-1) n y, где n ∈ Z.
- Для любых действительных чисел x и y из условия x = cos y следует, что x = 2nπ ± y, где n ∈ Z.
