Решить графически двойственную задачу: Двойственная задача линейного программирования онлайн

Решение двойственной задачи — линейное программирование

Здесь мы рассмотрим вопрос, как из решения прямой задачи, получить решение двойственной задачи.

Теоремы двойственности

Первая теорема двойственности

Если одна из пары двойственных задач имеет оптимальное решение, то и двойственная задача имеет оптимальное решение. При этом значения целевых функций прямой и двойственной задачи, для оптимальных решений, равны друг другу.

Если одна из пары двойственных задач не имеет решения вследствие неограниченности целевой функции, то двойственная задача не имеет решения вследствие несовместимости системы ограничений.

Вторая теорема двойственности

Пусть мы имеем симметричную пару двойственных задач (1) и (2):
(1.1)   ;
(1.2)  
(2.1)   ;
(2.2)  
Для того чтобы допустимые решения и являлись оптимальными решениями двойственных задач (1) и (2), необходимо и достаточно, чтобы выполнялись следующие равенства:
(3)   ,   .
(4)   ,   ;

Для наглядности, выпишем равенства (3) и (4) в развернутом виде:
(3.1)  
(3.2)  

(3.m)  

(4.1)  
(4.2)  

(4.n)  

Метод решения двойственной задачи

Применяя теоремы двойственности, можно получить решение двойственной задачи из решения прямой. Опишем метод решения двойственной задачи.

Пусть мы нашли решение прямой задачи (1) с оптимальным значением целевой функции и с оптимальным планом . Подставим найденные значения в систему ограничений (1.2). Тогда если -е неравенство не является равенством, то есть если
,
то, согласно (3.i),
.
Рассматривая все строки системы ограничений (1.2), мы найдем, что часть переменных двойственной задачи равна нулю.

Далее замечаем, что если , то, согласно (4.k), -я строка системы ограничений (2.2) является равенством:
.
Составив все строки системы ограничений (2.2), для которых , мы получим систему уравнений, из которой можно найти ненулевые значения переменных .

На основании первой теоремы двойственности, минимальное значение целевой функции
.

Если известно решение задачи (2), то аналогичным образом можно найти решение задачи (1).

Примеры решения двойственной задачи из решения прямой

Пример 1

Пусть дана задача линейного программирования:
;

Известно решение этой задачи:
;   .

Составить двойственную задачу и получить ее решение из решения прямой.

Решение

Составляем двойственную задачу.

;

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи.
(П1.1.1)   ;
(П1.1.2)   ;
(П1.1.3)   ;
(П1.1.4)   .
Поскольку первая и четвертая строки являются строгими неравенствами (не являются равенствами), то
  и   .

Поскольку   и   , то 2-я и 4-я строки двойственной задачи являются равенствами:

Подставим уже найденные значения     и   , имеем:

Отсюда
;
;   .

Ответ

Двойственная задача имеет вид:
;

Ее решение
;  

Пример 2

Дана задача линейного программирования:
(П2.1.1)   ;
(П2.1.2)  
Найти решение этой задачи, решив двойственную задачу графическим методом.

Решение

Составляем двойственную задачу.

(П2.2.1)   ;
(П2.2.2)  

Решение задачи (П2.2) приводится на странице “Решение задач линейного программирования графическим методом”. Решение задачи (П2.2) имеет вид:
;   .

Согласно первой теореме двойственности, оптимальное значение целевой функции равно
.

Применим вторую теорему двойственности. Подставим оптимальные значения переменных в систему ограничений прямой задачи (П2.2).
;
;
.
Поскольку третья строка является строгим неравенством (не являются равенством), то
.

Поскольку   и   , то 1-я и 2-я строки двойственной задачи (П2.1) являются равенствами:

Подставим найденное значение   .

Решаем систему уравнений.
;
;
;
;   ;
.

Ответ

Решение исходной задачи (П2.1) имеет вид:
;   .

Линейное программирование. Некоторые примеры экономических задач, приводящих к модели линейного программирования. Геометрическая интерпретация и графическое решение задачи ЛП, страница 16

                                            

Ограничения и целевая функция  прямой задачи  «записаны» в строках таблицы 5, ограничения и целевая функция двойственной задачи «читаются» по столбцам. Ограничению с номером   прямой задачи соответствует переменная   двойственной; переменной   прямой задачи —  ограничение двойственной.

  Пример 15. Записать условие  задачи, двойственной к стандартной  задаче из примера 11.

     Решение. Воспользуемся схемой из таблицы 5. Рядом с ограничениями каждой из  задач записаны в скобках соответствующие переменные другой задачи:

Прямая задача

Двойственная задача

     Двойственную задачу примера 15 можно привести к стандартному виду, затем записать условие двойственной к ней и снова привести к стандартному виду. Проверьте, что результатом таких преобразований будет исходная (прямая) задача. Нетрудно понять, что и в общем случае задача, двойственная к двойственной совпадает с исходной. Поэтому  прямую и двойственную задачи называют также взаимодвойственными  или  двойственной парой.

В теории ЛП доказаны следующие утверждения (теоремы двойственности), устанавливающие связи между свойствами задач двойственной пары.

     Теорема 1. Если одна из  задач двойственной пары разрешима, т. е имеет оптимальные планы, то разрешима и другая задача. При этом для оптимальных планов имеет место равенство  . Для разрешимости одной (а, значит, и другой) задачи необходимо и достаточно, чтобы каждая из них имела хотя бы один допустимый план.

     Теорема 2. Для того, чтобы допустимые планы  

пары двойственных задач (14) – (16) и (31) – (33) были их оптимальными планами, необходимо и достаточно, чтобы они удовлетворяли системе уравнений

                              

                               

   Теорема 1 – центральный результат всей теории ЛП. Теорема 2 позволяет найти оптимальный план одной из задач двойственной пары по оптимальному плану другой.

     Пример 16. Решить задачу ЛП

                                                  ,

                                                  

     Решение.  Запишем условие двойственной задачи

                                                    

                                                   

Эту задачу можно решить графически (проделайте самостоятельно), в результате получим   По теореме 1 исходная (прямая) задача также имеет оптимальный план   Чтобы найти   подставим 

 в систему уравнений из теоремы 2:

                         

                  

Второе и третье  уравнения представляют собой тождества 0 =  0. Из остальных уравнений находим единственный оптимальный план исходной задачи                                      

 Для определения   даже не обязательно подставлять эти числа в выражение для целевой функции  F, так как из теоремы 1 следует  (проверьте подстановкой).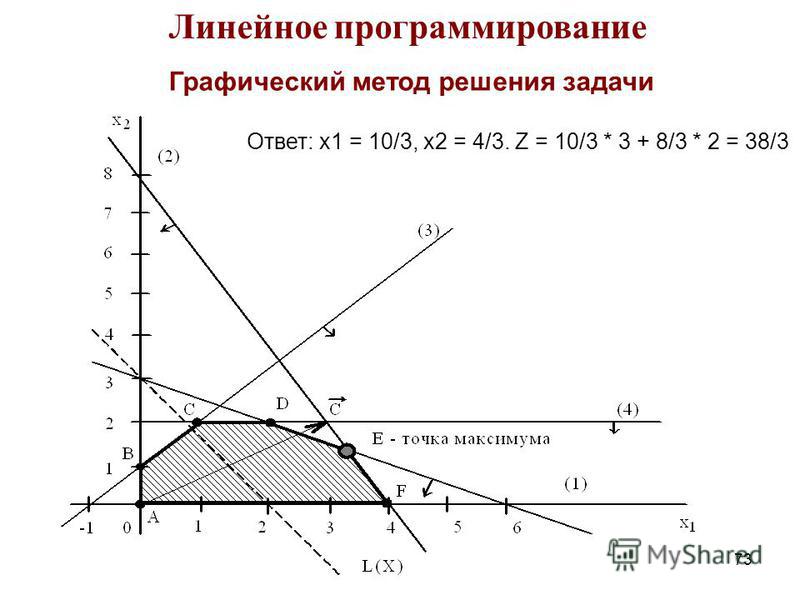

     В разобранном примере  решалось более «легкая» из пары двойственных задач, ответ другой задачи получался после решения системы линейных уравнений. В случае , когда оптимальный план одной из задач находится симплекс-методом, оптимальный план другой можно найти непосредственно по заключительной симплексной таблице без дополнительных вычислений.    

     Пример 17. Приведем обе задачи двойственной пары из предыдущего примера к канонической форме. В прямой задаче заменим   и введем балансовые переменные  в двойственной задаче введем балансовые переменные            

Прямая задача	Двойственная задача

     Примем за базисные переменные   в прямой  задаче  (тогда  свободные) и переменные   в двойственной задаче  (тогда  свободные). Каждая базисная переменная  , содержатся в определенном ограничении  одной  из задач двойственной  пары; этому ограничению соответствует определенная  свободная  переменная другой задачи. Это позволяет установить следующее соответствие между переменными  взаимодвойственных задач:

4.3: Минимизация симплексным методом

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

38581

• Рупиндер Секон и Роберта Блум
• Колледж Де Анза

Цели обучения

В этом разделе вы научитесь решать задачи минимизации линейного программирования с использованием симплекс-метода.

1. Определение и настройка линейной программы в стандартной форме минимизации
2. Сформулируйте двойственную задачу в стандартной форме максимизации
3. Используйте симплекс-метод для решения задачи двойной максимизации
4. Определите оптимальное решение исходной задачи минимизации по оптимальной симплексной таблице.

В этом разделе мы будем решать стандартные задачи минимизации линейного программирования, используя симплекс-метод. Еще раз напомним читателю, что в стандартных задачах минимизации все ограничения имеют вид \(ax + by ≥ c\).

Процедура решения этих проблем была разработана доктором Джоном фон Нейманом. Он включает в себя решение связанной задачи, называемой двойственной задачей

. Каждой задаче минимизации соответствует двойственная задача. Решение двойственной задачи используется для нахождения решения исходной задачи. Двойственная задача — это задача максимизации, которую мы научились решать в предыдущем разделе. Сначала решим двойственную задачу симплекс-методом.

Затем из окончательной симплексной таблицы мы извлекаем решение исходной задачи минимизации.

Однако прежде чем двигаться дальше, мы сначала научимся преобразовывать задачу минимизации в соответствующую задачу максимизации, называемую ее двойной .

Пример \(\PageIndex{1}\)

Преобразуйте следующую задачу минимизации в двойственную.

\[\begin{array}{ll}
\textbf { Свернуть } & \mathrm{Z}=12 \mathrm{x}_{1}+16 \mathrm{x}_{2} \\
\textbf { С учетом: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\

& \mathrm{x}_{1}+\mathrm{x }_2 \geq 30 \\
& \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
\end{array} \nonumber \]

Решение

Чтобы достичь нашей цели, мы сначала представим нашу задачу в виде следующей матрицы.

\[\begin{array}{cc|c}
1 & 2 & 40 \\
1 & 1 & 30 \\
\hline 12 & 16 & 0
\end{array} \nonumber \]

Обратите внимание, что эта таблица выглядит как исходная симплексная таблица без резервных переменных. Далее пишем матрицу, столбцы которой являются строками этой матрицы, а строки — столбцами. Такая матрица называется транспонированной исходной матрицы. Получаем:

\[\begin{array}{cc|c}
1 & 1 & 12 \\
2 & 1 & 16 \\
\hline 40 & 30 & 0
\end{array} \nonumber \ ]

Следующая задача максимизации, связанная с приведенной выше матрицей, называется двойственной ей.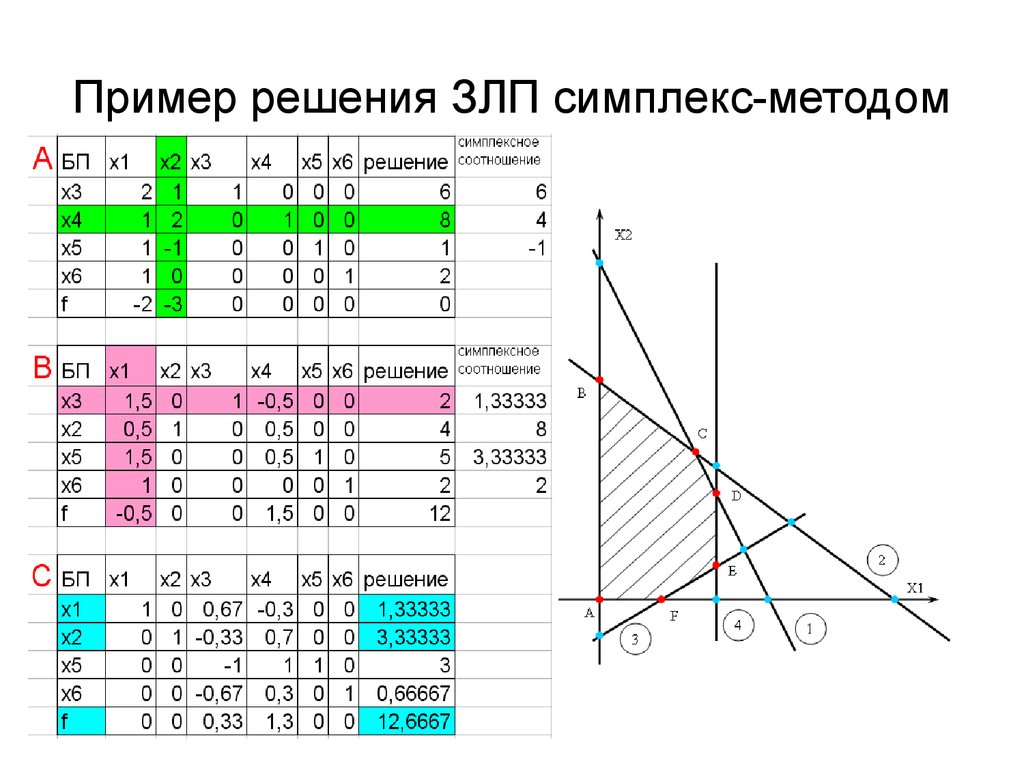

\[\begin{array}{ll}
\textbf {Увеличить} & \mathrm{Z}=40 \mathrm{y}_{1}+30 \mathrm{y}_{2} \\
\ textbf { При условии: } & \mathrm{y}_{1}+\mathrm{y}_{2} \leq 12 \\
& 2 \mathrm{y}_1+\mathrm{y}_2 \leq 16 \ \
& \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0
\end{array} \nonumber \]

Обратите внимание, что мы выбрали переменные как y, а не x, чтобы различать две проблемы.

Пример \(\PageIndex{2}\)

Графически решить как задачу минимизации, так и задачу двойной максимизации.

Решение

Наша задача минимизации состоит в следующем.

\[\begin{array}{ll}
\textbf { Свернуть } & \mathrm{Z}=12 \mathrm{x}_1+16 \mathrm{x}_2 \\
\textbf { Подлежит: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\
& \mathrm{x}_{1}+\mathrm{x}_{2} \geq 30 \\
& \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
\end{array} \nonumber \]

Теперь построим графики неравенств:

Мы построили график, заштриховали допустимую область и пометили угловые точки . Угловая точка (20, 10) дает наименьшее значение целевой функции, и это значение равно 400.

Теперь его двойник:

\[\begin{array}{ll}
\textbf {Увеличить} & \mathrm{Z}=40 \mathrm{y}_1+30 \mathrm{y}_{2} \\
\textbf { При условии: } & \mathrm{y}_{1}+\mathrm{y}_{2} \leq 12 \\
& 2 \mathrm{y}_1+\mathrm{y} 2 \leq 16 \\
& \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0
\end{array}\nonumber \]

Нарисуем неравенства:

Опять же, мы построили график, заштриховали допустимую область и пометили угол точки. Угловая точка (4, 8) дает наивысшее значение целевой функции со значением 400.

Читатель может заметить, что приведенный выше пример \(\PageIndex{2}\) совпадает с примером 3.1.1 в разделе 3.1. Это та же задача, что и в примере 4.1.1 в разделе 4.1, где мы решили ее симплекс-методом.

Заметим, что минимальное значение задачи минимизации совпадает с максимальным значением задачи максимизации; в примере \(\PageIndex{2}\) минимум и максимум равны 400. Это не совпадение. Сформулируем принцип двойственности.

Принцип двойственности

Целевая функция задачи минимизации достигает минимума тогда и только тогда, когда целевая функция двойственной задачи достигает максимума. И когда они это делают, они равны.

Наша следующая цель — извлечь решение нашей задачи минимизации из соответствующего двойственного числа. Для этого решим двойственное симплекс-методом.

Пример \(\PageIndex{3}\)

Найдите решение задачи минимизации в примере \(\PageIndex{1}\) путем решения двойственной задачи симплекс-методом. Переписываем нашу задачу.

\[\begin{array}{ll}
\textbf { Свернуть } & \mathrm{Z}=12 \mathrm{x}_{1}+16 \mathrm{x}_{2} \\
\ textbf { При условии: } & \mathrm{x}_{1}+2 \mathrm{x}_{2} \geq 40 \\
& \mathrm{x}_{1}+\mathrm{x}_ {2} \geq 30 \\
& \mathrm{x}_{1} \geq 0 ; \mathrm{x}_{2} \geq 0
\end{array} \nonumber \]

Решение

\[\begin{array}{ll}
\textbf {Увеличить} & \mathrm{Z }=40 \mathrm{y}_{1}+30 \mathrm{y}_{2} \\
\textbf { При условии: } & \mathrm{y}_{1}+\mathrm{y}_ {2} \leq 12 \\
& 2 \mathrm{y}_{1}+\mathrm{y}_{2} \leq 16 \\
& \mathrm{y}_{1} \geq 0 ; \mathrm{y}_{2} \geq 0
\end{array} \nonumber \]

Напомним, что указанную выше задачу мы решили симплекс-методом в примере 4. 1.1, раздел 4.1. Поэтому мы показываем только начальную и конечную симплексную таблицу.

Начальная симплексная таблица:

\[\begin{array}{ccccc|c}
\mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \mathrm{x }_{2} & \mathrm{Z} & \mathrm{C} \\
1 & 1 & 1 & 0 & 0 & 12 \\
2 & 1 & 0 & 1 & 0 & 16 \\
\hline-40 & -30 & 0 & 0 & 1 & 0
\end{массив} \nonumber \]

Обратите внимание на важное изменение. Здесь нашими основными переменными являются \(\mathrm{y}_1\) и \(\mathrm{y}_2\), а резервными переменными являются \(\mathrm{x}_1 и \mathrm{x}_2\).

Окончательная симплексная таблица выглядит следующим образом:

\[\begin{array}{ccccc|c}
\mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \ mathrm{x}_{2} & \mathrm{Z} & \\
0 & 1 & 2 & -1 & 0 & 8 \\
1 & 0 & -1 & 1 & 0 & 4 \\
\hline 0 & 0 & 20 & 10 & 1 & 400
\end{массив} \nonumber \]

Более пристальный взгляд на эту таблицу показывает, что значения \(\mathrm{x}_1\) и \(\mathrm{x}_2\) вместе с минимальным значением для задачи минимизации могут быть получены из последняя строка финальной таблицы. Мы выделили эти значения стрелками.

\[\begin{array}{ccccc|c}
\mathrm{y}_1 & \mathrm{y}_2 & \mathrm{x}_{1} & \mathrm{x}_{2} & \ матрм {Z} & \\
0 & 1 & 2 & -1 & 0 & 8 \\
1 & 0 & -1 & 1 & 0 & 4 \\
\hline 0 & 0 & 20 & 10 & 1 & 400 \\
& & \ uparrow & \uparrow & & \uparrow
\end{array} \nonumber \]

Переформулируем решение следующим образом:

Задача минимизации имеет минимальное значение 400 в угловой точке (20, 10)

Мы теперь подведем итоги нашего обсуждения.

Минимизация симплекс-методом

1. Установить проблему.
2. Напишите матрицу, строки которой представляют каждое ограничение с целевой функцией в нижней строке.
3. Запишите транспонирование этой матрицы, поменяв местами строки и столбцы.
4. Теперь напишите двойную задачу, связанную с транспонированием.
5. Решите двойственную задачу симплекс-методом, изученным в разделе 4.1.
6. Оптимальное решение находится в нижней строке итоговой матрицы в столбцах, соответствующих резервным переменным, а минимальное значение целевой функции совпадает с максимальным значением двойственной.

---

Эта страница под названием 4.3: Минимизация с помощью симплексного метода распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Рупиндер Сехон и Роберта Блум

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Показать страницу TOC

   нет

2. Теги

   1. двойной
   2. двойная проблема
   3. Симплексный метод
   4. источник@https://www. deanza.edu/faculty/bloomroberta/math21/afm3files.html.html

Графический метод линейного программирования – задачи с решениями

Графический метод решения задач линейного программирования

Графический метод решения задач линейного программирования — это метод, в котором для решения задачи используется граф. Граф используется для определения допустимой области, которая представляет собой область графа, представляющую все возможные решения проблемы. График также помогает определить оптимальное решение, которое дает наилучшие результаты.

Методы, используемые для решения задач линейного программирования

Задачи

Существует ряд методов, которые можно использовать для решения задач линейного программирования. Наиболее распространенными методами являются графический метод, симплексный метод и двойной симплексный метод.

Графический метод — это графический метод, который можно использовать для решения задач линейного программирования. Метод включает в себя нанесение на график точек, представляющих задачу линейного программирования. Затем допустимая область заштриховывается на графике и находится оптимальное решение.

Симплекс-метод — это математический прием, который можно использовать для решения задач линейного программирования. Метод включает решение ряда линейных уравнений для нахождения оптимального решения.

Метод двойного симплекса — это математический метод, который можно использовать для решения задач линейного программирования. Метод включает решение ряда линейных уравнений для нахождения оптимального решения. Метод аналогичен симплекс-методу, но учитывает двойственность задачи линейного программирования.

Важные моменты

1. Использование VPN может помочь защитить вашу конфиденциальность в Интернете, скрывая ваш IP-адрес и шифруя ваш трафик.

2. VPN можно использовать для доступа к заблокированным веб-сайтам и контенту, а также для защиты ваших данных при использовании общедоступной сети Wi-Fi.