Логарифмические неравенства
Логарифмические неравенстваОпределение. Логарифмические неравенства — это неравенства, содержащие переменную под знаком логарифма.
Например: log3 (x2 — 3 x + 3) > 1.
При решении логарифмических неравенств помним:
общие свойства неравенств;
свойства монотонности логарифмической функции;
область определения логарифмической функции.
Основные методы решения логарифмических неравенств
loga f(x) > ba > 1 <=> f(x) > ab
loga f(x) > b0 < a < 1 <=> 0 < f(x) < ab
loga f(x) < ba > 1 <=> 0 < f(x) < ab
loga f(x) < b0 < a < 1 <=> f(x) > a
logg(x) f(x) > b <=> f(x) > g(x)bg(x) > 1f(x) < g(x)b0 < g(x) < 1f(x) > 0
logg(x) f(x) < b <=> f(x) < g(x)bg(x) > 1f(x) > 0f(x) > g(x)b0 < g(x) < 1
loga f(x) > loga h(x)a > 1 <=> f(x) > h(x)h(x) > 0
loga f(x) > loga h(x)0 < a < 1 <=> f(x) < h(x)f(x) > 0
loga f(x) < loga h(x)a > 1 <=> f(x) < h(x)f(x) > 0
loga f(x) < loga h(x)0 < a < 1 <=> f(x) > h(x)h(x) > 0
logg(x) f(x) > logg(x) h(x) <=> f(x) > h(x)g(x) > 1h(x) > 0f(x) < h(x)0 < g(x) < 1f(x) > 0
logg(x) f(x) < logg(x) h(x) <=> f(x) < h(x)g(x) > 1f(x) > 0f(x) > h(x)0 < g(x) < 1h(x) > 0
Примеры решения логарифмических неравенств
Пример 1.
Решить неравенство log2 (x2 + 3x) ≤ 2.
Так как основа логарифма 2 > 1, то используем третий метод для решения неравенства
log2 (x2 + 3x) ≤ 2 => 0 < x2 + 3x ≤ 22 => x2 + 3x ≤ 4x2 + 3x > 0 => x2 + 3x -4 ≤ 0x(x + 3) > 0 => (x + 4)(x -1) ≤ 0x(x + 3) > 0
Найдем общее решение:
x ∈ [-4; -3) ∪ (0; 1]
Ответ: x ∈ [-4; -3) ∪ (0; 1].
Пример 2.
Решить неравенство logx — 3 (x — 1) < 2.
Используем вторую схему для решения неравенства
logx — 3 (x — 1) < 2 => x — 1 < (x — 3)2x — 3 > 1x — 1 > 0x — 1 > (x — 3)20 < x — 3 < 1 => x — 1 < x2 — 6x + 9x > 4x > 1x — 1 > x2 — 6x + 93 < x < 4 => x2 — 7x + 10 > 0x > 4x2 — 7x + 10 < 03 < x < 4 => (x — 2)(x -5) > 0x > 4(x — 2)(x -5) < 03 < x < 4 => x ∈ (-∞; 2) ∪ (5; +∞)x > 4x ∈ (2; 5)3 < x < 4 => x ∈ (5; +∞)x ∈ (3; 4) => x ∈ (3; 4) ∪ (5; +∞)
Ответ: x ∈ (3; 4) ∪ (5; +∞).
Пример 3.
Решить неравенство log20.5 x + log0.5 x — 2 ≤ 0.
ОДЗ x > 0.
Сделаем замену log0.5 x = t
t2 + t — 2 ≤ 0
(t + 2)(t — 1) ≤ 0
-2 ≤ t ≤ 1
Вернемся обратно к переменной x и с учетом ОДЗ решим неравенство:
t ≥ -2t ≤ 1 => log0.5 x ≥ -2log0.5 x ≤ 1 =>
Так как основа логарифма 0.5 < 1
=> x ≤ 0.5-2x ≥ 0.51 => x ≤ 4x ≥ 0.5
Ответ: x ∈ [0.5; 4].
Пример 4.
Решить неравенство: log0.4 x + log0.4 (x — 1) ≥ log0.4 (x + 3).
ОДЗ: x > 0x — 1 > 0x + 3 > 0 => x > 0x > 1x > -3 => x > 1
Используя свойство, суммы логарифмов, перепишем неравенство:
log0.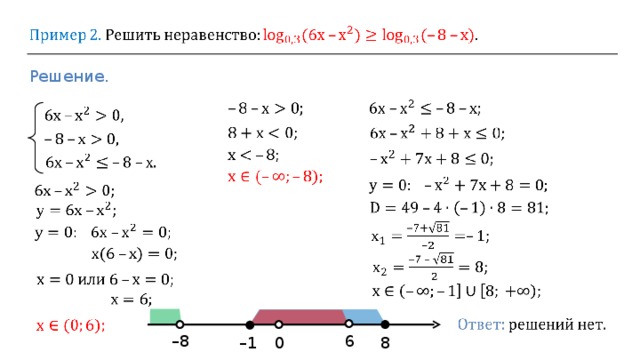
4 x(x — 1) ≥ log0.4 (x + 3)
Так как основа логарифма 0.4 < 1 используем 8 схему решения неравенств, с учетом ОДЗ:
x(x — 1) ≤ x + 3x > 1 => x2 — x ≤ x + 3x > 1 => x2 — 2x — 3 ≤ 0x > 1 => (x + 1)(x — 3) ≤ 0x > 1
Найдем общее решение:
Ответ: x ∈ (1; 3].
Пример 5.
Решить неравенство: (3 — 2x) log0.1 x < 0.
ОДЗ: x > 0
Найдем нули функции, стоящей в левой части неравенства:
(3 — 2x) log0.1 x = 0 => 3 — 2x = 0log0.1 x = 0 => x = 1.5x = 1
Используя метод интервалов найдем решение:
Ответ: x ∈ (1; 1.5).
Логарифмы
Логарифм числа, основное логарифмическое тождество
Формулы и свойства логарифмов
Логарифм произведения. Сумма логарифмов
Логарифм частного.
Разность логарифмов
Логарифм степени
Логарифм корня
Логарифмирование
Потенцирование
Десятичный логарифм
Натуральный логарифм
Число е
Логарифмическая функция
Логарифмические уравнения
Логарифмические неравенства
Логарифмические неравенства — презентация онлайн
Лекция по алгебре.
Тема: логарифмические
неравенства.
Преподаватель математики Хохлова С.Н., Мещенко Н.В.
Определение:
Неравенства, содержащие переменную
под знаком логарифма, называются
логарифмическими.
Например:
1) log5 x 2;
2) lg( x 5) 5;
3) ln( x 1) ;
4) log
3
2
( x 2 x 6)
25 2
I. Типы простейших
логарифмических неравенств
Неравенства вида
1) loga x b или
loga x b
называются простейшими
логарифмическими неравенствами
Неравенства можно переписать
loga x loga
b или
a
loga x loga a
b
Решение логарифмических неравенств
основано на свойстве монотонности
функции y = logat : при a > 1
логарифмическая функция возрастает и
при
0 < a < 1 убывает.
y
y
y = logat, a > 1
0
1
t
0
y = logat, 0 < a < 1
1
t
Методы решения
логарифмических неравенств.
І) Неравенство вида logaf(x) > c (или < c ).
Если a > 1,то
logaf(x) > c,
logaf(x) > c logaa , функция y = logat
возрастает на R+ и
c
logaf(x ) > logaa .
неравенствоlogaf(x)> c
равносильно системе
a>1
f(x) > 0 – это ОДЗ
или
c
f(x) > a – это монотонность
f(x) > ac
Пример. Решить неравенство
log7(4x + 1) 2
Решение.
log7(4x + 1) log749
Так как (a = 7 > 1)
4x + 1 > 0 – это ОДЗ
4x + 1 49
4x + 1 49,
x 12
Ответ: x 12 .
2) Если 0 < a < 1, то функция y = logat
убывает на R+ и неравенство
logaf(x) > c равносильно системе
f(x) > 0 – это ОДЗ
f(x) < ac – это монотонность
Систему в этом случае упростить
нельзя.
Пример. Решить неравенство
log1/2(1 – x) > 2
Решение.
log1/2(1 – x) > log1/2(1/4)
1 – x > 0 – это ОДЗ
1 – x < 1/4 (a = 1/2 < 1)
3/4 < x < 1
x<1
x > 3/4
Ответ: ( 0,75; 1) .
І І. Неравенство вида logaf(x) > logaφ(x)
или logaf (x) < logaφ(x).
1) Если a > 1, то функция y = logat
возрастает на R+ и неравенство
log a f (x) > log aφ(x) равносильно системе
f(x) > 0
– это ОДЗ
φ(x) > 0
f(x) > φ(x) – это монотонность
f(x) > φ(x)
φ(x) > 0
Пример. Решить неравенство
lgx2 > lg(5x – 4)
Решение.
x2 > 5x – 4
5x – 4 > 0
x2
>0
– это ОДЗ
5x – 4 > 0
x2 > 5x – 4 (a = 10 > 1)
(x – 1)(x – 4) > 0
x > 4/5
1
4
x
4/5
Ответ: (0,8;1) (4;∞).
І І. Неравенство вида
logaf(x) > logaφ(x) или logaf (x) < logaφ(x).
2) Если 0 < a < 1, то функция y = logat
убывает на R+ и неравенство
logaf(x) > logaφ(x) равносильно системе
f(x) > 0
– это ОДЗ
φ(x) > 0
f(x) < φ(x) – это монотонность
φ(x) > f(x)
f(x) > 0
Пример.
Решить неравенство
log1/3(3x – 4) ≥ log1/3(x2 – 2)
Решение.
3x – 4 > 0
– это ОДЗ
x2 – 2 > 0
3x – 4 ≤ x2 – 2 (a = 1/3 < 1)
(x – 1)(x – 2) ≥ 0
x > 4/3
x2 – 2 ≥ 3x – 4
3x – 4 > 0
1
4/3
2
Ответ: [ 2; ∞).
x
Простейшие логарифмические
неравенства.
f x 1,
logа f x 0, logа f x loga 1,
a 1
0 f x 1,
logа f x loga 1,
0 a 1
0 a 1
1)
a 1
logа f x 0,
2)
0 a 1
a 1
logа f x 0,
3)
a 1
logа f x loga 1,
0 f x 1,
a 1
a 1
logа f x 0,
4)
0 a 1
logа f x loga 1,
f x 1,
0 a 1
0 a 1
І І І) Неравенства, требующие предварительных
преобразований.
1) Находят ОДЗ неравенства.
2) Преобразуют неравенство к виду І
или І І и решают полученное
неравенство, используя свойство
монотонности.
3) Находят пересечение множества
решений с ОДЗ неравенства и
записывают ответ.
Пример. Решить неравенство
log 2(x – 1) + log 2x ≤ 1
Решение.
1) ОДЗ :
x–1>0
x>0
2) log 2(x – 1)·x ≤ log 22
x2
– x ≤ 2, (x + 1)(x – 2) ≤ 0
x>1
a=2>1
-1
2
3) Пересечение множества решений с ОДЗ.
-1
1
2
x
Ответ: ( 1; 2].
x
III.Метод замены переменной в
логарифмическом неравенстве.
Пример. Решить неравенство
Решение.
lg x 3 lg x 3
1
lg x 1
2
Пусть lgx = t, t – любое число, тогда
2
t
3
t
3
неравенство примет вид
1 0
t 1
2
Отсюда
имеем
t 4t 4
0 Нули числителя
:
2(
кратность четная)
lg x < 1;
t 1 2
Нули знам.:1(кратность нечетная)
lg x < lg10
t 2 0
+
+
т. к.
> 1, x >0, то
t 1
— a = 10 2
1 0 < x < 10
t 1
Ответ:
0; 10
17. IV. Решение логарифмических неравенств, содержащих переменную в основании логарифма
Теорема 1.Если а > 0,
a ≠1, b> 0, c> 0,
1) неравенство logab > logac равносильно неравенству
(a -1)(b — c) > 0;
2) неравенство logab ≥ logac равносильно неравенству
(a -1)(b — c) ≥ 0;
3) неравенство logab < logac равносильно неравенству
(a -1)(b — c) < 0;
4) неравенство logab ≤ logac равносильно неравенству
(a -1)(b — c) ≤ 0;
18.
Решение логарифмических неравенств, содержащих переменную в основании логарифмаЗамечание- соглашение.Для упрощения записей целесообразно
ввести символ v ,
понимая, что там, где стоит этот символ,
должен стоять один из знаков ≥, ≤,>либо<.
Тогда теорема 1 может быть
сформулирована более коротко: при всех
допустимых значениях a ,b и с неравенство
logab v logac равносильно (a -1)(b — c) v 0.
Если в процессе решения смысл неравенства
должен измениться, то пишется символ .
Пример 1. Решите неравенство
logx+7(2×2-6x+8)≤logx+7(x2+x-2).
Решение: logx+7(2×2-6x+8) ≤ logx+7(x2+x-2)
x 7 1 2 x 2 6 x 8 x 2 x 2 0,
x 7 0 , x 7 1,
2 x 2 6 x 8 0,
x 2 x 2 0
x 6 x 5 x 2 0,
x 7, x 6,
x 2 x 1 0
x 6 x 2 7 x 10 0,
x 7, x 6,
2
x 3x 4 0,
x 2 x 1 0
6,
7 x -6
2 x 5.
-7 -6
x 3x 4 0
2
Так как D<0,то
x 3x 4 0
2
на x R
2
-2
5
1
Ответ: 7; 6 2;5 .
-7
-6
2
5
20.
Следствие 1. При допустимых значениях a ,b и c неравенство logab — logac v 0 равносильно неравенству (a -1)(b — c) v 0Следствие 1. При допустимых значениях a ,bи c неравенство logab — logac v 0
(a -1)(b — c) v 0
Следствие 2. При допустимых значениях a и b
равносильно неравенству
неравенство logab
a
v
0 равносильно
неравенству ( -1)(b — 1) v 0
Пример .
Решите неравенство
log10-х(x2-5x+6) — log10-х(2x-4)≥0.
Решение:
10 x 1 x 2 5 x 6 2 x 4 0, x 9 x 2 x 5 0,
x 10, x 9,
x 9 x 5 x 2
10 x 0 , 10 x 1,
2
3 x 10, x 9,
x
2
x
3
0
,
x 5 x 6 0,
2 x 4 0
x 2
0,
5 x 9
Ответ: 5; 9
1. Решите неравенство :
x
2
2 x 8 log x 5 2 x 7 0.
Ответ : 4; 3 2;4 .
2. Решите неравенство
log x x 3 log x 9 x
log x 1 x
0.
Ответ : 3;6
Теорема 2.
При допустимых значениях a ,b , c, d неравенство
logab logcd v 0 равносильно неравенству
(a -1)(b — 1)(c-1)(d-1) v 0
2
x
log
log
x
1 0.
Решите неравенство:
1 x 1
x 2
x
Решение:
1 x
2
1
1
x
3
x
1 1 0
, 1 x 1
x 1 x 3
2
x x 1
0,
x x 1 x 3 x 0, x3 x 1
1 0, x 1,
x 2,
x
x 0, x 1,
x 3
x
x 1 0,
0,
x 1
x 2, x 3
x 2 0, x 2 1
2 x 3.
Ответ:
2;3 .
Теорема 3.
При допустимых значениях a ,b , c неравенство
logab — logcb v 0 равносильно неравенству
(a -1)(b — 1)(c-1)(c-a) v 0.
Решите неравенство:
log x x 1 log x 1 x 1 0.
Решение:
x 1 x 1 1 x 1 1 x 1 x 0,
x x 1 x 2 0,
x 0, x 1,
1 x 2.
x 1
x
1
0
,
x 1 0, x 1 1
Ответ: 1;2 .
Домашнее
задание.
1) Разобрать приёмы решений логарифмических
уравнений и неравенств по лекции.
2) Никольский 10 кл.
I. № 6.33 – 6. 34, 6.37(а, б), 6.38(а),6.41(a,г)
II. № 6.37(а, б), 6. 39(в, г), 6.41(б, в), 6.42(в, г).
Логарифмические неравенства — Практика решения задач Проблемы онлайн
Каков диапазон xxx, который удовлетворяет приведенному выше логарифмическому неравенству?
25≤x≤625 25 \leq x \leq 625 25≤x≤625 0≤x≤25 0 \leq x \leq 25 0≤x≤25 0View wiki
Уровень силы звука (измеряется в децибелах) определяется по формуле:
LI=10log(II0) (дБ), L_I=10\log\left(\frac{I}{I_0}\right)\text{ (дБ)},LI=10log(I0I) (дБ ),
где III обозначает интенсивность звука, а I0I_0I0 — эталонную интенсивность звука.
2,I0=1 пВт/м2, в каком диапазоне порога интенсивности звука xxx может воспринимать человек с тугоухостью средней степени тяжести? ? 921 мкВт/м2
View wiki
A,BA, B A,B и CCC — положительные целые числа, удовлетворяющие условиям A≥2,B≥4,C≥8 A \geq 2, B \geq 4, C \geq 8 A≥2,B≥ 4,С≥8. Каково минимальное целое значение
logA(BC)+logB(CA)+logC(AB)? \log_A (BC) + \log_B (CA) + \log_C (AB) ? logA(BC)+logB(CA)+logC(AB)?
Детали и предположения 92-2x\log_{9}a+4\log_{9}a=0 x2−2xlog9a+4log9a=0 положительный, а другой корень отрицательный, каков диапазон a?a?a?
19View wiki
Урок Решение логарифмических неравенств
Урок Решение логарифмических неравенствАлгебра -> Решатели логарифмов, тренажеры и текстовые задачи -> Урок Решение логарифмических неравенств Войти
|
