Решить систему уравнение онлайн: Решение систем уравнений · Калькулятор Онлайн

alexxlab / / Разное

Тест к уроку: “Современное общество”

Решение систем уравнений второй степени

План урока

  1. Способ (метод) подстановки;
  2. Способ (метод) сложения.

Цели урока

  • Знать алгоритм решения систем уравнений второй степени способом подстановки;
  • Знать суть метода сложения для решения систем уравнений второй степени;
  • Уметь использовать метод подстановки для решения систем уравнений второй степени;
  • Уметь использовать метод сложения для решения систем уравнений второй степени.

Разминка

  • Какие способы решения систем линейных уравнений вы изучали?
  • Сколько решений имеет система линейных уравнений?

Метод подстановки

 

Системы линейных уравнений можно решить, например, способом подстановки или способом сложения. Оба эти метода решения вам знакомы, и вы умеете их использовать. Каждый из них можно применить и для решения других систем.

 

Рассмотрим сначала способ подстановки. Вспомним алгоритм решения системы уравнений для этого метода.

Алгоритм решения систем уравнений второй степени способом подстановки:

1. Выразить из уравнения первой степени одну переменную через другую;

2. Подставить полученное выражение в уравнение второй степени, в результате чего получается уравнение с одной переменной;

3. Решить получившееся уравнение с одной переменной;

4. Подставить решения уравнения в выражение из пункта 1 и найти соответствующее значение второй переменной.

Воспользуемся этим способом для решения следующей системы.

Пример 1

Решить систему уравнений:

 

x2+y2=25x+y=-7

Решение

 

1. Выразим из второго уравнения переменную y:

 

x+y=-7, y=-7-x.

 

2. Подставим полученное выражение в первое уравнение и решим уравнение с одной переменной:

 

x2+(-x-7)2=25

x2+x2+14x+49-25=0

2×2+14x+24=0

x2+7x+12=0

x1=-3; x2=-4.

 

3. Подставим полученные значения для переменной x в выражение из пункта 1, y=-7-x

 

y1=-7-(-3)=-7+3=-4 

y2=-7-(-4)=-7+4=-3

 

4. Таким образом, решение системы уравнений – две пары значений (-3; -4) и (-4; -3).

 

Ответ: (-3; -4), (-4; -3).

Упражнение 1

Решить систему уравнений:

 

3x-y=2×2-4x+8=y

Метод сложения

 

Второй способ решения – метод сложения. Суть метода состоит в том, что при сложении (или вычитании) уравнений системы можно получить уравнение с одной переменной.

Алгоритм решения систем уравнений второй степени методом сложения:

1. Умножить или разделить, при необходимости, уравнения (или оба) на число, так чтобы в обоих уравнениях была одна из переменных с одинаковыми или противоположными коэффициентами;

2. Сложить (если коэффициенты одинаковые) или вычесть (если коэффициенты противоположные) уравнения;

3. Решить получившееся уравнение с одной переменной;

4. Подставить решения уравнения в любое из исходных уравнений и найти соответствующее значение второй переменной.

Оба способа пользуются широким распространением и изучение обоих необходимо. 

 

Рассмотрим применение метода сложения на примере.

Пример 2

Решить систему уравнений:

 

5×2+y2=3610×2+2y2=36x

Решение

 

1. Умножим первое уравнение на 2 и получим:

 

10×2+2y2=7210×2+2y2=36x

 

2. Из первого уравнения вычтем второе:

 

10×2+2y2-(10×2+2y2)=72-36x

72-36x=0

 

3. Решим полученное уравнение:

 

72-36x=0

x=2

 

4. Подставим полученное значение для переменной x в уравнение 5×2+y2=36:

 

5·22+y2=36

y2=36-20

y2=16

y1=4, y2=-4.

 

5. Таким образом, решение системы уравнений – две пары значений (2; 4) и (2; -4).

 

Ответ: (2; 4), (2; -4).

Если система состоит из двух уравнений второй степени с двумя переменными, то решить ее бывает трудно. Для ее решения в отдельных случаях применяют метод подстановки и метод сложения.

Упражнение 2

Решить систему уравнений:

 

18×2+21y2=61x6x2+7y2=61

Пример 3 

Решите систему уравнений:

 

x2y2-xy=yx-y2x2,x+y=4.

Решение 

 

Перепишем систему уравнений в виде: 

 

x2y2+y2x2=xy+yx,x+y=4.

 

Пусть t=xy+yx. Возведем обе части этого равенства во вторую степень:

 

t2=x2y2+2·xy·yx+y2x2,

 

x2y2+y2x2=t2-2.

 

Первое уравнение примет вид t2-t-2=0, решением которого являются числа 2 и -1. 

 

Тогда из исходной системы уравнений получаем две системы: 

 

xy+yx=2,x+y=4, и xy+yx=-1,x+y=4.

 

Решим каждую из них.

 

1) xy+yx=2,x+y=4, 4-yy+y4-y=2,x=4-y.

 

Решим отдельно первое уравнение: 

 

4-yy+y4-y=2,

 

16-8y+y2+y2-2y4-yy4-y=0,

 

y2-4y+4=0 при y≠0; y≠4, 

 

y=2.

 

Если y=2, то x=2.

 

2) xy+yx=-1,x+y=4, 4-yy+y4-y=-1,x=4-y.

 

Решим отдельно первое уравнение:

 

4-yy+y4-y=-1,

 

16-8y+y2+y2+4y-y2y4-y=0,

 

y2-4y+16=0 при y≠0; y≠4.

 

Последнее уравнение не имеет действительных корней, значит, и система уравнений не имеет решений. 

 

Ответ: 2; 2.

Пример 4

Решите систему уравнений:

 

xy+2x-y=10,5xy-3x-y=11.

Решение

 

Пусть xy=t, x-y=m. Тогда система уравнений примет вид: 

 

t+2m=10,5t-3m=11, t=10-2m,50-10m-3m=11, t=4,m=3.

 

Имеем: 

 

xy=4,x-y=3, y3+y=4,x=3+y.

 

Решения первого уравнения: y1=1; y2=-4.

 

Если y=1, то x=4. 

 

Если y=-4, то x=-1.  

 

Ответ: (4; 1), (−1; −4).

Пример 5

Решите систему уравнений:

 

x+4y-1=x2+5x+4,x2-xy-3x+8=0.

Решение

 

Разложим квадратный трехчлен из правой части первого уравнения на множители: 

 

x2+5x+4=x+4x+1.

 

Первое уравнение примет вид: 

 

x+4y-1=x+4x+1.

 

Перенесем все в левую часть и вынесем за скобки общий множитель:

 

x+4y-x-2=0,

 

откуда, x=-4 или y=x+2. 

 

Если x=-4, то из второго уравнения получим y=-9. 

 

Если y=x+2, то из второго уравнения x=1,6, тогда y=3,6. 

 

Ответ: (−4; −9), 1,6; 3,6.

Контрольные вопросы:

 

1. Как решить систему уравнений методом подстановки?

2. Чем метод сложения отличается от метода подстановки?

Ответы

Упражнение 1

 

(2; 4), (5; 13)

 

Упражнение 2

 

(3; 1), (3; -1)

Системы уравнений

Репетиторы ❯ Математика ❯ Системы уравнений

Автор: Валентин В.

, онлайн репетитор по математике

●

10.10.2011

●

Раздел: Математика

Если перед нами ставится задача найти все общие решения двух уравнений с двумя переменными, то говорят, что нужно решить систему уравнений. Решением системы уравнений называется каждая пара значений переменных, обращающая каждое уравнение системы в верное равенство. Иными словами, решить систему – это значит найти все решения этой системы или доказать, что их нет.

Запись системы уравнений сопровождается фигурной скобкой {.

Две системы уравнений называются равносильными, если эти системы имеют одни и те же решения. Системы уравнений считаются равносильными также и в случае, когда каждое уравнение системы не имеет решения.

Теорема 1. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение системы оставить без изменения, а другое уравнение системы заменить уравнением, ему равносильным, то полученная система будет равносильна заданной.

{х – 3у = 10,                                     {х = 3у + 10
{3х – 2у = 2                                      {3х – 2у = 2

Следствие. Если каждое уравнение системы заменить равносильным уравнением, то получится система, равносильная данной. Так, равносильными являются системы:

{х – 3у = 10,                                     {х = 3у + 10

{3х – 2у = 2                                      {х = 2/3у + 2/3.

Теорема 2. Пусть дана система двух уравнений с двумя переменными. Если одно уравнение оставить без изменения, а другое уравнение заменить суммой или разностью обоих уравнений системы, то полученная системы будет равносильна данной.

Так, равносильны системы:

{х – 3у = 10,                                    {(х – 3у) + (3х – 2у) = 10 + 2
{3х – 2у = 2                                     {3х – 2у = 2.

Существует несколько методов решения систем уравнений с двумя переменными.

Метод подстановки реализуется так:

1. В одном из уравнений мы выражаем одну переменную через другую (например, х через у).

2. Полученное выражение подставляем во второе уравнение вместо х. В результате получается уравнение с одной переменной.

3. Находим корни этого уравнения.

4. Воспользовавшись нашим выражением из пункта 1, находим вторую переменную.

Решим систему уравнений:

{х – 3у = 10,
{х2 – 24у = 100.

Решение.

1. В уравнении 1 выразим х через у и получим: х – 3у = 10 → х = 3у + 10

2. В уравнение 2 подставим полученное выражение: х2 – 24у = 100 – (3у + 10)2 – 24 у = 100.

3. Решим преобразованное уравнение 2 и получим корни 0 и -4.

4. Исходя из полученных значений у, найдем значения х.

Если у = 0, х = 10.

Если у = -4, х = -2.

Т.о., система уравнений имеет два решения: (-2; -4) и (10; 0).

Ответ. (-2; -4) и (10; 0).

Метод сложения основан на рассмотренных нами теориях. Изучим данный метод, работая с примером:

Решим систему:

{2х + 3у = 7,
{3х – у = 16.

Решение.

1. Умножим обе части второго уравнения на 3, получим систему:

{2х + 3у = 7,
{9х – 3у = 48.

Эта система, в соответствии с теоремами, равносильна первоначальной.

2. Сложим оба уравнения новой системы и получим:

{2х + 3у = 7,
{(2х + 3у) + (9х – 3у) = 7 + 48.

3. Преобразуем полученную систему:

{2х + 3у = 7,
{11х = 55.

4. Из уравнения 2 получаем х = 5. Подставим получившееся значение в уравнение 1 и получим у = -1 .

Ответ. х = 5, у = -1.

Метод введения новых переменных работает так: либо мы вводим новую переменную только для одного уравнения, либо вводим две новых переменных сразу для обоих уравнений.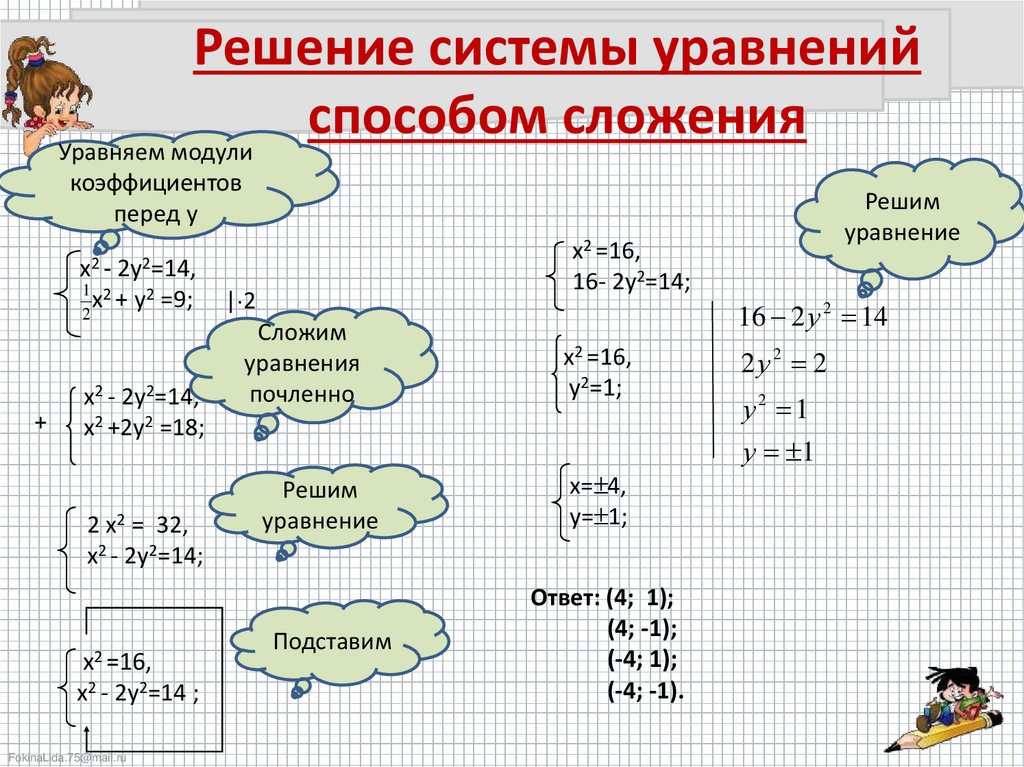

Решим систему

{х/у = у/х = 13/6
{х = у = 5.

Решение.

1. Предположим, что х/у = a, тогда у/х = 1/а → уравнение 1 примет вид: а + 1/а = 13/6.

Решим полученное уравнение относительно переменной а: 6а2 + 6 = 13а

6а2 – 13а + 6 = 0. Корнями уравнения являются а1 = 2/3 и а2 = 3/2.

2. Отсюда получим, что либо х/у = 2/3, т.е. у = 3х/2, либо х/у = 3/2, т.е. у = 2х/3.

3. Т.к. с учетом полученных результатов, уравнение 1 распалось на два уравнения, нам предстоит решить совокупность двух систем:

{у = 2х/3,                       {у = 2х/3.
{х + у = 5                        {х + у = 5.

Из системы 1 находим  х = 2, у = 3, из системы 2 находим х = 3, у = 2.

Ответ: (2; 3) и (3; 2).

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Задать вопрос

Математика

Курсы по математике 10 класс

Математика

Курсы по математике 9 класс

Математика

Математика 11 класс

Математика

Курсы по геометрии 7 класс

Математика

Курсы по алгебре 7 класс

Математика

Алгебра 8 класс

Математика

Курсы по геометрии 8 класс

Французский язык

Курсы французского языка для начинающих

Онлайн калькулятор: Решатель линейных уравнений с двумя переменными

Учеба Математика Алгебра

Калькулятор решает систему уравнений первой степени с двумя неизвестными. Вы вводите шесть коэффициентов, он находит значения неизвестных и обнаруживает случаи отсутствия решения или бесконечных решений.

Система уравнений первой степени с двумя неизвестными:

где a, b, c, d, e и f действительные числа, а x и y неизвестны.

Необходимо ввести коэффициенты a, b, c, d, e и f в форму ниже, и калькулятор выдаст x и y .

Формулы, используемые для решения уравнений, находятся под калькулятором.

Решение системы уравнений первой степени с двумя неизвестными

Точность вычислений

Знаки после запятой: 2

Комментарии

Решение уравнений

Для решения уравнений необходимо найти значения x и y, удовлетворяющие обоим уравнениям одновременно.

Шаги, связанные с решением системы уравнений первой степени с двумя неизвестными, включают исключение одного из неизвестных путем сложения или вычитания двух уравнений, а затем решение оставшихся неизвестных. Это можно сделать с помощью методов замены или исключения. Подстановка включает решение одного уравнения для одной переменной и подстановку этого значения в другое уравнение, в то время как исключение включает добавление или вычитание двух уравнений для исключения одной из переменных.

Однако есть общие формулы:

Эти формулы легко запомнить, если ввести понятие определителя второго порядка как

Тогда решение уравнений можно записать в виде

т.е. неизвестных равна дроби, знаменателем которой является определитель, состоящий из коэффициентов при неизвестных, а числитель получается из этого определителя заменой коэффициентов при соответствующем неизвестном на абсолютный член.

Возможны три различных решения:

  1. Коэффициенты при неизвестных в уравнениях непропорциональны

    в этом случае система уравнений имеет единственное решение, представленное формулой

  2. Коэффициенты при неизвестных пропорциональны, но непропорциональны свободным слагаемым

    в этом случае система уравнений не имеет решений, так как мы имеем здесь противоречивые уравнения.

  3. Все коэффициенты уравнений пропорциональны

    Система уравнений имеет бесконечное множество решений, потому что на самом деле у нас одно уравнение вместо двух.

URL скопирован в буфер обмена

Похожие калькуляторы
  • • Решение неоднородной системы линейных уравнений с помощью обратной матрицы
  • • Общее решение системы линейных уравнений с помощью метода исключения Гаусса
  • • Метод исключения Гаусса
    • 9 0064 • Правило Крамера
  • • Решатель уравнений 3×3
  • • Раздел алгебры (110 калькуляторов)

 Алгебра Математическая система уравнений

PLANETCALC, двухпеременная линейная Equation Solver

Тимур 07.03.2023 07 :34:38 ​​

Легко решить систему уравнений

Калькулятор системы уравнений

Мы представляем вам лучший Калькулятор системы уравнений с шагами, с помощью которых вы можете решают системы линейных уравнений , систему квадратных уравнений , линейные квадратные системы  и систему нелинейных уравнений в целом.

Этот калькулятор идеально подходит для обучения решению систем уравнений методами подстановки и исключения, так как он представляет решения с пошаговым объяснением. Так что, если вы изучаете алгебру, этот калькулятор системы уравнений будет вам очень полезен.

Этот калькулятор идеально подходит для обучения решению систем уравнений методами подстановки и исключения, так как он представляет решения с пошаговым объяснением. Так что, если вы изучаете алгебру, этот калькулятор системы уравнений будет вам очень полезен.

А если вы учитель математики, этот инструмент поможет вам создать новый учебный материал для использования в классе.

В следующем разделе вы найдете инструкции по использованию решателя системы уравнений.

Содержание

  • 1 Калькулятор системы уравнений
  • 2 Инструкции по использованию Решателя системы уравнений
  • 3 Что такое система уравнений?
  • 4 Типы систем уравнений
  • 5 Как решить систему уравнений
    • 5. 1 Метод замены
    • 5.2 Метод исключения

Инструкции по использованию Решателя систем уравнений

Для решения систем уравнений с помощью этого калькулятора выполните следующие действия:

  1. Введите уравнения одно за другим, используя поле ввода и кнопку «+ Добавить». Введенные уравнения будут располагаться под полем ввода, их можно отредактировать, нажав кнопку со значком карандаша, или удалить, нажав красную кнопку «x».
  2. Нажмите кнопку «Решить», чтобы получить решение системы уравнений. Автоматически появится окно с подробным пошаговым решением. В этом поле вы можете выбрать метод, используемый для решения системы уравнений.

В этом видеоуроке более подробно показано, как пользоваться калькулятором системы уравнений.

5x-3y+4z=-1
-3x-6y=14z

5x-32y=-1
-3x-6y=14