Решить уравнение дробное онлайн с решением: Решение уравнений с дробями онлайн · Как пользоваться Контрольная Работа РУ

Содержание

Уравнения . Решение уравнений — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Уравнения . Решение уравнений.

Девиз урока:
«Вся математика – это, собственно,
одно большое уравнение для других
наук»
Новалис
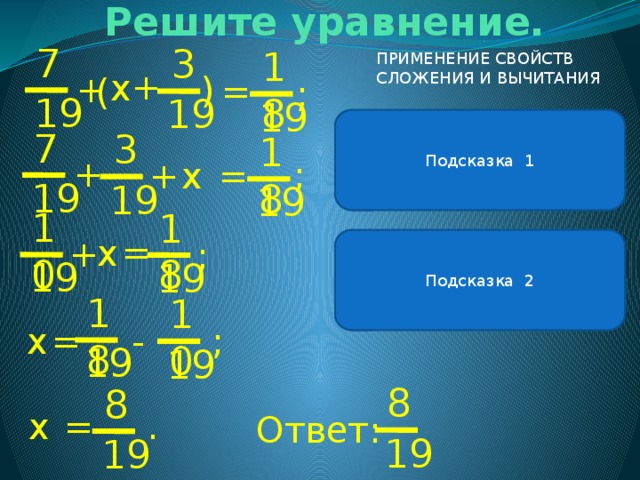
Решите уравнение.
1вариант
2вариант
1. 3х²+х =0
1. 3х-х² = 0
2. 3(2+1,5х)=0,5х+24
2. 2х-5,5=3( 2х-1,5)
.
3. 2х²-8=0
4.
5
4
1 x 3 x
3.

3х²-27=0
4.
5
3
x 2 x 4
Решите уравнение.
1вариант
2 вариант
5.
x x
5
3 12
x x
3
5 2
6. Каждое уравнение, имеющее корни, соотнесите
с множеством его корней.
1. х² = х
2. х²= -х
3. х² = -1
4. х² =1
а) 1и-1
б) 0 и 1
в) 0 и-1
1.х² -1=0
2.х²+1=0
3.х² = х
4.х² = -х
а) 0 и-1
б) 0и1
в) 1 и-1
Ответы.
1
вариант
1. 0
и
2.
4,5
3.
-2 и 2
4.
11
5.
-12
6. 1-б
2-в
4-а
2.
-0,25
3.
-3 и 3
4.
13
5.
10
6. 1-в
3-б
4-а
1
3
2
вариант
1.
0и3
Решите уравнение.( 2 балла)
1) x 2 x 8 0
4
2
2) x x 4 0
4
2
1
2
2
3)
x 6 x 2 x 6
4 балла
Решите уравнение.
1) x x 20 0
2) x 6 x 27 0
При каких значениях k уравнение x²+ kх+2=0
имеет корни? Приведите пример положительного
значения k, при котором выполняется условие.

7. Решите уравнение. 6 баллов

x 4
x
11
2
0
x
x 3x 4
2
2

8. Уравнения. Уравнение-это равенство с переменной или переменными. Те значения переменной или переменных, при которых уравнение

обращается в верное
равенство, называют корнями
уравнения.
Решить уравнение-это, значит
найти все его корни или
доказать , что корней нет.

9. Основные свойства уравнений.

1.Любой член уравнения можно
перенести из одной части в другую,
изменив его знак на противоположный.
2. Обе части уравнения можно
умножить или разделить на одно и то
же число, не равное нулю.

10. Линейное уравнение с одной переменной. Уравнение вида ax = b,где x — неизвестное, a и b — некоторые числа, называется линейным

уравнением с одним
неизвестным.
1. Если a 0, то уравнение имеет
единственный корень x = — b/a.
2. Если а = 0, b ≠ 0,то уравнение не имеет
корней.
3. Если a = 0, b = 0, то уравнение имеет
бесконечно много корней: корнем
уравнения является любое действительное
число.

11. Определение квадратного уравнения.

Опр. 1. Квадратным уравнением
называется уравнение вида ах2 + bх + с = 0,
где х –переменная, а, b и с — некоторые
числа, причем а 0.
Числа а, b и с — коэффициенты
квадратного уравнения. Число а называют
первым коэффициентом, b – вторым
коэффициентом и с – свободным членом.

12. Дискриминант квадратного уравнения

Опр. 2. Дискриминантом квадратного
уравнения ах2 + bх + с = 0 называется
выражение b2 – 4ac.
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0

13. Если D  0

Если D 0
В этом случае уравнение ах2 + bх + с = 0
имеет два действительных корня:
b D
x1
2a
b D
и x2
.
2a

14. Если D = 0

В этом случае уравнение ах2 + bх + с = 0
имеет один действительный корень:
b 0
x
2a
b
x
2a

15. Если D  0

Если D 0
Уравнение ах2 + bх + с = 0 не имеет
действительных корней.

16. Формула корней квадратного уравнения

Обобщив рассмотренные случаи получаем
формулу корней квадратного уравнения
ах2 + bх + с = 0.
b D
x1,2
, где D b2 4ac.
2a

17. Определение приведенного квадратного уравнения

Опр. 3. Приведенным квадратным уравнением
называется квадратное уравнение, первый
коэффициент которого равен 1.
х2 + bх + с = 0

18. Теорема Виета: Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а

произведение корней равно
свободному члену.
Х2 + рх+q = 0 (приведённое квадратное уравнение)
р – второй коэффициент
q – свободный член
Итак, х1+ х2 = -р.
х1· х2 = q
Теорема, обратная теореме Виета.
Если числа p, q, х1и х2 таковы, что
х1+ х2 = -р, х1· х2 = q,
то х1и х2
корни уравнений
Х2 + рх+q = 0 .

19. Дробно -рациональные уравнения. Уравнение дробное – уравнение вида где Р(х) и Q(х) –некоторые многочлены.

Решение дробногоДробно -рациональные уравнения.
Уравнение дробное – уравнение вида
P( x)
0
Q( x)
где Р(х) и Q(х) –некоторые многочлены.
Решение дробного уравнения можно
разбить на два этапа:
1.Решить уравнение Р(х) = 0.
2.Проверить условие: Q (х)
≠0.

20. Рациональные уравнения. Уравнение вида P(x)=0, P(x)/Q(x)=0, где Р(х), Q(x)-многочлены. При решение рациональных уравнений в

основном используются
два метода:
1. разложение на множители;
2. введение новых переменных.

English Русский Правила

Исчисление дробей 分数阶微积分 Дифференциальные уравнения дробных чисел 分数阶微分方程

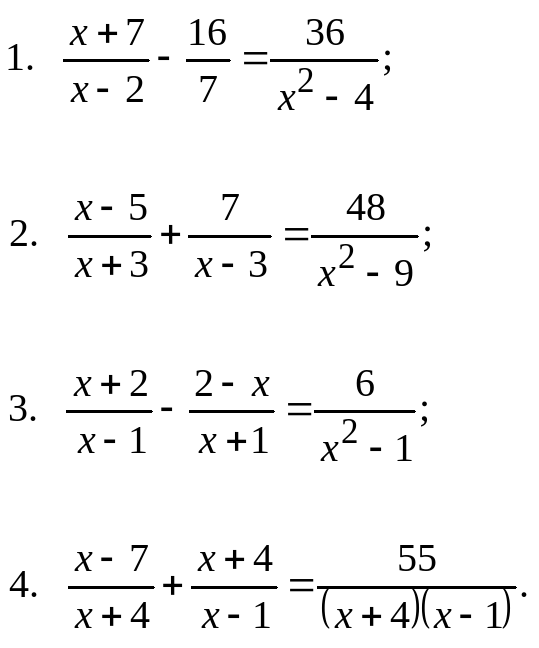
Введение Наука физика в основном построена на дифференциальных уравнениях. Многие из наиболее полезных дифференциальных уравнений, появляющихся в физике, представляют собой дифференциальные уравнения в частных производных, известные как математические физические уравнения. так что понимание решений, которые могут возникнуть, и их взаимосвязей может многое сказать о возможных системах, пригодных для анализа физических проблем.

В математике дифференциальное уравнение в частных производных (УЧП) — это дифференциальное уравнение, содержащее неизвестные функции многих переменных и их частные производные. УЧП используются для формулировки задач, включающих функции нескольких переменных, и либо решаются компьютерами, либо используются для создания компьютерной модели. Особый случай — обыкновенные дифференциальные уравнения (ОДУ), которые имеют дело с функциями одной переменной и их производными.

PDE можно использовать для описания широкого спектра явлений, таких как звук, тепло, диффузия, электростатика, электродинамика, гидродинамика, упругость, гравитация и квантовая механика. Эти, казалось бы, разные физические явления можно аналогичным образом формализовать в терминах УЧП. Точно так же, как обыкновенные дифференциальные уравнения часто моделируют одномерные динамические системы, уравнения в частных производных часто моделируют многомерные системы.

Дифференциальные уравнения дробного порядка (ДДУ) могут описывать динамику нескольких сложных и нелокальных систем с памятью. Они возникают во многих областях науки и техники, таких как физика, химия, биология, биофизика, экономика, теория управления, обработка сигналов и изображений и т. д. В частности, нелинейные системы, описывающие различные явления, можно моделировать с помощью дробных производных. В некоторых фракционных моделях также сообщалось о хаотическом поведении. Имеются теоретические результаты, касающиеся существования и единственности решений начальных и краевых задач с дробными дифференциальными уравнениями [1-5].

В этой статье показано, что аналитическое решение уравнения дробного деления решается с помощью MathHand.com. MathHand.com — математический онлайн-калькулятор, бывший SymbMath [6-7]. Он рассматривается как Math Handbook Calculator [8]. Примеры включали дробное дифференциальное уравнение, дробное уравнение в частных производных, дробное интегральное уравнение, уравнение смешанного дробного дифференциального и интегрального порядков, система дифференциального уравнения дробного порядка, дифференциальное уравнение комплексного порядка и дифференциальное уравнение переменного порядка. По умолчанию определение дробного исчисления Капуто [9] используется здесь.

Дифференциальное уравнение По умолчанию неизвестная функция — y(x), а ее начальное значение — y(0). Независимой переменной является x для обыкновенного дифференциального уравнения. Для уравнения в частных производных неизвестной функцией является y( ), а двумя ее независимыми переменными являются x и t. Для системы уравнений две неизвестные функции — это x(t) и y(t) с независимой переменной t.

Таблица 1. Сравнение различных заказов 9((1))(х) — 2у = ехр(х)`
Или введите функцию dsolve(), нажмите кнопку « = » для решения, затем нажмите кнопку « test «, чтобы проверить решение. например
введите dsolve( ds(y) — 2y = exp(x)) для
dsolve `dy/dx — 2y = exp(x)`
Ее решение находится в таблице 2.

Таблица 2. Сравнение дифференциальных уравнений разных порядков

Заказ	наименование 9cos(x))`	-exp(x)

решение = общее решение + частное решение = gsolution() + psolution()

Приведенная выше таблица показывает, что частные решения их дифференциальных уравнений одинаковы независимо от их порядка.

Решить ОДУ графически

Некоторые дифференциальные уравнения не могут быть решены в символьном виде, но могут быть решены численно и графически с помощью функции графика ОДУ odeplot(), например вход sin(x)-cos(y) для y’ = sin(x)-cos(y), затем отметьте y’= или y»= флажок для решения дифференциального уравнения первого или второго порядка. по умолчанию это ODE первого порядка.
y»=y’-y для ОДУ второго порядка

Уравнение в частных производных Введите уравнение УЧП, нажмите кнопку PDE , затем нажмите кнопку plot2D чтобы показать его кривую, где можно изменить значение времени t, или нажмите кнопку plot3D чтобы показать его трехмерный график, где вы можете вращать график. 90,5 у = 2у` )

Его решение находится в таблице 2. Свойство дифференциального уравнения дробного типа такое же, как и у дифференциального уравнения:

Решение уравнения линейной дроби = общее решение + частное решение = gsolution( ) + psolution( )

Оно похоже на линейное дифференциальное уравнение, поэтому метод решения дробного дифференциального уравнения аналогичен дифференциальному уравнению [3-5].

Дробное уравнение в частных производных Когда PDE расширяется до дробного времени, временной порядок в PDE изменяется на дробный временной порядок. Рассмотрим дифференциальное уравнение в частных производных дробного времени с дифференциальным временем дробного порядка. Приведенные выше уравнения диффузии и волновые уравнения можно заменить уравнениями дробной диффузии и волновыми уравнениями. путем изменения порядка времени на дробный порядок, например. 0,5 порядка.

Уравнение теплопроводности с дробным временным порядком 90,5` — 2у = ехр(х)

Его решение находится в Таблице 2. По умолчанию определение дробного исчисления Капуто используется функцией

dsolve() . Если вы хотите использовать определение Римана, используйте решатель преобразования Лапласа lasolve() . Разница между определением Капуто и определением Римана-Лиувилля (RL) заключается в разделе 6 дробного исчисления [8]. например

dsolve(y(-0.5,x)=1) дают ноль.
lasolve(y(-0.5,x)=1) дает ненулевое значение. 9n x` на анимации ниже Рис.1.

Рис. 1. Анимация изменения порядка между 1 и -1.

Сравнение дифференциальных уравнений разных порядков Интересно сравнить дифференциальные уравнения разных порядков в табл. 2. В таблице 2 показано, что все решения уравнений постоянного порядка имеют один и тот же формат exp(k x). При уменьшении порядка дифференциальных уравнений с 2 до 0,5 их общее решение возрастало с exp(sqrt(2)*x) до exp(4x). При уменьшении порядка интегральных уравнений с -0,5 до -2 их общее решение также увеличилось с exp(1/4 x) до exp(1/sqrt(2) x), но все их частные решения не изменились. 90,5 у = 2у)`

f:= 2y+1, eq:=y’-f=0, s:=dsolve(eq), test(s, eq)
f:= 2y+1, eq:=ds(y,x,0.5)-f=0, s:=dsolve(eq), test(s, eq)

ntest( ) числовой тест для положить случайное число в независимую переменную обратно в уравнение с помощью ntest(решение, уравнение) .

Заключение Представлен обзор методов решения дифференциальных уравнений в функции dsolve MathHandbook. Дополнительные примеры доступны на странице документации [10], и примеры включали дифференциальные уравнения [11], которые другие программы не могут, например. Ошибки Вольфрама [12].

Мы надеемся, что примеры и идеи, изложенные в этой статье, будут полезны для элементарные и углубленные курсы по дифференциальным уравнениям, а также для решение дифференциальных уравнений, возникающих в исследовательских и конструкторских задачах на практике.

Ссылки

К.Б. Олдхэм, Дж. Спаниер, Дробное исчисление, Academic Press, Нью-Йорк, Лондон (1974).
Б.Росс. дробное исчисление и его приложения. Springer, Берлин, Гейдельберг, 1975.
К.Б. Миллер, Б. Росс, Введение в дробное исчисление и дробные дифференциальные уравнения, Wiley, Нью-Йорк (1993).
И. Подлубный, Дробные дифференциальные уравнения, Academic Press, Нью-Йорк (1999).
Ю. Ху, Ю. Луо, З. Лу, Аналитическое решение линейного дробно-дифференциального уравнения методом разложения Адомиана, Том 215, Выпуск 1, 15 мая 2008 г., стр. 220-229.
В. Хуанг, SymbMath: программа символической математики, Int. Дж. Матем. Эду. науч. Техн., 1992, 23(1), 160-165.

В. Хуанг, SymbMath Update to Version 2.0, Abs. амер. Мат. Соц., 1992, 13(6), 535.
Math Handbook Calculator, https://blog.actorsfit.com/a?ID=00550-3e2ed6ca-f8f1-49ba-aafd-2b44cee0ab44, последний доступ 21/07/2021.
Дробное исчисление, http://drhuang.com/science/mathematics/fractional_calculus/, последний доступ 21/07/2021.
Примеры системы компьютерной алгебры дробного исчисления, http://drhuang.com/index/example/, последний доступ 21/07/2021.
Специальное дифференциальное уравнение, https://jingyan.baidu.com/article/19020a0a6bb358529d284293.html, последний доступ 21//07/2021.
Ошибки Wolfram, http://drhuang.com/index/bugs/, последний доступ 21/07/2021.

уникальный калькулятор матрицы решений — Googlesuche

AlleBilderShoppingVideosMapsNewsBücher

suchoptionen

Gauss-Jordan Elimination — Matrix Calculator — Reshish

matrix.reshish.com › Gauss-JordanElimination

, который имеет уникальное решение в системах, а также может решать как однократные, так и неопределенные системы с помощью калькулятора. бесконечно много решений.

Решение систем линейных уравнений — Калькулятор матриц

matrixcalc.org › slu

Этот калькулятор решает системы линейных уравнений с использованием метода исключения Гаусса, метода обратной матрицы или правила Крамера. Также вы можете вычислить количество …

Ähnliche Fragen

Как найти единственное решение матрицы?

Какова формула уникального решения?

Как узнать, имеет ли матрица одно решение и нет решения?

Как узнать, что матрица имеет бесконечно много решений?

Найдите значение h,k, при котором система уравнений имеет Уникальное . ..

atozmath.com › LinearEqn_HK

Найдите значение h,k, при котором система уравнений имеет Уникальное решение Калькулятор — Найдите значение h,k, при котором система уравнений …

Калькулятор матриц — Решатель систем Он-лайн — Mathstools

www.mathstools.com › раздел › главная › system_equations_solver

Решатель линейных систем — это калькулятор линейных систем линейных уравнений и матричный калькулятор для квадратных матриц. Он вычисляет собственные значения и …

Комплексные матрицы и линейные системы — Калькулятор матриц

calculates-math.com › комплексный матричный калькулятор

1,99 $

Матричный калькулятор для выполнения матричной алгебры и решения систем линейные уравнения методом исключения Гаусса-Жордана. Все матрицы могут быть комплексными матрицами.

Общее решение системы линейных уравнений с использованием …

planetcalc.com › …

Этот онлайн-калькулятор решает систему линейных алгебраических уравнений, используя метод исключения Гаусса. Он дает результат, если у вас есть уникальный …

Калькулятор матриц — Symbolab

www.symbolab.com › … › Матрицы и векторы

Бесплатный калькулятор матриц — решение матричных операций и функций … Чтобы умножьте две матрицы вместе, внутренние размеры матриц должны совпадать.

Онлайн-решатель систем уравнений — Wolfram|Alpha

www.wolframalpha.com › калькулятор системных уравнений

Wolfram|Alpha способен решать самые разные системы уравнений. Он может решать системы линейных уравнений или системы, включающие нелинейные уравнения, …

Калькулятор системы линейных уравнений — eMathHelp

www.eathhelp.net › калькуляторы › алгебра-2 › система…

Этот калькулятор решить систему линейных уравнений любого типа с показанными шагами, используя либо метод исключения Гаусса-Жордана, либо обратную матрицу.

Калькулятор исключения Гаусса-Жордана — eMathHelp