Определители и системы линейных уравнений
2.3.1. Определители матриц второго порядка
При отыскании обратной матрицы А-1 для матрицы второго порядка с помощью элементарных преобразований в примере 2.10 оказалось, что все элементы обратной матрицы получаются делением элементов матрицы, присоединенной к матрице А, на число ∆ = a11a22 − a12 a21 . Поэтому рассмотрим ве-
личину ∆ подробнее.
Пример 3.1. Рассмотрим систему двух линейных алгебраических уравнений с двумя неизвестными и произвольными матрицей коэффициентов при неизвестных и матрицей-столбцом правых частей:
a11 x1 + a12 x2 = b1a21 x1 + a22 x2 = b2
Указание. Если действовать с буквами затруднительно, сначала можно задаться системой с числовыми коэффициентами.
Воспользуемся методом исключения неизвестной. Для исключения неизвестной х2 умножим первое уравнение системы на коэффициент при х2 во втором уравнении а22, а второе уравнение – на коэффициент при неизвестном х2 в первом уравнении а12. Тогда система примет вид:
Тогда система примет вид:
a22 (a11 x1 + a12 x2 ) = b1a22a12 (a21 x1 + a22 x2 ) = b2 a12
Теперь вычтем из первого уравнения второе. При этом неизвестное х2 исчезнет и останется одно уравнение с одним неизвестным х1:
(a22 a11 − a12 a21 )x1 = b1a22 −b2 a12
Аналогично, после исключения неизвестного х1, получим:
(a22 a11 − a12 a21 )x2 = b2 a11 −b1a21
Оба уравнения содержат в качестве коэффициента при оставшихся неизвестных ∆ = a11a22 − a12 a21 . Он возникал раньше при отыскании обратной матрицы. Правые части также представляют собой аналогичные разности произведений элементов матрицы А и правых частей исходной системы. Заметим, что в тех случаях, когда коэффициент ∆ не равен нулю, после деления на него получаются явные выражения для неизвестных х1 и х2. Для записи этих выражений удобно ввести понятие определителя матрицы второго порядка.
Определителем квадратной матрицы А второго порядка А=(аij), где i=1,2; j=1,2 называется число:
∆ = a22 a11 − a12 a21 .
Определитель матрицы второго порядка записывается А или det(А) и читается определитель А или детерминант А:
A = a11a22 −a12 a21
30
Можно сказать, что определитель второго порядка равен числу, которое получается после вычитания из произведения элементов на главной диагонали произведения элементов матрицы на побочной диагонали.
Пример 3.2. Вычислить определители | 3 | 5 | и | ab | b 2 |
| 4 | 7 |
| 1 | 2 |
|
|
|
|
|
|
Для первого определителя получаем: А =3×7-5×4=21-20=1. А для вто-
рого, аналогично находим: |
| A |
| = 2ab −b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||
Задача 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||||||
1) |
| 3 | 4 |
| 2) |
| 3 | 5 |
| 3) |
| 4 | 3 |
|
| 4) |
| 6 4 |
| 5) |
| 5 −4 |
| 6) |
| 2 | 11 |
| 7) |
| 3 | 19 |
| 8) |
| 3 | 4 |
| |||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||||||||
|
| 5 | 7 |
|
|
| 4 | 7 |
|
|
| 7 | 5 |
|
|
|
| 10 7 |
|
|
| 10 −8 |
|
|
| 4 | 22 |
|
|
| 5 | 32 |
|
|
| 2 | 3 |
| |||
Сравните получившиеся результаты и обратите внимание на совпадение некоторых результатов (точное или с точностью до знака), а также на равенство определителя нулю.
2.3.2. Свойства определителя матриц второго порядка
Определители матриц второго порядка зависят от величины всех элементов матрицы А. Справедливы следующие свойства определителей:
1)определитель матрицы А совпадает с определителем транспонированной матрицы Ат;
2)после перестановки двух строк (или столбцов) матрицы местами величина определителя меняет знак;
3)если определитель имеет совпадающие строки (или столбцы), то определитель равен нулю;
4)общий множитель всех элементов строки (или столбца) можно вынести за знак определителя;
5)если в определителе имеются пропорциональные строки или столбцы, то определитель равен нулю;
6)определитель не изменится, если к любой из его строк прибавить другую строку, умноженную на произвольное число;
7)определитель матрицы равен нулю тогда и только тогда, когда строки(столбцы) этой матрицы пропорциональны;
8)если строка (или столбец) определителя равна сумме двух слагаемых, то определитель равен сумме двух определителей, в которых эта строка (столбец) заменена слагаемыми.
Рекомендация. Доказательства этих свойств можно использовать в качестве задач для вычисления определителей. При этом полезно перейти от численных примеров к алгебраической записи свойства и его анализу.
В качестве примера докажем шестое свойство.
Надо доказать, что величина определителя матрицы A = a22 a11 − a12 a21 не
изменится, если ко второй строке матрицы А прибавить первую строку, умноженную на произвольное число λ. Действительно, элементы второй стро-
31
ки получающегося после такого преобразования определителя равны a21 + λa11 и a22 + λa12 . Поэтому для величины нового определителя получаем:
a11 (a22 + λa12 ) − a12 (a21 + λa11 ) = a11a22 − a12 a21 +λ(a11a12 −a12 a11 ) = A.
Свойства определителей можно использовать для их вычисления. Это полезно делать, когда элементы определителя большие числа, с помощью свойств 4),5),6),8). Применяя эти свойства так же, как для матриц элементарные преобразования, нередко удается сделать хотя бы один из элементов равным нулю или значительно уменьшить элементы определителя, как это было в определителях 1), 7) и 8) задачи 3. 1.
1.
Пример 3.3. Используя свойства определителей, вычислить:
1) | ab | b2 | 2) | 3 | 11 | 3) | 13 | 35 | |
| a | 2 | 45 | 165 | 6 | 16 | ||||
|
|
|
Здесь при вычислении первого определителя полезно заметить, что из первой строки и из первого столбца можно вынести общие множители. По-
сле этого остается | ab | 1 | b | = ab(2 −b). Здесь сначала вынесли общий множи- |
|
| 1 | 2 |
|
тель, а затем нашли оставшийся множитель.
Во втором определителе точно так же полезно сначала вынести общие множители 3 из первого столбца и 11 из второго. Тогда строки определителя оказываются пропорциональными, и по свойству 5) определитель равен 0. Этот результат можно получить иначе, если вычесть из второй строки исходного определителя первую строку, умноженную на 15. Тогда вторая строка окажется нулевой, и, следовательно, определитель равен нулю.
В последнем примере вычисление упрощается, если сначала вычесть из первой строки умноженную на 2 вторую строку. Тогда остается:
1 | 3 | = 2 | 1 | 3 | = 2(8 −9) = −2 |
6 | 16 |
| 3 | 8 |
|
Указание. Также как при решении примеров 3.2, преобразования определителя можно делать разными способами, но результат всегда должен оставаться одинаковым. Это обстоятельство очень полезно использовать для контроля вычислений. Если результаты оказываются одинаковыми, возникает удовлетворение и даже радость победы в тех случаях, когда вычисления казались сложными. Тем самым сомнения порождают удовольствие.
Это обстоятельство очень полезно использовать для контроля вычислений. Если результаты оказываются одинаковыми, возникает удовлетворение и даже радость победы в тех случаях, когда вычисления казались сложными. Тем самым сомнения порождают удовольствие.
Задача 3.2. Используя свойства определителя матрицы второго порядка, вычислить определители:
1) |
| 3 | 5 |
| 2) |
| 4 8 |
| 3) |
| 5 | 45 |
| 4) |
| 3 | − 21 |
| 5) |
| a | 5a |
| 6) |
| 14 7a |
| 7) |
| 4 3 |
| 8) |
| 11 | 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||||||||
|
| 6 | 7 |
|
|
| −3 5 |
|
|
| 2 | 9 |
|
|
| 3 | 7 |
|
|
| 2 | 15 |
|
|
| 3 2a |
|
|
| 16 12 |
|
|
| 33 | 9 |
|
32
2.
 3.3. Решение системы двух уравнений с двумя неизвестными с помощью определителей
3.3. Решение системы двух уравнений с двумя неизвестными с помощью определителейВ примере 3.1. решение системы двух уравнений с двумя неизвестными методом исключения переменных привело к уравнениям с одним неизвестным. Все коэффициенты в полученных уравнениях представляют собой определители матриц второго порядка. Коэффициент при неизвестных равен A матрицы коэффициентов при неизвестных исходной системы (его обычно
обозначают ∆). Выражения в правых частях представляются в виде:
∆ | 1 | = | b1 | a12 | ∆ | 2 | = | a11 |
| b1 |
| |||||||
|
|
|
| b2 | a 22 |
|
| a 21 |
| b2 |
| |||||||
|
|
|
|
|
|
|
|
|
| |||||||||
Следовательно, решение исходной системы есть: | ||||||||||||||||||
x1 = |
|
| ∆1 |
| = | ∆1 | x 2 | = |
| ∆2 |
| = | ∆2 | |||||
|
| ∆ |
|
| ∆ | |||||||||||||
|
|
|
| A |
|
|
|
|
|
|
| A |
|
| ||||
Заметим, что определители ∆1 и ∆2 получаются из определителя ∆ заменой первого и второго столбцов соответственно столбцом правых частей.
Выражение неизвестных в виде отношения определителей ∆1, ∆2 и ∆ на-
зывается правилом Крамера.
Пример 3.4. С помощью правила Крамера решить систему уравнений:
15x −8y = −1017x − 4 y =14
Здесь
∆ = |
| A |
| = | 15 | −8 | = −4 | 15 | 2 | = −4(15 − 34) = 76, ∆ | = | −10 | −8 | = 40 +112 =152 | ||||||
|
| |||||||||||||||||||
|
|
|
|
|
| 17 | − 4 |
|
| 17 | 1 |
|
|
| 1 |
| 14 | − 4 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
∆2 = | 15 | −10 | = | 5 | 3 | − 2 | =10 | 3 | −1 | =10(21 +17) = 380 |
|
| ||||||||
17 | 14 |
| 17 | 14 | 17 | 7 |
|
| ||||||||||||
Поэтому получаем:
x1 | = | 152 | = 2 | x 2 | = | 380 | =5 | ||
| 76 | 76 | |||||||
|
|
|
|
|
| ||||
Подстановка найденных значений неизвестных в исходную систему 15×2-8×5=-10,17×2-4×5=14 показывает, что действительно получено решение.
Указание. Полученное решение всегда следует проверять подстановкой в исходную систему для контроля возможных ошибок.
Задача 3.3. Найдите решения систем двух уравнений с двумя неизвестными с помощью определителей:
1) | 13x +5y =1 | 2) | 31x −8y = −3 | 3) | 17x + 25y =1 | 4) | 23x −8y = −4 |
|
|
|
| ||||
| 11x + 4 y = 2 |
| 12x −5y = −24 |
| 11x +16 y =1 |
| 27x −5y = 48 |
Правило Крамера можно обобщить и аналогично записать и вычислить решение любой линейной алгебраической системы n уравнений с n неизвестными через определители матриц порядка n. Поэтому перейдем к понятиям, которые необходимы для определителей матриц порядка n.
33
Особенности вычисления определителя матрицы (стр. 1 из 2)
Содержание
Введение…………………………………………………………………………………………….. 2
1. Постановка задачи………………………………………………………………………….. 3
2. Математические и алгоритмические основы решения задачи……………… 5
2.1 Определитель матрицы………………………………………………………………….. 5
2.2 Метод Гаусса для решения систем линейных уравнений…………………… 6
2.3 Метод Гаусса для вычисления определителя……………………………………. 8
3. Функциональные модели и блок-схемы решения задачи…………………….. 9
4. Программная реализация решения задачи………………………………………. 11
5. Пример выполнения программы…………………………………………………….. 16
Заключение. ……………………………………………………………………………………… 18
……………………………………………………………………………………… 18
Список использованных источников и литературы……………………………… 19
Введение
Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему алгебраических уравнений.
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной.
При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности. Этот метод (который также называют методом последовательного исключения неизвестных) известен в различных вариантах уже более 2000 лет.
Помимо аналитического решения СЛАУ, метод Гаусса также применяется для нахождения матрицы, обратной к данной, определения ранга матрицы и нахождения определителя.
Целью данной курсовой работы является реализация вычисления определителя методом исключения Гаусса.
1. Постановка задачи
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Вычисление определителя матрицы заключается в выполнении над матрицей алгоритма Гаусса для решения систем линейных алгебраических уравнений. В результате выполнения алгоритма получаем диагональную матрицу, её определитель равен произведению элементов, стоящих на диагонали.
Пример 1.
Вычислить определитель матрицы методом A исключения Гаусса.
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
~
.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.
Знак определяется количеством обменов строк, следовательно определитель матрицы
.
Пример 2.
Вычислить определитель матрицы методом A исключения Гаусса.
.
Решение:
Приведем матрицу к диагональному виду методом Гаусса.
~
.
Тогда определитель матрицы равен произведению ее элементов, стоящих на диагонали:
.
Знак определяется количеством обменов строк, следовательно определитель матрицы
.
2. Математические и алгоритмические основы решения задачи
2. 1 Определитель матрицы
1 Определитель матрицы
Введем определение определителя квадратной матрицы любого порядка. Это определение будет рекуррентным, то есть чтобы установить, что такое определитель матрицы порядка n, нужно уже знать, что такое определитель матрицы порядка n-1. Отметим также, что определитель существует только у квадратных матриц.
Определитель квадратной матрицы A будем обозначать
или det A.
Определение. Определителем квадратной матрицы
второго порядка называется число
.
Определителем
квадратной матрицы порядка n,
, называется число
где
— определитель матрицы порядка n-1, полученной из матрицы A вычеркиванием первой строки и столбца с номером k.
2.2 Метод Гаусса для решения систем линейных уравнений
Пусть дана квадратная матрица A размером NxN. Требуется вычислить её определитель.
Воспользуемся идеями метода Гаусса решения систем линейных уравнений.
Дана система:
a11 x1 + a12 x2 + … + a1n xn = b1
a21 x1 + a22 x2 + … + a2n xn = b2
…
an1 x1 + an2 x2 + … + ann xn = bn
Выполним следующий алгоритм.
На первом шаге найдём в первом столбце наибольший по модулю элемент, поставим уравнение с этим элементом на первую строчку (обменяв две соответствующие строки матрицы A и два соответствующих элемента вектора B), а затем будем отнимать это уравнение от всех остальных, чтобы в первом столбце все элементы (кроме первого) обратились в ноль. Например, при прибавлении ко второй строке будем домножать первую строку на -a21/a11, при добавлении к третьей — на -a31/a11, и т.д.
На втором шаге найдём во втором столбце, начиная со второго элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на вторую строчку, и будем отнимать это уравнение от всех остальных (в том числе и от первого), чтобы во втором столбце все элементы (кроме второго) обратились в ноль. Понятно, что эта операция никак не изменит первый столбец — ведь от каждой строки мы будем отнимать вторую строку, домноженную на некоторый коэффициент, а во второй строке в первом столбце стоит ноль.
Т.е. на i-ом шаге найдём в i-ом столбце, начиная с i-го элемента, наибольший по модулю элемент, поставим уравнение с этим элементом на i-ю строчку, и будем отнимать это уравнение от всех остальных. Понятно, что это никак не повлияет на все предыдущие столбцы (с первого по (i-1)-ый).
В конце концов, мы приведём систему к так называемому диагональному виду:
c11 x1 = d1
c22 x2 = d2
…
cnn xn = dn
Т.е. мы нашли решение системы.
Замечание 1. На каждой итерации найдётся хотя бы один ненулевой элемент, иначе система бы имела нулевой определитель, что противоречит условию.
Замечание 2. Требование, что на каждом шаге мы выбираем наибольший по модулю элемент, очень важно в смысле численной устойчивости метода. Если выбирать произвольный ненулевой элемент, то это может привести к гигантской погрешности, когда получившееся решение будет отличаться в разы от правильного.
2.3 Метод Гаусса для вычисления определителя
Будем выполнять те же самые действия, что и при решении системы линейных уравнений, исключив только деление текущей строки на a[i][i] (точнее, само деление можно выполнять, но подразумевая, что число выносится за знак определителя). Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Тогда все операции, которые мы будем производить с матрицей, не будут изменять величину определителя матрицы, за исключением, быть может, знака (мы только обмениваем местами две строки, что меняет знак на противоположный, или прибавляем одну строку к другой, что не меняет величину определителя).
Но матрица, к которой мы приходим после выполнения алгоритма Гаусса, является диагональной, и определитель её равен произведению элементов, стоящих на диагонали. Знак, как уже говорилось, будет определяться количеством обменов строк (если их нечётное, то знак определителя следует изменить на противоположный). Таким образом, мы можем с помощью алгоритма Гаусса вычислять определитель матрицы за O(N3).
Осталось только заметить, что если в какой-то момент мы не найдём в текущем столбце ненулевого элемента, то алгоритм следует остановить и вернуть 0.
3. Функциональные модели и блок-схемы решения задачи
Блок-схема решения задачи представлена на рисунке 1.
Рисунок 1 – Блок-схема решения задачи для функции DETERMINATE
4 Программная реализация решения задачи
;ФУНКЦИЯ, ВЫЧИСЛЯЮЩАЯ ОПРЕДЕЛИТЕЛЬ
(DEFUN DETERMINANT (MATRIX SIZE)
;ОБЪЯВЛЕНИЕ ПЕРЕМЕННЫХ
;ОПРЕДЕЛИТЕЛЬ
(DECLARE (SPECIAL DET))
;ВСПОМОГАТЕЛЬНЫЕ МАССИВЫ И ПЕРЕМЕННЫЕ
(DECLARE (SPECIAL PAR))
(DECLARE (SPECIAL R))
(DECLARE (SPECIAL T_))
(DECLARE (SPECIAL I))
(DECLARE (SPECIAL II))
;*********************
(SETQ R (MAKE-ARRAY SIZE :ELEMENT-TYPE ‘FLOAT :INITIAL-ELEMENT 0))
(SETQ T_ 1)
(SETQ DET 1)
(DO
((J 0))
((>= J (- SIZE 1)))
;ИСКЛЮЧАЕМ ДЕЛЕНИЕ НА 0
(IF (= (AREF MATRIX J J) 0)
(PROGN
(SETQ II (+ J 1))
;ИЩЕМ СТРОКУ В КОТОРОЙ J-Й ЭЛЕМЕНТ НЕ 0
(DO
(())
((OR (/= (AREF MATRIX II J) 0) (= II (- SIZE 1))))
(SETQ II (+ II 1))
)
;ЕСЛИ НЕТ ТАКОЙ СТРОКИ ОПРЕДЕЛИТЕЛЬ РАВЕН 0
(IF (AND (= (AREF MATRIX II J) 0) (= II (- SIZE 1))) (SETQ T_ 0))
Матрица строка решение.
 Решение матричных уравнений: теория и примеры
Решение матричных уравнений: теория и примерыРешение матриц – понятие обобщающее операции над матрицами. Под математической матрицей понимается таблица элементов. О подобной таблице, в которой m строк и n столбцов, говорят что это матрица размером m на n.
Общий вид матрицы
Основные элементы матрицы:
Главная диагональ . Её составляют элементы а 11 ,а 22 …..а mn
Побочная диагональ. Её слагают элементы а 1n ,а 2n-1 …..а m1 .
Перед тем как перейти к решению матриц рассмотрим основные виды матриц:
Квадратная – в которой число строк равно числу столбцов (m=n)
Нулевая – все элементы этой матрицы равны 0.
Транспонированная матрица — матрица В, полученная из исходной матрицы A заменой строк на столбцы.
Единичная – все элементы главной диагонали равны 1, все остальные 0.
Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.
Матрица может быть симметричной относительно главной и побочной диагонали. То есть, если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 . то матрица симметрична относительно главной диагонали. Симметричными бывают только квадратные матрицы.
То есть, если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 . то матрица симметрична относительно главной диагонали. Симметричными бывают только квадратные матрицы.
Теперь перейдем непосредственно к вопросу, как решать матрицы.
Матрицы можно алгебраически складывать, если они обладают одинаковой размерностью. Чтобы сложить матрицу А с матрицей В, необходимо элемент первой строки первого столбца матрицы А сложить с первым элементом первой строки матрицы В, элемент второго столбца первой строки матрицы А сложить с элементом элемент второго столбца первой строки матрицы В и т.д.
Свойства сложения
А+В=В+А
(А+В)+С=А+(В+С)
Матрицы можно перемножать, если они согласованы. Матрицы А и В считаются согласованными, если количество столбцов матрицы А равно количеству строк матрицы В.
Если А размерностью m на n, B размерностью n на к, то матрица С=А*В будет размерностью m на к и будет составлена из элементов
Где С 11 – сумма папарных произведений элементов строки матрицы А и столбца матрицы В, то есть элемента сумма произведения элемента первого столбца первой строки матрицы А с элементом первого столбца первой строки матрицы В, элемента второго столбца первой строки матрицы А с элементом первого столбца второй строки матрицы В и т. д.
д.
При перемножении важен порядок перемножения. А*В не равно В*А.
Любая квадратная матрица может породить определитель или детерминант. Записывает det. Или | элементы матрицы |
Для матриц размерностью 2 на 2. Определить есть разница между произведением элементов главной и элементами побочной диагонали.
Для матриц размерностью 3 на 3 и более. Операция нахождения определителя сложнее.
Введем понятия:
Минор элемента – есть определитель матрицы, полученной из исходной матрицы, путем вычеркивания строки и столбца исходной матрицы, в которой этот элемент находился.
Алгебраическим дополнением элемента матрицы называется произведение минора этого элемента на -1 в степени суммы строки и столбца исходной матрицы, в которой этот элемент находился.
Определитель любой квадратной матрицы равен сумме произведения элементов любого ряда матрицы на соответствующие им алгебраические дополнения.
Обращение матрицы — это процесс нахождения обратной матрицы, определение которой мы дали в начале. Обозначается обратная матрица также как исходная с припиской степени -1.
Обозначается обратная матрица также как исходная с припиской степени -1.
Находиться обратная матрица по формуле.
А -1 = A * T x (1/|A|)
Где A * T — Транспонированная матрица Алгебраических дополнений.
:
Если хотите разобраться, смотрите обязательно.
Это основные операции по решению матриц. Если появится дополнительные вопросы о том, как решить матрицы , пишите смело в комментариях.
Если все же вы не смогли разобраться, попробуйте обратиться к специалисту.
Это понятие, которое обобщает все возможные операции, производимые с матрицами. Математическая матрица — таблица элементов. О такой таблице, где m строк и n столбцов, говорят, что это матрица имеет размерность m на n .
Общий вид матрицы:
Для решения матриц необходимо понимать, что такое матрица и знать основные ее параметры. Основные элементы матрицы:
- Главная диагональ, состоящая из элементов а 11 ,а 22 ….
 .а mn .
.а mn . - Побочная диагональ, состоящая из элементов а 1n ,а 2n-1 …..а m1 .
Основные виды матриц:
- Квадратная — такая матрица, где число строк = числу столбцов (m=n ).
- Нулевая — где все элементы матрицы = 0.
- Транспонированная матрица — матрица В , которая была получена из исходной матрицы A путем замены строк на столбцы.
- Единичная — все элементы главной диагонали = 1, все остальные = 0.
- Обратная матрица — матрица, при умножении на которую исходная матрица даёт в результате единичную матрицу.
Матрица может быть симметричной относительно главной и побочной диагонали. Т.е., если а 12 =а 21 , а 13 =а 31 ,….а 23 =а 32 …. а m-1n =а mn-1 , то матрица симметрична относительно главной диагонали. Симметричными могут быть лишь квадратные матрицы.
Методы решения матриц.
Почти все методы решения матрицы заключаются в нахождении ее определителя n -го порядка и большинство из них довольно громоздки. Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.
Чтобы найти определитель 2го и 3го порядка есть другие, более рациональные способы.
Нахождение определителей 2-го порядка.
Для вычисления определителя матрицы А 2го порядка, необходимо из произведения элементов главной диагонали вычесть произведение элементов побочной диагонали:
Методы нахождения определителей 3го порядка.
Ниже приведены правила для нахождения определителя 3го порядка.
Упрощенно правило треугольника, как одного из методов решения матриц , можно изобразить таким образом:
Другими словами, произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «+»; так же, для 2го определителя — соответствующие произведения берутся со знаком «-«, то есть по такой схеме:
При решении матриц правилом Саррюса , справа от определителя дописывают первые 2 столбца и произведения соответствующих элементов на главной диагонали и на диагоналях, которые ей параллельны, берут со знаком «+»; а произведения соответствующих элементов побочной диагонали и диагоналей, которые ей параллельны, со знаком «-«:
Разложение определителя по строке или столбцу при решении матриц.
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку либо столбец, по которой/ому ведется разложение, будут обозначать стрелкой.
Приведение определителя к треугольному виду при решении матриц.
При решении матриц методом приведения определителя к треугольному виду, работают так: с помощью простейших преобразований над строками либо столбцами, определитель становится треугольного вида и тогда его значение, в соответствии со свойствами определителя, будет равно произведению элементов, которые стоят на главной диагонали.
Теорема Лапласа при решении матриц.
Решая матрицы по теореме Лапласа, необходимо знать непосредственно саму теорему. Теорема Лапласа: Пусть Δ — это определитель n -го порядка. Выбираем в нем любые k строк (либо столбцов), при условии k ≤ n — 1 . В таком случае сумма произведений всех миноров k -го порядка, содержащихся в выбранных k строках (столбцах), на их алгебраические дополнения будет равна определителю.
Решение обратной матрицы.
Последовательность действий для решения обратной матрицы :
- Понять, квадратная ли данная матрица. В случае отрицательного ответа становится ясно, что обратной матрицы для нее не может быть.
- Вычисляем алгебраические дополнения.
- Составляем союзную (взаимную, присоединённую) матрицу C .
- Составляем обратную матрицу из алгебраических дополнений: все элементы присоединённой матрицы C делим на определитель начальной матрицы. Итоговая матрица будет искомой обратной матрицей относительно заданной.
- Проверяем выполненную работу: умножаем матрицу начальную и полученную матрицы, результатом должна стать единичная матрица.
Решение систем матриц.
Для решения систем матриц наиболее часто используют метод Гаусса.
Метод Гаусса — это стандартный способ решения систем линейных алгебраических уравнений (СЛАУ) и он заключается в том, что последовательно исключаются переменные, т. е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
е., при помощи элементарных изменений систему уравнений доводят до эквивалентной системы треугольного вида и из нее, последовательно, начиная с последних (по номеру), находят каждый элемент системы.
Метод Гаусса является самым универсальным и лучшим инструментом для нахождения решения матриц. Если у системы бесконечное множество решений или система является несовместимой, то ее нельзя решать по правилу Крамера и матричным методом.
Метод Гаусса подразумевает также прямой (приведение расширенной матрицы к ступенчатому виду, т.е. получение нулей под главной диагональю) и обратный (получение нулей над главной диагональю расширенной матрицы) ходы. Прямой ход и есть метод Гаусса, обратный — метод Гаусса-Жордана. Метод Гаусса-Жордана отличается от метода Гаусса лишь последовательностью исключения переменных.
Материал из ВикиПро: Отраслевая энциклопедия. Окна, двери, мебеля
Мне нравится
31
Иероглифы: Хосин Канри
Хосин канри (яп. : 方針管理, англ.: Hoshin Kanri) – это метод стратегического управления компанией, в процессе реализации которого устанавливаются направления деятельности предприятия, цели и применяемые для
их достижения инструменты и способствующий вовлечению руководителей и персонала в выработку общего видения и общего плана действий.
: 方針管理, англ.: Hoshin Kanri) – это метод стратегического управления компанией, в процессе реализации которого устанавливаются направления деятельности предприятия, цели и применяемые для
их достижения инструменты и способствующий вовлечению руководителей и персонала в выработку общего видения и общего плана действий.
Хосин канри иногда также рассматривается как процесс развертывания политики (англ.: Policy Deployment) или управление политикой .
Прежде всего, хосин канри это инструмент, связывающий макро и микро уровни организации. Хосин канри помогает увидеть самый верхний уровень целей компании, работая на микроуровне, и в тоже время понимать возможности, творческий потенциал и проблемы микро-уровня, находясь на самых высоких уровнях управления .
Этимология
Примерно в то же время, когда Джозеф Джуран находился в Японии, вышла книга Питера Друкера Практика менеджмента (The Practice of Management ), в которой описана концепция управления по целям (MBO). В ней подразумевается, что сотрудники самостоятельно включаются в процесс постановки целей и выбора направления действий, необходимых для их достижения , при таких условиях сотрудники более мотивированы на исполнение своих обязанностей.
В ней подразумевается, что сотрудники самостоятельно включаются в процесс постановки целей и выбора направления действий, необходимых для их достижения , при таких условиях сотрудники более мотивированы на исполнение своих обязанностей.
Все эти методы получили в Японии широкое распространение и последующее развитие, и непосредственно способствовали появлению концепции «Хосин Канри».
Впервые методологию «Хосин Канри» во второй половине 1960-х годов внедрила японская компания «Бриджстоун» , получившая в 1968 г. премию Деминга в области качества. В 1964 году «Бриджстоун» ввела в обращение термин «Хосин Канри», а в июле 1965 года опубликовав доклад «Руководство по хосин канри» сформулировала основные принципы хосин . Так появилось официальное название «Хосин Канри».
Термин «хосин канри» стал широко применяться в Японии в середине 1970-х гг. в таких компаниях, как Toyota , Nippon Denso , Komatsu и Matsushita Electric Industrial Co. (Panasonic Corporation). К концу 1970-х гг. аккумулированный опыт привел к формализации принципов, и первые книги на данную тему вышли в свет.
Во второй половине 1980-х годов, после успеха японских подразделений американских корпораций, а также работам Ёджи Акао, система «хосин канри» привлекла к себе внимание и в Америке. Первой из западных компаний этот подход переняла Hewlett-Packard и при сотрудничестве с Н. Кано внедрила ее в свою систему стратегического управления.
Успех HP привлек к этой теории внимание других крупных американских корпораций которые также начали внедрять её: Florida Power & Light , Procter & Gamble , Exxon , Texas Instruments, Xerox ; Intel .
В России работы по хосин канри начали появляться относительно недавно, в 2008 году была переведена и опубликована на русском языке книга Томаса Джексона «Хосин канри: как заставить стратегию работать», в которой содержится подробное описание концепции хосин канри. Книга уже получившая общее признание в США, по сути, стала первым в России практическим пособием по внедрению хосин канри.
Основы Хосин Канри
Система хосин канри направлена на совершенствование процесса управления стратегией компании и является ключевым элементом бережливого производства . Данный подход ориентирован на развитие качеств и характеристик, обеспечивающих конкурентоспособность всей компании благодаря повышению прибыли. Данный подход используется для интеграции единого процесса производства, в рамках которого хосин канри и бережливые идеи являются единым интегрированным процессом .
При этом хосин канри не поощряет внедрение случайных, неупорядоченных усовершенствований и ориентирует организацию на реализацию проектов, которые планомерно продвигают ее к достижению стратегических целей.
Данный подход ориентирован на развитие качеств и характеристик, обеспечивающих конкурентоспособность всей компании благодаря повышению прибыли. Данный подход используется для интеграции единого процесса производства, в рамках которого хосин канри и бережливые идеи являются единым интегрированным процессом .
При этом хосин канри не поощряет внедрение случайных, неупорядоченных усовершенствований и ориентирует организацию на реализацию проектов, которые планомерно продвигают ее к достижению стратегических целей.
Сила этого подхода заключена в его тесной увязке с системой повседневного управления предприятием, основанной на принципах непрерывного совершенствования (система kaizen) .
В отличие от общепринятого подхода к управлению стратегией, подход хосин канри основан на применении цикла Деминга, или PDCA в масштабе всей компании и представляет собой концепцию циклического управления. За счет систематического применения PDCA в системе хосин канри, интегрируются функции планирования и исполнения на всех уровнях организации. Данная концепция подразумевает одновременное так называемое двухуровневое планирование и управление:
Данная концепция подразумевает одновременное так называемое двухуровневое планирование и управление:
- Уровень стратегического планирования. Основная ориентация данного уровня заключена в достижение значительных улучшений эффективности или обеспечение выполнения ключевых целей компании.
- Ежедневный уровень. Это уровень текущей деятельности, на котором переводятся установленные стратегические цели на язык конкретных действий.
Правильное сочетание указанных двух уровней в согласованном процессе управления движением организации к целям, разделяемым всеми ее сотрудниками, является ключевым условием надлежащего развертывания политики хосин канри.
Хосин канри представляет собой комплексный замкнутый процесс планирования, установления и доведения до исполнителей целей предприятия и оперативного анализа его работы, который обеспечивает координацию всех действий, направленных на достижение установленных стратегических целей компании .
Процесс внедрения системы хосин канри требует жесткого подхода и долгосрочной приверженности, а также терпения и усилий высшего исполнительного руководства.
Помимо всего прочего хосин Канри, как часть всеобщего процесса постоянного совершенствования, эффективен для укрепления корпоративной среды и морального климата в компании . Подход хосин канри содействует комплексному развертыванию стратегических планов компании при объединении усилий всех сотрудников компании.
Цикл Деминга (или PDCA) — ключевой элемент политики Хосин Канри
Классический цикл PDCA
Цикл PDCA (англ.: «Plan/Do/Check/Act») является главным инструментом процесса непрерывного улучшения. Цикл PDCA подразумевает принцип повторения в решении какого-либо вопроса – поэтапное достижение улучшения, и повторение цикла преобразования много раз. Цикл PDCA – это непрерывный процесс улучшений , представленный в виде циклической повторяющейся последовательности:
Применение циклов PDCA осуществляется до того момента, пока результат не совпадет с заранее определенным планом. Это обусловлено тем, что в соответствии с требованиями потребителей планируемые критерии качества подвержены изменениям, цикл PDCA служит непрерывному улучшению качества и является эффективным инструментом для достижения наилучших результатов.
В классическом понимании цикл PDCA представляет собой систему, в рамках которой члены высшего руководства создают и реализуют стратегию, не привлекая к этому тех, кто находится на нижних иерархических уровнях организации, что в итоге приводит к слабому пониманию людьми стратегии и слабой заинтересованности в их реализации. В отличие от классического подхода, в структуре хосин канри циклы PDCA встраиваются друг в друга образуя систему в рамках которой топ-менеджмент компании обеспечивает развернутое внедрение своего стратегического плана, привлекая менеджеров среднего звена и квалифицированных рабочих, как к планированию, так и к выполнению стратегических решений. Так возникает новый высокоэффективный тип организационного саморегулирования, в основе которого лежат четкое понимание всеми менеджерами и рабочими стратегических целей и высокая заинтересованность в их реализации . Со временем такая саморегулирующаяся организация становится гибкой бережливой организацией, потому что все эксперименты PDCA в системе хосин встроены друг в друга или связаны между собой и соответственно изменение, произведенное в одном из циклов, быстро транслируется и вызывает перемены во всех остальных.
Циклы PDCA в системе Хосин Канри
«Хосин Канри» процесс достаточно разнонаправленный. Он включает в себя реализацию циклов PDCA на разных уровнях менеджмента в оперативном, среднеднесрочном и долгосрочном масштабе.
Циклы PDCA в системе хосин канри :
Долгосрочная стратегия:
Общий план деятельности на длительный период (5-100 лет) — направлен на осуществление важнейших преобразований или внесение изменений в миссию организации.
Среднесрочная стратегия:
Это почти законченный план действий, который включает в себя критерии улучшений существующих процессов и рассчитанный на среднесрочную перспективу (3-5 лет). Ориентирован на формирование необходимых характеристик.
Ежегодный план (Тактика):
Конкретный план действий на ближайший период (6-18 месяцев), который подразумевает формирование свойств и характеристик, способствующих повышению конкурентоспособности компании.
Оперативная деятельность:
Достаточно конкретные проекты (3-6 месяцев) реализуемые с целью применения инноваций в стандартизированных процессах.
Применение циклов в системе хосин канри проводятся специально созданными для этого сетью рабочих групп, в состав которых входят высшее руководство, менеджеры среднего звена и в обязательном порядке весь рабочий персонал компании. Такие группы или команды создаются и объединяются по принципу иерархии, обязанности по планированию и внедрению распределяются между ними следующим образом:
- Хосин-команда – это управленческая команда самого высокого уровня, которая отвечает в целом за стратегическое планирование и процесс реализации политики.
- Тактическая команда — разрабатывают и управляют проведением определенных тактик по формированию некоторых характеристик, улучшающих конкурентоспособность организации.
- Оперативная команда — разрабатывает и осуществляет оперативные проекты по совершенствованию конкретных процессов.
- Команда исполнителей — разрабатывает и руководит проведением периодических относительно крупных усовершенствований () и осуществлением непрерывного улучшения (кайдзен).

У каждого цикла PDCA в системе хосин канри имеет свою определенную задачу, зависимую от продолжительности и того, каким образом он связан с общими целями компании. В итоге, чем длиннее определенный цикл, тем выше степень ответственности в управленческой иерархии организации. В целом процесс хосин канри не имеет конечной точки и циклы стратегических преобразований повторяются с периодичностью 1-2 раза в год. Процесс применения циклов PDCA в системе хосин канри, проводимый в контролируемых условиях стандартизированных рабочих процессов, позволяет вовлечь всех сотрудников компании для проверки правильности выбранной компанией стратегии .
Х-матрица. Хосин Канри в формате А3
Одним из основных условий реализации политики хосин канри является создание документа, в котором фиксируются результаты процесса разработки стратегии компании. Для этого в системе хосин применяют такой инструмент, как «Х-матрица», которая дает возможность представить весь процесс разработки стратегии на одном листе бумаги. Важно, что этот документ выполняет функции итогового документа, в котором фиксируются принятые решения и обсуждаемые аргументы, необходимые для формулировки и претворения в жизнь эффективной стратегии .
Важно, что этот документ выполняет функции итогового документа, в котором фиксируются принятые решения и обсуждаемые аргументы, необходимые для формулировки и претворения в жизнь эффективной стратегии .
Х-матрица представляет собой пакет планов работы команд, которые описывают в практических, а также стратегических терминах основную суть бережливой организации: создать и укрепить конкурентоспособность, измеряемую в конкретных показателях, современных технологиях, высшем уровне качества, низких затратах и поставке «точно в срок» . Каждый план работы команды, который включается в систему Х-матриц, призван решить конкретную задачу: ликвидировать непроизводительные потери и уменьшить нестабильность, которые мешают одержать победу над конкурентами.
Х-матрица оформляется в формате А3 (), так как данный формат наиболее нагляден, лаконичен и мобилен, он является самым оптимальный форматом, для того чтобы ничего не упустить и в то же время избежать написание чего-либо лишнего. Данная форма используется для разработки и применения среднесрочной стратегии и годового хосин-плана компании, а также предназначена для объединения многочисленных планов команд различных уровней в единый масштабный документ, направленный на реализацию стратегии.
Х-матрица состоит из четырех основных блоков:
- Стратегии – это основной движущий фактор в матрице, описание того, что будет делаться, как на текущий период, так и в ближайшие 2-3 года.
- Тактики – описание того как будет достигаться выбранная стратегия в период ближайших 6-18 месяцев.
- Процесс – критерии оценки, с помощью которых будет оцениваться ход развития всего процесса.
- Результаты – описание всех результатов качественного управления процессом.
Дополнительные блоки матрицы:
- Члены команды – перечисляются участники всех процессов;
- Ответственность – отмечается, кто за какой процесс несет ответственность;
- Взаимосвязи – фиксируются имеющиеся взаимоотношения между процессами.
Процесс разработки Х-матрицы.
Перед тем как заполнять Х-матрицу, требуется выполнить стратегический анализ и определить пути развития организации . Только после этого заполняется первый блок матрицы, содержащий сформулированную стратегию. Следующим шагом выбираются и заносятся тактики, которые позволят обеспечить выполнение выбранной стратегии. Далее необходимо описать проекты, то есть, что необходимо выполнить, чтобы реализовать сформулированные тактики. Затем прописываются планируемые финансовые итоги, то есть то, для чего всё это делается.
В дальнейшем определяются взаимосвязи между выбранными стратегией и тактиками. В итоге установление этих взаимосвязей позволяет понять, насколько тактики способны реализовать стратегии. Далее необходимо определить, с помощью, каких проектов можно реализовать выбранные тактики и сколько это будет стоить. Взаимосвязи также устанавливаются и между проектами и тактиками. Определение взаимосвязей позволит понять, какой проект способен выполнить ту или иную тактику, а также какая тактика сможет реализовать выбранную стратегию. В результате будет получено видение далекой цели и конкретных шагов, позволяющих ее достичь.
Только после этого заполняется первый блок матрицы, содержащий сформулированную стратегию. Следующим шагом выбираются и заносятся тактики, которые позволят обеспечить выполнение выбранной стратегии. Далее необходимо описать проекты, то есть, что необходимо выполнить, чтобы реализовать сформулированные тактики. Затем прописываются планируемые финансовые итоги, то есть то, для чего всё это делается.
В дальнейшем определяются взаимосвязи между выбранными стратегией и тактиками. В итоге установление этих взаимосвязей позволяет понять, насколько тактики способны реализовать стратегии. Далее необходимо определить, с помощью, каких проектов можно реализовать выбранные тактики и сколько это будет стоить. Взаимосвязи также устанавливаются и между проектами и тактиками. Определение взаимосвязей позволит понять, какой проект способен выполнить ту или иную тактику, а также какая тактика сможет реализовать выбранную стратегию. В результате будет получено видение далекой цели и конкретных шагов, позволяющих ее достичь. На последнем этапе выбираются ответственные лица. И после этого в матрице проставляется связь между проектами и результатами (то есть позволяют ли эти проекты получить желаемые результаты) и устанавливается связь результатов со стратегиями.
На последнем этапе выбираются ответственные лица. И после этого в матрице проставляется связь между проектами и результатами (то есть позволяют ли эти проекты получить желаемые результаты) и устанавливается связь результатов со стратегиями.
Х-матрица – это ключевой документ в системе хосин канри, который призван обеспечить максимально четкую реализацию данного подхода. В результате внедрения этого метода менеджеры начинают обсуждать ход выполнения поставленных задач чаще и в непосредственном контакте со своими подчиненными, а также с вышестоящими руководителями.
Поймай мяч или «кэтчбол» в методологии Хосин канри
Успешная реализация стратегии невозможна без активного участия коллектива в процессе ее развертывания и без заинтересованности каждого в конечных результатах. В системе хосин канри стратегии не просто спускаются с верхних уровней управленческой иерархии на нижние, а согласуются по определённой схеме, которая называется «поймай мяч». Прием «поймай мяч» или «кэтчбол» (англ. catch-ball) является ключевым элементом стратегии хосин канри, и представляет собой способ интерактивного построения плана.
catch-ball) является ключевым элементом стратегии хосин канри, и представляет собой способ интерактивного построения плана.
Смысл метода в том, что стратегия как мяч перекидывается между различными уровнями, до тех пор пока не будет достигнуто окончательное согласование. Мяч политики перебрасывается между менеджерами всех уровней, и только потом принимается окончательное решение. Задача приема «поймай мяч» – преобразовать цели высшего руководства в цели всех сотрудников .
«Поймай мяч» — это процесс, с помощью которого руководители команд разрабатывают годовой хосин-план и передают его всем командам в организации. Свое название он получил из-за многочисленных обсуждений и активных переговоров, происходящих между командами при создании и обсуждении уставов и планов, в соответствии с которыми проходит внедрение системы хосин канри. В таком контексте процесс охватывает все уровни и все сектора вашей организации как в вертикальном (сверху вниз и снизу вверх), так и в горизонтальном направлениях, обеспечивая активное обсуждение будущего компании и возможность прийти к соглашению о целевых показателях, основных средствах, ролях, обязанностях и сферах ответственности, распределении и развитии ресурсов.
Ёсио Кондо описывает форму процесса «перебрасывания мяча» при развертывании планов на финансовый год в рамках концепции хосин канри следующим образом :
- Высшее руководство компании разрабатывает проект плана на будущий год. В проекте учитываются итоги работы прошлого года. Формулируется среднесрочная и долгосрочная стратегия и основная философия компании.
- Проект политики подвергается обсуждению во всех подразделении организации их руководителями вместе с менеджерами.
- Каждое подразделение выдвигает свои собственные идеи, относящиеся к планам организации, меняя первоначальный проект стратегии, если в этом есть необходимость.
- Проект с внесёнными предложениями затем обсуждается в каждом из отделов компании менеджерами следующих более мелких уровней, после чего каждый отдел выдвигает свой вариант предложенной политики.
- После того как в этом процессе будет учтено мнение как можно большего числа сотрудников компании информация возвращается по иерархии высшему руководству, и уже только после этого стратегия компании на следующий год окончательно принимается после дальнейшего обсуждения и изменения, если требуется.

Таким образом, в приеме «поймай мяч» планы политики для каждого подразделения компании, от высшего до низшего, неоднократно пересматриваются, начиная с высшего уровня в подразделениях, и доходят до нижних уровней. Политика компании утверждается только после того, как высшее руководство учтет информацию, полученную снизу. Благодаря процессу «поймай мяч» циклы PDCA оказываются вмонтированными один в другой по мере того, как стратегический план последовательно развертывается на различных этапах управления иерархии.
Выгоды данного метода заключаются в том, что обсуждение планов компании ее работниками углубляет понимание процессов преобразования и позволяет им думать одновременно о «необходимости» и о «возможности» реализации этих преобразований, т. е. включиться в процесс совершенствования. С помощью приема «поймай мяч» компания осуществляет качественный переход от нисходящих принудительных целей к добровольным восходящим. Вместо того, чтобы просто говорить людям, что делать, метод «поймай мяч» дает каждому менеджеру голос, а это чрезвычайно эффективный путь мотивации людей для достижения поставленных перед ними целей . Применение метода «поймай мяч» в системе хосин канри позволяет каждому работнику почувствовать, что ему доверяют, и поэтому он должен сделать все возможное, чтобы оправдать это доверие. Осознание работниками своей значимости для компании – это именно то, что необходимо руководству для эффективного внедрения концепции всеобщего управления качеством в компании .
Применение метода «поймай мяч» в системе хосин канри позволяет каждому работнику почувствовать, что ему доверяют, и поэтому он должен сделать все возможное, чтобы оправдать это доверие. Осознание работниками своей значимости для компании – это именно то, что необходимо руководству для эффективного внедрения концепции всеобщего управления качеством в компании .
Фундаментальная предпосылка, на которой основывается идея хосин канри, заключена в том, что главным условием достижения организацией требуемых результатов является понимание всеми ее работниками выбранного стратегического направления развития и их участия в выработке практических действий, ведущих к достижению желаемых результатов.
Хосин канри требует, чтобы каждый сотрудник компании стал обученным и сертифицированным специалистом, способным применять методы PDCA. Для этого требуется активное внедрение различных обучающих программ.
В конечном итоге развертывание политики хосин канри заключается в системном планировании, позволяющем увязать стратегию компании с фундаментальными основами, обеспечивающими ее успешную ежедневную деятельность. Применение данного подхода позволяет руководителям оценивать эффективность предлагаемых проектов, осуществлять контроль их выполнения и тем самым управлять изменениями в стратегии и развитии компании.
Применение данного подхода позволяет руководителям оценивать эффективность предлагаемых проектов, осуществлять контроль их выполнения и тем самым управлять изменениями в стратегии и развитии компании.
Примечания
- Лайкер Д. Дао. Toyota: 14 принципов менеджмента ведущей компании мира//Серия «Модели менеджмента ведущих корпораций»/ перев. с англ. — М.: Альпина Бизнес Букс, 2005. — С. 332 — 402 с. — ISBN 5-9614-0124-3.
- Shook J. Policy Deployment: aka Strategy Alignment, aka Hoshin Kanri.
- Корпоративный университет ЭКСWord. Стратегическое управление. Хосин канри.
- Governica.com. Hoshin Kanri.
- Нив Р.Г. Пространство доктора Деминга: Принципы построения устойчивого бизнеса// Модели менеджмента ведущих корпораций/ перев.: Ю. Рубаник, Ю. Адлер, В. Шпер. – М.: Альпина Паблишер, 2005. — С. 18 – 376 с. – ISBN 5-9614-0238-X.
- Управление технологией и инновациями в Японии/сборник статей/перев. с англ./ред. Корнелиус Х. и др. – М.
 : Волтерс Клувер, 2009. — С. 237 – 512 с.- ISBN 978-5-466-00269-0
: Волтерс Клувер, 2009. — С. 237 – 512 с.- ISBN 978-5-466-00269-0 - Всеобщее управление качеством. Материал из Википедии.
- Практика менеджмента. — М.: Вильямс, 2003. — 397c. — ISBN 5-8459-0085-9
Назначение сервиса . Матричный калькулятор предназначен для решения систем линейных уравненийматричным способом (см. пример решения подобных задач).
Инструкция . Для онлайн решения необходимо выбрать вид уравнения и задать размерность соответствующих матриц.
где А, В, С — задаваемые матрицы, Х — искомая матрица. Матричные уравнения вида (1), (2) и (3) решаются через обратную матрицу A -1 . Если задано выражение A·X — B = C , то необходимо, сначала сложить матрицы C + B , и находить решение для выражения A·X = D , где D = C + B (). Если задано выражение A*X = B 2 , то предварительно матрицу B надо возвести в квадрат .
Рекомендуется также ознакомиться с основными действиями над матрицами .
Пример №1
. Задание . Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1:Умножаем обе части этого равенства слева на A -1 и справа на B -1: A -1 ·A·X·B·B -1 = A -1 ·C·B -1 . Так как A·A -1 = B·B -1 = E и E·X = X·E = X, то X = A -1 ·C·B -1
Обратная матрица A -1:
Найдем обратную матрицу B -1 .
Транспонированная матрица B T:
Обратная матрица B -1:
Матрицу X ищем по формуле: X = A -1 ·C·B -1
Ответ:
Пример №2
. Задание. Решить матричное уравнение
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3
. Задание. Найти решение матричного уравнения
Найти решение матричного уравнения
Решение . Обозначим:
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим справа обе части уравнения на A -1: X·A·A -1 = B·A -1 , откуда находим, что X = B·A -1
Найдем обратную матрицу A -1 .
Транспонированная матрица A T:
Обратная матрица A -1:
Матрицу X ищем по формуле: X = B·A -1
Ответ: >
линейная алгебра — Поиск решения, когда определитель равен нулю
$\begingroup$
У меня есть набор уравнений $$x+y-z=-5$$ $$x-y-z=-3$$ $$x+y-z=0$$ Я хотел бы указать здесь, что первое и третье уравнения в основном то же самое — просто приравняйте два разных числа. Я не знаю, означает ли это автоматически, что решений нет. Затем я представил это в матричной форме и получил $$\begin{bmatrix} 1&1&-1\\1&-1&-1\\1&1&-1 \end{bmatrix}\begin{bmatrix}x\\y\\z\ end{bmatrix}=\begin{bmatrix}-5\\-3\\0\end{bmatrix}$$ (я буду называть эту первую матрицу $A$. ) Я нашел определитель $A$ и он равен нулю, то есть обратного нет. Я действительно застрял здесь.
) Я нашел определитель $A$ и он равен нулю, то есть обратного нет. Я действительно застрял здесь.
Я знаю, что для решения этой проблемы нужно использовать эшелонированную форму строк, пустое пространство и пространство столбцов. Я поместил $A$ в форму эшелона строк и получил $$\begin{bmatrix}1&0&-1\\0&1&0\\0&0&0\end{bmatrix}$$, но перевод этого обратно дал $$x-z=-5$$ $$ y=-3$$ $$0=0$$ Попытка решить первое уравнение дала противоречивые ответы.
Итак, у меня есть три основных вопроса:
- Как найти здесь решение (или понять, что решения нет)?
- Как рассчитать пустое пространство/столбец? (Обратите внимание, что я погуглил это, и я просто не могу его получить.)
- Как нулевое пространство/колоночное пространство связано с поиском решения здесь, если вообще связано?
Спасибо! Пожалуйста, имейте в виду, что я в 8-м классе пытаюсь понять это, поэтому чем проще ответ, тем лучше. Я готов попытаться выяснить вещи, хотя. Любые ответы будут оценены.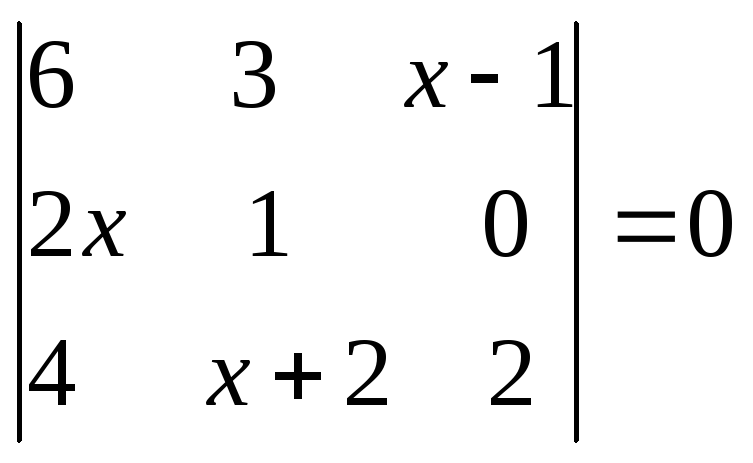
Редактировать: Да, эта конкретная система неразрешима (спасибо Джеку Д’Аурицио и другим), но мне как бы хотелось узнать, как найти общий способ вычисления решений или отсутствия решений, когда определитель равен нулю и матрица не имеет обратной. Другими словами, сейчас в основном вопросы два и три.
- линейная алгебра
- матрицы
- матричные уравнения
$\endgroup$
9
$\begingroup$
В форме $Ax=b$ будет хотя бы одно решение тогда и только тогда, когда $b$ находится в столбце $A$.
Если $A$ — квадратная матрица, то существует единственное решение тогда и только тогда, когда $\det(A) \ne 0$.
Объединив эти тесты, мы получим для всех квадратных матриц $A$, $Ax=b$ имеет
- нет решения, если $b$ не находится в пространстве столбцов $A$.
- единственное решение, если $\det(A) \ne 0$.

- бесконечно много решений, если $b$ находится в столбце $A$, но $\det(A) = 0$.
Более общий, но и немного более утомительный (иногда) метод, который будет работать для неквадратных матриц, заключается в уменьшении строки расширенной матрицы $[A\mid b]$. Если вы получите
- строку с $[0\mid a]$, где $0$ представляет собой строку нулей, а $a\ne 0$, то решения нет.
- точка опоры в каждом столбце и нет строк с $[0\mid a]$, где $a\ne 0$, то существует единственное решение.
- хотя бы один столбец без стержня и ни одной строки с $[0\mid a]$, где $a\ne 0$, то решений бесконечно много.
$\endgroup$
4
$\begingroup$
Чтобы превратить комментарий Джека Д’Аурицио в ответ:
Первое уравнение говорит, что
$$x+y-z=-5$$
, но второе уравнение говорит, что
$$x+y-z=0$$
Поскольку оба эти утверждения не могут быть истинными (так как это означало бы, что $5=0$), решений нет. Заметим также, что если определитель матрицы коэффициентов $A$ равен $0$, это означает, что одно выражение можно представить в виде линейной комбинации двух других, и, таким образом, система либо имеет бесконечно много решений, либо вообще не имеет решений.
Заметим также, что если определитель матрицы коэффициентов $A$ равен $0$, это означает, что одно выражение можно представить в виде линейной комбинации двух других, и, таким образом, система либо имеет бесконечно много решений, либо вообще не имеет решений.
$\endgroup$
2
$\begingroup$
Вы не правильно привели линейную систему в рядно-эшелонную форму.
\begin{bmatrix}1&0&-1\\0&1&0\\0&0&0\end{bmatrix}
По ходу работы вы отбрасывали решения. Строко-ступенчатая форма возникает из расширенной матрицы, которая включает \begin{bmatrix}-5\\-3\\0\end{bmatrix}
Таким образом, правильная форма начинается с \begin{bmatrix} 1&1&-1&-5 \\1&-1&-1&-3\\1&1&-1&0 \end{bmatrix}
Вы должны закончить выражением типа $0=5$ (см. комментарий Джека)
Поскольку вы тоже учитесь в 8-м классе, вот несколько понятий:
1) Система линейных уравнений либо не имеет решения, либо имеет единственное решение, либо бесконечно много решений.
2) Для квадратной матрицы $A$ $det(A) \ne 0$ тогда и только тогда, когда система имеет единственное решение. Всегда.
3) Если после строчно-ступенчатой формы осталось выражение типа $x+y=2$, это означает, что ваша система имеет бесконечно много решений. Наивно, это линия, так сколько точек составляет линию?
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
линейная алгебра — Если $\det(A)=0$, как мы узнаем, что $A$ не имеет решений или их бесконечно много?
Спросил
Изменено 2 года, 2 месяца назад
Просмотрено 65 тысяч раз
$\begingroup$
Если определитель $\det(A)$ матрицы $A$ неоднородной системы уравнений равен $0$, то как узнать, не имеет ли она решений или имеет бесконечно много решений?
И пока мы этим занимаемся, пожалуйста, ответьте на следующие «подвопросы», вытекающие из этого. Я буду вам очень признателен, так как это будет иметь решающее значение для моего понимания всего этого:
а) Поскольку определитель, равный нулю, означает, что возникает ситуация «Деление на ноль» (с использованием правила Крамера), вариант «нет решения» понятен, поскольку деление на ноль не определено.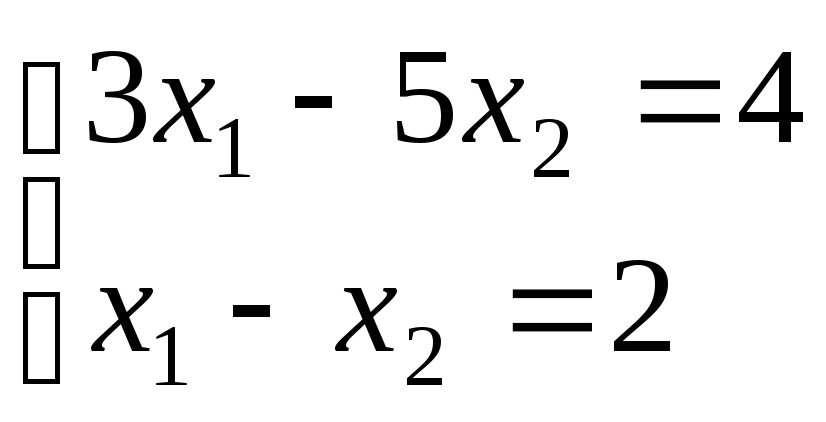 Но меня смущает, как тогда, при любых обстоятельствах , система может иметь бесконечно много решений. Я имею в виду, не будем ли мы сталкиваться с делением на ноль во всех случаях, когда определитель равен нулю? Итак, , пожалуйста, , дайте мне интуитивное и проницательное объяснение этому.
Но меня смущает, как тогда, при любых обстоятельствах , система может иметь бесконечно много решений. Я имею в виду, не будем ли мы сталкиваться с делением на ноль во всех случаях, когда определитель равен нулю? Итак, , пожалуйста, , дайте мне интуитивное и проницательное объяснение этому.
б) Буду ли я неправ, если предположу, что в случае, когда определитель равен нулю, существует бесконечно много решений тогда и только тогда, когда это однородная система уравнений? Пожалуйста, объясните, почему или почему нет.
И, пожалуйста, не забудьте главный вопрос — «для определителя $=0$, как узнать, что решений нет или бесконечно много?»
- линейная алгебра
- матрицы
- определитель
$\endgroup$
4
$\begingroup$
Для любой квадратной линейной системы $\,A\vec x=\vec b\,$ над некоторым полем существует единственное решение тогда и только тогда, когда $\,\det A\neq 0\,$ , так как тогда мы можем использовать обратная матрица: 9{-1}\vec b=\vec x $$
Что касается (а) и вашего «основного вопроса»: если $\,\det A=0\,$, то можно еще проверить, нет ли решений или бесконечные решения (при условии, что мы работаем с бесконечным полем). Например, если система однородна (над бесконечным полем), она должна иметь бесконечные решения, тогда как если система неоднородна, она может не иметь решений или их может быть несколько:
Например, если система однородна (над бесконечным полем), она должна иметь бесконечные решения, тогда как если система неоднородна, она может не иметь решений или их может быть несколько:
$$\begin{cases}x+y=1 \\x+y=1\end{cases} \Longleftrightarrow \begin{pmatrix}1&1\\1&1\end{pmatrix}\binom{x}{y}=\binom{1}{1}\longrightarrow\,\ ,\text{бесконечное количество решений}$$
$$\begin{case}x+y=1\\x+y=0\end{cases} \Longleftrightarrow \begin{pmatrix}1&1\\1&1\end{pmatrix}\binom{x}{y} =\binom{1}{0}\longrightarrow\,\,\text{вообще нет решений}$$
и, конечно, в обоих вышеприведенных случаях имеем $\,\det A=0\,$
$\endgroup$
3
$\begingroup$
Для случая линейной системы неоднородных уравнений необходимо рассмотреть расширенную матрицу и сравнить ее ранг с рангом матрицы коэффициентов системы.
$\endgroup$
2
$\begingroup$
На самом деле возможны два случая:
Если вектор b не находится в пространстве столбцов матрицы A, он не будет иметь решений. Если b находится в пространстве столбцов A и поскольку det(A)=0, то у него будет бесконечно много решений.
Надеюсь, это может быть хорошей отправной точкой для вас.
Если b находится в пространстве столбцов A и поскольку det(A)=0, то у него будет бесконечно много решений.
Надеюсь, это может быть хорошей отправной точкой для вас.
$\endgroup$
$\begingroup$
Пусть система уравнений: $$ \оставил\{ \начать{массив}{л} топор+by=е \\ сх+dy=f \конец{массив} \Правильно. $$ Если мы умножим определитель на $x$ и воспользуемся некоторыми свойствами определителей, то получим: $$x\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} топор и б \\ сх & д \\ \конец{массив} \Rightarrow$$
$$\стрелка вправо
х\начало{массив}{|cc|}
а и б \\
CD \\
\end{массив}= \begin{массив}{|cc|}
е-б&б\
ф-ды&д\
\конец{массив}
\Rightarrow$$
$$\стрелка вправо
х\начало{массив}{|cc|}
а и б \\
CD \\
\end{массив}= \begin{массив}{|cc|}
е & б \\
ж и д \\
\конец{массив}+
\begin{массив}{|cc|}
-by&b\
-ды&д\
\конец{массив}
\Rightarrow$$
$$ \Rightarrow x\begin{массив}{|cc|}
а и б \\
CD \\
\end{массив}= \begin{массив}{|cc|}
е & б \\
ж и д \\
\конец{массив}+ 0
\Rightarrow$$
$$\Rightarrow x\begin{массив}{|cc|}
а и б \\
CD \\
\end{массив}= \begin{массив}{|cc|}
е & б \\
ж и д \\
\конец{массив}
$$
Если у нас есть система, в которой $\begin{array}{|cc|}
а и б \\
CD \\
\end{массив}=0$ и $\begin{массив}{|cc|}
е & б \\
ж и д \\
\end{array}=0$, тогда $x$ может быть любым вещественным числом.
То же самое можно сделать и с $y$, но в этом случае мы получим: $$\Rightarrow y\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}= \begin{массив}{|cc|} а & е \\ с и ж \\ \конец{массив} $$ Опять же, если $\begin{массив}{|cc|} а и б \\ CD \\ \end{массив}=0$ и $\begin{массив}{|cc|} а & е \\ с и ж \\ \end{массив}=0$, $y$ может принимать множество значений в зависимости от значений $x$ или наоборот.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
линейная алгебра — Что значит иметь определитель равный нулю?
Спросил
Изменено 2 года 10 месяцев назад
Просмотрено 483k раз
$\begingroup$
После нескольких часов поиска в моей книге я все еще не понимаю, что означает для $(n\times n)$-матрицы $A$ наличие определителя, равного нулю, $\det(A )=0$.
Надеюсь, кто-нибудь объяснит мне это простым языком.
- линейная алгебра
- матрицы
- терминология
- определитель
$\endgroup$
5 9$
Матрица необратима.
Объем параллелепипеда, определяемый векторами-столбцами матрицы, равен $0$.
Объем параллелепипеда, определяемый векторами-строками матрицы, равен $0$.
Система однородных линейных уравнений, представленная матрицей, имеет нетривиальное решение.
Определитель линейного преобразования, определяемого матрицей, равен $0$.
Свободный коэффициент в характеристическом многочлене матрицы равен $0$.
В зависимости от определения определителя, которое вы видели, доказательство каждой эквивалентности может быть более или менее сложным.
$\endgroup$
7
$\begingroup$
Для меня это самое наглядное видео в сети, объясняющее детерминанты, и всем, кто хочет глубокого и наглядного понимания этой темы, стоит посмотреть его:
Определитель от 3Blue1Brown
Весь плейлист доступен по этой ссылке:
Суть линейной алгебры от 3Blue1Brown
Ключевая часть серии «Линейные преобразования и матрицы». Если вы это хорошо понимаете, все остальное будет как кусок пирога. Буквально: простой английский + визуальный.
Если вы это хорошо понимаете, все остальное будет как кусок пирога. Буквально: простой английский + визуальный.
$\endgroup$
5
$\begingroup$
Если определитель квадратной матрицы $n\times n$ $A$ равен нулю, то $A$ равен необратимый . Это важный тест, который помогает определить, является ли квадратная матрица обратимой, т. Е. Есть ли у матрицы обратная. Когда у него есть обратное, это позволяет найти единственное решение, например, уравнения $Ax = b$ при заданном векторе $b$.
Когда определитель матрицы равен нулю, связанная с ним система уравнений линейно зависима; то есть, если определитель матрицы равен нулю , по крайней мере одна строка такой матрицы является скалярно кратной другой.
[Когда определитель матрицы не равен нулю, линейная система, которую она представляет, линейно независима. ]
]
Когда определитель матрицы равен нулю, ее строки являются линейно зависимыми векторами, а ее столбцы являются линейно зависимыми векторами.
$\endgroup$
5
$\begingroup$
Определитель матрицы – это ориентированный объем изображения единичного куба. Если он равен нулю, единичный куб отображается внутри плоскости и имеет нулевой объем. 9{-1} = \dfrac{1}{detA} adjA$$
Следовательно, если определитель равен нулю, обратная матрица не существует.
$\endgroup$
9
$\begingroup$
Определитель имеет геометрическую интерпретацию. В дополнение к интерпретации в другом ответе, еще одной привлекательной, связанной с определителем, является его интерпретация как объема $N$-мерного параллелепипеда. Это более выражено в трехмерном пространстве. Если вы возьмете трехмерные трехмерные векторы, они могут образовывать или не образовывать углы параллелепипеда, если вы возьмете определитель матрицы с этими тремя векторами в качестве столбцов (или строк), если определитель равен нулю, он означает, что они не образуют вместе параллелепипед, если он отличен от нуля, это означает, что они действительно образуют 3 ребра параллелепипеда с объемом, заданным определителем. Знак значения определителя дает своеобразную информацию об ориентации этого тела.
Это более выражено в трехмерном пространстве. Если вы возьмете трехмерные трехмерные векторы, они могут образовывать или не образовывать углы параллелепипеда, если вы возьмете определитель матрицы с этими тремя векторами в качестве столбцов (или строк), если определитель равен нулю, он означает, что они не образуют вместе параллелепипед, если он отличен от нуля, это означает, что они действительно образуют 3 ребра параллелепипеда с объемом, заданным определителем. Знак значения определителя дает своеобразную информацию об ориентации этого тела.
$\endgroup$
$\begingroup$
Когда вы думаете о матрице как о преобразовании, определитель — это площадь (или объем в более высоком измерении), созданная базисом после преобразования. Этот тип мышления даст вам визуальную помощь. Например, при $n=3$ определитель матрицы равен нулю, значит, отображение по этой матрице переводит плоскость в прямую (площадь основания в преобразованной плоскости равна нулю). Идея может быть обобщена для более высокой размерности.
Идея может быть обобщена для более высокой размерности.
Обратите внимание, что невозможно обратно сопоставить линию с плоскостью. Значит, обратной матрицы, у которой определитель равен нулю, не существует.
$\endgroup$
$\begingroup$
Возьмите матрицу 2 x 2, назовите ее A, начертите ее в системе координат.
А= [[2,1],[4,2]] . —> Обозначение матрицы Numpy
Следующие два вектора записываются из A
x=[2,4]
y=[1,2]
Если вы построите это, вы увидите, что они находятся в тот же промежуток. Это означает, что векторы x и y не образуют площадь. Следовательно, det(A) равен нулю. Det относится к области, образованной векторами.
$\endgroup$
$\begingroup$
Другими словами:
Если взять $2$ вектора в $2D$ пространстве, можно показать, что площадь образованного параллелограмма является просто определителем матрицы, образованной этими двумя векторами. Это общий результат для $n$-мерностей — определитель матрицы есть объем $n$-параллелограмма, образованного строками матрицы.
Это общий результат для $n$-мерностей — определитель матрицы есть объем $n$-параллелограмма, образованного строками матрицы.
Если определитель равен нулю, это означает, что объем равен нулю. Это может произойти только тогда, когда один из векторов «перекрывает» один из других или, более формально, когда два вектора либо линейно зависимы.
$\endgroup$
1
$\begingroup$
Если матрица A имеет обратную, это означает, что умножение матриц AB = I, единичная матрица. Говоря простым языком, если матрица обратима, то она может иметь решение.
Если определитель матрицы отличен от нуля, матрица может иметь решение. Если определитель равен нулю, то матрица необратима и, следовательно, не имеет решения, поскольку одна из строк может быть удалена заменой другой строки в матрице.
Обычная причина обратимости матрицы заключается в том, что одна или несколько строк в матрице являются скалярами другой.

 1. Вычислить определители:
1. Вычислить определители: .а mn .
.а mn .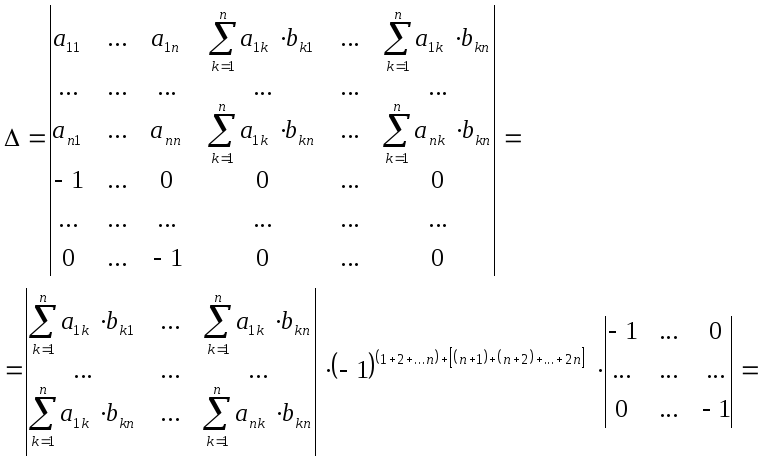

 : Волтерс Клувер, 2009. — С. 237 – 512 с.- ISBN 978-5-466-00269-0
: Волтерс Клувер, 2009. — С. 237 – 512 с.- ISBN 978-5-466-00269-0