Решить уравнение с модулем икс и зачем нужна логика
Давайте попробуем решить довольно простое, на первый взгляд, уравнение с модулем икс. Для его решения, вроде бы, не нужно ничего знать, кроме алгебры: 2х — |х| = -1
Содержание
- Если убрать модуль х из уравнения
- Как решить уравнение с модулем икс
- Икс равен нулю
- Получим уравнение без знака модуля:
- Икс в уравнении отрицательный
- Проверка гипотез в других областях
Если убрать модуль х из уравнения
Что будет, если приведенного уравнения убрать х по модулю, то есть если заменить |х| просто на х? Тогда уравнение с модулем икс можно решить в уме, не прибегая к сложным выкладкам:
2х — х = х = -1. Очевидно, что х = -1.
Но знак модуля |х| нам все портит. И значение х = -1 не является решением первоначального уравнения, так как
2 * (-1) — |-1| = -2 — 1 = -3. Но никак не -1 !!!
Как решить уравнение с модулем икс
Давайте вместе с алгеброй применим логику. Логика позволяет нам делать некоторые предположения. Применительно к первоначальному уравнению, сделаем сразу 3 логических допущения.
Логика позволяет нам делать некоторые предположения. Применительно к первоначальному уравнению, сделаем сразу 3 логических допущения.
1. Предположим, что х=0.
2. Допустим, что х>0.
3. Предположим, что х<0.
Этими тремя предположениями мы «перекрыли» весь диапазон возможных значений икс х, которые могут стать решением данного уравнения, так ведь? Значение х может быть нулевым, положительным или отрицательным.
Теперь давайте проверим каждое сделанное предположение. Выполним своеобразную «проверку гипотез» о том, что х может быть нулевым, положительным или отрицательным.
Икс равен нулю
Проверим первое предположение, что икс равен нулю (х=0):
2 * 0 — |0| = 0 — 0 = 0, но никак не -1, как записано в исходном уравнении.
Значит, первая гипотеза о том, что х = 0 оказывается не верна, поэтому отбросим ее.
Если в уравнении икс положительный
Проверим вторую гипотезу о том, что х является числом положительным. Тогда можно избавиться от знака модуля в исходном уравнении. Ведь если х является положительным числом, то |х| = х. Это очевидно, не так ли?!
Тогда можно избавиться от знака модуля в исходном уравнении. Ведь если х является положительным числом, то |х| = х. Это очевидно, не так ли?!
Получим уравнение без знака модуля:
2х — |х| = 2х — х = х = -1
Итак, в результате решения нового уравнения, когда знак модуля был отброшен, получили ответ х = -1.
Однако в начале этой статьи мы получали такой же ответ, который не «проходил» элементарную проверку путем подстановки -1 в уравнение вместо х. Что не так?
Почему в результате решения уравнения мы получили х = -1, но проверка показывает неверный результат? Дело в том, что мы нарушили нашу собственную логику.
Второе предположение состояло в том, что значение х должно быть положительным (х>0). Но в результате подстановки положительного значения х в уравнение после его решения мы получили отрицательное значение х = -1.
А раз логика нарушена, значит наше предположение о том, что х является положительным числом НЕ ВЕРНО. Мы должны отбросить второе наше предположение, что х>0 так же, как мы отбросили первое предположение, что х=0.
Икс в уравнении отрицательный
Что же у нас остается? Остается третье логическое предположение, что значение х отрицательное (х<0). Давайте попробуем решить исходное уравнение при данном логическом предположении.
Итак, если х<0, то |х| = -х — это факт. Подставим в наше уравнение с модулем икс вместо |х| значение (-х). Тогда получим следующее:
2х — |х| = 2х — (-х) = 2х + х = 3х = -1.
Решаем полученное уравнение:
3х = -1, что означает х = -1/3.
Получается, если предположить, что х<0, решением уравнения будет значение х = -1/3, то есть отрицательное число «одна треть». Логика соблюдена? Да, конечно: мы предположили, мы построили гипотезу, что х<0, и в результате получили х = -1/3, мы получили отрицательное число, как и предположили. Значит, мы, действуя логически, наконец, решили уравнение.
Наше решение: х = -1/3.
Давайте на всякий случай проверим, действительно ли мы правы, решая исходное уравнение таким «замысловатым» логическим способом, делая предположения, гипотезы и затем их проверяя на логическую непротиворечивость:
2 * (-1/3) — |-1/3| = -2/3 — 1/3 = -3/3 = -1, что и требовалось получить в конечном итоге!
Итак, решением уравнения с модулем икс:
2х — |х| = -1
является значение х = -1/3.
Вот что значит действовать логически при решении уравнения: делать логические предположения, далее пытаться решить уравнение на основе сделанных логических предположений. И в конце, после даже кажущегося удачного решения уравнения, проверять логическую непротиворечивость сделанных гипотез.
И тогда можно решать не только данное уравнение, являющееся не таким уж сложным, но и находить решения других более сложных задач.
Проверка гипотез в других областях
Метод проверки гипотез работает не только в математике, алгебре, но и в других науках. Даже в гуманитарных дисциплинах применяют методы проверки гипотез. Скажем, в управлении, в менеджменте.
Допустим, на заводе выпускается продукция, но по какой-то неясной причине некоторые производимые изделия стали бракованными. В чем проблема? Менеджеры начинают строить гипотезы: оборудование износилось и требует ремонта, сырье привезли уже бракованное, рабочий на линии перестал соблюдать установленные требования и так далее.
Может быть даже построено «дерево возможных причин». Оно визуально выглядит, не как дерево с разветвляющимися ветками, а как скелет рыбы, лежащий на боку, где на конце каждой косточки надписана та или иная гипотеза, предположение, почему стали выпускать бракованную продукцию. Подобная схема имеет несколько вполне официальных, признанных наукой названий: «рыбная кость», «рыба Исикавы» (по фамилии ее изобретателя из Японии) и другие.
И затем, «косточка за косточкой», гипотеза за гипотезой, последовательно проверяя их все, менеджеры находят одну или сразу несколько причин возникшей проблемы.
Так что проверка гипотез, логический подход к решению задач, на самом деле, широко распространен в наше время. Изучение этого подхода на простых алгебраических уравнениях, на самом деле, очень полезно, поскольку логика таких решений, возможно, нам всем потребуется в дальнейшей работе и жизни. Причем, совершенно не обязательно, что мы будем решать уравнения, а не заниматься другими делами, скажем, управлением производством или обслуживанием.
«Математика уж тем хороша, что она ум в порядок приводит» — М.В.Ломоносов. Лучше не скажешь, особенно применительно к решению логических задач, так как логика очень часто нужна в повседневной жизни в работе.
Решение для двух переменных в уравнениях линейного модуля — Ответы MATLAB
30 просмотров (последние 30 дней)
11 февраля 2019 г.
Принятый ответ: Джон Д’Эррико
В настоящее время я работаю над проектом по взлому текстового файла, закодированного с помощью аффинного шифра с использованием неизвестных ключей. Текстовый файл содержит расширенный ASCII, поэтому мой модуль будет равен 256 (указанный в инструкциях к проекту).
Я пытаюсь избежать грубой силы, и мне нравится алгебраически решать мой ключ, используя частотный анализ зашифрованного текста. Проблема, с которой я сталкиваюсь, заключается в том, что я не очень хорошо знаком с Matlab, но это то, что мы используем в курсе.
Вот что я пробовал, используя известный ключ (251,69)
S = решить(32*a+b==165, 101*a+b==76)
S. a = -89 /69
a = -89 /69
S.b = 14233/69
Вот что я хотел бы сделать, так это:
S = решить(mod(32*a+b,256)==165, mod(101*a+b, 256)==76)
S.a = 251
S.b = 69
Однако это не работает. Я искал и пробовал MuPAD и lincongruence, но это не кажется подходящим для двух переменных. Я также пробовал linsolve и устанавливал Domain = Dom::IntegerMod(256). Но это вызвало следующую ошибку:
Ошибка: «Домен = R», где R — домен категории «Cat::Field», ожидаемый. [linsolve]
Заранее спасибо!
(с использованием Matlab R2018b для учебных заведений)
Ответ принят
Отредактировано: Джон Д’Эррико 11 февраля 2019 г.
- rrefgf.m
Довольно просто, правда. У вас есть линейная система модульных уравнений.
mod(32*a+b,256)==165
mod(101*a+b,256)==76
Просто вычтите два, что вполне допустимо. Затем мы узнаем, что
mod((101 — 32)*a,256) == 76 — 165
Это сводится к одномерной задаче
mod(69*a,256) == 167
69, мод 256 существует, так как gcd(69,256)==1.
[G, A, B] = GCD (69,256)
G =
1
A =
-115
B =
31
MOD (A, 256)
ANS =
31
MOD (A, 256)
ANS =
0003
141
Таким образом, пока gcd возвращает 1 для gcd, тогда модульная инверсия 69 равна mod(a,256)==141. (Прочитайте справку по gcd, где вы узнаете, что означают второй и третий выходные данные GCD.)
Это говорит нам о том, что мы можем найти просто как…
a = mod(167*141,256)
a =
251
И мы находим b как:
b = mod(165 — 32*a, 256)
b =
69
Шаг проверки:
b, 25*6a
ans =
165
mod(101*a + b, 256)
ans =
76
Если бы задача была более общей, она все равно была бы такой же простой, если бы она была линейной. система. Посмотрим, кажется, я совсем недавно разместил rrefgf на файлообменнике. Это может сделать работу.
Ared = rrefgf([A,eye(2)],256)
Ared =
1 0 115 141
0 1 161 96
rhs = [165 ; 76];
ab = mod(Ared(:,3:4)*rhs,256)
ab =
251
69
Итак, a равно ab(1), b = ab(2).
(Черт, я думал, что разместил rrefgf на FEX. Я прикреплю его к этому ответу.)
Больше ответов (0)
Произошла ошибка
Не удалось выполнить действие из-за изменений, внесенных на страницу. Перезагрузите страницу, чтобы увидеть ее обновленное состояние.
Выберите сеть Сайт
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и посмотреть местные события и предложения. На основе ваше местоположение, мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Обратитесь в местный офис
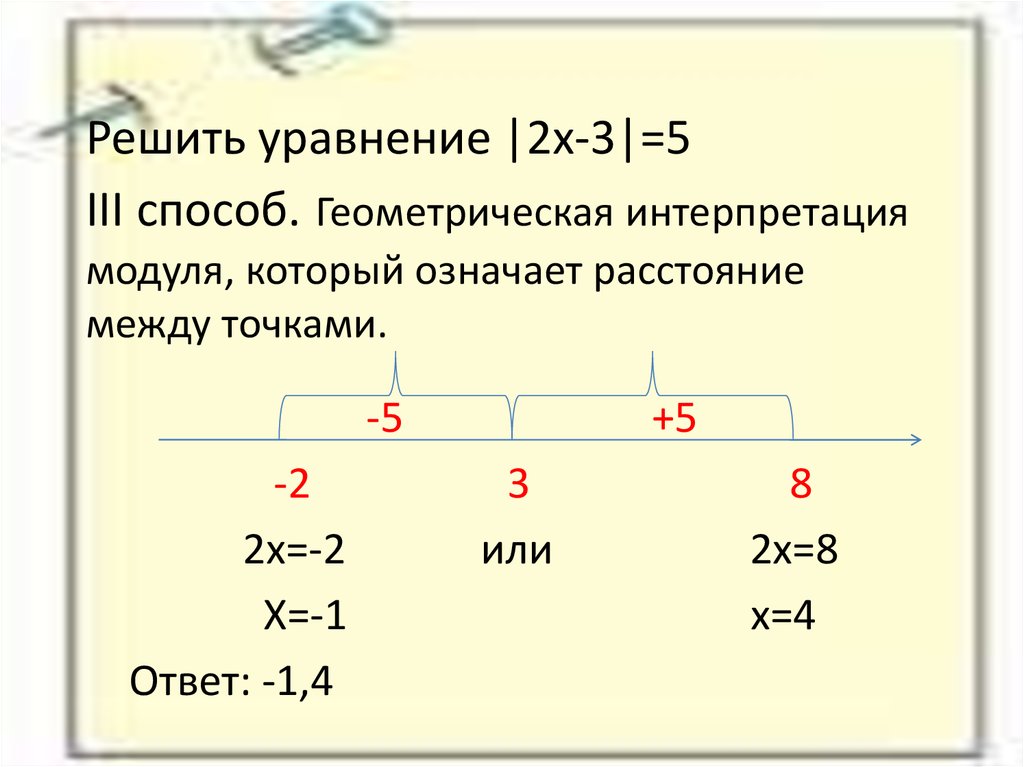
Решение уравнений абсолютного значения — JustQuant.com
В этом посте мы увидим, как решать задачи на абсолютное значение (модуль ) уравнения и неравенства. Чтобы понять основы абсолютного значения, нажмите здесь – Абсолютное значение
youtube.com/embed/eKrissCglI0?feature=oembed&enablejsapi=1&origin=https://www.justquant.com» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Решение задач абсолютного значения типа |f(x)| + g(x) = k
Как найти значение x в абсолютных уравнениях, содержащих |f(x)| + г(х) = к
Мы можем подойти к таким задачам, сделав уравнение независимым от знака модуля.
Чтобы уравнение не зависело от знака абсолютного значения, давайте сначала посмотрим на определение абсолютного значения f(x)
Мы знаем, что абсолютное значение всегда положительно,
Итак, если f(x)≥0, значение f(x) положительно и, следовательно, |f(x)| будет равно f(x), а если f(x)<0, то значение отрицательно, поэтому |f(x)| будет равно -f(x), чтобы сделать результирующее значение положительным.
Следовательно, на основании определения модуля f(x) мы можем выделить те значения x, при которых f(x) меняет знак и на основании которых мы можем классифицировать наш подход к проблеме на случаи,
Случай 1: f(x) ≥ 0
Когда f(x)≥0, |f(x)| = f (х). Следовательно,
Следовательно,
|f(x)| + g(x) = k => f(x) + g(x) = k.
Случай 2: f(x) < 0 Когда f(x)≥0, |f(x)| = f (х). Следовательно, |f(x)| + g(x) = k => -f(x) + g(x) = k.
Теперь у нас есть два уравнения относительно f(x), которые не зависят от знака модуля. Теперь мы можем решить эти уравнения относительно x.
Примечание. Как только вы найдете значение x в каждом случае, проверьте, удовлетворяет ли x условию для этого случая. Если x удовлетворяет условию, то это верное решение.
1. Найти x: |x-3| + 2x = 7
Имеем,
Следовательно,
Случай 1 : x ≥ 3
|x-3| + 2x = 7 => x – 3 + 2x = 7 => x = 10/3
Здесь x = 10/3 удовлетворяет условию x≥3. Там x = 10/3 является допустимым решением.
Случай 2 : x < 3 |x-3| + 2x = 7 => -(x – 3) + 2x = 7 => x = 4,92 – 9}$
3. Найти x: |x + 3y|=5, |y| = 4
Случай 1: x + 3y = 5, y = 4
=> x = -7, y = 4
Случай 2: x + 3y = 5, y = -4
=> x = 17, y = -4
Случай 3: x + 3y = -5, y = 4
=> x = -17, y = 4
Случай 4: x + 3y = -5, y = -4
=> x = 7, y = -4
Math Tricks Workout
Пожалуйста, попробуйте наше приложение для Android – Math Tricks Workout.