розв’язування рівнянь алгебри з додаванням і відніманням
Рівняння
Одним з основних понять алгебри є рівняння. Головне, що слід знати про рівняння, це те, що все, що знаходиться на одній стороні знака рівності (=), має дорівнювати всьому на іншій стороні знака рівності.
Змінні
Змінні — це речі, які можуть змінюватися або мати різні значення. В алгебрі ми зазвичай намагаємося знайти значення однієї або декількох змінних. В алгебраїчних рівняннях змінна представлена буквою.
На цій сторінці наші змінні будуть представлені буквами ‘x’ та ‘y’.
Просте рівняння
Ось просте рівняння із змінною x:
x + 5 = 7
Що означає x =?
x = 2, оскільки 2 + 5 = 7.
Розв’язування рівняння
У наведеному вище рівнянні ми могли б просто сказати, дивлячись на нього, що x = 2, однак це не завжди так. Іноді нам доводиться більше працювати, щоб вирішити рівняння.
Іноді ми можемо розв’язати рівняння, додавши або віднявши одне і те ж число до обох сторін рівняння.
Ми знаємо, що це нормально, тому що поки ми виконуємо одну і ту ж операцію з обома сторонами рівняння, тоді рівняння не змінюється.
Спробуємо розв’язати цей простий приклад, додавши або віднявши обидві сторони:
x + 5 = 7
Ми хочемо з’ясувати, що дорівнює x, тому нам потрібно отримати x само по собі на одній стороні рівняння. Якщо відняти 5 з лівого боку, x буде саме собою. Слідуючи нашому попередньому правилу, нам потрібно зробити те ж саме з правою стороною.
(x + 5) — 5 = (7) — 5
х = 2
Інший приклад:
Вирішити для x:
x — 2y + 7 = y + 15
Нам потрібно отримати х саме по собі, тому давайте почнемо з віднімання 7 з кожної сторони:
(x — 2y + 7) — 7 = (y + 15) — 7
x — 2y = y + 8
Тепер нам потрібно позбутися — 2y, ми можемо зробити це, додавши 2y на кожну сторону:
(x — 2y) + 2y = (y + 8) + 2y
x = 3y + 8
Тепер ми повинні ще раз перевірити цю відповідь, підключивши її назад до початкового рівняння:
x — 2y + 7 = y + 15
Підставляємо 3y + 8 на x
3y + 8 — 2y + 7 = y + 15
3y — 2y + 8 + 7 = y + 15
y + 15 = y + 15
Тут ми дізналися, як розв’язувати рівняння, додаючи і віднімаючи до кожної сторони, але що, якщо ми маємо щось на зразок 2x = 4? Щоб вирішити це рівняння, нам потрібно множити і ділити з кожної сторони.
Зайдіть сюди, щоб навчитися розв’язувати алгебраїчні рівняння за допомогою множення та ділення .
Що слід пам’ятати
- Завжди виконуйте одну і ту ж операцію з обох сторін рівняння.
- Ви можете додавати і віднімати числа з обох сторін рівняння, щоб розв’язати для x або y.
- Завжди двічі перевіряйте свою відповідь, підключаючи її назад до початкового рівняння.
Більше предметів алгебри
Словник алгебри
Експоненти
Лінійні рівняння — Вступ
Лінійні рівняння — форми нахилу
Порядок операцій
Співвідношення
Співвідношення, частки та відсотки
Розв’язування рівнянь алгебри з додаванням і відніманням
Розв’язування рівнянь алгебри за допомогою множення та ділення
Рівняння. Розв’язування рівнянь — презентация онлайн
Похожие презентации:
Правильний опуклий многогранник ікосаедр
Десяток. Лічба десятками
Похідна та її застосування
Паралельне проектування і його властивості.
Зображення фігур у стереометрії
Правильні многокутники. (9 клас)
Тригонометричні функції в житті людини
Додатні та від’ємні числа. (6 клас)
Порівняння швидкості рухів тварин і техніки
Прямокутні координати в просторі
Дія ділення.(2 клас)
1. Р І В Н Я Н Н Я
РІВНЯННЯВчитель математики Цой І.Ф.
Іллінської ЗОШ І-ІІІ ступенів
Чаплинського району
Херсонської області
2. після уроку учні зможуть
— дати визначення рівняння зоднією змінною;
— складати алгоритм
розв’язування таких рівнянь
Ніколи не пізно
порозумнішати.
Д.Дефо
Дуже багато типових ситуацій з
нашого побуту, наприклад
звичайний похід у магазин,
може обернутися необхідністю
розв’язати деяку задачу. А
значну кількість цих задач
набагато легше розв’язати
склавши відповідне рівняння.
«Не вважай невдачею
те, що можна
виправити»
Катон
6. ІНТЕЛЕКТУАЛЬНА РОЗМИНКА
1.
Рівність що містить змінну, називається…а) виразом; б) рівнянням; в) нерівністю.
2. Щоб знайти невідоме зменшуване, треба від’ємник і різницю …
а) додати;, б) відняти; в) поділити.
3. Рівняння 3х + 6 = -12 має
а) один корінь; б) два корені; в) три корені.
4. Число, яке задовольняє рівняння, називається його…
а) змінною; б) розв’язком; в) значенням.
5. У рівнянні 4х – 15 = х + 15 сума х + 15 називається його…
а) лівою частиною; б) правою частиною; в) серединою.
3
x є число…
6. Коренем рівняння
=15
4
45
а) -20; б)
в) 20.
4
7. Рівняння 5 – у = 8 – у
а) не має розв’язків; б) має безліч розв’язків; в) має один розв’язок.
8. Число – 1 задовольняє рівняння…
а) х + 15 = 2х; б) 4 – 6х = 8; в) 10 + 7х = 3.
7. ІНТЕЛЕКТУАЛЬНА РОЗМИНКА
9. Щоб знайти множник, треба добуток… на відомиймножник
а) помножити; б) поділити; в) відняти.
10. Знайти всі корені рівняння або довести, що їх немає,
означає …
а) розв’язати рівняння; б) спростити рівняння;
в) допустити помилку в рівнянні.
11. Яке рівняння відповідає умові задачі : «Я задумала
число. Потім знайшла його третю частину, а до здобутого
результату додала 6. Після чого дістала 18. Яке я
задумала число?»
x
а) 3х + 6 = 18; б) 3 + 6 = 18; в) + х + 6 = 18.
12. Чому дорівнює шукане число в попередній задачі.
а) 36;
б) 4;
в) 12.
«Практика багатша і
складніша за будь-які
штучні побудови та
абстрактні схеми»
9. Скласти рівняння за схемою і розв’язати його
х—
5
—
х
2
+
х
10. Розв’язання
(5 — х) – (2 + х) = х5–х–2–х=х
-3х = -3
х=1
Відповідь: 1
11. Скласти рівняння за схемою і розв’язати його
8 (…)9
5 (…)
2х
2
3х
12. Розв’язання
8 (9 + 2х) = 5 (2 – 3х)72 + 16х = 10 – 15х
31х = — 62
х = -2
Відповідь: -2
«Єдиний шлях, що
веде до знань діяльність»
Б.Щоц
На фермерській ділянці зібрали
2050 т овочів. Картоплі зібрали в 4
рази більше, ніж буряків, а капусти
на 250 т більше ніж буряків.
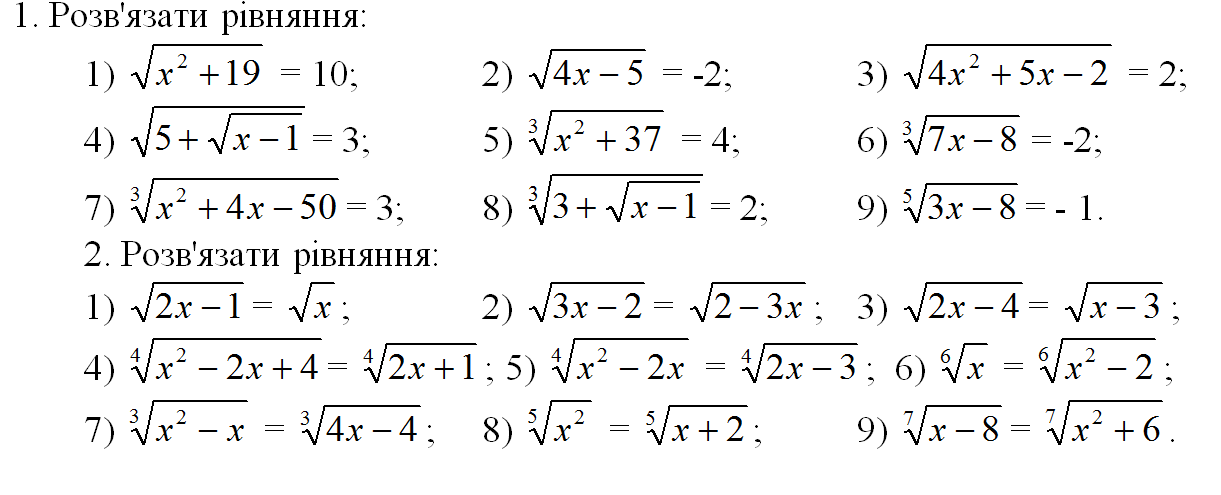
Скільки зібрали картоплі, буряків і
капусти окремо.
Картопля
— в 4 рази більше
2050 т
Буряк
Капуста
— на 250 т більше
16. Розв’язання:
Нехай буряків зібрали х т, тоді картоплі – 4х т, акапусти (х + 250) т. Знаючи, що всіх овочів зібрали
2050 т, складаємо рівняння.
х + 4х + х + 250 = 2050
6х = 1800
х = 1800 : 6
х = 300
Отже, буряків зібрали 300 т.
300* 4 = 1200 (т) картоплі
300+ 250= 550 (т) капусти.
Відповідь: 300 т, 550 т, 1200 т
Фермер Садаєв засіяв пшеницею
три поля, загальна площа яких
становить 50% площі другого, а
площа третього більша від площі
першого в 3 рази. Яка площа
кожного поля
http://www.caringbahlearningcentre.com.au/assets/imag
es/calc.JPG
http://www.mathknowledge.com/images/custom/LOGO.
GIF
http://www.proshkolu.ru/content/media/pic/std/100000
0/248000/247659-a3befaa6af58cffa.jpg
English Русский Правила
Розвязка ривнян трекег и четвртог корака.
Povijest prve etape treće i četvrte etapeZavdannya Broj 1
Podignite Razinu Trećeg Koraka Za Cardanovu formulu:
x 3 -3x 2 -3x -1 = 0.
odluka: prijejejejeje -lega. али не я осветить себе другим koraku, koji nije kod kuće. За брзу особу с формулой
х = у -, учетовитость при х 2.
Махмо: х = у + 1.
(у + 1) 3 -3 (у + 1) 2 -3 (у + 1) -1 = 0,
Наконе что смо отворили луковы и циепили поделе, можно указать:
За кубни корижен у 3 + ру + q = 0 ê Формула Карданова:
yi = (i = 1,2,3,), decimalno mjesto za radikal
, = .
Neka je α1 — jedna / be-yake / vrijednost radikala α. Todi dva značenja poznata su kao ofenzivni rang:
α 2 = α 1 ε 1, α 3 = α 1 ε 2, de ε 1 = + i, ε 2 = — i je korijen trećeg koraka iz jedinice.
Ako je u području β 1 = -, онда может направить мо β 2 = β 1 ε 2, β 3 = β 1 ε 1
Уведимо значение формулы yi = αi + βi, znamo korijen
y 1 = α 1 + β 1,
y 2 = -1/2 (α 1 + β 1) + i (α 1 -β 1),
y 3 = -1/2 (α 1 + β 1) — i (α 1 -β 1),
U trenucima p = -6, q = — 6.
α= =
Jedna od vrijednosti radikala je jednaka. Одговару α1 =. Todi β 1 = — = — =,
y 2 =) — i).
Слово же, знамо полезность х по формуле х = у + 1.
х 2 =) + и) + 1,
х 3 =) — и) + 1.
Завдання №2
Виришити по Феррари методы четвёртой корака:
x 4 -4×3 + 2×2-4x + 1 = 0.
x 4 -4x 3 = -2x 2 + 4x-1,
x 4 -4x 3 + 4x 2 = 4x 2 -2x 2 + 4x-1,
(x 2 -2x) 2 = 2x 2 + 4х-1.
Уведено на нов начин, у оваквом ряд:
(х 2 -2х +) 2 = 2х 2 + 4х-1 + (х 2 -2х) у +,
(х 2 -2х +) 2 = (2 + у) х 2 + (4-2у) ) х + () / 1 /.
Подберем у со, щоб и казнити права квадрат.
Mahmo: B 2 -4AC = 16-16y + 4y 2 -y 3 -2y 2 + 4y + 8 = 0
Abo y 3 -2y 2 + 12y-24 = 0.
od korijena ê y = 2. Vrijednost y = 2/1 /,
Otrimaêmo (x 2 -2x + 1) 2 = 4x 2. Signali (x 2 -2x + 1) 2 — (2x) 2 = 0 или ( х 2 -2х + 1-2х) (х 2 -2х + 1 + 2х) = 0,
Отримаемо два квадратна ривняня:
х 2 -4х + 1 = 0 i х 2 + 1 = 0.
Выришучи их, знамо корижен клипа ривняня:
+х 1 = 2, х 1 = 2-2-2 = -I, х 4 = I.
Завдання брой 1
Укажите большую корижен багатолена
f (x) = 8x 5 -14x 4 -77x 3 + 128×2 + 45x-18.
Odluka : Da bi se razumnije spoznalo korijen torbe izoštrava se novim teoremima.
Теорема 1. Kao ne-kratki pokretač, f (x) je ukorijenjen s mnogo funkcija, zatim je ime valjanog člana, a q je ime starijeg člana polinoma f (x).
Номер: Teorem 1 da treba um da bi bio racionalan broj . Bulo po corijenu polinoma, crveni um i nedostatak, tobto. S teoremom 1 možemo vidjeti vrijednost za takav razlomak, koji nije korijenska točka.
Теорема 2: Kao nekratki dib ê po korijenu polinoma f(x)s nizom factora, tada za bilo koje cijelo m, danog tipa, broj f(m) proširuje broj p-qm, tj. брой.
Зокрем, вважаючи m=1, а понекад и m=-1, можно речи:
ako korijen polinoma nije veći od ± 1, tada je f (x) (p-q) i f (-x):.
Номер: Teorem 2 daje još jedan neophodan razlog za racionalni korijen Problema. Qia umova je prijateljski tim, lako ga je promijeniti u praksi. Znamo raspon f (1) i f (-1), a zatim se za frakciju kože, prije pokušaja, promijeni na um. Ako želite b jedan od brojeva razlomka, tada je korijen vrećice izostren f (x) nije ê.
Одлука: Prema teoremu 1, korijen ovog polinoma nalazi se uz srednje skraćene razlomke ciji su brojevi jednaki 18, a nazivnici 8. Također, budući da je nekratki korijen f (x), tada je p je jedan prema jedan od, ± brojeva: 2, ±3, ±6, ±9, ±18; q jedan jedan z brojevi
± 1, ± 2, ± 4, ± 8.
Vrahoyuchi scho знак равно , знак равно , nazivnici razlomaka su manje-više pozitivni.
Такомер, racionalni korijeni ovog polinoma mogu biti rastući brojevi: ± 1, ± 2, ± 3, ± 6, ± 9, ± 18, ±, ±, ±, ±, ±, ±, ±, ±, ±.
Natječite se za other koje trebate.
Oskílki f (1) = 72, f (-1) = 120, звезда крема, scho 1 í -1 ê korijeni f (x).
Sada, za skin junior, razlomak se može povno pretvoriti s teoremima 2 za m = 1 í m = -1, tako da ga je moguće postaviti, bilo pomoću razlomka: = í =
Rezultati se stavljaju u tablicu, del literi «c » i «d» znače točno, cilim abo snimamo ê broj abo
Iz otrimanih tablica se vidi da vipada više nema, ako je jedan od brojeva: 2, -2, 3, -3,.
Као результат Безутовых теорема, брой α-корижен ф(х)и тоди, ако йе ф(х)(х-α). Ozhe, za inverziju rješenja devet cijelih brojeva moguće je popraviti Hornerovu shemu dodavanjem dva člana.
2 — корижен.
Zvidsi maêmo: x = 2 — jednostavan korijen f (x). Korijen датчанин vrećice se izvlači iz korijena vrećice.
F 1 (x) = 8×4 + 2×3-73×2-18x + 9.
Slično, moguće je mijenjati brojeve.
2 — не корижен, 3 — корижен, -3 — корижен, 9 — не корижен, ½ — не корижен, -1/2 — корижен, 3/2 — не корижен, ¼ — корижен.
Opet, polinom f (x) = 8x 5 -14x 4 -77x 3 + 128x 2 + 45x-18 je pet racionalnih korijena: (2, 3, -3, -1/2, ¼).
ekvivalentni Koraci
VrШенджак Леонарда да Винсиджа, Професор Скипион дель Ферро -Бололог (Soba 1526), Доджелджудж Сэв Живот джеци Алгебарски Свеини Свейнсенам, Свейнсенам, Свеженам, Свеженам, Свейн.
Како су нам нешто показали, zadnji put kad su matematičari srednje Europe bili u toku, otishli su na algebru, na temeljito razumijevanje aparata i simbola. Regiomontane je naučio razumjeti brojke, uvodeći radikale i operacije iz njih. To je omogućilo da se postavi problem relativno široke klase rivljana među radikalima. У првом реду у самой регии постигнути су први успехи — показало се у радикалима 3. и 4. этап.
Зелено светло, плетено из броя упита, изврсно се чита у литератури. Здебильный победити такой. Profesor na Sveučilištu u Bologni Scipion del Ferro viviv формула za značenje pozitivnog korijena određene vrste x 3 + px = q (p ›0, q ›0). Osvojite obrezivanje u taunnitsi, spašavajući их противников njihovih противников u znanstvenim sporovima, ili prije smrti, nakon što su vidjeli svog rođaka, prijestupnika Anibalu della Nave i naučili na svoj način — Fiorea.
На клипу 1535. mau nalazi se znanstveni susret između Fiorea i Nicola Tartaglie (1500.-1557.). Ostanniy buv je Talirani znanstvenik, vještica iz svoje domovine, koja ima mnogo novca za život u povijesti matematike i mehanike u mjestima antičkog svijeta. Znajući da Fiore Volodya koristi Ferro формула и priprema свог противника за новую версию кубических продуктов, Tartalya zumira како би поновно primijenila формулу.
Na debati, Fiore predlaže hranu Tartalus kilka, jer zahtijeva jasniju razinu virishuvati trećeg koraka. Ale Tartaglia je već prije znao kako ujediniti takve ryvnyane, i štovise, nije lišen jednog od onih zamjenskih vipadkua, kao što je Ferrov bulo, i dva other istog vipadkiva. Tartaglia je uzela wiklik я предложил Fiorea са svojim nastojanjima. Rezultat smanjenja metka je novi rez ostatka. Tartalya je virishiv proponated yomu prodannya stretching dvije godine, samo jedan sat otkako Fiore nije propustio virishnost zhodny zhodannya predložene yomu (s obje strane bilo je 30 projekata).
Незабаром тарталья змиг виршувати рівняння на уму х 3 = px + q (p ›0, q ›0). Nareshty vín naizgled x 3 + q = px biti izgrađen prije pogleda sprijeda, ale bez davanja mjesta za izgradnju. Tartaglia nije objavio svoj rezultat. Два su razloga za to: u Perche, sam razlog, koji zupiny í Ferro. Na otheračiji način, zle volje da se uklopi u omraženi vipad. Останный поляга у тома, нижняя x 3 = px + q yaki može biti pozitivan korijen. Međutim, Tartagliina формула nije dala rješenje za to, ako je bilo potrebno vidjeti korijene negativnih brojeva, onda nije bilo moguće ispravno protumačiti očite brojeve, već izaći s tsyomom. Mrski vipadok pojavio se u Tartalu i na vidiku x 3 + q = px.
Меджутим, младич ние дуго нестао. С 1539 г. кубическими ривняннными почестями заматися Кардано (1501-1576). Osjećajući Tartaglinu poruku, prijavljujem bagato Zusila, a idem u život na tajno mjesto u zaštitno i nesuđeno mjesto za objavljivanje njegove knjige «Velika мистерия, или правила алгебры».
Međutim, Cardano nije razuman samo za pravila, već im to i dokaže. Nevažno na danu obitsyanka, vin je objavio Tartalovu metodu i cijeli način gledanja na «Cardan pravila». I knjiga se sudbini pojavila 1545. godine.
Незащищенный бульо идкрито рішення рівнян 4. корака. Talijanski matematičar D. Kolla iznio je spoznaju da je do tog časa vladao neadekvatno, a prije svega bilo je pristrano. Većina matematicara je poštovala cijenu nerazumljivosti. Ale Cardano je predložio vlastitog znanstvenika Luidzhija Ferrara, koji je djevica tvornice, a on zna kako napraviti četvrti korak uzgal, koji vodi do trećeg koraka.
Тако велики успехи у познатим формулы за развой 3. и 4. ступня представили су математическую проблему развоя веза изменчивых ступнева.
Mnogo je pitanja, Zusillas od većine učenika nije donio uspjeh. U šalama je bilo око 300 ракет. Liche u XIX stoljeću Abel (1802-1829) doviv, isti koraci n ›4, vzagalí očito, radikali ne upadaju u nevolje.
Na putu do kapije strana teorija Algebarski svećenici i načini stiha bili su još dva koraka: preklapanje, nedostatak Talenta opsjednutih формула i nedostatak jasnoće omraženog vipadku. Perche je postao немного praktičnog netalenta. Його Кардано научил, пропоньючи знай и корижен обитель е отприлике изван правила двию милостивих одредби, кое су, успей речено, запеле у наше дане на видику единство или линейное интерполацие. Još jedna pereshkoda je manje od korijena, a nakon što su pokušali ovu podolannyu iznijeli su još važnije naslijeđe.
Ugodno i odvažno pokušati se uklopiti u nepouzdano vrijeme kako bi pristajalo talijansko matematicaru i inženjeru R. Bombelli iz Bologne. У стваранью «Алгебра» (1572 г.), формально су била правила за джелованье над эксплицитным и комплексным броевима.
Nakon pritiska na gumb «Dodaj arhivu», možete dodati datoteku koja vam je potrebna bez kopije.
Prije preuzimanja ove datoteke pogodite one dobre sažetke, testove, tečajeve, robote za diplome, statistiku i other dokumente, koji nisu potrebni na vasem računalu. Tse vaš svećenik, braća su kriva za sudbinu razvoja suspenzije koja donosi prijekor ludima. Узнай роботе и пожалуйста их у базы знаний.
Svi studenti, postdiplomci, mladi lyudi, koji su zamjenska baza znanja u vlastitim pridošlicama i robotima, bit ćemo i dalje uz vas.
Заполните архив с документом в поле инесайте петерознаменные брошюры, брошюры е манджи, и кликните на гумб «Омогучу архив»
Выше документ
Opis života talijanskog svijeta tog dana, ako je bila živa, radi Girolamo Cardano. Знание o matematicharima, promatrajuci njihove matematičare i poze razvoja kubičnih ekvivalenata među radikalima. Načini razvoja razine trećeg i četvrtog koraka.
технический робот, допуне 26.08.2011
Povijest razvoja matematike u Europi VI-XIV stoljeća, njen predstavnici tog postignuća. Развой математики добы Видродження. Razvoj književnog broja, djelatnost Francoisa Vinte. Udokonallennia nabrajanje на primjer XVI — на клипу XVI stoljeća.
презентация, пожертвование 20.09.2015
Европейская математическая доби Видродження. Рад слова računice Франсуа Вит и метод izračunavanja Ривляна. Adekvatan izračun na primjer XVI — na uhu XVII stoljeća: deseci razlomaka, logaritmi. Уведена ссылка тригонометрия и алгебра.
презентация, пожертвование 20.09.2015
Из повижести десэтака тих изванредних фракций. Uradi više desetaka frakcija. Dodavannya (vidnimannya) desetke frakcija… Množenje desetina razlomaka. Розподил десетке фракция.
sažetak, dodaci 29.05.2006
Gretski matematicari i njena filozofija. Međusobna povezanost spilnog puta filozofije i matematike od početka epohe preporoda do kraja 17.
stoljeća. Филозофия и математика у эпохи образования. Анализ природы математических знаний классической философии.
диплом робота, допуна 07.09.2009
Ровняня у диеловима броя знака коже е написао Коми; Практические значения теории desetaka razlomaka. Samoodređivanje robota са sirokim varijacijama rezultata, направленный je izračun.
презентация, додано 02.07.2010
Победа в математике и математических методах Древна Кина… Особняк градевина Кинеза темелье се на бройчаним ознакама Ривляна и оних геометрических накрта, кои се могу довести до разине тречег ступня. Поглядел на математику древнего кино.
СТОРИЧНЫЕ ТРЕЧИ И ЧЕТВЕРТИ КОРАК
Кинец XV — столица XVI века. Tijekom razdoblja burnog razvoja u povijesti matematike, a posebno algebre. Bulo je poznato u stražnjem dijelu trga rivnyannya, kao i puno privatnih veza u trećem i četvrtom koraku. Postalo je ružna manifestacija vođenja turneja na vrhuncu stoljeća. Najranije u 16.
stoljeću u Bologni, profesor matematike Scipio del Ferro pronašao je rješenje zanapadnu kubnu rivnju:
Ю.С. Антонов,
9-r2.Poznato je da je r = ± A [P + P.
z3 + az2 + bx + c = 0,
Zamjena x = g — cijena linije se diže na oko: 3
x3 + px = q = 0.
Ферро виришив шукати развязання цго рывняня на вигляди х = А + В,
де а = 3 — 2 + р, = 3 — 2 — стр.
Подставляючи цей вираз на ривняння (1), принимаем:
1 + r + 3A2B + 3AB2 r + p (A + B) + I = 0.
Scipion del Ferro (1465. — 1526. ул.) — talijanski matematicar
метод разведения неупорных костей
Na fotografiji su jegulje — matematicari XVI стол (миниатюра среднего размера)
У таквом рангу, виходне івняння маэ развязок x = A + B, de:
* = Гр? ■ v = ■ ®
Ferro je tajnu principa prenio svom znanstveniku Mariju Fioreu. Останный, раскрывающий секрет, почтовый журнал на едином од математических оборотов.
Mnogi turniri nisu sudjelovali na pobjedničkim turnirima Nikkola Tartaglie. Sigurno je nakon susreta Tartaliyu i Maria Fiorea uslijedio obrok. Tartalya je bio upućen u riječi autoritativnog matematičara Pich-cholija, da je bio težak, ali radikalima je neugodno to učiniti, jer je to zbog preopterećenosti njegovog permozija. Međutim, dva dana prije klipa, može se saznati da Ferro zna rješenje kocke ryvnyannya i da svoju tajnu prenosi Mariju Fioreu. Usvajanje doslovno titanski zusilla, kriv za nekoliko dana prije otvaranja preokret je oduzeo njihovu kubičnu rivnyania rješenje (1). 12 жестоких 1535 руб. турнир видбулся. Кожен судионик пропоновал свой противник 30 завдан. Onaj koji je радиопрограмма био je kriv što je mogao posjetiti ostale prijatelje s čistim prekršajem, a štoviše, nekoliko traženih prijatelja bilo je dovoljno malo da se vrati od broja prijatelja od kojih je traženo da pobijede. Tartaglia je već dvije godine postala uspješna. Його неприятель je zhodnoi. Povijest znanosti objasniti cijenu na takav način.
Ровняня:
х3 + 3 х — 4 = 0.
Tse rivnyannya maê jednostruki korijen govora x = 1. Todi prema formuli Ferro mi otrimaêmo:
х = 3/2 + / 5 + -1 / 5.
Viraz, koji je dostojan znaka žara, kriv je za dragog. Slajd znači da je Tartaglia promatrao nedostatak takve kubične rivnyannya, i A i B nasilnički govor.
Koristeći Tartaglia формула, prisjetio sam se stajališta učenja Gerolama Cardana. Tartalia predaje vašu odluku na pamet, tako da Cardano može biti objavljen bez pomoći Tartalijine publikacije. Кардано на своем последнем блюде из Тартала. Win заткавился випад, ако í Vê su kompleksni brojevi. Ровняня: 92 +111
Cardanov veleposlanik, Rafael Bombelli, bio je dobar u tome, kao takav viraziv ispraviti rješenje Kubanki. Pobjeda, scho iz zadanog kubika jednako je A = 2 +1, B = 2 -1. Тоди х = А + В = 4,
Никколо Фонтана
Тарталья (ул. 1499 — 1557) — Талианский математический
тобто. бит će korijen rívnannya (3).
Важается, шо Кардано может украсить такво ржешенье за неке кубанске Ривняне.
Desetak sati kasnije, nakon što je odbacio формула Tartaglie Cardano, Ferrova odluka je donesena. Vín buv zdivaniyu povnim zbígom ríshen Tartaglia i Ferro. Нешто кардано зна о Ферровом ржешеню, нешто из неког разлога, али за свою книгу «Велики мистерий» объявио je Tartaglinu формулу, с правом, приписавши авторство Tartaglii i Ferru. Znajući za izlazak Cardanove knjige, Tartaglia će smrtno vrištati. Я, можда, не узалюд. Za kretanje по trenutnoj формуле (2) najčešće se naziva формула Cardano. Tartaglia wiklikav Cardano na matematicčkoj utakmici, ali još nije viđena. Zamijeniti novi wiklik prihvaćanjem studija Cardana, Ferrarija, koji nije lišen razvoja kubične ryvnannya, već četvrti korak. U svakodnevnim oznakama, veza četvrtog koraka je takva viglyad:
Nekhay maêmo rívnyannya z4 + pzi + qz2 + sz + r = 0,
Zrobimo zamijenimo m = x + p. Тоди ривняння набуде вигляд x4 + ax2 + bx + c = 0.
Укажите додатну промйену т и шукатимемо ржешенье за вигляд:
Джероламо Кардано (ул. 1501 — 1576) — талийский математик, инженер, философ, работник и астролог
Лодовико (Луиджи) Феррари (1522. — 1565. р.р.) — итальянский математический, koji poznaje okosnicu četvrtog koraka
x2 + ti = 2tx2 — bx + 1 t2 + at + c 92T0x+-b
U takvom rangu, rješenje etvrtog koraka Ferrarinom metodom dopiralo je do razvoja dvaju kvadrata (6) i kubika (5).
Par Tartaglia — Ferrari отбился 10 серпня 1548 руб. код Милана. Погледали смо razinu trećeg i četvrtog koraka. Чудесно, але Tartalya kilka je i dalje istinita (у Ferrariju, мелодично, sav bully je dizajniran za razvoj kubičnih felgi iz complexa A, B je za razvoj etvrte faze). Ferrarí je viríshivílíst í ako im se predloži zaposlenicima. Kao rezultat Tartagliine umišljenosti prosjačkog praza.
Практики, застой добитых растений, как велик. Числовым методом, ци ривняння варира с великом прецизионным. Međutim, формула су dale veliki doprinos razvoju algebre i zokrema, u razvoju method razvoja viših stepenica. Da zavrshimo priču, da je početak krokodila kod Rivnjana Vir_shenna slomljen i lišen u devetnaestom stoljeću. Abel je ustao, što je jednako n-tom koraku na n> 5, na vipadku, neugodno je visjeti u radikalima. Зокрема, показавши да се одно х5 + х4 + х3 + х2 + х +1 = 0 може повезти у радикала, али честно, на први поглед, одно х5 + 2х = 2 = 0 у радикалима е неповезан. Galois je pokupio hranu o razvoju rabina među radikalima. Як гуза ривняння, завжуваный у радикалима, может поставить исту ривняння:
Sve je postalo moguće pojavom nove teorije i same teorije grupa.
Популярная литература
1. Виленкин Н.Я. Иза маргиневодителя математики / Н.Я. Виленкин, Л.П. Шибасов, Е.Ф. Шибасова. — М.: Образование: АТ «Навчальная литература», 1996. — 320 стр.
2. Гиндикин, С.Г. Раскрытия физики и математики / С.Г. Гиндикин. — 2. врста. — М: Наука, 1985. — 182 стр.
ЛФХШ му и р ис думок
Znanost je manje nego korisna, ako se ne prihvaća srcem, nego srcem.
Д. И. Менделёв
Vsesvit se ne može izgraditi do razine ljudske inteligencije, a kasnije je moguće proširiti i razviti ludsku inteligenciju, tako da možete uzeti sliku Vsesvita u svijetu yo vidkrittya.
Фрэнсис Бэкон
Белешка. На статистических викторианских иллюстрациях на странице http://lesequations.net
Циклюши:
- Систематизировать для явного знания да vminnya на тему: Odluka trećeg i četvrtog koraka.
- Ubijte znanje obilakom niza zgrada, dio onih koji nisu poznati ni po vrsti, ni po načinu na koji se vide.
- Формирование интереса за математику кроз разной новых гран математики, развой графической культуры кроз индустрии графики Ровно.
Vrsta lekcije : комбинация.
Почтовый индекс: графоскоп.
Стварно: Vidi tablicu «Vijtin teorem».
Иди на лекцию
1. Усный рахунок
а) Zašto je višak u raspodjeli polinoma p n (x) = a n x n + a n-1 x n-1 + … + a 1 x 1 + a 0 u binarni x-a?
б) Колико кориена может проначи кубних кориена?
c) Што стои иза помощи тко е виришуэмо трэг и четвртог ступня?
г) Якшо б момак брой у квадратно, колико су онда врата Д и х 1; х 2
2. Самостальный робот (за группу)
Područje vnyannya, kao u domu korijena (od izvora do tvornice je kodirano)
1 группа
Корижен: x1 = 1; х 2 = -2; х 3 = -3; х 4 = 6
Ровняня:
Б = 1-2-3 + 6 = 2; б = -2
ч = -2-3 +6 + 6-12-18 = -23; с = -23
д = 6-12 + 36-18 = 12; д = -12
е = 1 (-2) (- 3) 6 = 36
х 4 — 2 х 3 — 23 х 2 — 12 х + 36 = 0
Одлука … Средина дана йе брой 36.
р = ± 1; ± 2; ± 3; ± 4; ± 6 …
р 4(1)=1-2-23-12+36=0 Иза Хорнерова схема
р 3 (х) = х 3 -х 2 -24х -36
р 3 (-2) = -8 -4 +48 -36 = 0, х 2 = -2
р 2 (х) = х 2 -3х -18 = 0
х 3 = -3, х 4 = 6
Врста: 1; -2; -3; 6 korijena zbroja 2 (P)
2 группы
Корижен: x1 = -1; х 2 = х 3 = 2; х 4 = 5
Ровняня:
В = -1 + 2 + 2 + 5-8; б = -8
с = 2 (-1) + 4 + 10-2-5 + 10 = 15; ч = 15
Д = -4-10 + 20-10 = -4; д = 4
е = 2 (-1) 2 * 5 = -20; е = -20
8 + 15 + 4x-20 = 0
р = ± 1; ± 2; ± 4; ± 5; ± 10; ± 20,
р 4 (1) = 1-8 +15 + 4-20 = -8
р 4 (-1) = 1 +8 + 15 -4 -20 = 0
р 3 (х) = х 3 -9х 2 + 24х -20
р 3 (2) = 8 -36 +48 -20 = 0
р 2 (х) = х 2 -7 х +10 = 0 х 1 = 2; х 2 = 5
Просмотрел: -1; 2; 2; 5 сума кориена 8 (R)
3 группы
Корижен: x1 = -1; х 2 = 1; х 3 = -2; х 4 = 3
Ровняня:
В = -1 + 1-2 + 3 = 1; В = -1
с = -1 + 2-3-2 + 3-6 = -7; с = -7
Д = 2 + 6-3-6 = -1; д = 1
е = -1 * 1 * (- 2) * 3 = 6
х 4 — х 3 — 7х 2 + х + 6 = 0 (Це ривняння виришу потим за группу дошци 4)
Одлука.
Срце срча дана дже 6.
р = ± 1; ± 2; ± 3; ± 6
р 4 (1) = 1 — 1 — 7 +1 +6 = 0
р 3 (х) = х 3 — 7х -6
р 3 (-1) = -1 + 7-6 = 0
р 2 (х) = х 2 -х -6 = 0; х 1 = -2; х 2 = 3
Просмотрел: -1; 1; -2; 3 Зброй Кориена 1 (О)
4 группы
Корижен: x1 = -2; х 2 = -2; х 3 = -3; х 4 = -3
Ровняня:
В = -2-2-3 + 3 = -4; б = 4
с = 4 + 6-6 + 6-6-9 = -5; с = -5
Д = -12 + 12 + 18 + 18 = 36; д = -36
е = -2 * (- 2) * (- 3) * 3 = -36; е = -36
х 4 + 4х 3 — 5х 2 — 36х -36 = 0 (Це ривняння виришу потом 5 група на дощи)
Одлука. Cílí kornnya shukaêmo usred dana na broj -36
р = ± 1; ± 2; ± 3 …
р (1) = 1 + 4-5-36-36 = -72
р 4 (-2) = 16 -32 -20 + 72 -36 = 0
р 3 (х) = х 3 + 2х 2 -9х-18 = 0
р 3 (-2) = -8 + 8 + 18-18 = 0
р 2 (х) = х 2 -9 = 0; х = ± 3
Просмотрел: -2; -2; -3; 3 Сума корижен-4 (Ж)
5 групп
Корижен: x1 = -1; х 2 = -2; х 3 = -3; х 4 = -4
г.
Ровняня
х 4 + 10х 3 + 35х 2 + 50х + 24 = 0 (Це ривняння виришу потом 6 группа на дощи)
Одлука … Srce srca dana je 24.
р = ± 1; ± 2; ± 3
р 4 (-1) = 1 -10 + 35 -50 + 24 = 0
р 3 (х) = х-3 + 9х 2 + 26х + 24 = 0
р 3 (-2) = -8 + 36-52 + 24 = О
р 2 (х) = х 2 + 7х + 12 = 0
Врста: -1; -2; -3; -4 Зброй-10 (И)
6 групп
Корижен: x1 = 1; х 2 = 1; х 3 = -3; х 4 = 8
г. Ровняня
В = 1 + 1-3 + 8 = 7; б = -7
ч = 1-3 + 8-3 + 8-24 = -13
Д = -3-24 + 8-24 = -43; д = 43
х 4 — 7 х 3 — 13 х 2 + 43 х — 24 = 0 (Це ривняння виришу потом 1 группа на доще)
Одлука … Средина дана je -24.
р 4 (1) = 1-7-13 + 43-24 = 0
р 3 (1) = 1-6-19 +24 = 0
р 2 (х) = х 2 -5х — 24 = 0
х 3 = -3, х 4 = 8
Просмотрено: 1; джедан; -3; 8 зброй 7 (л)
3.
Внесение изменений в параметры
1. Развязать ривняня х 3 + 3х 2 + тх — 15 = 0; као онадж из кориена врата (-1)
Molimo pišite redoslijedom rasta
Р = Р 3 (-1) = — 1 + 3-м-15 = 0
х 3 + 3 х 2 -13 х — 15 = 0; -1 + 3 + 13-15 = 0
За пранье х 1 = — 1; Д = 1 + 15 = 16
Р 2 (х) = х 2 + 2х-15 = 0
х 2 = -1-4 = -5;
х 3 = -1 + 4 = 3;
Приказ: — 1; -5; 3
Редом раста: -5; -1; 3. (Л Н И)
2. Знать сав кориен торбе йе х 3 — 3х 2 + топор — 2а + 6, гдже йе вишак из овог пододжелка х-1 и х +2 пивн.
Одлука: Р = Р 3 (1) = Р 3 (-2)
Р 3 (1) = 1-3 + а-2а + 6 = 4-а
Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а
х 3 -3х 2 -6х + 12 + 6 = х 3 -3х 2 -6х + 18
х 2 (х-3) -6 (х-3) = 0
(х-3) (х 2 -6) = 0
3) а = 0, х 2 -0 * х 2 +0 = 0; х 2 = 0; х 4 = 0
а = 0; х = 0; х = 1
а > 0; х = 1; х = а ± √а
2. Словения
1 группа .
.. Корння: -4; -2; джедан; 7;
2 группа … Корння: -3; -2; джедан; 2;
3 группа … Корня: -1; 2; 6; 10;
4 группа … Корння: -3; 2; 2; 5;
5 группа … Корння: -5; -2; 2; 4;
6 группа … Корння: -8; -2; 6; 7.
Розвязання ривнян е хапаве тë третэ дхе тэ катерт. Historia e fazës së pare të fazës së tretë dhe të katërt
Zavdannya numri 1
ngritni nivelin e hapit të tretë pë formulën e cardanos:
x 3 -3x 2 -3x -1 = 0.
Vendimi: Mbi të gjitha, për këndvështrimin, por jo pë hakmarrou тэ памбиккйурурве. Пэр нй человек тэ шпейтэ мне формулу
х = у -, позволими и эфикаситетит нэ х 2.
Мамо: х = у + 1.
(у + 1) 3 -3 (у + 1) 2 -3 ( y + 1) -1 = 0.
Pasi kemi hapur harqet dhe kemi shartuar nënndarjet, mund të bëjmë:
Për rrënjën e ekuivalentit kub y 3 + py + q = 0 є Formula e Cardanos:
yi = (i = 1,2,3,), vend dhjetor per radikalin
, = .
Лэ тэ а1 — нджэ / бэ-яке / влера е радикалит α. Këto janë dy nga kuptimet e gradës sulmuese:
α 2 = α 1 ε 1, α 3 = α 1 ε 2, de ε 1 = + i, ε 2 = — i është rrënja e hapit të tretë nga një.
Nëse në zonën β 1 = -, atëherë mund të dallojmë mo β 2 = β 1 ε 2, β 3 = β 1 ε 10005
y 1 = α 1 + β 1,
y 2 = -1/2 (α 1 + β 1) + i (α 1 -β 1),
y 3 = -1/2 (α 1 + β 1) — i (α 1 -β 1),
Нë импульс p = -6, q = — 6.
α= =
Një nga vlerat e radikalit është e barabartë. Kjo është akomodimi α1 =. Todi β 1 = — = — =,
y 2 =) — i).
Пергжигья еште, не е димэ влерэн е х па формуле х = у + 1.
х 2 =) + и) + 1,
х 3 =) — и) + 1.
Завд04а0003 №2
virishiti me metodën ferrari të hapit të katërt:
x 4 -4×3 + 2×2-4x + 1 = 0.
Vendimi: Transferimi I Treeeve të Mbetura në anou ehe hi -në në në në në në në në në në në në në në në në në në në në në nou , mundësisht në sheshin kryesor.
x 4 -4x 3 = -2x 2 + 4x-1,
x 4 -4x 3 + 4x 2 = 4x 2 -2x 2 + 4x-1,
(x 2 -2x) 2 = 2x 2 + 4х-1.
Prezantuar në një mënyrë të re, në një gradë tëtilë:
(x 2 -2x +) 2 = 2x 2 + 4x-1 + (x 2 -2x) y +,
(х 2 -2х +) 2 = (2 + у) х 2 + (4-2у) х + () / 1 /.
Подберемо у со, щоб и тë дрейтат е ндэшкимит катроре.
Mahmo: B 2 -4AC = 16-16y + 4y 2 -y 3 -2y 2 + 4y + 8 = 0
Abo y 3 -2y 2 + 12y-24 = 0. një nga rrënjët є y = 2. Влера y = 2/1 /,
Otrimaєmo (x 2 -2x + 1) 2 = 4x 2. Sinjalet (x 2 -2x + 1) 2 — (2x) 2 = 0 ose (х 2 -2х + 1-2х) (х 2 -2х + 1 + 2х) = 0.
Ка ды ривняняс каторе:
х 2 -4х + 1 = 0 дхе х 2 + 1 = 0.
Виришучи їх, не е димэ ррэнджэн е каллирит рывняння:
х 1 = 2-, х 2 = 2+, х 3 = -I , х 4 = я.
Zavdannya numri 1
Njihni më mirë rrënjën e bagatolenës
f (x) = 8x 5 -14x 4 -77x 3 + 128×2 + 45x-18.
Vendimi : Për të ditur më me efikasitet rrënja e thesit mprehet nga teoremat e reja.
Teorema 1. Si një drejtues jo i shkurtër, f (x) është i rrënjosur me shumë funksione, atëherë është emri i një anëtari të vlefshëmeme eshtou emri’tritrite finerithy eritrite fine
Код: Teorema 1 po duhet një mendje në mënyrë që të jetë një racional numër . Bulo nga rrënja e një polinomi, një mendje e kuqe dhe një mungesë, tobto. Nga teorema 1, ne mund të shohim se për një fraksion tëtilë, e cila nuk është një rrënjë është e mjaftueshme.
Teorema 2: Si Një Dib Jo I Shkurtër є nga rrënja e polinomit f (x) me një numër koeficeshsh, atëherë për çdo m të tërë, nou varësi të llojit, numri f (m) zgrë nerinon zgjjj д.м.т. числа и плоте.
Zokrema, vvazhayuchi m = 1, dhe nganjëherë m = -1, mund të themi:
nëse rrënja e polinomit nuk është e barabartë me ± 1, atëherë f (x) (p-q) dhe f (-x):. (p + q), пра. — нумеровать и плоте.
Шиним: Teorema 2 jep një arsye më shumë të nevojshme për rrënjën racionale të Problemit.
Qia umova është një ekip miqësor, kështu që është e lehtë ta ndryshosh atë në praktikë. Ne e dimë gamën e f (1) dhe f (-1), dhe më pas për fraksionin e lëkurës, përpara se të përpiqem të provoj, do tanryshoj mendjen. Нэсе деширони ндже нга нумрат нэ тиесэ, атехер ррнджа э шантэс нук еште.
Vendimi: Sipas Teoremës 1, Rrënja e TheSit Të Dhënë mprehet nou numrin e thyesave të shkurtuara nou mes, Numrat e të Cylave Janing x) , atëherë p është një me një nga numrat: ± 1, ± 2, ± 3, ± 6, ± 9, ± 18; q numrat një deri në një z
± 1, ± 2, ± 4, ± 8.
Vrahoyuchi karrierës знак равно , знак равно , emëruesit e thyesave janë pak a shumë pozitivë.
Gjithashtu, rrënjët racionale të këtij polinomi mund të jenë numra rritës: ± 1, ± 2, ± 3, ± 6, ± 9, ± 18, ±, ±, ±, ±, ±, ±, ±, ±, ±, ±.
Konkurroni për të tjerët që ju nevojiten.
Осколки f (1) = 72, f (-1) = 120, yjet e kremit, scho 1 и -1 є rrënjët f (x). Тани, пэр скин джуниор, фраксиони мунд тэ риконвертохет мне теоремат 2 пэр м = 1 и м = -1, нэ мэнйрэ кэ тэ джетэ е мундур тэ вендосет, кофтэ ме анэ тэ нджэ numri thiesor: = іj =
Результ tabelë, del literi «c» dhe «d» do të thotë saktësisht, cilim abo ne shkrepim є numrin abo
Nga tabelat e otrimano shihet se nuk ka më vipad, nëse njëri është një nga numrat: 2, -2, 3, -3,.
Си ндже трэшэгими е теоремаве тэ Безу, нумри и рренджэв а ф(х) и тоді, нсэ ф(х)(х-α). Otzhe, për të ndryshuar zgjidhjen e nëntë numrave të plotë, mund të përdorni skemën e Horner-it për ta kthyer atë në dy terma.
2 — ррендже.
Звидси маємо: х = 2 — ррэнджэ е тъештэ ф (х). Рренджа э шантес се дхенэ нксиррет нга рранджет э шантеш.
F 1 (х) = 8х4 + 2х3-73х2-18х + 9.
Në mënyrë të ngjashme, është e mundur të ndryshohen numrat.
2 — джо ррэндже, 3 — ррэндже, -3 — ррэндже, 9 — йо ррэндже, ½ — йо ррэндже, -1/2 — ррэндже, 3/2 — йо ррэндже, ¼ — ррэндже.
Përsëri, polinomi f (x) = 8x 5 -14x 4 -77x 3 + 128x 2 + 45x-18 është pesë rrënjë racionale: (2, 3, -3, -1/2, ¼).
Hapat ekuivalent
Bashkëmoshatari I Leonardo da Vinçit, Profesor Scipion del Ferro nga Bolonja (Dhoma 1526), герцог U Caktuar Gjithhy Jetën fëmijehehehë jehehry hehhyrehry hehhtyrehry hehhthhyrehry hehhthyrehrahehry hehhtyrehrahehrahehhonhehhyrhehrahehrahehhyrehrahehhyrehrahehhyhhonhehhyhhyhehhyhehhyhehhyhehhyhehhyhehhyh , Булат Джан Мадхешторе.
Ata na treguan një gjë, matematikanët e rinj të Evropës së mesme kaluan epoka, ata shkuan në algjebrën galusa, në kuptimin e plotë të aparateve dhe simboleve. Regiomontan ка mësuar të kuptojë numrat duke futur radikale dhe operacione prej tyre. Kjo bëri të Mundur Shtrimin e Problemit të klasës relativisht më të gjerë të rivnyanëve midis radikalëve. Në radhë të parë në vetë rajonin u arritën sukseset e para — u tregua në radikalët e fazave të 3-të dhe të 4-të.
Legjenda, e thurur nga simpatitë e udhëzimeve, lexohet shkëlqyeshëm në literaturë. Здебильный фитон такой. Profesor në Universitetin e Bolonjës Scipion del Ferro viviv формула për kuptimin e rrënjës положительная характеристика x 3 + px = q (p > 0, q > 0). Duke fituar në taunnitsa, duke i shpëtuar ata kundër kundërshtarëve të tire në mosmarrëveshjet shkencore, përpara se të vdisnin, pasi kishin par kushëririn e tyre në taunnitsa, shkelësin anibalu della nave dhe mëresuan.
Në kallirin e vitit 1535 ka një takim shkencor midis Fiores dhe Николо Тарталья (1500-1557).
Ostanniy buv është një shkencëtar я Taltuar, një shtrigë нга vendlindja е tij, я cili ка шуме пункт për të jetuar në historinë e matematikës dhe mekanikës në vendet e historisë personale. Герцог е ditur себе Fiore Володя по përdorte формула e Ferros dhe po bënte që kundërshtari i tij të shihte ritet kubane, Tartalya zmadhoi përsëri për të rifutur формулу.
Në debat, Fiore propozon ushqimin Tartal kilka, i cili do të kërkojë një zhvillim më të qartë të nivelit të hapit të tretë. Але Tartaglia tashmë dinte si t’i bashkonte ryvnianë tëtilë dhe per më tepër, nuk ishte i privuar nga një nga ata vipadku mëkëmbës, siç është buloja e Ferros, por dy nga vipadtjerikhet e. Tartaglia ka pranuar wiklik dhe proponuvav në Fiore me përpjekjen e saj. Rezultati i zvogëlimit të plumbit është një prerje e re e pjesës tjetër. Tartalya i është propozuar virishiv yomu prodannya që shtrihet për dy vjet, në atë kohë Fiore nuk e humbi virishiti zhodnogo zavdannya propozuar në yomu (nga të dyja anët kishte 30 ndërtesa).
Незабаром Тарталья сміг вирішувати рівняння на мене х 3 = px + q (p ›0, q ›0). Нарешти він повідомів, менджен е карриерівння x 3 + q = px т ндертохет дери не памьен е перпарме, але па у дхэне руге за тунгритур. Tartaglia nuk e publikoi rezultatin e saj. Ka dy arsye per këtë: në Pershe, vetë arsyeja, e cila zupiny і Ferro. Në një mënyrë tjetër, pakënaqësia është të pushosh kundër vipadit të urryer. Останный поляна на улице, Карьерный рівняння x 3 = пикселей + q yaki mund të jetë një rrënjë положительный. Sidoqoftë, formula e Tartaglia nuk i dha zgjidhje kësaj çështjeje, nëse do të ishte e nevojshme të shiheshin rrënjët e numrave negativë, atëherë nuk ishte e mundur të interpretoheshin saktë numrat e dukshëm, por të dilnin në një kohë. Vipadok i urryer u shfaq në Tartal dhe në pamje të qartë x 3 + q = px.
Megjithatë, i riu nuk u zhduk për një kohë të gjatë. Меня 1539 куб ровнянний заматися Кардано (1501-1576).
Pasi ndjeva mesazhin e Tartaglias, по raportoj një bagato zusil dhe po shkoj në gjallërinë e një njeriu të fshehtë dhe të padyshimtë për botimin e librit të tij «Mister i madh, por rregullat e algjebrës». Vetëm nëse Cardano do të betohej mbi ungjillorin dhe do t’i jepte fjalën e tij nderit të fisnikut, por ai nuk e shihte mënyrën e Tartaglias për ta konvertuar familjen dhe për ta shkruar atëqet nëqet nëqet nëqet nëqet nëqet nëqet nëqet nëqet nëqy; Фитони герцог трегуар rregullat për zhvillimin e ryvnyanëve kub, Viklavshi në krye, dhe është e mjegullt per të përfunduar.
Мегжитатэ, Кардано нук еште ветэм и нджешем ндадж rregullave, пор эдхе пер та провуар атэ пер та. E parëndësishme për obitsyanka-në e dhënë, vin botoi metodën e Tartalit dhe të gjithë mënyrën e shikimit të «rregullave të Cardan». Dhe libri u shfaq në 1545 duke u tronditur.
Було и путь открыто ришення ровнян и хапит тэ 4-тэ. Matematikani итальянский Д. Колла propozoi njohurinë себе дери нë atë orë ai sundonte në mënyrë joadekuate dhe në radhë të parë sundohej нга rregulla bikuadratike.
Shumica e matematikanëve respektuan çmimin e të qenit të pakuptueshëm. Але Кардано пропозой шкенкэтарин е тий Луиджи Феррари, я кили ештэ вирджэреша е фабрики дхе ди тэ беджэ хапин е катерт взгал, кэ тэ сон нэ хапин е трэт.
Сукшесет е тилла тэ мэдха нэ формула е нджохура пэр жвиллимин е этапаве тэ 3-тэ дхе тэ 4-тэ пэрбенин ндже проблема пэр математиканэт нэ жвиллимин е лидхджеве мидис нивелеве. Një numër я madh sondash, Zusillas nga shumica e dishepujve nuk sollën sukses. Në shaka isin rreth 300 ракет. Личе не шекуллин XIX Авель (1802-1829) довился, т. е. хапа н › 4, взял меня на дукет, радикалет нук футен нэ телаше.
rrugës për nou portë teori e huaj priftërinjtë algebrikë dhe monyrat e vargjeve qëndronin më shumë se dy hapa: palosshmëria, mungesa e zbutjes sou formure thourathere. Perche u bë thelbi я jotalentit praktik. Yogo Cardano mësoi, proponyuchi e di rrënja e familjes është afërsisht përtej rregullit të dy dispozitave të hirshme, të cilat, meqë ra fjala, janë ngecur në ditët tona linear në pamjen e interpojelimit të.
Нджэ перешкода тджэтэр эште мэ шумэ се ндже ррнджэ, дхе паси провои кэтэ подолання ата соллен трэшэгими эдхе мэ тэ рэндэсишме.
E këndshme dhe e guximshme për t’u përshtatur me kohën jo të besueshme për t’u miqësuar me matematikanin dhe inxhinierin итальянский R. Bombella nga Bolonja. Në krijimin e «Algjebrës» (1572 г.), ekzistojnë zyrtarisht rregulla për veprim mbi numrat explicit dhe komplexs.
Фрагмент Тексти Цей є месони ндже. Паси тë кэни штыпур бутонин «Шкарко архив», до тэ штони скедарин кэ ю невожит па косстовно.
Përpara se të shkarkoni këtë skedar, merrni me mend për ato abstrakte të mira, teste, kurse, robotë Digram, statistika dhe dokumente tjera, të cilat nuk kërkohen nga kompjuteri juaj. Tse prifti juaj, vëllezërit janë fajtorë për fatin e zhvillimit të pezullimit që sjell sharje për njerëzit. Njihni robotet dhe dërgojini në bazën e njohurive.
Të gjithë studentët, pasuniversitarët, të rinjtë, të cilet janë baza mëkëmbëse e njohurive në të ardhurit dhe robotet e tyre, ne do të jemi gjithashtu me ju.
Për të riregjistruar archivat me dokumentin, futni një numër pesëshifror në fushë, numri është më i ulët dhe klikoni në butonin «Aktivizon arkivat»
Мой документ
Një përshkrim i jetës së italianes dhe drita e asaj ore, nëse do të ishte gjallë, Duke Krijuar Girolamo Cardano. Shkenca е matematikanëve, герцог parë тë mbrojturit и шины matematikor dhe pozicionet е bashkimit të ekuivalentëve kub midis radikalëve. Mënyrat për të zhvilluar nivelin e hapave të tretë dhe të katërt.
робот курси, штэса 26.08.2011
Historia e zhvillimit të matematikës në Evropë shekujt VI-XIV, її përfaqësues të asaj arritje. Жвиллими и математика добы Видродження. Жвиллими и нумрит летрар, вепримтариа и Франсуа Вінта. Удосконалення numërimi për sembull XVI — në kalli shekulli XVI.
prezantim, donacione 20.09.2015
Математикани европейская доби Видродження. Пуна е llogaritjes се shkronjave Франсуа Вит дхе метод е llogaritjes се rivnyanëve.
Llogaritja adekuate për sembull XVI — në veshin e shekullit XVII: dhjetëra fraksione, logaritme. Prezantimi я lidhjes Së trigonometrisë dhe algjebrës.
prezantim, donacione 20.09.2015
Nga historia e dhjetëra prejatyre fraksioneve ekstravagante. Diy mbi dhjetëra fraksione. Dodavannya (vidnimannya) dhjetra thiesa… Riprodhimi i dhjetëra thiesave. Розподил дхьетера фраксионе.
реферат, штэса 29.05.2006
Математика Греческая философия її. Ndërlidhja e rrugës së ndyrë të filozofisë dhe matematikës nga veshi i epokës së ringjalljes deri në fund të shekullit të 17-të. Философия dhe matematika në epokën e arsimit. Analiza e natyrës Së njohurive matematikore Të filozofisë klasike.
диплом робота, штэса 07.09.2009
Ривняння не фраксионе тэ нумрит тэ шенджаве тэ шкруара нга коми; Rëndësia praktike e teorisë së dhjetëra tyesave. Vetëvendosja e robotit me një gamë të gjerë rezultatesh, llogaritje.
презантим, штуар 02.
07.2010
Fitorja e Matematikës dhe e Metodave Matematikore Kina e lashtë… Veçoritë e ndërtesave të kinezëve bazohen në zgjidhjet numerike të rivnyanëve dhe në strukturat gjeometrike, të cilat mund të ngrihen në nivelin e fazës së tretë. Pamje электронной matematikës се Кинес се lashtë.
ИСТОРИЯ HAPI I TRETË DHE I KATËRT
Кинет XV — вещи и шекуллит XVI. Periudha Boolean e zhvillimit të vrullshëm në historinë e matematikës dhe veçanërisht të algjebrës. Bulo njihet në dhomën e pasme të katit katror, si dhe shumë lidhje private në shkallën e tretë dhe të katërt. Është bërë një manifestim i shëmtuar i kryerjes së turneve në krye të skenës. Në fillim të shekullit të 16-të në Bolonja, profesori i matematikës Scipio del Ferro gjeti zgjidhjen e rivnya kubike sulmuese: 9-r2.
Dihet se r = ± A [P + P.
z3 + az2 + bx + c = 0,
Zëvendësimi i x = g — çmimi i linjës është ngritur në sy: 3
x3 + px = q = 0.
Ферро виришив шукати развязки этого ривняння вигляд х = А + В,
де а = 3 — 2 + р, = 3 — 2 — р.
Подставляючи цей вираз не ривняння (1), отправляем:
1 + r + 3A2B + 3AB2 r + p (A + B) + I = 0.
Scipio del Ferro (1465 — 1526 fq.) — математический итальянский
метод и шкэпутджес сэ ндже лине кубике джо идентике
Në foto ka ngjala — matematikanë të shekullit të 16-të (миниатюра e periudhës së mesme)
Нет градэ тэ тилле, виходне івняння має развязок x = A + B, de:
* = Гр? ■ в = ■ ®
Ferro ia ka transmetuar sekretin e virgjërisë (1) shkencëtarit të tij Mario Fiore. Rri, corystyuyuchit cym sekret, duke u bërë fitues në një nga turnetë matematikore. Shumë turne nuk morën pjesë në turnetë fitimtare të Nikkolo Tartaglia. Me siguri, pas Tartaliyu dhe Mario Fiore kishte një vakt. Tartalya njohu fjalët e matematikanit autoritar Pich-choli, se ai ishte një sturdzhuvav, por është e pakëndshme për radikalet ta bëjnë këtë, sepse është faji për mbingarkimin e tij. Megjithatë, dy ditë para kallirit, mund të mësohet se si Ferro e njeh zgjidhjen e një ryvnyannya kub dhe ia kalon sekretin e tij Maryo Fiores.
Герцог адоптуар фьяле пер фьяле зусилла титанике, файэсони пер диса дитэ пара хапджес се ктесес герцог хекур згджидхен туадж куб рывняння (1). 12 и ашпер 1535 р. Памье Турнир. Кожен pjesëmarrës proponuvav kundërshtarin e tij 30 zavdan. Ai qou e kishte bërë, ishte fajtor qou mundi të vinte të vizitonte shokun e atij shokut për një shkelje të pastër dhe për mou tepër, numri i miqve të nemuerea uresha uresha uresha uresha uresha re. Tartaglia për dy vjet është bërë një sukses. Yogo armiku është zhodnoi. Historia e shkencës për të shpjeguar çmimin në një mënyrë tëtilë. Ровняня:
х3 + 3 х — 4 = 0.
Tse rivnannya maє rrënjë e vetme e të folurit x = 1. Todi sipas формула Ferro mi otrimaєmo:
х = 3/2 + / 5 + -1 / 5.
Viraz, i cili qëndron i vetem në shenjë padurimi, është fajtor per zyrtaret e lartë. Rrëshqitni për të nënkuptuar që Tartaglia shikonte pa fjalë vetëm një rivnyannya të tilë kub, si boulat A dhe B.
Me Formulën Tartaglia, ne kujtuam vidomitë e mësimeve të Gerolamo Cardano.
Tartalia të jep vendimin tënd per mendjen, në mënyrë që Cardano të mund të publikohet pa ndihmën e botimit të Tartalia. Cardano në agimin e tij të tartalit. Фитони закавив випад, несёт в себе джан нумра комплекс. Ровняня: 92 +111
Ambasadori i Cardanos, Rafael Bombelli, ishte i zoti në këtë, si itilë viraziv për të korrigjuar zgjidhjen e grand kubaneze. Fitues, karrieres nga kubiku i dhënë është i barabartë A = 2 +1, B = 2-1. Тоди х = А + В = 4,
Никколо Фонтана
Tartaglia (1499 — 1557 fq.) — математический итальянский
тобто. сделать të jetë rrënja e rівняння (3). Вважается, шо Cardano mund të otrimav zgjidhje të tilë të дейки кубичных привняний.
Një duzinë orë më vonë, pasi hodhi poshtë формула e Tartaglia Cardano, u mor vendimi i Ferros. Вена був здивания вечным збигом ришен Тартал дхе Ферро. Diçka që Cardano di për zgjidhjen e Ferros, për disa arsye, ai botoi Formulan e Tartaglia në librin e tij «Misteri i madh», dhe me të drejtë, Duke vleresuar autorësinë e Tartaglia dhe Ferro.
Duke ditur për publikimin e librit të Cardanos, Tartaglia buv bërtet vdekjeprurëse. Унэ, ндошта, джо пер асгдже. Për të lundruar формула aktuale (2) më spesh quhet формула Cardano. Tartaglia wiklikav Cardano në një lojë matematikore, por ende e pa parë. Për të zëvendësuar një wiklik të ri duke pranuar studimin e Cardano, Ferrari, i cili nuk është i privuar nga zhvillimi i rivnannya kubike, por hapi i katërt. Në emërtimet e përditshme, lidhja e hapit të katërt është një viglyad itilë:
Нехай маємо рівняня z4 + pzi + qz2 + sz + r = 0.
Zrobimo zëvendësojë m = x + p. Тоди рівняння набуде вигляд x4 + ax2 + bx + c = 0. Презантони ндже ндрышим штесэ т дхе згжидхэ шукатімімі вигляді:
Джероламо Кардано (1501 — 1576 fq.) — математик, инженер, философ, мьек дхе астролог итальянский
Lodovico (Luiji) Ferrari (1522 — 1565 rr.) -Matematican Italian, i cili njeh styllën kurrizore të fazës së fazës së katërt
x2 + ti = 2tx2 — bx + 1 t2 + në + c 92T0x+-b
Në një renditje tëtilë, zgjidhja e hapit të katërt me metodën e Ferrarit ishte zhvillimi i dy katrorëve të barabartë (6) dhe kub të barabartë (5).
Чифти Тарталья — Феррари отбился 10 серпня 1548 фший. нэ Милано. Ne shikuam nivelin e hapit të tretë dhe të katërt. Чудитеришт, але Тарталья килка ештэ энде е вэртэтэ (нэ Феррари, мелодиозишт, и гитхэ нгакмуэси эштэ крижуар пэр жвиллимин е римаве кубике нга комплекси А, Бэштэ пэр жвиллимин е фазет сэрт). Феррари еште виришивілистіф нга пропонуар нэ фабрики йом. Si rezultat i mendjemadhësisë së Tartaglias për humbjen lypëse.
Praktikisht, staza e zgjidhjeve të fituara nuk është shumë e madhe. Ме методу нумерике, нивели и шактесише аррихет ме шактеси тэ мадхе. Megjithatë, формула dhanë një contribut të madh në zhvillimin e algjebrës dhe zokremit, në zhvillimin e metodave të zhvillimit të hapave më të lartë. Për të përfunduar historinë, se fillimi i croc në Vir_shenna Rivnyans u thye dhe u privua në shekullin e nëntëmbëdhjetë. Абели, герцог кендруар дери нэ нивелин е хапит тэ н-тэ нэ н> 5, эште нэ випадку, нук эште е лехте тэ вареш нэ радикалет. Zokrema, pasi ka treguar se e barabartë x5 + x4 + x3 + x2 + x +1 = 0 mund të lidhet në radikale, dhe më thjesht, për herë të parë, e barabartë x5 + 2x = 2 = 0 në radikale nuk është e лидхур.
Galois mori ushqim për zhvillimin e radikalëve. Як прапаникэ ривняння, завжуваний нэ радикалет, ю мунд тэ вендосни тэ нджэйтэн ривняння:
Gjithka u bë e mundur permes shfaqjes së një teorie të re, dhe vetë teorisë së grupeve.
Список и письмо
1. Виленкин Н.Я. Прапа анаш тэ траджтуесит тэ математика / Н.Я. Виленкин, Л.П. Шибасов, Е.Ф. Шибасова. — М.: Эдукими: АТ «Навчальная литература», 1996. — 320 л.
2. Гиндикин, С.Г. Распознай физику и математику / С.Г. Гиндикин. — Лоджи и дыте. — М: Наука, 1985. — 182 л.
ЛФХШ му и р ис думок
Shkenca është më pak se e dobishme, nëse pranohet jo me zemër, por me zemër.
Д. И. Мендель
vsesvit nuk mund të ndertohet deri nou nivelin e inteligjences njerëzore, ale mou vonë ështe e mundur të zgjerohet dhe zhvillohet inteligjenca njerëzore, nea munyrety yeshrite yeshrite yeshrite yeshrite yeshrite vishrite vishrite yrishrite vishrite vishrite.
Фрэнсис Бэкон
Шэним.
Нет статистики и иллюстраций Виктории Нга Факья http://lesequations.net
Циклет:
- Систематизувати кë uzagalniti znannya që vminnya në temën: Rozvyazannya rivnyan e fazës së tretë dhe të katërt.
- Вритни нджохуритэ, паси кэни визитуар ндже сере ндэртешаш, ндже пьесе тэ атире кэ нук нджихен ас нга ллоджи, ас нга мэнйра се си шихен.
- Формими я интересуюсь математикой пермес zhvillimit të degëve të reja të matematikës, zhvillimit të kulturës grafike permes induksionit të arteve grafike.
Льоджи и Месимит : комбинация.
Поседьми: проектор ларт.
Vërtet: Шини табелен «Теорема и Вийтас».
Шкони не месим
1. Усный рахунок
а) Pse teprica në shpërndarjen e polinomit p n (x) = a n x n + a n-1 x n-1 + … + a 1 x 1 + a 0 në x-a diadik?
b) Sa rrënjë mund të gjeni rrënjë kubike?
c) Çfarë qëndron pas ndihmës së kujt fshihet Rituali i Hapit të tretë dhe të katërt?
г) Якшо б гай нумрин нэ нэ мэнырэ катроре, атэхэрэ чфарэ эштэ дера Д и х 1; х 2
2.
Робот и ветеринар (не группа)
Зона е ривняння, си нë штепинэ е ррэнджес (нга бурими нэ фабрике ештэ и кодуар)
1 группа
Рренджа: x1 = 1; х 2 = -2; х 3 = -3; х 4 = 6
Ровняня:
Б = 1-2-3 + 6 = 2; б = -2
ч = -2-3 +6 + 6-12-18 = -23; с = -23
д = 6-12 + 36-18 = 12; д = -12
е = 1 (-2) (- 3) 6 = 36
х 4 — 2 х 3 — 23х 2 — 12 х + 36 = 0
Вендими … Mesi i ditës është numri 36.
р = ± 1; ± 2; ± 3; ± 4; ± 6 …
p 4 (1) = 1-2-23-12 + 36 = 0 Pas skemës së Hornerit
р 3 (х) = х 3 -х 2 -24х -36
р 3 (-2) = -8 -4 +48 -36 = 0, х 2 = -2
р 2 (х) = х 2 -3х -18 = 0
х 3 = -3, х 4 = 6
Лоджи: 1; -2; -3; 6 rrënjë shuma 2 (P)
2 группа
Рренджа: x1 = -1; х 2 = х 3 = 2; х 4 = 5
Ровняня:
В = -1 + 2 + 2 + 5-8; б = -8
с = 2 (-1) + 4 + 10-2-5 + 10 = 15; ч = 15
Д = -4-10 + 20-10 = -4; д = 4
е = 2 (-1) 2 * 5 = -20; е = -20
8 + 15 + 4x-20 = 0
р = ± 1; ± 2; ± 4; ± 5; ± 10; ± 20,
р 4 (1) = 1-8 +15 + 4-20 = -8
р 4 (-1) = 1 +8 + 15-4-20 = 0
р 3 (х) = х 3 -9х 2 + 24х -20
р 3 (2) = 8 -36 +48 -20 = 0
р 2 (х) = х 2 -7 х +10 = 0 х 1 = 2; х 2 = 5
Память: -1; 2; 2; 5 ррендже сума 8 (R)
3 группа
Рренджа: x1 = -1; х 2 = 1; х 3 = -2; х 4 = 3
Ровняня:
В = -1 + 1-2 + 3 = 1; В = -1
с = -1 + 2-3-2 + 3-6 = -7; с = -7
Д = 2 + 6-3-6 = -1; д = 1
е = -1 * 1 * (- 2) * 3 = 6
х 4 — х 3 — 7х 2 + х + 6 = 0 (Це рівняння вішу потим пір групін дощи 4)
Вендими.
Земра э земрэс сэ дитэс эштэ 6.
р = ± 1; ± 2; ± 3; ± 6
р 4 (1) = 1 -1 -7 +1 +6 = 0
р 3 (х) = х 3 — 7х -6
р 3 (-1) = -1 + 7-6 = 0
р 2 (х) = х 2 -х -6 = 0; х 1 = -2; х 2 = 3
Лоджи: -1; 1; -2; 3 rrënjë сума 1 (O)
4 группа
Рренджа: x1 = -2; х 2 = -2; х 3 = -3; х 4 = -3
Ровняня:
В = -2-2-3 + 3 = -4; б = 4
с = 4 + 6-6 + 6-6-9 = -5; с = -5
Д = -12 + 12 + 18 + 18 = 36; д = -36
е = -2 * (- 2) * (- 3) * 3 = -36; е = -36
х 4 + 4х 3 — 5х 2 — 36х -36 = 0 (Це ривняння виришу потом 5 груп не дощи)
Вендими. Цили корння шукаємо нэ мес тэ дитэвэ нэ нумрин -36
р = ± 1; ± 2; ± 3 …
р (1) = 1 + 4-5-36-36 = -72
р 4 (-2) = 16 -32 -20 + 72 -36 = 0
р 3 (х) = х 3 + 2х 2 -9х-18 = 0
р 3 (-2) = -8 + 8 + 18-18 = 0
р 2 (х) = х 2 -9 = 0; х = ± 3
Память: -2; -2; -3; 3 Сума Коренев-4 (Ф)
5 группа
Рренджа: x1 = -1; х 2 = -2; х 3 = -3; х 4 = -4
г.
Ровняня
х 4 + 10 х 3 + 35 х 2 + 50 х + 24 = 0 (Це ривняння виришує потом 6груп не дошці)
Вендими … Меси и дитёс еште 24.
р = ± 1; ± 2; ± 3
р 4 (-1) = 1 -10 + 35 -50 + 24 = 0
р 3 (х) = х-3 + 9х 2 + 26х + 24 = 0
р 3 (-2) = -8 + 36-52 + 24 = О
р 2 (х) = х 2 + 7х + 12 = 0
Лоджи: -1; -2; -3; -4 шума-10(И)
6 группа
Рренджа: x1 = 1; х 2 = 1; х 3 = -3; х 4 = 8
г. Ровняня
В = 1 + 1-3 + 8 = 7; б = -7
ч = 1-3 + 8-3 + 8-24 = -13
Д = -3-24 + 8-24 = -43; д = 43
x 4 — 7x 3 — 13×2 + 43 x — 24 = 0 (Це ровняння вирішу потом 1 группа не дитё)
Вендими … Меси и дитёс ёштэ -24.
р 4 (1) = 1-7-13 + 43-24 = 0
р 3 (1) = 1-6-19 +24 = 0
р 2 (х) = х 2 -5х — 24 = 0
х 3 = -3, х 4 = 8
Память: 1; 1; -3; 8 шума 7 (л)
Параметры 3.
Вишення ивнян и
1. Развязать ровняня х 3 + 3х 2 + мх — 15 = 0; си ндже нга рренджет е дерес (-1)
Ju lutemi shkruani sipas rendit të rritjes
Р = Р 3 (-1) = — 1 + 3-м-15 = 0
х 3 + 3 х 2 -13 х — 15 = 0; -1 + 3 + 13-15 = 0
Длина x 1 = — 1; Д = 1 + 15 = 16
Р 2 (х) = х 2 + 2х-15 = 0
х 2 = -1-4 = -5;
х 3 = -1 + 4 = 3;
Память: — 1; -5; 3
Сипас рендит тэ рритжес: -5; -1; 3. (Л Н И)
2. Пëр тë дитур тэ гджитхэ ррэнджэн э тесит ештэ х 3 — 3х 2 + сепатэ — 2а + 6, ку теприка нга кй нэнсексион ештэ х-1 дхэ х +2 пивні.
Зджидхье: R = P 3 (1) = P 3 (-2)
Р 3 (1) = 1-3 + а-2а + 6 = 4-а
Р 3 (-2) = -8-12-2а-2а + 6 = -14-4а
х 3 -3х 2 -6х + 12 + 6 = х 3 -3х 2 -6х + 18
х 2 (х-3) -6 (х-3) = 0
(х-3) (х 2 -6) = 0
3) а = 0, х 2 -0 * х 2 +0 = 0; х 2 = 0; х 4 = 0
а = 0; х = 0; х = 1
а > 0; х = 1; х = а ± √а
2.