Ряд тейлора котангенс: c++ — Разложение котангенса в ряд Тейлора и вычисление его приближенного значения

2f_{yy}(a,b)\right\}+\cdots$
где $f_x(a,b), f_y(a,b),\cdots$ означают частные производные по $x, y,\cdots$ взятые в точках $x=a, y=b$.

13. Разложение в ряд Тейлора

С помощью меню.

13.1. Выделить в выражении переменную, по которой производится разложение в ряд.

13.2. Выбрать пункт меню Символика/Переменная/Расширение в числовых последовательностях.

13.3. В появившемся диалоговом окне ввести порядок приближения.

С помощью ключевого слова series.

13.4. Ввести выражение и ключевое слово series панели Символы.

13.5. В появившиеся местозаполнители ввести имя переменной и порядок приближения.

Пример.

14. Получение численного значения выражения (действительного или комплексного)

Действительное значение выражения вычисляется с помощью меню Символика/Оценивание

/Плавающая точка или ключевого слова float панели Символы. Для вычисления необходимо задать точность вывода в окне диалога после выбора пункта меню или в местозаполнителе после ключевого слова float.

Комплексное значение выражения в виде вычисляется с помощью меню Символика/Оценивание/Комплексный или ключевого слова complex панели Символы.

Примеры.

100! float,20→ 9.332621544394415268210¹⁵⁷

e²ⁱ(4+3i) complex→ 4cos(2) – 3sin(2) + i(3cos(2) + 4sin(2))

Кроме того, с помощью пунктов меню Символика/Трансформация или панели Символика можно производить прямые и обратные интегральные преобразования Фурье, Лапласа и Z-преобразование.

Задание по работе

Выполните символьные вычисления в каждом задании в соответствии со своим вариантом

двумя способами: с помощью меню и ключевых слов. Работу оформите по аналогии с лабораторной работой №1. Сохраните результаты выполнения работы в своей папке на диске.

Задание 1. Упростите выражение.

Варианты задания 1:

1.

2.

3.

4.

5.

6.

Задание 2. Расширьте выражение.

Варианты задания 2:

1. sin(x) – 2sin(2x) + 4sin(3x) 4. ctg(2x) – sin(x)· cos(3

x)

2. cos(2x) – sin(2x) + sin(3x) 5. cos(2x) · sin(x) · sin(3x)

3. tg(2x) + ctg(2x) +cos(2x) 6. tg(2x) · sin(2x) – sin(3x)

Задание 3. Разложите на множители.

Варианты задания 3:

1. 2x⁴ + x³ – 20x² –13x + 30

2. x⁴ + x³ – 19x² +11x + 30

3. x⁴ –12

x³ – 3x² +178x – 264

4. 3x⁴ + 8x³ – 33x² –62x + 24

5. 3x⁴ –7 x³ – 13x² +23x – 6

6. 6x⁴ –11 x³ – 30x² +29x – 6

Задание 4. Приведите подобные слагаемые полинома. Определите коэффициенты полинома.

Варианты задания 4:

1. (2x²+1)( 12 x³ – 5x+3) +3x – 1

2. (3x+1)( 2 x⁴ – 4x+7) +3

x – 5

3. (x² –1)( x³ – 3x²+3) +3x² + 6

4. 5x – 1 – (x² –1)( x³ – 5x²+1)

5. 2x² + 5 – (x –1)( 2x⁴ – 3x+6)

6.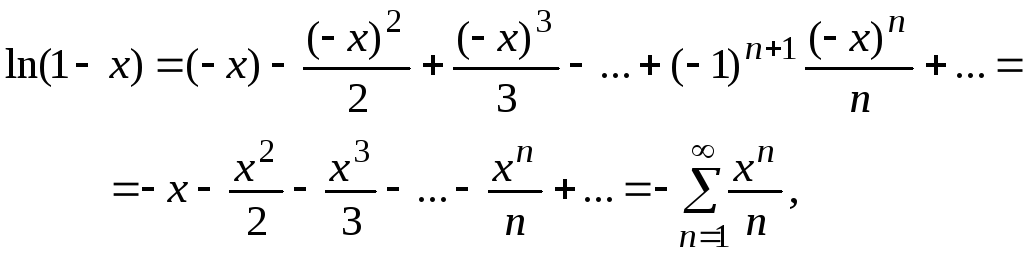 3x² – 4 + (x² –x)( 5x³ – 2x²+ 1)

Задание 5. Разложите на простые дроби.

Варианты задания 5:

1.

2.

3.

4.

5.

6.

Задание 6. Решите уравнение, упростите сложные результаты.

Варианты задания 6:

1.

2.

3.

4.

5.

6.

Задание 7. Произведите символьные вычисления, упростите сложные результаты.

Варианты задания 7:

1.

2.

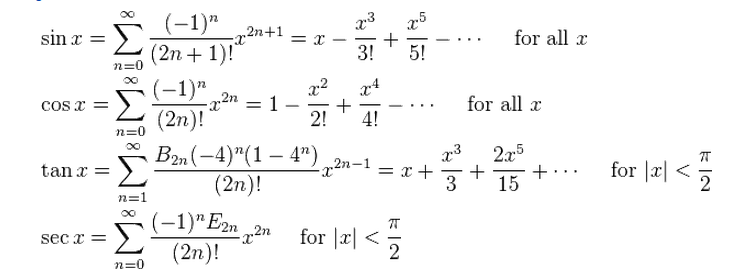
3.

4.

5 .

6.

Задание 8. Разложите выражение в ряд до 8 порядка.

Варианты задания 8:

1. 4. tg(x)

2. sin(x) 5. ln(1+x)

3. cos(x) 6.

комплексный анализ — ряд Лорана для $\cot(z)$

спросил 6 лет, 2 месяца назад

Изменено 3 года, 9 месяцев назад

Просмотрено 23 тысячи раз

$\begingroup$

Я ищу разъяснения о том, как вычислить ряд Лорана для

$\cot z$

Я начал с попытки найти $\frac{1}{\sin z}$. Я нашел несколько ссылок, которые ведут от разложения Тейлора для $\sin z$ непосредственно к выражению для $\frac{1}{\sin z}$, но я не могу понять, как они туда попали. Эта тема Вычислить ряд Лорана для $1/\sin(z)$ начала отвечать на мой вопрос, но я не понимаю, как использовать данные формулы для «итеративного вычисления» коэффициентов, а в приведенном примере есть несколько коэффициентов, и я Я не знаю, как они были получены. 9{2 n-1}$$

$\endgroup$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

комплексный анализ — ряд Лорана котангенса

спросил 7 лет, 6 месяцев назад

Изменено 7 лет, 6 месяцев назад

Просмотрено 1к раз

$\begingroup$

Вычислить главную часть ряда Лорана $\cot(\pi z)$ на $1<|z|<2$. 92}\тег{2} $$ или же: $$ \cot(\pi z)=\frac{1}{\pi z}+\frac{2}{\pi}\sum_{n\geq 1}\left(\frac{1}{z-n}+ \frac{1}{z+n}\right).\tag{3}$$ Вы можете закончить оттуда?

$\endgroup$

1

$\begingroup$

Другой подход: в $\{|z|<2\}$ $\cot \pi z$ имеет только три особенности, а именно простые полюса в точках $0,1,-1.