Самые сложные уравнения: Математики решили самую сложную задачу в мире

Содержание

Более сложные примеры уравнений | Математика

52. Более сложные примеры уравнений.
Пример 1.

5/(x – 1) – 3/(x + 1) = 15/(x² – 1)

Общий знаменатель есть x² – 1, так как x² – 1 = (x + 1)(x – 1). Умножим обе части этого уравнения на x² – 1. Получим:

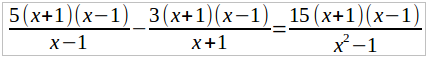
или, после сокращения,

5(x + 1) – 3(x – 1) = 15

или

5x + 5 – 3x + 3 = 15

или

2x = 7 и x = 3½

Рассмотрим еще уравнение:

5/(x-1) – 3/(x+1) = 4(x² – 1)

Решая, как выше, получим:

5(x + 1) – 3(x – 1) = 4
5x + 5 – 3x – 3 = 4 или 2x = 2 и x = 1.

Посмотрим, оправдываются ли наши равенства, если заменить в каждом из рассмотренных уравнений x найденным числом.

Для первого примера получим:

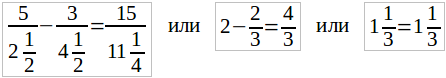
Видим, что здесь нет места никаким сомнениям: мы нашли такое число для x, что требуемое равенство оправдалось.

Для второго примера получим:

5/(1-1) – 3/2 = 15/(1-1) или 5/0 – 3/2 = 15/0

Здесь возникают сомнения: мы встречаемся здесь с делением на нуль, которое невозможно. Если в будущем нам удастся придать определенный, хотя бы и косвенный, смысл этому делению, то тогда мы можем согласиться с тем, что найденное решение x – 1 удовлетворяет нашему уравнению. До этой же поры мы должны признать, что наше уравнение вовсе не имеет решения, имеющего прямой смысл.

Подобные случаи могут иметь место тогда, когда неизвестное входит как-либо в знаменатели дробей, имеющихся в уравнении, причем некоторые из этих знаменателей, при найденном решении, обращаются в нуль.

Пример 2.

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

Можно сразу видеть, что данное уравнение имеет форму пропорции: отношение числа x + 3 к числу x – 1 равно отношению числа 2x + 3 к числу 2x – 2. Пусть кто-либо, в виду такого обстоятельства, решит применить сюда для освобождения уравнения от дробей основное свойство пропорции (произведение крайних членов равно произведению средних). Тогда он получит:

(x + 3) (2x – 2) = (2x + 3) (x – 1)

или

2x² + 6x – 2x – 6 = 2x² + 3x – 2x – 3.

Здесь может возбудить опасения, что мы не справимся с этим уравнением, то обстоятельство, что в уравнение входят члены с x². Однако, мы можем от обеих частей уравнения вычесть по 2x² — от этого уравнение не нарушится; тогда члены с x² уничтожатся, и мы получим:

6x – 2x – 6 = 3x – 2x – 3

Перенесем неизвестные члены влево, известные вправо — получим:

3x = 3 или x = 1

Вспоминая данное уравнение

(x + 3)/(x – 1) = (2x + 3)/(2x – 2)

мы сейчас же подметим, что найденное значение для x (x = 1) обращает в нуль знаменателей каждой дроби; от такого решения мы, пока не рассмотрели вопроса о делении на нуль, должны отказаться.

Если мы подметим еще, что применение свойства пропорции усложнило дело и что можно было бы получить более простое уравнение, умножая обе части данного на общий знаменатель, а именно на 2(x – 1) — ведь 2x – 2 = 2 (x – 1), то получим:

2(x + 3) = 2x – 3 или 2x + 6 = 2x – 3 или 6 = –3,

что невозможно.

Это обстоятельство указывает, что данное уравнение не имеет таких, имеющих прямой смысл решений, которые не обращали бы знаменателей данного уравнения в нуль.
Решим теперь уравнение:

(3x + 5)/(x – 1) = (2x + 18)/(2x – 2)

Умножим обе части уравнения 2(x – 1), т. е. на общий знаменатель, получим:

6x + 10 = 2x + 18

или

4x = 8 и x = 2

Найденное решение не обращает в нуль знаменатель и имеет прямой смысл:

или 11 = 11

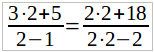
Если бы кто-либо, вместо умножения обеих частей на 2(x – 1), воспользовался бы свойством пропорции, то получил бы:

(3x + 5)(2x – 2) = (2x + 18)(x – 1) или
6x² + 4x – 10 = 2x² + 16x – 18.

Здесь уже члены с x² не уничтожались бы. Перенеся все неизвестные члены в левую часть, а известные в правую, получили бы

4x² – 12x = –8

или

x² – 3x = –2

Это уравнение мы теперь решить не сумеем. В дальнейшем мы научимся решать такие уравнения и найдем для него два решения: 1) можно взять x = 2 и 2) можно взять x = 1. Легко проверить оба решения:

1) 2² – 3 · 2 = –2 и 2) 1² – 3 · 1 = –2

Если мы вспомним начальное уравнение

(3x + 5) / (x – 1) = (2x + 18) / (2x – 2),

то увидим, что теперь мы получим оба его решения: 1) x = 2 есть то решение, которое имеет прямой смысл и не обращает знаменателя в нуль, 2) x = 1 есть то решение, которое обращает знаменателя в нуль и не имеет прямого смысла.

Пример 3.

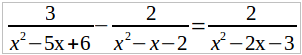
Найдем общего знаменателя дробей, входящих в это уравнение, для чего разложим на множители каждого из знаменателей:

1) x² – 5x + 6 = x² – 3x – 2x + 6 = x(x – 3) – 2(x – 3) = (x – 3)(x – 2),

2) x² – x – 2 = x² – 2x + x – 2 = x (x – 2) + (x – 2) = (x – 2)(x + 1),

3) x² – 2x – 3 = x² – 3x + x – 3 = x (x – 3) + (x – 3) = (x – 3) (x + 1).

Общий знаменатель равен (x – 3)(x – 2)(x + 1).

Умножим обе части данного уравнения (а его мы теперь можем переписать в виде:

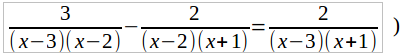
на общего знаменателя (x – 3) (x – 2) (x + 1). Тогда, после сокращения каждой дроби получим:

3(x + 1) – 2(x – 3) = 2(x – 2) или
3x + 3 – 2x + 6 = 2x – 4.

Отсюда получим:

–x = –13 и x = 13.

Это решение имеет прямой смысл: оно не обращает в нуль ни одного из знаменателей.

Если бы мы взяли уравнение:

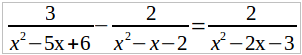
то, поступая совершенно так же, как выше, получили бы

3(x + 1) – 2(x – 3) = x – 2

или

3x + 3 – 2x + 6 = x – 2

или

3x – 2x – x = –3 – 6 – 2,

откуда получили бы

0 = –11,

что невозможно. Это обстоятельство показывает, что нельзя найти для последнего уравнения решения, имеющего прямой смысл.

Сложные системы уравнений

2015-03-26 | Автор: Анна

Я решила сделать отдельную запись с решениями таких систем. Здесь часто помогает замена, однако догадаться, какая замена оптимальна, не всегда легко. В записи рассмотрены системы как с радикалами, так и с логарифмами, поэтому не забываем про область допустимых значений.Тем не менее, как будет видно из одного из примеров, полученные корни необходимо проверять подстановкой в исходную систему, так как даже удовлетворяя ОДЗ, корни могут оказаться посторонними.

Пример 1. Решить систему уравнений.

$delim{lbrace}{matrix{3}{1}{{x^2-xy+y^2=21} {y^2-2xy+15=0} {} }}{ }$

Показать

Пример 2. Решить систему уравнений.

Показать

Пример 3. Решить систему уравнений.

$delim{lbrace}{matrix{2}{1}{{y^4+19=20(x+y)} {sqrt{x}+sqrt{2y+x}=sqrt{2}} }}{ }$

Показать

Пример 4. Решить систему уравнений.

$delim{lbrace}{matrix{2}{1}{{x^{2log_x y}=4x+3} {log_x y^2=log_y (xy)} }}{ }$

Показать

Пример 5. Решить систему уравнений.

$delim{lbrace}{matrix{2}{1}{{(log_{3/2} (x+y))^2+(log_{3/2} (x-y))^2-(log_{3/2} (2x))^2=1} {log_{2/3} (x+y)*log_{2/3} (x-y)-log_{2/3} (2x)=0} }}{ }$

Показать

Задачи тысячелетия. Просто о сложном / Хабр

Привет, хабралюди!

Сегодня я бы хотел затронуть такую тему как «задачи тысячелетия», которые вот уже десятки, а некоторые и сотни лет волнуют лучшие умы нашей планеты.

После доказательства гипотезы (теперь уже теоремы) Пуанкаре Григорием Перельманом, основным вопросом, который заинтересовал многих, был: «А что же он собственно доказал, объясните на пальцах?» Пользуясь возможностью, попробую объяснить на пальцах и остальные задачи тысячелетия, или по крайней мере подойти в ним с другой более близкой к реальности стороны.

Равенство классов P и NP

Все мы помним из школы квадратные уравнения, которые решаются через дискриминант. Решение этой задачи относится к классу P (Polynomial time) — для нее существует быстрый (здесь и далее под словом «быстрый» подразумевается как выполняющийся за полиномиальное время) алгоритм решения, который и заучивается.

Также существуют NP-задачи (Non-deterministic Polynomial time), найденное решение которых можно быстро проверить по определенному алгоритму. Для примера проверка методом перебора компьютером. Если вернуться к решению квадратного уравнения, то мы увидим, что в данном примере существующий алгоритм решения проверяется так же легко и быстро как и решается. Из этого напрашивается логичный вывод, что данная задача относится как к одному классу так и ко второму.

Таких задач много, но основным вопросом является, все или не все задачи которые можно легко и быстро проверить можно также легко и быстро решить? Сейчас для некоторых задач не найдено быстрого алгоритма решения, и неизвестно существует ли такой вообще.

На просторах интернета также встретил такую интересную и прозрачную формулировку:

Допустим, что вы, находясь в большой компании, хотите убедиться, что там же находится ваш знакомый. Если вам скажут, что он сидит в углу, то достаточно будет доли секунды, чтобы, бросив взгляд, убедиться в истинности информации. В отсутствие этой информации вы будете вынуждены обойти всю комнату, рассматривая гостей.

В данном случае вопрос стоит все тот же, есть ли такой алгоритм действий, благодаря которому даже не имея информации о том, где находится человек, найти его так же быстро, как будто зная где он находится.

Данная проблема имеет большое значение для самых различных областей знаний, но решить ее не могут уже более 40 лет.

Гипотеза Ходжа

В реальности существуют множество как простых так и куда более сложных геометрических объектов. Очевидно, что чем сложнее объект тем более трудоемким становится его изучение. Сейчас учеными придуман и вовсю применяется подход, основная идея которого заключается в том, чтобы вместо самого изучаемого объекта использовать простые «кирпичики» с уже известными свойствами, которые склеиваются между собой и образуют его подобие, да-да, знакомый всем с детства конструктор. Зная свойства «кирпичиков», становится возможным подступиться и к свойствам самого объекта.

Гипотеза Ходжа в данном случае связана с некоторыми свойствами как «кирпичиков» так и объектов.

Гипотеза Римана

Всем нам еще со школы известны простые числа которые делятся только на себя и на единицу (2,3,5,7,11…). С давних времен люди пытаются найти закономерность в их размещении, но удача до сих пор так никому и не улыбнулась. В результате ученые применили свои усилия к функции распределения простых чисел, которая показывает количество простых чисел меньше или равных определенного числа. Например для 4 — 2 простых числа, для 10 — уже 4 числа. Гипотеза Римана как раз устанавливает свойства данной функции распределения.

Многие утверждения о вычислительной сложности некоторых целочисленных алгоритмов, доказаны в предположении верности этой гипотезы.

Теория Янга — Миллса

Уравнения квантовой физики описывают мир элементарных частиц. Физики Янг и Миллс, обнаружив связь между геометрией и физикой элементарных частиц, написали свои уравнения, объединяющие теории электромагнитного, слабого и сильного взаимодействий. Одно время теория Янга-Миллса рассматривалась лишь как математический изыск, не имеющий отношения к реальности. Однако, позже теория начала получать экспериментальные подтверждения, но в общем виде она все еще остается не решенной.

На основе теории Янга-Миллса построена стандартная модель физики элементарных частиц в рамках которой был предсказан и не так давно обнаружен нашумевший бозон Хиггса.

Существование и гладкость решений уравнений Навье — Стокса

Течение жидкостей, воздушные потоки, турбулентность. Эти, а также множество других явлений описываются уравнениями, известными как уравнения Навье — Стокса. Для некоторых частных случаев уже найдены решения, в которых как правило части уравнений отбрасываются как не влияющие на конечный результат, но в общем виде решения этих уравнений неизвестны, и при этом даже неизвестно, как их решать.

Гипотеза Бёрча — Свиннертон-Дайера

Для уравнения x² + y² = z² в свое время еще Эвклид дал полное описание решений, но для более сложных уравнений поиск решений становится чрезвычайно трудным, достаточно вспомнить историю доказательства знаменитой теоремы Ферма, чтобы убедиться в этом.

Данная гипотеза связана с описанием алгебраических уравнений 3 степени — так называемых эллиптических кривых и по сути является единственным относительно простым общим способом вычисления ранга, одного из важнейших свойств эллиптических кривых.

В доказательстве теоремы Ферма эллиптические кривые заняли одно из важнейших мест. А в криптографии они образуют целый раздел имени себя, и на них основаны некоторые российские стандарты цифровой подписи.

Гипотеза Пуанкаре

Думаю если не все, то большинство точно о ней слышали. Чаще всего встречается, в том числе и на центральных СМИ, такая расшифровка как «резиновую ленту натянутую на сферу можно плавно стянуть в точку, а натянутую на бублик — нельзя». На самом деле эта формулировка справедлива для гипотезы Тёрстона, которая обобщает гипотезу Пуанкаре, и которую в действительности и доказал Перельман.

Частный случай гипотезы Пуанкаре говорит нам о том, что любое трехмерное многообразие без края (вселенная, например) подобно трехмерной сфере. А общий случай переводит это утверждение на объекты любой мерности. Стоит заметить, что бублик, точно так же как вселенная подобна сфере, подобен обычной кофейной кружке.

Заключение

В настоящее время математика ассоциируется с учеными, имеющими странный вид и говорящие о не менее странных вещах. Многие говорят о ее оторванности от реального мира. Многие люди как младшего, так и вполне сознательного возраста говорят, что математика ненужная наука, что после школы/института, она нигде не пригодилась в жизни.

Но на самом деле это не так — математика создавалась как механизм с помощью которого можно описать наш мир, и в частности многие наблюдаемые вещи. Она повсюду, в каждом доме. Как сказал В.О. Ключевский: «Не цветы виноваты, что слепой их не видит».

Наш мир далеко не так прост, как кажется, и математика в соответствии с этим тоже усложняется, совершенствуется, предоставляя все более твердую почву для более глубокого понимания существующей реальности.

Задачи современной математики, которые до сих пор не решены

На протяжении веков лучшие умы человечества решали одну математическую задачу за другой, однако есть несколько, не поддавшихся до сих пор никому. За нахождение алгоритма их решения некоторые фонды и компании готовы заплатить большие деньги.

1 октября 2019 14:00

Гипотеза Коллатца

Другие названия: гипотеза 3n+1, сиракузская проблема, числа-градины. Если взять любое натуральное число n и совершить с ним следующие преобразования, рано или поздно всегда получится единица. Четное n нужно разделить надвое, а нечетное — умножить на 3 и прибавить единицу. Для числа 3 последовательность будет такой: 3×3+1=10, 10:2=5, 5×3+1=16, 16:2=8, 8:2=4, 4:2=2, 2:2=1. Очевидно, что если продолжить преобразование с единицы, то начнется цикл 1,4,2. Достаточно быстро количество шагов в вычислениях начинает превышать сто и на решение каждой новой последовательности требуется все больше ресурсов.

Небольшой прогресс в решении этой задачи почти вековой давности наметился буквально в прошлом месяце. Однако знаменитый американской математик Терренс Тао лишь ближе всех подошел к нему, но ответа все равно пока не нашел. Гипотеза Коллатца является фундаментом такой математической дисциплины, как «Динамические системы», которая, в свою очередь, важна для множества других прикладных наук, например, химии и биологии. Сиракузская проблема выглядит, как простой безобидный вопрос, но именно это делает ее особенной. Почему ее так сложно решить?

Проблема Гольдбаха (бинарная)

Еще одна задачка, формулировка которой выглядит проще пареной репы — любое четное число (больше 2) можно представить в виде суммы двух простых. И это краеугольный камень современной математики. Данное утверждение легко проверяется в уме для небольших значений: 18=13+5, 42=23+19. Причем рассматривая последнее, можно достаточно быстро понять всю глубину проблемы, ведь 42 представляется и как 37+5 и 11+31, а еще как 13+29 и 19+23. Для чисел больше тысячи количество пар слагаемых становится просто огромным. Это очень важно в криптографии, но даже самые мощные суперкомпьютеры не могут перебирать все значения до бесконечности, поэтому нужно какое-то четкое доказательство для всех натуральных чисел.

Проблема была сформулирована Кристианом Гольдбахом в его переписке с другим величайшим светилом математики Леонардом Эйлером в 1742 году. Сам Кристиан ставил вопрос несколько проще: «каждое нечетное число, больше 5, можно представить в виде суммы трех простых чисел». В 2013 году перуанский математик Харальд Хельфготт нашел окончательное решение этого варианта. Однако предложенное Эйлером следствие этого утверждения, которое и назвали «бинарной проблемой Гольдбаха», до сих пор не поддается никому.

Гипотеза о числах-близнецах

Близнецами называются такие простые числа, которые отличаются всего на 2. Например, 11 и 13, а также 5 и 3 или 599 и 601. Если бесконечность ряда простых чисел была доказана множество раз начиная с античности, то бесконечность чисел-близнецов находится под вопросом. Начиная с 2, среди простых чисел нет четных, а начиная с 3 — делящихся на три. Соответственно, если вычесть из ряда все, подходящие под «правила деления», то количество возможных близнецов становится все меньше. Единственный модуль для формулы нахождения таких чисел — 6, а формула выглядит следующим образом: 6n±1.

Как и всегда в математике, если проблема не решается «в лоб», к ней подходят с другого конца. Например, в 2013 году было доказано, что количество простых чисел, отличающихся на 70 миллионов, бесконечно. Тогда же, с разницей менее чем в месяц, значение разницы было улучшено до 59 470 640, а затем и вовсе на порядок — до 4 982 086. На данный момент существуют теоретические обоснования бесконечности пар простых чисел с разницей в 12 и 6, однако доказанной является лишь разность в 246. Как и прочие проблемы такого рода, гипотеза о числах-близнецах особенно важна для криптографии.

Гипотеза Римана

Если кратко, то Бернхард Риман предположил, что распределение простых чисел по множеству всех натуральных чисел не подчиняется каким-либо законам. Но их количество на заданном участке числового ряда коррелирует с распределением определенных значений на графике дзета-функции. Она расположена выше и для каждого s дает бесконечное количество слагаемых. Например, когда в качестве s подставляется 2, то в результате получается уже решенная «базельская задача» — ряд обратных квадратов (1 + ¼ + 1/9 + 1/16 + …).

Одна из «проблем тысячелетия», за решение которой назначен приз в миллион долларов, а также вхождение в пантеон «богов» современной математики. На деле, доказательство этой гипотезы настолько сильно толкнет вперед теорию чисел, что это событие по праву будет называться историческим. Многие вычисления и утверждения в математике строятся на предположении о том, что «гипотеза Римана» верна, и до сих пор никого не подводили. Немецкий математик сформулировал знаменитую задачу 160 лет назад, и с тех пор к ее решению подступались неисчислимое количество раз, однако прогресс очень скромен.

Гипотеза Берча и Суиннертон-Дайера

Еще одна «задача тысячелетия», за решение которой Институт Клэя одарит миллионом долларов. Не-математику достаточно трудно хотя бы в общих чертах сформулировать и понять, в чем же суть гипотезы. Берч и Свиннертон-Дайер предположили определенные свойства эллиптических кривых. Идея заключалась в том, что ранг кривой можно определить зная порядок нуля дзета-функции. Как говорится, ничего не понятно, но очень интересно.

Эллиптическими кривыми называются такие линии на графике, которые описываются, на первый взгляд, безобидными уравнениями вида y²=x³+ax+b. Некоторые их свойства чрезвычайно важны для алгебры и теории чисел, а решение данной задачи может серьезно продвинуть науку вперед. Наибольший прогресс был достигнут в 1977 году коллективом математиков из Англии и США, которые смогли найти доказательство гипотезы Берча и Суиннертон-Дайера для одного из частных случаев.

Проблема плотной упаковки равных сфер

Это даже не одна, а целая категория схожих проблем. Причем мы сталкиваемся с ними ежедневно, например, когда хотим разложить фрукты на полке в холодильнике или как можно плотнее расставить бутылки на полке. С математической точки зрения необходимо найти среднее количество контактов («поцелуев», также называется контактным числом) каждой сферы с остальными. На данный момент есть точные решения для размерностей 1−4 и 8.

Под размерностью или измерением понимается количество линий, вдоль которых размещаются шары. В реальной жизни больше третьей размерности не встречается, однако математика оперирует и гипотетическими значениями. Решение этой задачи может серьезно продвинуть не только теорию чисел и геометрию вперед, но также поможет в химии, информатике и физике.

Проблема развязывания

И снова каждый день встречающаяся проблема. Казалось бы, что сложного — узел развязать? Тем не менее, вычисление минимального времени, необходимого для этой задачи является еще одним краеугольным камнем математики. Трудность в том, что мы знаем, вычислить алгоритм развязывания можно, но его сложность может быть такой, что даже самый мощный суперкомпьютер будет считать слишком долго.

Первые шаги на пути решения этой задачи были сделаны в 2011 году американским математиком Грегом Купербергом. В его работе развязывание узла из 139 вершин было сокращено со 108 часов до 10 минут. Результат впечатляющий, но это лишь частный случай. На данный момент существует несколько десятков алгоритмов разной степени эффективности, однако ни один из них не является универсальным. Среди применений этой области математики — биология, в частности, процессы сворачивания белков.

Самый большой кардинал

Какая бесконечность самая большая? На первый взгляд бредовый вопрос, но так и есть — все бесконечности разные по размеру. А точнее, по мощности, ведь именно так различают множества чисел в математике. Под мощностью понимается общее количество элементов множества. Например, самая маленькая бесконечность — натуральные числа (1, 2, 3, …), потому что она включает в себя только целые положительные числа. Ответа на этот вопрос пока нет и математики постоянно находят все более мощные множества.

Мощность множества характеризуется его кардинальным числом или просто кардиналом. Существует целая онлайн-энциклопедия бесконечностей и примечательных «конечностей», названная в честь Георга Кантора. Этот немецкий математик первым обнаружил, что неисчислимые множества могут быть больше или меньше друг друга. Более того, он смог доказать разницу в мощностях различных бесконечностей.

Что не так с суммой числа π и e?

Является ли сумма этих двух иррациональных чисел алгебраическим числом? Мы оперируем этими константами сотни лет, но так и не узнали о них все. Алгебраическое число — корень многочлена с целыми коэффициентами. На первый взгляд кажется, что все вещественные числа алгебраичны, но нет, наоборот. Большинство чисел трансцендентны, то есть не являются алгебраическими. Более того, все вещественные трансцедентные числа иррациональны (например, π и e), но вот их сумма может быть любой.

Если от предыдущего абзаца у читателя не заболела голова, то вот продолжение загадки — а что с πe, π/e и π-e? Также неизвестно, а знать это наверняка довольно важно для теории чисел. Трансцедентность числа доказал в конце XIX века Фердинанд фон Линдеман вместе с невозможностью решения задачи квадратуры круга. С тех пор значимых подвижек в решении вопроса не было.

Является ли γ рациональной?

Вот еще одна проблема, которую очень легко написать, но трудно решить. Является ли постоянная Эйлера-Маскерони иррациональной или нет? Рациональные числа можно записать в виде p/q, где p и q — целые числа. Таким образом, 42 и -11/3 являются рациональными, а и √2 — нет. Формула выше позволяет вычислить постоянную, которая является пределом разности между частичной суммой гармонического ряда и натуральным логарифмом числа. За определение ее рациональности миллион долларов, конечно, не светит, зато вполне можно рассчитывать на кресло профессора в Оксфорде.

Значение γ было вычислено до нескольких тысяч знаков после запятой, первые четыре из которых — 0,5772. Она достаточно широко используется в математике, в том числе вместе с другим числом Эйлера — e. Согласно теории цепных дробей, если постоянная Эйлера-Маскерони является рациональной дробью, то ее знаменатель должен быть больше 10 в 242 080 степени.

Самая красивая теорема математики: тождество Эйлера / Хабр

Посмотрев лекцию профессора Робина Уилсона о тождестве Эйлера, я наконец смог понять, почему тождество Эйлера является самым красивым уравнением. Чтобы поделиться моим восхищением это темой и укрепить собственные знания, я изложу заметки, сделанные во время лекции. А здесь вы можете купить его прекрасную книгу.

Что может быть более загадочным, чем взаимодействие мнимых чисел с вещественными, в результате дающее ничто? Такой вопрос задал читатель журнала Physics World в 2004 году, чтобы подчеркнуть красоту уравнения Эйлера «e в степени i, умноженного на пи равно минус единице».

Рисунок 1.0: тождество Эйлера — e в степени i, умноженного на пи, плюс единица равно нулю.

Ещё раньше, в 1988 году, математик Дэвид Уэллс, писавший статьи для американского математического журнала The Mathematical Intelligencer, составил список из 24 теорем математики и провёл опрос, попросив читателей своей статьи выбрать самую красивую теорему. И после того, как с большим отрывом в нём выиграло уравнение Эйлера, оно получило званием «самого красивого уравнения в математике».

Рисунок 2.0: обложка журнала The Mathematical Intelligencer
Рисунок 3.0: опрос Дэвида Уэллса из журнала

Леонарда Эйлера называют самым продуктивным математиком за всю историю. Других выдающихся математиков вдохновляли его работы. Один из лучших физиков в мире, Ричард Фейнман, в своих знаменитых лекциях по физике назвал уравнение Эйлера «самой примечательной формулой в математике». Ещё один потрясающий математик, Майкл Атья, назвал эту формулу «…математическим аналогом фразы Гамлета — «быть или не быть» — очень короткой, очень сжатой, и в то же время очень глубокой».

Существует множество интересных фактов об уравнении Эйлера. Например, оно встречалось в некоторых эпизодах «Симпсонов».

Рисунок 4.0: в этой сцене уравнение Эйлера можно заметить на второй книге в самой правой стопке.
Рисунок 5.0: в этой сцене уравнение Эйлера написано на футболке второстепенного персонажа.

Также уравнение Эйлера стало ключевым пунктом в уголовном деле. В 2003 году аспирант Калифорнийского технологического института Билли Коттрелл писал краской на чужих спортивных автомобилях уравнение Эйлера. На суде он сказал: «Я знал теорему Эйлера с пяти лет, и её обязаны знать все«.

Рисунок 6.0: марка, выпущенная в 1983 году в Германии в память о двухсотлетии со смерти Эйлера.
Рисунок 7.0: марка, выпущенная Швейцарией в 1957 году в честь 250-й годовщины Эйлера.

Почему уравнение Эйлера так важно?

Вы имеете полное право задаться вопросом: почему Билли Коттрелл считал, что об уравнении Эйлера обязаны знать все? И был настолько в этом уверен, что начал писать его на чужих машинах? Ответ прост: Эйлер воспользовался тремя фундаментальными константами математики и применил математические операции умножения и возведения в степень, чтобы записать красивую формулу, дающую в результате ноль или минус один.

Константа e связана со степенными функциями.
Константа i является не вещественным, а мнимым числом, равным квадратному корню из минус единицы.
Знаменитая константа π (пи) связана с окружностями.

Впервые тождество Эйлера появилось в 1748 году в его книге Introductio in analysin infinitorum. Позже другие люди увидели, что эта формула связана с тригонометрическими функциями синуса и косинуса, и эта связь удивительна, ведь степенная функция стремится к бесконечности, а тригонометрические функции колеблются в интервале от — 1 до -1.

e в степени i, умноженного на ϕ (фи) = cos ϕ + i * sin ϕ

Рисунок 8.0: экспоненциальная функция y=e^x.
Рисунок 8.1: график тождества Эйлера.
Рисунок 8.2: частоты, испускаемые LC-цепью.

Показанные выше уравнения и графы могут показаться абстрактными, но они важны для квантовой физики и вычислений обработки изображений, и при этом зависят от тождества Эйлера.

1: число для счёта

Число 1 (единица) является основой нашей системы исчисления. С неё мы начинаем счёт. Но как мы считаем? Чтобы считать, мы используем цифры 0–9 и систему разрядов, определяющую значение цифры.

Например, число 323 означает 3 сотни, 2 десятка и 3 единицы. Здесь число 3 исполняет две разные роли, которые зависят от его расположения.

323 = (3*100) + (2*10) + (3*1)

Существует и другая система исчисления, называемая двоичной. В этой системе вместо 10 используется основание 2. Она широко применяется в компьютерах и программировании. Например, в двоичной системе:

1001 = (2³) + (0²) + (0¹) + (2⁰) = [9 в системе с основанием 10]

Кто создал системы исчисления? Как первые люди считали предметы или животных?

Как возникли наши системы исчисления? Как считали первые цивилизации? Мы точно знаем, что они не пользовались нашей разрядной системой. Например 4000 лет назад древние египтяне использовали систему исчисления с разными символами. Однако они комбинировали символы, создавая новый символ, обозначающий числа.

Рисунок 11: показанные здесь иероглифы образуют число 4622; это одно из чисел, вырезанных на стене в храме в Карнаке (Египет).
Рисунок 12: иероглифы — это изображения, обозначающие слова, а в данном случае — числа.

В то же время, но в другом месте ещё один социум обнаружил способ подсчёта, но в нём тоже использовались символы. Кроме того, основанием их системы исчисления было 60, а не 10. Мы используем их метод счёта для определения времени; поэтому в минуте 60 секунд, а в часе 60 минут.

Рисунок 13: вавилонские числа из шестидесятиричной системы счисления (с основанием 60).

Тысячу лет спустя древние римляне изобрели римские числа. Для обозначения чисел они использовали буквы. Римская нотация не считается разрядной системой, потому что для многих значений нашей системы счисления в ней использовались разные буквы. Именно по этой причине для счёта они использовали абакус.

Рисунок 14: романский абакус в шестнадцатеричной (с основанием 16) системе счисления
Рисунок 15: таблица преобразования из арабских в римские числа

Древние греки тоже не использовали разрядную систему счисления. Греческие математики обозначали числа буквами. У них были специальные буквы для чисел от 100 до 900. Многие люди в то время считали греческие числа запутанными.

Рисунок 15: таблица букв древних греков.

В то же самое время китайские математики начали использовать для расчётов небольшие бамбуковые палочки. Этот китайский способ счёта называют первой десятичной разрядной системой.

Рисунок 16: китайский способ счёта с числами-палочками. Использовался как минимум с 400 года до нашей эры. Квадратная счётная доска использовалась примерно до 1500 года, когда её заменил абакус.

Однако самая уникальная система счёта использовалась индейцами майя. Их система счисления имела основание 20. Для обозначения чисел от 1 до 19 они использовали точки и линии. Чем же отличалась их система счисления? Для каждого числа они использовали изображения голов и отдельный символ нуля 0.

Рисунок 17: Система счисления майя с основанием 20, в которой числа обозначались головами
Рисунок 18: ещё один способ записи чисел майя.

0: число для обозначения ничего

Некоторые цивилизации использовали пробелы, чтобы, например, отличать число 101 от 11. Спустя какое-то время начало появляться особое число — ноль. К примеру, в пещере в индийском городе Гвалиор археологи обнаружили на стене число 270, в котором был ноль. Самое первое зафиксированное использование нуля можно увидеть в Бодлианской библиотеке.
Рисунок 19: вырезанный на стене храма в Гвалиоре круг обозначает ноль. Ему примерно 1500 лет.
Рисунок 20: чёрные точки в манускрипте Бакхшали обозначают нули; это самый старый письменный пример использования числа, ему примерно 1800 лет.

Примерно 1400 лет назад были записаны правила вычислений с нулём. Например, при сложении отрицательного числа и нуля получается то же отрицательное число. Деление на нуль не допускается, потому что если разделить на ноль, то мы получим число, которое может быть равно любому нужному нам числу, что должно быть запрещено.

Вскоре после этого многими людьми были опубликованы книги по арифметике, распространяющие использование индо-арабской записи чисел. Ниже показана эволюция индо-арабских чисел. В большинстве стран используется индо-арабская система чисел, но арабские страны до сих пор пользуются арабскими числами.

Рисунок 21: на этой схеме показана эволюция чисел, происходящих от чисел брахми и заканчивающаяся числами, которыми мы используем и сегодня.
Рисунок 22: классическая гравюра «Арифметика» из Margarita Philosophica Грегора Рейша, на которой изображено соревнование между Боэцием, улыбающимся после открытия индо-арабских чисел и письменных вычислений, и нахмуренным Пифагором, до сих пор пытающимся пользоваться счётной доской.

Пи (π): самое известное иррациональное число

Пи — самое популярное из известных нам иррациональных чисел. Пи можно найти двумя способами: вычислив соотношение длины окружности к её диаметру, или соотношение площади круга к квадрату его радиуса. Евклид доказал, что эти соотношения постоянны для всех окружностей, даже для луны, пенни, шины и т.д.

π = окружность / диаметр ИЛИ π = площадь круга / радиус²

Рисунок 22: анимированная связь между окружностью и диаметром в отношении пи.

Так как иррациональные числа наподобие пи бесконечны и не имеют повторений, мы никогда не закончим записывать пи. Оно продолжается вечно. Есть люди, запомнившие множество десятичных разрядов пи (нынешний рекорд — 70 000 цифр! Источник: «Книга рекордов Гиннесса» ).

Рисунок 23: данные опроса 941 респондентов для определения процента людей, способных запомнить знаки пи после запятой.
Рисунок 24: На стене станции метро Karlsplatz в Вене записаны сотни разрядов пи.

На данный момент компьютеры смогли вычислить всего 2,7 триллиона разрядов пи. Может казаться, что это много, но на самом деле этот путь бесконечен.

Как я сказал выше, число пи нашёл Евклид. Но как поступали люди до Евклида, когда им нужно было найти площадь круга? Историки обнаружили вавилонскую глиняную табличку, в которой было записано отношение периметра шестиугольника к диаметру описанной вокруг него окружности. После вычислений полученное число оказалось равным 3.125. Это очень близко к пи.

Рисунок 24: вавилонская глиняная табличка с отношением периметра шестиугольника к длине описанной окружности.
Рисунок 25: Numberwarrior

Древние египтяне тоже близко подобрались к значению пи. Историки обнаружили документ, показывающий, как древние египтяне нашли число пи. Когда историки перевели документ, то нашли такую задачу:

Например, чтобы найти площадь поля диаметром 9 хета (1 хет = 52,35 метра), нужно выполнить следующее вычисление:
Вычесть 1/9 диаметра, а именно 1. Остаток равен 8. Умножить его на 8, что даёт нам 64. Следовательно, площадь будет равна 64 setjat (единица измерения площади).
Другими словами, диаметр равен 2r, а 1/9 радиуса равно (1/9 • 2r). Тогда если мы вычтем это из исходного диаметра, то получим 2r — (1/9 • 2r) = 8/9(2r). Тогда площадь круга равна 256/81 r². То есть пи равно почти 3,16. Они обнаружили это значение пи примерно 4000 лет назад.

Рисунок 26: математический папирус Ахмеса.

Однако греческие математики нашли для вычисления пи способ получше. Например, Архимед предпочитал работать с периметрами. Он начал рисовать окружности, описывающие многоугольники разного размера. Когда он чертил шестиугольник, то рисовал окружность с диаметром 1. Затем он видел что каждая сторона шестиугольника равна 1/2, а периметр шестиугольника равен 1/2 x 6 = 3. Затем он увеличивал количество сторон многоугольника, пока он не становился похожим на круг. Работая со 96-сторонним многоугольником и применив тот же способ, он получил 2 десятичных разряда пи после запятой: 3 и 10/71 = 3,14084. Спустя много лет китайский математик Лю Ху использовал 3072-сторонний многоугольник и получил число 3,14159 (5 верных десятичных разрядов числа пи после запятой). После этого ещё один китайский математик Цзу Чунчжи провёл ещё более впечатляющую работу. Он работал со 24000-сторонним многоугольником и получил 3,1415926 — семь верных десятичных разрядов пи после запятой.

Спустя тысячу лет немецкий математик Людольф Цейлен работал со 2⁶²-сторонним многоугольником и получил 35 десятичных разрядов пи. Это число, названное Людольфовым, было высечено на его могильном камне.

В 1706 году англичанин Джон Мэчин, долгое время работавший профессором астрономии, использовал формулу сложения, чтобы доказать, что пи равно
Не беспокоясь о том, как откуда взялась эта формула, Мэчин начал постоянно ею пользоваться, а затем записал показанный ниже ряд. Это был самый большой на то время шаг в количестве разрядов пи.
Рисунок 29: Формула Мэчина для пи

Однако первое упоминание пи появилось в 1706 году. Преподаватель математики Уильям Джонс написал книгу и впервые предложил пи для измерения окружностей. Так пи впервые появилась в книгах!

Рисунок 30: Juliabloggers

В 1873 году Уильям Шэнкс воспользовался формулой Джона Мэчина и получил 707 десятичных разрядов пи. Эти цифры написаны в комнате пи парижского Дворца открытий. Однако позже математики выяснили, что верными являются только 527 разрядов.

Рисунок 31: комната пи

С другой стороны, более интересный способ нахождения пи обнаружил Буффон. Его эксперимент основывался на случайном разбрасывании иголок для оценки пи. Он нарисовал на доске несколько параллельных линий на расстоянии D и взял иголки длиной L. Затем он случайным образом начал бросать иголки на доску и записывал долю иголок, пересекавших линию.

Рисунок 32.0: Science Friday

А после этого другой математик по имени Ладзарини подбросил иголку 3408 раз и получил шесть десятичных разрядов пи с соотношением 355/113. Однако если бы одна иголка не пересекла линию, он получил бы только 2 разряда пи.

Рисунок 32.1: бросание 1000 иголок для оценки приблизительного значения пи

e: история экспоненциального роста

e — это ещё одно знаменитое иррациональное число. Дробная часть e тоже бесконечна, как и у пи. Мы используем число e для вычисления степенного (экспоненциального) роста. Другими словами, мы используем e, когда видим очень быстрый рост или уменьшение.

Один из величайших, а возможно и лучший математик Леонард Эйлер открыл число e в 1736 году и впервые упомянул это особое число в своей книге Mechanica.

Рисунок 33: источник

Чтобы разобраться в экспоненциальном росте, мы можем использовать историю об изобретателе шахмат. Когда он придумал эту игру, то показал её властителю Севера. Царю понравилась игра и он пообещал, что отдаст автору любую награду. Тогда изобретатель попросил нечто очень простое: 2⁰ зерна на первую клетку шахматной доски, 2¹ зерна на вторую клетку доски, 2² зерна — на третью, и так далее. Каждый раз количество зерна удваивалось. Царь Севера подумал, что просьбу будет выполнить легко, но он ошибался, потому то на последнюю клетку нужно было бы положить 2⁶³ зёрен, что равно 9 223 372 036 854 775 808. Это и есть экспоненциальный рост. Он начался с 1, постоянно удваивался, и через 64 шага вырос в огромное число!

Если бы изобретатель шахмат выбрал линейное уравнение, например 2n, то получил бы 2, 4, 6, 8, … 128… Следовательно, в дальней перспективе экспоненциальный рост часто намного превышает полиномиальный.

Кстати, 9 223 372 036 854 775 808–1 — это максимальное значение 64-битного целого числа со знаком.

Рисунок 34: источник: Wikipedia

Число e открыл Эйлер. Однако Якоб Бернулли тоже работал с числом e, когда вычислял сложный процент, чтобы заработать больше денег. Если вложить 100 долларов под 10% дохода, то как будет расти эта сумма? Во-первых, это зависит от того, как часто банк рассчитывает проценты. Например, если он рассчитывает один раз, то мы получим в конце года 110 долларов. Если мы передумаем и будем брать проценты каждые 6 месяцев, то в этом случае мы получим больше 110 долларов. Дело в ттом, что процент, полученный за первые 6 месяцев, тоже получит свой процент. Общая сумма будет равна 110,25 долларов. Можно догадаться, что мы можем получить больше денег, если будем забирать деньги каждый квартал года. А если мы будем делать временной интервал всё короче, то окончательные суммы будут продолжать расти. Такой бесконечный сложный процент сделает нас богатыми! Однако наш общий доход стремится к ограниченному значению, связанному с e.

Бернулли не называл число 2,71828 именем e. Когда Эйлер работал с 2,71828, он возвёл экспоненциальную функцию e в степень x. Свои открытия он изложил в книге The Analysis of Infinite.

В 1798 году Томас Мальтус использовал экспоненциальную функцию в своём эссе, посвящённом пищевому дефициту будущего. Он создал линейный график, показывающий производство пищи и экспоненциальный график, показывающий население мира. Мальтус сделал вывод, что в дальней перспективе экспоненциальный рост победит, и мир ждёт серьёзный дефицит пищи. Это явление назвали «мальтузианской катастрофой». Ньютон тоже использовал эту модель, чтобы показать, как охлаждается чашка чая.

Рисунок 35: закон Ньютона-Рихмана
Рисунок 36: мальтузианская катастрофа

Мнимость числа: i, квадратный корень -1

Долгое время для решения своих задач математикам было достаточно обычных чисел. Однако в какой-то момент для дальнейшего развития им потребовалось открыть нечто новое и загадочное. Например, итальянский математик Кардано пытался разделить число 10 на 2 части, произведение которых было бы равно 40. Чтобы решить эту задачу, он записал уравнение: x (10-x) = 40. Когда он решил это квадратное уравнение, то получил два решения: 5 плюс √-15 и 5 минус √-15, что в то время не имело никакого смысла. Этот результат был бессмысленным, потому что по определению квадратного корня ему нужно было найти число, квадрат которого был бы отрицательным. Однако и положительное, и отрицательное числа в квадрате имеют положительное значение. Как бы то ни было, он нашёл своё уникальное число. Однако первым математиком, назвавшим √-1 (квадратный корень из минус единицы) мнимым числом i, был Эйлер.

Лейбниц дал такой комментарий о мнимом числе √-1:

Комплексные числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием.

Мы можем складывать, вычитать, умножать и делить мнимые числа. Сложение, вычитание и умножение просты, а деление немного сложнее. Вещественные и мнимые части складываются по отдельности. В случае умножения i² будет равно -1.

После Эйлера математик Каспар Вессель представил мнимые числа геометрически с создал комплексную плоскость. Сегодня мы представляем каждое комплексное число a + bi как точку с координатами (a,b).

Рисунки 37 и 38: комплексные числа

В викторианскую эпоху многие относились к мнимым числам с подозрением. Однако ирландский математик и астроном Уильям Роуэн Гамильтон покончил с этими сомнениями, определив комплексные числа применительно к кватернионам.

Самое красивое уравнение: тождество Эйлера

Тождество Эйлера связывает экспоненциальную функцию с функциями синуса и косинуса, значения которых колеблются от минус единицы до единицы. Чтобы найти связь с тригонометрическими функциями, мы можем представить их в виде бесконечного ряда, истинного для всех значений

Рисунок 39: открытие тождества Эйлера

Рисунок 40: тождество Эйлера

Эйлер никогда не записывал это тождество в явном виде, и мы не знаем, кто впервые записал его. Тем не менее, мы связываем его с именем Эйлера в знак почтения перед этим великим первопроходцем математики.

Формулы и уравнения, которые изменили мир

Математик Ян Стюарт (Ian Stewart) в своей новой книге «В поисках неизвестного: 17 уравнений, которые изменили мир» рассматривает несколько наиболее важных уравнений всех времен и приводит примеры их практического применения.

Теорема Пифагора

Согласно Теореме Пифагора в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Важность: Теорема Пифагора — важнейшее уравнение в геометрии, которое связывает ее с алгеброй и является основой тригонометрии. Без него было бы невозможно создать точную картографию и навигацию.

Современное использование: Триангуляция используется и по сей день, чтобы точно определить относительное расположение для GPS навигации.

Логарифм и его тождество

Логарифм — это степень, в которую надо возвести основание, чтобы получить аргумент.

Важность: Логарифмы стали настоящей революцией, позволив астрономам и инженерам делать расчеты более быстро и точно. С появлением компьютеров они не потеряли своего значения, поскольку все еще существенны для ученых.

Современное использование: Логарифмы важная составляющая для понимания радиоактивного распада.

Основная теорема анализа

Основная теорема анализа или формула Ньютона — Лейбница дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной.

Важность: Теорема анализа фактически создала современный мир. Исчисление имеет важное значение в нашем понимание того, как измерять тела, кривые и площади. Она является основой многих природных законов и источником дифференциальных уравнений.

Современное использование: Любая математическая проблема, где требуется оптимальное решение. Существенное значение для медицины, экономики и информатики.

Классическая теория тяготения Ньютона

Классическая теория тяготения Ньютона описывает гравитационное взаимодействие.

Важность: Теория позволяет рассчитать силу гравитации между двумя объектами. Хотя позднее она была вытеснена теорией относительности Эйнштейна, теория все равно необходима для практического описания того, как объекты взаимодействуют друг с другом. Мы используем ее и по сей день для проектирования орбит спутников и космических аппаратов.

Современное использование: Позволяет найти наиболее энергоэффективные пути для вывода спутников и космических зондов. Также делает возможным спутниковое телевидение.

Комплексные числа

Комплексное число

Комплексные числа — расширение поля вещественных чисел.

Важность: Многие современные технологии, в том числе цифровые фотокамеры, не могли быть изобретены без комплексных чисел. Кроме того, они позволяют проводить анализ, который нужен инженерам для решения практических задач в авиации.

Современное использование: Широко используется в электротехнике и сложных математических теориях.

Эйлерова характеристика полиэдров

Важность: Внесла вклад в понимание топологического пространства, в котором рассматриваются только свойства непрерывности. Необходимый инструмент для инженеров и биологов.

Современное использование: Топология используется, чтобы понять поведение и функции ДНК.

Нормальное распределение

Важность: Уравнение является основой современной статистики. Естественные и социальные науки не могли бы существовать в своей нынешней форме без него.

Современное использование: Используется в клинических испытаниях для определения эффективности лекарств по сравнению с отрицательными побочными эффектами.

Волновое уравнение

Дифференциальное уравнение, описывающее поведение волн.

Важность: Волны исследуются с целью определения времени и места землетрясений, а также для прогнозирования поведения океана.

Современное использование: Нефтяные компании используют взрывчатку, а затем считывают данные от последующих звуковых волн для определения геологических формаций.

Преобразование Фурье

Важность: Уравнение позволяет разбивать, очищать и анализировать сложные шаблоны.

Современное использование: Используется при сжатии информации изображений в формате JPEG, а так же для обнаружения структуры молекул.

Уравнения Навье—Стокса

В левой части уравнения — ускорение небольшого количества жидкости, в правой — силы, которые воздействуют на него.

Важность: Как только компьютеры стали достаточно мощными, чтобы решить это уравнение, они открыли сложную и очень полезную области физики. Она особенно полезна для создания более качественной аэродинамики у транспортных средств.

Современное использование: Среди прочего, уравнение помогло в усовершенствовании современных пассажирских самолетов.

Уравнения Максвелла

Описывают электромагнитное поле и его связь с электрическими зарядами и токами в вакууме и сплошных средах.

Важность: Помогли в понимании электромагнитных волн, что способствовало созданию многих технологий, которые мы используем сегодня.

Современное использование: Радар, телевидение и современные средства связи.

Второй закон термодинамики

Вся энергия и тепло со временем исчезнет.

Важность: Имеет существенное значение для нашего понимания энергии и Вселенной через понятие энтропии. Открытие закона помогло улучшить паровой двигатель.

Современное использование: Помог доказать, что материя состоит из атомов, физики до сих пор пользуются этим знанием.

Теория относительности Эйнштейна

Энергия равна массе, умноженной на квадрат скорости света.

Важность: Наверное, самое известное уравнение в истории. Оно полностью изменило нашу точку зрения на материю и реальность.

Современное использование: Помогло создать ядерное оружие. Используется в GPS навигации.

Уравнение Шрёдингера

Нелинейное уравнение Шрёдингера

Описывает материю как волну, а не как частицу.

Важность: Перевернула представления физиков — частицы могут существовать в диапазоне возможных состояний.

Современное использование: Существенный вклад в использование полупроводников и транзисторов, и, таким образом, в большинство современных компьютерных технологий.

Информационная энтропия Шаннона

Оценивает количество данных в куске кода путем расчета вероятности его символов.

Важность: Это уравнение, которое открыло дверь в Информационную Эпоху.

Современное использование: В значительной степени все, что связано с обнаружением ошибок в кодировании (программировании).

Логистическая модель роста популяций

Оценка изменений в популяции живых существ из поколения в поколение с ограниченными ресурсами.

Важность: Помогла в развитии теории хаоса, которая полностью изменила наше понимание того, как работают природные системы.

Современное использование: Используется для моделирования землетрясений и прогноза погоды.

Модель Блэка-Скоулза

Модель Блэка Скоулза

Одна из моделей ценообразования опционов.

Важность: Помогла создать несколько триллионов долларов. Согласно некоторым экспертам, неправильное использование формулы (и ее производных) способствовало финансовому кризису. В частности, уравнение имеет несколько предположений, которые не справедливы на реальных финансовых рынках.

Современное использование: Даже после кризиса используются для определения цен.

Вместо заключения

В мире существует множество других важных уравнений и формул, которые изменили судьбу человечества в целом и нашу личную жизнь в частности. Среди них, модель Ходжкина—Хаксли, Фильтр Калмана и, конечно, уравнение поисковой системы Google. Мы надеемся, что нам удалось показать насколько важна математика, и насколько бесценен ее вклад для всех людей.

Самые элегантные математические уравнения

Математические уравнения не только полезны – они также могут быть и красивы. И многие ученые признают, что они часто любят определенные формулы не только за их функциональность, но еще и за их форму, некую особую поэтичность. Есть те уравнения, которые известны на весь мир, как, например, E = mc^2. Другие не столь широко распространены, но красота уравнения не зависит от его популярности.

Общая теория относительности

Уравнение, описанное выше, было сформулировано Альбертом Эйнштейном в 1915 году как часть инновационной общей теории относительности. Теория на самом деле произвела революцию в мире науки. Это удивительно, как одним уравнением можно описать абсолютно все, что есть вокруг, в том числе пространство и время. Весь истинный гений Эйнштейна воплощен в нем. Это очень элегантное уравнение, которое кратко описывает, как все вокруг вас связано – например, как присутствие Солнца в галактике искривляет пространство и время так, чтобы Земля вращалась вокруг него.

Стандартная модель

Стандартная модель – это еще одна из важнейших теорий физики, в ней описываются все элементарные частицы, из которых состоит вселенная. Существуют различные уравнения, способные описать эту теорию, однако чаще всего пользуются уравнением Лагранжа, французского математика и астронома 18 века. Он успешно описал абсолютно все частицы и силы, которые на них воздействуют, за исключением гравитации. Это также включает недавно открытый бозон Хиггса. Оно в полной мере сочетается с квантовой механикой и общей теорией относительности.

Математический анализ

В то время как первые два уравнения описывают конкретные аспекты вселенной, данное уравнение может быть использовано во всех возможных ситуациях. Фундаментальная теорема математического анализа формирует основу математического метода, известного как исчисление, и связывает две свои основные идеи – концепцию интеграла и понятие производной. Зародился математический анализ еще в древности, однако все теории были собраны воедино Исааком Ньютоном в 17 веке – он использовал их для вычисления и описания движения планет вокруг Солнца.

Теорема Пифагора

Старым добрым известным всем уравнением выражается знаменитая теорема Пифагора, которую учат все школьники на уроках геометрии. Это формула описывает, что в любом прямоугольном треугольнике квадрат длины гипотенузы, самой длинной из всех сторон (c), равен сумме квадратов двух других сторон, катетов (a и b). В итоге, уравнение выглядит следующим образом: a^2 + b^2 = c^2. Эта теорема удивляет многих начинающих математиков и физиков, когда они только учатся в школе и еще не знают, что им готовит новый мир.

1 = 0.999999999….

Это простое уравнение указывает на то, что число 0.999 с бесконечным количеством девяток после запятой, на самом деле, равно единице. Это уравнение замечательно тем, что оно крайне простое, невероятно наглядное, но все же умудряется удивить и поразить многих. Некоторые люди не могут поверить в то, что это на самом деле так. Более того, красиво и само по себе уравнение – левая его часть представляет собой простейшую основу математики, а правая скрывает в себе тайны и загадки бесконечности.

Специальная теория относительности

Альберт Эйнштейн снова попадает в список, на этот раз со своей специальной теорией относительности, которая описывает, как время и пространство являются не абсолютными понятиями, а относительными – к скорости смотрящего. Это уравнение показывает, как время «расширяется», тем сильнее замедляясь, чем быстрее человек движется. На самом деле, уравнение не является таким уж сложным, простые производные, линейная алгебра. Однако то, что оно собой воплощает, представляет абсолютно новый способ смотреть на мир.

Уравнение Эйлера

Эта простая формула включает в себя основные знания о природе сфер. Она говорит о том, что если вы разрезаете сферу и получаете грани, ребра и вершины, то если F принять за число граней, E — за число ребер, а V – за число вершин, то вы всегда получите одно и то же: V — E + F = 2. Именно так и выглядит данное уравнение. Поражает то, что какую бы сферическую форму вы ни взяли – будь-то тетраэдр, пирамида или любая другая комбинация граней, ребер и вершин, у вас всегда получится одинаковый результат. Эта комбинаторика рассказывает людям нечто фундаментальное о сферических формах.

Уравнение Эйлера-Лагранжа и теорема Нетер

Эти понятия являются довольно абстрактными, но очень сильными. Самое интересное заключается в том, что данный новый способ мышления о физике смог пережить несколько революций в данной науке, таких как открытие квантовой механики, теории относительности и так далее. Здесь L означает уравнение Лагранжа, которое является мерой энергии в физической системе. А решение этого уравнения расскажет вам о том, как конкретная система будет развиваться с течением времени. Вариантом уравнения Лагранжа является теорема Нетер, которая является фундаментальной для физики и роли симметрии. Суть теоремы заключается в том, что если ваша система симметрична, то в ней действует соответствующий закон сохранения. Собственно говоря, главная идея этой теоремы заключается в том, что законы физики действуют повсеместно.

Уравнение ренормгруппы

Это уравнение также называется по имени его создателей, уравнением Каллана-Симанчика. Оно является жизненно важным базовым уравнением, написанным в 1970 году. Оно служит для того, чтобы продемонстрировать, как наивные ожидания рушатся в квантовом мире. Уравнение также имеет множество приложений, позволяющих оценить массу и размер протона и нейтрона, которые составляют ядро атома.

Уравнение минимальной поверхности

Данное уравнение невероятным образом вычисляет и кодирует те самые красивые мыльные пленки, которые образуются на проволоке, когда ее окунают в мыльную воду. Данное уравнение, однако, сильно отличается от привычных линейных уравнений из той же области, например, уравнения тепла, образования волн и так далее. Это уравнение – нелинейно, оно включает в себя воздействие сторонних сил и производных продуктов.

Прямая Эйлера

Возьмите любой треугольник, нарисуйте наименьший круг, который может включить в себя треугольник, и отыщите его центр. Найдите центр массы треугольника – ту точку, которая позволила бы треугольнику балансировать, например, на острие карандаша, если бы его можно было вырезать из бумаги. Нарисуйте три высоты этого треугольника (линии, которые были бы перпендикулярны тем сторонам треугольника, от которых они рисуются) и найдите точку их пересечения. Суть теоремы заключается в том, что все три точки будут находиться на одной прямой, именно это и есть прямая Эйлера. Теорема заключает в себе всю красоту и мощь математики, открывая удивительные закономерности в самых простых вещах.

Нашли нарушение? Пожаловаться на содержание

21 самый сложный вопрос по математике для ACT

Вы учились и теперь готовы к математическому разделу ACT (ууу!). Но готовы ли вы ответить на самые сложные математические вопросы, которые предлагает ACT? Вы хотите точно знать, почему эти вопросы так сложны и как их лучше всего решать? Если вы настроены на этот высший балл (или вам просто очень любопытно посмотреть, какие будут самые сложные вопросы), то это руководство для вас.

Мы собрали, по нашему мнению, 21 самый сложный вопрос, который ACT задавал учащимся за последние 10 лет, со стратегиями и ответами на каждый из вопросов.Все это настоящие вопросы по математике ACT, поэтому их понимание и изучение — один из лучших способов улучшить свой текущий результат ACT и выбить его из общего ряда в день экзамена.

Краткий обзор раздела ACT Math

Как и все тематические разделы ACT, математический раздел ACT представляет собой один законченный раздел, который вы будете изучать сразу. Это всегда будет второй раздел теста, и у вас будет 60 минут, чтобы ответить на 60 вопросов .

ACT размещает свои вопросы в порядке возрастания сложности . Как правило, вопросы 1-20 будут считаться «легкими», вопросы 21-40 будут считаться «средними», а вопросы 41-60 будут считаться «сложными».

Способ, которым ACT классифицирует «легкий» и «сложный», основан на том, сколько времени требуется среднему учащемуся, чтобы решить задачу, а также проценту студентов, которые ответили на вопрос правильно. Чем быстрее и точнее средний ученик решит задачу, тем «легче» это сделать. Чем больше времени уходит на решение проблемы и чем меньше людей ответят на нее правильно, тем «сложнее» проблема.

(Примечание: мы помещаем слова «легкий» и «сложный» в кавычки по какой-то причине — у всех есть свои сильные и слабые стороны в математике, поэтому не все сочтут «легкий» легким или «сложный» вопрос трудным. Эти категории усреднены для многих студентов по определенной причине, и не каждый студент вписывается в эту точную форму.)

С учетом всего сказанного, , за очень немногими исключениями, самые сложные математические задачи ACT будут сгруппированы в дальнем конце теста. Помимо того, что они попали в тест, эти вопросы имеют несколько общих черт. Мы рассмотрим примеры вопросов и способы их решения, а также то, что общего у этих типов вопросов, всего через мгновение

10 самых важных уравнений в истории

Уравнения — важный инструмент для описания того, сколько вещей в естественном мире функционируют и взаимодействуют. Но одни уравнения оказали более сильное влияние, чем другие.

Здесь мы представляем 10 таких уравнений, а также помогаем ответить на некоторые общие вопросы об уравнениях в сети.

СВЯЗАННЫЕ: 15 НАИБОЛЕЕ ВАЖНЫХ АЛГОРИТМОВ, ПОМОГЛИ ОПРЕДЕЛЕНИЯ МАТЕМАТИКИ, ВЫЧИСЛЕНИЙ И ФИЗИКИ

Какое уравнение является самым длинным в мире?

По данным Sciencealert, самое длинное математическое уравнение содержит около 200 терабайт текста.Эта задача, получившая название булевой проблемы троек Пифагора, была впервые предложена математиком из Калифорнии Рональдом Грэхемом еще в 1980-х годах.

Почему уравнения важны?

Уравнения используются каждый день для многих, многих вещей. Они помогают вам искать в Интернете, заставлять ваш компьютер функционировать и удерживать самолеты в воздухе, и это лишь некоторые из них.

Что такое уравнение теории хаоса?

«Теория хаоса — это раздел математики, изучающий поведение динамических систем, которые очень чувствительны к начальным условиям.Теория хаоса — это междисциплинарная теория, утверждающая, что в пределах очевидной случайности хаотических сложных систем есть лежащие в основе закономерности, постоянные петли обратной связи, повторение, самоподобие, фракталы и самоорганизация ». — Википедия.

Уравнение выглядит следующим образом : —

Изменено с news.bitofnews.com

Эта теория эффективно помогает нам иметь дело со сложными системами, поведение которых очень чувствительно к незначительным изменениям условий, так что небольшие изменения могут привести к непредвиденным последствиям.

Теория хаоса — это наука сюрпризов, а не всегда приятных сюрпризов.

10 уравнений, изменивших мир

Вот десять самых важных уравнений, которые изменили мир. Этот список далеко не исчерпывающий и в нем нет определенного порядка.

1. Теорема Пифагора

Источник: Maxpixel

Являясь основным продуктом школьных уроков математики, это уравнение фактически изменило мир.Это позволило нам составить более точные карты и помочь найти кратчайшее расстояние между объектами; среди других вещей.

Он также широко используется в архитектуре, деревообработке и многих других областях.

2. Исчисление

«Исчисление, первоначально называвшееся исчислением бесконечно малых или« исчислением бесконечно малых », представляет собой математическое исследование непрерывных изменений, точно так же, как геометрия — это изучение формы и алгебры. это изучение обобщений арифметических операций.»- Википедия.

Он был разработан независимо великим Исааком Ньютоном и сэром Готфридом Лейбницем. После его изобретения он объединил алгебру и геометрию в качестве одного из столпов математики.

3. Логарифмы

Логарифмы — это еще один тип уравнений, который изменил мир. Они помогали нам делать утомительные вычисления до того, как появились калькуляторы.

Логарифм — это величина, представляющая степень, до которой должно быть возведено фиксированное число (основание), чтобы получить заданное число.Использование таблиц логарифмов позволило исключить многие утомительные шаги в вычислениях в таких областях, как геодезия, навигация и инженерия.

4. Относительность

Источник: Peat Bakke / Flickr

Знаменитые уравнения Эйнштейна по теории относительности не только ответили на многие ранее нерешенные вопросы, но и помогли изменить наш взгляд на время, пространство и гравитацию.

Он используется для объяснения всего, от черных дыр до Большого взрыва и ядерной энергетики, а также GPS на наших телефонах.

5. Нормальное распределение

Сегодня мы все знакомы с графиками колоколообразной кривой. Они помогают описать распределение данных в заданном наборе.

Его можно использовать для чего угодно, от IQ в популяции до результатов экзамена в группе студентов. В рамках нормального распределения большинство точек данных попадают где-то посередине, с меньшим количеством людей в каждую крайность.

6. Уравнение Шредингера

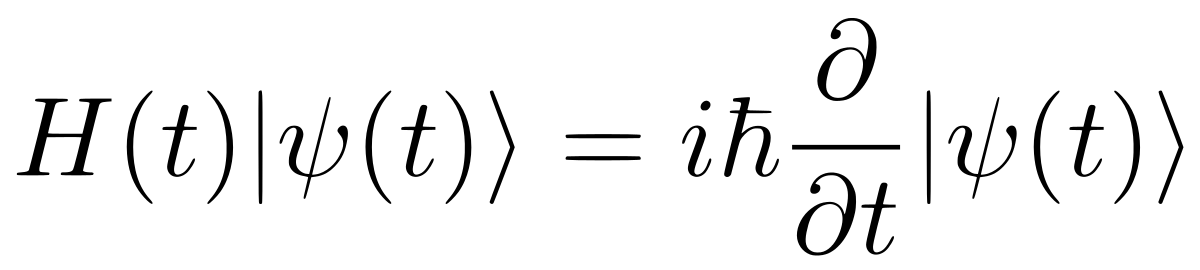Источник: YassineMrabet / Wikimedia Commons

Уравнение Шредингера необходимо для современных компьютерных микросхем и лазеров.Это также помогает держать кошек в состоянии анабиоза между жизнью и смертью.

А если серьезно, это уравнение навсегда изменило область квантовой физики. Это линейное уравнение в частных производных, описывающее волновую функцию квантово-механической системы. Его открытие стало важной вехой в развитии квантовой механики.

7. Закон всемирного тяготения Ньютона

«Закон всемирного тяготения Ньютона гласит, что каждая частица притягивает каждую другую частицу во Вселенной с силой, которая прямо пропорциональна произведению их масс и обратно пропорциональна квадрат расстояния между их центрами.»- Википедия.

Закон всемирного тяготения Ньютона — одно из самых фундаментальных уравнений в физике.

8. Волновое уравнение

« Волновое уравнение описывает поведение волн — вибрирующая струна гитары, рябь в пруду за камнем. брошен или свет выходит из лампы накаливания. Волновое уравнение было ранним дифференциальным уравнением, и методы, разработанные для его решения, открыли дверь для понимания и других дифференциальных уравнений », — businessinsider.ком.

Он эффективно образует важный компонент электромагнетизма, оптики, гидродинамики и теплопередачи.

9. Второй закон термодинамики

«Это означает, что в замкнутой системе энтропия (S) всегда постоянна или возрастает. Термодинамическая энтропия, грубо говоря, является мерой того, насколько неупорядочена система Система, которая начинается в упорядоченном, неравномерном состоянии — скажем, в горячей области рядом с холодной — всегда будет иметь тенденцию к выравниванию, при этом тепло будет течь из горячей области в холодную до тех пор, пока не будет равномерно распределено.»- businessinsider.com.

Это помогает нам, среди прочего, понять направление теплопередачи. Эта теория может быть выражена в терминах изменения энтропии системы (dS). В этом уравнении рассчитывается dS путем измерения количества тепла, поступившего в замкнутую систему (δQ), деленного на обычную температуру (T) в точке, где произошла теплопередача.

10. Преобразование Фурье

Это уравнение в основном имеет вид сердце современной обработки сигналов.Это также важно для анализа сигналов и сжатия данных.

«Преобразование Фурье необходимо для понимания более сложных волновых структур, таких как человеческая речь. Учитывая сложную беспорядочную волновую функцию, такую как запись разговора человека, преобразование Фурье позволяет нам разбить беспорядочную функцию на комбинацию чисел. простых волн, что значительно упрощает анализ ». — businessinsider.com.

.2, боров большинство общественной славы, многие менее известные формулы имеют своих чемпионов среди ученых. LiveScience запросил у физиков, астрономов и математиков их любимые уравнения; вот что мы обнаружили:

Общая теория относительности

(Изображение предоставлено: Shutterstock / RT Wohlstadter)

Приведенное выше уравнение было сформулировано Эйнштейном как часть его новаторской общей теории относительности в 1915 году. Теория произвела революцию в том, как ученые понимали гравитацию, описывая сила как искривление ткани пространства и времени.

«Мне до сих пор удивительно, что одно такое математическое уравнение может описать, что такое пространство-время», — сказал астрофизик Института космического телескопа Марио Ливио, который назвал это уравнение своим любимым. «В этом уравнении воплощен весь истинный гений Эйнштейна». [Викторина Эйнштейна: проверьте свои знания о гении]

«Правая часть этого уравнения описывает энергетический состав нашей Вселенной (включая« темную энергию », которая движет текущим космическим ускорением)», — пояснил Ливио.«Левая часть описывает геометрию пространства-времени. Равенство отражает тот факт, что в общей теории относительности Эйнштейна масса и энергия определяют геометрию и, соответственно, кривизну, которая является проявлением того, что мы называем гравитацией». [6 странных фактов о гравитации]

«Это очень элегантное уравнение», — сказал Кайл Кранмер, физик из Нью-Йоркского университета, добавив, что уравнение показывает взаимосвязь между пространством-временем, материей и энергией. «Это уравнение говорит вам, как они связаны — как присутствие солнца искажает пространство-время, так что Земля движется вокруг него по орбите и т. Д.В нем также рассказывается, как эволюционировала Вселенная после Большого взрыва, и предсказывается, что должны быть черные дыры ».

Стандартная модель

(Изображение предоставлено Shutterstock / RT Wohlstadter)

Еще одна господствующая теория физики, стандартная модель описывает совокупность фундаментальных частиц, из которых в настоящее время считается наша Вселенная.

Теория может быть заключена в главное уравнение, называемое стандартным модельным лагранжианом (названное в честь французского математика и астронома 18-го века Жозефа Луи Лагранжа), которое было выбрано физик-теоретик Лэнс Диксон из Национальной ускорительной лаборатории SLAC в Калифорнии в качестве своей любимой формулы.

«Он успешно описал все элементарные частицы и силы, которые мы наблюдали в лаборатории на сегодняшний день, за исключением гравитации», — сказал Диксон LiveScience. «Сюда входит, конечно, недавно открытый (подобный) бозон Хиггса, фи в формуле. Это полностью самосогласовано с квантовой механикой и специальной теорией относительности».

Однако стандартная модельная теория еще не была объединена с общей теорией относительности, поэтому она не может описывать гравитацию. [Инфографика: объяснение стандартной модели]

Calculus

(Изображение предоставлено: Shutterstock / agsandrew)

Хотя первые два уравнения описывают определенные аспекты нашей Вселенной, другое любимое уравнение можно применить ко всем ситуациям.Фундаментальная теорема исчисления составляет основу математического метода, известного как исчисление, и связывает две его основные идеи: понятие интеграла и понятие производной.

«Простыми словами, [он] говорит, что чистое изменение плавной и непрерывной величины, такой как пройденное расстояние, за данный интервал времени (т. Е. Разница в значениях величины в конечные моменты времени интервал) равен интегралу скорости изменения этой величины, т.е.е. интеграл скорости «, — сказала Мелкана Бракалова-Тревитик, заведующая математическим факультетом Фордхэмского университета, которая выбрала это уравнение в качестве своего любимого.» Фундаментальная теорема исчисления (FTC) позволяет нам определить чистое изменение за интервал на основе от скорости изменения за весь интервал ».

Зародыши исчисления зародились в древние времена, но большая часть их была собрана в 17 веке Исааком Ньютоном, который использовал расчеты для описания движения планет вокруг Солнца. ,

Теорема Пифагора

(Изображение предоставлено Shutterstock / igor.stevanovic)

Уравнение «старое, но хорошее» — это знаменитая теорема Пифагора, которую изучает каждый начинающий студент-геометр.

Эта формула описывает, как для любого прямоугольного треугольника квадрат длины гипотенузы c (самая длинная сторона прямоугольного треугольника) равен сумме квадратов длин двух других сторон. ( a и b ). Таким образом, a ^ 2 + b ^ 2 = c ^ 2

«Самым первым математическим фактом, который меня поразил, была теорема Пифагора, — сказала математик Дайна Таймина из Корнельского университета.«Я был тогда ребенком, и мне казалось таким удивительным, что это работает с геометрией и с числами!» [5 серьезных математических фактов]

1 = 0,999999999….

(Изображение предоставлено: Shutterstock / Турсунбаев Руслан)

Это простое уравнение, которое утверждает, что величина 0,999, за которой следует бесконечная строка девяток, эквивалентна единице, является любимым математиком Стивеном Строгацем из Корнельского университета.

«Мне нравится, насколько это просто — все понимают, что в нем говорится, — но насколько это провокационно», — сказал Строгац.«Многие люди не верят, что это может быть правдой. Он также прекрасно сбалансирован. Левая сторона представляет собой начало математики; правая часть представляет тайны бесконечности».

Специальная теория относительности

(Изображение предоставлено: Shutterstock / optimarc)

Эйнштейн снова попадает в список со своими формулами специальной теории относительности, которые описывают, что время и пространство не являются абсолютными понятиями, а скорее являются относительными в зависимости от скорости движения. наблюдатель. Приведенное выше уравнение показывает, как время расширяется или замедляется по мере того, как человек движется в любом направлении.

«Дело в том, что это действительно очень просто», — сказал Билл Мюррей, физик элементарных частиц из лаборатории CERN в Женеве. «В нем нет ничего, что не мог бы сделать ученик A-level, никаких сложных производных и алгебр трассировки. Но то, что он воплощает, — это совершенно новый взгляд на мир, целостное отношение к реальности и наше отношение к ней. неизменный космос сметается и заменяется личным миром, связанным с тем, что вы наблюдаете.Вы переходите от того, чтобы быть вне вселенной, глядя вниз, к одному из компонентов внутри нее.Но концепции и математику может усвоить любой, кто хочет ».

Мюррей сказал, что предпочитает специальные уравнения относительности более сложным формулам более поздней теории Эйнштейна.« Я никогда не смогу следовать математике общей теории относительности », — сказал он. .

Уравнение Эйлера

(Изображение предоставлено: Shutterstock / Jezper)

Эта простая формула инкапсулирует нечто чистое о природе сфер:

«Это говорит о том, что если вы разрежете поверхность сферы на грани, края и вершины и пусть F будет числом граней, E числом ребер и V числом вершин, вы всегда получите V — E + F = 2 «, — сказал Колин Адамс, математик из колледжа Уильямс в Массачусетсе.

«Возьмем, к примеру, тетраэдр, состоящий из четырех треугольников, шести ребер и четырех вершин», — пояснил Адамс. «Если вы сильно дунете в тетраэдр с гибкими гранями, вы можете округлить его до сферы, так что в этом смысле сферу можно разрезать на четыре грани, шесть ребер и четыре вершины. И мы видим, что V — E + F = 2. То же самое верно для пирамиды с пятью гранями — четырьмя треугольными и одним квадратом — восемью гранями и пятью вершинами », и любой другой комбинацией граней, ребер и вершин.

«Очень крутой факт! Комбинаторика вершин, ребер и граней улавливает кое-что очень фундаментальное о форме сферы», — сказал Адамс.

Уравнения Эйлера-Лагранжа и теорема Нётер

(Изображение предоставлено Shutterstock / Марк Пинтер)

«Это довольно абстрактные, но удивительно мощные», — сказал Кранмер из Нью-Йоркского университета. «Круто то, что такой способ мышления о физике пережил несколько крупных революций в физике, таких как квантовая механика, теория относительности и т. Д.«

Здесь L означает лагранжиан, который является мерой энергии в физической системе, такой как пружины, рычаги или фундаментальные частицы.« Решение этого уравнения показывает, как система будет развиваться со временем », — сказал Кранмер.

Побочный результат уравнения Лагранжа называется теоремой Нётер, в честь немецкого математика 20 века Эмми Нётер. «Эта теорема действительно фундаментальна для физики и роли симметрии», — сказал Кранмер. обладает симметрией, то существует соответствующий закон сохранения.Например, идея о том, что фундаментальные законы физики сегодня такие же, как и завтра (временная симметрия), подразумевает, что энергия сохраняется. Идея о том, что законы физики здесь такие же, как и в космическом пространстве, подразумевает, что импульс сохраняется. Симметрия, возможно, является движущей концепцией фундаментальной физики, в первую очередь благодаря вкладу [Нётер] ».

Уравнение Каллана-Симанзика

(Изображение предоставлено: Shutterstock / RT Wohlstadter)

« Уравнение Каллана-Симанзика является жизненно важным первым — «Уравнение принципов 1970 года, необходимое для описания того, как наивные ожидания терпят неудачу в квантовом мире», — сказал физик-теоретик Мэтт Страсслер из Университета Рутгерса.

Уравнение имеет множество применений, в том числе позволяет физикам оценивать массу и размер протона и нейтрона, которые составляют ядра атомов.

Основы физики говорят нам, что гравитационная сила и электрическая сила между двумя объектами пропорциональны обратному квадрату расстояния между ними. На простом уровне то же самое верно и для сильного ядерного взаимодействия, которое связывает протоны и нейтроны вместе, чтобы сформировать ядра атомов, и которое связывает кварки вместе, чтобы сформировать протоны и нейтроны.Однако крошечные квантовые флуктуации могут немного изменить зависимость силы от расстояния, что имеет драматические последствия для сильного ядерного взаимодействия.

«Это предотвращает уменьшение этой силы на больших расстояниях, заставляет ее захватывать кварки и объединять их, чтобы сформировать протоны и нейтроны нашего мира», — сказал Штрасслер. «Уравнение Каллана-Симанзика связывает этот драматический и трудно поддающийся расчету эффект, важный, когда [расстояние] примерно равно размеру протона, с более тонкими, но более простыми для расчета эффектами, которые можно измерить, когда [ расстояние] намного меньше протона.«

Уравнение минимальной поверхности

(Изображение предоставлено Shutterstock / MarcelClemens)

« Уравнение минимальной поверхности каким-то образом кодирует красивые мыльные пленки, которые образуются на границах проводов, когда вы погружаете их в мыльную воду », — сказал математик Фрэнк Морган из Williams. Колледж. «Тот факт, что уравнение является» нелинейным «и включает в себя степени и произведения производных, является закодированным математическим намеком на удивительное поведение мыльных пленок. Это контрастирует с более известными линейными уравнениями в частных производных, такими как уравнение теплопроводности, волновое уравнение и уравнение Шредингера квантовой физики.«

Математик обсуждает решение, казалось бы, неразрешимого уравнения

Mathematician discusses solving a seemingly unsolvable equation

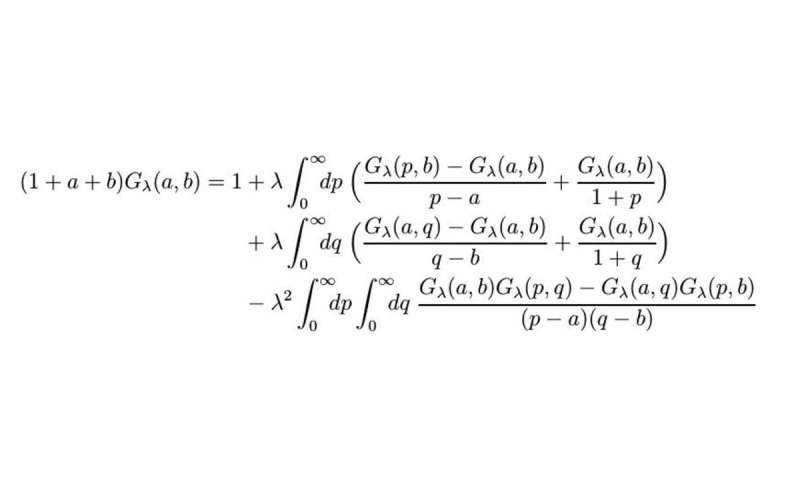Математическое уравнение. Предоставлено: WWU / Раймар Вулкенхаар.

Спустя 10 лет профессор Раймар Вулкенхаар из Математического института Мюнстерского университета и его коллега доктор Эрик Панцер из Оксфордского университета решили математическое уравнение, которое считалось неразрешимым. Уравнение будет использоваться для поиска ответов на вопросы физики элементарных частиц.В этом интервью с Кристиной Хеймкен Вулкенхаар оглядывается на проблемы, с которыми пришлось столкнуться при поиске формулы решения, и объясняет, почему работа еще не завершена.

Вы работали над решением уравнения в течение 10 лет.Что сделало это уравнение таким трудным для решения?

Это нелинейное интегральное уравнение с двумя переменными. Такое уравнение настолько сложно, что вы действительно думаете, что не может быть никакой формулы для решения. Сами по себе две переменные являются проблемой, и не существует установленных подходов к поиску решения для нелинейных интегральных уравнений. Тем не менее, снова и снова в течение этих 10 лет появлялись проблески надежды, и в результате, несмотря на все трудности, я думал, что найти явную формулу решения, выраженную через известные функции, действительно возможно.

Для чего можно использовать это уравнение?

Речь идет о математическом понимании квантовых теорий поля. Они относятся к области физики и участвуют в крупномасштабных экспериментах, например, в ЦЕРНе. Цель состоит в том, чтобы математически описать элементарные частицы, то есть мельчайшие известные компоненты материи. Но это настолько сложно, что вместо этого математически описываются мнимые частицы, которые обладают определенными свойствами реальных частиц.Есть надежда, что когда-нибудь реальные частицы можно будет описать с помощью установленных таким образом методов.

Проработав 10 лет над проблемой, в этом году вы совершили прорыв. Как это произошло?

Ближе к концу мая я опробовал идею, по которой получил степень доктора философии. Студент Александр Хок дал решающий импульс. Я разработал новое уравнение — более простое, чем предыдущее — и начал решать его циклами. Это означает, что вы подходите к решению шаг за шагом, т.е.е. цикл за циклом, вычисляя левую часть уравнения на каждом предыдущем шаге и используя ее для правой части уравнения на следующем шаге.

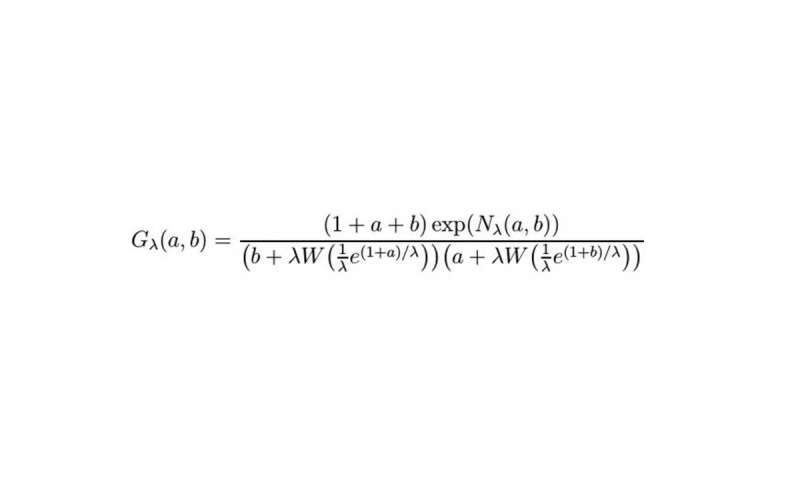Решение. Предоставлено: WWU / Раймар Вулкенхаар.

В четвертом цикле мне нужно было вычислить сумму 46 интегралов, содержащих, помимо прочего, полилогарифмы. Эти полилогарифмы, которые являются одними из наиболее требовательных функций, усложнялись в каждом цикле.Мне повезло в том, что в итоге почти все было вычеркнуто, а осталась лишь небольшая сумма степеней нормальных логарифмов. Я сразу понял, что здесь можно найти сокровища.

Пятую петлю решить было не так просто — но мне снова повезло. Во время летней школы во французских Альпах у меня была возможность поговорить с экспертами по таким функциям.Одним из этих экспертов был доктор Эрик Панцер из Оксфордского университета. Он написал компьютерную программу по символической математике гиперлогарифмов и оказал ей поддержку. За ночь эта программа вычислила мое уравнение до седьмого цикла. Он подтвердил мои результаты вплоть до четвертого цикла, а после четвертого цикла чудо продолжалось — все можно было разбить на нормальные логарифмы. Начали появляться закономерности!

Что это значит?

Возможно, вы помните Треугольник Паскаля со школьной скамьи с биномиальными коэффициентами? В треугольнике каждое число, введенное в строку треугольника, является суммой двух чисел, введенных над ним.И это как раз такая треугольная структура, которую мы находим в наших циклах, хотя и более сложную, чем в треугольнике Паскаля.

9 июня завершились восьмой и девятый петли. И вот наступил, пожалуй, самый важный момент. Эрик Панцер расшифровал так называемую рекурсивную формулу, которая порождает каждую последнюю строку в треугольнике из строки над ним и, таким образом, позволяет нам экстраполировать от известного к неизвестному.

О чем вы думали в этот момент?

Одна из вещей, которые я подумал, было: «Никто не может быть настолько удачливым.«Я понял, что мы решим уравнение. За ужином на нашем столе стояла бутылка вина…

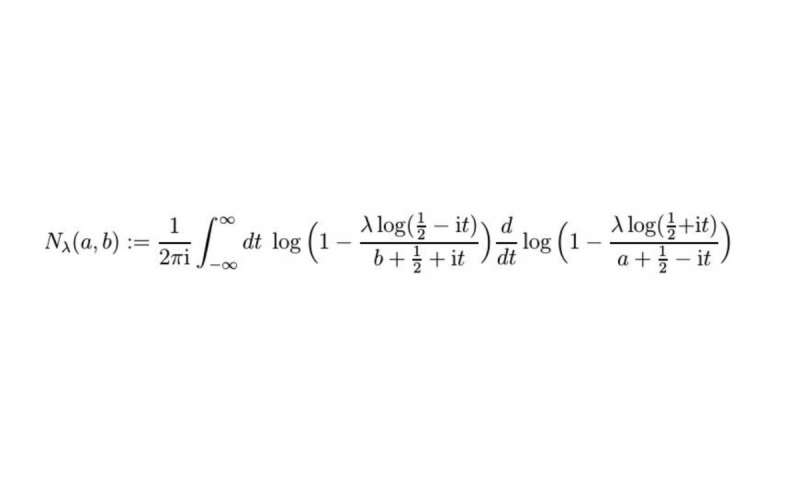Функция Нильсена является частью решения. Профессор Раймар Вулкенхаар и доктор Эрик Панцер открыли эту новую функцию в ходе своей работы. Предоставлено: WWU / Раймар Вулкенхаар.

… прежде чем вы вернетесь к работе.

Да. На следующий день мне удалось свести часть уравнения к простой серии производных.Поначалу все остальное казалось сложным. Только поздно вечером мне пришла в голову идея использовать формулу Коши для ее решения. На следующее утро я поставил будильник на 5:30 и сразу же попробовал. Это сработало с первой попытки, а на следующем шаге я нашел формулу, которую часто видел. Я знал, что это будет решено с помощью функции Ламберта W. Через несколько минут я получил электронное письмо от Эрика Панцера: он тоже думал о функции Ламберта, но совершенно другим путем.В результате мы достигли того, чего не было возможно в течение 10 лет: решения интегрального уравнения, описывающего модель квантовой теории поля. Это было просто невероятно.

Вы используете идеи и методы, разработанные математиками в 18 веке, которые сегодня почти полностью забыты.

Эти старые формулы нам очень помогли. Функция Ламберта W, которая является элементарной частью нашего решения, названа в честь швейцарского математика Иоганна Генриха Ламберта.Это уравнение возникает в большом количестве совершенно разных вопросов. Из-за недостаточной осведомленности об основах Ламберта функция Ламберта изобреталась снова и снова, и только в 1993 году она была введена в качестве стандарта. Мы также использовали формулу Лагранжа-Бюрмана, которая помогла нам решить интеграл с помощью функция Ламберта, а также формула Коши. Вообще математика очень уважает своих предков. Такие имена, как Эйлер, Ламберт, Лагранж, Коши, Гаусс и Гильберт, упоминаются с наибольшим признанием за их достижения.Но есть два современных инструмента, без которых я бы не хотел остаться: Википедия и компьютерная алгебра. Вы можете найти в Википедии исчерпывающую информацию, охватывающую известные — и менее известные — математические структуры и функции. Компьютеры могут решать уравнения несравнимо быстрее, чем вручную, и без ошибок

Каковы следующие шаги?

В нашем решении появилась новая функция, которую мы назвали функцией Нильсена. Когда мы лучше поймем это и определим, например, как это соотносится с другими известными функциями, мы отправим нашу работу, которая находится в свободном доступе в Интернете в виде препринта, для публикации в специализированном журнале с рецензированием.

После этого я хотел бы продолжить работу, которой я занимался с 2002 года с моим коллегой профессором Харальдом Гроссе из Вены. Он посвящен квантовой теории поля для математических частиц. Теперь мы сможем полностью понять эту модель с помощью решенного уравнения.

Математики находят новые решения древней головоломки

Дополнительная информация: Ламберт-W решает некоммутативную Φ ⁴ -модель.arxiv.org/abs/1807.02945 Предоставлено Мюнстерский университет

Ссылка : Математик обсуждает решение, казалось бы, неразрешимого уравнения (2018, 7 августа) получено 16 августа 2020 с https: // физ.орг / Новости / 2018-08-математик-обсуждаетс-казалось бы, неразрешимый-equation.html

Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, нет часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.