2+n-72)=1/(n+9)Sin 360 градусов — Найдите значение Sin 360 градусов
LearnPracticeDownload
Значение sin 360 градусов равно 0 . Sin 360 градусов в радианах записывается как sin (360° × π/180°), то есть sin (2π) или sin (6,283185…). В этой статье мы обсудим методы определения значения sin 360 градусов на примерах.
- Sin 360°: 0
- Грех (-360 градусов): 0
- Sin 360° в радианах: грех (2π) или грех (6,2831853 . . .)
Какова ценность греха 360 градусов?
Значение sin 360 градусов равно 0. Sin 360 градусов также можно выразить с помощью эквивалента заданного угла (360 градусов) в радианах (6,28318 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 360 градусов = 360° × (π/180°) рад = 2π или 6,2831. . .
∴ sin 360° = sin(6.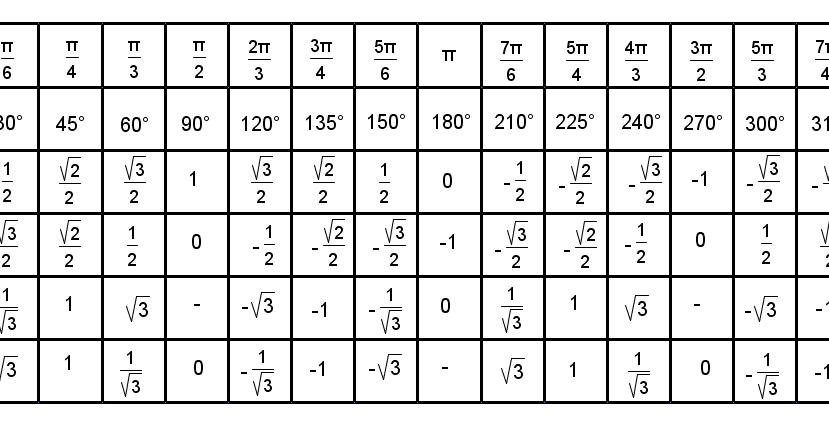
2831) = 0
Объяснение:
Для sin 360 градусов угол 360° лежит на положительной оси x. Таким образом, значение sin 360° = 0
Поскольку функция синуса является периодической функцией, мы можем представить sin 360° как sin 360 градусов = sin(360° + n × 360°), n ∈ Z.
⇒ sin 360° = sin 720° = sin 1080° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-360°) = -sin(360°) = 0.
Методы определения значения Sin 360 градусов
Значение sin 360° дается как 0. Мы можем найти значение sin 360 градусов по:
- Использование тригонометрических функций
- Использование единичного круга
Sin 360° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin 360 градусов как:
- ± √(1-cos²(360°))
- ± тангенс 360°/√(1 + тангенс²(360°))
- ± 1/√(1 + раскладушка²(360°))
- ± √(сек²(360°) — 1)/сек 360°
- 1/косек 360°
Примечание.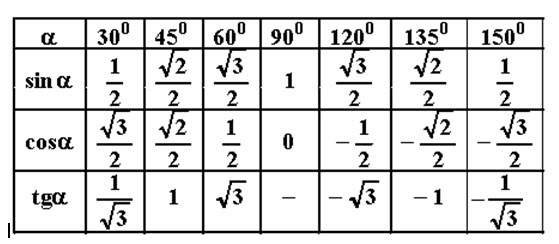
Поскольку 360° лежит на положительной оси x, конечное значение sin 360° будет равно 0,9.0003
Мы можем использовать тригонометрические тождества для представления sin 360° как
- sin(180° — 360°) = sin(-180°)
- -sin(180° + 360°) = -sin 540°
- cos(90° — 360°) = cos(-270°)
- -cos(90° + 360°) = -cos 450°
Sin 360 градусов с помощью единичной окружности
Чтобы найти значение sin 360 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы сформировать угол 360° или 0° с положительной осью x.
- Грех 360 градусов равен координате y(0) точки пересечения (1, 0) единичной окружности и r.
Отсюда значение sin 360° = y = 0
☛ Также проверьте:
- sin 50 градусов
- грех 37 градусов
- грех 3 градуса
- грех 129 градусов
- грех 70 градусов
- грех 130 градусов
Примеры использования Sin 360 градусов
Пример 1.
Найдите значение 5 sin(360°)/7 cos(0°). Решение:
Используя тригонометрические тождества, мы знаем, что sin(360°) = 0 и cos(0°) = 1,
⇒ Значение 5 sin(360°)/7 cos(0°) = 0Пример 2: Упростить: 2 (sin 360°/sin 90°)
Решение:
Мы знаем sin 360° = 0 и sin 90° = 1
⇒ 2 sin 360°/sin 90° = 2(0)
= 0Пример 3: Используя значение sin 360°, решите: (1-cos²(360°)).
Решение:Мы знаем, (1-cos²(360°)) = (sin²(360°)) = 0
⇒ (1-cos²(360°)) = 0
Найдите значение 5 sin(360°)/7 cos(0°). перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 360 Degrees
Что такое Sin 360 Degrees?
Sin 360 градусов — значение тригонометрической функции синуса для угла, равного 360 градусам.
Значение sin 360° равно 0.
Каково точное значение sin 360 градусов?
Точное значение sin 360 градусов равно 0.
Как найти Sin 360° в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin 360° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(360°))
- ± тангенс 360°/√(1 + тангенс²(360°))
- ± 1/√(1 + раскладушка²(360°))
- ± √(сек²(360°) — 1)/сек 360°
- 1/косек 360°
☛ Также проверьте: таблицу тригонометрии
Каково значение Sin 360 градусов в пересчете на Cot 360°?
Мы можем представить функцию синуса в терминах функции котангенса, используя тригонометрические тождества, sin 360° можно записать как 1/√(1 + cot²(360°)).
Как найти значение греха 360 градусов?
Значение sin 360 градусов можно вычислить, построив угол 360° с осью x и затем найдя координаты соответствующей точки (1, 0) на единичной окружности.
Значение sin 360° равно координате y (0). ∴ sin 360° = 0.
Скачать БЕСПЛАТНО учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
тригонометрические соотношения 360 минус тета|sin(360
Проверка тригонометрических тождеств — G…
Включите JavaScript
В тригонометрических отношениях 360 минус тета (360 — θ) конечные стороны котерминальных углов совпадают, следовательно, их тригонометрические отношения равны.
| sin(- θ ) = — sin θ cos (- θ ) = cos θ tan(- θ ) = — tan θ θ ) = сек θ раскладушка (- θ ) = — раскладушка θ |
Ясно, что 360 — θ и — θ являются коконцевыми углами.
sin(360 — θ) = Sin(- θ)
Но мы знаем, что sin(- θ) = — sinθ
$\underline{sin(360 — θ)= -sin θ} $
Опять же,
cos( 360 — θ) = cos (- θ)
Но мы знаем, что cos (- θ) = cos θ
$ \ underline {cos (360 — θ) = cos θ} $
Теперь
tan (360 — θ) = tan(- θ)
Но мы знаем, что tan(- θ) = — tanθ
$\underline{tan(360 — θ)= — tan θ} $
Как мы знаем, csc θ = $\frac{1 {sinθ}$
∴ csc (360-θ) = $\frac{1}{sin(360-θ)}$
∴ csc (360-θ)= $\frac {1}{-sin θ}$
$\underline{csc(360 — θ)= -csc θ} $
И,
сек θ = $\frac{1}{cosθ}$
∴ сек (360- θ) = $\frac{1}{cos(360-θ)}$
Но cos(360-θ) = cos(θ)
∴ сек (360-θ)= $\frac{1}{cos θ} $
$ \ underline {sec (360 — θ) = cos θ} $
Опять же,
кроватка θ = $ \ frac {1} {tanθ} $
∴ кроватка (360-θ) = $ \ frac {1} {tan(360-θ)}$
Но tan(360-θ) = — tan(θ)
∴ cot (360-θ)= $\frac{1}{-tan θ}$ 9{0}$ = tan (360 -60) = -tan 60
Но tan(60) = $\sqrt{3}$
⇒ tan (270) = — $\sqrt{3}$
От тригонометрических соотношений 360 минус тета (360 -Θ) до Home
Мы в ask-math считаем, что учебные материалы должны быть бесплатными для всех.