Sin (a — b) — Формула, Доказательство, Примеры | Что такое Sin(a
) Sin(a — b) является одним из важных тригонометрических тождеств, используемых в тригонометрии, также называемым формулой составного угла sin(a — b). Тождество Sin (a — b) используется при нахождении значения тригонометрическая функция синуса для разницы заданных углов, скажем, «а» и «b». Расширение sin (a — b) может быть применено для представления синуса составного угла (в виде разницы двух углов) в терминах тригонометрических функций синуса и косинуса Давайте разберемся в тождестве sin(a — b) и его доказательстве подробно в следующих разделах.
| 1. | Что такое Sin(a — b) Тождество в тригонометрии? |
| 2. | Sin(a — b) Формула составного угла |
| 3. | Доказательство греха (a — b) Формула |
| 4. | Как применить Sin(a — b)? |
5. | Часто задаваемые вопросы о Sin(a — b) |
Что такое Sin(a — b) Тождество в тригонометрии?
Sin(a — b) является тригонометрическим тождеством для составного угла, который задается в виде разности двух углов. Он применяется, когда угол, для которого должно быть вычислено значение синусоидальной функции, задается в виде составного угла для разности двух углов. Здесь угол (a — b) представляет собой составной угол.
Sin(a — b) Формула составного угла
Формула Sin(a — b) также называется разностной формулой в тригонометрии. Формула sin(a — b) для составного угла (a — b) может быть представлена как
sin (a — b) = sin a cos b — cos a sin b,
, где a и b — меры любых двух углов.
Доказательство греха (a — b) Формула
Разложение формулы sin(a — b) можно доказать геометрически. Чтобы дать пошаговый вывод формулы тригонометрической синусоидальной функции разности двух углов геометрически, давайте сначала предположим, что ‘a’, ‘b’ и (a — b) являются положительными острыми углами, такими что (a > б).
Чтобы доказать: sin (a — b) = sin a cos b — cos a sin b
Конструкция: Пусть OX — вращающаяся линия. Поверните его вокруг точки O против часовой стрелки, чтобы сформировать лучи OY и OZ так, что ∠XOZ = a и ∠YOZ = b. Тогда ∠XOY = a — b.
На луче OY возьмем точку P и:
- проведем перпендикуляры PQ и PR к OX и OZ соответственно.
- Снова проведите перпендикуляры RS и RT из R на OX и PQ соответственно.
Доказательство: Мы увидим, как мы написали ∠TPR = a на рисунке выше.
- Из прямоугольного треугольника OPQ ∠OPQ = 180 – (90 + a – b) = 90 – a + b;
- Из прямоугольного треугольника OPR ∠OPR = 180 — (90 + b) = 90 — b
Теперь, исходя из рисунка, ∠OPQ, ∠OPR и ∠TPR — это углы в точке на прямой линии, следовательно, их сумма составляет 180 градусов.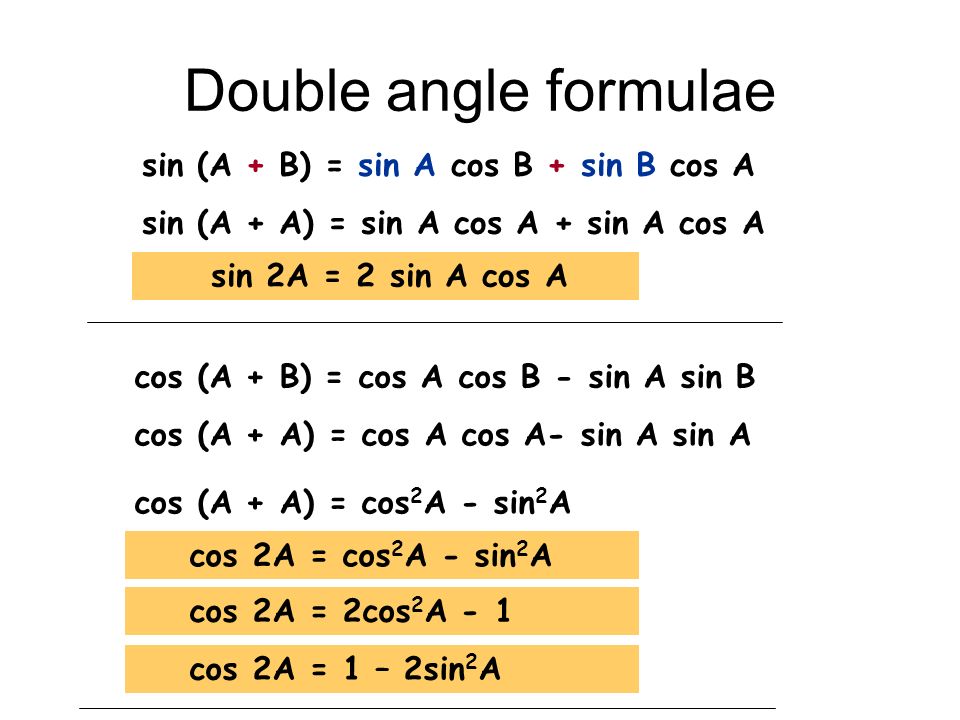
∠OPQ + ∠OPR + ∠TPR = 180
(90 — а + b) + (90 — b) + ∠TPR = 180
180 — а + ∠TPR = 180
∠TPR = a
Теперь из прямоугольного треугольника PQO получаем
sin (a — b) = PQ/OP
= (QT-TP)/OP
= QT/OP — TP/OP
= РС/ОП — ТР/ОП
= РС/ОР ∙ ИЛИ/ОП — ТП/ПР ∙ ПР/ОП
= sin a cos b — cos ∠TPR sin b
= sin a cos b — cos a sin b, (так как мы знаем, ∠TPR = a)
Следовательно, sin ( a — b) = sin a cos b — cos a sin б.
Как применить Sin(a — b)?
В тригонометрии разложение sin(a — b) может использоваться для вычисления значения тригонометрической функции синуса для углов, которые могут быть представлены как разность стандартных углов. Мы можем выполнить приведенные ниже шаги, чтобы научиться применять идентичность sin (a — b). Давайте оценим sin(60º — 30º), чтобы лучше понять это.
- Шаг 1: Сравните выражение sin(a — b) с данным выражением, чтобы определить углы ‘a’ и ‘b’.
Здесь a = 60º и b = 30º. - Шаг 2: Мы знаем, что sin (a — b) = sin a cos b — cos a sin b.
⇒ sin(60º — 30º) = sin 60ºcos 30º — sin 30ºcos 60º
Так как sin 30º = 1/2, sin 60º = √3/2, cos 30º = √3/2, cos 60º = 1/2
⇒ sin(60º — 30º) = (√3/2)(√3/2) — (1/2)(1/2) = 3/4 — 1/4 = 2/4 = 1/2
Также мы знаем, что sin(60º — 30º) = sin 30º = 1/2. Поэтому результат проверен.
Здесь a = 60º и b = 30º.☛ Связанные темы о грехе (a-b):
Вот некоторые темы, которые могут вас заинтересовать при чтении о грехе (a — b).
- Тригонометрическая таблица
- Тригонометрические функции
- грех кост загар
- Закон синусов
Давайте рассмотрим несколько решенных примеров для лучшего понимания концепции формулы sin(a — b).
Часто задаваемые вопросы о грехе (a — b)
Что такое грех (а-б)?
В тригонометрии существует множество тождеств составных углов. sin(a — b) — одно из важных тригонометрических тождеств, также называемое формулой разности синусов.
Sin(a — b) может быть задан как sin (a — b) = sin a cos b — cos a sin b, где «a» и «b» — углы.
Что такое Формула Греха (а — б)?
Формула sin(a — b) используется для выражения формулы составного угла sin через значения тригонометрических функций sin и косинуса отдельных углов. Формула Sin(a — b) в тригонометрии задается как sin (a — b) = sin a cos b — cos a sin b.
Что такое расширение sin (a — b)
Расширение sin(a — b) задается как sin (a — b) = sin a cos b — cos a sin b, где a и b равны меры углов.
Как доказать формулу греха (а — б)?
Доказательство формулы sin(a — b) может быть дано методом геометрического построения. Сначала мы предполагаем, что ‘a’, ‘b’ и (a — b) — положительные острые углы, такие, что (a > b). Нажмите здесь, чтобы понять пошаговый метод получения формулы sin(a — b).
Каково применение формулы Sin(a — b)?
Sin(a — b) можно использовать для нахождения значения функции синуса для углов, которые можно представить как разность простых или стандартных углов.
Таким образом, эта формула помогает упростить вывод значений триггерных функций. Его также можно применять при выводе формул расширения других формул двойного и кратного угла.
Как найти значение Sin 15º, используя Sin(a — b) Identity.
Значение sin 15º с использованием тождества (a — b) можно вычислить, сначала записав его как sin[(45º — 30º], а затем применив тождество sin(a — b). ⇒sin[(45º — 30º)] = sin 45ºcos30º — sin30ºcos 45º = (√3/2√2) — (1/2√2) = (√3 — 1)/2√2 = (√6 — √2 )/4.
Как найти Sin(a — b + c), используя Sin(a — b)?
Мы можем выразить sin(a — b + c) как sin((a — b) + c) и расширить, используя формулу sin(a + b), как sin(a — b + c) = sin(a — b )·cos c + sin c·cos(a — b) = cos c·(sin a cos b — cos a sin b) + sin c·(cos a cos b + sin a sin b) = sin a cos b cos c — cos a sin b cos c + cos a cos b sin c + sin a sin b sin c.
найти точные значения sin(a+b) и cos(a-b)
Математическая тригонометрия Тригонометрические тождества
Лорен Г.
Учитывая, что sin(a)=2/3 и cos(b)=-1/5, причем a и b оба находятся в интервале pi — pi/2
Подписаться І 2
Подробнее
Отчет
1 ответ эксперта
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Виктория В. ответил 31.07.17
Репетитор
5,0 (402)
Более 15 лет опыта преподавания тригонометрии
См. таких репетиторов
Смотрите таких репетиторов
Привет Лорен.
Это можно сделать сложением триггера. Вот формулы:
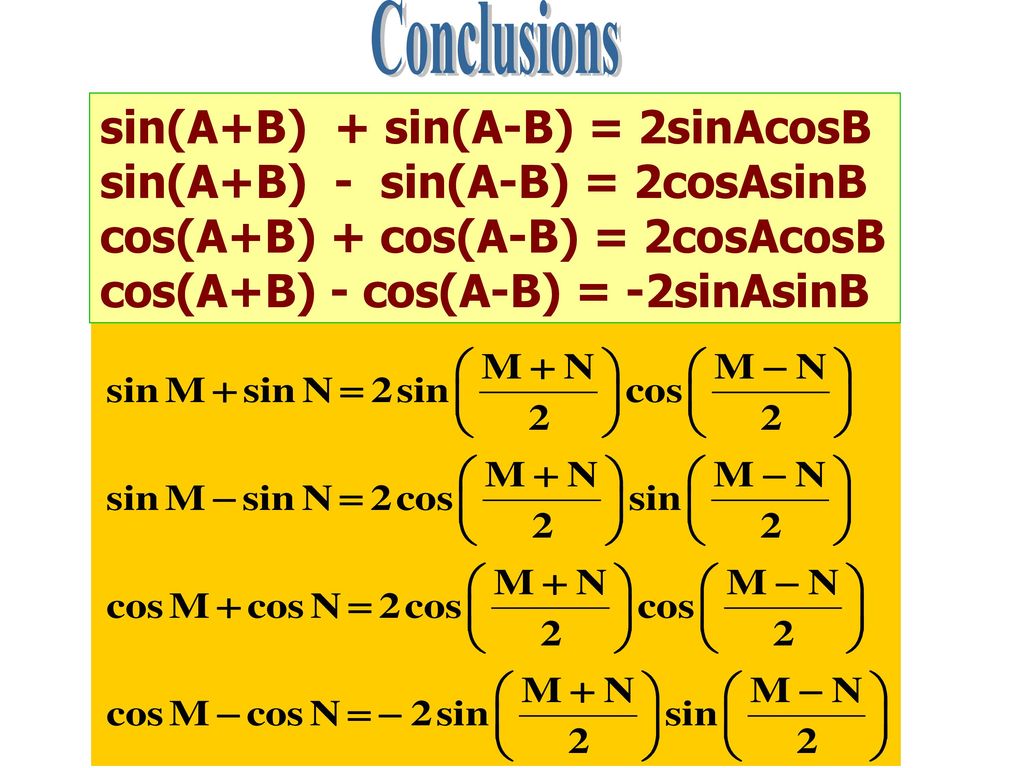
sin(a+b)=sin(a)cos(b) + sin(b)cos(a)
sin(a-b)=sin(a)cos(b) — sin(b) cos(a)
cos(a+b) = cos(a)cos(b) — sin(a)sin(b)
cos(a-b) = cos(a)cos(b) + sin(a)sin(b)
Итак.
.. при ваших значениях sin(a) = 2/3 и cos(b) = -1/5 нам нужно найти cos(a) и грех (б).
Опять же, используя треугольник и помещая угол во 2-й квадрант, угол a находится в нижней правой вершине (угол от отрицательной оси x и луча, завершающего угол), противоположная сторона вертикальная сторона = 2. Гипотенуза = 3. Итак, горизонтальный катет равен √5. Поскольку он находится во 2-м квадранте, он будет отрицательным. Получается, что cos(a)=(-√5/3).
Повторите то же самое для угла b. Сделайте угол, начинающийся в начале координат и поднимающийся влево во 2-й квадрант. Угол b — это нижняя правая вершина между отрицательной осью x и лучом из начала координат. На этот раз смежная сторона, горизонтальная сторона равна -1, а гипотенуза равна 5. С помощью теории Пифага найдите, что вертикальная сторона равна √24 = 2√6. Это делает sin(b)=(2√6)/5.
Теперь просто подставьте эти значения в формулы:
sin(a+b)=sin(a)cos(b) + sin(b)cos(a) = (2/3)(-1/5) + (2√6/5)(-√5/ 3) = -2/15 — 2√30/15
cos(a-b)=cos(a)cos(b) + sin(a)sin(b) = (-√5/3)(-1 /5) + (2/3)(2√6/5) = √5/15 + 4√6/15
Голосовать за 0 Понизить голос
Подробнее
Отчет
Все еще ищете помощь? Получите правильный ответ, быстро.
