Sin Cos Tan: Введение в тригонометрию
На колесе есть две точки, где вы будете находиться на нужной высоте (две красные точки на рисунке). Следовательно, существует два нужных нам угла α
1 и α2. Обратите внимание на два прямоугольных треугольника, выделенных зелёным цветом. Они одинаковые, так как являются зеркальным отображением друг друга. Давайте так же зеркально отобразим правый треугольник, но уже «вверх». Этот треугольник, выделенный красным цветом, имеет гипотенузу равную 1 (радиус колеса) и противолежащий катет (высота над центром) равный 1/2. В силу того, что все три треугольника одинаковые, они имеют одинаковые острые углы. Давайте найдём острый угол красного треугольника, при котором его синус равен 1/2. Поступим также, как древние астрономы, и заглянем в таблицу значений синуса для различных углов. Итак, sin α = 1/2 при = 30°. Интуитивно понятно, что наши три угла и значения их синусов связаны.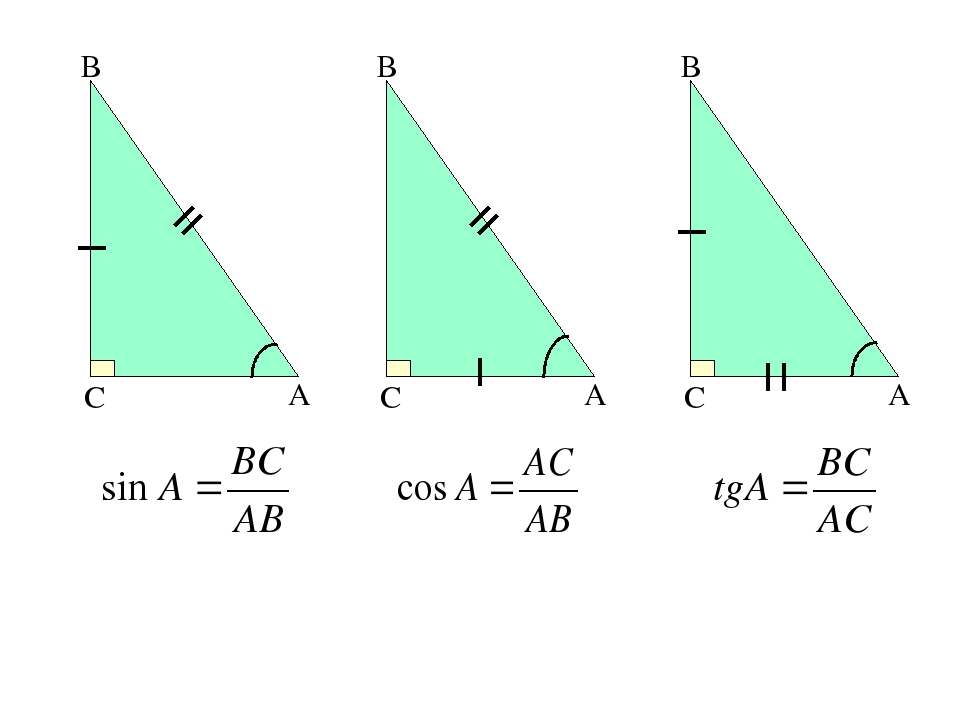
Полный круг составляет 360°. Разделим его на четыре четверти по 90° и пронумеруем их. Первая точка находится в третьей четверти. Так как две четверти в общем дают 180°, а угол α = 30°, то искомый угол α 1 = 210°. Нашли первый угол. Вторая точка находится в четвертой четверти. Три четверти в общем дают 270°, но прибавлением 30° тут не отделаешся, так как нужно прибавить угол β, а не угол α. Так как угол α + β= 90°, то угол β = 90°− 30°=60°. И второй искомый угол равен 270°+ 60°=330°. Остался один маленький ньюанс. Помните, как мы говорили о том, что тригонометрические функции описывают повторяющиеся процессы? Если наше колесо не остановится после того, как совершит полный оборот в 360°, то с каждым новым оборотом вы будет проходить через две точки, находящиеся на уровне –1/2. Эти точки определяются простым прибавлением 360° к найденным нами углам.
При этом n – любое целое число, то есть, на нашем примере это количество оборотов колеса.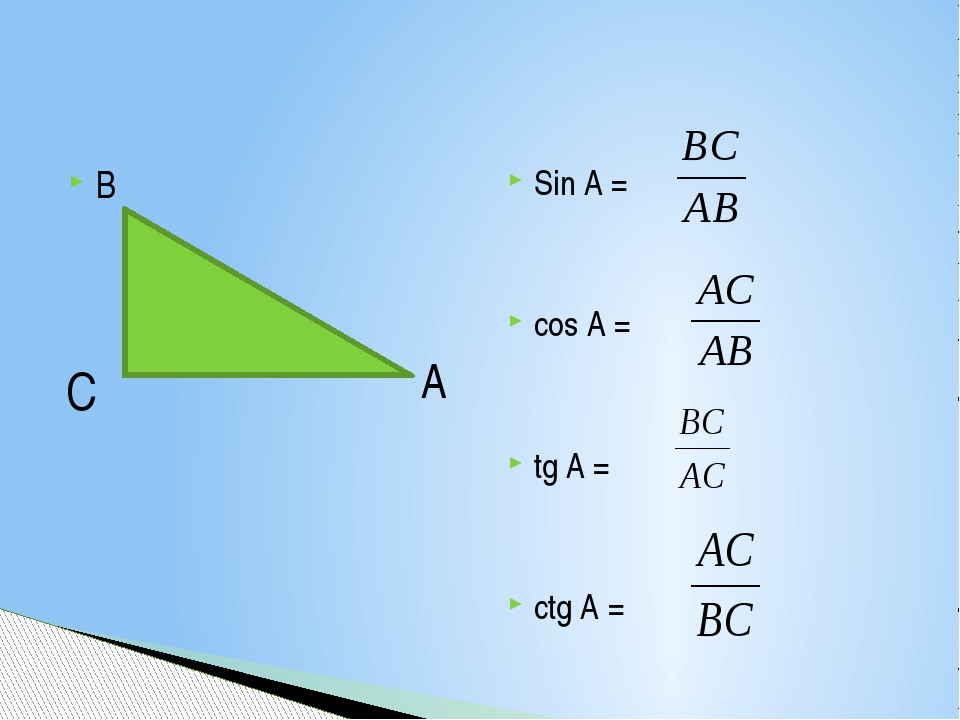 Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.
Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.
Равенстно sin α=−1/2 мы решили. Перейдем к неравенству sin α ≥ −1/2. Если для решения равенства мы нашли значения углов, при которых наша высота над центром колеса равна −1/2, то для решения неравенства нам нужно найти все углы, при которых наша высота больше либо равна −1/2. Помните мы говорили о том, что угол может быть отрицательным? Сейчас нам это пригодится. Определим угол α2 не как 330°, а как −30° (330°−360°) На рисунке эта область выделена зелёным цветом.
Для того, чтобы правильно записать решение неравенства, обратите внимание на рисунок синусоиды и прямой y=−1/2(высота). Нас интересуют области синусоиды, которые выше прямой y=−1/2. На рисунке они заштрихованы красным цветом. Обратите внимание на точки, которые выделяют эти отрезки. Это те же точки, которые мы получили при решении равенства sin α=−1/2 и они повторяются каждые 360°.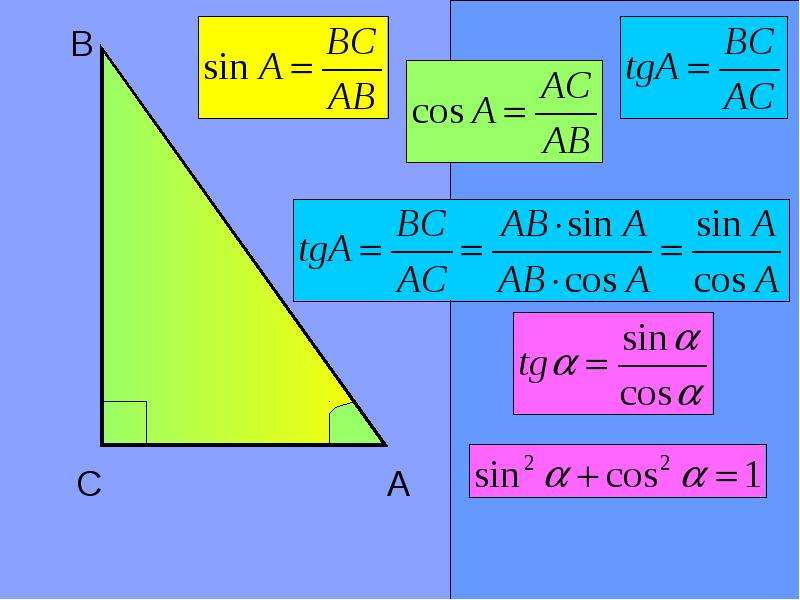
Дело осталось за малым. Во-первых, вспомнить, что математики обозначают 180° как π, когда записывают формулы с углами, и переписать решение так:
Во-вторых, произвести обратную замену α на 3x − π/4.
Путём нехитрых алгебраических преобразований, а именно прибавления π/4 и деления на 3 ко всем частям неравенства, получаем:
Ответ:
Миссия выполнена!
Функции Acos, Acot, Asin, Atan, Atan2, Cos, Cot, Degrees, Pi, Radians, Sin и Tan в Power Apps — Power Apps
- Чтение занимает 3 мин
В этой статье
Вычисление тригонометрических значений.
Описание
Основные функции
Функция Cos возвращает косинус аргумента, при этом угол указан в радианах.
Функция Cot возвращает котангенс аргумента, при этом угол указан в радианах.
Функция Sin возвращает синус аргумента, при этом угол указан в радианах.
Функция Tan возвращает тангенс аргумента, при этом угол указан в радианах.
Обратные функции
Функция Acos возвращает арккосинус или обратный косинус аргумента. Арккосинус — это угол, косинус которого является аргументом. Возвращаемый угол указывается в радианах в диапазоне от 0 (нуля) до π.
Функция Acot возвращает основное значение арккотангенса (или обратный котангенс) аргумента. Возвращаемый угол указывается в радианах в диапазоне от 0 (нуля) до π.
Функция Asin возвращает арксинус (или обратный синус) аргумента. Арксинус — это угол, синус которого является аргументом.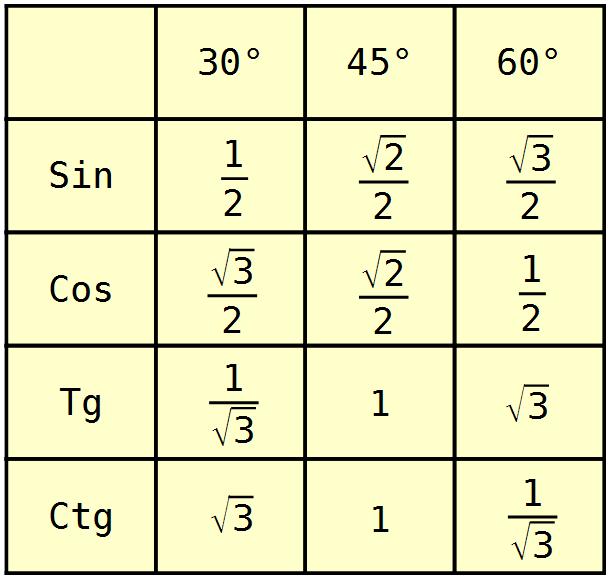 Возвращаемый угол указывается в радианах в диапазоне от -π/2 до π/2.
Возвращаемый угол указывается в радианах в диапазоне от -π/2 до π/2.
Функция Atan возвращает арктангенс (или обратный тангенс) своего аргумента. Арктангенс — это угол, тангенс которого является аргументом. Возвращаемый угол указывается в радианах в диапазоне от -π/2 до π/2.
Функция Atan2 возвращает арктангенс (или обратный тангенс), в качестве аргументов которого указаны координаты x и y. Арктангенс — это угол между осью x и линией, проходящей через точку начала координат (0, 0) и точку с координатами (x, y). Угол указывается в радианах между -π и π, исключая -π. Положительный результат соответствует углу, расположенному против часовой стрелки относительно оси x; отрицательный же результат представляет угол, расположенный по часовой стрелке. Atan2( a, b ) равно Atan( b/a ), за исключением случаев, когда a может быть равно 0 (нулю) в функции ** Atan2**.
Вспомогательные функции
Функция Degrees преобразует радианы в градусы. π радиан равно 180 градусам.
Функция Pi возвращает трансцендентное число π, которое начинается с 3,141592…
Функция Radians преобразует градусы в радианы.
Заметки
Если этим функциям передать одно число, возвращается один результат. Если передать таблицу с одним столбцом, содержащим числовые значения, возвращается таблица с одним столбцом, содержащим результаты вычислений — по одному результату для каждой записи в таблице аргументов. Таблицу с несколькими столбцами можно преобразовать в таблицу с одним столбцом, как описано в статье об использовании таблиц.
Если для аргумента не определено значение функции, возвращается пустое значение. Это может произойти, например, при использовании обратных функций с аргументами, которые выходят за пределы диапазона.
Синтаксис
Основные функции
Cos( Radians )
Cot( Radians )
Sin( Radians )
Tan( Radians )
- Radians — обязательный аргумент.
 Угол, для которого нужно выполнить операцию.
Угол, для которого нужно выполнить операцию.
Cos( SingleColumnTable )
Cot( SingleColumnTable )
Sin( SingleColumnTable )
Tan( SingleColumnTable )
- SingleColumnTable — обязательный аргумент. Таблица с одним столбцом, для углов в котором нужно выполнить операцию.
Обратные функции
Acos( Number )
Acot( Number )
Asin( Number )
Atan( Number )
- Number — обязательный аргумент. Число, для которого нужно выполнить операцию.
Acos( SingleColumnTable )
Acot( SingleColumnTable )
Asin( SingleColumnTable )
Atan( SingleColumnTable )
- SingleColumnTable — обязательный аргумент.

Atan2( X, Y )
- X — обязательный аргумент. Координата по оси X.
- Y — обязательный аргумент. Координата по оси Y.
Вспомогательные функции
Degrees( Radians )
- Radians — обязательный аргумент. Угол в радианах, преобразуемый в градусы.
Pi()
Radians( Degrees )
- Degrees — обязательный аргумент. Угол в градусах, преобразуемый в радианы.
Примеры
Одно число
| Формула | Описание | Результат |
|---|---|---|
| Cos( 1.047197 ) | Возвращает косинус 1,047197 радиана или 60 градусов. | 0.5 |
| Cot( Pi()/4 ) | Возвращает котангенс 0,785398. .. радиана или 45 градусов. .. радиана или 45 градусов. | 1 |
| Sin( Pi()/2 ) | Возвращает синус 1,570796 радиана или 90 градусов. | 1 |
| Tan( Radians(60) ) | Возвращает тангенс 1,047197… радиана или 60 градусов. | 1.732050… |
| Acos( 0.5 ) | Возвращает арккосинус аргумента 0,5 в радианах. | 1.047197… |
| Acot( 1 ) | Возвращает арккотангенс аргумента 1 в радианах. | 0.785398… |
| Asin( 1 ) | Возвращает арксинус аргумента 1 в радианах. | 1.570796… |
| Atan( 1.732050 ) | Возвращает арктангенс аргумента 1,732050 в радианах. | 1.047197… |
| Atan2( 5, 3 ) | Возвращает арктангенс угла (который составляет приблизительно 31 градус) между осью Х и линией, проходящей через точку начала координат (0, 0) и точку с координатами (5, 3).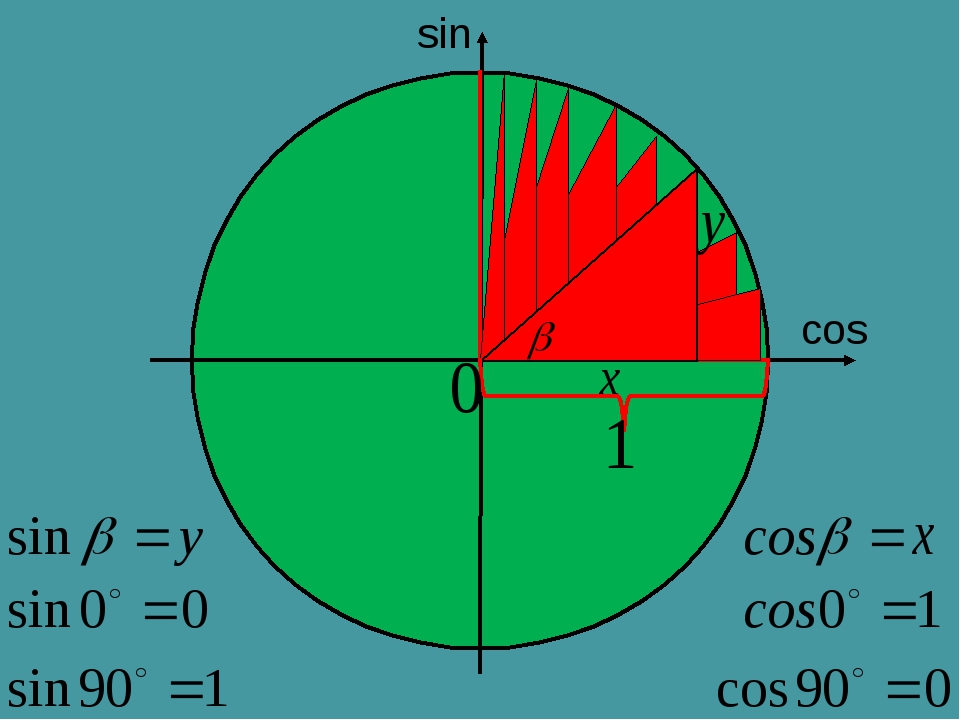 | 0.540419… |
| Atan2( 4, 4 ) | Возвращает арктангенс угла (который составляет ровно π/4 радиана или 45 градусов) между осью Х и линией, проходящей через точку начала координат (0, 0) и точку с координатами (4, 4). | 0.785398… |
| Degrees( 1.047197 ) | Возвращает число в градусах, соответствующее 1,047197 радиана. | 60 |
| Pi() | Возвращает трансцендентное число π. | 3.141592… |
| Radians( 15 ) | Возвращает число в радианах, соответствующее 15 градусам. | 0.261799… |
Таблица с одним столбцом
В примерах этого раздела используется источник данных с именем ValueTable, который содержит следующие данные. Последняя запись в таблице — π/2 радиана или 90 градусов.
Формулы приведения [Love Soft]
Формулы приведения — сокращенное название формул, которые позволяют привести синусы и косинусы к соответствующим значениям синусов и косинусов острых углов (т.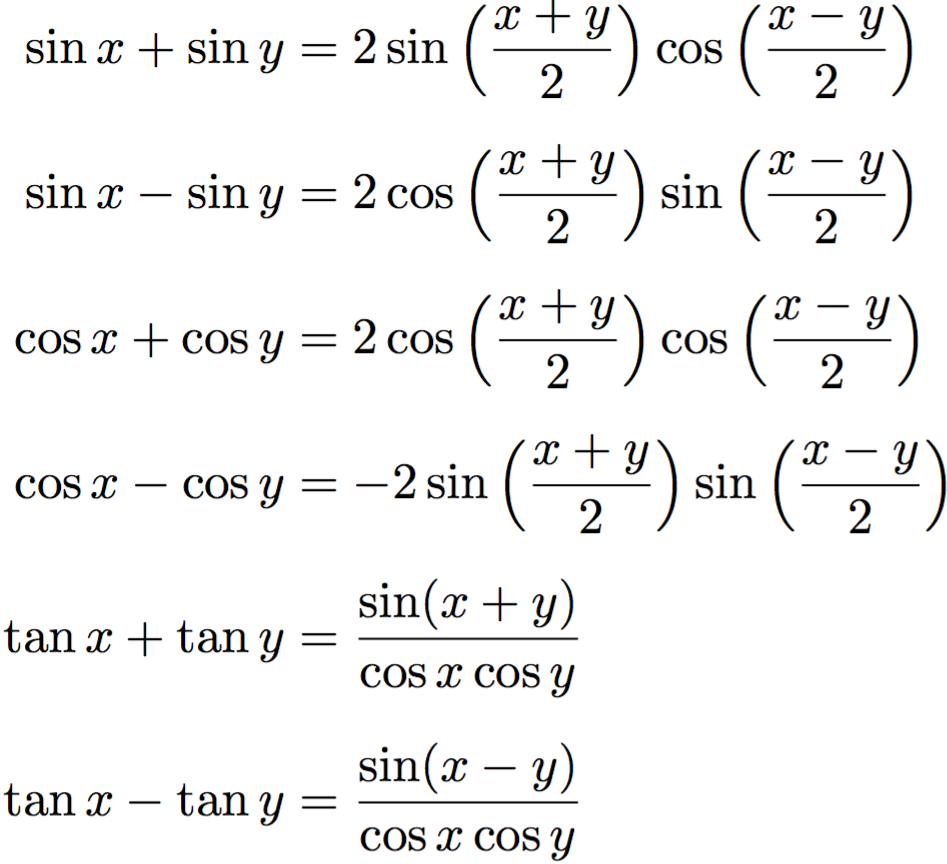 е. от 0 до 90 градусов).
е. от 0 до 90 градусов).
Формулы приведения косинуса
Формулы приведения синуса
Формулы приведения тригонометрических функций
Мнемоническое правило
Подготовительный шаг: аргумент исходной функции представляется в виде
$\pm \alpha + 2\pi z$ или $\pi/2 \pm \alpha + 2\pi z$ или $\pi \pm \alpha + 2\pi z$ или $3\pi/2 \pm \alpha + 2\pi z$,
причем угол должен быть от 0 до 90 градусов (острый). Это замечание про угол альфа очень важно, так как для других углов мнемоническое правило может приводить к неверным результатам.
При приведении функции от аргумента вида kp/2 ± α, где k – целое число, к функции от аргумента α:
Дальше определяется знак, который имеет исходная функция. Функция в правой части записываемой формулы приведения будет иметь такой же знак как и приводимая функция.
название функции сохраняется для 1-го и 3-го случая (нечетный квадрант), и меняется на «дополнительное» (кофункцию), для 2-го и 4-го случая (четный квадрант) [синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс]
Например, при приведении ctg (α – p/2) убеждаемся, что α – p/2 при 0 < α < p/2 лежит в четвертом квадранте, где котангенс отрицателен, и, по второму правилу, меняем название функции: ctg (α – p/2) = –tg α. \circ$.
\circ$.
Правило лошади
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет своё название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
Пример
sin(120) = sin(90+30) = [лошадь говорит да] = cos(30) = $\frac {\sqrt 3} 2 $
или
sin(120) = sin(180-60) = [лошадь говорит нет] = sin(60) = $\frac {\sqrt 3} 2 $
Новоселов — таблица
Формулы приведения в особом доказательстве не нуждаются.
Формулы первой строки выражают свойства четности и нечетности тригонометрических функций, прочие же формулы вытекают из теорем сложения для косинуса и синуса.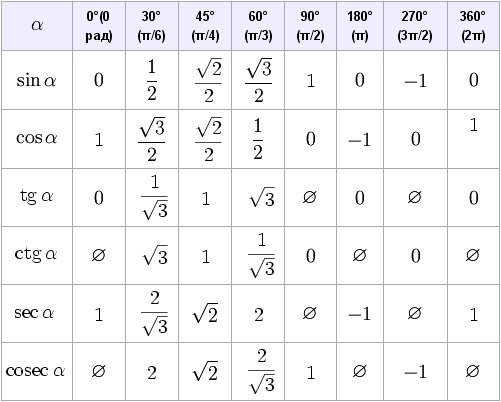
В последнем столбце дано геометрическое пояснение формул приведения для острого угла α (равные треугольники заштрихованы).
Формулы четвёртой и восьмой строк легко вывести также и геометрически. Если к углу α прибавить π, т. е. половину полного оборота, то подвижной радиус займёт диаметрально противоположное положение. Абсцисса х и ордината у конца подвижного радиуса, т. е. косинус и синус угла, изменят знаки (не изменяя абсолютной величины) на противоположные, а их отношения не изменятся.
Формулы приведения показывают, что в практических вычислениях достаточно знать значения тригонометрических функций лишь острых углов (и даже не больших 45°).
Обоснование:
Пример. Вычислить cos(-1000°)
mat/trig/sin-cos-privedenie.txt · Последние изменения: 2020/09/23 22:28 — kc
Модуль для анализа данных инкрементального датчика SINAMICS S120 SMC20 SIN/COS 1VPP абсолютный датчи
Код товара 2467002
Артикул 6SL3055-0AA00-5BA3
Страна Германия
Наименование SINAMICS S120 МОДУЛЬ ДАТЧИКА SMC20 МОДУЛЬ ДЛЯ АНАЛИЗА ДАННЫХ ИНКРЕМЕНТАЛЬНОГО ДАТЧИКА: SIN/COS 1VPP АБСОЛЮТНЫЙ ДАТЧИК: ENDAT БЕЗ КАБЕЛЯ DRIVE-CLIQ МОНТАЖНАЯ ШИРИНА 30 ММ
Упаковки
Сертификат
RU Д-DE. HA10.B01502-18
HA10.B01502-18
Тип изделия Модуль
Характеристики
Код товара 2467002
Артикул 6SL3055-0AA00-5BA3
Страна Германия
Наименование SINAMICS S120 МОДУЛЬ ДАТЧИКА SMC20 МОДУЛЬ ДЛЯ АНАЛИЗА ДАННЫХ ИНКРЕМЕНТАЛЬНОГО ДАТЧИКА: SIN/COS 1VPP АБСОЛЮТНЫЙ ДАТЧИК: ENDAT БЕЗ КАБЕЛЯ DRIVE-CLIQ МОНТАЖНАЯ ШИРИНА 30 ММ
Упаковки
Сертификат
RU Д-DE. HA10.B01502-18
HA10.B01502-18
Тип изделия Модуль
Похожие товары
Это также называют: 6SL3055-0AA00-5BA3, 6SL30550AA005BA3, 6SL3055 0AA00 5BA3, инвертор, привод, ПРЧ, частотник, частотный, преобразователь, ПЧ, ЧП, 6SL3O55-OAAOO-5BA3
Всегда поможем:
Центр поддержки
и продаж
Скидки до 10% +
баллы до 10%
Доставка по городу
от 150 р.
Получение в 150
пунктах выдачи
Sin, cos — это отношения сторон в прямоугольном треугольнике
Тригонометрия — математическая наука о тригонометрических функциях sin и cos. Эти отношения — базовые понятия, без их понимания не получится изучать что-то новое в этой области. Это не сложно, главное понимать, откуда берутся значения косинусов и синусов и как их рассчитать.
Из истории появления
В работах древнегреческих математиков уже в III веке до нашей эры встречаются отношения отрезков треугольников. В древнем Риме их исследовал Менелай. Математик Ариабхата из Индии также дал определения этим понятиям. Вычисления синуса он связывал с «архадживами» (дословный перевод — половина тетивы лука) — полухордами окружности. Позднее понятие сократилось до слова «джива». Арабские математики использовали термин «джайб» (выпуклость).
А что насчет cos? Это отношение значительно моложе. Понятие представляет собой сокращение от латинского выражения completely sinus, что в переводе звучит как дополнительный синус (синус дополнительной дуги).
Современные краткие латинские обозначения sin и cos введены Уильямом Отредом в VII веке и закреплены в трудах Эйлера.
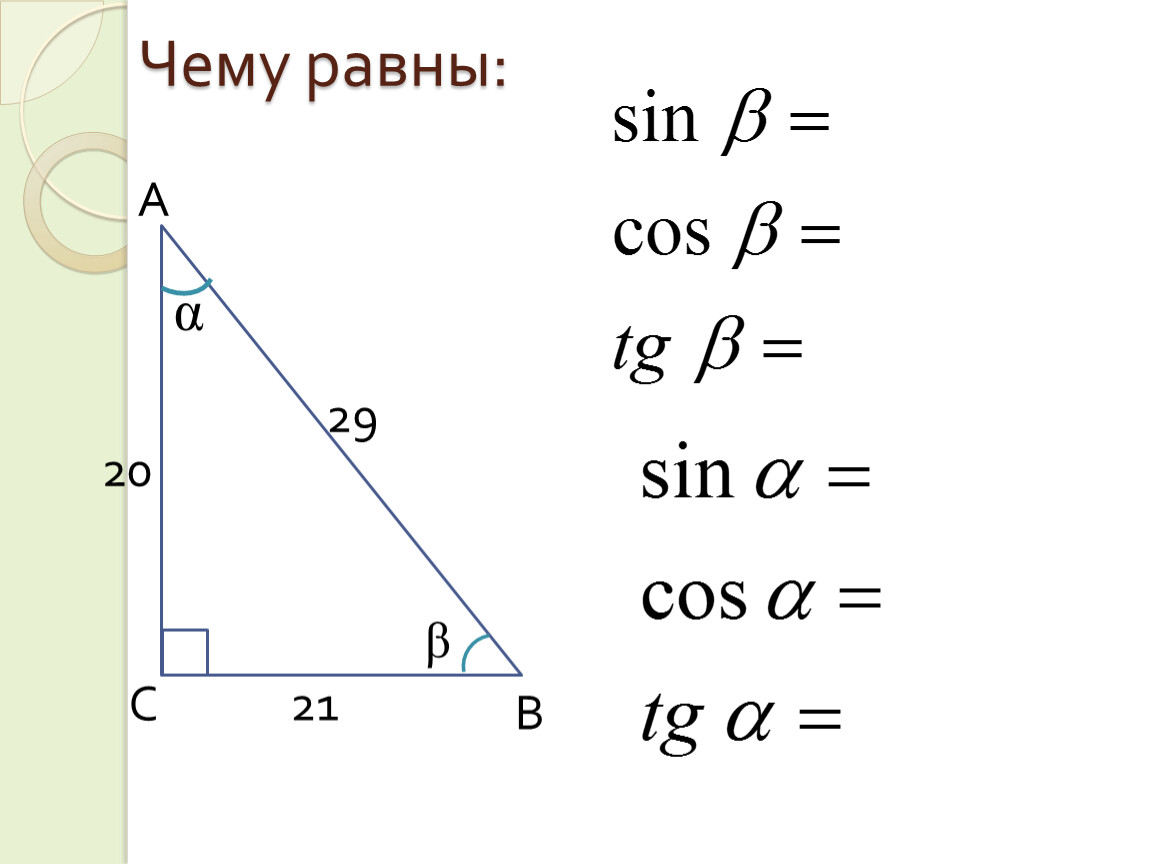
Что такое прямоугольный треугольник?
Поскольку sin и cos — это отношения величин этой фигуры, то необходимо знать, что она собой представляет. Это вид треугольника, у которого один из углов прямой, то есть составляет 90 градусов.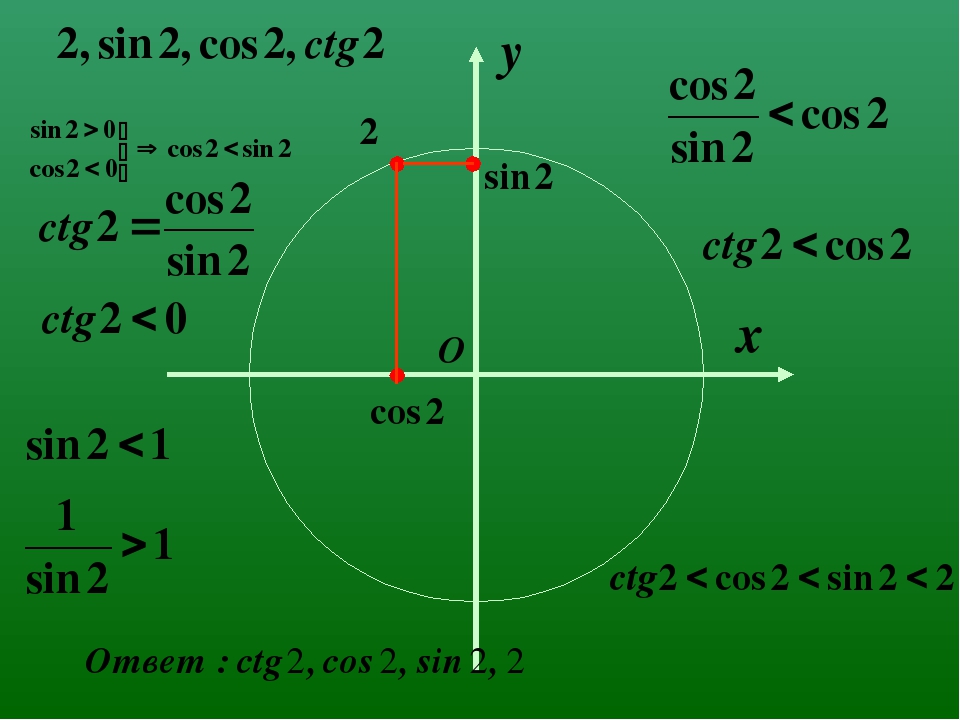 Катетами называют стороны, прилежащие к прямому углу (лежат напротив острых), а гипотенузой — противолежащую сторону.
Катетами называют стороны, прилежащие к прямому углу (лежат напротив острых), а гипотенузой — противолежащую сторону.
Они связаны между собой теоремой Пифагора.
sin — это отношение противолежащего катета к гипотенузе.
cos — это отношение прилежащего катета к гипотенузе.
Зная численные значения сторон треугольника можно определить обе эти величины.
Если рассмотреть единичную окружность с центром в точке (0,0) декартовой системы координат, тогда, взяв точку на оси абсцисс и повернув ее на острый угол альфа, опустим перпендикуляр на ось абсцисс. Длина катета, прилежащего к гипотенузе в полученном прямоугольном треугольнике, будет равна абсциссе точки.
Следовательно, определение через отношение сторон cos(sin) острого угла в этой фигуре эквивалентно нахождению косинуса (синуса) угла поворота при альфа, лежащем в пределах от 0 до 90 градусов.
Для чего нужны данные тригонометрические функции?
Известно, что сумма углов в прямоугольном треугольнике равна 180 градусам. Значит, зная два угла, можно найти третий. С помощью теоремы Пифагора находят значение любой из сторон по двум другим. А их отношения через sin и cos помогут, если известен один угол и одна любая сторона.
Значит, зная два угла, можно найти третий. С помощью теоремы Пифагора находят значение любой из сторон по двум другим. А их отношения через sin и cos помогут, если известен один угол и одна любая сторона.
Вопрос решения такой задачи возник при составлении карт звездного неба, когда точно невозможно было измерить все величины.
С другой стороны, отношения sin и cos — это тригонометрические функции угла. Если известно его значение, то с помощью специальных таблиц получится найти все необходимые показатели.
Sohcahtoa: синус, косинус, тангенс
Sohca … что? Просто простой способ запомнить , как работают синус, косинус и тангенс:
Soh … | S ine = O pposite / H ypotenuse |
. | C осин = A djacent / H ypotenuse |
…toa | T angent = O pposite / A djacent |
Прямой треугольник
Хорошо, давайте посмотрим, о чем идет речь.
Во-первых, названия Противоположный, Смежный и Гипотенуза происходят от прямоугольного треугольника:
- «Напротив» противоположно углу θ
- «Соседний» примыкает (рядом) к углу θ
- «Гипотенуза» — длинная
Соседний всегда находится рядом с углом
И Напротив , напротив угла
Синус, косинус и тангенс
И Синус , Косинус и Касательный — три основные функции в тригонометрии.
Их часто сокращают до sin , cos и tan .
Вычисление — это просто , одна сторона прямоугольного треугольника делится на другую сторону … нам просто нужно знать, какие стороны, и именно здесь «sohcahtoa» помогает.
Для треугольника с углом θ функции рассчитываются следующим образом:
Синус: | soh… | с дюймов ( θ ) = o pposite / h ypotenuse |
Косинус: | … ка … | c os ( θ ) = a djacent / h ypotenuse |
Касательная: | …toa | t an ( θ ) = o pposite / a djacent |
Пример: каковы синус, косинус и тангенс 30 °?
Треугольник 30 ° имеет гипотенузу (длинную сторону) длиной 2 , противоположную сторону длиной 1 и смежную сторону √3 , вот так:
Теперь мы знаем длины, можем вычислить функции:
Синус | soh.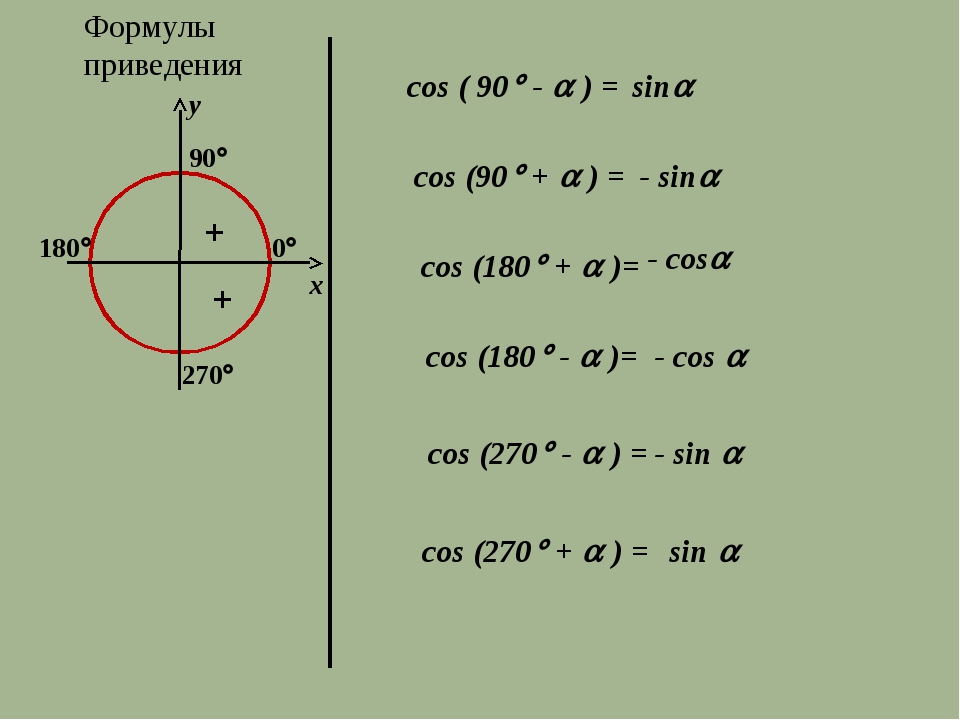 .. .. | sin (30 °) = 1 2 = 0,5 |
Косинус | … ка … | cos (30 °) = 1,732 … 2 = 0,866 … |
Касательная | … toa | тангенс (30 °) = 1 1,732… = 0,577 … |
(возьмите калькулятор и проверьте его!)
Как помнить
Я считаю, что «sohcahtoa» легко запомнить … но вот и другие способы, если хотите:
- S ailors O ften H ave C urly A uburn H air T ill O ld A ge.
- S ome O ld H orses C an A lways H ear T наследник O wners A pproach.

- S ome O ld H en C aught A nother H en T aking O ne A way.
Практика здесь:
Sin, Cos и Tan — Математика GCSE Revision
В этом разделе рассматриваются Sin, Cos и Tan в области тригонометрии.
Прямоугольный треугольник — это треугольник, в котором один из углов является прямым.Гипотенуза прямоугольного треугольника — это самая длинная сторона, противоположная прямому углу. Соседняя сторона — это сторона, которая находится между рассматриваемым углом и прямым углом. Противоположная сторона противоположна рассматриваемому углу.
В любом прямоугольном треугольнике , для любого угла:
Синус угла = длина противоположной стороны
длина гипотенузы
Косинус угла = длина соседней стороны
длина гипотенузы
Тангенс угла = длина противоположной стороны
длина соседней стороны
Итак, в сокращенной записи:
sin = o / h cos = a / h tan = o / a
Часто вспоминается по: soh cah toa
Пример
Найдите длину стороны x на схеме ниже:
Угол 60 градусов. Нам дана гипотенуза, и нам нужно найти прилегающую сторону. Эта формула, которая связывает эти три, следующая:
Нам дана гипотенуза, и нам нужно найти прилегающую сторону. Эта формула, которая связывает эти три, следующая:
cos (угол) = смежный / гипотенуза
, следовательно, cos60 = x / 13
, следовательно, x = 13 × cos60 = 6,5
, следовательно, длина стороны x составляет 6,5 см.
Это видео объясняет, как работают формулы.
Графики Sin, Cos и Tan — (ВЫСШИЙ УРОВЕНЬ)
На следующих графиках показано значение sinø, cosø и tanø в зависимости от ø (ø представляет собой угол).Из графика sin мы видим, что sinø = 0, когда ø = 0 градусов, 180 градусов и 360 градусов.
Обратите внимание, что график tan имеет асимптоты (линии, к которым график приближается, но никогда не пересекает). Это красные линии (на самом деле они не являются частью графика).
Также обратите внимание, что графики sin, cos и tan являются периодическими. Это означает, что они повторяются. Следовательно, например, sin (ø) = sin (360 + ø).
Обратите внимание на симметрию графиков.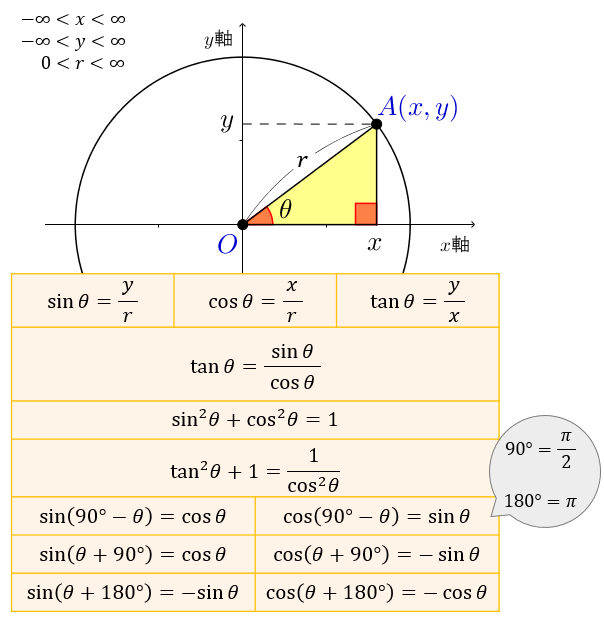 Например, cos симметричен по оси y, что означает, что cosø = cos (-ø). Так, например, cos (30) = cos (-30).
Например, cos симметричен по оси y, что означает, что cosø = cos (-ø). Так, например, cos (30) = cos (-30).
Кроме того, sin x = sin (180 — x) из-за симметрии sin в прямой ø = 90.
Для получения дополнительной информации о тригонометрии щелкните здесь
косинусов
Затем рассмотрим углы 30 ° и 60 °.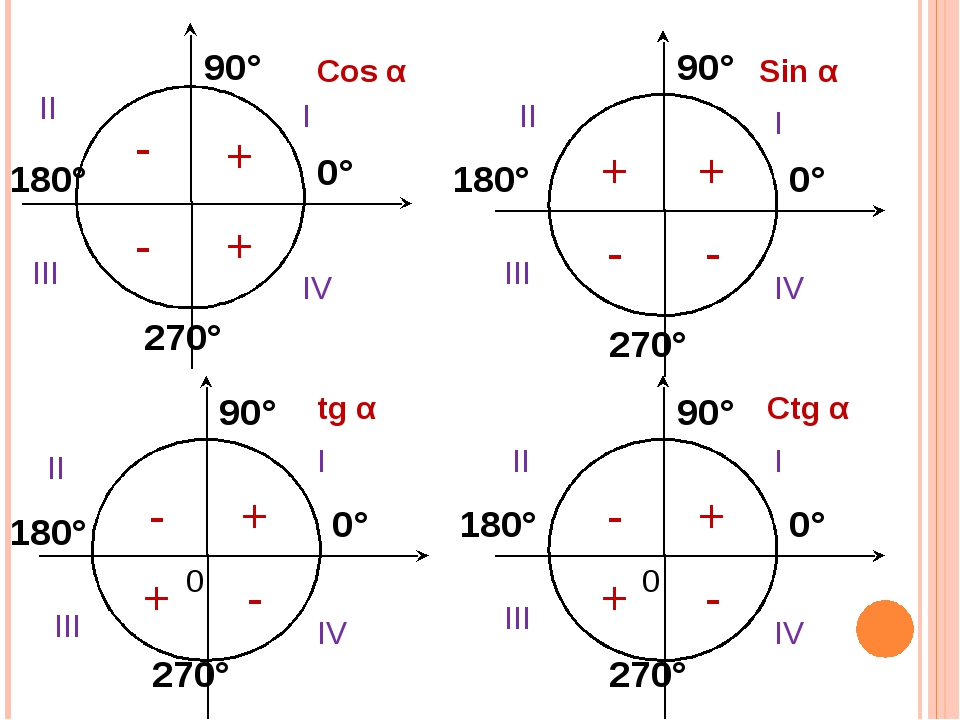 В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
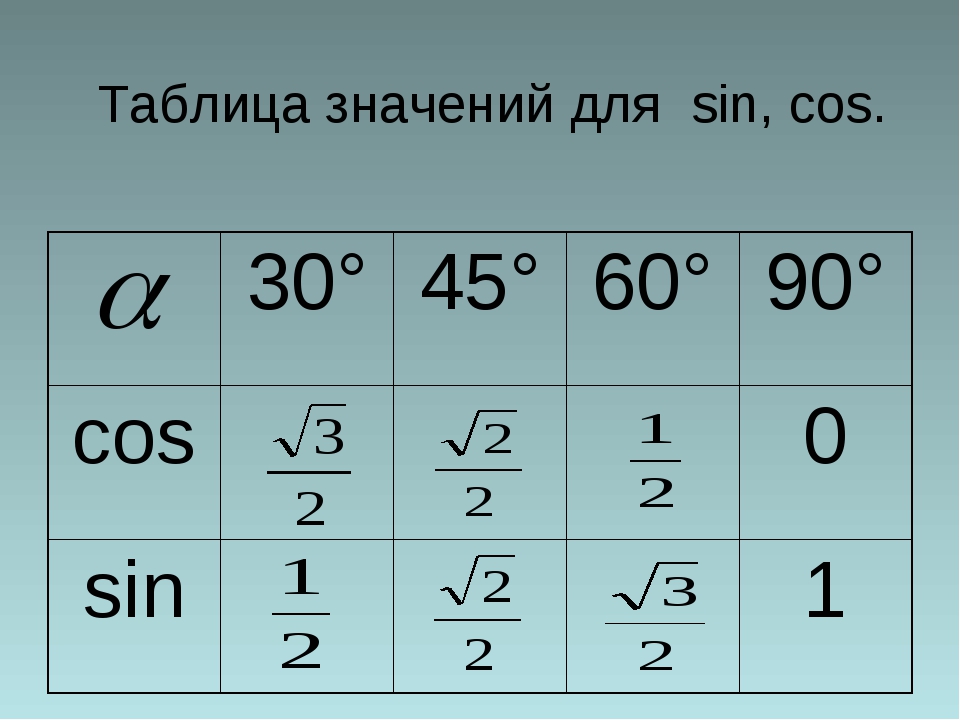
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
В прямоугольном треугольнике 30 ° -60 ° -90 ° отношения
сторон равны 1: √3: 2. Отсюда следует, что
sin 30 ° = cos 60 ° = 1/2, и
sin 60 ° = cos 30 ° = √3 / 2.
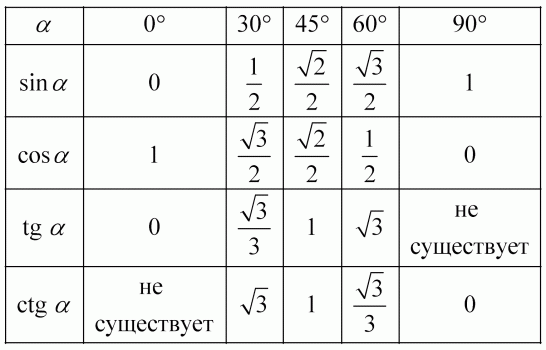
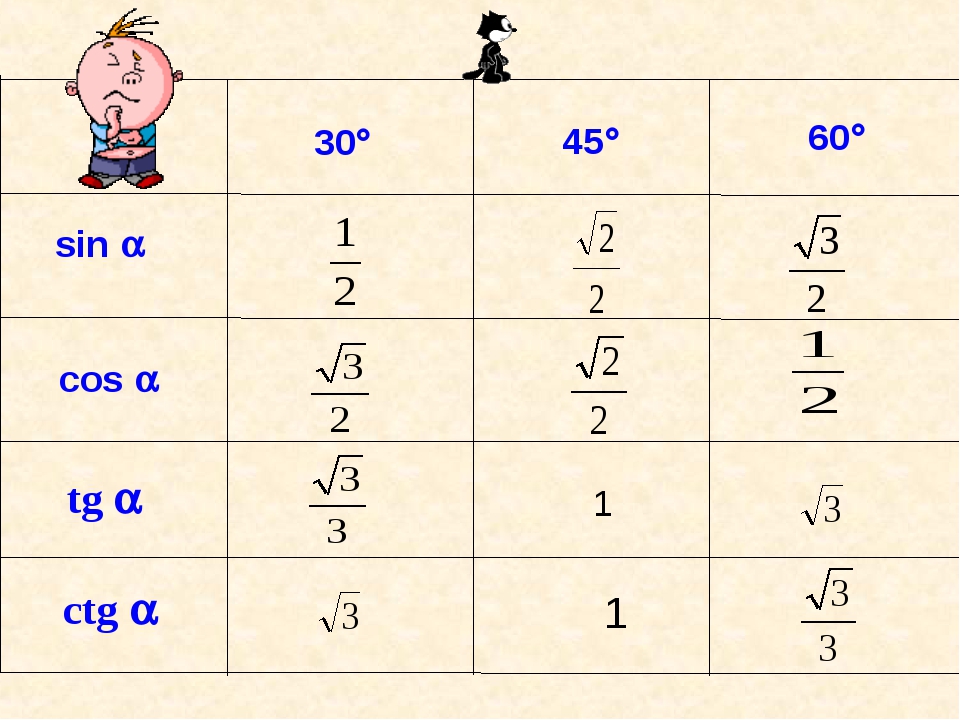
Эти результаты занесены в эту таблицу.
| Угол | Градусы | Радианы | косинус | синус | ||||
|---|---|---|---|---|---|---|---|---|
| 90 ° | π /2 | 0 | 1 | 09 | 9 /3 | 1/2 | √3 / 2 | |
| 45 ° | π /4 | √2 / 2 | √2 / 2 | |||||
| 30 ° | π /6 | √3 / 2 | 1/2 | |||||
| 0 ° | 0 | 1 | 0 |
Упражнения
Все эти упражнения относятся к прямоугольным треугольникам со стандартной маркировкой. 30. b = 2,25 метра и cos A = 0,15.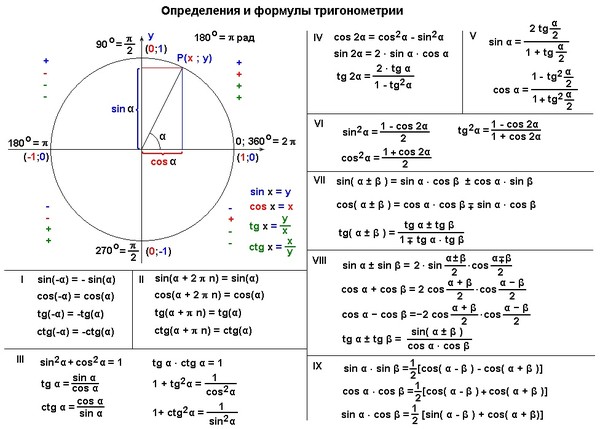 Найдите a и c.
Найдите a и c.
33. b = 12 футов и cos B = 1/3. Найдите c и a.
35. b = 6,4, c = 7,8. Найдите A и a.
36. A = 23 ° 15 ‘, c = 12.15. Найдите a и b.
Подсказки
30. Косинус A связывает b с гипотенузой c, , поэтому вы можете сначала вычислить c. Если вы знаете b и c, , вы можете найти a по теореме Пифагора.
33. Вы знаете b и cos B. К сожалению, cos B — это отношение двух сторон, которых вы не знаете, а именно a / c. Тем не менее, это дает вам уравнение, с которым можно работать: 1/3 = a / c. Тогда c = 3 a. Тогда из теоремы Пифагора следует, что a 2 + 144 = 9 a 2 . Вы можете решить это последнее уравнение для a , а затем найти c.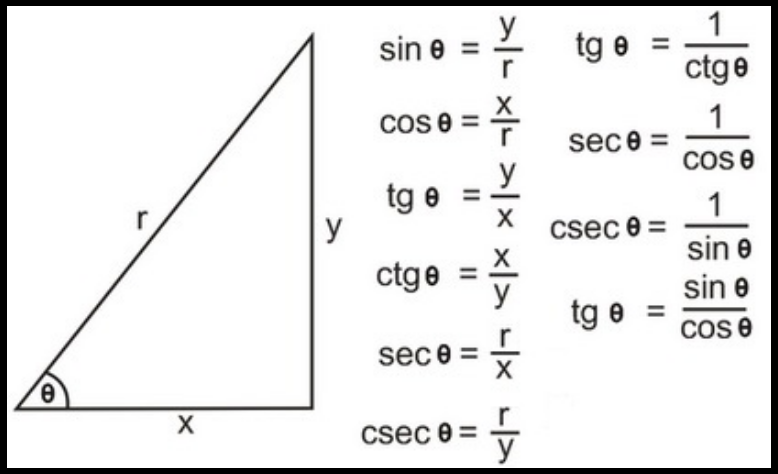
35. b и c дают A по косинусам и a по теореме Пифагора.
36. A и c дают a по синусам и b по косинусам.
ответы
30. c = b / cos A = 2,25 / 0,15 = 15 метров; a = 14,83 метра.
33. 8 a 2 = 144, поэтому a 2 = 18. Следовательно, a равно 4,24 ‘или 4’3 «.
c = 3 a , что равно 12.73 ‘или 12’9 «.
35. cos A = b / c = 6,4 / 7,8 = 0,82. Следовательно, A = 34,86 ° = 34 ° 52 ‘, или около 35 °.
a 2 = 7,8 2 — 6,4 2 = 19,9, поэтому a составляет около 4,5.
36. a = c sin A = 12,15 sin 23 ° 15 ‘= 4,796.
b = c cos A = 12,15 cos 23 ° 15 ‘= 11.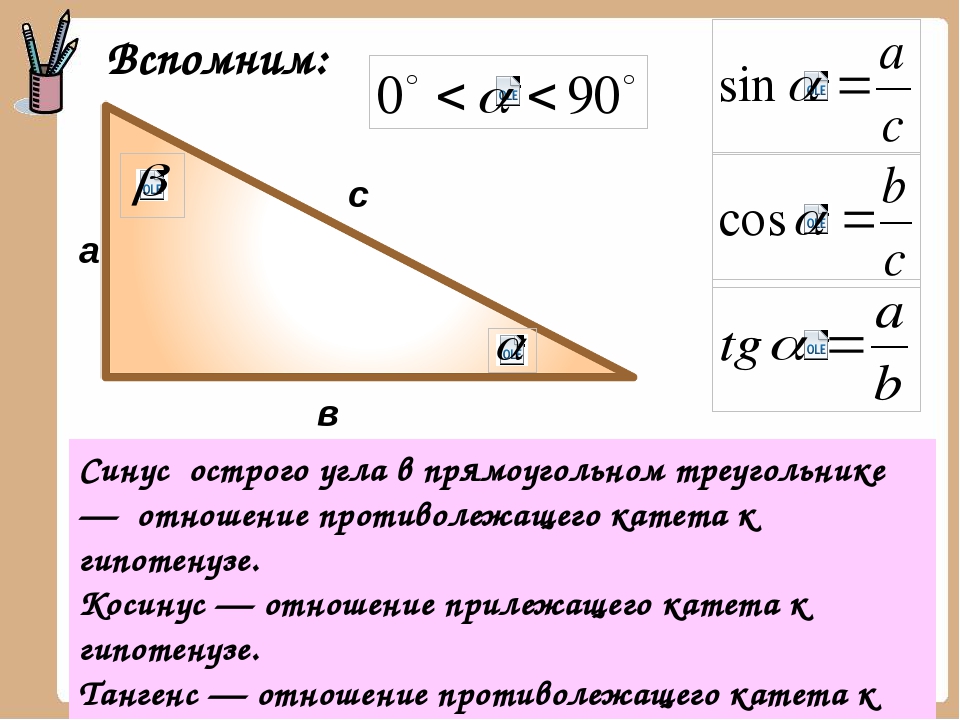 17.
17.
Графики: синус и косинус
Чтобы увидеть, как изображены функции синуса и косинуса, воспользуйтесь калькулятором, компьютером или набором тригонометрических таблиц, чтобы определить значения функций синуса и косинуса для ряда различных степеней (или радиан) меры (см. таблицу 1).
Затем постройте эти значения и получите основные графики функции синуса и косинуса (рисунок 1).
Рисунок 1
Один период а) синусоидальной функции и б) косинусной функции.
Синус-функция и косинус-функция имеют периоды 2π; поэтому образцы, показанные на рисунке, непрерывно повторяются слева и справа (рисунок 2).
Несколько периодов а) синусоидальной функции и б) косинусной функции.К функциям синуса и косинуса можно добавить несколько дополнительных членов и множителей, которые изменяют их форму.
Дополнительный член A в функции y = A + sin x допускает вертикальный сдвиг в графике синусоидальных функций.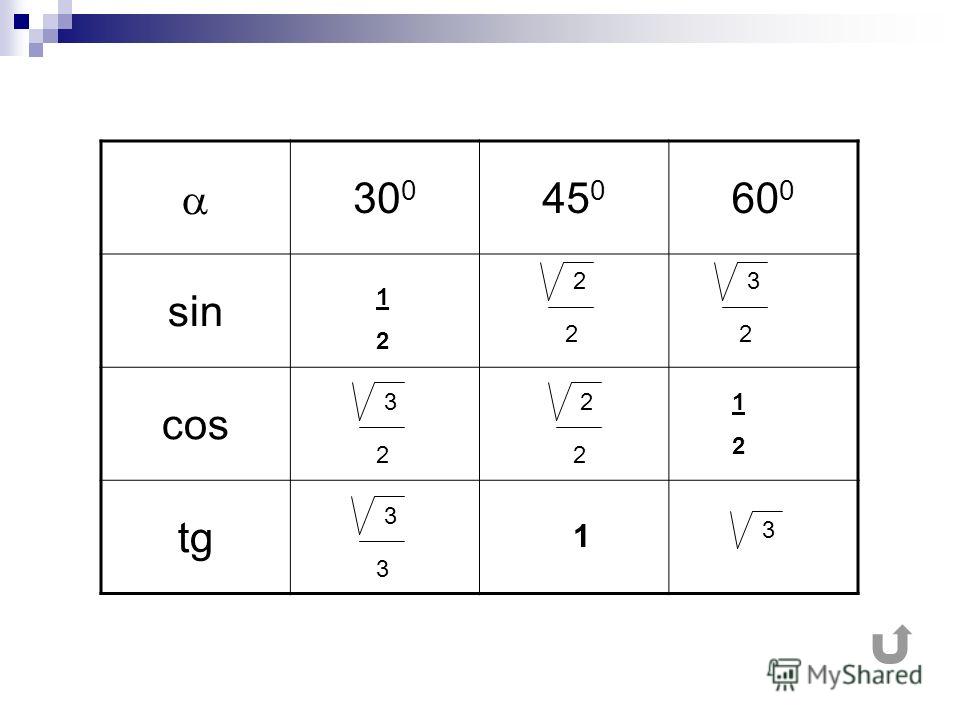 Это также верно для функции косинуса (рисунок 3).
Это также верно для функции косинуса (рисунок 3).
Рисунок 3
Примеры нескольких вертикальных сдвигов синусоидальной функции.
Дополнительный множитель B в функции y = B sin x допускает изменение амплитуды и синусоидальной функции. Амплитуда, | B | — максимальное отклонение от оси x , то есть половина разницы между максимальным и минимальным значениями графика.Это также верно для функции косинуса (рисунок 4).
Рисунок 4
Примеры нескольких амплитуд синусоидальной функции.
Объединение этих цифр дает функции y = A + B sin x , а также y = A + B cos x . Эти две функции имеют минимальных и максимальных значений, как определено следующими формулами.Максимальное значение функции — M = A + | B |.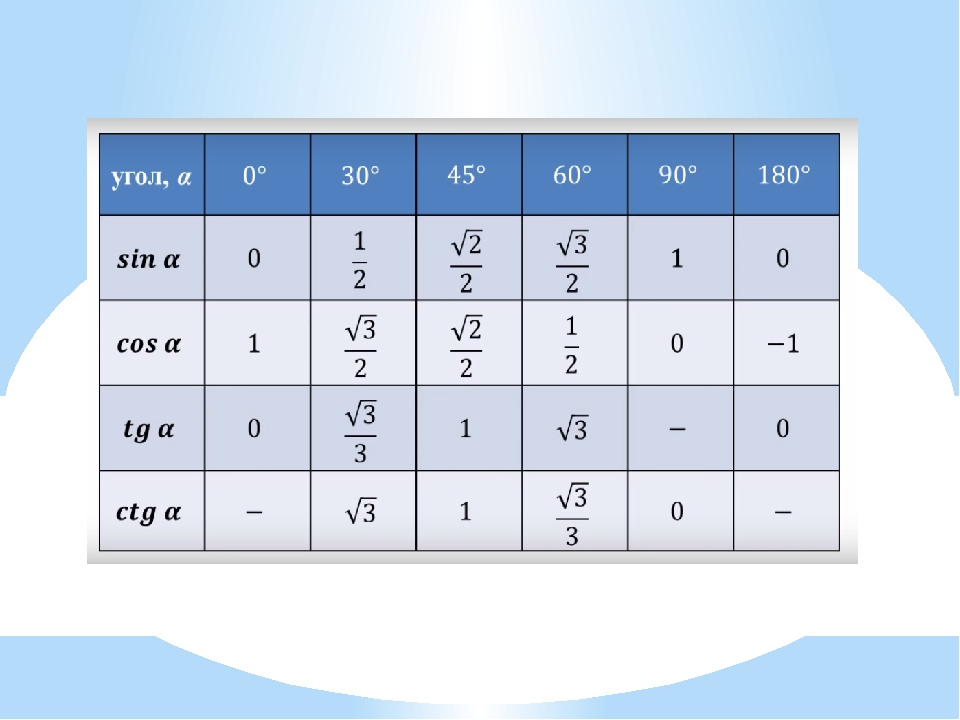 Это максимальное значение возникает всякий раз, когда sin x = 1 или cos x = 1. Минимальное значение функции составляет m = A — | B |. Этот минимум возникает всякий раз, когда sin x = -1 или cos x = -1.
Это максимальное значение возникает всякий раз, когда sin x = 1 или cos x = 1. Минимальное значение функции составляет m = A — | B |. Этот минимум возникает всякий раз, когда sin x = -1 или cos x = -1.
Пример 1: Постройте график функции y = 1 + 2 sin x . Какие максимальные и минимальные значения функции?
Максимальное значение: 1 + 2 = 3.Минимальное значение — 1 −2 = −1 (Рисунок 5).
Рисунок 5
Чертеж для примера 1.
Пример 2: Постройте график функции y = 4 + 3 sin x . Какие максимальные и минимальные значения функции?
Максимальное значение 4 + 3 = 7. Минимальное значение 4 — 3 = 1 (Рисунок 6).
Рисунок 6
Рисунок для примера 2.
Дополнительный коэффициент C в функции y = sin Cx допускает изменение периода (продолжительность цикла) синусоидальной функции на период. (Это также верно для функции косинуса.) Период функции y = sin Cx равен 2π / | C |. Таким образом, функция y = sin 5 x имеет период 2π / 5. На рисунке 7 показаны дополнительные примеры.
(Это также верно для функции косинуса.) Период функции y = sin Cx равен 2π / | C |. Таким образом, функция y = sin 5 x имеет период 2π / 5. На рисунке 7 показаны дополнительные примеры.
Рисунок 7
Примеры нескольких частот а) синусоидальной функции и б) косинусоидальной функции.
Дополнительный член D в функции y = sin ( x + D ) учитывает фазовый сдвиг (перемещение графика влево или вправо) на графике синусоидальных функций. (Это также верно для функции косинуса.) Сдвиг фазы равен | D |. Это положительное число. Не имеет значения, будет ли сдвиг влево (если D положительный) или вправо (если D отрицательный). Функция синуса нечетная, а функция косинуса четная.Функция косинуса выглядит точно так же, как функция синуса, за исключением того, что она сдвинута на π / 2 единицы влево (рисунок 8). Другими словами,
Рисунок 8
Примеры нескольких фазовых сдвигов синусоидальной функции.
Пример 3: Каковы амплитуда, период, фазовый сдвиг, максимальное и минимальное значения
y = 3 + 2 sin (3 x -2)
y = 4 cos2π x
Пример 4: Нарисуйте график y = cosπ x .
Поскольку cos x имеет период 2π, cos π x имеет период 2 (рисунок 9).
Рисунок 9
Рисунок для примера 4.
Пример 5: Нарисуйте график y = 3 cos (2x + π / 2).
Поскольку cos x имеет период 2π, cos 2x имеет период π (рисунок 10).
Рисунок 10Рисунок для примера 5.
График функции y = — f ( x ) находится путем отражения графика функции y = f ( x ) относительно оси x . Таким образом, рисунок может также представлять график y = −3 sin 2 x .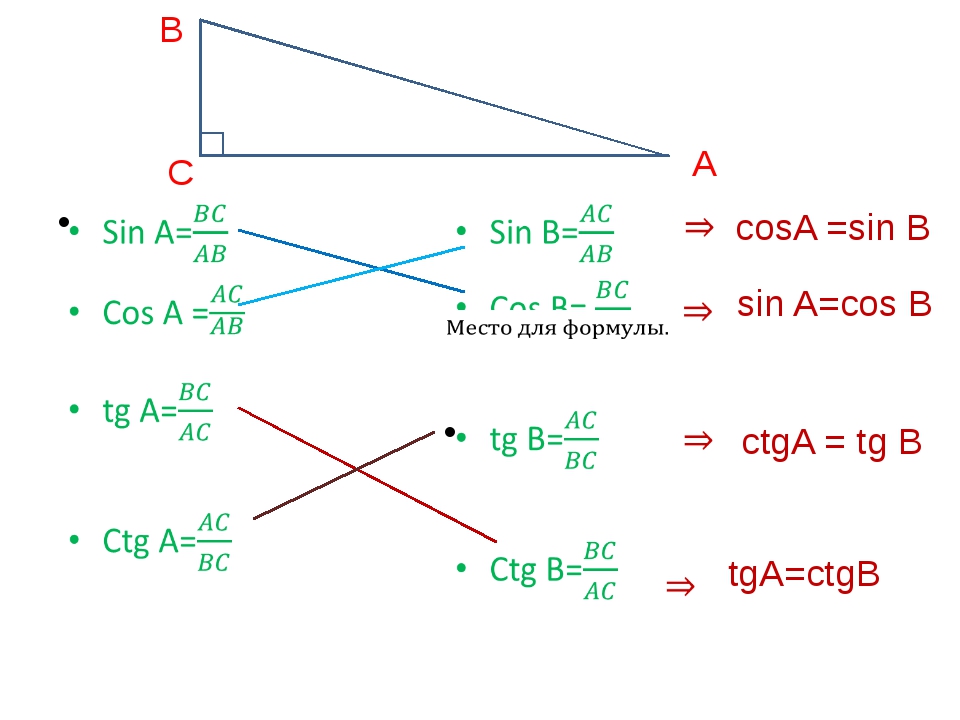 В частности,
В частности,
Важно понимать отношения между функциями синуса и косинуса и то, как сдвиги фазы могут изменять их графики.
sin cos tan — определения, факты и решаемые примеры
В этом мини-уроке мы исследуем тригонометрические отношения sin, cos и tan.
Тригонометрия — это исследование взаимосвязи между углами и сторонами треугольника (особенно прямоугольного).
Теорема Пифагора и тригонометрия были наиболее важными понятиями при построении пирамид.
Пифагор работал над соотношением сторон прямоугольного треугольника, тогда как люди, подобные Гиппарку, работали над соотношением сторон и углов прямоугольного треугольника.
Sin, cos и tan являются основными тригонометрическими отношениями и основами тригонометрии.
Давайте подробно рассмотрим sin, cos и tan.
План урока Что мы подразумеваем под Sin Cos Tan? Sin, cos и tan — три основных тригонометрических отношения, каждое из которых дает отношение двух (из трех) сторон прямоугольного треугольника.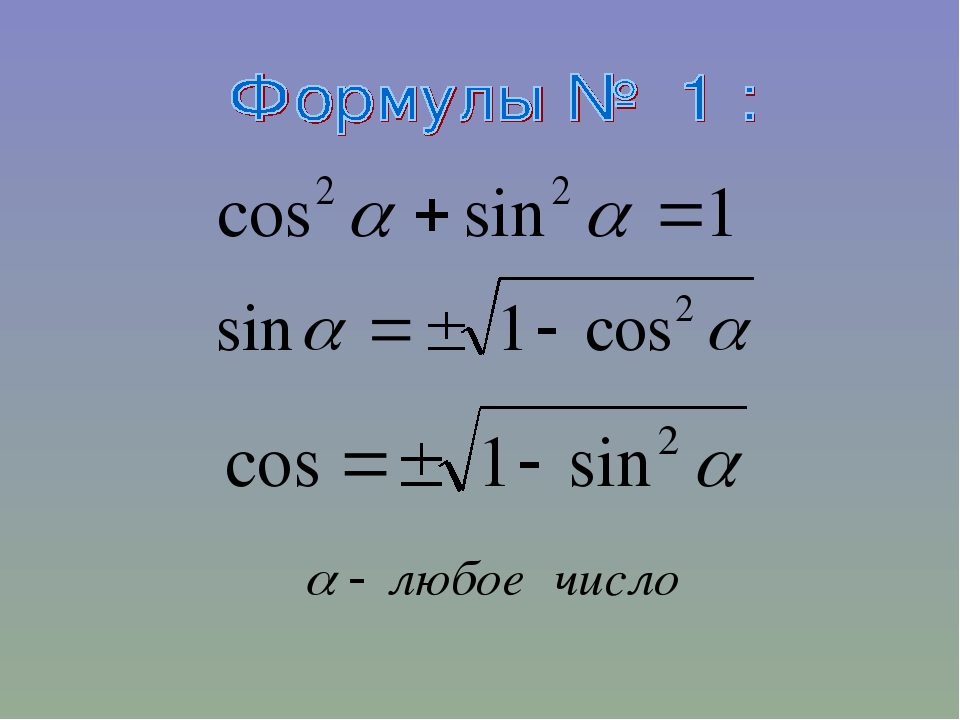
Мы знаем, что самая длинная сторона прямоугольного треугольника известна как «гипотенуза», а две другие стороны известны как «катеты».«
В тригонометрии самая длинная сторона прямоугольного треугольника все еще известна как «гипотенуза», но два других катета имеют следующие названия:
- противоположная сторона и
- смежная сторона
Мы определяем «противоположную» и «смежную» стороны, исходя из угла, о котором мы говорим.
Важные примечания
- «Противоположная сторона» — это сторона, которая прямо «противоположна» углу.
- «Смежная сторона» — это сторона, которая «касается» угла.
Sin, cos и tan определяются в терминах двух из трех сторон (противоположной, смежной и гипотенузы) прямоугольного треугольника.
ФормулыВот формулы sin, cos и tan.
\ [\ begin {align} \ sin \ theta & = \ dfrac {\ text {Opposite}} {\ text {Hypotenuse}} \\ [0. 2 см] \ cos \ theta & = \ dfrac {\ text {Adjancent}} {\ text {Hypotenuse}} \\ [0,2 см] \ tan \ theta & = \ dfrac {\ text {Opposite}} {\ text {Смежно }} \\ [0,2 см] \ end {align} \]
2 см] \ cos \ theta & = \ dfrac {\ text {Adjancent}} {\ text {Hypotenuse}} \\ [0,2 см] \ tan \ theta & = \ dfrac {\ text {Opposite}} {\ text {Смежно }} \\ [0,2 см] \ end {align} \]
Помимо этих трех тригонометрических соотношений, у нас есть еще три соотношения, называемые csc, sec и cot, которые являются обратными величинами sin, cos и tan соответственно.
Пример
Найдите sin, cos и tan следующего треугольника для заданного угла \ (\ theta \).
Раствор
В треугольнике самая длинная сторона (или) сторона, противоположная прямому углу, — это \ (AC \), и, следовательно, \ (AC \) — гипотенуза.
Угол, противоположный \ (\ theta \), равен \ (AB \), поэтому \ (AB \) — противоположная сторона.
Угол, примыкающий к \ (\ theta \), равен \ (BC \), поэтому \ (BC \) является прилегающей стороной.
Теперь мы находим \ (\ sin \ theta, \ cos \ theta, \) и \ (\ tan \ theta \), используя приведенные выше формулы:
\ [\ begin {align} \ sin \ theta & = \ dfrac {\ text {Opposite}} {\ text {Hypotenuse}} = \ dfrac {AB} {AC} = \ dfrac {3} {5} \\ [0,2 см] \ cos \ theta & = \ dfrac {\ text {Adjancent}} {\ text {Hypotenuse}} = \ dfrac {BC} {AC} = \ dfrac {4} {5} \\ [0.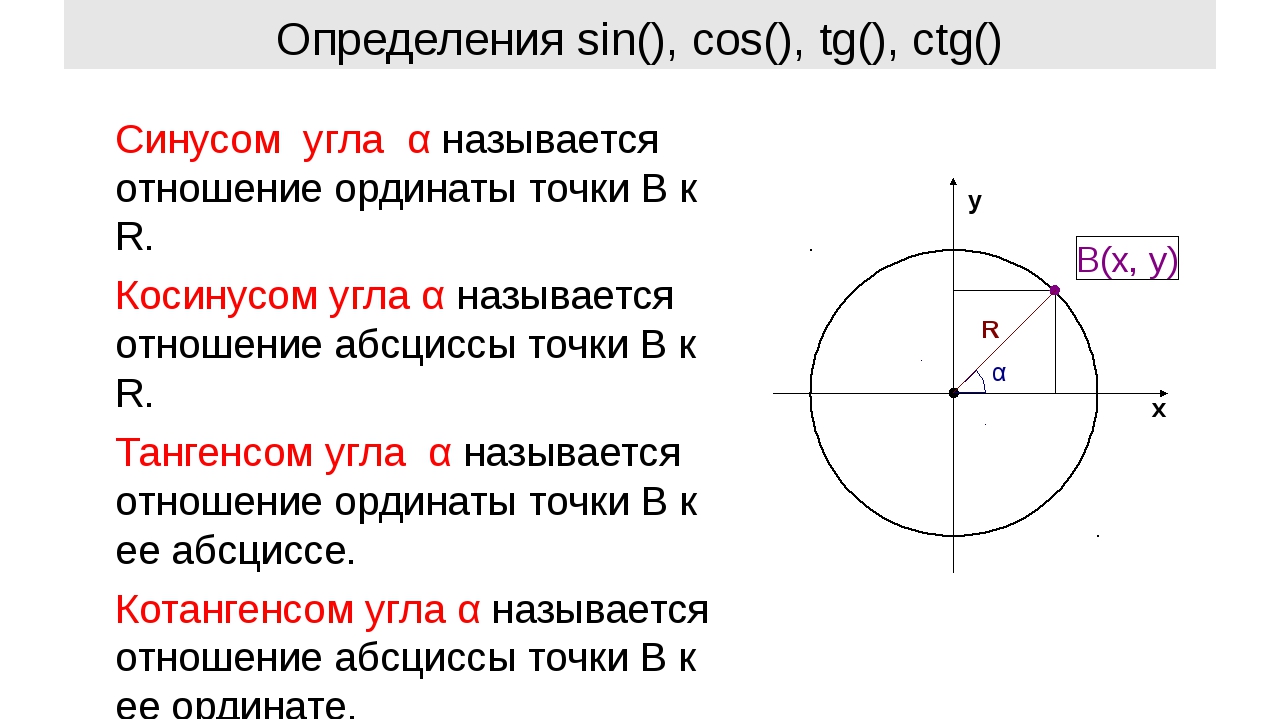 2 см] \ tan \ theta & = \ dfrac {\ text {Противоположный}} {\ text {Смежный}} = \ dfrac {AB} {BC} = \ dfrac {3} {4} \\ [0,2 см] \ end {align} \]
2 см] \ tan \ theta & = \ dfrac {\ text {Противоположный}} {\ text {Смежный}} = \ dfrac {AB} {BC} = \ dfrac {3} {4} \\ [0,2 см] \ end {align} \]
Советы и хитрости
- Вы пытаетесь запомнить эти формулы? Вот уловка, чтобы запомнить формулы sin, cos и tan.
Помните, что тригонометрические отношения не зависят от длин сторон треугольника, а зависят от угла, потому что в конечном итоге мы берем соотношение сторон.
Вот иллюстрация, где вы можете изменить угол с помощью данного ползунка; и где можно изменить длину сторон, перетащив точку B.
Вы все еще можете видеть, что значения тригонометрических соотношений остаются постоянными под определенным углом, хотя длины сторон меняются.
Мы можем найти sin, cos и tan любого угла с помощью графического калькулятора, используя следующие кнопки и задав угол в градусах / радианах по мере необходимости.
Вот калькулятор Sin Cos Tan.«
Вы можете ввести любой угол в градусах / радианах и выбрать любую тригонометрическую функцию.
Показывает значение выбранной тригонометрической функции по отношению к заданному углу.
Sin Cos Tan ДиаграммаХотя мы можем найти значения cos, sin и tan с помощью калькулятора, есть таблица с некоторыми стандартными углами 0 o , 30 o , 45 o , 60 o и 90 o. .
Полезные советы sin cos tan table:
Из этой таблицы вам нужно запомнить:
- Углы 0 o , 30 o , 45 o , 60 o и 90 o по порядку.
- Первую строку (греха) можно запомнить так: \ (\ dfrac {\ sqrt 0} {2}, \ dfrac {\ sqrt 1} {2}, \ dfrac {\ sqrt 2} {2}, \ dfrac {\ sqrt 3} {2}, \) и \ (\ dfrac {\ sqrt 4} {2} \)
Это все, что вам нужно запомнить, потому что:
- Строка cos такая же, как и строка sin, только в обратном порядке.

- Каждое значение в строке tan получается делением соответствующих значений sin на cos, потому что tan = sin / cos.
Вы можете увидеть, как tan = sin / cos здесь:
\ [\ begin {align} \ dfrac {\ sin \ theta} {\ cos \ theta} & = \ dfrac {\ text {Opposite}} {\ text {Hypotenuse}} \ div \ dfrac {\ text {смежные} } {\ text {Гипотенуза}} \\ [0.2 см] & = \ dfrac {\ text {Противоположно}} {\ text {Гипотенуза}} \ times \ dfrac {\ text {Гипотенуза}} {\ text {Смежные}} \\ [0,2 см] & = \ dfrac {\ текст {Противоположный}} {\ text {Смежный}} \\ [0,2 см] & = \ tan \ theta \ end {align} \]
Где мы используем Sin Cos Tan в реальной жизни?
Мы действительно используем sin, cos и tan для решения многих реальных проблем. Вот пример.
Пример
Лестница прислоняется к кирпичной стене под углом 50 o к горизонту.
Если лестница находится на расстоянии 10 футов от стены, то до какой высоты стены она достигает?
Раствор
Предположим, что лестница достигает \ (x \) футов стены.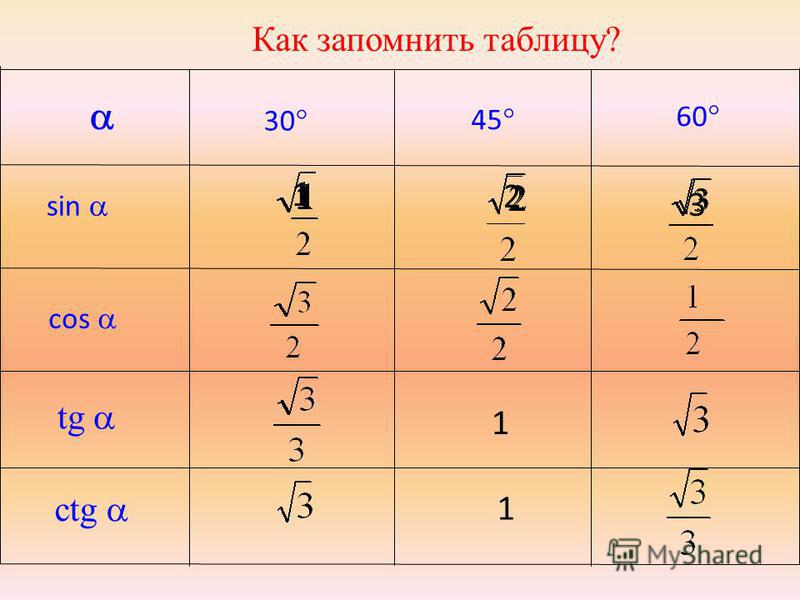
Используя предоставленную информацию:
Здесь мы знаем соседнюю сторону (которая составляет 10 футов), и мы должны найти противоположную сторону (которая равна \ (x \) ft).
Итак, мы используем отношение между противоположной и соседней сторонами, которое является желтовато-коричневым.\ circ \\ [0,2 см] x & \ приблизительно 11,9 \ text {ft} \ end {align} \]
Здесь tan 50 o вычисляется с помощью калькулятора, а окончательный ответ округляется до 1 десятичного знака.
Таким образом, лестница достигает 11,9 фута стены.
Решенные примеры
Можем ли мы помочь Рэйчел найти \ (\ cos \ theta \) относительно следующего треугольника?
Раствор
Чтобы найти \ (\ cos \ theta \), нам нужны прилегающая сторона и гипотенуза.2 \\ [0,2 см] & = 100 \\ [0,2 см] AC & = \ sqrt {100} = 10 \ end {align} \]
Следовательно, \ [\ cos \ theta = \ dfrac {\ text {смежный}} {\ text {Hypotenuse}} = \ dfrac {8} {10} = \ dfrac {4} {5} \]
| \ (\ cos \ theta = \ dfrac {4} {5} \) |
Найдите точную длину тени, отбрасываемой 15-футовым фонарным столбом, когда угол наклона солнца составляет 60º.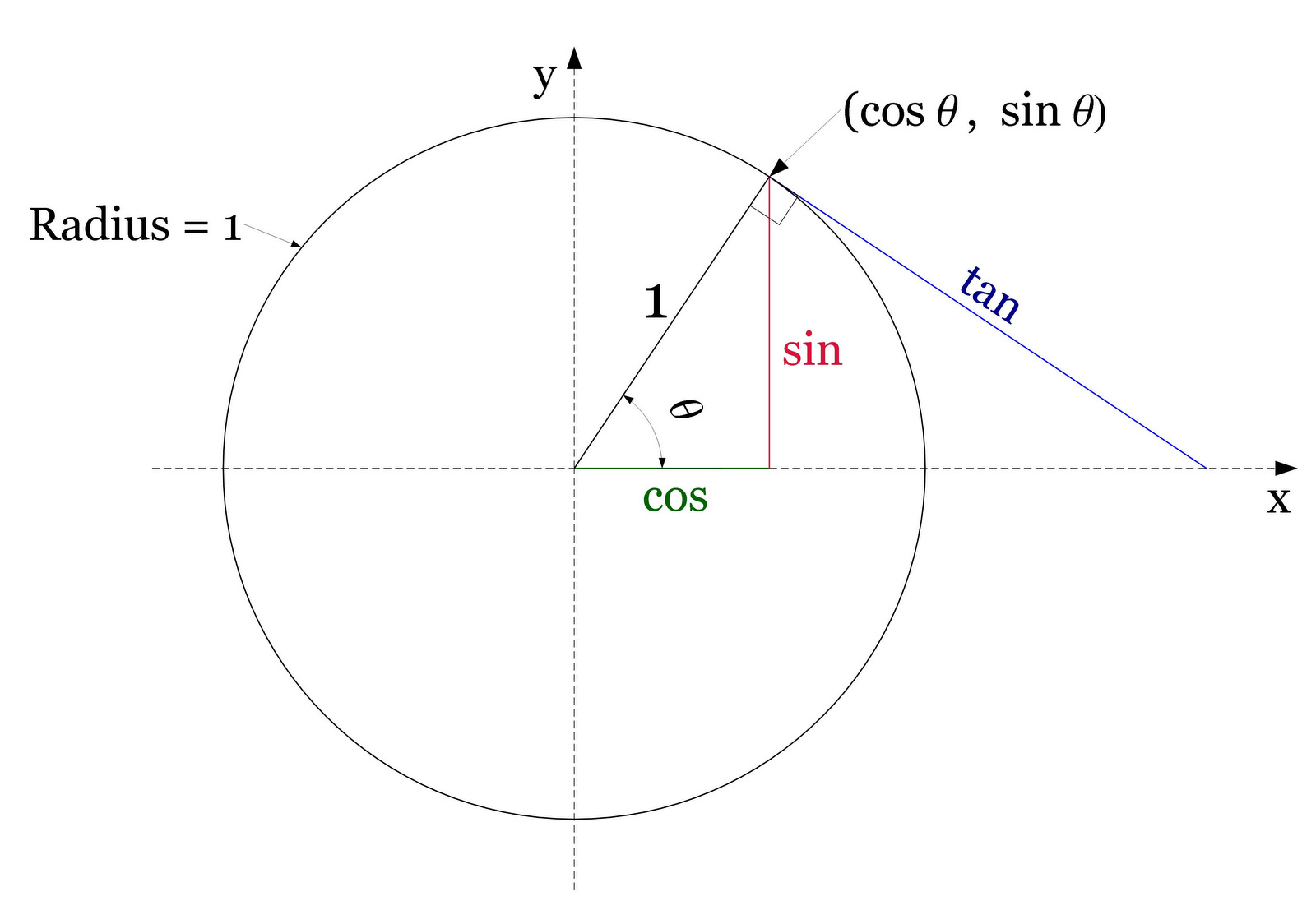
Раствор
Предположим, что длина тени фонарного столба составляет \ (x \) футов.\ circ} \\ [0,2 см] x & = \ dfrac {15} {\ sqrt 3} \, \, \, \ text {(с использованием диаграммы)} \\ [0,2 см] x & = \ dfrac {15 \ sqrt 3} {3} \ end {align} \]
| \ (\ следовательно \) Длина тени фонарного столба составляет \ (\ dfrac {15 \ sqrt 3} {3} \) футов |
Интерактивные вопросы
Вот несколько занятий для вас.
Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции sin cos tan. Математическое путешествие вокруг sin cos tan начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению.
Часто задаваемые вопросы (FAQ)
1. Как использовать sin cos tan?
Мы можем использовать sin cos и tan для решения реальных проблем.
Чтобы решить любую проблему, мы сначала рисуем рисунок, который описывает проблему, и используем соответствующее тригонометрическое соотношение для решения проблемы.
2.
 Как найти sin cos tan?
Как найти sin cos tan?Чтобы найти sin, cos и tan, мы используем следующие формулы:
\ [\ begin {align} \ sin \ theta & = \ dfrac {\ text {Opposite}} {\ text {Hypotenuse}} \\ [0,2 см] \ cos \ theta & = \ dfrac {\ text {Adjancent} } {\ text {Hypotenuse}} \\ [0,2 см] \ tan \ theta & = \ dfrac {\ text {Opposite}} {\ text {Adjacent}} \\ [0,2 см] \ end {align} \]
Чтобы найти sin, cos и tan стандартных углов, вы можете использовать таблицу, упомянутую на этой странице.
Чтобы найти sin, cos и tan для любого угла, вы можете использовать калькулятор на этой странице (или) графический калькулятор.
3. Как сделать sin cos tan?
Чтобы найти sin, cos и tan, мы используем следующие формулы:
\ [\ begin {align} \ sin \ theta & = \ dfrac {\ text {Opposite}} {\ text {Hypotenuse}} \\ [0,2 см] \ cos \ theta & = \ dfrac {\ text {Adjancent} } {\ text {Hypotenuse}} \\ [0,2 см] \ tan \ theta & = \ dfrac {\ text {Opposite}} {\ text {Adjacent}} \\ [0,2 см] \ end {align} \]
Чтобы найти sin, cos и tan стандартных углов, вы можете использовать таблицу, упомянутую на этой странице. 2 \\ [0.2 \\ [0,2 см] \ text {Смежный} & = \ sqrt {5} k \ end {align} \]
2 \\ [0.2 \\ [0,2 см] \ text {Смежный} & = \ sqrt {5} k \ end {align} \]
Следовательно, \ (\ cos \ theta = — \ dfrac {\ text {смежный}} {\ text {Hypotenuse}} = — \ dfrac {\ sqrt {5} k} {3k} \\ = — \ dfrac {\ sqrt 5} {3} \)
Синус-косинус-касательная
Чтобы лучше понять некоторые проблемы, связанные с самолетами и двигательная установка необходимо использовать некоторые математические идеи из тригонометрия, изучение треугольников. Начнем с некоторых определений и терминологии. который мы будем использовать на этом слайде.Прямоугольный треугольник — это трехсторонняя фигура с одним углом, равным 90 градусам. Угол 90 градусов называется прямым углом , что дает название прямоугольному треугольнику. Выбираем один из двух оставшихся углов и маркируем его c а третий угол обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , тогда мы знаем, что значение d :
90 + с + г = 180
г = 180 — 90 — в
d = 90 — c
Определим сторону треугольника противоположную от прямого угла к
— гипотенуза .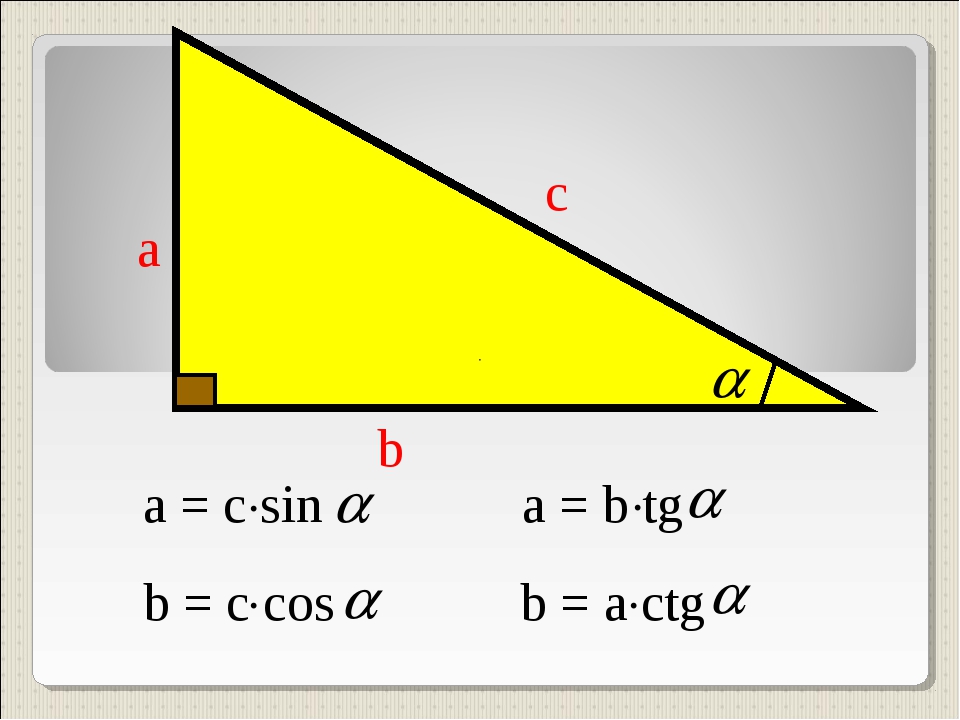 Это самая длинная из трех сторон.
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов.
означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h .
Есть сторона, противоположная углу c , которую мы обозначаем o .
для «противоположного». Оставшуюся сторону мы маркируем как для «смежных».
Угол c образован пересечением гипотенузы h .
и соседняя сторона а .
Это самая длинная из трех сторон.
прямоугольного треугольника. Слово «гипотенуза» происходит от двух греческих слов.
означает «растягивать», так как это самая длинная сторона. Обозначим гипотенузу символом h .
Есть сторона, противоположная углу c , которую мы обозначаем o .
для «противоположного». Оставшуюся сторону мы маркируем как для «смежных».
Угол c образован пересечением гипотенузы h .
и соседняя сторона а .
Нас интересует соотношение сторон и углов прямоугольный треугольник. Начнем с некоторых определений. Мы будем называть соотношение стороны прямоугольного треугольника, противоположной гипотенузе синус и присвоить ему символ sin .
грех = о / ч
Отношение смежной стороны прямоугольного треугольника к гипотенузе называется косинус и обозначен символом cos .
cos = а / ч
Наконец, отношение противоположной стороны к соседней стороне называется
касательная и обозначена символом tan .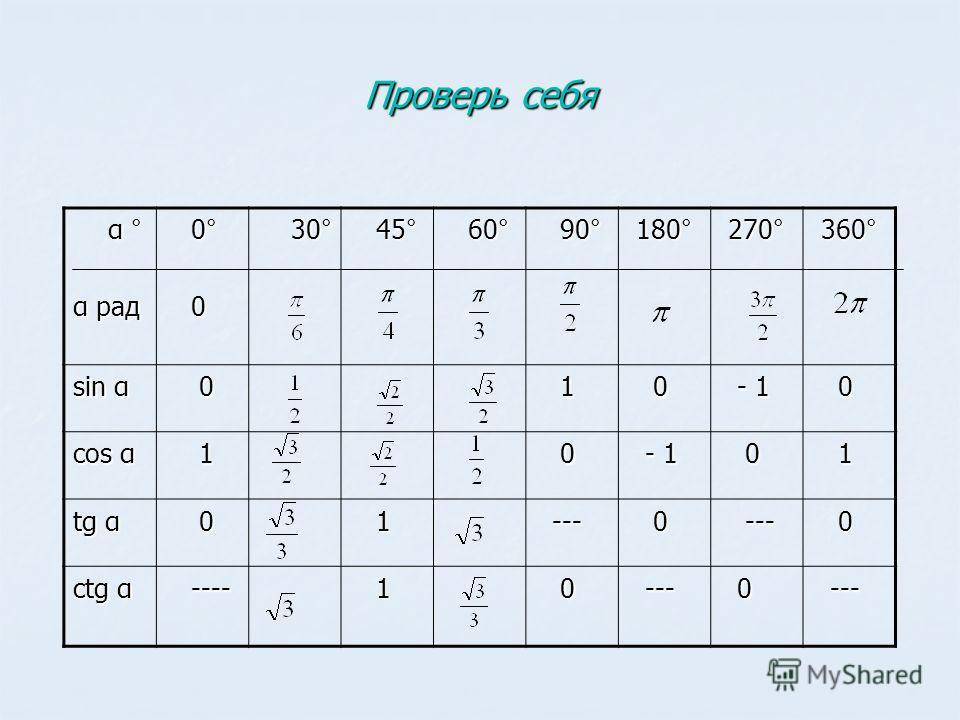
загар = о / а
Мы утверждаем, что значение каждого коэффициента зависит только от значения
угол c , образованный смежной и гипотенузой.
Чтобы продемонстрировать этот факт,
давайте изучим три фигуры в середине страницы.В этом примере у нас есть
8-футовая лестница, которую мы собираемся прислонить к стене. Стена
8 футов высотой, и мы нарисовали белые линии на стене
и синие линии на земле с интервалом в один фут.
Длина лестницы фиксированная.
Если наклонить лестницу так, чтобы ее основание находилось на расстоянии 2 фута от стены,
лестница образует угол около 75,5 градусов с землей.
Лестница, земля и стена образуют прямоугольный треугольник. Соотношение расстояния от
стены (а — прилегающая) к длине лестницы (h — гипотенуза) составляет 2/8 =.25.
Это определено как косинус c = 75,5 градусов. (На
другая страница
покажем, что если бы лестница была вдвое длиннее (16 футов),
и наклонена под тем же углом (75,5 градуса), чтобы он сидел вдвое больше
далеко (4 фута) от стены.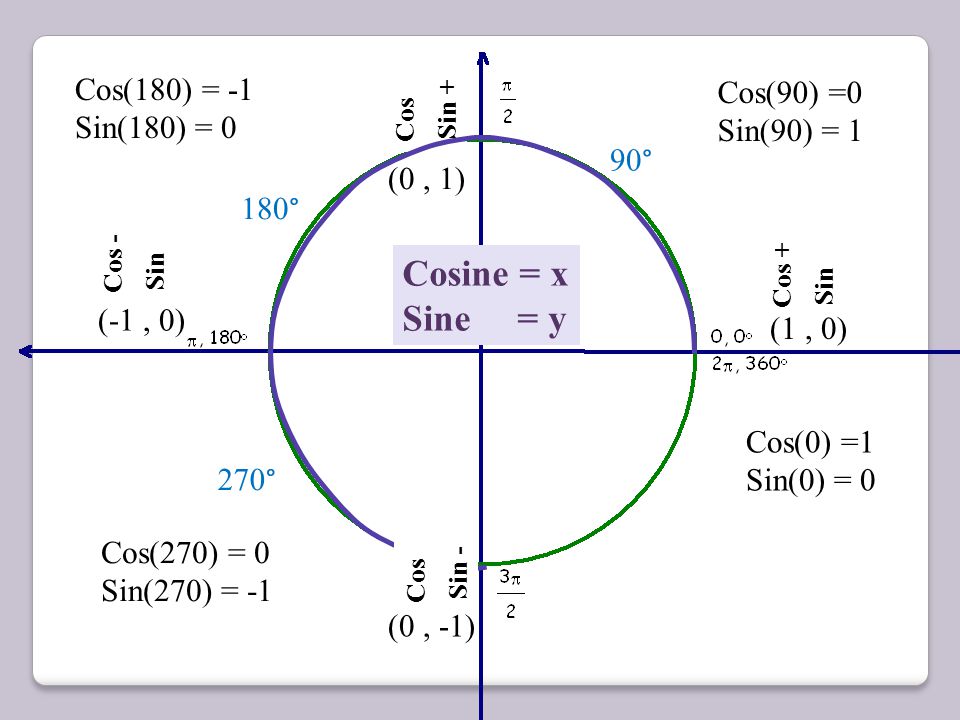 2 = 64 — 4 = 60
2 = 64 — 4 = 60
о = 7.745
Отношение противоположности к гипотенузе равно 0,967 и определяется как синус угла c = 75,5 градусов.
Теперь предположим, что мы наклоняем 8-футовую лестницу так, чтобы ее основание находилось на 4 футах от стены.
Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем в
первый пример. Угол составляет 60 градусов, а соотношение прилегающих к
гипотенуза теперь 4/8 = 0,5. Уменьшение угла c увеличивает косинус угла, потому что гипотенуза фиксирована
а соседний увеличивается с уменьшением угла.Если мы наклоним 8 футов
лестнице так, чтобы ее основание находилось на расстоянии 6 футов от стены, угол уменьшается до
около 41,4 градуса, и соотношение увеличивается до 6/8, что составляет 0,75.
Как видите, для каждого угла
на земле есть уникальная точка, которой соприкасается 8-футовая лестница,
И это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом.
Математики называют эту ситуацию
функция. Соотношение соседних
сторона гипотенузы является функцией угла c , поэтому мы можем записать
символ как cos (c) = значение .
Соотношение соседних
сторона гипотенузы является функцией угла c , поэтому мы можем записать
символ как cos (c) = значение .
Также обратите внимание, что по мере увеличения cos (c) уменьшается sin (c) . Если мы наклоним лестницу так, чтобы основание находилось на расстоянии 6,938 фута от стены, угол c становится 30 градусов, а отношение соседнего к гипотенуза 0,866. Сравнивая этот результат со вторым примером, мы обнаруживаем, что:
cos (c = 60 градусов) = sin (c = 30 градусов)
sin (c = 60 градусов) = cos (c = 30 градусов)
Мы можем обобщить это соотношение:
sin (c) = cos (90 — c)
90 — c — величина угла d .Вот почему мы назовем соотношение смежного и гипотенузы «косинусом» угла.
sin (c) = cos (d)
Поскольку синус, косинус и тангенс являются функциями угла c , мы можем
определить (измерить) коэффициенты один раз и составить таблицы значений
синус, косинус и тангенс для различных значений c . Позже, если мы узнаем
значение угла в прямоугольном треугольнике, таблицы покажут нам соотношение
сторон треугольника.Если нам известна длина одной стороны, мы можем найти длину другой.
стороны.
Или, если мы знаем соотношение любых двух сторон прямоугольного треугольника, мы можем
найти значение угла между сторонами. Мы можем использовать таблицы для решения проблем. Некоторые примеры проблем, связанных с треугольниками и углами, включают
силы
на самолете в полете,
применение
крутящие моменты,
и разрешение
составные части
вектора.
Позже, если мы узнаем
значение угла в прямоугольном треугольнике, таблицы покажут нам соотношение
сторон треугольника.Если нам известна длина одной стороны, мы можем найти длину другой.
стороны.
Или, если мы знаем соотношение любых двух сторон прямоугольного треугольника, мы можем
найти значение угла между сторонами. Мы можем использовать таблицы для решения проблем. Некоторые примеры проблем, связанных с треугольниками и углами, включают
силы
на самолете в полете,
применение
крутящие моменты,
и разрешение
составные части
вектора.
Вот таблицы синуса, косинуса и тангенса, которые вы можете использовать для решения проблемы.
Действия:
Экскурсии с гидом
Навигация ..
- Руководство для начинающих Домашняя страница
Функции синуса, косинуса и тангенса
Функции синуса, косинуса и тангенсаФункции синуса, косинуса и тангенса
Предыстория: В дальнейшем мы предполагаем, что вы знакомы с тригонометрия. Функции синуса, косинуса и тангенса (обозначаемые sin, cos и tan) важны в тригонометрии и многих других областях математики.
Вот как они получены. Рассмотрим вектор (красная стрелка) на картинке справа.
Он имеет хвост в начале координат, имеет длину х и ориентирован по
угол θ .
Функции синуса, косинуса и тангенса (обозначаемые sin, cos и tan) важны в тригонометрии и многих других областях математики.
Вот как они получены. Рассмотрим вектор (красная стрелка) на картинке справа.
Он имеет хвост в начале координат, имеет длину х и ориентирован по
угол θ .Пусть ( x, y ) обозначают координаты голова вектора (т.е. пусть x и y будут движения в направлении x , а затем в направлении y требуется, чтобы добраться от хвоста до головы вектора.) Три стрелки образуют треугольник в стандартной позиции .
Теперь представьте изменение угла θ . Вектор укажет на другой
направление, но его голова все еще будет где-то в пунктирном круге
(потому что его длина х неизменна).
Значения x и y изменятся. Например на картинке справа значения x и y отрицательны.
| Определения: Функции синуса, косинуса и тангенса (обозначаемые sin, cos и tan) определяются как возвращающие следующие отношения: Эти отношения являются функциями θ , потому что x и y изменяются с θ .  |
График функции синуса: На рисунке слева показан красный вектор указывает под разными углами θ а график справа показывает результирующую функцию sin ( θ ):
График функции косинуса: На следующем рисунке слева снова показано красный вектор, указывающий под разными углами θ а график справа показывает результирующую функцию cos ( θ ):
График касательной функции: На следующем графике показана функция tan ( θ ).Пунктирная вертикаль линии — это асимптоты (линии, к которым функция приближается, но никогда не касается):
На трех приведенных выше графиках угол θ измеряется в радианах. Если вы хотите, чтобы θ измерялось в градусах , тогда просто измените горизонтальный масштаб так что θ проходит от 0 до 360 ° вместо от 0 до 2π радиан; в остальном формы графиков не изменились. Функции синуса, косинуса и тангенса называются периодическими .
 Это означает
что они повторяются в горизонтальном направлении после
определенный интервал называется периодом . Функции синуса и косинуса имеют период
2π радиан, а тангенциальная функция имеет период π радиан.
Это означает
что они повторяются в горизонтальном направлении после
определенный интервал называется периодом . Функции синуса и косинуса имеют период
2π радиан, а тангенциальная функция имеет период π радиан.Домен и диапазон: Из графиков выше мы видим, что для функций синуса и косинуса область является всей действительные числа и диапазон действительных чисел от -1 до +1 включительно. Для касательной функции доменом являются все действительные числа, кроме ± π / 2, ± 3π / 2, ± 5π / 2,…, (или в градусах: ± 90 °, ± 270 °, ± 450 °,…), где касательная функция не определена.Диапазон касательной функции — это все действительные числа.
Определения синуса, косинуса и тангенса могут быть
расширенный до комплексных чисел
определяя функции их рядами Тейлора
вместо соотношения двух длин.
В этом случае область и диапазон функций синуса и косинуса все
комплексные числа, а область определения касательной функции — все комплексные числа
кроме ± π / 2, ± 3π / 2, ± 5π / 2,…,
где касательная функция не определена,
а диапазон — это все комплексные числа.
Специальные значения: Для двух треугольников, показанных ниже, теорема Пифагора дает простой точные значения длин сторон и, следовательно, значений функции синуса, косинуса и тангенса. В следующей таблице приведены эти значения, а также для углов 0 ° и 90 °:
Алгоритмы вычисления синуса, косинуса и тангенса: Вы когда-нибудь задумывались, как калькуляторы и компьютеры умеют вычислять такие функции, как синус, косинус и тангенс? Ответ в том, что они используют такие формулы:
Эти формулы называются полиномиальными приближениями и основаны на рядах Тейлора.Для их использования x должно быть указано в радианах. Они очень точны при x близко к 0, но теряет точность по мере увеличения x . Когда x = π / 4 радиан (т. Е. 45 °), формула sin точна только с точностью до ± 0,00004, cos с точностью до ± 0,000004 и tan до в пределах ± 0,004.
Если x больше, чем π / 4, эти формулы слишком неточны для непосредственного использования.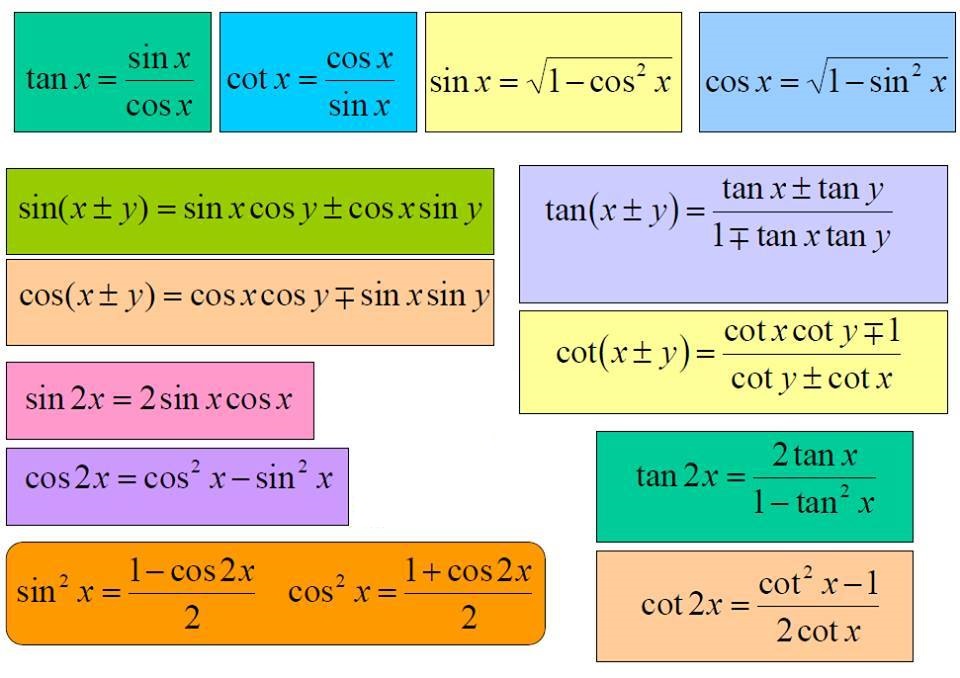 Вместо этого объединяются функции и симметрии синуса, косинуса и тангенса.
используется для уменьшения угла x и повышения точности.Например, чтобы вычислить
sin (440 °), используется тот факт, что это то же самое, что sin (80 °),
что то же самое, что cos (10 °), то же самое, что cos (0,174533 радиан),
который затем вычисляется по формуле cos.
Щелкните здесь, чтобы увидеть алгоритмы, которые компьютеры используют для расчета
синусоидальная функция,
функция косинуса и
касательная функция.
Вместо этого объединяются функции и симметрии синуса, косинуса и тангенса.
используется для уменьшения угла x и повышения точности.Например, чтобы вычислить
sin (440 °), используется тот факт, что это то же самое, что sin (80 °),
что то же самое, что cos (10 °), то же самое, что cos (0,174533 радиан),
который затем вычисляется по формуле cos.
Щелкните здесь, чтобы увидеть алгоритмы, которые компьютеры используют для расчета
синусоидальная функция,
функция косинуса и
касательная функция.
Как использовать функции синуса, косинуса и тангенса в Algebra Coach
- Введите sin (x), cos (x) или tan (x) в текстовое поле, где x — аргумент.Аргумент должен быть заключен в квадратные скобки.
- Установите соответствующие параметры:
- Установите опцию с точной / с плавающей запятой . (Точный режим позволяет используйте специальные значения.)
- Установите режим градусов / радиан. .
 (Режим Radian более универсален и рекомендуется. Тогда любые углы, которые
предполагается, что вы вводите в радианах, но вы все равно можете
введите углы в градусах, поставив за ними букву d;
см. следующий пункт.)
(Режим Radian более универсален и рекомендуется. Тогда любые углы, которые
предполагается, что вы вводите в радианах, но вы все равно можете
введите углы в градусах, поставив за ними букву d;
см. следующий пункт.) - Установить d означает / не представляет опцию символа ° . (Этот параметр доступен только в режиме радиан. Если этот параметр равен на , вы можете например, введите cos (30d + 2), чтобы обозначить косинус 30 градусов плюс 2 радиан.)
- Набор p не представляет собой вариант π.
- Включите комплексных чисел , если вы хотите иметь возможность оценивать синус, косинус или тангенс комплексного числа.
- Нажмите кнопку «Упростить».
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его. .

 Угол, для которого нужно выполнить операцию.
Угол, для которого нужно выполнить операцию.
 .. cah …
.. cah … 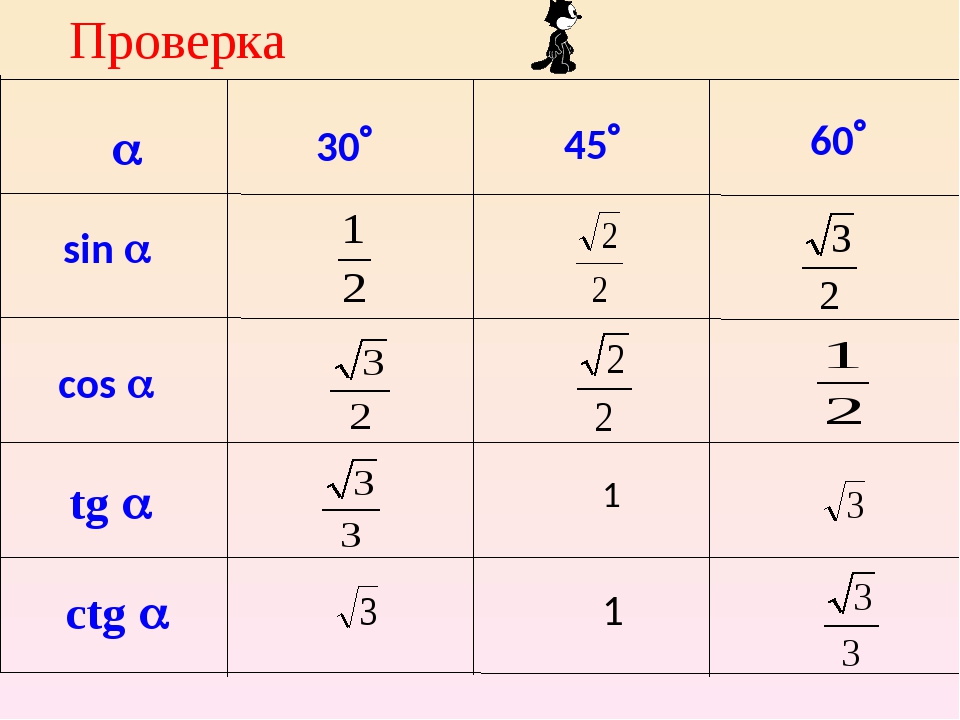
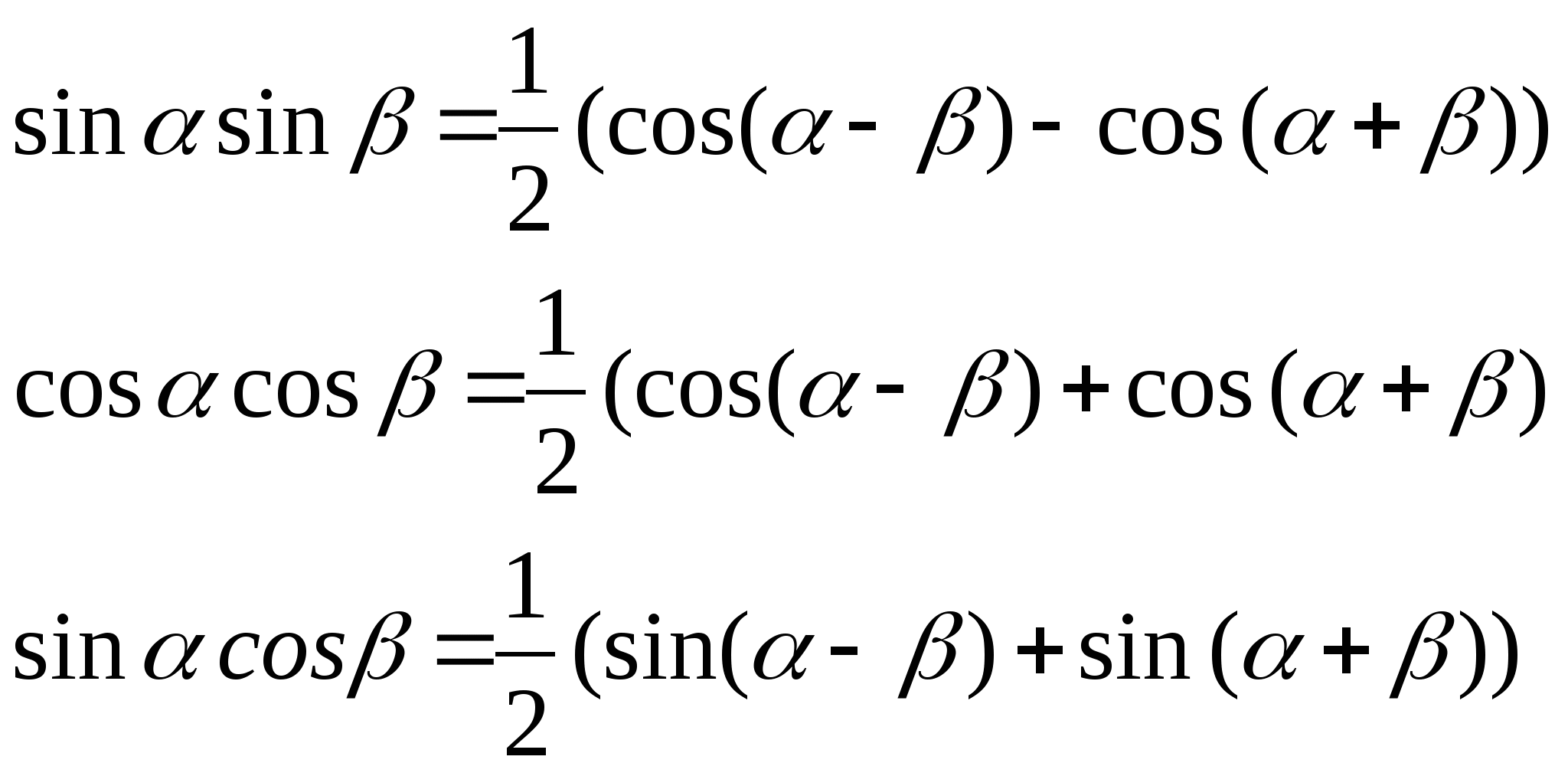
 (Режим Radian более универсален и рекомендуется. Тогда любые углы, которые
предполагается, что вы вводите в радианах, но вы все равно можете
введите углы в градусах, поставив за ними букву d;
см. следующий пункт.)
(Режим Radian более универсален и рекомендуется. Тогда любые углы, которые
предполагается, что вы вводите в радианах, но вы все равно можете
введите углы в градусах, поставив за ними букву d;
см. следующий пункт.)