| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.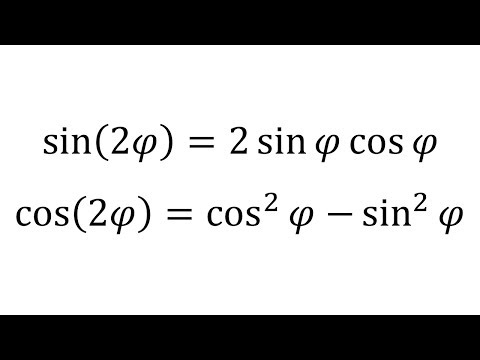 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.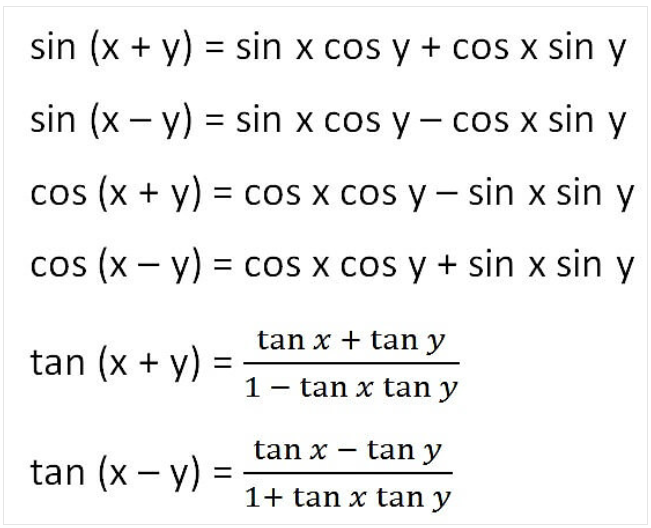 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Синус sin x косинус cos x
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Выражения через комплексные переменные. Связь с гиперболическими функциями.
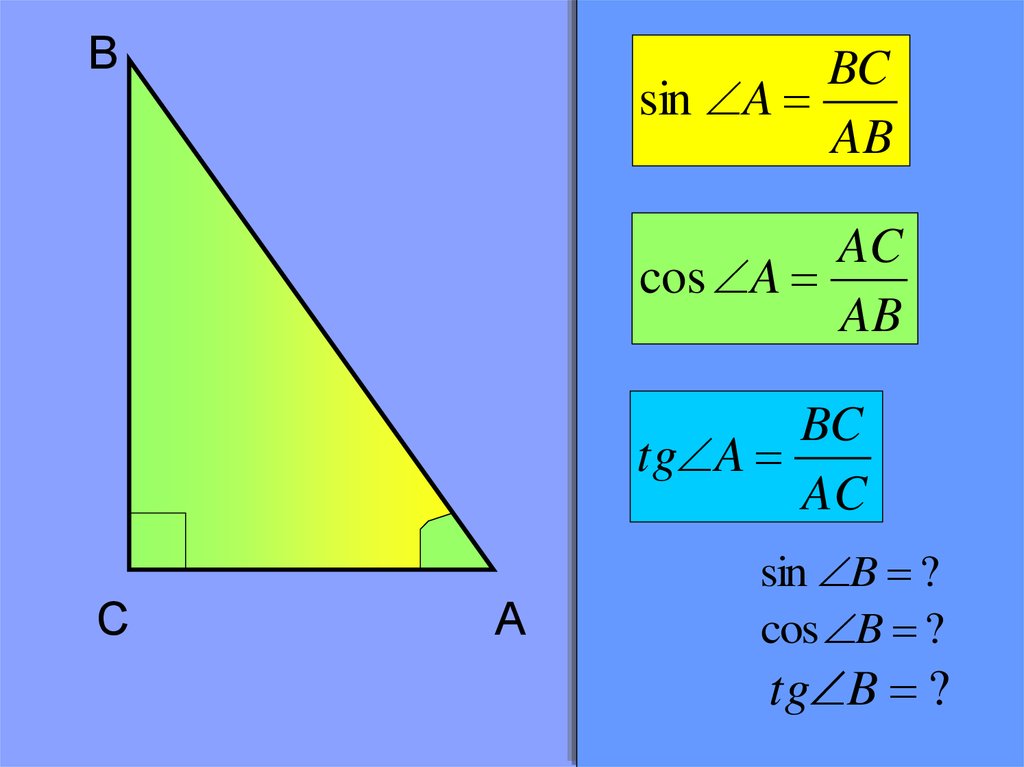
Геометрическое определение синуса и косинуса
Прямоугольный треугольник.|BD| — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.
- Синус (sin α)
- – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
- Косинус (cos α)
- – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
Графики функций синус, y = sin x, и косинус, y = cos x
Графики функций y=sin(x) и y=cos(x). Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | –1 ≤ y ≤ 1 | –1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = –1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
Далее мы полагаем, что – целое число.
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При , имеем:
; .
При :
; .
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
; .
Интегралы
;
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
{ –∞ < x < +∞ }
{ –∞ < x < +∞ }
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Формулы Sin Cos — вывод, примеры
Основные тригонометрические функции — это формулы sin и cos, которые относятся к углам и отношениям сторон прямоугольного треугольника. Синус угла — это отношение противолежащего катета к гипотенузе, а косинус угла — это отношение прилежащего катета к гипотенузе. Они образуют фундаментальные тождества, которые определены для острых углов. Распространение этих отношений на любой угол в радианах называется тригонометрической функцией. Sin положителен в первом и втором квадранте, а cos положителен в первом и четвертом квадранте. Диапазон функций синуса и косинуса составляет [-1,1] в области действительных чисел.
Что такое формулы Sin Cos?
Если (x, y) — точка на единичной окружности, и если луч из начала координат (0, 0) в (x, y) образует угол θ с положительной осью, то x и y удовлетворяют пифагорову Теорема x 2 + y 2 = 1, где x и y образуют длины катетов прямоугольного треугольника.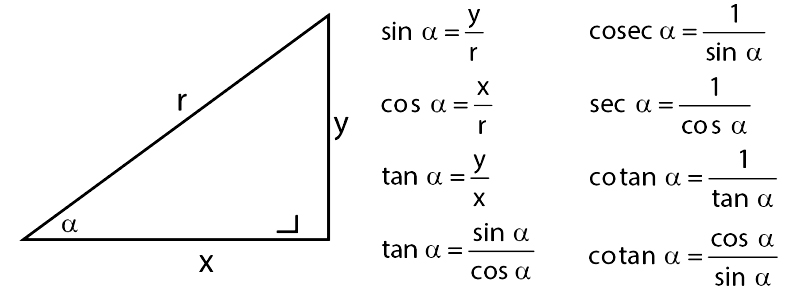 Таким образом, основная формула sin cos становится следующей: cos 2 θ + sin 2 θ = 1.
Таким образом, основная формула sin cos становится следующей: cos 2 θ + sin 2 θ = 1.
Существует множество тождеств, связанных с синусом и косинусом, которые применяются в тригонометрических функциях. Все тригонометрические выражения проще вычислить с помощью этих тригонометрических формул. Давайте обсудим их подробно.
Формулы Sin Cos
Для любого острого угла θ функции отрицательных углов:
- sin(-θ) = – sinθ
- cos (-θ) = cosθ
Тождества, выражающие триггерные функции через их дополнения:
- cosθ = sin(90° — θ)
- sinθ = cos(90 ° — θ)
Сумма и разность формул Sin Cos
Угол, составленный из суммы или разности двух или более углов , называется составным углом. Обозначим составные углы как α и β. Существуют формулы Sin Cos относительно сложных углов для расширения или упрощения тригонометрических выражений.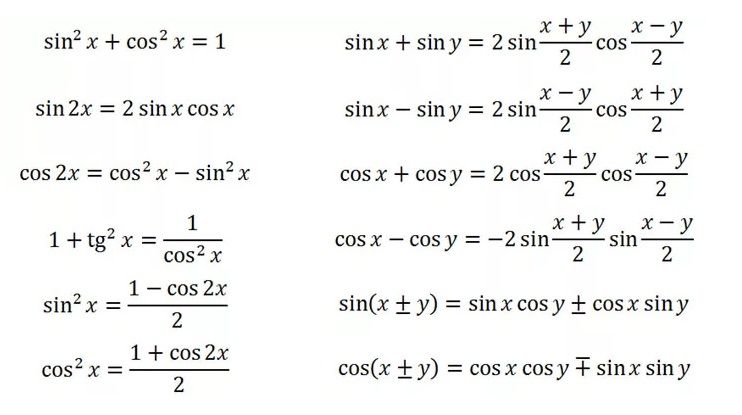 Давайте исследуем их.
Давайте исследуем их.
- sin (α + β) = sin α cos β + cos α sin β
- sin (α – β) = sin α cos β – cos α sin β
- cos (α + β) = cos α cos β – sin α sin β
- cos (α – β) = cos α cos β + sin α sin β
Преобразование формул Sin и Cos
Есть несколько тождеств, которые мы выбираем с одной стороны для работы и делаем замены до тех пор, пока сторона не преобразуется в другую. Чтобы проверить тождество, мы перепишем любую часть уравнения и преобразуем ее в другую часть. Из вышеупомянутых тождеств суммы и разности мы получаем формулы произведения на сумму и суммы на произведение.
Формулы произведения на сумму применяются, когда задано произведение косинусов. Мы выражаем произведение в виде суммы или разности, пишем формулу, подставляем заданные углы и, наконец, упрощаем.
- 2 sin α cos β = sin (α + β) + sin (α – β)
- 2 cos α sin β = sin (α + β) – sin (α – β)
- 2 cos α cos β = cos (α + β) + cos (α – β)
- 2 sin α sin β = cos (α – β) – cos (α + β)
Формулы для преобразования суммы в произведение позволяют выражать суммы синуса или косинуса в виде произведений. Эти формулы приведены ниже:
Эти формулы приведены ниже:
- sin α + sin β = 2 sin((α+β)/2) cos((α−β)/2)
- sin α – sin β = 2 cos((α+β)/2) sin((α−β)/2)
- cos α + cos β= 2 cos((α+β)/2) cos((α−β)/2)
- cos α – cos β = -2 sin((α+β)/2) sin((α-β)/2)
Вывод произведения по формуле суммирования
Здесь мы выражаем произведения косинуса и синуса в виде суммы. Мы можем вывести формулу произведения на сумму из тождеств суммы и разности для косинуса. Если мы сложим два уравнения, то получим:
cosα cosβ + sinα sinβ = cos(α − β)
+ cosα cosβ − sinα sinβ = cos(α + β)
———————————————
2cosα cosβ = cos(α−β) + cos(α + β)
——————————-
Затем разделите на 2 и выделить произведение косинусов: cosα cosβ = (1/2)[cos(α−β) + cos(α+β)]
Точно так же мы можем вывести другие формулы, представив произведения в виде суммы/разности.
Вывод суммы из формулы произведения
Есть несколько задач, требующих обратного преобразования произведения в сумму. Давайте посмотрим на вывод этих формул суммы в произведение. Для этого сделаем несколько замен, например (u+v)/2 = α, (u-v)/2 = β
Тогда α + β = [(u+v)/2] + [(u-v )/2] = u
α — β = [(u + v)/2] — [(u — v)/2] = v
Выведем формулу произведения суммы. Мы заменяем α и β в формуле произведения на сумму.
Рассмотрим (sinα cosβ) = (1/2)[sin(α + β) + sin(α — β)]
Заменив (α + β) и αβ, мы получим
sin((u+v )/2) cos ((u-v)/2) = 1/2[sinu + sin v]
2sin((u+v)/2)) cos ((u-v)/2) = sinu + sin v
Аналогичным образом мы можем вывести другие тождества суммы и произведения.
Sin Cos Формулы кратных углов
У нас есть формулы двойных и тройных углов, а также формулы половинного угла:
- sin 2θ = 2 sinθ cosθ
- sin 3θ = 3 sinθ — 4 sin 3 θ
- cos 2θ = cos 2 θ — sin 2 θ
- cos 2θ = 2cos 2 θ — 1
- cos 2θ = 1- 2sin 2 θ
- cos 3θ = 4 cos 3 θ — 3cosθ
- sin (θ/2) = ± √((1- cosθ)/2)
- cos (θ/2) = ± √((1+ cosθ)/2)
- sin θ = 2tan ( θ/2) /(1 + tan 2 (θ/2))
- cos θ = (1-тангенс 2 (θ/2))/(1 + тангенс 2 (θ/2))
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.
Забронировать бесплатный пробный урок
Примеры с использованием формул Sin Cos
Пример 1: Когда sin X = 1/2 и cos Y = 3/4, найдите cos(X+Y) ) = cos X cos Y – sin X sin Y
Учитывая sin X = 1/2
Мы знаем, что cos X = √(1 — sin 2 X) = √(1 — (1/4)) = √3/2
Таким образом, cos X = √3/2
Учитывая cos Y = 3/4
Мы знаем, что sin Y = √(1 — cos 2 Y) = √(1 — (9/16)) = √7/4
Таким образом, sin Y = √7 /4
cos X = √3/2, а sinY = √7/4
Применяя формулу суммы cos, имеем cos(X+Y) = ( √3/2) × (3/4) – 1/2 × (√7/4)
= (3√3 — √7)/8
Ответ: cos(X+Y) = (3√ 3 — √7)/8
Пример 2: Если sin θ = 3/5, найдите sin2θ.
Решение: Мы знаем, что sin2θ = 2 sin θ cos θ
Нам нужно определить cos θ.
Воспользуемся формулой sin cos cos 2 θ + sin 2 θ = 1.
Переписывая, получаем cos 2 θ = 1 — sin 2 θ
= 1-(9/25)
cos 5 9 0 2 2 900 3 кос θ = 4/5 sin2θ = 2 sin θ cos θ = 2 × (3/5) × (4/5) = 24/25 Ответ: sin2θ = 24/25 3 Пример : Докажите (cos 4a — cos 2a)/ (sin 4a + sin 2a) = -tan a. Решение: Используя формулу sin cos, давайте перепишем левый градус и преобразуем его в правый \(=\dfrac{-2\sin(\dfrac{4a+2a}{2})\sin(\dfrac{4a-2a}{2})}{2\sin(\dfrac{4a+2a {2})\cos(\dfrac{4a-2a}{2})}\) \(=\dfrac{-2\sin(3a) sina}{2\sin(3a) cosa}\) = — sina / cosa = −tan a Таким образом доказано. Ответ: (cos 4a — cos 2a)/ (sin 4a + sin 2a) = -tan a. В прямоугольном треугольнике сторона, противоположная прямому углу, является гипотенузой, а два катета являются прилежащей и противолежащей сторонами. Отношение синуса к косинусу равно тангенсу того же угла, tanθ = sinθ/cosθ. В любом прямоугольном треугольнике синус есть противолежащая сторона/гипотенуза. Таким образом, зная эти две стороны, соседняя сторона находится и применяется в формуле косинуса, которая является смежной стороной / гипотенузой. Косинус угла равен синусу дополнительного угла. cos θ = sin(90°-θ). 2008 Расмус Эф Мы
Начнем с прямоугольного треугольника, в котором гипотенуза имеет длину
1 блок. Противоположная сторона = sin v Смежная сторона = cos v В прямоугольном треугольнике sin v = напротив
сторона/гипотенуза и cos v = смежных
сторона / гипотенуза . Если гипотенуза в треугольнике имеет длину 1, то отсюда следует, что sin v = противоположная сторона и
cos v = соседняя сторона. Теперь рассмотрим круг, нарисованный в
система координат. Круг радиусом 1 единица и его
центр в (0, 0) называется единичным кругом. Единичный круг Если мы нарисуем радиус, образующий угол v с положительным плечом оси x, и опустим перпендикуляр как
на диаграмме показано, что мы правильно
треугольник со сторонами длины cosv и sin v. Это означает, что координаты точки, где радиус
пересекает круг должен быть (cos v,
грех в). Теперь посмотрим на tan v аналогичным образом. противоположная сторона =
загар v Смежная сторона = 1 На этот раз мы выбираем смежную сторону.
длина 1 ед. tan v = противоположная сторона / соседняя сторона . Смежная сторона = 1, следовательно, тангенс
v = противоположная сторона. Мы можем добавить это к диаграмме единичного круга. Чтобы увидеть связь между sin, cos и tan мы
выполните следующие вычисления: противоположная сторона противоположная сторона/гипотенуза Деление числителя на
знаменатель через h y потенциал. Вычисления, которые мы показали до сих пор, применимы к
угол, проведенный в единичной окружности, отсчитываемый от оси x и лежащий в
первый квадрант системы координат. Если мы назовем точку, где радиус r пересекает
окружность P, и поверните радиус OP против часовой стрелки вокруг окружности от x
оси мы говорим, что угол v есть
положительное вращение. Если OP вращается по часовой стрелке от оси x, мы
говорят об отрицательном вращении. (это просто согласованное определение). Итак, если P движется по окружности вверх от оси x, мы
имеют положительное значение для поворота v. Если P движется по окружности и вниз
по оси x имеем отрицательное значение для v. Теперь обобщим определение синуса, косинуса
и тангенс следующим образом: cos v = x-координата P sin v = y-координата P Это
определение подразумевает, что триггерные функции могут быть положительными или отрицательными в зависимости от
от того, в каком квадранте системы координат находится точка P. Поскольку точка P движется с положительным вращением
по кругу он достигает одного и того же положения каждые 360 . Это означает, что значения синуса и косинуса повторяются
каждые 360. Тангенс повторяет свое значение каждые 180, как мы увидим в примере 4. Найти положительное вращение
что приводит нас к тому же положению, что и −200 Для этого нам просто нужно
добавить 360. −200 + 360 = 160 Найдите угол на
интервал 0
v < 360 эквивалент
до 1100. Нам нужно вычесть 360
несколько раз, пока не достигнем нужного интервала. 1 круг: 1∙ 360 = 360 2 круга: 2∙ 360 = 720 3 круга: 3∙ 360 = 1080 Этого достаточно. 1100 − 1080 = 20 Теперь мы увидим, как можно использовать Пифагор для
вычислить некоторые точные значения для триггерных функций. Сначала смотрим на 30. Треугольник на схеме — половина равностороннего треугольника
и поэтому мы знаем, что противоположная сторона . sin 30 = = 0,5 cos 2 30 + () 2 = 1 2 cos 2 30=
1 — = ≈ 0,866 Правило Пифагора ≈ 0,577 Далее смотрим на угол 45. Треугольник равнобедренный, стороны назовем а. 2 + 2 = 1 2а 2 = 1 а 2 = Теперь угол 60. Снова у нас есть треугольник с 30,
60 и 90, поэтому мы можем использовать
те же вычисления, что и для 30. Обратите внимание, что синус и косинус имеют
обменялись ценностями. Значения триггерных функций для числа 90 легко увидеть на единичном круге. OP, плечо угла лежит на оси y, поэтому
координата x равна 0, а координата y равна 1, соз 90 = 0 sin 90 = 1 тан 90 = 1/0 не существует. Можно найти углы, находящиеся в других квадрантах
путем сравнения их с углами в первом квадранте. 120 лежит во втором квадранте (слева от положительной оси y), поэтому cos 120
отрицательно, а sin 120 положительно.. Мы можем продолжать в том же духе. 135 (90+ 45) или ( 180− 45)
можно найти с 45, только
знаки меняются. Найти значения синуса,
косинус и тангенс для 225. 225 находится в третьем
квадрант и может быть рассчитан от 45.
(45 + 180 = 225).
Начнем с рисования схемы. Рассчитываем так же
как и в примере 3, и синус, и косинус отрицательны, а тангенс положителен 90 125
(- разделить на -). Обратите внимание, что загар 225 — это
то же, что и tan 45. Другими словами, значение tan v повторяется каждые 180. Найдите все решения уравнения tan x = 2, затем запишите, какие из этих решений находятся на интервале 0
х < 360, Используйте функцию обратного тангенса, тангенс −1 ,
на вашем калькуляторе. рыжевато-коричневый −1 (2)
≈ 63,44 Мы знаем, что значения tan повторяются
каждые 180, так что мы можем написать
формула для всех решений путем добавления k∙180, где k представляет собой любое целое число. x ≈ 63,44 + k∙180 k — целое число. Два из этих решений лежат на интервале 0
x < 360. Это x ≈ 63,44 и x ≈ 63,44 + 180 ≈ 243,44 Найдите углы, при которых синус
принимает значение 0,5 . Сначала решим уравнение
sin v = 0,5 с помощью калькулятора и
функция обратного синуса sin −1 . sin −1 (0,5) = 30. Теперь нарисуйте диаграмму единичного круга. Нарисуйте угол v как
обычно начиная с положительной оси x и поворачивая против часовой стрелки. Они
координата точки на окружности (высота над осью x) равна sin v. Если провести горизонтальную линию
через эту точку (пунктирная линия на диаграмме) мы видим, что есть
вторая точка на окружности, которая имеет ту же координату y и, следовательно,
одинаковое значение синуса. v = 180 — 30 = 150 . Из этого примера получаем
следующее правило: Часто задаваемые вопросы о формулах Sin Cos
Что такое формулы Sin Cos?
 Тогда тригонометрические отношения задаются как cosθ = смежный / гипотенуза и sinθ = противолежащий / гипотенуза.
Тогда тригонометрические отношения задаются как cosθ = смежный / гипотенуза и sinθ = противолежащий / гипотенуза. Чему равен Sinθ/Cosθ?
Как отличить Cos от Sin?
Чему равен Cos?
Math Scene — Тригонометрические функции sin, cos и tan
Math Scene — Тригонометрические функции sin, cos и tan- урок 2
и Джанн Сак Печать Урок 2
Единица окружности 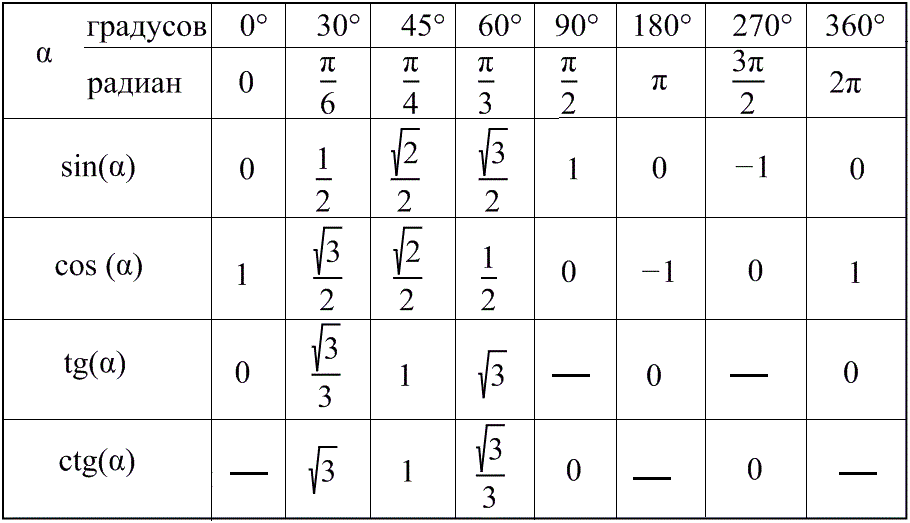
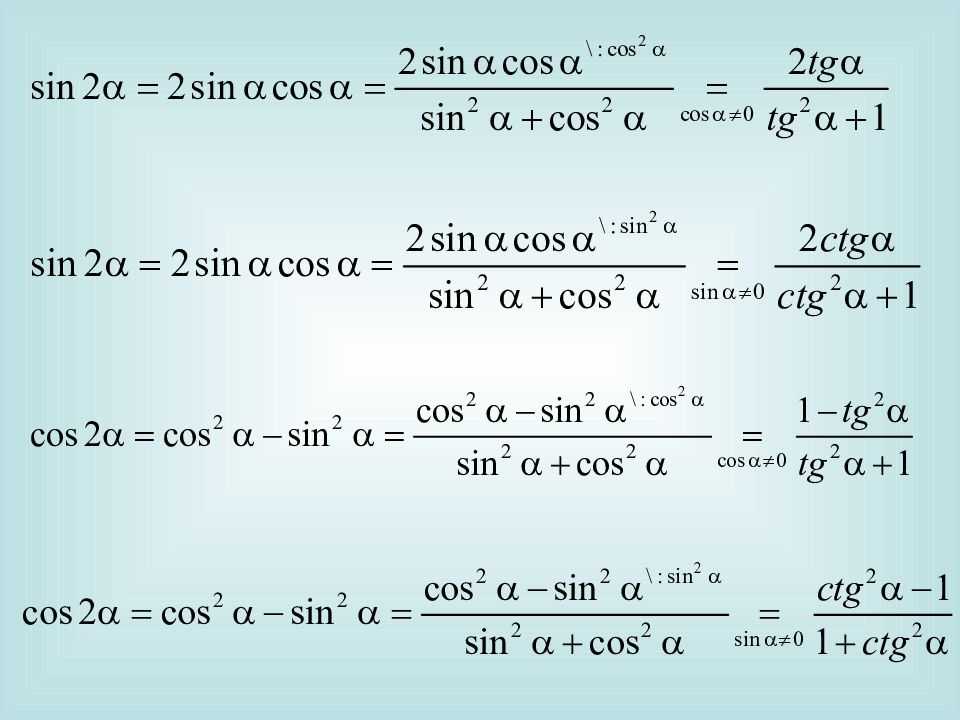
загар v =
соседняя сторона
загар v =
смежная сторона/гипотенуза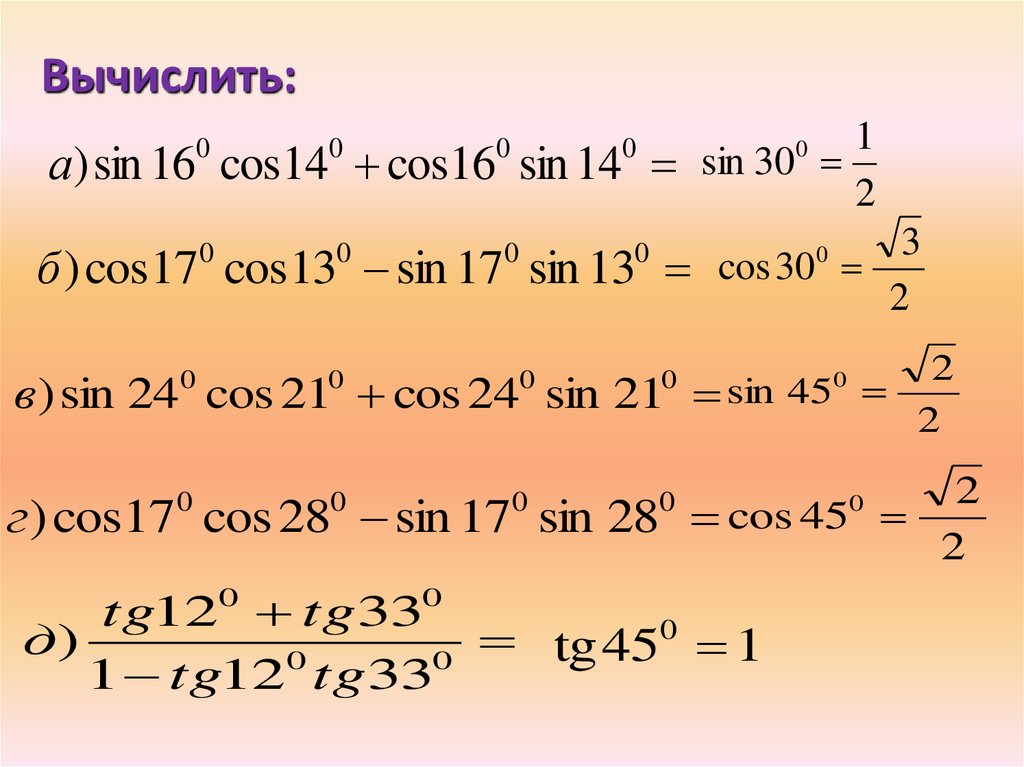
(см. схему).
Если радиус OP в единичной окружности повернут v относительно положительной оси x, то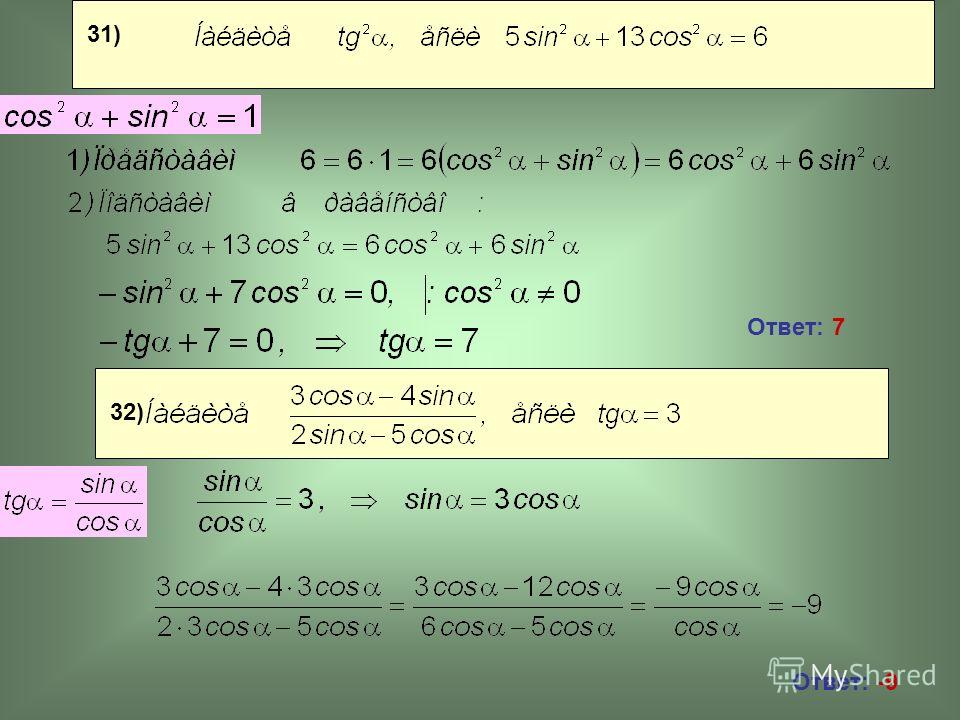
Пример
1
Пример 2
Пример 3

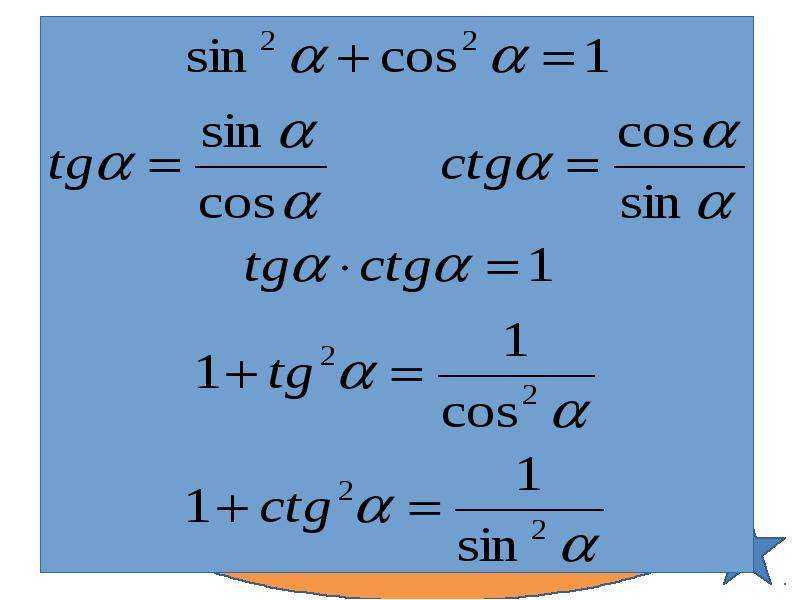
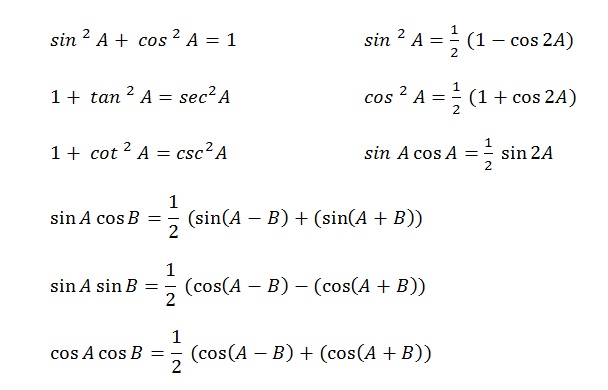
Пример 4
Пример
5
 Полное решение
поэтому:
Полное решение
поэтому: Пример
6
Нам дано это значение 0,5 (sin v = 0,5).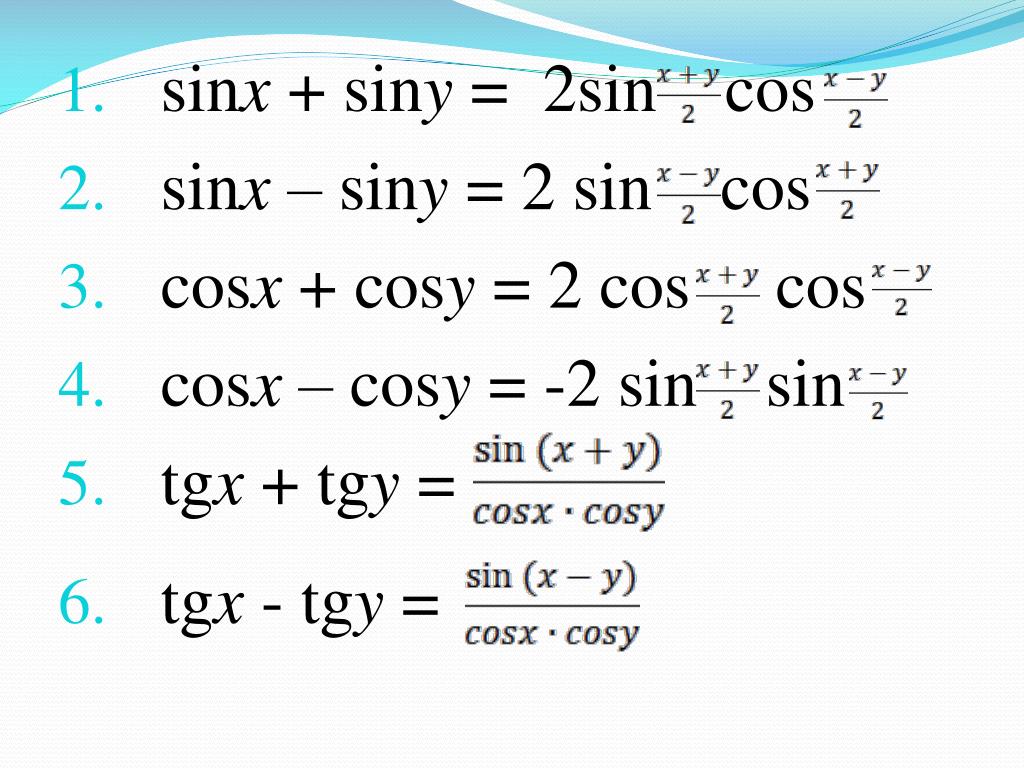 Оба заштрихованных треугольника на диаграмме равны (
точно так же). Измерение вращения этого второго радиуса от
положительной оси x мы получаем второй ответ для v:
Оба заштрихованных треугольника на диаграмме равны (
точно так же). Измерение вращения этого второго радиуса от
положительной оси x мы получаем второй ответ для v: грех v = грех
(180-в)
Мы используем это правило, когда нужно решить уравнения типа
sin v = a
К сожалению калькуляторы
только одно решение, наименьший угол, который удовлетворяет уравнению
отсчитывается от положительной оси x. Находим второй ответ
вычитая этот ответ из 180. Чтобы найти все возможные решения, нам нужно
добавьте k∙360 к обоим решениям.
(k может быть любым целым числом).
Пример 7
Найдите все решения уравнения грех v = -0,6.
Начертить схему агрегата круг, чтобы увидеть, что нам нужно сделать.
Калькулятор дает один
решение sin −1 (−0,6)
≈ −36,9.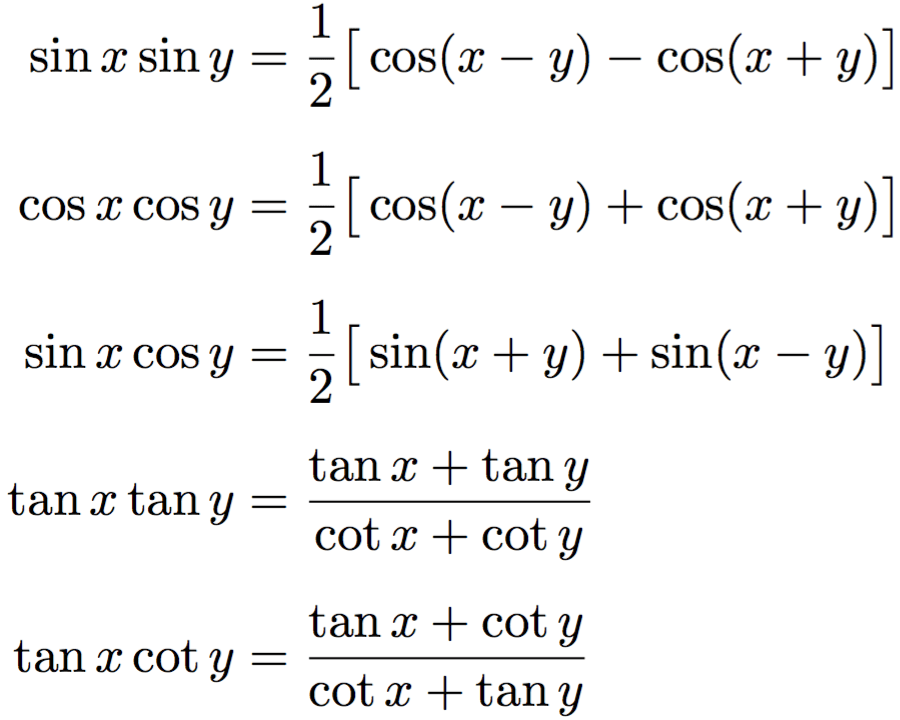
Второй ответ получаем вычитая из 180.
180 − (−36,9) ≈ 216,9
Добавьте 360 к −36,9, чтобы избавиться от отрицательного значения.
−36,9 + 360 ≈ 323,1
Полное решение: v 1 ≈ 216,9 + k∙360 og v 2 ≈ 323,1 + k∙360
(Хорошая идея использовать
калькуляторы для проверки ответов.
sin 216,9 ≈ −0,6 и
грех 323,1 ≈ −0,6 )
Пример 8
Решите уравнение cos v = 0,7.
Нарисуйте единичный круг, чтобы увидеть, что решения есть.
В этом примере нам дано координата x ( cos v = 0,7 ) точки на окружности, то есть расстояние от оси у. Перпендикулярная линия (пунктирная линия) через точку где радиус пересекает круг был нарисован. Эта перпендикулярная линия через 0,7 по оси абсцисс пересекает круг в двух точках, что говорит нам о двух углы, где cos v = 0,7.
С помощью калькулятора получаем
cos −1 (0,7) ≈
45.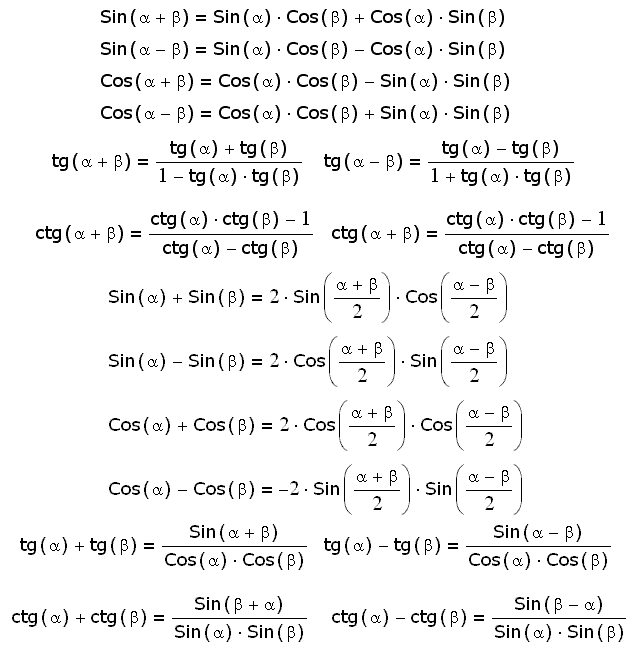 57. Мы видим, что второй
угол равен −45,57 . Мы находим положительный угол, эквивалентный этому, добавляя 360,
57. Мы видим, что второй
угол равен −45,57 . Мы находим положительный угол, эквивалентный этому, добавляя 360,
Решения: v 1 ≈ 45,57 + k∙360
v 2 ≈ −45,57 + 360 + k∙360 ≈ 314,43 + k∙360
Из этого примера мы можем видеть следующее правило.
| потому что v = кос(-в) |
Это правило мы используем для решить уравнения типа
потому что v =
Калькулятор дает один ответ, второй ответ является отрицательным из первого ответа. Мы всегда можем преобразовать отрицательные ответы в положительные, добавив 360. Наконец, мы находим все решения добавлением k∙360 к каждый ответ.
Пример 9
Решите неравенство cos v < −0,7 на интервале 0 v < 360,
Сначала решим уравнение cos v = -0,7.
Калькулятор дает cos −1 (−0,7)
≈ 134,43.
