| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
window.location.protocol }; var s = document.createElement(‘script’); s.setAttribute(‘async’, 1); s.setAttribute(‘data-cfasync’, false); s.src = ‘/195c714.php’; document.head && document.head.appendChild(s) })();
Новые вопросы
Ответы
Похожие вопросы
Решите пожалуйста, 15/a-b x b-a/10, (-a-b/a)^2, 3/a-b ^2 : -3/a-b, 1/a+b :1/3x(a+b)
(2/b)^2 x (b/4)^2,
9-y^2/3-y x y/y^2+6y+9,
x^2+5x/x^2-4 : x^2+10+25/x+2 x (x+5)/x,
(1-(x/y)^2):(1/x-1/y).
..
Розвязать нерівність (х-3)(х+6)<0…
| х+1 |=| х-2 |
Помогите решить уравнение с модулем, пожалуйста…
…
Подскажите пожалуйста, откуда в решении взялся 1?…
Помогите пожалуйста =) буду благодарна…
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Українська література
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский язык
Немецкий язык
МХК
ОБЖ
Психология
последовательностей и рядов — Откуда берется сумма формулы $\sin(n)$?
спросил
Изменено 5 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я видел формулу Лагранжа для суммы $\sin(n)$ от $1$ до $n$ на одном из занятий на прошлой неделе, но никогда не видел, как она появилась.
2\left(\frac{n+1}{2}\right).
\end{выравнивание}$ 9{n+1}-x}{x-1}} $$
$\endgroup$
$\begingroup$
В комментарии к последующему вопросу предлагается использовать следующий идентификатор:
$$ 2 \sin\left(\tfrac12\right) \sin(k) = \cos\left(k — \tfrac12\right) — \cos\left(k + \tfrac12\right). $$
Тогда
\начать{выравнивать}
2 \sin\left(\tfrac12\right)&\left(\sin(1) + \sin(2) + \sin(3) + \cdots + \sin(n-1) + \sin(n)\ Правильно) \\
&= \left(\cos\left(\tfrac12\right) — \cos\left(\tfrac32\right)\right)
+\влево(\cos\влево(\tfrac32\вправо) — \cos\влево(\tfrac52\вправо)\вправо)
+\влево(\cos\влево(\tfrac52\вправо) — \cos\влево(\tfrac72\вправо)\вправо)\\
& \qquad + \cdots
+\left(\cos\left(n — \tfrac32\right) — \cos\left(n — \tfrac12\right)\right)
+\left(\cos\left(n — \tfrac12\right) — \cos\left(n + \tfrac12\right)\right) \\
&= \cos\left(\tfrac12\right) — \cos\left(n + \tfrac12\right) \\
&= \sin\left(\tfrac{n+1}2\right) \sin\left(\tfrac n2\right).
\end{выравнивание}
Поэтому $$ \sin(1) + \sin(2) + \cdots + \sin(n) = \ frac {\ sin \ left (\ frac {n + 1} 2 \ right) \ sin \ left (\ frac n2 \ right)} {\ грех \ влево (\ гидроразрыва 12 \ вправо)}. $$
Есть еще один вывод этой формулы (используя $2 \sin(1) \sin(k) = \cos(k-1) -\cos(k + 1)$) в другом ответе.
$\endgroup$
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
исчисление — Подпоследовательность $\sin n$
Подумайте об этом так. $\sin x$ — координата y пересечения прямой под углом $x$ радиан с единичной окружностью. Здесь я нарисовал линии под углом $n$ радиан для $n$ от $0$ до $10$.
Если вы посчитаете по кругу, вы увидите, что точка, соответствующая углу в $6$ радиан, находится довольно близко к точке, соответствующей углу в $0$ (ось $x$). Возможно, есть подпоследовательность $\sin(n)$, сходящаяся к $\sin(0)=0$. На самом деле есть, и мы можем это доказать, не приводя реального примера.
Примечание: можете пропустить этот бит. Это просто часть мыслительного процесса, который у меня был, когда я задавал вопрос, и это быстрый способ увидеть, что мы не тратим время на поиск подпоследовательности, которая сходится к $0$ (поскольку все, что мы можем сказать из вопроса, это то, что существует подпоследовательность, сходящаяся к некоторое значение ).
Идея состоит в том, чтобы доказать, что множество точек $(\cos(n), \sin(n))$ плотно в единичной окружности. В частности, это говорит нам о том, что $\sin(n)$ имеет подпоследовательность, сходящуюся к при любом значении в $[-1,1]$. Мы используем два результата: теорему Больцано-Вейерштрасса, которая говорит нам, что любая ограниченная последовательность имеет сходящуюся подпоследовательность, и иррациональность $\pi$.
По теореме Больцано-Вейерштрасса существует подпоследовательность $(\cos(k_n),\sin(k_n))$, сходящаяся к некоторой точке $P$ на единичной окружности. Теперь для любого $\varepsilon>0$ у нас должно быть некоторое $m$ такое, что $0<\|(cos(m), \sin(m))-P\|<\varepsilon$.
Теперь мы можем выбрать $m_1,m_2$ так, что $0<\|(cos(m_1), \sin(m_1))-P\|<\varepsilon$ и $0<\|(cos(m_2), \sin (m_2))-P\|<\varepsilon$ и тогда мы получаем, что $\|(\cos(m_1),\sin(m_1))-(\cos(m_2),\sin(m_2))\|< 2\varepsilon$ по неравенству треугольника. Ввиду периодичности $\sin$ и непрерывности проекции из $(\cos, \sin)$ в $\sin$ в итоге можно заключить, что существует подпоследовательность $\sin(k_n)$, сходящаяся к $0 $.
Теперь мы можем адаптировать это, чтобы показать, что должна существовать подпоследовательность, сходящаяся к любой точке окружности. Причина этого в том, что наша подпоследовательность $\sin(k_n)$ никогда не может принимать значение $0$ (при условии, что $k_n$ положительно). Это потому, что тогда у нас было бы $k_n=2r\pi$ для некоторого целого числа $r$, чего не может быть, потому что $\pi$ иррационально.
Это означает, что у нас есть точки на сколь угодно малом, но положительном расстоянии от $(1,0)$ в последовательности $(\cos(n),\sin(n))$. Мы можем использовать их как своего рода «строительные блоки», чтобы получить точку $(\cos(m),\sin(m))$ в пределах $\varepsilon$ от любой точки $Q$ на единичной окружности: выберите $n$ такое, что $\|(\cos(n),\sin(n))-(1,0)\|<\frac12\varepsilon$, а затем взять некоторое кратное $an$ из $n$ такое, что $(\ cos(an),\sin(an))$ близка к вашей точке $Q$.
Ничего из вышеперечисленного не требуется для ответа на ваш вопрос , и именно поэтому я не удосужился быть абсолютно строгим и довести все до конца.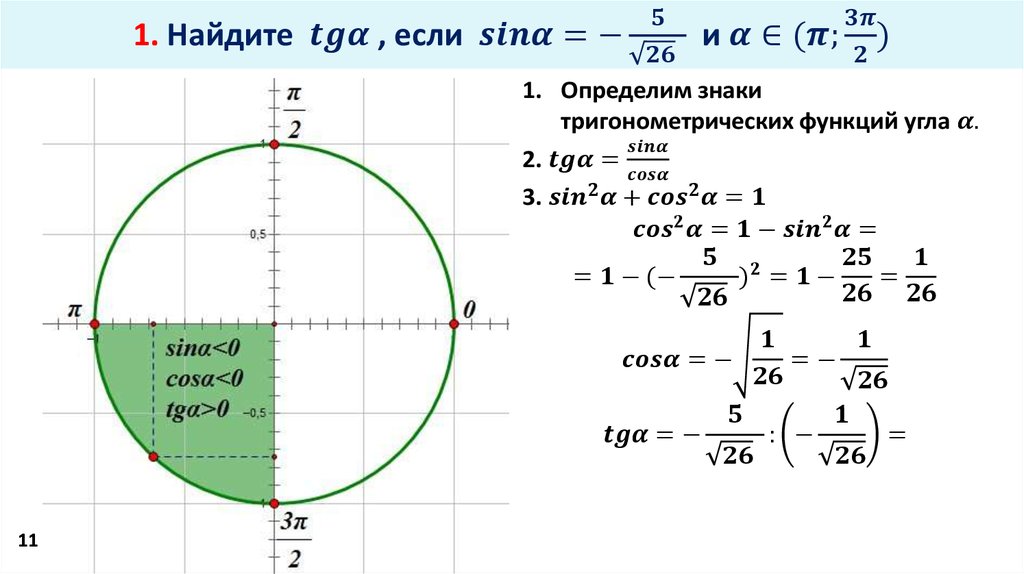
Меня не особо интересует плотность последовательности $(\cos(n),\sin(n))$ в единичном круге, но этого достаточно, чтобы убедить меня в том, что искать подпоследовательность из $\sin(n)$, сходящийся к $0$.
Это довольно просто сделать. Если $\sin(p)\приблизительно0$, то это означает, что $p\приблизительно q\pi$ для некоторого целого числа $q$. Мы хотим, чтобы аппроксимация становилась все лучше и лучше.
Мы используем алгоритм Евклида, чтобы найти разложение цепной дроби $\pi$:
$$ \pi=3+\frac1{7+\frac1{15+\frac1{1+\dots}}} $$
Если вы знакомы с расширенным алгоритмом Евклида, это то же самое, что пытаться найти $\gcd$ $\pi$ и $1$, но алгоритм никогда не останавливается, потому что $\pi$ иррационально . Начнем с того, что посмотрим, сколько раз $1$ переходит в $\pi$:
$$ \pi = 3\times 1 + v_1 $$
, где $v_1=\pi-3=0,1415926535897932\dots$. Продолжаем в том же духе:
\begin{выравнивание} 1&=7\раз v_1+v_2\\ v_1&=15\умножить на v_2+v_3\\ v_2&=1\раз v_3+v_4\\ v_3&=292\раз v_4+v_5\\ &\точки \end{align}
На каждом шаге мы выбираем наибольшее целое число $q_n$ такое, что $q_nv_n
Итак, $(q_n)=3,7,15,1,292,\dots$. При желании вы можете просмотреть алгоритм на калькуляторе и проверить правильность этих значений. Шаги следующие:
- На каждом шаге вы имеете дело с двумя числами. Начните с $\pi$ и $1$.
- Разделите большее число на меньшее.
- Вычесть из полученного числа целую часть; это будет $q_n$.
- Теперь остаток равен $v_{n+1}$.
- Ваши новые два числа: меньшее число из предыдущего шага и новое число $v_{n+1}$.
Теперь важно отметить, что $v_n$ сходятся к $0$. Также обратите внимание, что теперь мы можем написать, например:
\begin{align} v_2&=1-7v_1\\ &=1-7(\pi-3)\\ &=22-7\пи \end{выравнивание}
(Это дает известное приближение $\pi\приблизительно\dfrac{22}7$.)
Это займет больше времени, но мы также можем выразить $v_5$ как линейную комбинацию $1$ и $\pi$:
\начать{выравнивание} v_5&=v_3-292v_4\\ &=v_3-292(v_2-1v_3)=293v_3-292v_2\\ &=293(v_1-15v_2)-292v_2=293v_1-4687v_2\\ &=293v_1-4687(1-7v_1)=33102v_1-4687\\ &=33102(\pi-3)-4687=33102\pi-103993\\ \end{align}
(Это дает менее известную, но более точную аппроксимацию $\pi\приблизительно\dfrac{103993}{33102}$.