Ответов пока нет | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение заданий тригонометрия по материалам открытого банка задач ЕГЭ по математике
Similar presentations:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай».
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Решение заданий тригонометрия по материалам открытого банка задач ЕГЭ по математике
Задания открытого банка задач1. Найдите значение выражения
Решение.
2 sin 11 cos11
.
sin 22
2 sin 11 cos11 sin 22
1.
sin 22
sin 22
Использована формула: sin 2t = 2sin t · cos t
2. Найдите значение выражения
Решение.
22 sin 2 9 cos2 9
.
cos18
22 sin 2 9 cos 2 9
22 cos 2 9 sin 2 9
22cos 2 9
cos18
cos18
cos18
22cos18
22.
cos18
Использована формула: сos 2t = cos2 t – sin2 t
Задания открытого банка задач
Решение.
33 cos 63
.
sin 27
33cos 63 33cos 90 27 33 sin 27
33.
sin 27
sin 27
sin 27
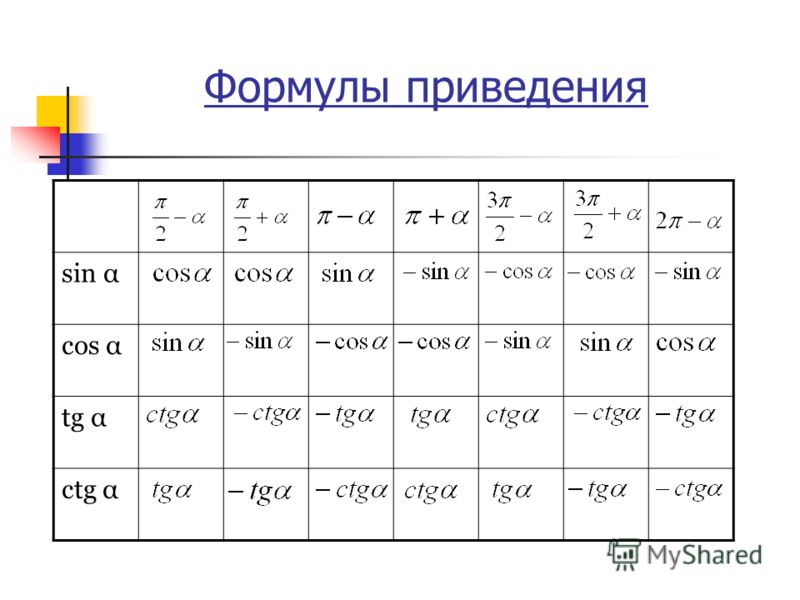
Использована формула приведения: cos (90º – t) = sin t
π
6
π
6
4. Найдите значение выражения 6 3tg sin .
Решение.
6 3 tg
π
π
1 1 6 3
sin 6 3
3.
6
6
3 2 2 3
Использована таблица значений тригонометрических
функций.
5. Найдите значение выражения
Решение.
60
.
π
31
π
19
sin
cos
6
3
60
60
π
5π
19π
31π
sin
cos
sin 3 2π cos 3 2π
3
6
3
6
60
60
60
60
60
80.
π
5π
3
3
π
3
π
3 3
sin cos
cos π
cos
3
6
4
2
6
2
6
2 2
Использованы:
а) свойство нечетности функции sin t: sin (−t) = − sin t
б) свойство периодичности функций sin t и cos t:
sin (2πn ± t) = ± sin t, cos (2πn ± t) = cos t, где n ∈ Z
в) свойство четности функции cos t: cos (−t) = cos t
г) формула приведения: cos (π – t) = − cos t.
д) таблица значений тригонометрических функций.
Задания открытого банка задач
6. Найдите значение выражения 24 3 cos 750 .
Решение.
24 3 cos 750 24 3 cos 2 360 30 24 3 cos 30
24 3
3 24 3 3
12 3 36.
2
2
Использованы:
а) свойство четности функции cos t: cos (−t) = cos t
б) свойство периодичности функции cos t:
cos (2πn ± t) = cos t, где n ∈ Z
в) таблица значений тригонометрических функций.
Задания открытого банка задач
7. Найдите значение выражения 34 sin 100 .
sin 260
Решение.
34 sin 100 34 sin 90 10 34cos10
34.
sin 260
cos10
Использованы формулы приведения:
sin (90º + t) = cos t и sin (270º − t) = − cos t
8. Найдите значение выражения 5 tg 154 tg 244 .
Решение.
5 tg 154 tg 244 5 tg 90 64 tg 180 64
5 ctg 64 tg 64 5.
Использованы:
а) формулы приведения: tg (90º + t) = − ctg t и tg (180º + t) = tg t
б) тождество: tg t · ctg t = 1.
Задания открытого банка задач
9.
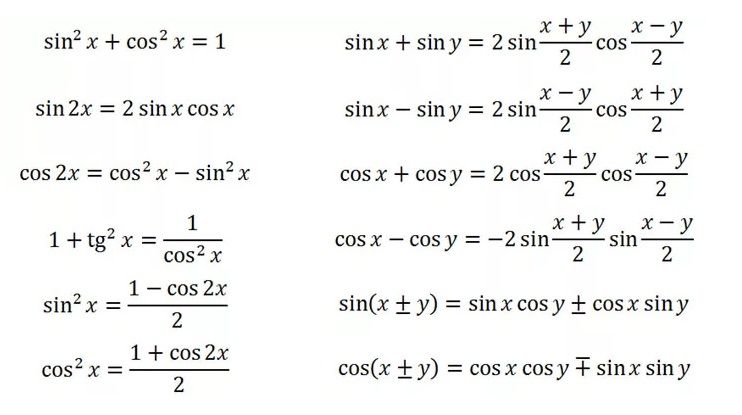Найдите значение выражения37
.
2
2
sin 173 sin 263
Решение.
37
37
2
2
2
2
sin 173 sin 263 sin 90 83 sin 180 83
37
37
37.
2
2
cos 83 sin 83
1
Использованы:
а) формулы приведения:
sin (90º + t) = cost и sin (180º + t) = − sin t
sin2 (180º + t) = (− sin t) 2 = sin2 t
б) тождество: sin2 t + cos2 t = 1.
Задания открытого банка задач
5 29
3π
, t
; 2π .
10. Найдите tg t, если cos t
29
2
Решение.
5 29
cos t
29
5
29
2
25 29 25
4
5
2
2
sin t 1 cos t 1
1
29
29
29
29
29
4
2
3π
, где t
; 2π sin t 0
29
29
2
2
sin t
29 2 0,4.
tgt
5
cos t
5
29
sin t
Использованы тождества:
sin2
t+
cos2
sin t
t = 1 и tg t =
.
cos t
Задания открытого банка задач
11. Найдите −20cos 2t, если sin t = −0,8
Решение.
20 cos 2t 20 1 2 sin 2 t 20 1 2 0,8
2
20 1 2 0,64 20 1 1,28 20 0,28 5,6.
Использована формула: сos 2t = 1 – 2sin2 t
12. Найдите
Решение.
2 sin 4t
5 cos 2t
, если sin 2t = −0,7.
2 sin 4t 4 sin 2t cos 2t 4 sin 2t 4 0,7 2,8
0,56.
5 cos 2t
5 cos 2t
5
5
5
Использована формула: sin 2t = 2sin t cos t
13. Найдите значение выражения
Решение.
3π
cos 3π t sin
t
2
.
5 cos t π
3π
3π
cos 3π t sin
t cos t sin
t
2
2
5 cos t π
5 cos π t
cos t cos t 2cos t 2
0,4.
5 cos t
5 cos t 5
Использованы:
а) свойство нечетности функции sin t: sin (−t) = − sin t
б) свойство четности функции cos t: cos (−t) = cos t
в) формулы приведения:
cos (3π − t) = −cos t, sin (3π/2 − t) = − cos t, cos (π − t) = − cos t.
Задания открытого банка задач
14. Найдите значение выражения:
4tg(−3π – t) – 3tg t, если tg t = 1.
Решение.
4tg 3π t 3tgt 4tg 3π t 3tgt 4tgt 3tgt 7tgt
7 1 7.
Использованы:
а) свойство нечетности функции tg t: tg (−t) = − tg t
б) формула приведения: tg (3π + t) = tg t.
Задания открытого банка задач
3π
t , если sin t = 0,96, t ∈ (0; 0,5π).
2
15. Найдите 4 sin
Решение.
cos 2 t 1 sin 2 t 1 0,96
2
2
625 576
49
24
1
25
625 625 625
49
7
28
0,28, где t 0; 0,5π cos t 0
625 25 100
3π
4 sin
t 4 cos t 4 0,28 1,12.
2
cos t
Использованы:
а) формула приведения: sin (3π/2 − t) = − cos t
б) тождество: sin2 t + cos2 t = 1.
Задания открытого банка задач
16. Найдите tg t
5π
, если tg t = 0,1.
2
Решение.
5π
π
1
1
π
tg t
10.
tg 2π t tg t ctgt
2
2
tgt
0,1
2
Использованы:
а) формула приведения: tg (5π/2 + t) = − ctg t
б) тождество: tg t · ctg t = 1.
Задания открытого банка задач
17.
Найдите tg2 t, если 5sin2 t + 12cos2 t = 6.Решение.
: cos 2 t
5 sin 2 t 12cos 2 t
6
cos 2 t
cos 2 t
cos 2 t
1
5tg 2t 12 6
cos 2 t
5tg 2t 12 6 tg 2t 1
5tg 2t 6tg 2t 6 12
tg 2t 6
tg 2t 6.
Использовано тождество:
tg2
1
t+1=
.
2
cos t
Задания открытого банка задач
7 cos t 6 sin t
18. Найдите
,
3 sin t 5 cos t
если tg t = 1.
Решение.
Поделим числитель и знаменатель дроби на cos t ,
где cos t 0 :
7 cos t 6 sin t
7 cos t 6 sin t
cos t 7 6tgt 7 6 1 1 0,5.
cos t
3 sin t 5 cos t 3 sin t 5 cos t 3tgt 5 3 1 5 2
cos t
cos t
Использовано тождество: tg t =
sin t
.
cos t
Задания открытого банка задач
10 cos t 2 sin t 10
19. Найдите
, если tg t = 5.
sin t 5 cos t 5
Решение.
Поделим числитель и знаменатель дроби на cos t ,
где cos t 0 :
10 cos t 2 sin t
10
10
10 2tgt
10 cos t 2 sin t 10
cos t
cos t
cos t
cos t
sin t 5 cos t
5
5
sin t 5 cos t 5
tgt 5
cos t
cos t
cos t
cos t
10
10
10 2 5
cos t cos t 2.
5
5
5 5
cos t
cos t
Использовано тождество: tg t =
sin t
.
cos t
Задания открытого банка задач
20. Найдите tg t, если
7 sin t 2cos t
2.
4 sin t 9 cos t
Решение.
7sint 2cost 2
4sint 9cost 1
7sint 2cost 2 4sint 9cost
16cost sint
: cost
16cost sint
cost
cost
16 tgt
tgt 16.
Использовано тождество: tg t =
sin t
.
cos t
Задания открытого банка задач
21. Найдите tg t, если
3 sin t 5 cos t 1 1
.
2 sin t cos t 4 4
Решение.
3 sin t 5 cos t 1 1
2 sin t cos t 4 4
4 3 sin t 5 cos t 1 2 sin t cos t 4
12 sin t 20 cos t 4 2 sin t cos t 4
12 sin t 2 sin t cos t 20 cos t
10 sin t 19 cos t
10 sin t 19 cos t
cos t
cos t
10tgt 19
19
tgt
10
tgt 1,9.
: cos t
Использовано тождество: tg t =
sin t
.
cos t
Задания открытого банка задач
22. Найдите значение выражения
2
3
если cos t .
Решение.
π
2cos 2π t 5 sin t ,
2
π
π
2cos 2π t 5 sin t 2cos t 5 sin t 2cos t 5 cos t
2
2
2
3 cos t 3 2.
3
Использованы формулы приведения:
cos (2π + t) = cos t, sin (π/2 − t) = cos t.
Задания открытого банка задач
23. Найдите значение выражения
6 sin 142
.
sin 71 sin 19
Решение.
6 sin 142
6 2 sin 71 cos 71 12cos 71
12.
sin 71 sin 19 sin 71 sin 90 71
cos 71
Использованы:
а) формула sin 2t = 2sin t · cos t
б) формула приведения sin (90º – t) = cos t.
Задания открытого банка задач
13π
13π
cos
.
24. Найдите значение выражения 2 2 sin
8
8
Решение.
2 2 sin
13π
13π
13π
13π
cos
2 sin 2
2
sin
8
8
8
4
3π
3π
2
3π
2 sin 4π
2
1.
2 sin
2 sin
4
4
2
4
Использованы:
а) формула sin 2t = 2sin t · cos t
б) свойство периодичности функции sin t:
sin (2πn ± t) = ± sin t, где n ∈ Z
в) свойство нечетности функции sin t: sin (−t) = − sin t
г) таблица значений тригонометрических функций.
Задания открытого банка задач
25. Найдите значение выражения 27 cos 2
13π
13π
27 sin 2
.
12
12
Решение.
13π
13π
13π
13π
27 sin 2
27 cos 2
sin 2
12
12
12
12
π
π
13π
13π
27 cos 2
27 cos
27 cos 2π 27 cos
12
6
6
6
27 cos 2
3 3
3 9
4,5.
2
2
Использованы:
а) формула cos 2t = cos2 t – sin2 t.
б) свойство периодичности функции cos t:
cos (2πn ± t) = cos t, где n ∈ Z
в) таблица значений тригонометрических функций.
Задания открытого банка задач
26. Найдите значение выражения
Решение.
72 cos 2
15π
72 cos
18.
8
2
15π
15π
15π
18 18 2cos 2
1 18 cos 2
8
8
8
π
π
2
15π
18 cos
3.
18 cos 4π 18 cos 3 2
4
4
4
2
Использованы:
а) формула cos 2t = 2cos2 t – 1.
б) свойство периодичности функции cos t:
cos (2πn ± t) = cos t, где n ∈ Z
в) таблица значений тригонометрических функций.
Задания открытого банка задач
27. Найдите значение выражения
Решение.
8 32 sin 2
11π
8 32 sin
.
8
2
11π
11π
11π
8 1 2 sin 2
8 cos 2
8
8
8
3π
3π
2
11π
2 .
8 cos
2 2
8 cos 2π
8 cos
4
4
4
2
Использованы:
а) формула cos 2t = 1 – 2sin2 t.
б) свойство периодичности функции cos t:
cos (2πn ± t) = cos t, где n ∈ Z
в) таблица значений тригонометрических функций.
English Русский Rules
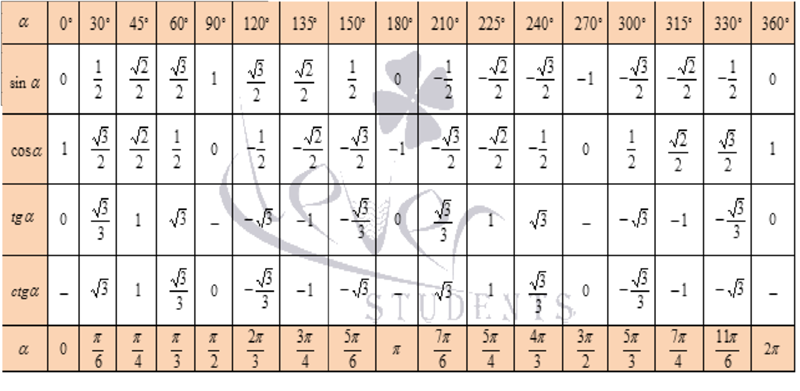
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
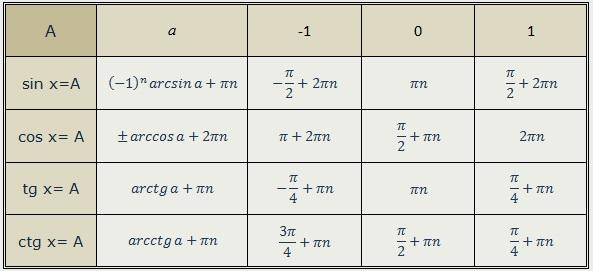
Найти все решения уравнения sin t — cos t = 1
Тригонометрия
Наталья М.
экспресс-результаты в радианах
Подписаться І 1
Подробнее
Отчет
2 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Марк Н. ответил 03.03.20
Репетитор
5,0 (1354)
Математика, статистика, программирование на C/C++? Марк поможет!
Смотрите таких репетиторов
Смотрите таких репетиторов
Пусть y = sin t и x = cos t. Тогда нам дано, что y — x = 1 или, что то же самое, y = x + 1. Из тождества Пифагора мы также должны иметь y 2 + x 2 = 1. Подстановка y = x + 1 дает (x+1 ) 2 + х 2 = 1, что упрощается до 2x 2 + 2x = 0.
Последнее уравнение выполняется только тогда, когда x равно 0 или -1. То есть, когда cos t = 0 или cos t = -1. Это также происходит, когда t = (2k + 1) π / 2 и t = (2k + 1) π соответственно, принимая k за любое целое число. Однако мы должны отбросить значения t = (4k+3)π/2, так как они не удовлетворяют данному уравнению. Это оставляет t = (4k+1)π/2 или t = (2k+1)π.
Голосовать за 0 Понизить
Подробнее
Отчет
Уильям В. ответил 02.02.20
Репетитор
5,0 (839)
Опытный репетитор и инженер на пенсии
См. таких репетиторов
Смотрите таких репетиторов
Диапазон как sin(t), так и cos(t) равен [-1, 1], что означает, что наибольшее значение get равно 1, а наименьшее значение get равно -1.
Это означает, что sin(t) — cos(t) может быть равен 1, только если sin(t) = 1, в то же время, когда cos(t) = 0 (1 — 0 = 1) или когда sin(t) = 0 в то же время, что cos(t) = -1 (0 — -1 = 1).
Чемодан 1 . sin(t) = 1 И cos(t) = 0
Это происходит только при π/2
Случай 2 sin(t) = 0 И cos(t) = -1
Это происходит только при π
Однако задача не дает ограничений на область. Это означает, что нам нужно включить оба этих значения, а также каждое приращение 2π. Итак, ответ:
t = π/2 + 2πk и t = π + 2πk, где k — любое целое число
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.
Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.