Син угла: Что такое синус угла — ответ на Uchi.ru

Содержание

Как находить синус угла :: SYL.ru

Открываем мадженту: самый модный цвет на 2023 в макияже, одежде и не только

Колесо жизни и другие практики, которые помогут начать новую жизнь в 2023 году

Уютные тренды и главные секреты офисного стиля на зиму 2023

Делаем праздничный блестящий маникюр без специального лака: способы и лайфхаки

Обычный картофель превращаем в изысканное блюдо. Легко готовить, вкусно есть

Любимчики фортуны. Какие знаки зодиака в новом году будут на коне

Особенности и актуальные модели джинсовых юбок макси — стильного хита 2023 года

Антибиотик или белок? Когда стоит снимать пенку с бульона, а когда нет

Как делать не надо: ошибки в использовании модных трендов при составлении образа

Не поверят, что сами сделали: рецепт шоколадно-мятного печенья

Автор Лео Север December 8, 2016

Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.

Игры с линейкой и карандашом

Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.

Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.

В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.

Найти синус для угла больше 90°

Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.

Вычисление синуса по другим тригонометрическим функциям

Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.

Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.

Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.

Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.

Как находить синус по трём сторонам треугольника

Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.

Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.

синусов

Синус — это половина хорды.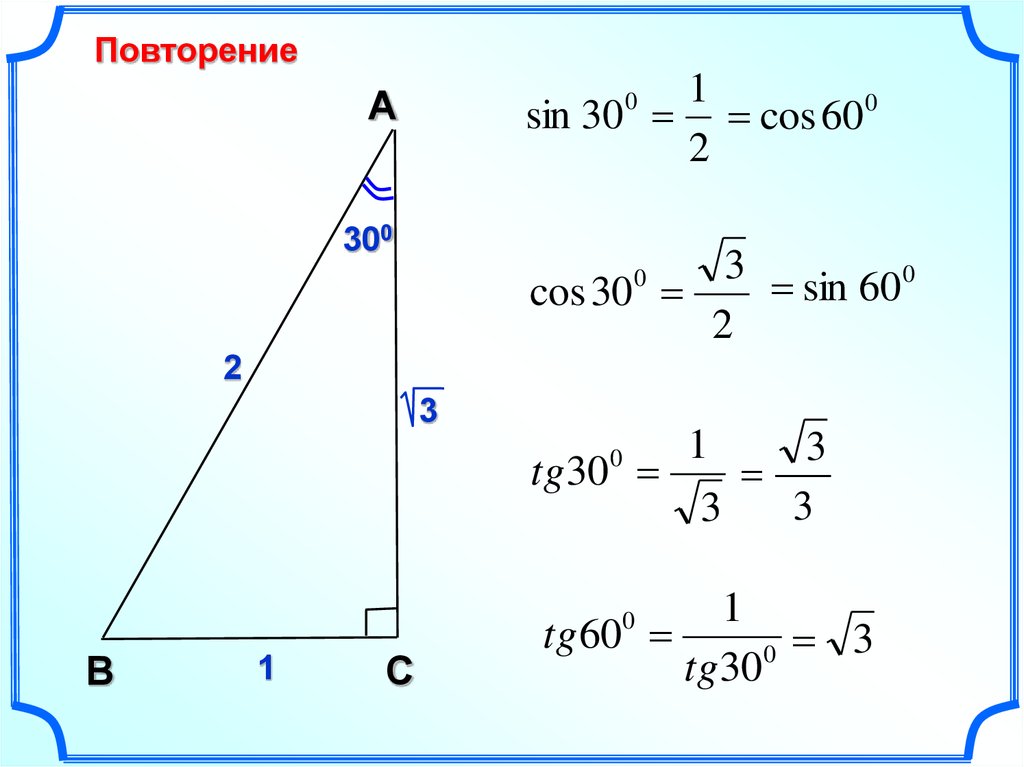 Точнее, синус угла равен половине хорды удвоенного угла.

Схема лука и стрел

Рассмотрим угол BAD на этом рисунке и предположим, что AB имеет единичную длину. Пусть точка C будет основанием перпендикуляра, опущенного из B на прямую AD. Тогда синус угла БАД определяется как длина линии до н.э., и записывается как sin BAD. Вы можете удвоить угол BAD , чтобы получить угол

BAE, и хорда угла BAE равна BE. Таким образом, синус BC угла BAD составляет половину хорды BE угла BAE, , а угол BAE вдвое больше угла BAD. Следовательно, как было сказано ранее, синус угла равен половине хорды удвоенного угла.

Смысл этого в том, чтобы показать, что синусы так сложно понять. (Ой, это описка! Я хотел написать «, а не , все это сложно понять».)

Значение слова «синус»

Санскритское слово, обозначающее половину аккорда, было джья-ардха, , которое иногда сокращалось до джива.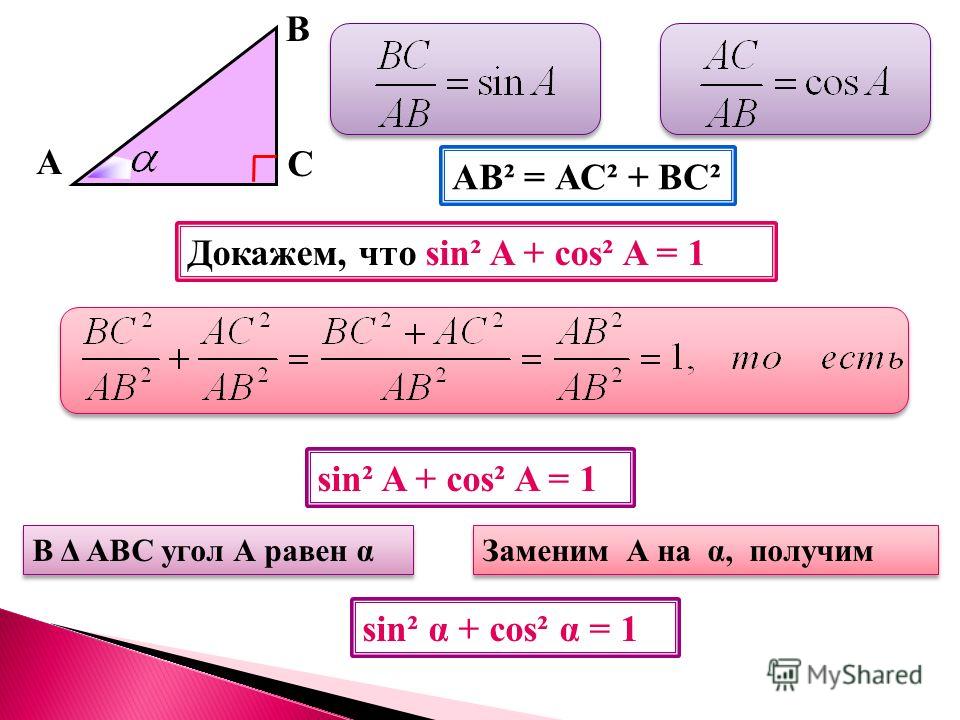 Это было перенесено на арабский язык как jiba, и написано по-арабски просто двумя согласными jb, 9.0009 гласных не пишется. Позже латинские переводчики выбрали слово sinus для перевода jb , думая, что это слово было арабским словом

jaib, означало грудь, а sinus имело два значения грудь и залив. В английском языке sinus было импортировано как «sine».
История этого слова для синуса интересна тем, что следует по пути тригонометрии из Индии через арабский язык из Багдада через Испанию в Западную Европу на латинском языке, а затем в современные языки, такие как английский и остальной мир. .
Синусы и прямоугольные треугольники
Мы можем использовать свойства подобных треугольников, чтобы связать синусы с прямоугольными треугольниками. На рисунке выше треугольник ABC является прямоугольным треугольником с прямым углом при угле C и гипотенузой длины 1. Рассмотрим аналогичный прямоугольный треугольник AB’C’ с гипотенузой произвольной длины. веб-браузер с поддержкой Java, вы можете перетаскивать точки B’ , чтобы изменить размер прямоугольного треугольника
АБ’С’. )

Поскольку треугольники подобны, отношение BC к AB равно отношению B’C’ к AB’. Но AB равно 1. Следовательно,
до н.э. = до н.э.’ / AB’
но до н.э. = sin A, так
sin A = B’C’ / AB’
Этот результат легче всего запомнить, поскольку синус угла в прямоугольном треугольнике равен противолежащему катету, деленному на гипотенузу:
Стандартное обозначение прямоугольного треугольника
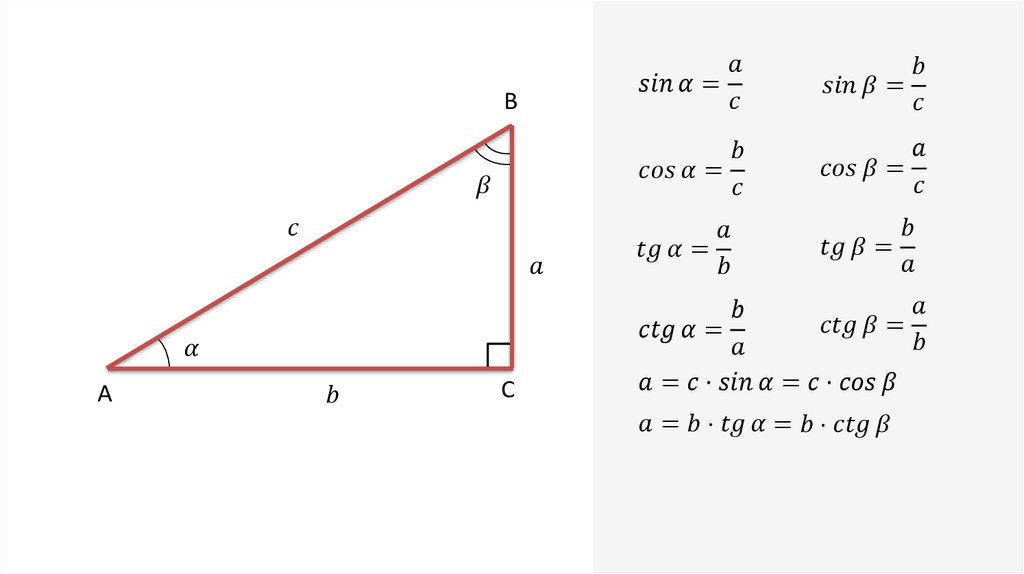
Какое-то время мы будем рассматривать в основном прямоугольные треугольники, поэтому было бы полезно использовать стандартные обозначения для углов и сторон этих треугольников.
Рассмотрим прямоугольный треугольник

ABC с прямым углом C. Обычно мы будем использовать букву a для обозначения стороны, противоположной углу A, букву b для обозначения стороны, противоположной углу В, и буква с для обозначения стороны, противолежащей углу С, то есть гипотенузе.
При таком обозначении sin A = a/c, и sin B = b/c.
Далее мы рассмотрим косинусы. Косинусы — это просто синусы дополнительного угла. Отсюда и название «косинус» («ко» — первые две буквы слова «дополнение»). Для треугольника ABC , потому что A просто sin Б.
Упражнения
28. В прямоугольном треугольнике гипотенуза c = 15 дюймов, а синус одного угла A, равен sin /5 /5. Найдите а, сторону, противоположную А, и найдите b, оставшуюся сторону.

44. В прямоугольном треугольнике B = 55° 30′, а b = 6,05. Найдите c и a.
191. Если высота фронтона крыши составляет 22,5 фута, а длина стропил 30 футов 8 дюймов, под каким углом наклоняются стропила и какой ширины фронтон у основания?
194. Верх лестницы длиной 50 футов упирается в здание на высоте 43 фута от земли. Под каким углом наклонена лестница и каково расстояние ее основания от стены?
Подсказки
28. Гипотенуза c равно 15″. Так как sin A = a/c, , следовательно, a = c sin A. Это дает вам a. и и с
44. Поскольку sin B = b/c, можно определить c. Когда у вас есть b и c, , вы можете определить a по теореме Пифагора.

191. Фронтон ABD крыши представляет собой равнобедренный треугольник, основание которого равно ширине дома, а две равные наклонные стороны — стропила на конце крыши. Если опустить перпендикуляр из вершины B треугольника, вы получите два конгруэнтных прямоугольных треугольника, ABC и DBC. Поскольку вы знаете две стороны прямоугольного треугольника ABC, , вы можете вычислить третью, используя теорему Пифагора. Вы можете использовать синусы для определения угла наклона, так как sin A = BC/AB = 22,5’/30’8″ = 0,7337. Чтобы найти угол A, , вам понадобится так называемый арксинус 0,7337.
Функция арксинуса обратна функции синуса, и ваш калькулятор может их вычислить. Обычно на калькуляторе есть кнопка с надписью «inv» или «arc», которую вы нажимаете перед нажатием кнопки «sin». Тогда у вас будет угол. Ваш калькулятор, вероятно, может быть установлен либо в градусный режим, либо в радианный режим. Если он установлен в градусный режим, вы получите угол в градусах; и если он установлен в радианном режиме, то вы получите угол в радианах. Всегда знайте, в каком режиме установлен ваш калькулятор.

194. Нарисуйте треугольник ABC , как указано выше. Вы знаете гипотенузу с и вертикальную сторону а. Расстояние b можно найти по теореме Пифагора. Просто возьмите квадратный корень из c ² – a ² . Наклон, то есть угол А, можно найти с помощью синусов. Вы знаете, что sin A = a/c = 43/50 = 0,86. Как и в задаче 191, используйте arcsin, чтобы найти угол А.
Ответы
28.
a = c sin A = 15 (2/5) = 6 дюймов.
b ² = c ² – a ² = 189, поэтому b = 13,7 дюйма.
44. c = b /sin B = 6,05/sin 55°30′ = 7,34.
a = 4,16.
191. Угол A равен 0,824 радиана, или 47,2° = 47°12′. Ширина фронтона 41,7 фута = 41 фут 8 дюймов.
194. Поскольку c ² – a ² = 651, следовательно, расстояние b равно квадратному корню, а именно 25,5 футов.
Теперь sin A = 0,86, поэтому A составляет 1,035 радиана, или около 59,32° = 59°20′.
Как использовать функцию SIN в Excel (6 простых примеров)
Функция SIN используется для определения синуса углов в Excel. По умолчанию функция SIN принимает углы в радианах. Однако с помощью других функций вы можете вставлять углы как в радианах, так и в градусах. Чтобы помочь вам в этом, в этой статье мы обсудим использование функции SIN в Excel на 6 подходящих примерах.
Приведенный выше снимок экрана представляет собой обзор статьи, представляющий несколько приложений 9Функция 0376 SIN в Excel. Вы узнаете больше о методах наряду с другими функциями для использования функции SIN именно в следующих разделах этой статьи.
Скачать практическую рабочую тетрадь
Введение в функцию SIN
Что такое синус в тригонометрии?
6 примеров использования функции SIN в Excel
1. Используйте функцию SIN в Excel для углов в радианах.
2. Используйте функцию SIN в Excel для углов в градусах
3. Используйте функцию SIN с функцией PI в Excel для углов в градусах.
4. Рассчитайте высоту здания с помощью функции SIN.
5. Решите уравнение с функцией SIN
6. Функция SIN в макросах VBA
То, что нужно запомнить
Заключение
Статьи по Теме
Загрузить учебную тетрадь
Вам рекомендуется скачать файл Excel и попрактиковаться вместе с ним.
Знакомство с функцией SIN
Назначение функции:
Функция SIN используется для определения синуса углов в Excel.
Синтаксис:
=SIN(число)
Аргументы Объяснение:
Аргумент Требуется/дополнительно Пояснение
номер Обязательно Угол в радианах для вычисления синуса заданного угла.
Возвращаемый параметр:
Значение синуса заданных углов.
Что такое синус в тригонометрии?
Отношение Синус в тригонометрии — это отношение между гипотенузой и противоположной стороной треугольника.
Для приведенного выше рисунка sin(a)=гипотенуза/противоположная
6 примеров использования функции SIN в Excel
В зависимости от входных значений использование функции SIN делится на две основные категории. Первый — это входные углы в радианах, которые являются угловой метрикой по умолчанию для функции SIN . Второй наклонен в градусах. В следующих разделах мы обсудим обе категории одну за другой.
Мы также обсудим функцию SIN в Excel VBA . Итак, без дальнейшего обсуждения, давайте сразу перейдем ко всем примерам один за другим.
1. Используйте функцию SIN в Excel для углов в радианах
Если вы хотите вставить углы в радианах, то использовать функцию SIN очень просто. Потому что функция SIN по умолчанию может работать с углами в радианах. В любом случае выполните следующие шаги, чтобы увидеть, как использовать функцию SIN для углов в радианах.
🔗 Шаги:
❶ Выберите ячейку C5 ▶ для сохранения результата формулы.
❷ Затем введите формулу в ячейку:
=SIN(B6)
❸ Теперь нажмите кнопку ВВОД ▶ для выполнения формулы.
❹ Наконец, завершите весь процесс, перетащив значок Ручка заполнения в конец столбца синуса.
Это все, что вам нужно сделать. В любом случае, когда вы выполните все шаги, упомянутые выше, вы увидите конечный результат, как на картинке ниже:
Как мы видим на картинке выше, синус заданных углов представляет собой значения длинной дроби. Не всегда удобно пользоваться.
Итак, если вы хотите, вы можете обрезать эти длинные числа по своему усмотрению, используя ОКРУГЛ функцию . Все, что вам нужно сделать, это:
🔗 Шаги:
❶ Нажмите на ячейку D5 ▶ для сохранения результата формулы.
❷ Затем введите в ячейку формулу:
=ОКРУГЛ(C5,2)
❸ Нажмите кнопку ENTER ▶ для выполнения формулы.
❹ Наконец, завершите весь процесс, перетащив значок Ручка заполнения в конец столбца синуса.
Это все, что вам нужно сделать. В любом случае, когда вы выполните все шаги, упомянутые выше, вы увидите конечный результат, как на картинке ниже:
Подробнее: 51 Наиболее часто используемые математические и триггерные функции в Excel
2.
Используйте функцию SIN в Excel для углов в градусах
Когда у вас есть углы в градусах, то для вычисления синуса углов вам придется выполнить дополнительную задачу. То есть перевести угол из градусов в радианы. Как функция SIN принимает только углы в радианах.
Итак, мы можем конвертировать углы в градусы двумя разными способами. Первый использует функцию RADIAN . Это встроенная в Microsoft Excel функция, с помощью которой вы можете мгновенно преобразовывать углы в градусах в углы в радианах.
Следующие шаги помогут вам сделать это.
🔗 Шаги:
❶ Нажмите на ячейку C5 ▶, чтобы сохранить результат формулы.
❷ Теперь введите следующую формулу в ячейку C5 :
=SIN(РАДИАНЫ(B5))
❸ Нажмите кнопку ВВОД ▶ для выполнения формулы.
❹ Наконец, перетащите значок Ручка заполнения в конец столбца синуса.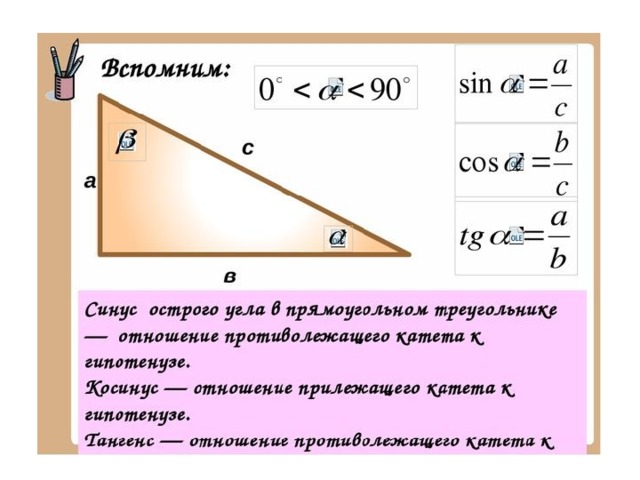
Это все, что вам нужно сделать. В любом случае, когда вы выполните все шаги, упомянутые выше, вы увидите конечный результат, как на картинке ниже:
Подробнее: 44 Математические функции в Excel (Скачать PDF бесплатно)
3. Использование функции SIN с функцией PI в Excel для углов в градусах
Существует еще один способ преобразования углов в градусах в углы в радианах. Все, что вам нужно сделать, это умножить углы на PI()/180 . Позвольте мне показать вам весь процесс шаг за шагом:
🔗 Шаги:
❶ Сначала выберите ячейку C5 ▶ для сохранения результата формулы.
❷ Затем введите формулу:
=SIN(B5*PI()/180)
внутри ячейки.
❸ Теперь нажмите кнопку ВВОД ▶ для выполнения формулы.
❹ Наконец, завершите весь процесс, перетащив значок Ручка заполнения в конец столбца синуса.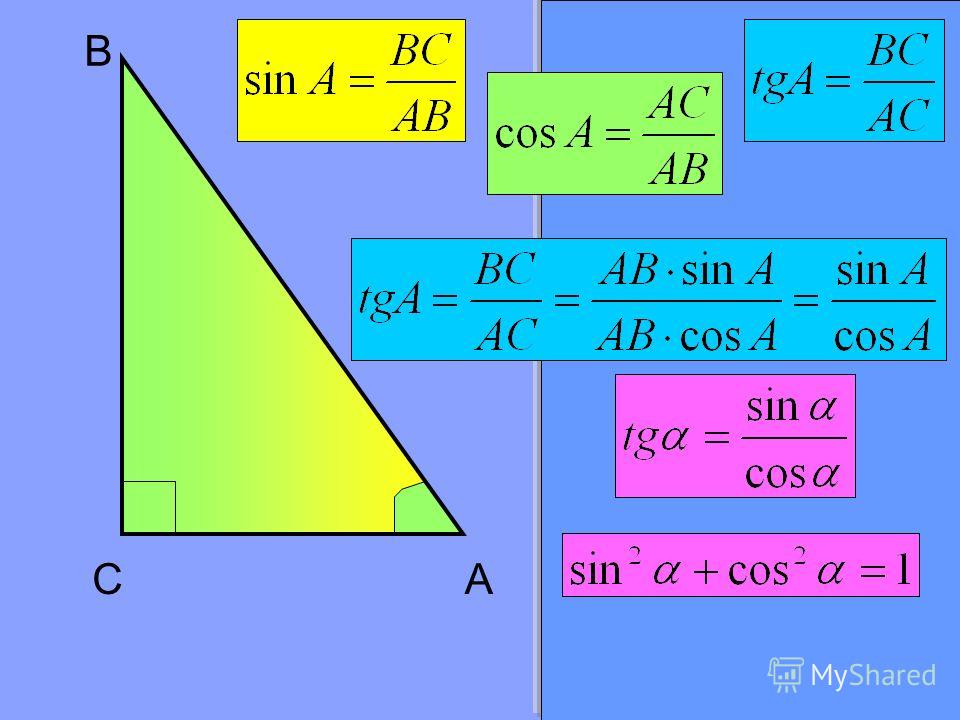
Это все, что вам нужно сделать. В любом случае, когда вы выполните все шаги, упомянутые выше, вы увидите конечный результат, как на картинке ниже:
Как мы видим на картинке выше, синус заданных углов представляет собой значения длинной дроби. Не всегда удобно пользоваться.
Итак, если вы хотите, вы можете обрезать эти длинные числа по своему усмотрению, используя функцию ОКРУГЛ . Все, что вам нужно сделать, это:
🔗 Шаги:
❶ Выберите ячейку D5 ▶ для сохранения результата формулы.
❷ Затем введите формулу:
=ОКРУГЛ(C5,2)
внутри ячейки.
❸ Теперь нажмите кнопку ВВОД ▶ для выполнения формулы.
❹ Наконец, завершите весь процесс, перетащив значок Ручка заполнения в конец столбца синуса.
Это все, что вам нужно сделать. В любом случае, когда вы выполните все шаги, упомянутые выше, вы увидите конечный результат, как на картинке ниже:
Подробнее: Как использовать функцию Excel PI (7 примеров)
Аналогичные показания
Как использовать функцию FLOOR в Excel (11 примеров)
Функция VBA EXP в Excel (5 примеров)
Как использовать функцию МУМНОЖ в Excel (6 примеров)
Использование функции TRUNC в Excel (4 примера)
Как использовать функцию TAN в Excel (6 примеров)
4.
Расчет высоты здания с помощью функции SIN
Мы можем рассчитать высоту здания, используя функцию SIN . Например, высота дома h. Он дал тень длиной 50м. Воображаемая линия соединения высоты здания с тенью образует с тенью угол 0,5 рад. Теперь посчитаем высоту здания.
🔗 Шаги:
❶ Нажмите на ячейку C7 ▶ для сохранения результата формулы.
❷ Затем введите формулу:
=C5*SIN(0.5)
внутри ячейки.
❸ Теперь нажмите кнопку ВВОД ▶ для выполнения формулы.
Теперь вы можете видеть, что высота здания составляет 23,97 метра.
5. Решение уравнения с функцией SIN
Теперь мы будем следовать приведенному ниже уравнению, используя SIN и COS 9.2А=1
Введите все формулы, как показано на рисунке ниже:
Когда вы закончите писать, вы увидите следующий результат:
Подробнее: Решение уравнений в Excel (полиномиальные, кубические, квадратичные и линейные)
6.
Функция SIN в макросах VBA
Чтобы реализовать функцию SIN в VBA , выполните следующие действия:
🔗 Шаги:
❶ Нажмите ALT + F11 , чтобы открыть редактор VBA .
❷ Перейти к Вставка ▶ Модуль.
❸ Скопируйте следующий код:
Sub CalSin() Dim sin_val1 как двойной Dim sin_val2 как двойной Dim sin_val3 как двойной sin_val1 = грех (90) Ячейки (5, 3). Значение = sin_val1 sin_val2 = Грех (45) Ячейки (6, 3). Значение = sin_val2 sin_val3 = Грех (0) Ячейки (7, 3). Значение = sin_val3 Конец суб
❹ Вставьте и сохраните код.
❺ Вернитесь к листу Excel.
❻ Нажмите ALT + F8 , чтобы открыть макрос .
❼ Запустить функцию.
Когда вы выполните все описанные выше шаги, вы увидите следующий результат:
Что нужно помнить
📌 Функция SIN ожидает углы в радианах.
No related posts.