Sin x 1 cos x 2: sin(x-1)=cos(x+2) — Школьные Знания.com

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88
Найти точное значение		tan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

sinx*cosx — AvBj

March 21, 2023 by

30 mai 2016 — Sinx – cosx = 1/5, what is sin x and cos x equivalent to? 5,722 Views. The expression for sin x + cos x in terms of sine is sin x + sin (π/2 – x).15 apr. 2015 — Explanation: ; cos · =±√1 ; sin · +cosx=sinx±√1 ; cos · = · ( …The tangent function is positive in the first and third quadrants. To find the second solution, add the reference angle from π π to find the solution in the …Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, …sin(x)*cos(x). Natural Language; Math Input. Use Math Input Mode to directly enter textbook math notation. Try it. ×.9 apr. 2018 — (sin 2x)/2 = 2sin x * cos x /2 =six*cosx. Explorează toate răspunsurile similare. arrow right. heart outlined. Mulţumesc 5.sinx + cosx. 1. Vezi răspunsul. Insigna care arată cizma unui astronaut atingând luna este deblocată. Vezi ce spune comunitatea și deblochează insigna.Click here to get an answer to your question ✍️ The general solution of |sin x| = cos x is (when nepsilon Z) given by.Click here to get an answer to your question ✍️ The minimum value of sin x + cos x is.

2x By signing up, you’ll get thousands of step-by-step solutions to your homework…Example 1. Solve the equation sin x = cos x and then the inequality. sin x > cos x on the interval 0 …We know that sinx/cosx = tanx. Therefore we can write sinx – cosx = 0 as sinx = cosx . By diving both sides by cosx, we get tanx = 1.28 iul. 2022 — Answer: The maximum value of sinx.cosx is ½. The detailed solution can be seen below. … Now, we know that the maximum value of sinx = 1, hence …4 Answers · √2 x 1/√2 ( sinx – cosx) · =√2 x { (1/√2)sinx – (1/√2)cosx } · =√2 sin (x – pi/4) · range of sine function is [-1,1] · so range of f(x) will be [- …sin(2x) = 2 sin(x) cos(x). cos(2x) = cos2(x) − sin2(x) = 1 − 2 sin2(x) = 2 cos2(x) − 1. tan ⁡ ( 2 x ) = 2 tan ⁡ ( x ) 1 − tan ⁡ 2 ( x ) tan(2x) …The issue : when you write out sinx=cosx implies sin2x=cos2x, there is no problem with the implication. However, an implication leads to a …Why is sin (x+x) = sinx cosx + cosx sinx ? Simple explanation required please. Free Pre-Algebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators step-by-step.Given: (frac{{sin x + cos x}}{{sin x – cos x}} = frac{6}{5}) Concept Used: Componendo & dividendo a/b = c/d then (a + b)/(a – b) =(c …If sinx + cosx = a, then |sinx – cosx| = ______.Prove the following: cosx+sinxcosx-sinx-cosx-sinxcosx+sinx = 2tan2x.Hint: In this question, we need to find the maximum value of sinx-cosx. Suppose $fleft( x right)=sin x-cos x$ for this, …11 mar. 2018 — Surprisingly, it appears as though sin(x) + cos(x) is itself a sine function. And while its period is the same as sin(x), its amplitude has …Question 1112839: If +log%28sinx%2C+cosx%29+=+1%2F2+ , and 0 < x < pi/2, compute sin x. Answer by solver91311(24713) · About Me (Show Source):.31 aug. 2018 — The number of distinct real roots of |(sinx cosx cosx), (cosx sinx cosx), (cosx cosx sinx)| = 0 in the … (A) 0 (B) 2 (C) 1 (D) 3.cos(X – Y) = cosX cosY + sinX sinY sin(X + Y) = sinX cosY + … sin(X – Y) = sinX cosY – cosX sinY … sinX + sinY = 2sin[ (X + Y) / 2 ] cos[ (X – Y) / 2 ] …13 feb. 2 x. Verify that the equation is an identity. Show that sinx – cosx sinx+cosx.Does the above mean either of the following?. tan x = sin x/cos x, equation 1. … Aug 22, 2015 tanx + secx = 1 tanx = sinx cosx and secx = 1 cosx sinx cosx …Tan X Sec X 1tanx+secx=1 tanx=sinx/cosx and secx=1/cosx sinx/cosx+1/cosx=1 … calculate the values of sin x and cos x (2 decimal places) on the.sin 2 x sin x + cos x d x Put sin x …, int sinx + cosx√(sin2x)dx Maths Questions – Toppr Ask Web∫1+cosxdx is equal to A 2sin(2x)+C B 2sin(2x)+C C …For real number x, the notations sin x, cos x, etc. refer to the value of the trigonometric functions evaluated at an angle of x rad.Derivation of Integral of Sin x Cos x Using Sin 2x Formula. For | A | < 1, we can use the Weierstrass substitution (or alternatively, …X tan x 1 Step 3: cos x sinx COS X Step 4: sec x + 1 tan x Step 5: cscx+ … we take the help of trigonometric identities. tan x = sin x/cos x, equation 1.Formulas of the derivatives of trigonometric functions sin (x), cos (x), tan (x), cot (x), sec (x) and csc (x), in calculus, are presented along with several …t a n ( x ) = sin ⁡ ( x ) cos ⁡ ( x ) tan (x)= frac{sin(x)}{cos(x)} tan(x)=cos(x)sin(x)​. 2 x + sin x = 4; Solve the following equation giving value of x between 0 degrees to 360 degrees (or (0, 2 pi)). The calculations to …sinx, cosx.Improper Integral — Two Infinite Limits of Integration. Determine whether ∫∞−∞xsin(x2)dx ∫ − ∞ ∞ x sin ⁡ ( x 2 ) d x is convergent or divergent.The most common half angle identities are: sin (x/2) = ±√ { [1-cosx]/2} cos … list double angle identities by request step-by-step. sin x/cos x = tan x.

Click to rate this post!

[Total: 1 Average: 5]

Categories Uncategorized Tags sinx*cosx

Мэтуэй | Популярные задачи

92
1 Найти точное значение грех(30)
2 Найти точное значение грех(45)
3 Найти точное значение грех(30 градусов)
4 Найти точное значение грех(60 градусов)
5 Найти точное значение загар (30 градусов)
6 Найти точное значение угловой синус(-1)
7 Найти точное значение грех(пи/6)
8 Найти точное значение cos(pi/4)
9 Найти точное значение грех(45 градусов)
10 Найти точное значение грех(пи/3)
11 Найти точное значение арктан(-1)
12 Найти точное значение cos(45 градусов)
13 Найти точное значение cos(30 градусов)
14 Найти точное значение желтовато-коричневый(60)
15 Найти точное значение csc(45 градусов)
16 Найти точное значение загар (60 градусов)
17 Найти точное значение сек(30 градусов)
18 Найти точное значение cos(60 градусов)
19 Найти точное значение cos(150)
20 Найти точное значение грех(60)
21 Найти точное значение cos(pi/2)
22 Найти точное значение загар (45 градусов)
23 Найти точное значение arctan(- квадратный корень из 3)
24 Найти точное значение csc(60 градусов)
25 Найти точное значение сек(45 градусов)
26 Найти точное значение csc(30 градусов)
27 Найти точное значение грех(0)
28 Найти точное значение грех(120)
29 Найти точное значение соз(90)
30 Преобразовать из радианов в градусы пи/3
31 Найти точное значение желтовато-коричневый(30)
32
35 Преобразовать из радианов в градусы пи/6
36 Найти точное значение детская кроватка(30 градусов)
37 Найти точное значение арккос(-1)
38 Найти точное значение арктан(0)
39 Найти точное значение детская кроватка(60 градусов)
40 Преобразование градусов в радианы 30
41 Преобразовать из радианов в градусы (2 шт. )/3
42 Найти точное значение sin((5pi)/3)
43 Найти точное значение sin((3pi)/4)
44 Найти точное значение тан(пи/2)
45 Найти точное значение грех(300)
46 Найти точное значение соз(30)
47 Найти точное значение соз(60)
48 Найти точное значение соз(0)
49 Найти точное значение соз(135)
50 Найти точное значение cos((5pi)/3)
51 Найти точное значение cos(210)
52 Найти точное значение сек(60 градусов)
53 Найти точное значение грех(300 градусов)
54 Преобразование градусов в радианы 135
55 Преобразование градусов в радианы 150
56 Преобразовать из радианов в градусы (5 дюймов)/6
57 Преобразовать из радианов в градусы (5 дюймов)/3
58 Преобразование градусов в радианы 89 градусов
59 Преобразование градусов в радианы 60
60 Найти точное значение грех(135 градусов)
61 Найти точное значение грех(150)
62 Найти точное значение грех(240 градусов)
63 Найти точное значение детская кроватка(45 градусов)
64 Преобразовать из радианов в градусы (5 дюймов)/4
65 Найти точное значение грех(225)
66 Найти точное значение грех(240)
67 Найти точное значение cos(150 градусов)
68 Найти точное значение желтовато-коричневый(45)
69 Оценить грех(30 градусов)
70 Найти точное значение сек(0)
71 Найти точное значение cos((5pi)/6)
72 Найти точное значение КСК(30)
73 Найти точное значение arcsin(( квадратный корень из 2)/2)
74 Найти точное значение загар((5pi)/3)
75 Найти точное значение желтовато-коричневый(0)
76 Оценить грех(60 градусов)
77 Найти точное значение arctan(-( квадратный корень из 3)/3)
78 Преобразовать из радианов в градусы (3 пи)/4 
79 Найти точное значение sin((7pi)/4)
80 Найти точное значение угловой синус(-1/2)
81 Найти точное значение sin((4pi)/3)
82 Найти точное значение КСК(45)
83 Упростить арктан( квадратный корень из 3)
84 Найти точное значение грех(135)
85 Найти точное значение грех(105)
86 Найти точное значение грех(150 градусов)
87 Найти точное значение sin((2pi)/3)
88 Найти точное значение загар((2pi)/3)
89 Преобразовать из радианов в градусы пи/4
90 Найти точное значение грех(пи/2)
91 Найти точное значение сек(45)
92 Найти точное значение cos((5pi)/4)
93 Найти точное значение cos((7pi)/6)
94 Найти точное значение угловой синус(0)
95 Найти точное значение грех(120 градусов)
96 Найти точное значение желтовато-коричневый ((7pi)/6)
97 Найти точное значение соз(270)
98 Найти точное значение sin((7pi)/6)
99 Найти точное значение arcsin(-( квадратный корень из 2)/2)
100 Преобразование градусов в радианы 88 градусов

Formulaire de trigonométrie : ultime fiche

Les формул де trigonométrie sont essentielles quel que soit le niveau (au collège en 3ème, au lycée en 1ère ou Terminale, ou encore dans le superieur en prépa ou en MPSI), mais un rappel complete n’est pas superflu.

О том, что нужно для подготовки к спуску по формулам тригонометрии, по программе:

  • Основные отношения
  • Замечательные преобразования
  • Les Angles remarquables
  • Тригонометрические уравнения
  • Дополнительные формулы
  • Et enfin les формул де дублирования

Прекрасная лекция и n’hésitez pas à l’imprimer comme vous le feriez avec un pdf 😉

Rendez-vous également на форуме

I — Общие сведения о формулах триго

1.1 Основные отношения

tan (x) = sin⁡(x) cos⁡(x)tan (x) = \ frac{\sin(x)}{\cos(x)}tan(x)=cos(x)sin(x)​

Маленькая проницательность Нелли : Pour se сувенир из прежней формулы, je me dis que tangente c’est Soleil sur Carottes ! D’où sin sur cos…si ça peut aider!

1.2 Замечательные преобразования

Passons maintenant aux преобразования remarquables:

грех⁡(2π+x)=sin⁡(x)\sin (2\pi + x) = \sin (x)sin(2π+x)=sin(x)
cos⁡(2π+x)=cos ⁡(x)\cos (2\pi + x) = \cos (x)cos(2π+x)=cos(x)
tan⁡(2π+x)=tan⁡(x)\tan (2\pi + x) = \tan (x)tan(2π+x)=tan(x)

sin⁡(-x)=-sin⁡(x)\sin(-x) = — \sin (x)sin(-x)=-sin(x)
cos⁡(-x)=cos⁡(x )\cos (-x) = \cos (x)cos(-x)=cos(x)
tan⁡(-x)=-tan⁡(x)\tan (-x) = — \tan(x) загар(-х)=-загар(х)

sin⁡(π−x)=sin⁡(x)\sin (\pi — x) = \sin(x)sin(π−x)=sin(x)
cos⁡(π−x)=−cos ⁡(x)\cos (\pi — x) = — \cos(x)cos(π−x)=−cos(x)
tan⁡(π−x)=−tan⁡(x)\tan (\ pi — x) = — \tan(x)tan(π−x)=-tan(x)

sin⁡(π+x)=−sin⁡(x)\sin (\pi + x) = — \sin (x)sin(π+x)=−sin(x)
cos⁡(π+x)=−cos⁡(x)\cos (\pi + x) = — \cos (x)cos(π+x)=−cos(x)
tan⁡(π+x) = tan⁡(x)\tan (\pi + x) = \tan (x)tan(π+x)=tan(x)

sin⁡(π2−x)=cos⁡(x)\sin(\frac{\pi}{2} — x) = \cos (x)sin(2π​−x)=cos(x)
cos⁡ (π2−x)=sin⁡(x)\cos(\frac{\pi}{2} — x) = \sin (x)cos(2π​-x)=sin(x)
tan⁡(π2- x) = 1tan⁡(x)\tan(\frac{\pi}{2} — x) = \frac{1}{\tan (x)}tan(2π​−x)=tan(x)1​

sin⁡(π2+x)=cos⁡(x)\sin(\frac{\pi}{2} + x) = \cos (x)sin(2π​+x)=cos(x)
cos⁡ (π2+x)=-sin⁡(x)\cos(\frac{\pi}{2} + x) = — \sin (x)cos(2π​+x)=-sin(x)
tan⁡(π2+x)=-1tan⁡(x)\tan(\frac{\pi}{2} + x) = — \frac{1}{\tan (x)}tan(2π​+x )=−tan(x)1​

sin⁡(3π2−x)=−cos⁡(x)\sin(\frac{3\pi}{2} — x) = — \cos (x)sin(23π​−x)=−cos(x )
cos⁡(3π2−x)=−sin⁡(x)\cos(\frac{3\pi}{2} — x) = — \sin (x)cos(23π​−x)=−sin( x)
tan⁡(3π2−x)=1tan⁡(x)\tan(\frac{3\pi}{2} — x) = \frac{1}{\tan (x)}tan(23π​− х)=загар(х)1​

sin⁡(3π2+x)=−cos⁡(x)\sin(\frac{3\pi}{2} + x) = — \cos (x)sin(23π​+x)=−cos(x )
cos⁡(3π2+x)=sin⁡(x)\cos(\frac{3\pi}{2} + x) = \sin (x)cos(23π​+x)=sin(x)
tan⁡(3π2+x)=−1tan⁡(x)\tan(\frac{3\pi}{2} + x) = — \frac{1}{\tan (x)}tan(23π​+ x)=−tan(x)1​

1.

3. Углы remarquables
ххх грех⁡(х)\грех(х)грех(х) cos⁡(x)\cos(x)cos(x) загар⁡(х)\загар(х)загар(х) котан(х)\текст{котан}(х)котан(х)
0 0 1 0 /
π6\frac{\pi}{6}6π 12\фрак{1}{2}21​ 32 {\ frac {\ sqrt3} {2}} 23 33{\frac{\sqrt3}{3}}33​​ 3\sqrt33​
π4\frac{\pi}{4}4π 22 {\ frac {\ sqrt2} {2}} 22 22 {\ frac {\ sqrt2} {2}} 22 1 1
π3\frac{\pi}{3}3π 32 {\ frac {\ sqrt3} {2}} 23 12\фрак{1}{2}21​ 3\sqrt33​ 33{\frac{\sqrt3}{3}}33​
π2\frac{\pi}{2}2π 1 0 / 0
π\piπ 0 -1 0 /

1.

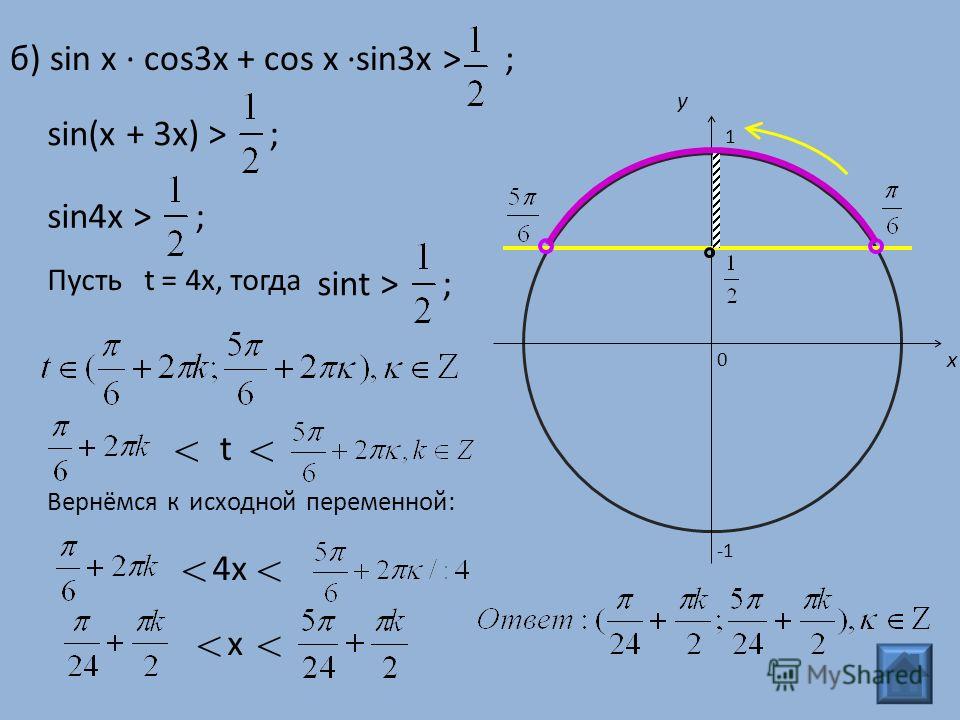
4. Тригонометрические уравнения

kkk appartient à Z

sin⁡(a)=sin⁡(b)\sin (a) = \sin(b)sin(a)=sin(b)
alors a=b+2kπa = b + 2k\pia=b+2kπ
или a=π−b+2kπa = \pi — b + 2k\pia=π−b+2kπ

cos⁡(a)=cos(b)\cos(a) = cos(b)cos(a)=cos(b)
alors a=b+2kπa = b + 2k\pia=b+2kπ
или a=−b+2kπa = -b + 2k\pia=−b+2kπ

tan⁡(a)=tan⁡(b)\tan (a) = \tan(b)tan(a)=tan(b)
alors a=b+kπa = b + k\pia=b+kπ

II — Дополнительные формулы

sin⁡(a+b)=sin⁡(a)cos⁡(b)+sin⁡(b)cos⁡(a)\sin(a+b)=\sin(a)\cos(b)+\ грех (b)\cos (a)sin(a+b)=sin(a)cos(b)+sin(b)cos(a)
sin⁡(a−b)=sin⁡(a)cos⁡( б)−sin⁡(b)cos⁡(a)\sin (a — b) = \sin (a)\cos (b) — \sin (b)\cos (a)sin(a−b)=sin (a) cos (b) − sin (b) cos (a)
cos⁡ (a + b) = cos⁡ (a) cos⁡ (b) − sin⁡ (a) sin⁡ (b) \ cos ( + b) = \cos (a)\cos (b) — \sin (a)\sin (b)cos(a+b)=cos(a)cos(b)−sin(a)sin(b)
cos⁡(a−b)=cos⁡(a)cos⁡(b)+sin⁡(a)sin⁡(b)\cos (a — b) = \cos(a)\cos(b) + \ sin (a)\sin (b)cos(a−b)=cos(a)cos(b)+sin(a)sin(b)
tan⁡(a+b)=tan⁡(a)+tan⁡ (b) 1−tan ⁡ (a) tan ⁡ (b) \ tan (a + b) = \ frac {\ tan (a) + \ tan (b)} {1 — \ tan (a) \ tan (b )}tan(a+b)=1−tan(a)tan(b)tan(a)+tan(b)​
tan⁡(a−b)=tan⁡(a)−tan⁡(b)1 +tan⁡(a)tan⁡(b)\tan (a — b) = \ frac{\tan (a) — \ tan (b)}{1 + \tan (a)\tan (b)}tan( a−b)=1+tan(a)tan(b)tan(a)−tan(b)​

sin⁡(p)+sin⁡(q)=2sin⁡(p+q2)cos⁡(p−q2)\sin (p) + \sin(q) = 2\sin(\frac{p + q} {2})\cos (\frac{p — q}{2})sin(p)+sin(q)=2sin(2p+q​)cos(2p−q​)
sin⁡(p)−sin⁡(q)=2sin⁡(p−q2)cos⁡(p+q2)\sin(p) — \sin(q) = 2\sin(\frac{p — q} {2})\cos (\frac{p + q}{2})sin(p)−sin(q)=2sin(2p−q​)cos(2p+q​)
cos⁡(p)+cos ⁡(q)=2cos⁡(p+q2)cos⁡(p−q2)\cos (p) + \cos(q) = 2\cos (\frac{p + q}{2})\cos (\ frac{p — q}{2})cos(p)+cos(q)=2cos(2p+q​)cos(2p−q​)
cos⁡(p)−cos⁡(q)=−2sin⁡ (p+q2)sin⁡(p−q2)\cos (p) — \cos(q) = -2\sin (\frac{p + q}{2})\sin (\frac{p — q} {2})cos(p)−cos(q)=−2sin(2p+q​)sin(2p−q​)
tan⁡(p)+tan⁡(q)=sin⁡(p+q)cos ⁡(p) cos(q)\tan (p) + \tan (q) = \frac{\sin (p + q)}{\cos (p)\ cos(q)}tan(p)+tan( q)=cos(p) cos(q)sin(p+q)​
tan⁡(p)−tan⁡(q)=sin⁡(p−q)cos⁡(p) cos(q)\tan(p) — \tan(q) = \frac{\sin(p — q) )}{\cos (p)\ cos(q)}tan(p)−tan(q)=cos(p) cos(q)sin(p−q)​

sin⁡(a)sin⁡(b)=12(cos⁡(a−b)−cos⁡(a+b))\sin(a)\sin(b) = \frac{1}{2}( \cos (a — b) — \cos (a + b))sin(a)sin(b)=21​(cos(a−b)−cos(a+b))
cos⁡(a)cos⁡ (b) = 12 (cos ⁡ (a + b) + cos ⁡ (a − b)) \ ​​cos (a) \ cos (b) = \ frac {1} {2} (\ cos (a + b) + \cos (a — b))cos(a)cos(b)=21​(cos(a+b)+cos(a−b))
sin⁡(a)cos⁡(b)=12(sin⁡ (a+b)+sin⁡(a−b))\sin(a)\cos(b) = \frac{1}{2}(\sin(a+b)+\sin(a-b)) sin(a)cos(b)=21​(sin(a+b)+sin(a−b)) 9{-i\theta})sin(θ)=2i1​(eiθ−e−iθ)

IV — Quand retrouve-t-on les формул тригонометрических ?

На ретроспективе тригонометрии 3ема (Vous pouvez en retrouver les détails sur ce cours), avec des notions simples sur l’hypoténuse, et la découverte du sinus et du cosinus. На l’utilise généralement dans le calcul de longueur ou la mesure d’angles.

Toutefois, формула тригонометрии плюс комплексы sot généralement abordées au lycée et plus particulièrement à partir de la Première S (nous vous renvoyons dans ce cas à notre fiche dédiée à ce niveau).

Pour ceux qui vont plus loin dans le domaine des mathématiques et qui peuvent in thégrer les filières d’excellence, les формул де тригонометрии sont également abordées dans la filière Math Sup, Math Spé, à des niveaux toutefois bien plus комплексы. Une complexité pas toujours évidente à appréhender pour tous les élèves. Les class préparatoirs sont en effet exigeantes et required énormement de travail. Elles nécessitent parfois d’avoir recours à des Cours particuliers ou des specialisés, avec un accompagnement personnalisé permettant aussi bien de reprendre les bases que d’approfondir определенных понятий.

Il Existe de nombreuxorganes proposant stage maths sup ou des stage maths spé, mais citons peut-être simplement les Cours Thalès, crées depuis 2007 et qui se sont spécialisés dans l’accompagnement des filières d’excellence comme les class préparatoires en maths.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *