Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
тригонометрия — Как получить точное значение $\sin(x)$, если $\sin(2x) = \frac{24}{25}$
спросил
Изменено 4 года, 10 месяцев назад
Просмотрено 2к раз
$\begingroup$
Как получить точное значение $\sin(x)$, если $\sin(2x) = \frac{24}{25}$ ?
Я проверил различные тригонометрические тождества, но не могу вывести $\sin(x)$ на основе данной информации.
Например: $\sin(2x) = 2 \sin(x) \cos(x)$
- тригонометрия
$\endgroup$
1
$\begingroup$
Поскольку $\cos 2x=\pm\frac{7}{25}$, $\tan x=\frac{\sin 2x}{1+\cos 2x}\in\left\{\frac{24} {32},\,\frac{24}{18}\right\}=\left\{\frac{3}{4},\,\frac{4}{3}\right\}$, так что $\ sin x = \ pm \ frac {\ tan x} {\ sqrt {1+ \ tan ^ 2 x}} \ in \ pm \ left \ {\ frac {3} {5}, \, \ frac {4} { 5}\right\}=\left\{-\frac{4}{5},\,-\frac{3}{5},\,\frac{3}{5},\,\frac{4 {5}\право\}$. 92$ и получаем $|\sin(x)|$. Возможны как положительные, так и отрицательные значения (подумайте, почему).
92$ и получаем $|\sin(x)|$. Возможны как положительные, так и отрицательные значения (подумайте, почему).
$\endgroup$
1
$\begingroup$
$tanx=\frac{sin2x}{1+cos2x}$. У вас есть $\sin2x$, и вы можете вычислить $\cos2x$ по теореме Пифагора. Если у вас есть $\tanx$, вы можете использовать SOHCATOA. Не забывайте о квадрантах
$\endgroup$
1
$\begingroup$
См. схему ниже.
$AD$ — биссектриса прямоугольного треугольника $\Delta ABC$.
Учитывая $BC=24$ и $AC=25$.
Пусть $\угол DAB = x$.
Из $\Delta ABC$ мы видим, что $\sin(2x) = \dfrac{24}{25}$.
Теперь по теореме о биссектрисе $BD:DC = 7:25$.
Следовательно, $BD = \dfrac{7}{7+25} \times 24 = \dfrac{21}4$.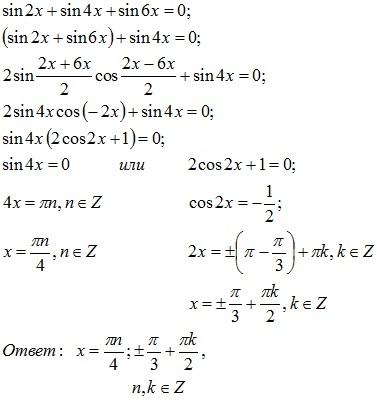 9{-1}(S))$, (где $S$ — решения, т. е. $\pm\frac 35, \pm \frac 45$), чтобы увидеть те, которые обеспечивают правильное решение, и отметить значения, которые работают $\frac 35, \frac 45$.
9{-1}(S))$, (где $S$ — решения, т. е. $\pm\frac 35, \pm \frac 45$), чтобы увидеть те, которые обеспечивают правильное решение, и отметить значения, которые работают $\frac 35, \frac 45$.
Мы можем увидеть их на графике здесь:
$\endgroup$
Как найти все значения x, такие что $\\sin 2x=\\sin x$ и $0\\le x\\le 2\\pi $?
Дата последнего обновления: 07 апреля 2023 г.
•
Всего просмотров: 231k
•
Просмотров сегодня: 6.06k
Ответ
Подтверждено
231k+ просмотров
Подсказка: В приведенном выше вопросе мы получили тригонометрическое уравнение, которое записывается как $\sin 2x=\sin x$. Для его решения мы можем применить тригонометрическое тождество $\sin 2x=2\sin x\cos x$, так что уравнение станет $2\sin x\cos x=\sin x$. Затем нам нужно вычесть $\sin x$ с обеих сторон, чтобы получить $\sin x\left( 2\cos x-1 \right)=0$. Отсюда получим два уравнения. On будет $\sin x=0$, а другой будет $\cos x=\dfrac{1}{2}$. Используя основные решения этих уравнений и по заданному интервалу $0\le x\le 2\pi $, мы получим все решения данных уравнений.
Отсюда получим два уравнения. On будет $\sin x=0$, а другой будет $\cos x=\dfrac{1}{2}$. Используя основные решения этих уравнений и по заданному интервалу $0\le x\le 2\pi $, мы получим все решения данных уравнений.
Полный пошаговый ответ:
Тригонометрическое уравнение, данное в вопросе:
$\Rightarrow \sin 2x=\sin x$
Мы знаем, что $\sin 2x=2\sin x\cos x$ . Подставляя это в приведенное выше уравнение, мы получаем
$\Rightarrow 2\sin x\cos x=\sin x$
Теперь, вычитая $\sin x$ из обеих частей приведенного выше уравнения, мы получаем
\[\ begin{align}
& \Стрелка вправо 2\sin x\cos x-\sin x=\sin x-\sin x \\
& \Стрелка вправо \sin x\left( 2\cos x-1 \right)=0 \
\end{align}\]
Используя правило нулевого произведения, получаем
$\begin{align}
& \Rightarrow \sin x=0,2\cos x-1=0 \\
& \Rightarrow \sin x=0,\cos x=\dfrac{1}{2} \\
\end{align}$
Учитывая первое уравнение, имеем
$\Rightarrow \sin x=0$
В заданном интервале $0\ le x\le 2\pi $ получаем решения в виде $x=0,\pi ,2\pi $.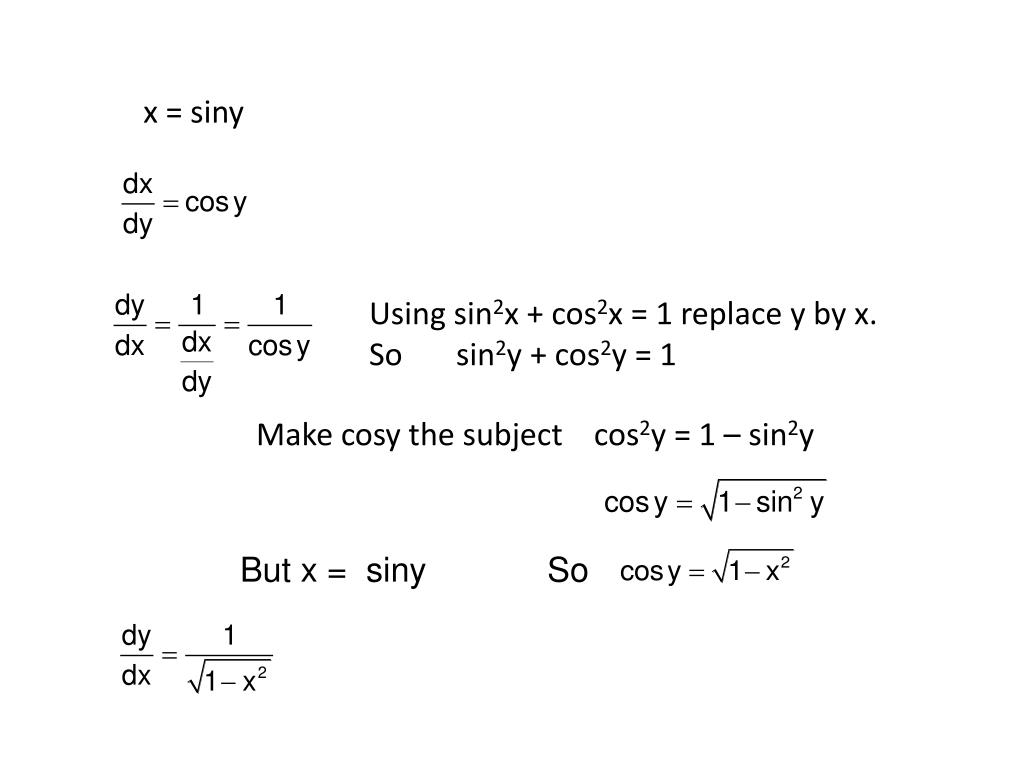

 3
3 14159..
14159..