Russian — Синус и косинус на единичной окружности. Пример
0:00 — 0:01
Здравствуйте!
0:01 — 0:06
Нас просят найти значения синуса и косинуса угла тета,
0:06 — 0:14
если тета равно П/3, 2П/3, 4П/3 и 5П/3.
0:14 — 0:17
Мера угла тета нам дана в радианах.
0:17 — 0:21
Что ж, приступим к выполнению задания.
0:21 — 0:27
Сейчас я вставлю сюда изображение единичной (тригонометрической) окружности.
0:27 — 0:35
Вот так. Эта окружность поможет нам в вычислении синуса и косинуса угла тета.
0:35 — 0:39
И я предлагаю еще перевести меру угла тета из радиан в градусы.
0:39 — 0:49
Потренируемся немного. Итак, первое значение тета – это П/3.
0:49 — 0:58
Запишем: П/3 радиан. Сколько это градусов?
0:58 — 1:02
Нам нужно выяснить, сколько градусов приходится на радиан.
1:02 — 1:08
Мы знаем, что на каждые 180° приходится П радиан.
1:08 — 1:14
Значит, мы умножаем П/3 на 180/П градусов на радиан.
1:14 — 1:20
П сокращаются, остается 180/3, а это 60,
1:20 — 1:24
в единицах измерения радианы уходят, остаются градусы.
1:24 — 1:32
Таким образом, это равно 60°. П/3 – это 60°.
1:32 — 1:35
Далее у нас идет значение 2П/3.
1:35 — 1:41
Мы только что выяснили, что П/3 – это 60 градусов.
1:41 — 1:45
Значит, чтобы узнать, сколько градусов в угле 2П/3,
1:45 — 1:48
нужно всего лишь 60° умножить на 2.
1:48 — 1:51
Это будет 120°. Можно проверить.
1:51 — 1:58
2П/3 радиан мы умножаем на 180 градусов, деленных на П радиан.
1:58 — 2:16
Если мы перемножим, то получим (2/3)*180, а это 120°.
2:05 —
Значит, 2П/3 радиан – это 120°. Вы, наверное, уже догадались,
Not Synced
Единицы измерения, радианы, у нас сокращаются, и остаются только градусы.
Not Synced
что градусная мера угла 4П/3 равна градусной мере угла 2П/3, умноженной на 2.
Not Synced
Мы можем сразу сказать, что это 240°, а можем все это расписать.
Not Synced
4П/3 радиан мы умножаем на 180°, деленных на П радиан.
Not Synced
В итоге П сокращается, и получается (4/3)*180 радиан, а это 240°.
Not Synced
По той же логике 5П/3 – это сколько градусов?
Not Synced
Можно рассуждать по-разному.
Not Synced
Мы можем рассматривать 5П/3 как 5 умножить на П/3.
Not Synced
А чему равно П/3, мы знаем. Это 60°.
Not Synced
Следовательно, чтобы выяснить, сколько градусов в 5П/3 радиан,
Not Synced
нужно всего лишь умножить 60° на 5. Это будет 300°.
Это будет 300°.
Not Synced
Или же можем выяснить это так: 5П/3 радиан мы умножаем на 180°,
Not Synced
деленных на П радиан. В итоге радианы уходят, П сокращаются.
Not Synced
И у нас остается (5180)/3, а это то же самое, что и 560, или 300°.
Not Synced
Вот мы и перевели все значения тета из радиан в градусы.
Not Synced
Теперь давайте изобразим эти все углы.
Not Synced
Потом используя определения синуса и косинуса,
Not Synced
на единичной окружности вычислим синус и косинус наших углов.
Not Synced
Начнем с угла 60°. Изобразим этот угол.
Not Synced
60° — это ровно 2/3 (две трети) угла 90°.
Not Synced
Вот примерно так он будет выглядеть. Это угол 60°.
Not Synced
Запомните, когда мы рассматриваем единичную окружность,
Not Synced
то синус и косинус угла, соответственно,
Not Synced
равны ординате и абсциссе в этой точке.
Not Synced
Исходя из всего этого, мы можем записать,
Not Synced
что координаты данной точки – это cos 60° и sin 60°.
Not Synced
Как можно вычислить, чему равны эти координаты?
Not Synced
cos 60° — это абсцисса нашей точки, а sin 60° — это ордината.
Not Synced
Давайте дорисуем здесь прямоугольный треугольник. Вот так.
Not Synced
Этот угол равен 90°, а этот 60°.
Not Synced
А так как сумма всех углов любого треугольника равна 180,
Not Synced
то третий угол должен быть равен 30°.
Not Synced
Значит, перед нами треугольник 30°-60°-90°.
Not Synced
Давайте вспомним свойства этого треугольника.
Not Synced
Предположим, у нас есть вот такой равносторонний треугольник.
Not Synced
Все его стороны равны. Допустим, они равны 1.
Not Synced
Поскольку это треугольник равносторонний, то и углы у него равны.
Not Synced
Каждый равен 60°. А что если мы разделим этот треугольник пополам,
Not Synced
проведем высоту из вершины к основанию.
Not Synced
В результате получились два симметричных треугольника.
Not Synced
Если мы разделим угол при вершине пополам,
Not Synced
то этот угол будет равен 30°, а эта сторона будет равна 1/2, правильно?
Not Synced
Высота в равностороннем треугольнике является также и медианой.
Not Synced
Итак, у нас есть прямоугольный треугольник.
Not Synced
Гипотенуза этого треугольника равна 1, этот угол равен 60°,
Not Synced
этот угол равен 30°, и эта сторона равна 1/2.
Not Synced
А чему будет равна третья сторона треугольника?
Not Synced
Она будет равна v3 умножить на длину этой стороны, а это v3/2.
Not Synced
Это все, что нам нужно знать о треугольнике с углами 30°-60°-90°.
Not Synced
Это у нас точно такой же треугольник.
Not Synced
Чему равны стороны этого треугольника.
Not Synced
Чему равна гипотенуза этого треугольника с углами 30°-60°-90°?
Not Synced
Это единичная окружность, и радиус этой окружности равен 1.
Not Synced
А это значит, что длина этой стороны равна 1.
Not Synced
Длина гипотенузы равна 1.
Not Synced
Зная длину гипотенузы, можем ли мы сказать, чему равна эта сторона?
Not Synced
Это треугольник с углами 30°-60°-90°.
Not Synced
Сторона, которая лежит напротив угла в 30° (самая маленькая сторона),
Not Synced
равна половине гипотенузы. Значит, этот катет равен 1/2.
Not Synced
А чему равна длина этого катета?
Not Synced
Она будет равна v3 умножить на длину этого катета.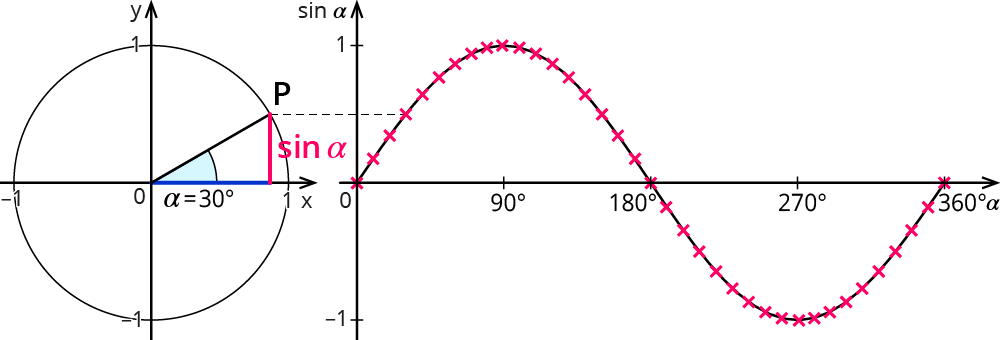 Это будет v3/2.
Это будет v3/2.
Not Synced
Теперь вернемся к вопросу: «Чему равен косинус 60°?»
Not Synced
Это координата х данной точки. Вот это значение.
Not Synced
А оно расположено на расстоянии 1/2 от начала координат.
Not Synced
Таким образом, косинус угла П/3, это то же самое,
Not Synced
что и косинус угла 60°,а он равен 1/2. А чему равен синус П/3?
Not Synced
Итак, синус П/3 – это то же самое, что и синус 60°, равен ординате этой точки.
Not Synced
А ордината, как видите, равна v3/2. Значит, синус равен v3/2.
Not Synced
Переходим к следующему значению тета.
Not Synced
Нам нужно вычислить синус и косинус угла 2П/3, или 120°.
Not Synced
Этот угол равен 90°, нам еще нужно отложить угол в 30°. Вот так.
Not Synced
Градусная мера этого угла равна 120°.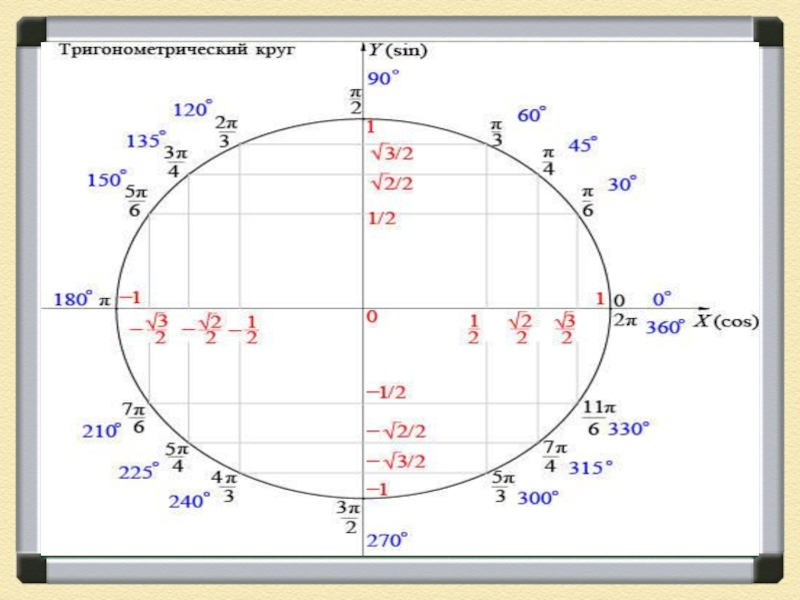
Not Synced
Как нам вычислить координаты этой точки?
Not Synced
Дорисовываем еще один прямоугольный треугольник. Это прямой угол.
Not Synced
А чему равен этот угол, как вы думаете?
Not Synced
Наш угол равен 120°, значит, до 180 не хватает 60°, следовательно,
Not Synced
градусная мера этого угла равна 60°.
Not Synced
Если мы сложим 60°и 120°, то получим развернутый угол, угол 180°.
Not Synced
Опять-таки перед нами треугольник с углами 30°-60°-90°.
Not Synced
Чему равны стороны этого треугольника?
Not Synced
Мы уже знаем, чему они равны.
Not Synced
Длина гипотенузы – это длина радиуса окружности, а она равна 1.
Not Synced
А чему равен катет напротив угла 60°? Он равен v3/2.
Not Synced
Это длина этой стороны. А длина катета напротив угла 30° равна 1/2.
А длина катета напротив угла 30° равна 1/2.
Not Synced
Исходя из этой информации, как вы думаете, чему равны координаты этой точки?
Not Synced
Мы знаем, что координата х – это значение косинуса угла тета,
Not Synced
а координата у, соответственно, — это синус угла тета.
Not Synced
Итак, косинус угла 2П/3 равен косинусу угла 120° и это равно чему?
Not Synced
Это равно значению абсциссы этой точки. Смотрим сюда.
Not Synced
Наша точка расположена на расстоянии 1/2 от начала координат
Not Synced
(в отрицательном направлении).
Not Synced
Значит, абсцисса в этой точке равна минус 1/2.
Not Synced
А чему равен синус? Синус 2П/3 равен синусу 120°, а это равно чему?
Not Synced
Это равно ординате этой точки, Значит, синус 120° равен v3/2.
Not Synced
Теперь рассмотрим угол 240° или 4П/3.
Not Synced
Это у нас угол 180°, значит, нам еще нужно отложить угол 60°.
Not Synced
Вот так будет выглядеть этот угол. Это 180°, а это 60°.
Not Synced
Дорисовываем прямоугольный треугольник.
Not Synced
И опять-таки это треугольник с углами 30°-60°-90°.
Not Synced
Мы уже знаем, что эта сторона равна 1, эта равна v3/2, а эта 1/2.
Not Synced
Следовательно, косинус 4П/3, а это то же самое, что и косинус 240°,
Not Synced
а он равен значению х в этой точке.
Not Synced
Точка расположена на расстоянии 1/2 от начала координат
Not Synced
(в отрицательном направлении). Значит, косинус равен минус 1/2.
Not Synced
Теперь синус. Синус 4П/3, а это то же самое, что и синус 240°…
Not Synced
Синус этого угла равен ординате этой точки.
Not Synced
А она равна длине этого катета только со знаком минус.
Not Synced
Значение у в этой точке равно минус v3/2.
Not Synced
Следовательно, синус 240° равен минус v3/2.
Not Synced
Остался последний угол, 5П/3, или угол 300°.
Not Synced
Здесь угол будет равен 270°, значит, еще нужно 30°.
Not Synced
Вот таким будет этот угол.
Not Synced
Этот угол равен 300°, и до полного поворота, до угла 360°, не хватает 60°.
Not Synced
Значит, градусная мера вот этого угла равна 60°.
Not Synced
Думаю, вы уже знаете, что будет дальше.
Дорисовываем прямоугольный треугольник. Это прямой угол.
Not Synced
И перед нами еще один треугольник с углами 30°-60°-90°.
Not Synced
Мы знаем, что это еще один радиус единичной окружности, он равен 1.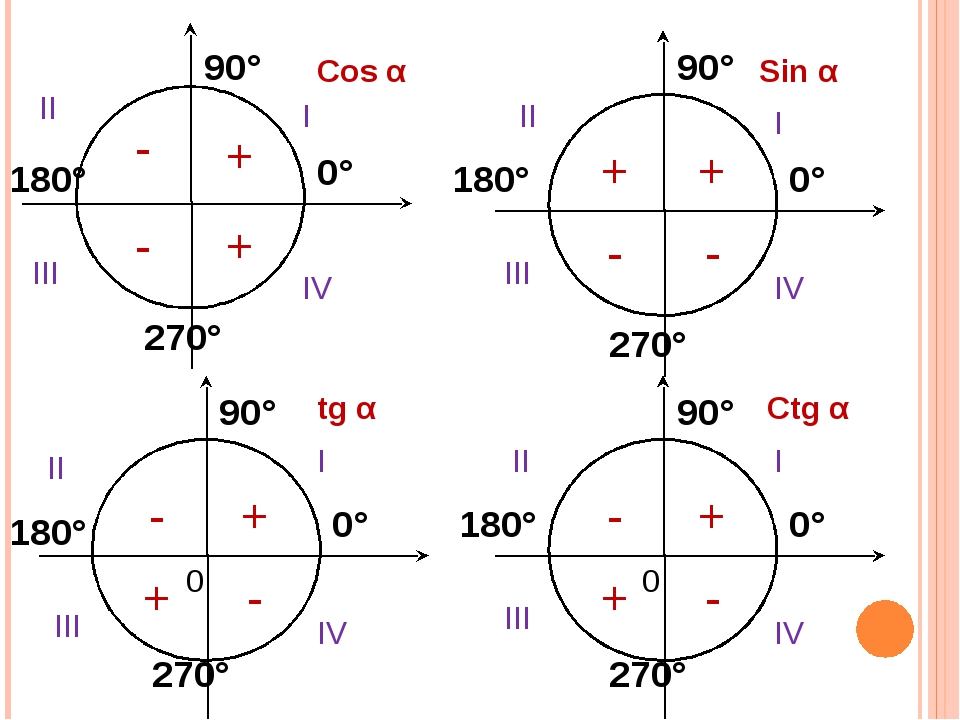
Not Synced
Самая маленькая сторона этого треугольника равна 1/2
Not Synced
(это катет напротив угла 30°), а сторона напротив угла 60°,
Not Synced
соответственно, равна v3/2.
Not Synced
Чему же равен косинус 5П/3, или косинус 300°?
Not Synced
Значение х в этой точке равно 1/2.
Not Synced
Точка расположена на расстоянии 1/2 от начала координат
Not Synced
(в положительном направлении). Значит, косинус равен 1/2.
Not Synced
А чему равен синус 5П/3, или синус 300°? Чему он равен?
Not Synced
Синус угла равен значению у в этой точке.
Not Synced
Точка расположена на расстоянии v3/2 от начала координат
Not Synced
(в отрицательном направлении).
Not Synced
Значит, синус 5П/3 будет равен минус v3/2.
Not Synced
Вот и все. Мы справились с заданием. До встречи!
Мы справились с заданием. До встречи!
Sin 240 градусов — Найдите значение Sin 240 градусов
LearnPracticeDownload
Значение sin 240 градусов равно -0,8660254. . . . Sin 240 градусов в радианах записывается как sin (240° × π/180°), т. е. sin (4π/3) или sin (4,188790…). В этой статье мы обсудим способы нахождения значения sin 240 градусов на примерах.
- Sin 240°: -0,8660254. . .
- Sin 240° в дробях: -(√3/2)
- Sin (-240 градусов): 0,8660254. . .
- Sin 240° в радианах: sin (4π/3) или sin (4,1887902 . . .)
Каково значение греха 240 градусов?
Десятичное значение sin 240 градусов равно -0,866025403. . .. Sin 240 градусов также можно выразить с помощью эквивалента заданного угла (240 градусов) в радианах (4,18879 . . .).
Используя преобразование градусов в радианы, мы знаем, что θ в радианах = θ в градусах × (pi/180°)
⇒ 240 градусов = 240° × (π/180°) рад = 4π/3 или 4,1887.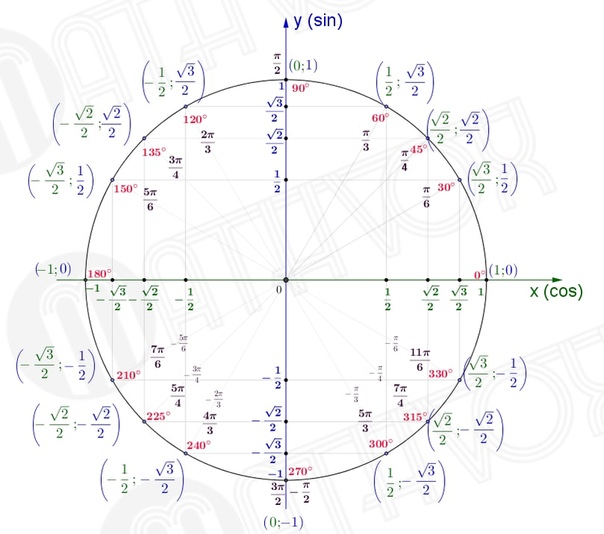 . .
. .
∴ sin 240° = sin(4,1887) = -(√3/2) или -0,8660254. . .
Объяснение:
Для sin 240 градусов угол 240° лежит между 180° и 270° (третий квадрант). Поскольку функция синуса в третьем квадранте отрицательна, значение sin 240° = -(√3/2) или -0,8660254. . .
Поскольку функция синуса является периодической функцией, мы можем представить sin 240° как sin 240 градусов = sin(240° + n × 360°), n ∈ Z.
⇒ sin 240° = sin 600° = sin 960° и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-240°) = -sin(240°).
Методы определения значения Sin 240 градусов
Функция синуса в 3-м квадранте отрицательна. Значение sin 240° равно -0,86602. . .. Мы можем найти значение sin 240 градусов по:
- Используя тригонометрические функции
- Использование единичного круга
Sin 240° в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить грех 240 градусов как:
- ± √(1-cos²(240°))
- ± тангенс 240°/√(1 + тангенс²(240°))
- ± 1/√(1 + раскладушка²(240°))
- ± √(сек²(240°) — 1)/сек 240°
- 1/косек 240°
Примечание. Поскольку 240° лежит в 3-м квадранте, конечное значение sin 240° будет отрицательным.
Поскольку 240° лежит в 3-м квадранте, конечное значение sin 240° будет отрицательным.
Мы можем использовать тригонометрические тождества для представления sin 240° как
- sin(180° — 240°) = sin(-60°)
- -sin(180° + 240°) = -sin 420°
- cos(90° — 240°) = cos(-150°)
- -cos(90° + 240°) = -cos 330°
Sin 240 градусов с помощью единичной окружности
Чтобы найти значение sin 240 градусов с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол 240° с положительной осью x.
- Синус 240 градусов равен координате y (-0,866) точки пересечения (-0,5, -0,866) единичной окружности и r.
Следовательно, значение sin 240° = y = -0,866 (приблизительно)
☛ Также проверьте:
- sin 0 градусов
- грех 15 градусов
- грех 150 градусов
- грех 600 градусов
- грех 510 градусов
- грех 33 градуса
Примеры использования Sin 240 градусов
Пример 1: Найдите значение 2 × (sin 120° cos 120°).
 [Подсказка: используйте sin 240° = -0,866]
[Подсказка: используйте sin 240° = -0,866] Решение:
Используя формулу sin 2a,
2 sin 120° cos 120° = sin(2 × 120°) = sin 240°
∵ sin 240° = -0,866
⇒ 2 × (sin 120° cos 120°) = -0,866Пример 2. Найдите значение sin 240°, если cosec 240° равно -1,1547.
Решение:
Поскольку sin 240° = 1/csc 240°
⇒ sin 240° = 1/(-1,1547) = -0,866Пример 3: Используя значение sin 240°, решите: (1-cos²(240°)).
Решение:
Мы знаем, (1-cos²(240°)) = (sin²(240°)) = 0,75
⇒ (1-cos²(240°)) = 0,75
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о Sin 240 Degrees
Что такое Sin 240 Degrees?
Sin 240 градусов — значение тригонометрической функции синуса для угла, равного 240 градусам. Значение sin 240° равно -(√3/2) или -0,866 (приблизительно).
Каково значение Sin 240° в терминах Sec 240°?
Поскольку функцию синуса можно представить с помощью функции секанса, мы можем записать sin 240° как √(sec²(240°) — 1)/sec 240°. Значение sec 240° равно -2.
Каково значение Sin 240 градусов в пересчете на Tan 240°?
Мы знаем, что, используя тригонометрические тождества, мы можем записать sin 240° как -tan 240°/√(1 + tan²(240°)). Здесь значение тангенса 240° равно 1,732050.
Как найти Sin 240° с точки зрения других тригонометрических функций?
Используя формулу тригонометрии, значение sin 240° может быть выражено через другие тригонометрические функции следующим образом:
- ± √(1-cos²(240°))
- ± тангенс 240°/√(1 + тангенс²(240°))
- ± 1/√(1 + раскладушка²(240°))
- ± √(сек²(240°) — 1)/сек 240°
- 1/косек 240°
☛ Также проверьте: таблицу тригонометрии
Как найти значение Sin 240 градусов?
Значение sin 240 градусов можно рассчитать, построив угол 240° с осью x и затем найдя координаты соответствующей точки (-0,5, -0,866) на единичной окружности. Значение sin 240° равно координате y (-0,866). ∴ sin 240° = -0,866.
Значение sin 240° равно координате y (-0,866). ∴ sin 240° = -0,866.
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядный учебный план
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктический(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc (45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найдите точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы | 45 | |
| 33 | Найти точное значение | соз(45) | |
| 34 | Упростить | sin(тета)^2+cos(тета)^2 | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | желтовато-коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найдите точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | соз(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найдите точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 шт.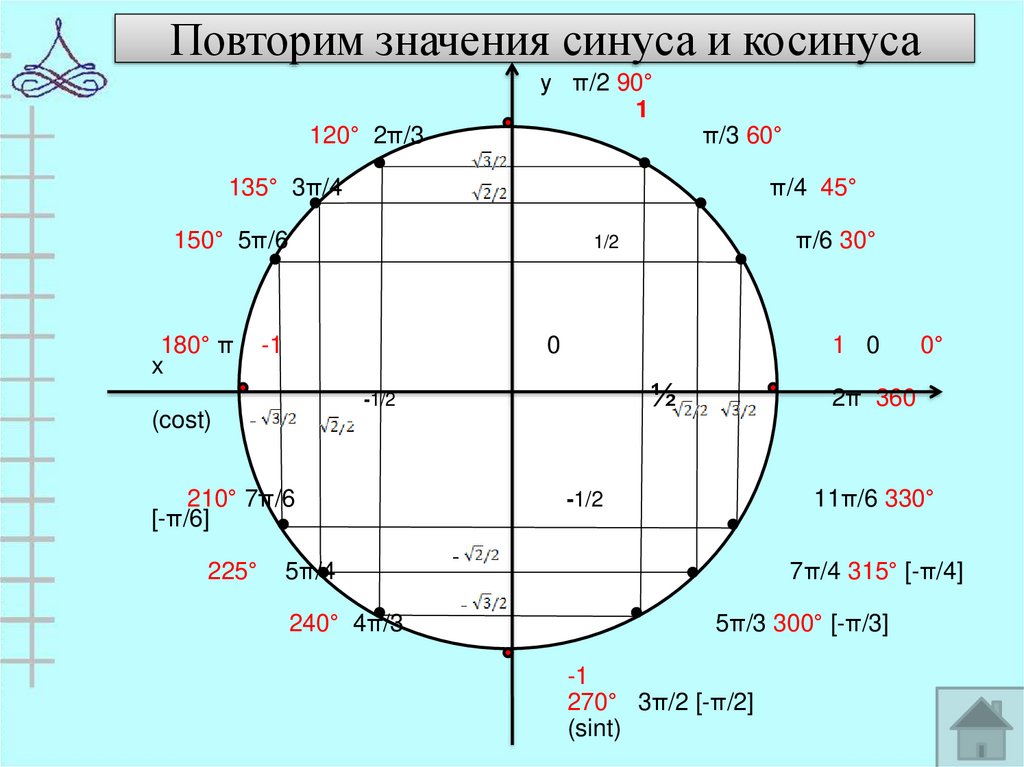 |

 [Подсказка: используйте sin 240° = -0,866]
[Подсказка: используйте sin 240° = -0,866]