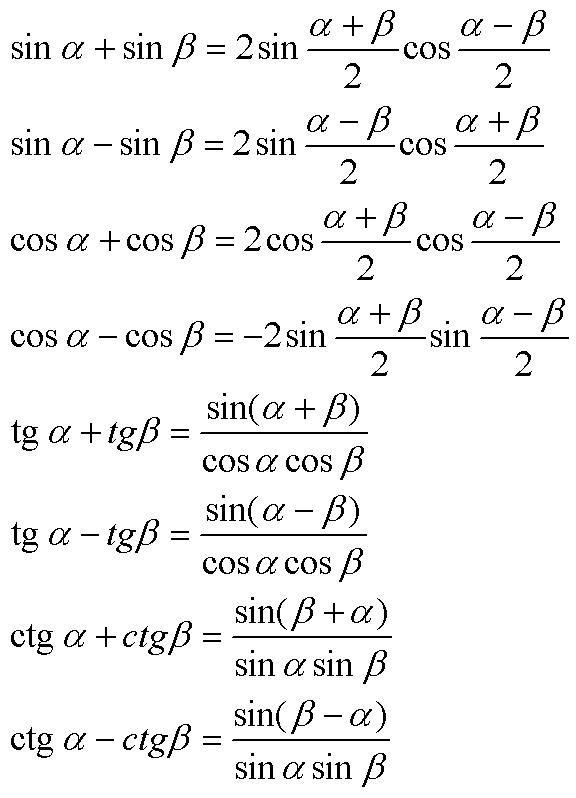Используя тождества \(\sin(-\beta)=-\sin(\beta)\) и \(\cos(-\beta)=\cos(\beta)\) получаем:
\[\sin(\alpha-\beta)=\sin(\alpha + (-\beta))=\sin \alpha \cos (-\beta) + \cos \alpha \sin (-\beta)= \sin\alpha\cos\beta — \cos\alpha\sin\beta\]
Формула сложения для косинуса
Загрузить рабочий лист GeoGebra
Измените углы, чтобы увидеть наблюдения во всех четырех квадрантах. 9\цирк\).\[-\cos(\alpha ‘ +\beta )=-\cos \alpha ‘ \cos \beta +\sin \alpha ‘ \sin\beta = \sin\alpha\cos\beta+\sin\beta\cos \альфа\]
Аналогичным образом можно доказать, что все формулы сложения верны для всех углов.
Малин Кристерссон в рамках Creative Commons Attribution-Noncommercial-Share Alike 2.5 Швеция Лицензия
www.malinc.se
интуиция — Как я могу понять и доказать «формулы суммы и разности» в тригонометрии?
Существуют простые геометрические доказательства формул для
$\sin(\alpha\pm\beta)$ и $\cos(\alpha\pm\beta)$
для случая, когда $\alpha,$ $\beta,$ и $\alpha \pm \beta$ — все острые углы.
Чтобы выйти за пределы острых углов, нужно иметь представление о том, что синусы и косинусы неострых углов. Графические доказательства можно распространить на другие случаи одно за другим, но разве не было бы неплохо охватить все возможные углы раз и навсегда? Итак, давайте воспользуемся несколькими дополнительными фактами, которые можно более или менее прочитать непосредственно из определения единичного круга, например $\sin(\tfrac\pi2 — \theta) = \cos(\theta)$ и $\sin(\pi — \theta) = \sin(\theta).$ 92(\альфа)\\ &= 1 = \sin(\alpha + \beta), \end{выравнивание} а также \начать{выравнивать} \cos(\alpha)\cos(\beta) — \sin(\alpha)\sin(\beta) &= \cos(\alpha)\cos(\tfrac\pi2 — \alpha) — \sin(\alpha)\sin(\tfrac\pi2 — \alpha) \\ &= \cos(\alpha)\sin(\alpha) — \sin(\alpha)\cos(\alpha) \\ &= 0 = \sin(\alpha + \beta), \end{выравнивание} поэтому в этом случае работают обе формулы суммы.
Если угол $\alpha + \beta$ тупой, то
\начать{выравнивать}
\sin(\alpha)\cos&(\beta) + \cos(\alpha)\sin(\beta) \\
&= \cos(\tfrac\pi2 — \alpha)\sin(\tfrac\pi2 — \beta)
+ \sin(\tfrac\pi2 — \alpha)\cos(\tfrac\pi2 — \beta) \\
&= \sin((\tfrac\pi2 — \alpha) + (\tfrac\pi2 — \beta)) \\
&= \sin(\pi — (\alpha + \beta)) \\
&= \sin(\альфа +\бета) \\
\end{выравнивание}
а также
\начать{выравнивать}
\cos(\alpha)\cos&(\beta) — \sin(\alpha)\sin(\beta) \\
&= \sin(\tfrac\pi2 — \alpha)\sin(\tfrac\pi2 — \beta)
— \cos(\tfrac\pi2 — \alpha)\cos(\tfrac\pi2 — \beta) \\
&= -\cos((\tfrac\pi2 — \alpha) + (\tfrac\pi2 — \beta)) \\
&= -\cos(\pi — (\alpha + \beta)) \\
&= \cos(\альфа +\бета), \\
\end{выравнивание}
так что обе формулы суммы работают и в этом случае.
Других случаев для суммы двух острых углов нет, но давайте также рассмотрим нулевой угол. Если $\alpha = 0$, то \начать{выравнивать} \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) &= 0 \cdot \cos(\beta) + 1\cdot \sin(\beta) \\ &= \грех(\бета) \\ &= \sin(\альфа +\бета) \end{выравнивание} а также \начать{выравнивать} \cos(\alpha)\cos(\beta) — \sin(\alpha)\sin(\beta) &= 1 \cdot \cos(\beta) + 0\cdot \sin(\beta) \\ &= \cos(\бета) \\ &= \cos(\альфа +\бета), \end{выравнивание} поэтому формулы работают в этом случае, и по симметрии они работают и при $\beta = 0$. Очевидно, они работают, когда оба угла равны нулю.
Это покрывает все возможные суммы углов $\alpha$ и $\beta$ где $0 \leq \alpha \lt \tfrac\pi2$ и $0 \leq \beta \lt \tfrac\pi2.$
Чтобы двигаться дальше, позвольте мне определить специальное обозначение, которое поможет более удобно выразить некоторые формулы. Специальное обозначение делает формулы менее загроможденными и (надеюсь) более легкими для понимания.
Тогда \начать{выравнивать} \sin_0(\theta) &= \sin(\theta + 0 \cdot \tfrac\pi2) = \sin(\theta), \\ \sin_1(\theta) &= \sin(\theta + 1 \cdot \tfrac\pi2) = \cos(\theta), \\ \sin_2(\theta) &= \sin(\theta + 2 \cdot \tfrac\pi2) = -\sin(\theta), \\ \sin_3(\theta) &= \sin(\theta + 3 \cdot \tfrac\pi2) = -\cos(\theta) \\ \end{выравнивание} для любого угла $\theta$ (не только острого угла), в чем легко убедиться с помощью единичного круга, а шаблон повторяется по четыре строки за раз (либо после, либо до этого набора уравнений) добавлением или вычитанием $2\pi$ из каждого угла; $\sin_{k+4}(\theta) = \sin_k(\theta) = \sin_{k-4}(\theta).$ Также обратите внимание, что $\sin_{k+2}(\theta) = -\sin_k(\theta) = \sin_{k-2}(\theta).$
Тогда для любых целых чисел $m$ и $n,$
\начать{выравнивать}
\sin_m(\alpha)\sin_{n+1}(\beta) &= (-\sin_{m+2}(\alpha))(-\sin_{n-1}(\beta)) \\
&= \sin_{m+2}(\alpha)\sin_{n-1}(\beta).
Отсюда следует, что \начать{выравнивать} \sin_m(\alpha)\sin_{n+1}&(\beta) + \sin_{m+1}(\alpha)\sin_n(\beta) \\ &= \sin_{m+1}(\alpha)\sin_n(\beta) + \sin_{m+2}(\alpha)\sin_{n-1}(\beta) \end{выравнивание} увеличив $m$ на $2$ и уменьшив $n+1$ на $2$ в $\sin_m(\alpha)\sin_{n+1}(\beta)$, а затем меняет порядок суммы на обратный. В результате индексы «$m$» увеличиваются на $1$. и индексы «$n$» уменьшаются на $1.$ Мы можем повторять этот набор операций столько раз, сколько захотим, вперед или назад, поэтому для любого целого числа $k,$ \начать{выравнивать} \sin_m(\alpha)\sin_{n+1}&(\beta) + \sin_{m+1}(\alpha)\sin_n(\beta) \\ &= \sin_{m+k}(\alpha)\sin_{n-k+1}(\beta) + \sin_{m+k+1}(\alpha)\sin_{n-k}(\beta). \end{выравнивание}
В частности, при $k = n,$ \начать{выравнивать} \sin_m(\alpha)\sin_{n+1}&(\beta) + \sin_{m+1}(\alpha)\sin_n(\beta) \\ &= \sin_{m+n}(\alpha)\sin_1(\beta) + \sin_{m+n+1}(\alpha)\sin_0(\beta). \end{align}
Теперь, когда у нас есть все эти механизмы, пусть $\alpha$ и $\beta$
любые углы любой величины, положительные или отрицательные. Напишите
\начать{выравнивать}
\alpha &= \bar\alpha + a\cdot \tfrac\pi2, \\
\beta &= \bar\beta + b\cdot \tfrac\pi2.
\end{выравнивание}
Напишите
\начать{выравнивать}
\alpha &= \bar\alpha + a\cdot \tfrac\pi2, \\
\beta &= \bar\beta + b\cdot \tfrac\pi2.
\end{выравнивание}
Тогда $$\sin(\alpha + \beta) = \sin(\bar\alpha + \bar\beta + (a + b)\tfrac\pi2) = \sin_{a+b}(\bar\alpha + \bar\beta).$$ Мы можем покрыть все возможные значения $\alpha$ и $\beta$ всего в четырех случаях, в зависимости от класса эквивалентности $a + b$ по модулю $4.$ В каждом случае мы можем полагаться на знание угла формулы сумм для острых углов $\bar\alpha$ и $\bar\beta.$
Случай $a + b \equiv 0 \pmod 4$:
\begin{align} \sin_{a+b}(\бар\альфа + \бар\бета) &= \sin(\бар\альфа + \бар\бета) = \sin(\bar\alpha)\cos(\bar\beta) + \cos(\bar\alpha)\sin(\bar\beta) \\ &= \sin_0(\bar\alpha)\sin_1(\bar\beta) + \sin_1(\bar\alpha)\sin_0(\bar\beta) \\ &= \sin_{a+b}(\bar\alpha)\sin_1(\bar\beta) + \sin_{a+b+1}(\bar\alpha)\sin_0(\bar\beta) \end{align}
Случай $a + b \equiv 1 \pmod 4$:
\begin{align} \sin_{a+b}(\бар\альфа + \бар\бета) &= \cos(\бар\альфа + \бар\бета) = \cos(\bar\alpha)\cos(\bar\beta) — \sin(\bar\alpha)\sin(\bar\beta) \\ &= \sin_1(\bar\alpha)\sin_1(\bar\beta) + \sin_2(\bar\alpha)\sin_0(\bar\beta) \\ &= \sin_{a+b}(\bar\alpha)\sin_1(\bar\beta) + \sin_{a+b+1}(\bar\alpha)\sin_0(\bar\beta) \end{выравнивание}
Случай $a + b \equiv 2 \pmod 4$:
\begin{align} \sin_{a+b}(\бар\альфа + \бар\бета) &= -\sin(\бар\альфа + \бар\бета) = -\sin(\bar\alpha)\cos(\bar\beta) — \cos(\bar\alpha)\sin(\bar\beta) \\ &= \sin_2(\bar\alpha)\sin_1(\bar\beta) + \sin_3(\bar\alpha)\sin_0(\bar\beta) \\ &= \sin_{a+b}(\bar\alpha)\sin_1(\bar\beta) + \sin_{a+b+1}(\bar\alpha)\sin_0(\bar\beta) \end{align}
Случай $a + b \equiv 3 \pmod 4$:
\begin{align} \sin_{a+b}(\бар\альфа + \бар\бета) &= -\cos(\бар\альфа + \бар\бета) = -\cos(\bar\alpha)\cos(\bar\beta) + \sin(\bar\alpha)\sin(\bar\beta) \\ &= \sin_3(\bar\alpha)\sin_1(\bar\beta) + \sin_0(\bar\alpha)\sin_0(\bar\beta) \\ &= \sin_{a+b}(\bar\alpha)\sin_1(\bar\beta) + \sin_{a+b+1}(\bar\alpha)\sin_0(\bar\beta) \end{выравнивание}
Обратите внимание, что во всех четырех случаях мы преобразовали $\sin_{a+b}(\bar\alpha + \bar\beta)$ в одно и то же выражение, поэтому мы можем завершить каждый случай следующим образом: \начать{выравнивать} \sin_{a+b}(\bar\alpha)\sin_1&(\bar\beta) + \sin_{a+b+1}(\bar\alpha)\sin_0(\bar\beta) \\ &= \sin_a(\bar\alpha)\sin_{b+1}(\bar\beta) + \sin_{a+1}(\bar\alpha)\sin_b(\bar\beta) \\ &= \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \end{align}
Следовательно, $\sin(\alpha + \beta) = \sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)$
для всех углов $\alpha$ и $\beta.