Площадь треугольника через синус и косинус
I. Площадь треугольника через синус
Если в задаче даны длины двух сторон треугольника и угол между ними, то можно применить формулу площади треугольника через синус.
Пример расчета площади треугольника через синус. Даны стороны a = 3, b = 4, и угол γ= 30°. По таблице синусов синус угла в 30° равен 0.5
Площадь треугольника будет равна 3 кв. см.
| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 3.000 | |||
Также могут быть и другие условия. Если дана длина одной стороны и углы, то для начала нужно вычислить недостающий угол. Т.к. сумма всех углов треугольника равняется 180°, то:
Т.к. сумма всех углов треугольника равняется 180°, то:
Площадь будет равна половине квадрата стороны, умноженной на дробь. В ее числителе находится произведение синусов прилегающих углов, а в знаменателе синус противолежащего угла. Теперь рассчитываем площадь по следующим формулам:
Например, дан треугольник со стороной a=3 и углами γ=60°, β=60°. Вычисляем третий угол:
Подставляем данные в формулу
Получаем, что площадь треугольника равняется 3,87 кв. см.
II. Площадь треугольника через косинус
Чтобы найти площадь треугольника, нужно знать длины всех сторон. По теореме косинусов можно найти не известные стороны, а уже потом использовать формулу Герона.
По теореме косинусов квадрат неизвестной стороны треугольника равняется сумме квадратов остальных сторон минус удвоенное произведение этих сторон на косинус угла, находящегося между ними.
Из теоремы выводим формулы для поиска длины неизвестной стороны:
Зная как найти недостающую сторону, имея две стороны и угол между ними можно легко посчитать площадь. Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Формула площади треугольника через косинус помогает легко и быстро найти решение различных задач.
Пример расчета формулы площади треугольника через косинус
Дан треугольник с известными сторонами a = 3, b = 4, и углом γ= 45°. Для начала найдем недостающую сторону с. По таблице косинусов косинус 45°=0,7. Для этого подставим данные в уравнение, выведенное из теоремы косинусов.
Теперь используя формулу, найдем площадь треугольника по трем сторонам:
| Сторона a= | Сторона b= | Угол γ ° | |
| Ответ: Площадь треугольника = 4.243 | |||
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Выполни необходимые вычисления и заполни таблицу! Округли до десятых! 1 проводник 2 проводник На всём участке цепи 𝐼, А 0,6 𝑈, В 𝑅, Ом 45 3
tga-? Если sina=-5/корень 26 и a пренадлежит (pi;3pi/2)
Идеальный пружинный маятник совершает колебания так, как показано на рисунке, последовательно проходя положения « 1 », « 2 », « 3 », « 4 » и « 5 ». Заполни пропуски в утверждениях, выбрав и отметив
Заполни пропуски в утверждениях, выбрав и отметив
Смешали воздух объемом 5 мы и относителтвой влажностью 22% при температуре 15°С с воздухом с относительнойина влажностью 46% при температуре 28°С.Определите относительно влажность смеси, если её
Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 5√3 см. Напишите решение плиииз
Пользуйтесь нашим приложением
Неправильные треугольники: закон синусов
Цели обучения
В этом разделе вы:
- Использовать закон синусов для решения косоугольных треугольников.
- Найдите площадь косоугольного треугольника с помощью функции синуса.
- Решение прикладных задач по закону синусов.
Предположим, что две радиолокационные станции, расположенные на расстоянии 20 миль друг от друга, обнаруживают самолет между собой.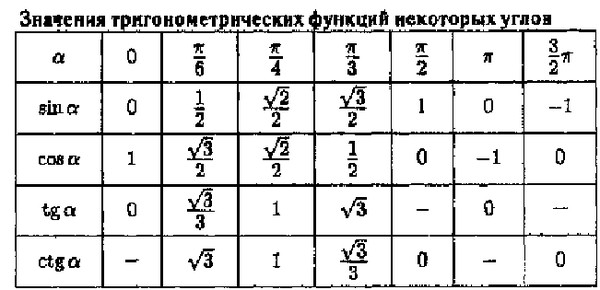 Угол места, измеренный первой станцией, составляет 35 градусов, тогда как угол места, измеренный второй станцией, равен 15 градусам. Как определить высоту самолета? Мы видим на (Рисунок), что треугольник, образованный самолетом и двумя станциями, не является прямоугольным, поэтому мы не можем использовать то, что знаем о прямоугольных треугольниках. В этом разделе мы узнаем, как решать задачи, связанные с неправильными треугольниками.
Угол места, измеренный первой станцией, составляет 35 градусов, тогда как угол места, измеренный второй станцией, равен 15 градусам. Как определить высоту самолета? Мы видим на (Рисунок), что треугольник, образованный самолетом и двумя станциями, не является прямоугольным, поэтому мы не можем использовать то, что знаем о прямоугольных треугольниках. В этом разделе мы узнаем, как решать задачи, связанные с неправильными треугольниками.
Рисунок 1.
Использование закона синусов для решения наклонных треугольников
В любом треугольнике мы можем провести высоту, перпендикулярную линию из одной вершины к противоположной стороне, образуя два прямоугольных треугольника. Однако было бы предпочтительнее иметь методы, которые можно было бы применять непосредственно к непрямоугольным треугольникам без предварительного создания прямоугольных треугольников.
Любой треугольник, не являющийся прямоугольным, является косоугольным. Решение косоугольного треугольника означает нахождение измерений всех трех углов и всех трех сторон. Для этого нам нужно начать как минимум с трех из этих значений, включая хотя бы одну из сторон. Мы исследуем три возможные ситуации в задаче о косом треугольнике:
Для этого нам нужно начать как минимум с трех из этих значений, включая хотя бы одну из сторон. Мы исследуем три возможные ситуации в задаче о косом треугольнике:
- ASA (угол-сторона-угол) Нам известны измерения двух углов и прилежащей стороны. См. (Рисунок).
Рисунок 2.
- AAS (угол-угол-сторона) Нам известны измерения двух углов и стороны, которая не находится между известными углами. См. (Рисунок).
Рис. 3.
- SSA (угол сторона-бок) Нам известны измерения двух сторон и угла, который не лежит между известными сторонами. См. (Рисунок).
Рисунок 4.
Знание того, как подходить к каждой из этих ситуаций, позволяет нам решать косоугольные треугольники без необходимости опускания перпендикуляра для образования двух прямоугольных треугольников. Вместо этого мы можем использовать тот факт, что отношение измерения одного из углов к длине его противоположной стороны будет равно двум другим отношениям измерения угла к противоположной стороне. Давайте посмотрим, как это утверждение получается, рассматривая треугольник, показанный на (Рисунок).
Давайте посмотрим, как это утверждение получается, рассматривая треугольник, показанный на (Рисунок).
Рисунок 5.
Используя соотношения прямоугольного треугольника, мы знаем, что [латекс]\,\mathrm{sin}\,\alpha =\frac{h}{b}\,[/latex]и[латекс]\ ,\mathrm{sin}\,\beta =\frac{h}{a}.\,\,[/latex]Решение обоих уравнений для [latex]\,h\,[/latex] дает два разных выражения для[ латекс]\,h.[/latex]
[латекс]h=b\mathrm{sin}\,\alpha \text{ и }h=a\mathrm{sin}\,\beta [/latex]
Затем мы устанавливаем выражения равными друг другу.
[латекс]\begin{array}{ll}\text{ }b\mathrm{sin}\,\alpha =a\mathrm{sin}\,\beta \hfill & \hfill \\ \text{ }\ влево(\frac{1}{ab}\right)\left(b\mathrm{sin}\,\alpha \right)=\left(a\mathrm{sin}\,\beta\right)\left(\ frac{1}{ab}\right)\begin{array}{cccc}& & & \end{array}\hfill & \text{Умножить обе части на}\,\frac{1}{ab}. \hfill \\ \text{ }\,\frac{\mathrm{sin}\,\alpha }{a}=\frac{\mathrm{sin}\,\beta}{b}\hfill & \hfill \end {массив}[/латекс]
Точно так же мы можем сравнить другие коэффициенты.
[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ gamma} {c} \ text {and} \ frac {\ mathrm {sin }\,\beta }{b}=\frac{\mathrm{sin}\,\gamma }{c}[/latex]
В совокупности эти соотношения называются Законом синусов .
[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm {sin} \, \ lambda }{c}[/latex]
Обратите внимание на стандартный способ маркировки треугольников: угол[латекс]\,\альфа \,[/латекс](альфа) противоположен стороне[латекс]\,а;\,[/ латекс]угол[латекс]\,\бета \,[/латекс](бета) является противоположной стороной[латекс]\,b;\,[/латекс]и угол[латекс]\,\гамма \,[/латекс] (гамма) находится на противоположной стороне[латекс]\,с.\,[/латекс]См. (рисунок).
При вычислении углов и сторон не забудьте ввести точные значения в окончательный ответ. Как правило, окончательные ответы округляются до десятых, если не указано иное.
Рисунок 6.
Закон синусов
Дан треугольник с углами и противоположными сторонами, обозначенными как на (рисунок), отношение измерения угла к длине его противоположной стороны будет равно другому два отношения меры угла к противоположной стороне. Все пропорции будут равны. Закон синусов основан на пропорциях и символически представлен двумя способами.
Все пропорции будут равны. Закон синусов основан на пропорциях и символически представлен двумя способами.
[латекс] \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm {sin} \, \ гамма }{c}[/latex]
[латекс]\frac{a}{\mathrm{sin}\,\alpha }=\frac{b}{\mathrm{sin}\,\beta }=\frac {c}{\mathrm{sin}\,\gamma }[/latex]
Чтобы решить косой треугольник, используйте любую пару применимых соотношений.
Решение для двух неизвестных сторон и угла треугольника AAS
Решите треугольник, показанный на (Рисунок), с точностью до десятых.
Рисунок 7.
Показать решение
Попробуйте
Решите треугольник, показанный на (Рисунок), с точностью до десятых.
Рис. 8.
Показать решение
Использование закона синусов для решения треугольников SSA
Мы можем использовать закон синусов для решения любого косоугольного треугольника, но некоторые решения могут быть непростыми. В некоторых случаях заданным критериям может удовлетворять более одного треугольника, что мы описываем как неоднозначный случай. Треугольники, классифицируемые как SSA, те, в которых мы знаем длины двух сторон и измерение угла, противоположного одной из данных сторон, могут иметь одно или два решения или даже не иметь решения.
В некоторых случаях заданным критериям может удовлетворять более одного треугольника, что мы описываем как неоднозначный случай. Треугольники, классифицируемые как SSA, те, в которых мы знаем длины двух сторон и измерение угла, противоположного одной из данных сторон, могут иметь одно или два решения или даже не иметь решения.
Возможные исходы для треугольников SSA
Косоугольные треугольники в категории SSA могут иметь четыре различных исхода. (Рисунок) иллюстрирует решения с известными сторонами[латекс]\,а\,[/латекс]и[латекс]\,b\,[/латекс]и известным углом[латекс]\,\альфа .[/латекс]
Рис. 9.
Решение косого треугольника SSA
Решите треугольник на (рис.) для отсутствующей стороны и найдите отсутствующий угол с точностью до десятых.
Рисунок 10.
Показать решение
Попробуйте
Дано[латекс]\,\альфа =80°,а=120,\,[/латекс]и[латекс]\,b=121,\,[/латекс]найдите недостающую сторону и углы . Если существует более одного возможного решения, покажите оба.
Если существует более одного возможного решения, покажите оба.
Показать раствор
Нахождение неизвестных сторон и углов треугольника SSA
В треугольнике, показанном на (рис.), найдите неизвестные стороны и углы. Округлите свои ответы до десятых.
Рис. 13.
Показать решение
Попробуйте
Дано[латекс]\,\альфа =80°,а=100,\,\,b=10,\,[/латекс]найдите недостающую сторону и углы. Если существует более одного возможного решения, покажите оба. Округлите свои ответы до десятых.
Показать раствор
Нахождение треугольников, удовлетворяющих заданным критериям
Найдите все возможные треугольники, если одна сторона имеет длину 4 напротив угла 50°, а вторая сторона имеет длину 10.
Показать решение
Попробуй
Определить возможное количество треугольников при условии [латекс]\,а=31,\,\,b=26,\,\,\бета =48°. \,\,[/латекс]
\,\,[/латекс]
Показать решение
Нахождение площади косоугольного треугольника с помощью функции синуса
Теперь, когда мы можем решить треугольник для пропущенных значений, мы можем использовать некоторые из этих значений и функцию синуса, чтобы найти площадь косоугольного треугольника. Напомним, что формула площади треугольника имеет вид[латекс]\,\текст{Площадь}=\фракция{1}{2}bh,\,[/латекс],где[латекс]\,b\,[/латекс ] — основание, а [латекс]\,h\,[/латекс] — высота. Для наклонных треугольников мы должны найти [латекс]\,h\,[/латекс], прежде чем мы сможем использовать формулу площади. Наблюдая за двумя треугольниками на (рисунке), одним острым и одним тупым, мы можем опустить перпендикуляр, чтобы представить высоту, а затем применить тригонометрическое свойство [латекс]\,\mathrm{sin}\,\alpha =\frac{\text {напротив}}{\text{гипотенуза}}\,[/latex]для записи уравнения площади в косоугольных треугольниках. В остроугольном треугольнике мы имеем [латекс]\,\mathrm{sin}\,\alpha =\frac{h}{c}\,[/latex]или[latex]c\mathrm{sin}\,\alpha =h. {\простое число},\,[/латекс]или[латекс]\,180-\альфа .[/латекс]
{\простое число},\,[/латекс]или[латекс]\,180-\альфа .[/латекс]
Рисунок 15.
Таким образом,
[латекс]\текст{Площадь}=\frac{1}{2}\left(\text{база}\right)\left(\text{height}\ right)=\frac{1}{2}b\left(c\mathrm{sin}\,\alpha \right)[/latex]
Аналогично,
[latex]\text{Area}=\frac{ 1}{2}a\left(b\mathrm{sin}\,\gamma\right)=\frac{1}{2}a\left(c\mathrm{sin}\,\beta \right)[/ латекс]
Площадь косоугольного треугольника
Формула площади косоугольного треугольника:
[латекс]\begin{array}{l}\text{Area}=\frac{1}{2} bc\mathrm{sin}\,\alpha \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}ac\mathrm {sin}\,\beta \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,=\frac{1}{2}ab\mathrm{sin} \,\gamma \hfill \end{массив}[/latex]
Эквивалентно половине произведения двух сторон и синуса прилежащего к ним угла.
Нахождение площади наклонного треугольника
Нахождение площади треугольника со сторонами[латекс]\,а=90,b=52,\,[/латекс]и углом[латекс]\,\гамма =102° . \,[/latex]Округлите площадь до ближайшего целого числа.
\,[/latex]Округлите площадь до ближайшего целого числа.
Показать раствор
Попробуйте
Найдите площадь заданного треугольника[латекс]\,\beta =42°,\,\,a=7,2\,\text{ft},\,\,c=3,4\,\text {ft}.\,[/latex]Округлите площадь до десятых.
Показать решение
Решение прикладных задач с использованием закона синусов
Чем больше мы изучаем тригонометрические приложения, тем больше мы обнаруживаем, что приложений бесчисленное множество. Некоторые из них представляют собой плоские ситуации типа диаграммы, но многие приложения в исчислении, технике и физике включают трехмерное пространство и движение.
Нахождение высоты
Нахождение высоты самолета в задаче, представленной в начале этого раздела, показанной на (рис.). Округлите высоту до ближайшей десятой мили.
Рисунок 16.
Показать решение
Диаграмма, показанная на (Рисунок), представляет высоту дирижабля, летящего над футбольным стадионом.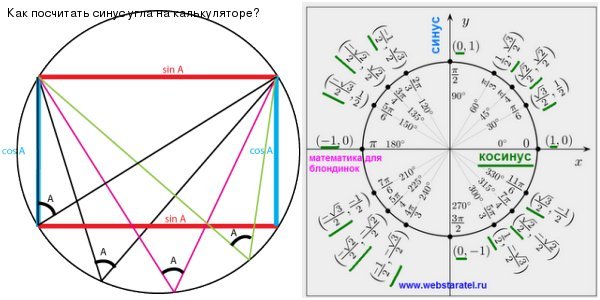 Найдите высоту дирижабля, если угол места в южной оконечности, точка А, равен 70°, а угол возвышения в северной оконечности, точка [латекс]\,В,\,[/латекс] равен 62°. °, а расстояние между точками обзора двух концевых зон составляет 145 ярдов.
Найдите высоту дирижабля, если угол места в южной оконечности, точка А, равен 70°, а угол возвышения в северной оконечности, точка [латекс]\,В,\,[/латекс] равен 62°. °, а расстояние между точками обзора двух концевых зон составляет 145 ярдов.
Рис. 17.
Показать решение
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с тригонометрическими приложениями.
- Закон синусов: основы
- Закон синусов: неоднозначный случай
Ключевые уравнения
| Закон синусов | [латекс] \ begin {array} {l} \ frac {\ mathrm {sin} \, \ alpha {a} = \ frac {\ mathrm {sin} \, \ beta} {b} = \ frac {\ mathrm{sin}\,\gamma}{c}\,\hfill \\\frac{a}{\mathrm{sin}\,\alpha}=\frac{b}{\mathrm{sin}\,\beta }=\frac{c}{\mathrm{sin}\,\gamma }\hfill \end{массив}[/latex] |
| Площадка для наклонных треугольников | [латекс]\begin{array}{r}\hfill \text{Area}=\frac{1}{2}bc\mathrm{sin}\,\alpha \\ \hfill \text{ }=\frac{ 1}{2}ac\mathrm{sin}\,\beta \\ \hfill \text{ }=\frac{1}{2}ab\mathrm{sin}\,\gamma \end{array}[/latex ] |
Ключевые понятия
- Закон синусов можно использовать для решения косоугольных треугольников, которые не являются прямоугольными треугольниками.

- По закону синусов отношение измерения одного из углов к длине его противоположной стороны равно двум другим отношениям измерения угла к противоположной стороне.
- Возможны три случая: ASA, AAS, SSA. В зависимости от предоставленной информации мы можем выбрать соответствующее уравнение для нахождения требуемого решения. См. (Рисунок).
- Неоднозначный случай возникает, когда косой треугольник может иметь разные исходы.
- Возможны три случая, возникающие из-за схемы SSA: одно решение, два возможных решения и отсутствие решения. См. (Рисунок) и (Рисунок).
- Закон синусов можно использовать для решения треугольников с заданными критериями. См. (Рисунок).
- Общая формула площади для треугольников преобразуется в косые треугольники, если сначала найти соответствующее значение высоты. См. (Рисунок).
- Существует множество тригонометрических приложений. Их часто можно решить, сначала нарисовав диаграмму данной информации, а затем используя соответствующее уравнение.
 См. (Рисунок).
См. (Рисунок).
Раздел Упражнения
Вербальные
Опишите высоту треугольника.
Показать раствор
Сравните прямоугольные и косоугольные треугольники.
Когда можно использовать закон синусов, чтобы найти недостающий угол?
Показать раствор
Каково соотношение между углом в числителе и стороной в знаменателе в законе синусов?
Какой тип треугольника приводит к неоднозначному случаю?
Показать раствор
Алгебраический
Для следующих упражнений предположим, что [латекс]\,\альфа \,[/латекс]противоположная сторона[латекс]\,а,\бета \,[/латекс]противоположная сторона[латекс]\, b,\,[/latex] и [латекс]\,\gamma \,[/latex]противоположная сторона[латекс]\,c.\,[/latex]Решите каждый треугольник, если это возможно. Округлите каждый ответ до десятых.
[латекс]\альфа=43°,\гамма=69°,а=20[/латекс]
[латекс]\альфа=35°,\гамма=73°,с=20[/латекс]
Показать решение
[латекс]\альфа =60°,\,\,\бета =60°,\,\гамма =60°[/латекс]
[латекс]а=4,\,\,\альфа =\, 60°,\,\beta =100°[/latex]
Показать решение
[латекс]b=10,\,\бета =95°,\гамма =\,30°[/латекс]
В следующих упражнениях используйте закон синусов, чтобы найти недостающую сторону для каждого косоугольного треугольника. . Округлите каждый ответ до сотых. Предположим, что угол[латекс]\,А\,[/латекс]противоположная сторона[латекс]\,а,\,[/латекс]угол[латекс]\,В\,[/латекс]противоположная сторона[латекс] \,b,\,[/latex]и угол[latex]\,C\,[/latex]является противоположной стороной[latex]\,c.[/latex]
. Округлите каждый ответ до сотых. Предположим, что угол[латекс]\,А\,[/латекс]противоположная сторона[латекс]\,а,\,[/латекс]угол[латекс]\,В\,[/латекс]противоположная сторона[латекс] \,b,\,[/latex]и угол[latex]\,C\,[/latex]является противоположной стороной[latex]\,c.[/latex]
Найти сторону[латекс]\,b\,[/латекс],когда[латекс]\,А=37°,\,\,В=49°,\,с=5.[/латекс]
Показать решение
Найти сторону[латекс]\,а[/латекс], когда[латекс]\,А=132°,С=23°,b=10.[/латекс]
Найти сторону[латекс]\,с\, [/latex]when[latex]\,B=37°,C=21°,\,b=23.[/latex]
Показать решение
В следующих упражнениях предположим, что [латекс]\,\альфа \,[/латекс]противоположная сторона[латекс]\,а,\бета \,[/латекс]противоположная сторона[латекс]\,b,\ ,[/latex]и[латекс]\,\гамма\,[/латекс]противоположная сторона[латекс]\,с.\,[/латекс]Определить, нет ли треугольника, один треугольник или два треугольника. Затем решите каждый треугольник, если это возможно. Округлите каждый ответ до десятых.
Округлите каждый ответ до десятых.
[латекс]\alpha =119°,a=14,b=26[/латекс]
[латекс]\gamma =113°,b=10,c=32[/латекс]
Показать решение
[латекс]b=3,5,\,\,c=5,3,\,\,\gamma =\,80°[/латекс]
[латекс]a=12,\,\,c=17,\ ,\,\alpha =\,35°[/latex]
Показать решение
[латекс]a=20,5,\,\,b=35,0,\,\,\beta=25°[/латекс]
[латекс]a=7,\,c=9,\,\,\ альфа =\,43°[/латекс]
Показать решение
[латекс]a=7,b=3,\beta=24°[/латекс]
[латекс]b=13,c=5,\gamma=\,10°[/латекс]
Показать решение
[латекс]a=2.3,c=1.8,\gamma=28°[/латекс]
[латекс]\beta=119°,b=8.2,a=11.3[/латекс]
Показать решение
В следующих упражнениях используйте закон синусов, чтобы найти недостающую сторону или угол для каждого треугольника или треугольников в неоднозначном случае. Округлите каждый ответ до десятых.
Округлите каждый ответ до десятых.
Найти угол[латекс]А[/латекс],когда[латекс]\,а=24,b=5,В=22°.[/латекс]
Найти угол[латекс]А[/латекс],когда[латекс] ]\,a=13,b=6,B=20°.[/латекс]
Показать решение
Найдите угол[латекс]\,В\,[/латекс],когда[латекс]\,А=12°,а=2,b=9.[/латекс]
Для следующих упражнений найдите площадь треугольник с заданными размерами. Округлите каждый ответ до десятых.
[латекс]a=5,c=6,\beta=\,35°[/латекс]
Показать решение
[латекс]b=11,c=8,\alpha=28°[/латекс]
[латекс]a=32,b=24,\gamma=75°[/латекс]
Показать решение
[латекс]a=7,2,b=4,5,\gamma=43°[/латекс]
Графический
Для следующих упражнений найдите длину стороны[латекс]\,х.\,[/латекс]Округлите до десятых.
Показать раствор
Показать раствор
Показать раствор
Для следующих упражнений найдите меру угла[латекс]\,х,\,[/латекс], если возможно. Округлите до десятых.
Округлите до десятых.
Показать раствор
Показать раствор
Обратите внимание, что [латекс]\,х\,[/латекс] — тупой угол.
Показать решение
В следующих упражнениях найдите площадь каждого треугольника. Округлите каждый ответ до десятых.
Показать раствор
Показать раствор
Показать раствор
Показать раствор
Расширения
Найдите радиус окружности на (рис.). Округлите до десятых.
Рис. 18.
Найдите диаметр окружности на (рис.). Округлите до десятых.
Рис. 19.
Показать решение
Найдите [латекс]\,m\угол АЦП\,[/латекс]в (Рисунок). Округлите до десятых.
Рисунок 20.
Найдите [латекс]\,AD\,[/латекс]в (рисунок). Округлите до десятых.
Рис. 21.
Показать решение
Решите оба треугольника на (Рисунок). Округлите каждый ответ до десятых.
Рис. 22.
Найдите[латекс]\,АВ\,[/латекс]в параллелограмме, показанном на (рис.).
Рисунок 23.
Показать решение
Решите треугольник на (Рисунок). (Подсказка: проведите перпендикуляр от [латекс]\,H\,[/латекс]к[латекс]\,JK).\,[/латекс]Округлите каждый ответ до десятых.
Рисунок 24.
Решите треугольник на (Рисунок). (Подсказка: проведите перпендикуляр от [латекс]\,N\,[/латекс]к[латекс]\,LM).\,[/латекс]Округлите каждый ответ до десятых.
Рис. 25.
Показать решение
На (Рисунок)[латекс]\,ABCD\,[/латекс]не является параллелограммом.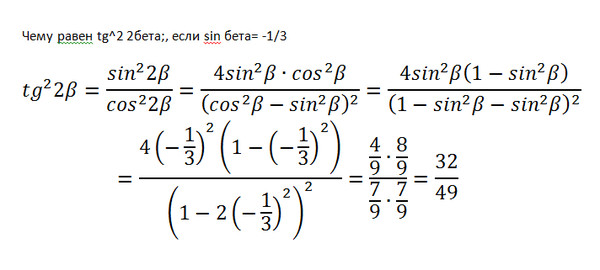 [латекс]\,\угол m\,[/латекс]тупой. Решите оба треугольника. Округлите каждый ответ до десятых.
[латекс]\,\угол m\,[/латекс]тупой. Решите оба треугольника. Округлите каждый ответ до десятых.
Рисунок 26.
Реальные приложения
Столб отклоняется от солнца под углом [латекс]\,7°\,[/латекс] к вертикали, как показано на (рисунок). Когда высота солнца составляет [латекс]\,55°,\,[/латекс] полюс отбрасывает тень длиной 42 фута на ровной поверхности. Какой длины столб? Округлите ответ до десятых.
Рис. 27.
Показать решение
Чтобы определить, насколько далеко лодка находится от берега, две радиолокационные станции, находящиеся на расстоянии 500 футов друг от друга, определяют углы от лодки, как показано на (Рисунок). Определите расстояние лодки от станции[latex]\,A\,[/latex]и расстояние лодки от берега. Округлите свои ответы до ближайшего целого фута.
Рисунок 28.
(Рисунок) показывает спутник, вращающийся вокруг Земли. Спутник проходит прямо над двумя станциями слежения [латекс]\,А\,[/латекс]и[латекс]\,В,\,[/латекс], которые находятся на расстоянии 69 миль друг от друга. Когда спутник находится по одну сторону от двух станций, углы места в точках [латекс]\,А\,[/латекс] и [латекс]\,В\,[/латекс] измеряются как [латекс]\ ,86,2°\,[/латекс] и [латекс]\,83,9°,\,[/латекс] соответственно. Как далеко находится спутник от станции[latex]\,A\,[/latex]и на какой высоте находится спутник над землей? Округлите ответы с точностью до целой мили.
Когда спутник находится по одну сторону от двух станций, углы места в точках [латекс]\,А\,[/латекс] и [латекс]\,В\,[/латекс] измеряются как [латекс]\ ,86,2°\,[/латекс] и [латекс]\,83,9°,\,[/латекс] соответственно. Как далеко находится спутник от станции[latex]\,A\,[/latex]и на какой высоте находится спутник над землей? Округлите ответы с точностью до целой мили.
Рисунок 29.
Показать решение
Башня связи расположена на вершине крутого холма, как показано на (Рисунок). Угол наклона холма составляет[латекс]\,67°.\,[/латекс]К вершине башни и к земле в 165 метрах вниз по склону от основания башни должна быть прикреплена оттяжка. Угол, образованный оттяжкой и холмом, равен[latex]\,16°.\,[/latex]Найдите длину троса, необходимого для оттяжки, с точностью до целого метра.
Рис. 30.
Крыша дома расположена под углом [латекс]\,20°\,[/латекс]. 8-футовая солнечная панель должна быть установлена на крыше и должна быть расположена под углом [латекс]\,38°\,[/латекс] по отношению к горизонтали для достижения оптимальных результатов.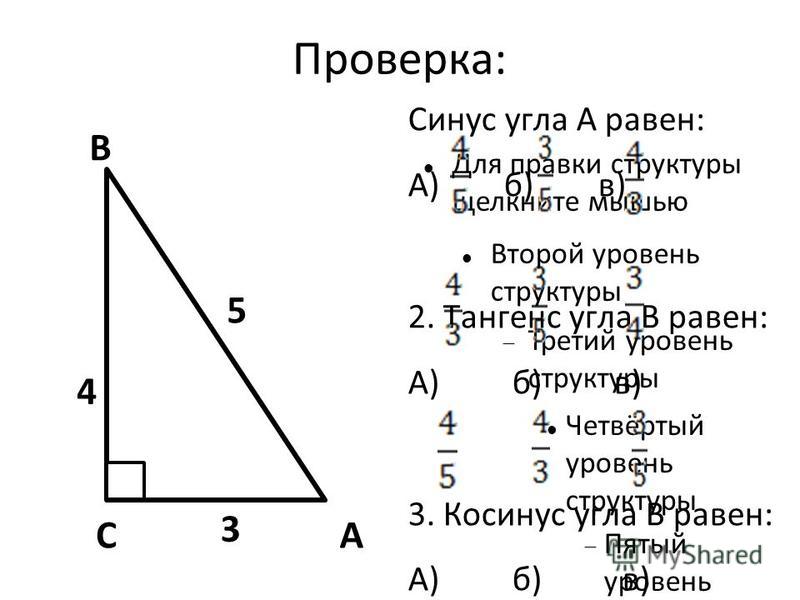 (См. (Рисунок)). Какой длины должна быть вертикальная опора, удерживающая заднюю часть панели? Округлите до десятых.
(См. (Рисунок)). Какой длины должна быть вертикальная опора, удерживающая заднюю часть панели? Округлите до десятых.
Рис. 31.
Показать решение
Аналогично углу подъема, угол наклона — острый угол, образованный горизонтальной линией и линией визирования наблюдателя на объект ниже горизонтали. Летчик летит по прямой трассе. Он определяет углы наклона к двум верстовым столбам, расположенным на расстоянии 6,6 км друг от друга, как [латекс]\,37°[/латекс] и [латекс]\,44°,[/латекс], как показано на (рис.). Найдите расстояние от точки [латекс]\,А\,[/латекс] до ближайшей десятой доли километра.
Рис. 32.
Пилот летит над прямой трассой. Он определяет углы падения к двум верстовым столбам, отстоящим друг от друга на 4,3 км, равными 32° и 56°, как показано на (рис.). Найдите расстояние от точки [латекс]\,А\,[/латекс] до ближайшей десятой доли километра.
Рисунок 33.
Показать решение
Чтобы оценить высоту здания, два ученика встают на определенном расстоянии от здания на уровне улицы. Отсюда они находят, что угол подъема от улицы до верха здания равен 39°. Затем они приближаются к зданию на 300 футов и обнаруживают, что угол подъема равен 50°. Предполагая, что улица ровная, оцените высоту здания с точностью до фута.
Чтобы оценить высоту здания, два ученика встают на определенном расстоянии от здания на уровне улицы. Отсюда они находят угол подъема от улицы до верха здания равным 35°. Затем они приближаются к зданию на 250 футов и обнаруживают, что угол возвышения составляет 53°. Предполагая, что улица ровная, оцените высоту здания с точностью до фута.
Показать решение
Точки[латекс]\,А\,[/латекс]и[латекс]\,В\,[/латекс]на противоположных сторонах озера. Точка[латекс]\,С\,[/латекс]находится в 97 метрах от[латекс]\,А.\,[/латекс]Мера угла[латекс]\,ВАС\,[/латекс] определяется как 101°, а мера угла [латекс]\,ACB\,[/латекс] определяется как 53°. Каково расстояние от [латекс]\,А\,[/латекс]до[латекс]\,В,\,[/латекс], округленное до ближайшего целого метра?
Каково расстояние от [латекс]\,А\,[/латекс]до[латекс]\,В,\,[/латекс], округленное до ближайшего целого метра?
Мужчина и женщина, стоящие[latex]\,3\frac{1}{2}\,[/latex]мили друг от друга, одновременно замечают воздушный шар. Если угол подъема от мужчины до воздушного шара равен 27°, а угол подъема от женщины к воздушному шару равен 41°, найдите высоту воздушного шара с точностью до ближайшего фута.
Показать решение
Две поисковые группы обнаруживают застрявшего в горах альпиниста. Первая поисковая группа находится в 0,5 мили от второй поисковой группы, и обе группы находятся на высоте 1 мили. Угол возвышения от первой поисковой группы до севшего на мель альпиниста составляет 15°. Угол возвышения от второй поисковой группы до альпиниста 22°. На какой высоте находится альпинист? Округлите до ближайшей десятой мили.
Уличный фонарь установлен на столбе. Мужчина ростом 6 футов стоит на улице недалеко от столба, отбрасывая тень. Угол возвышения от кончика тени человека до макушки его головы 28°. Женщина ростом 6 футов стоит на той же улице с противоположной от мужчины стороны столба. Угол возвышения от кончика ее тени до макушки составляет 28°. Если мужчина и женщина находятся на расстоянии 20 футов друг от друга, как далеко уличный фонарь от кончика тени каждого человека? Округлите расстояние до ближайшей десятой доли фута.
Угол возвышения от кончика тени человека до макушки его головы 28°. Женщина ростом 6 футов стоит на той же улице с противоположной от мужчины стороны столба. Угол возвышения от кончика ее тени до макушки составляет 28°. Если мужчина и женщина находятся на расстоянии 20 футов друг от друга, как далеко уличный фонарь от кончика тени каждого человека? Округлите расстояние до ближайшей десятой доли фута.
Показать решение
Три города,[латекс]\,А,В,[/латекс]и[латекс]\,С,[/латекс]расположены так, что город[латекс]\,А\,[/латекс]находится строго на восток города[латекс]\,В.\,[/латекс]Если город[латекс]\,С\,[/латекс] расположен в 35° к западу от севера от города[латекс]\,В\,[/латекс] и находится в 100 милях от города[латекс]\,А\,[/латекс]и в 70 милях от города[латекс]\,В,[/латекс]как далеко находится город[латекс]\,А\,[/латекс] from city[latex]\,B?\,[/latex]Округлите расстояние до ближайшей десятой мили.
Две улицы пересекаются под углом 80°.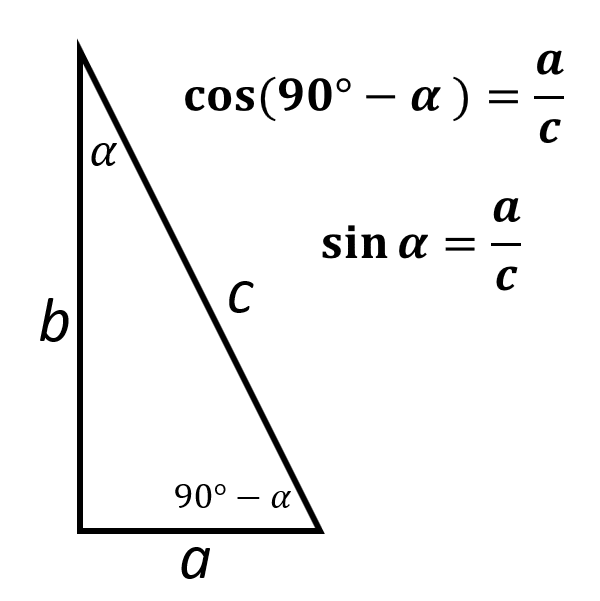 На углу строится парк в форме треугольника. Найдите площадь парка, если вдоль одной дороги длина парка составляет 180 футов, а по другой дороге — 215 футов.
На углу строится парк в форме треугольника. Найдите площадь парка, если вдоль одной дороги длина парка составляет 180 футов, а по другой дороге — 215 футов.
Показать решение
Дом Брайана находится на угловом участке. Найдите площадь переднего двора, если стороны имеют размеры 40 и 56 футов, как показано на (рис.).
Рисунок 34.
Бермудский треугольник — это регион Атлантического океана, соединяющий Бермудские острова, Флориду и Пуэрто-Рико. Найдите площадь Бермудского треугольника, если расстояние от Флориды до Бермудских островов составляет 1030 миль, расстояние от Пуэрто-Рико до Бермудских островов составляет 980 миль, а угол между двумя расстояниями равен 62°.
Показать решение
Знак доходности имеет размеры 30 дюймов со всех трех сторон. Какова площадь знака?
Наоми купила современный обеденный стол со столешницей в форме треугольника. Найдите площадь столешницы, если две стороны имеют размеры 4 фута и 4,5 фута, а меньшие углы равны 32° и 42°, как показано на (рис. ).
).
Рис. 35.
Показать решение
Глоссарий
- высота над уровнем моря
- перпендикулярная линия из одной вершины треугольника к противоположной стороне или, в случае тупоугольного треугольника, к прямой, содержащей противоположную сторону, образующая два прямоугольных треугольника
- неоднозначный случай
- сценарий, в котором более чем один треугольник является допустимым решением для данного наклонного треугольника SSA
- Закон синусов
- утверждает, что отношение измерения одного угла треугольника к длине его противоположной стороны равно двум оставшимся отношениям измерения угла к противоположной стороне; любая пара пропорций может быть использована для определения отсутствующего угла или стороны 90 582
- косой треугольник
- любой треугольник, не являющийся прямоугольным
Формулы сложения синусов.
 Задача 3
Задача 3Мы говорим о формулах сложения синусов, вот особенно сложный пример. В нем говорится, что если косинус альфа равен 7 больше 25, а альфа находится между 3 пи больше 2 и 2 пи, а синус бета равен 3/5 с бета между пи больше 5 и пи, найдите синус альфа минус бета и синус альфа плюс бета.
Чтобы решить эту проблему, мне нужно будет использовать единичный круг, потому что мне нужно больше, чем просто косинус альфа и синус бета.
Итак, начнем с альфы. Угол альфа находится между 3 пи на 2 и 2 пи, поэтому альфа находится в четвертом квадранте 3 пи на 2, 2 пи прямо здесь, а косинус альфа равен 7 на 25, так что это означает, что первая координата моей точки на единичном круге 7 на 25, так что я поставлю это прямо здесь, и я не знаю координату y, но я найду ее второй, так что это альфа.
Теперь помните, что это единичный круг, а единичный круг имеет уравнение x² плюс y² равно 1, поэтому каждая точка на единичном круге удовлетворяет этому уравнению, включая это, и это означает, что 7 на 25² плюс y² это y² равно 1. Возведем в квадрат это мы получаем 49больше 625 плюс y² равно 625 больше 625, и мы вычитаем y² равно чему-то больше 625. 625 минус 49, 625 минус 50 будет 575, поэтому минус 49 будет 576, и получается, что это оба идеальные квадраты, 576 это 24² и 625 равно 25², так что это плюс или минус 24 на 25. Итак, мы должны решить, плюс это или минус, но в четвертом квадранте координата y должна быть отрицательной, поэтому она должна быть отрицательной, -24 на 25. Хорошо, что позаботится об альфе.
Возведем в квадрат это мы получаем 49больше 625 плюс y² равно 625 больше 625, и мы вычитаем y² равно чему-то больше 625. 625 минус 49, 625 минус 50 будет 575, поэтому минус 49 будет 576, и получается, что это оба идеальные квадраты, 576 это 24² и 625 равно 25², так что это плюс или минус 24 на 25. Итак, мы должны решить, плюс это или минус, но в четвертом квадранте координата y должна быть отрицательной, поэтому она должна быть отрицательной, -24 на 25. Хорошо, что позаботится об альфе.
Теперь мы знаем косинус альфа и синус альфа, а бета? Что ж, бета находится между пи больше 2 и пи, а его синус равен 3/5, поэтому между пи больше 2 и пи поместите бета во второй квадрант этого квадранта, и если синус равен 3/5, это означает, что значение y точки на этом круге равно будет 3/5 ну это примерно здесь так что-то 3/5.
Так что это может быть бета-версия моего угла. Чтобы найти координату x, я проделал тот же трюк, что и здесь, я использовал уравнение x² плюс y² равно 1, поэтому я получаю x² плюс 3/5 в квадрате равно 1, и это означает, что x² плюс 9 на 25 равно 25 на 25, поэтому я вычитаю x² равно 16 на 25, а затем извлеките корни, чтобы получить плюс или минус 4/5.
Теперь координата x должна быть отрицательной, потому что мы находимся во втором квадранте, так что ответ -4/5, 3/5, и это дает мне косинус и синус моего угла бета, и теперь это все, что мне нужно, чтобы найти синус альфа минус бета и синус альфа плюс бета.
Теперь запомните формулу синуса и разности, это синус, косинус, косинус, синус альфа-бета, альфа-бета, альфа-бета, а затем, когда у вас есть знак минус с формулой синуса, она остается неизменной, поэтому я просто заполняю в ценностях. Синус альфа-24 больше 25, а косинус 7 больше 25, поэтому -24 и 7 больше 25, а как насчет бета? Косинус бета равен -4/5, синус бета равен 3/5, -4/5, 3/5.
Таким образом, у нас есть -24 на 25, умноженное на -4 на 5, два отрицательных числа сокращаются, наш знаменатель будет 125 25 на 5, а числитель 24 на 4, 24 на 2 будет 48, еще 2 будет 9.6, а затем минус знаменатель все еще 125, я получаю 21 сверху, так что в основном это 96 минус 21, это 75. Итак, 75 на 125, что очень хорошо сокращается до 3/5, и это мой ответ для синуса альфа минус бета.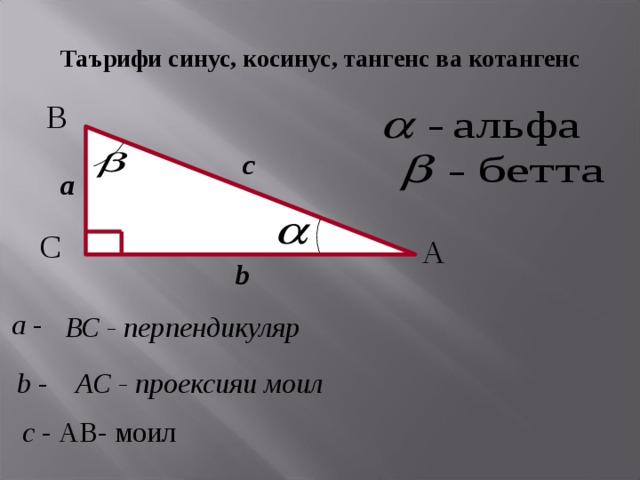

 02.21
02.21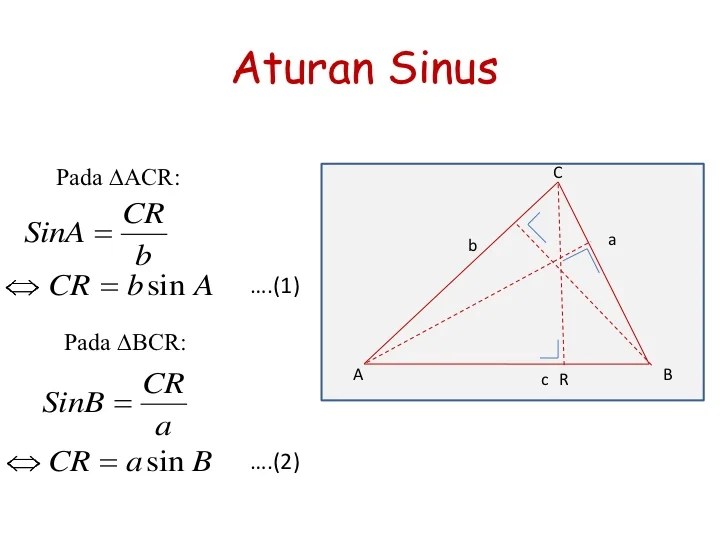
 См. (Рисунок).
См. (Рисунок).