Синус через тангенс: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа – StudyWay

В данной статье рассмотрим темы, которые встречаются в заданиях ЕГЭ по математике и содержатся в разделе алгебры, в ходе изучения темы подробно рассмотрим определения, используемые в теме, просмотрим рисунки, радианную меру углов, а также будем решать примерные задания. Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.

Переходим к более подробному изучению темы.

Для понятия о тригонометрических функциях следует рассмотреть окружность, радиус которой является единичным. У окружности есть центр, находящийся в начале координат, он расположен непосредственно на координатной плоскости. Для того, чтобы определить данную функцию, будем рассматривать вектор ОР. Он берёт начало в центре заданной окружности. Р – есть точка окружности. С помощью вектора ОР образуется угол с прилегающей осью, названной ОХ. ОР будет равен: OR = R = 1.

Рассмотрим соответствующий рисунок (рис. 1).

При проведении перпендикуляра из Р к оси ОХ получается прямоугольный треугольник, у которого есть гипотенуза и она равна единице.

При движении радиуса-вектора по часовой стрелке, будет получено отрицательное направление. А если радиус будет двигаться против часовой стрелки – положительное направление.

Для того чтобы осуществить вычисления синуса угла альфа, нужно обозначить на плоскости координату У. Как же получить это значение? Следует помнить, что в треугольнике, являющемся прямоугольным, синус произвольного угла будет равен отношению катета, являющегося противолежащим по отношению к гипотенузе. Получаем:

Sin a = У0 / R.

Радиус равен единице, исходя из этого: sin a = у0.

В окружности, являющейся единичной, ордината не должна быть больше единицы, а также меньше минус единицы: -1 < sin a < 1.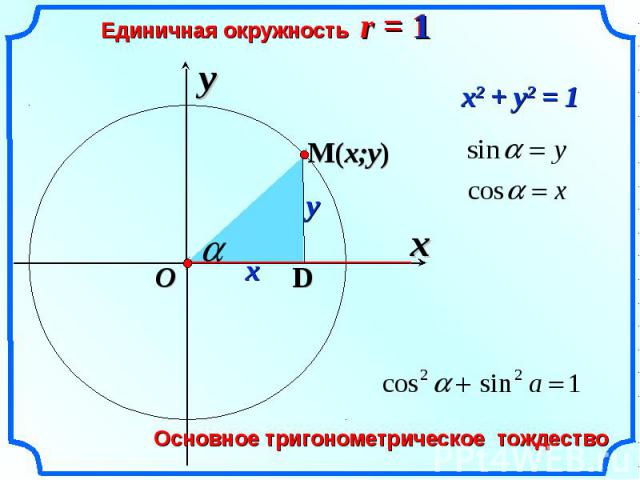

Синус будет являться положительным в первых и вторых четвертях окружности, являющейся единичной. Синус будет принимать отрицательное значение в третьей и четвёртой четверти окружности, являющейся единичной.

Выходит, для того чтобы получить косинус угла альфа, нужно определить на плоскости координату Х.

Косинус произвольного угла в треугольнике, являющемся прямоугольным, составляет отношение катета к гипотенузе. Получаем:

Cos a = х0 / R.

Поэтому, радиус равен единице, соответственно, cos a = x0.

У окружности, являющейся единичной, абсцисса не должна быть больше единицы и меньше минус единицы: -1 < cos a < 1.

Таким образом, косинус будет положительным в следующих четвертях окружности, являющейся единичной:

– В первой четверти;

– В четвёртой четверти.

Отрицательным:

– Во второй четверти;

– В третьей четверти.

Тангенсом угла, являющегося произвольным, считают отношение синуса и косинуса.

Представим произвольный треугольник, при условии, что он является прямоугольным.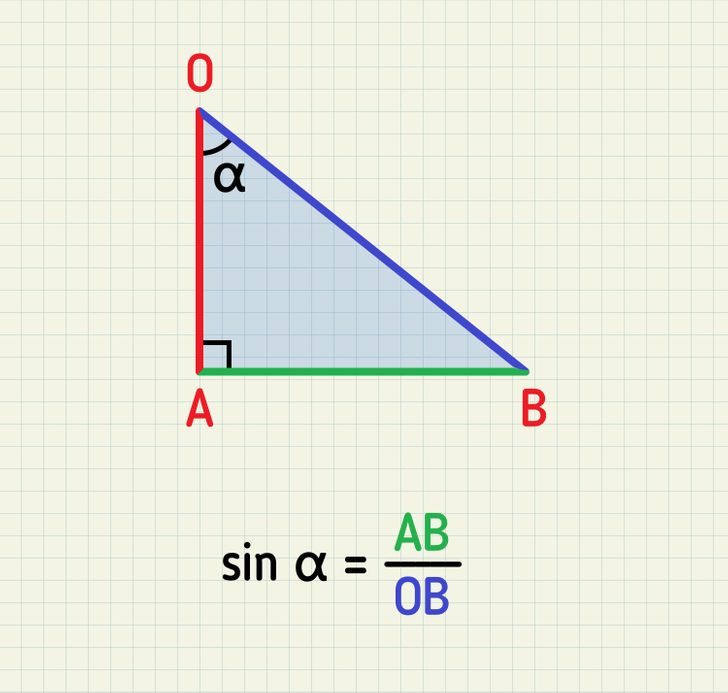 Здесь тангенсом будет отношение катета, названного противолежащим по отношению к прилежащему катету.

Если мы будем рассматривать единичную окружность – отношение её ординаты к абсциссе.

Получаем:

tg a = sin a / cos a; tg a = y0 / x0.

Следовательно, тангенс может быть при нулевом значении абсциссы, при этом, угол должен быть прямым. Тангенс вправе принимать и другие значения, такие как отрицательные и положительные.

Положительное значение тангенс будет иметь в первых и третьих четвертях окружности, являющейся единичной. Отрицательным тангенс является в четвёртой и второй четвертях.

Перейдём к рассмотрению котангенса. Котангенс угла, являющегося произвольным – косинус по отношению к синусу.

При рассмотрении прямоугольного треугольника это прилежащий катет по отношению к противолежащему:

Ctg a = cos a / sin a;

Ctg a = х0 / у0.

Если угол альфа равен нулю, то котангенса не существует. Это обусловлено тем, что в знаменателе дроби находится ордината.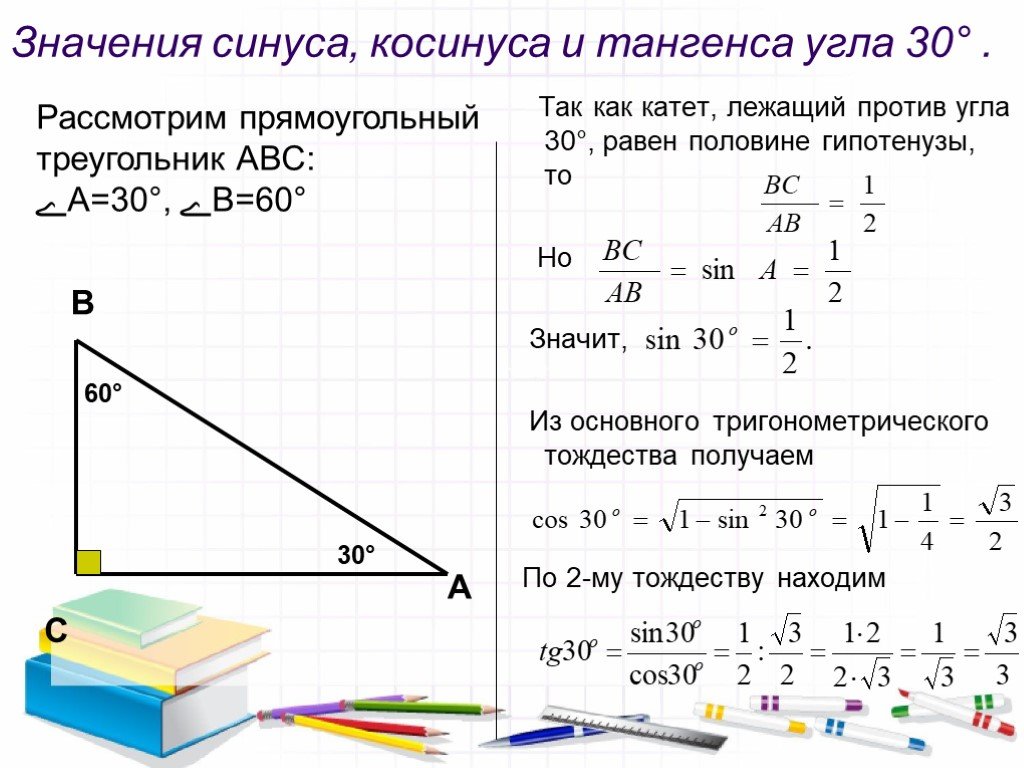

Котангенс так же как и тангенс, в четвертях окружности, имеет такие же значения.

Рассмотрим примеры заданий, а в точности — неравенства:

– Если n принадлежит Z, то:

Sin (a + 2 пn ) = sin a;

Cos ( a + 2 пn ) = cos a.

– Также, если n принадлежит Z, то:

Tg ( a + пn ) = tg a;

Ctg ( a + пn ) = ctg а.

Перейдём к рассмотрению радианной меры угла. Рассмотрим единичную окружность (рис. 2).

Проводим дугу, которая будет равна радиусу окружности. Далее нужно соединить центр с концами данной дуги с помощью радиана. Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.

Само понятие радиана открыл Томас Мюир и Джеймсон Томпсон в 1870 году. Таким образом, учёные измеряли углы на протяжении большого количества времени. К примеру, учёный Эйлер проводил исследования, он измерял углы с помощью длины дуги, которая отрезана в окружности, являющейся единичной.

Решим задачу ЕГЭ по математике на данную тему.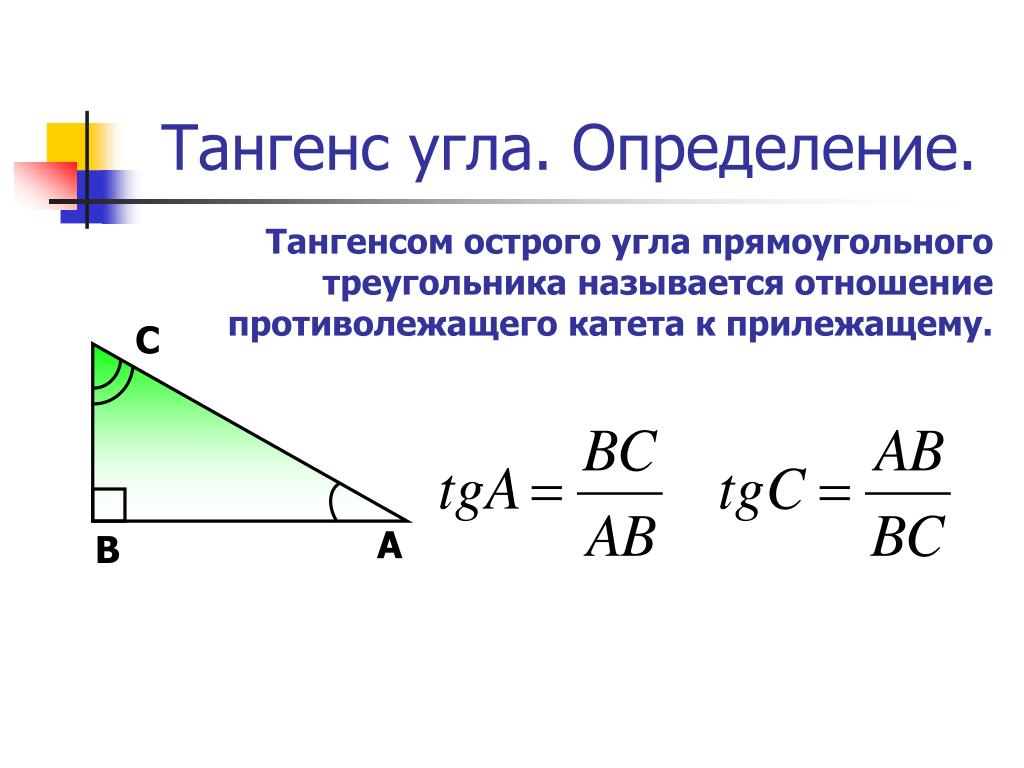

Нужно найти углы, при мере радиуса равной п / 2, п / 4, п / 8.

П / 2 * 180 / п = 90 градусов.

П / 4 * 180 / п = 45 градусов.

П / 8 * 180 / п = 22, 5 градуса.

Следует запомнить, что:

– 30 градусов равны п / 6;

– 45 градусов равны п / 4;

– 60 градусов равны п / 3;

– 90 градусов равны п / 2;

– 120 градусов равны 4п / 6;

– 180 градусов равны п.

Синус, тангенс, косинус, котангенс числа

Определением вышеописанных понятий считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.

Синусом, косинусом, тангенсом и котангенсом числа t считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.

Рассмотрим пример. Для любого действительного числа на окружности, являющейся единичной, определять точку. При этом, центр окружности должен находиться в начале системы координат. Все данные находят с помощью данной точки.

Начальной точкой окружности является точка А. Её координатами будут ( 1; 0 ).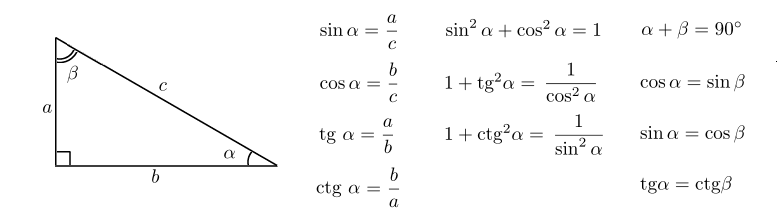 Пусть t – положительное число. Данному числу будет соответствовать точка, в неё осуществит переход изначальная точка. Если t отрицательное, то ему будет соответствовать точка, в которую осуществит переход исходная точка при направлении против часовой стрелки.

Рассмотрим определения основных понятий темы.

Синусом числа t является ордината точки окружности, являющейся единичной, она соответствует числу t. То есть sin t = y.

Косинусом числа t называют абсциссу точки окружности, являющейся единичной, она соответствует числу t. Получается: cos t = x.

Тангенсом числа t считают отношение ординаты к абсциссе точки окружности, являющейся единичной, она соответствует числу t. То есть: tg t = yx = sin t cos t.

Следует запомнить данные определения, а также необходимые неравенства, они пригодятся при решении заданий ЕГЭ по математике.

Данные определения не противоречат определению, которое дано в начале этой темы. Точка, лежащая на окружности, соответствует числу t, а также имеет совпадение с точкой. В эту точку переходит исходная точка, это происходит после осуществления поворота на угол, равный t радиан.

В процессе подготовки к экзамену рекомендуем внимательно просмотреть демоверсию ЕГЭ по математике базового уровня, а также решить примерные задания по теме. В демонстрационном варианте содержатся необходимые пояснения к ЕГЭ. Его назначением является ознакомление с примерным содержанием КИМОВ, заданиями, а также уровнем их сложности.

Синус, косинус и тангенс острого угла прямоугольного треугольника

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Синус, косинус и тангенс острого угла прямоугольного треугольника

2. Взаимосвязь между элементами прямоугольного треугольника.

В
Угол А – острый,
угол В –острый,
угол С – прямой.
с
А
b
а
С
Напротив ∟А катет а – противолежащий.
Рядом прилег катет b – прилежащий.
Напротив ∟В катет b – противолежащий.
Рядом прилег катет а –прилежащий.

3. Взаимосвязь между элементами прямоугольного треугольника.

М
Назовите гипотенузу,
катет противолежащий углу М,
катет прилежащий углу М
катет прилежащий углу К
Катет прилежащий углу Р
Катет противолежащий углу К
Р
К
Найти неизвестную сторону треугольника
№1
с
№2
13
6
12
8
Найти: РАВС и SАВС

5. Задачи ОГЭ-2016 с прямоугольным треугольником

6. ОГЭ-2016

№1
Найдите тангенс
угла В треугольника АВС,
изображенного на рисунке.
№2
В треугольнике ABC угол C
прямой, BC=8 , сosB=0,8. 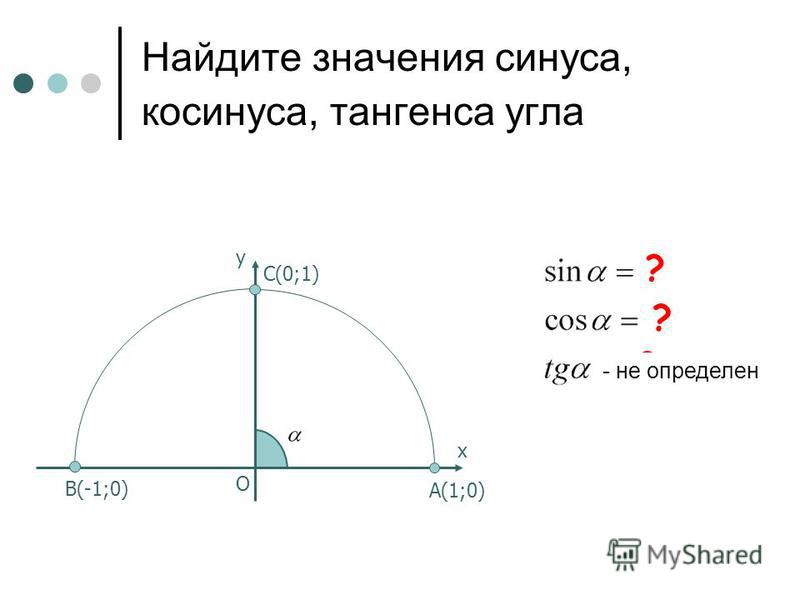Найдите AB.
№3
В треугольнике ABC угол C
прямой, AC=6 , sinВ=0,3. Найдите AB
Найти отношения сторон треугольника
№1
№2
10
6
12
13
8
ВС/АВ=
АС/АВ=
АС/ВС=
5

8. Определения:

Синусом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к гипотенузе
Косинусом острого угла прямоугольного
треугольника называется отношение
прилежащего катета к гипотенузе
Тангенсом острого угла прямоугольного
треугольника называется отношение
противолежащего катета к прилежащему

9. Стихотворение поможет запомнить определения

«Коль не знаешь правил – минус.
Если знаешь – тебе плюс!
Если «О», то будет синус,
Если «И», то косинус.

10. Соотнесите слова стихотворения с данным определением.

Противолежащий катет
Синус А =
гипотенуза
Прилежащий катет
Косинус А =
гипотенуза
«Коль не знаешь правил –
минус.
Если знаешь – тебе плюс!
Если «О», то будет синус,
Если «И», то косинус.
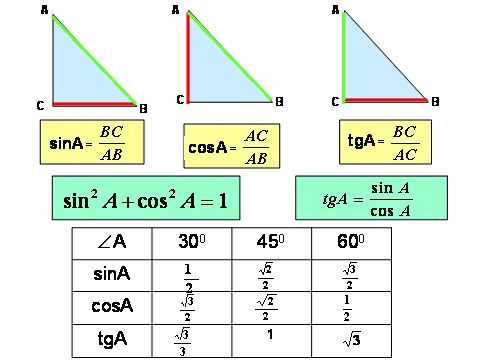
В
sin — синус альфа
cos — косинус альфа
tg — тангенс альфа
А
С
BC
sin A
AB
AC
cos A
AB
sin A BC AB BC
cos A AB AC AC
BC
tgA
AC
sin A
tgA
cos A
ТАНГЕНС УГЛА равен отношению синуса к
косинусу этого угла

12. Вывод:

Острый угол прямоугольного треугольника
зависит от гипотенузы, от катетов.
Примечание:
«Зная длины сторон прямоугольного
треугольника можно вычислить его острый
угол. Но для этого надо знать
тригонометрические функции: «синус»,
«косинус»,»тангенс»

13. Самостоятельная работа (практическая пятиминутка)

Задание. Дан прямоугольный треугольник
АВС с острым углом А и сторонами а = 4,
b = 3.Найдите:
В
1)Sin A =
Cos A =
5
4
2)Чему равно выражение:
c
Sin2 A + Cos2 A =
С
А
3

14. Всегда ли это равенство верное?

1. Ответ: Sin A = 4/5
Cos A = 3/5.
2. Ответ: Sin2 A + Cos2 A = 1.
Всегда ли это равенство верное?

15.

Основное тригонометрическое тождество«Тригонометрия» в переводе с греческого«измерение треугольников»
№593(в)

16. Домашнее задание.

Пункт 66, 67 повторить определения и
основное тригонометрическое тождество,
значения синуса, косинуса и тангенса
углов 30°, 60°, 45°.
Решить №591(а,б), №593 (а,б)
Решите задачу: В равнобедренной
трапеции меньшее основание равно 4 см,
боковая сторона равна 6см, а один из
углов трапеции равен 150°. Найдите
площадь трапеции.

17. ОГЭ-2016

№1
Найдите тангенс
угла В треугольника АВС,
изображенного на рисунке.
№2
В треугольнике ABC угол
C прямой, BC=8 ,сosB=0,8.
Найдите AB.
№3
В треугольнике ABC угол
C прямой, AC=6 , sinВ=0,3.
Найдите AB
если острый угол одного прямоугольного треугольника равен
острому углу другого прямоугольного треугольника, то
синусы этих углов равны, косинусы этих углов равны и
тангенсы этих углов равны
В
ABC
признаку
AB
BC
AC
A1 B1 B1C1 A1C1
А
В1
А1
A1B1C1- по первому
С1
С
BC B1C1
AB A1 B1
sin A sin A1
AC A1C1
AB A1 B1
cos A cos A1
BC B1C1
AC A1C1
tgA tgA1

English     Русский Правила

Касательная есть касательная!

В своем посте «Тригонометрическая йога» я обсуждал, как определение синуса и косинуса как длин сегментов единичного круга помогает развить интуицию для этих функций.

Я выучил круговые определения синуса и косинуса в первом классе старшей школы, в классе, который теперь будет называться предварительным исчислением (он назывался «Trig Senior Math»). Двумя годами ранее я выучил определения синуса, косинуса и тангенса треугольника на уроке геометрии. Я не помню, чтобы кто-нибудь из моих учителей когда-либо упоминал круговое определение касательной функции.

Геометрическое определение функции касательной, предшествующее определению треугольника, представляет собой длину отрезка, касательного к единичной окружности. Тангенс действительно является тангенсом! Как и для синуса и косинуса, это определение с одной переменной помогает развить интуицию. Вот определение, за которым следует апплет, чтобы помочь вам почувствовать это:

Пусть OA будет радиусом единичной окружности, пусть B = (1,0) и пусть \( \theta =\angle BOA\ ). Пусть C будет пересечением \(\overrightarrow{OA}\) и прямой x=1, т.е. касательной к единичной окружности в точке B. Тогда \(\tan \theta\) является координатой y точки C, т.е. длина отрезка BC со знаком.

Переместите синюю точку ниже; тангенс — это длина красного сегмента. (Если метка мешает, щелкните правой кнопкой мыши и выберите «показать метку» в меню).

Круговое определение функции тангенса приводит к геометрическим иллюстрациям многих стандартных свойств и тождеств. (Если бы это был мой класс, я бы остановился на этом и посоветовал вам исследовать его самостоятельно и вместе с другими).

 

На что следует обратить внимание:

\(\left| \tan \theta \right|\) становится больше по мере того, как \(\theta\) приближается к \(\pm 9\круг)\).

Приведенный ниже апплет показывает геометрию во всех квадрантах и ​​дает динамическое представление о связи между \(\tan\theta\) и \(\tan(-\theta)\). Снова переместите синюю точку:

Специальный бонус: функция секанса

Длина отрезка OC со знаком называется функцией секанса, \(\sec\theta\).

Используя подобные треугольники, мы видим, что \(\sec \theta = \dfrac{1}{\cos \theta}\). 2 \theta\).

Когда функция тангенса большая, то и функция секанса, а когда функция тангенса мала, то и функция секанса тоже. Также \(\sec \theta\) близко к \(\pm 1\), когда \(\theta\) близко к оси x и когда \(\tan \theta\) близко к 0.

Графики двух функций хорошо смотрятся вместе:

Видео-вопрос: нахождение синуса и тангенса углов в прямоугольных треугольниках, где гипотенуза в два раза больше противоположной стороны

Найдите sin 𝐴 и тангенс 𝐴, учитывая, что 𝐴𝐵𝐶 — прямоугольный треугольник в точке 𝐵, где 2𝐶𝐵 = 𝐴𝐶.

Стенограмма видео

Найдите sin 𝐴 и тангенс 𝐴, учитывая, что 𝐴𝐵𝐶 — прямоугольный треугольник с вершиной 𝐵, где два 𝐶𝐵 равны 𝐴𝐶.

Нам дана информация об этом прямоугольном треугольнике 𝐴𝐵𝐶, так что давайте начнем с его наброска. Прямоугольный треугольник находится в точке 𝐵, другими словами, стороны 𝐴𝐵 и 𝐵𝐶 перпендикулярны.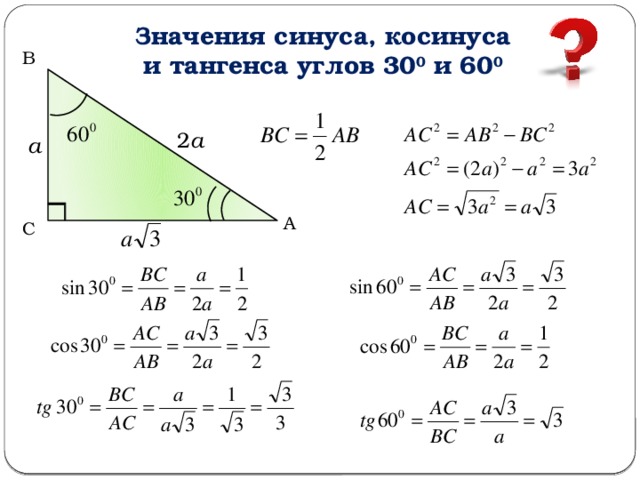

Нам также говорят, что два 𝐶𝐵 равны 𝐴𝐶, поэтому пусть сторона 𝐶𝐵 будет равна 𝑥 единицам длины. Тогда сторона 𝐴𝐶 должна быть равна двум 𝑥 единицам длины. Теперь мы собираемся вычислить грех 𝐴 и тангенс 𝐴. И мы знаем, что для прямоугольного треугольника с включенным углом 𝜃 тригонометрические соотношения синуса и тангенса говорят нам, что грех 𝜃 равен длине противоположного треугольника, деленной на длину гипотенузы. А тангенс 𝜃 равен противоположному деленному на соседнее.

Теперь мы пытаемся найти синус 𝐴 и тангенс 𝐴, так что это синус и тангенс этого угла. Относительно этого прилежащего угла мы знаем длину противоположного. Это длина 𝐵𝐶; это 𝑥 единиц. А гипотенуза в этом треугольнике равна двум 𝑥 единицам. Это означает, что мы можем довольно быстро вычислить значение греха 𝐴. Но нам нужно проделать еще немного работы, чтобы найти значение тангенса 𝐴.

Начнем с нахождения значения sin 𝐴. Это длина противоположной стороны, деленная на длину гипотенузы. Это 𝑥 разделить на два 𝑥. Но, конечно, мы можем упростить это выражение, разделив на 𝑥. Таким образом, 𝑥 разделить на два 𝑥 упрощается до половины, а грех 𝐴 равен половине. тангенс 𝐴, конечно же, есть противоположное деленное на прилежащее. Итак, давайте найдем выражение для длины прилежащей стороны.

Для этого воспользуемся теоремой Пифагора. А это говорит нам о том, что сумма квадратов двух меньших сторон в нашем треугольнике должна быть равна квадрату гипотенузы. Другими словами, 𝑥 в квадрате плюс 𝐴𝐵 в квадрате должно быть равно двум 𝑥 в квадрате. Два 𝑥 в квадрате равны четырем 𝑥 в квадрате. Итак, теперь мы возведем объект в квадрат 𝐴𝐵, вычитая 𝑥 в квадрате с обеих сторон. Тогда 𝐴𝐵 в квадрате равно трем 𝑥 в квадрате, а это означает, что 𝐴𝐵 равно положительному квадратному корню из трех 𝑥 в квадрате. В качестве альтернативы это можно записать как квадратный корень из трех умноженных на 𝑥. Таким образом, длина 𝐴𝐵 равна корню из трех 𝑥 единиц.

Теперь мы можем найти выражение для тангенса 𝐴. Поскольку оно противоположно соседнему, оно на 𝑥 больше корня три 𝑥.