| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.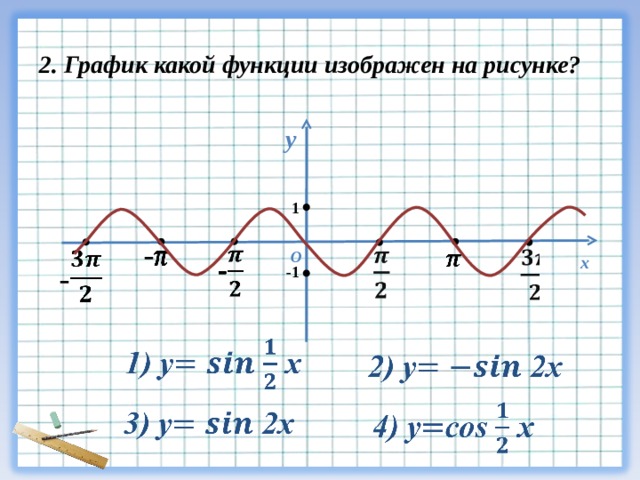 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град.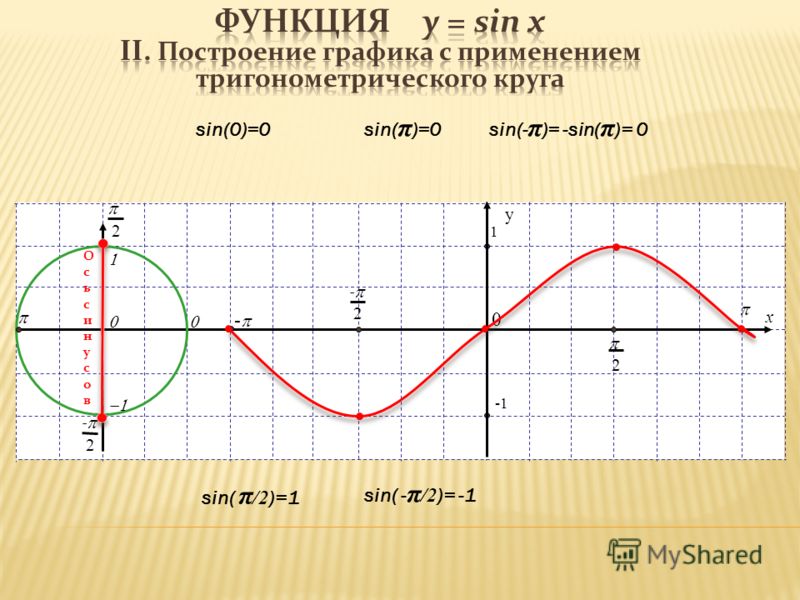 ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.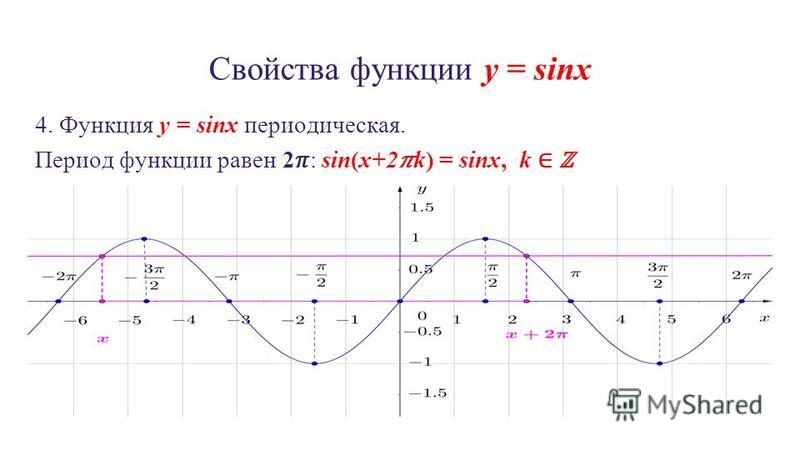 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град.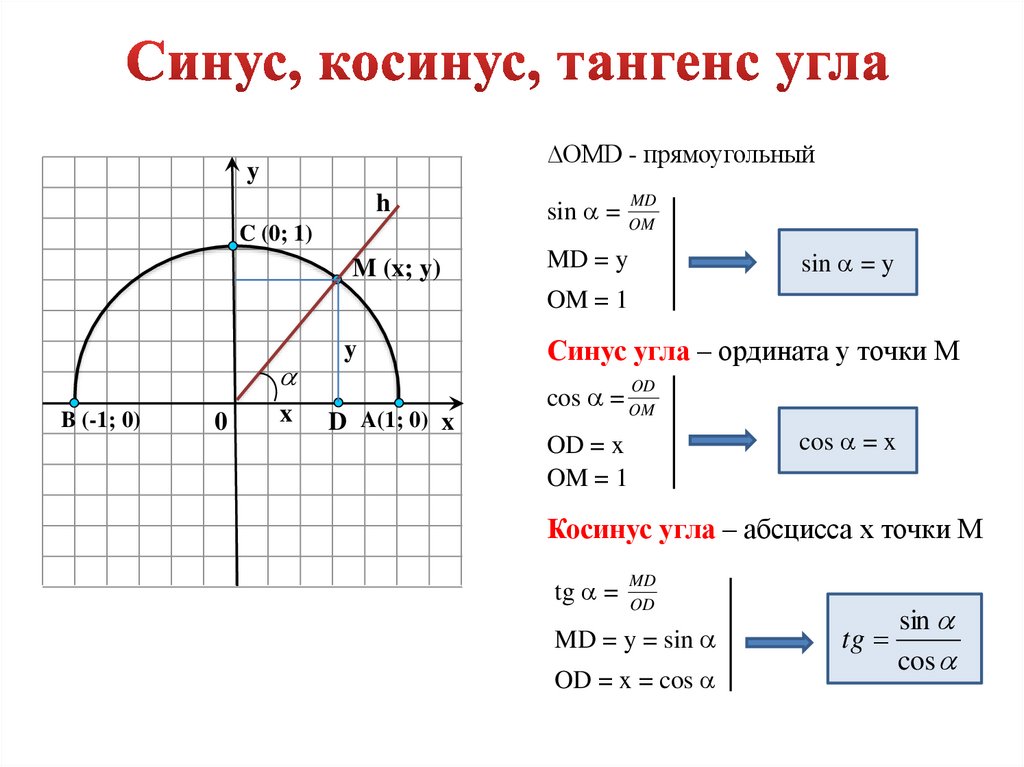 ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град.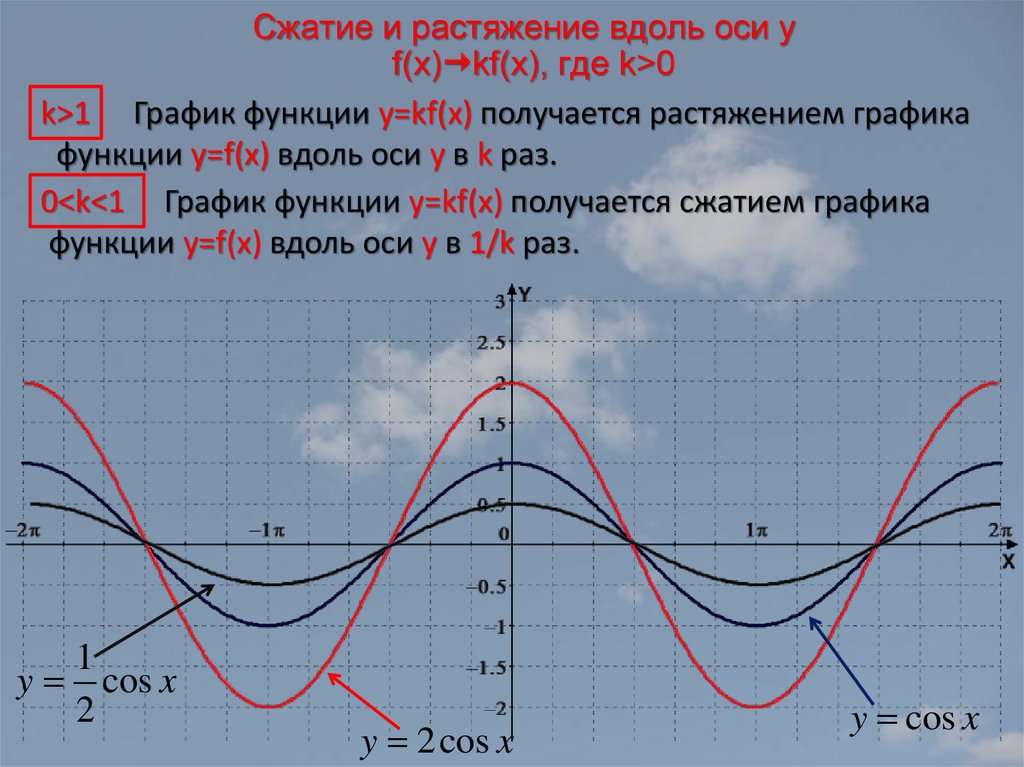 ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град.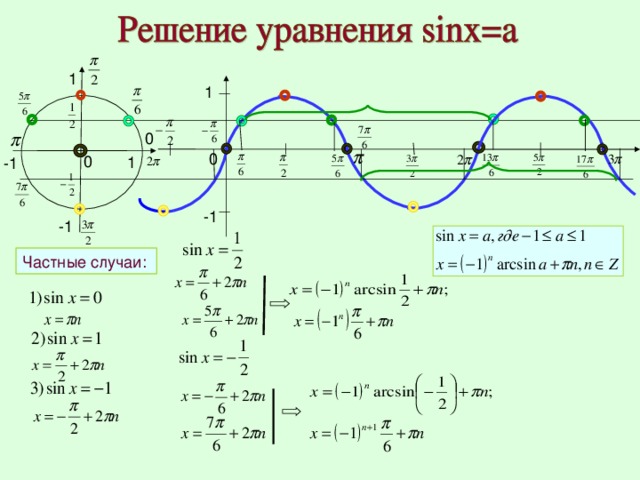 ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град.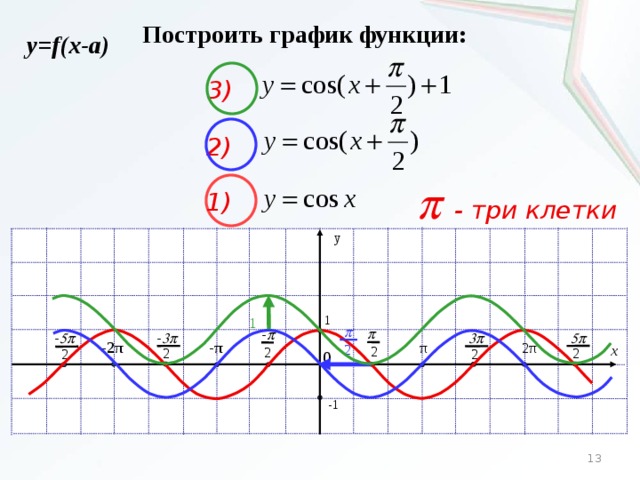 ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | arcsin(0) | ||
| 95 | Найти точное значение | sin(120 град.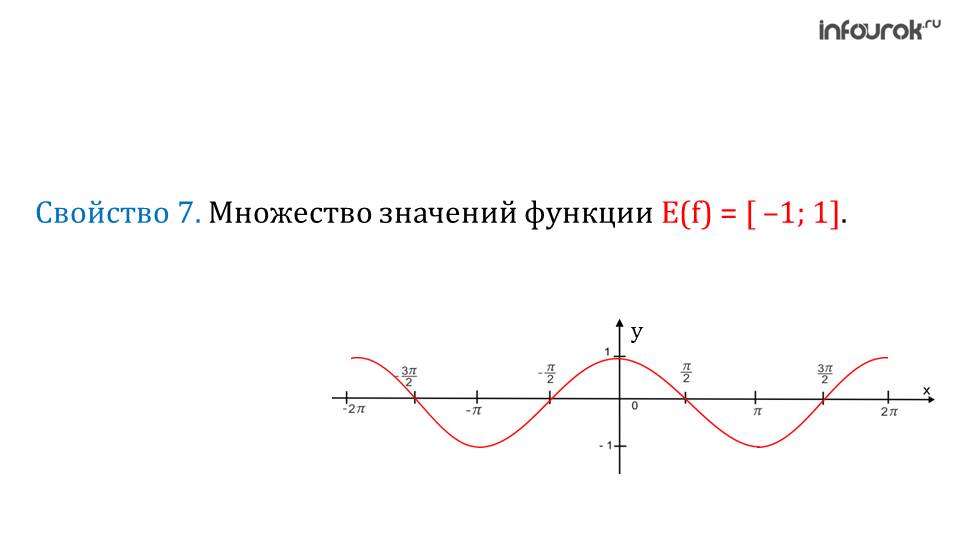 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
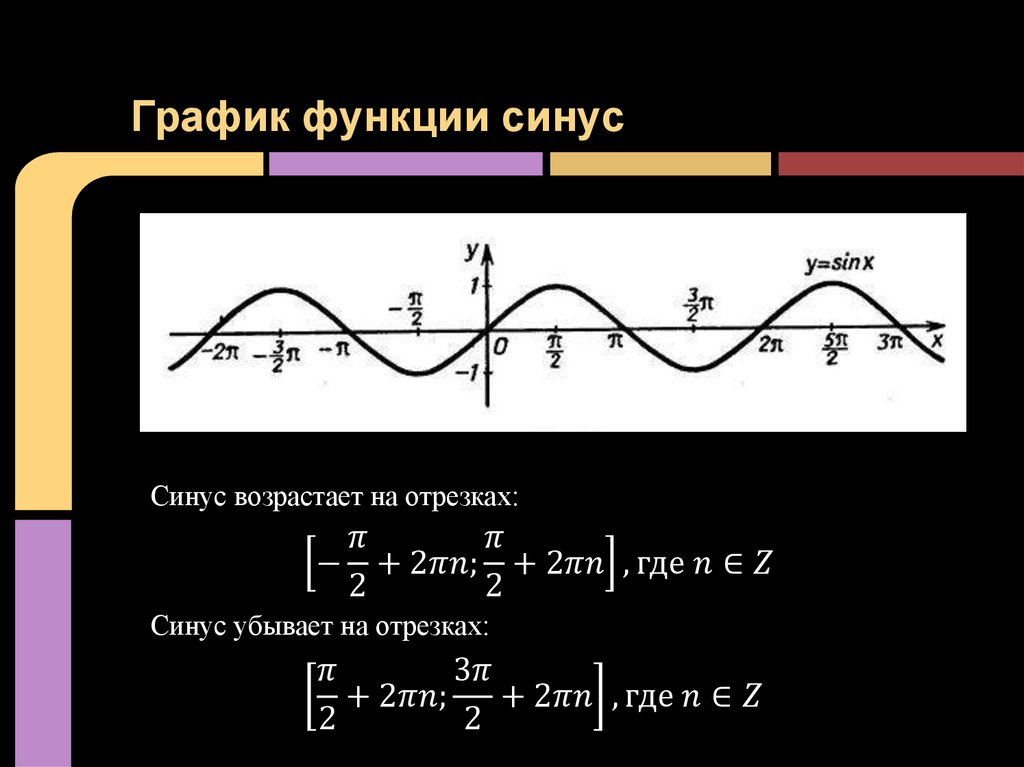
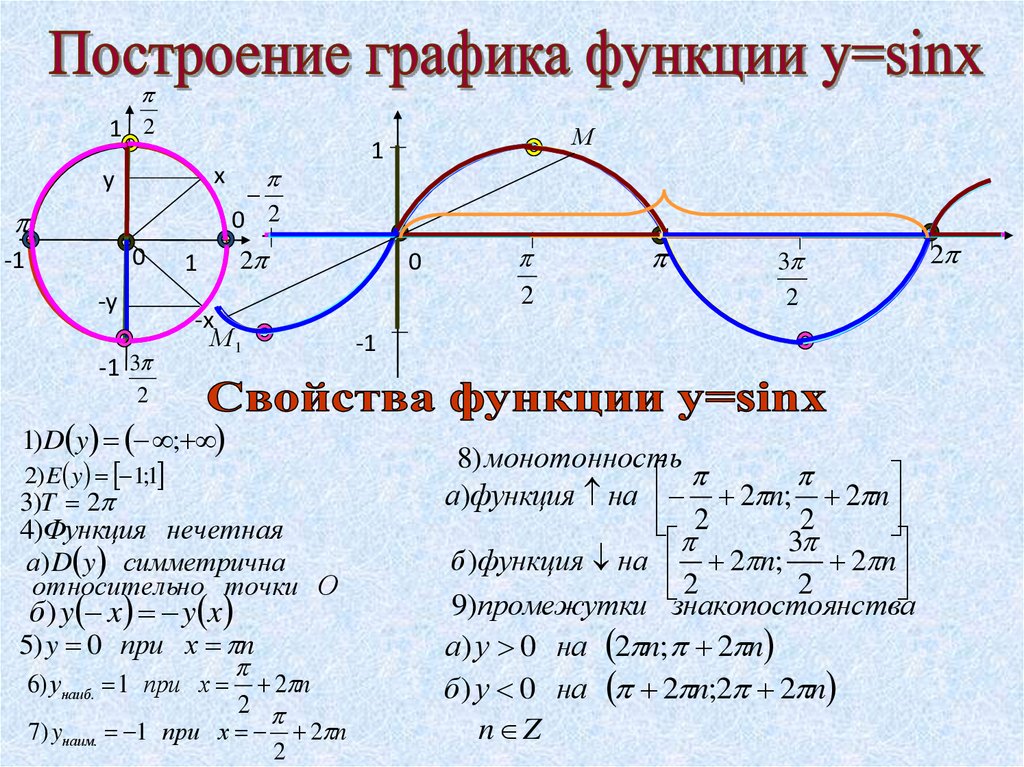
Графики тригонометрических функций. Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд — углы в радианах. Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0o до 360o, показаны на рисунках ниже.
Из графиков видно что:
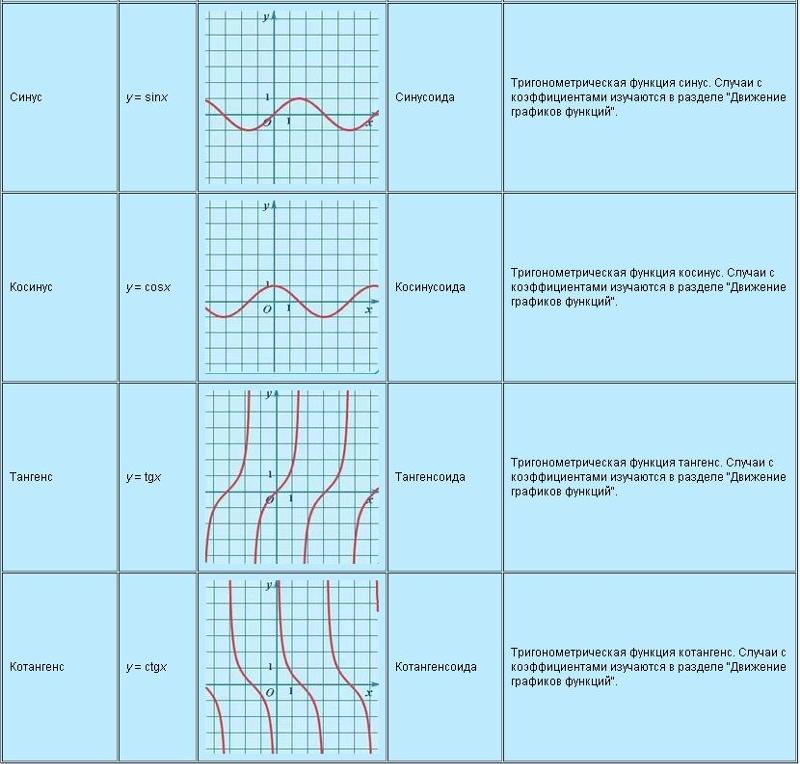
Углы произвольной величины На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О — отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке — отрицательным.
Пусть ОА вращается против часовой стрелки таким образом, что Θ1 — любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.
Пусть ОА вращается дальше таким образом, что Θ4— любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ4= -/+= -; cos Θ4=+/+=+; tg Θ4= -/+= -. В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем — только тангенс, в четвертом только косинус, что и показано на рис. График. Положительные и отрицательные значения синусов, косинусов и тангенсов.
Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины. Пример 1 Найти все углы в диапазоне от 0o до 360o , синус которых равен -0,7071 Решение: График. Нахождение всех углов по заданному значению синуса (пример)
Пример 2 Найти все углы между 0o и 360o , тангенс которых равен 1, 327. Решение: Из рис ниже Θ = arctg1,327= 53o . Построение синусоиды и косинусоиды Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30o вертикальная составляющая — это ТS, а горизонтальная — ОS.
Из определения тригонометрических функций Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30o на графике зависимости y от угла х.
Синусоидальные и косинусоидальные графики
Периодические функции и период
Амплитуда Пример 3. Решение: Пример 4. Решение:
Углы запаздывания и опережения Составив таблицу значений, можно построить график функции y=sin(A-60o), показанный на рис. слева. Если кривая y=sinA начинается в 0o, то кривая y=sin(A-60o) начинается в 60o (т.е. ее нулевое значение на 60o правее ). Таким образом, говорят, что y=sin(A-60o) запаздывает относительно y=sinA на 60o. Составив таблицу значений, можно построить график функции y=cos(A+45o), показанный на рис. ниже. В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α. Пример 5.
Пример 6. Решение: Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.
Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то Пример 7. Решение: Пример 8. Решение Пример 9. График. Колебательный механизм (пример, синусоида). v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35o или 0,611 рад. |
Открытая Математика. Функции и Графики. Синус и косинус
Синус и косинус
Положение точек на координатной окружности можно задавать не только длиной дуги, но и декартовыми координатами. Построим декартову систему координат с центром в точке O, осью абсцисс, проходящей через начало отсчета A (0), и осью ординат, проходящей через точку
Bπ2.
За единицу отсчета возьмем радиус этой окружности. Декартовы координаты точки M (x) единичной окружности называются косинусом и синусом числа x:
M (x) = M (cos x; sin x).
Построим декартову систему координат с центром в точке O, осью абсцисс, проходящей через начало отсчета A (0), и осью ординат, проходящей через точку
Bπ2.
За единицу отсчета возьмем радиус этой окружности. Декартовы координаты точки M (x) единичной окружности называются косинусом и синусом числа x:
M (x) = M (cos x; sin x).
Для x∈(0; π2) определение синуса и косинуса совпадает с геометрическим определением этих понятий, заданных при помощи прямоугольного треугольника OPM. В этом случае sinx=MPOM, cosx=OPOM.
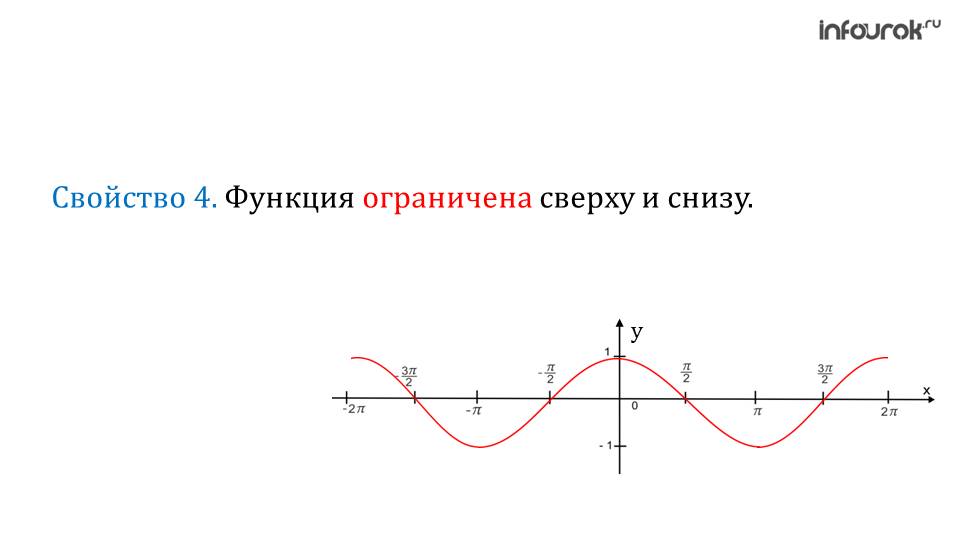
Так как координаты точек окружности единичного радиуса по модулю не превосходят 1, то |cos x| ≤ 1, |sin x| ≤ 1.
Таким образом, областью значений обеих функций является отрезок [–1; 1].
Ниже приведены значения косинуса и синуса для некоторых значений x:
| x | 0 | π6 | π4 | π3 | π2 | π | 3π2 |
|---|---|---|---|---|---|---|---|
| 0 | 30° | 45° | 60° | 90° | 180° | 270° | |
| sin x | 0 | 12 | 22 | 32 | 1 | 0 | –1 |
| cos x | 1 | 32 | 22 | 12 | 0 | –1 | 0 |
Функция sin x обращается в нуль при x = πn, функция cos x обращается в нуль при
x=πn+12,
n∈ℤ.
Промежутки монотонности и знакопостоянства:
| Функция | [0; π2] | [π2; π] | [π; 3π2] | [3π2; 2π] |
|---|---|---|---|---|
| sin x | Неотрицателен, возрастает от 0 до 1 | Неотрицателен, убывает от 1 до 0 | Неположителен, убывает от 0 до –1 | Неположителен, возрастает от –1 до 0 |
| cos x | Неотрицателен, убывает от 1 до 0 | Неположителен, убывает от 0 до –1 | Неположителен, возрастает от –1 до 0 | Неотрицателен, возрастает от 0 до 1 |
Синус достигает максимума в точках
xmax=π2+2πn
и минимумы в точках
xmin=-π2+2πn. Косинус достигает максимума в точках xmax = 2πn, минимума – в точках xmin = π + 2πn.
Косинус достигает максимума в точках xmax = 2πn, минимума – в точках xmin = π + 2πn.
Функция sin x нечетна, функция cos x четна:
cos (–x) = cos x sin (–x) = –sin xФормулы приведения, позволяющие свести тригонометрические функции от любого аргумента к функциям от углов из промежутка [0; π2] :
cos (x + π) = –cos x cos (π – x) = –cos x cosx+π2=-sinxcosπ2-x=sinxsin (x + π) = –sin x sin (π – x) = sin x sinx+π2=cosxsinπ2-x=cosxОсновное тригонометрическое тождество (следствие теоремы Пифагора):
sin2 x + cos2 x = 1Некоторые тригонометрические формулы приведены в таблице.
График функции y = sin x называется синусоидой, а функции y = cos x – косинусоидой. В обоих случаях достаточно построить графики на отрезке [0; 2π] или [–π; π], а затем периодически продолжать их на всю ось.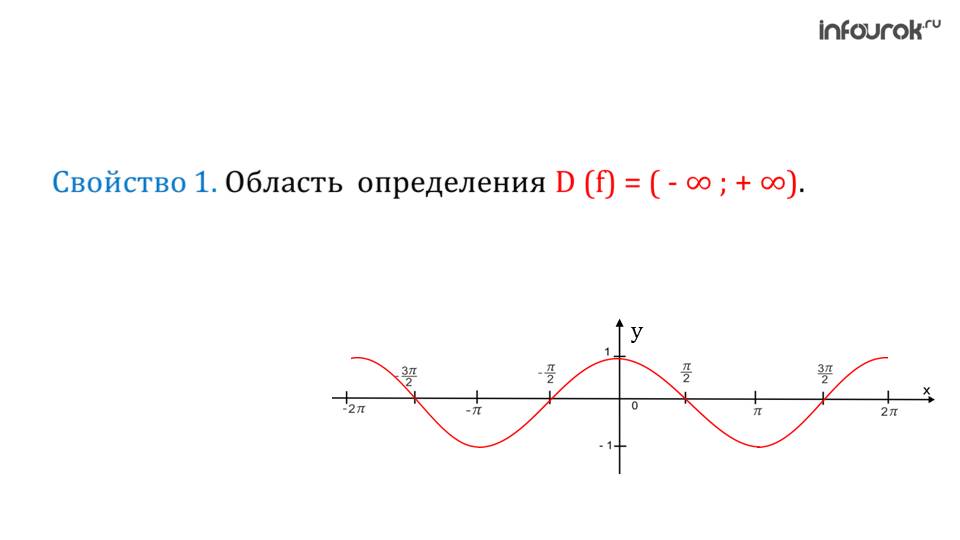 Более того, достаточно построить график y = sin x на отрезке
[0; π2],
отразить симметрично относительно оси
x=π2,
а затем отразить получившийся график относительно точки (π; 0). График y = cos x после построения на отрезке
[0; π2]
нужно отразить относительно точки
π2; 0,
а затем получившийся график – относительно оси x = π. Заметим также, что косинусоида получается из синусоиды сдвигом на π/2 влево, поэтому, как правило, используется только термин «синусоида».
Более того, достаточно построить график y = sin x на отрезке
[0; π2],
отразить симметрично относительно оси
x=π2,
а затем отразить получившийся график относительно точки (π; 0). График y = cos x после построения на отрезке
[0; π2]
нужно отразить относительно точки
π2; 0,
а затем получившийся график – относительно оси x = π. Заметим также, что косинусоида получается из синусоиды сдвигом на π/2 влево, поэтому, как правило, используется только термин «синусоида».
Синус и косинус применяются во многих областях физики и математики. Например, с их помощью удобно описывать гармонические колебания, задаваемые формулами y = A cos (ωx + φ) или y = A sin (ωx + φ). Здесь A – амплитуда, ω – частота, φ – начальная фаза колебаний. Для построения графика гармонического колебания необходимо последовательно выполнить следующие операции над синусоидой:
- сжать к оси ординат с коэффициентом ω,
- перенести вдоль оси абсцисс на φ влево,
- растянуть от оси абсцисс в A раз.

Если мы имеем дело с явлением, в котором одновременно происходят несколько различных колебательных процессов с соизмеримыми периодами, то зависимость колеблющейся величины от времени остается периодической, но график этой зависимости в общем случае уже не является синусоидой. Любую из функций, описывающих эту зависимость, можно представить в виде суммы постоянной составляющей и гармонических колебаний с частотами, кратными ω=2πT.
графиков функций синуса и косинуса
график функций синуса и косинусаВведение
Задачи: Построить графики функций синуса и косинуса;
находить графики функций синуса и косинуса.
«Функции синуса и косинуса определены для всех действительных чисел, и эти функции имеют много реальных приложения»
Например, «осциллограф — это электронный прибор, используемый для отображения изменяющихся электрических сигналов. Он отображает электрические или звуковые волны в виде узоров на флуоресцентном экране. Многие из графиков, показанных на осциллографе, являются синусоидальными или косинусоидальными. волны.»
Ресурс: Хейден, Джером Д. и Холл, Бетти. С. (1993). Тригонометрия . Прентис-холл: Энглвудские скалы, Нью-Джерси.
Занятие учащегося 1. Построение графика y = sinx по точкам
I. Во-первых, мы должны настроить таблицу координат некоторых точек, которые будут удовлетворять уравнению y = sinx.
1. Откройте электронную таблицу Excel. Метка столбца A «координаты x» и столбец B «координаты y». Установите оба столбца для округления до 4 знаков после запятой.
2. Заполните координаты x в столбце A.
в диапазоне от 0p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы используя радианы в качестве наших единиц.
3. Заполните координаты y в столбце B. используя уравнение, y = sinx.
Что вы заметили в значениях в эта колонка? Можете ли вы предсказать, как будет выглядеть график?
II. Графики в блокноте Geometer.
1. Откройте GSP и выберите Новый эскиз. Перейти к меню График и выберите «Создать оси».
2. Перейдите в меню «График» и выберите «График». Points». Введите значения из электронной таблицы Excel. Когда закончил, нажмите «Сюжет». У вас должно быть 9точки нанесены на график.
3. Выберите точку единицы измерения на оси x и перетащите его вправо до самой правой точки графика насколько это возможно, чтобы не «упасть» экран.
4. Выберите 1-ю, 2-ю и 3-ю точки ваш график (слева направо) именно в таком порядке. Перейти к конструкции Меню и выберите «Дуга через 3 точки».
Затем выберите 3-й, 4-й и 5-й пункты и сделайте то же самое. Повторите процесс для 5-го, 6-го и 7-го, а затем 7-го, 8-го и 9-гой точки.
Вы только что построили график синусоидальной функции!!
Какова область вашего графика? какая это диапазон?
III. Расширение графа.
1. Вы построили график функции синуса из от 0 до 2р. Но функция синуса подобна линии в том смысле, что она продолжается вечно. в двух направлениях. Итак, давайте нарисуем другую часть синусоидальной функции графически изобразив уравнение y = sinx от -2p до 0,
2. Следуйте частям I и II, но на этот раз пусть столбец A диапазон от -2p до 0 с шагом p/ 4. Нанесите точки на том же графике, который вы только что создали.
Что вы заметили в двух частях функции синуса, которую вы начертили?
IV. Проверь себя.
Нарисуйте (от руки!) что график y = sinx будет выглядеть, учитывая следующие ограничения домена.
Будьте внимательны к тому, где график пересекает ось x и где график достигает максимума и минимума.
а) 2 п до 4 п
б) -4 р до 0
в) -3 р к стр.
V. Сохраните файл GSP. Назовите его sinwavesmu.gsp, где сму ваши инициалы. Закройте файл.
Ключ учителя для задания для учащихся 1
И.
2. В ячейке A2 введите «0». В ячейке A3, введите «=A2+pi()/ 4». Перетащите, чтобы заполнить строку 10.
3. В ячейке B2 введите «=sin(A2)». Перетащите, чтобы заполнить строку 10.
Вот пример таблицы:
| 0 | 0 |
| 0,7854 | 0,7071 |
| 1,5710 | 1 |
| 2,3562 | 0,7071 |
3. 1416 1416 | 0 |
| 3,9270 | -0,7071 |
| 4,7124 | -1 |
| 5.4978 | -0,7071 |
| 6.2832 | 0 |
Обратите внимание, что значения y следуют шаблону!!
II.
4. Вот пример графика:
Домен графика — [0,2p], а диапазон равно [-1,1].
III.
2. Вот пример таблицы:
| -6,2832 | 0 |
| -5,4978 | 0,7071 |
| -4,7124 | 1 |
| -3,9270 | 0,7071 |
| -3,1416 | 0 |
| -2,3562 | -0,7071 |
| -1,5710 | -1 |
| -0,7854 | -0,7071 |
6. 2832 2832 | 0 |
Вот пример графика:
Обратите внимание, что две «части» графики идентичны.
IV.
а)
б)
в)
Задание 2 для учащихся. Построение графика y = cosx по точкам
I. Во-первых, мы должны настроить таблицу координат некоторых точек, которые будут удовлетворять уравнению y = sinx.
1. Откройте электронную таблицу Excel. Метка столбца A «координаты x» и столбец B «координаты y». Установите оба столбца для округления до 4 знаков после запятой.
2. Заполните координаты x в столбце A. в диапазоне от 0p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы используя радианы в качестве наших единиц.
3. Заполните координаты y в столбце B. используя уравнение, y = cosx.
Что вы заметили в значениях в эта колонка? Можете ли вы предсказать, как будет выглядеть график?
II. Графики в блокноте Geometer.
1. Откройте GSP и выберите Новый эскиз. Перейти к меню График и выберите «Создать оси».
2. Перейдите в меню «График» и выберите «График». Points». Введите значения из электронной таблицы Excel. Когда закончил, нажмите «Сюжет». У вас должно быть 9 точек на графике.
3. Выберите точку единицы измерения на оси x и перетащите его вправо до самой правой точки графика насколько это возможно, чтобы не «упасть» экран.
4. Выберите 1-ю, 2-ю и 3-ю точки ваш график (слева направо) именно в таком порядке. Перейти к конструкции Меню и выберите «Дуга через 3 точки». Затем выберите 3-й, 4-й и 5-й пункты и сделайте то же самое. Повторите процесс для 5-й, 6-й и 7-й, а затем 7-й, 8-й и 9-й точек.
Вы только что построили график косинуса функция!!
Какова область вашего графика? какая это диапазон?
III. Расширение графа.
1. Вы построили график функции косинуса из от 0 до 2р. Но функция косинуса подобна прямой в том смысле, что она продолжается. навсегда в двух направлениях. Итак, давайте нарисуем другую часть функции косинуса, построив график уравнения y = cosx от -2p до 0,
2. Следуйте частям I и II, но на этот раз пусть столбец A диапазон от -2p до 0 с шагом p/ 4. Нанесите точки на том же графике, который вы только что создали.
Что вы заметили в двух частях функции косинуса, которую вы нарисовали?
IV. Проверь себя.
Нарисуйте (от руки!) что график y = cosx будет выглядеть с учетом следующих ограничений домена. Будьте внимательны к тому, где график пересекает ось x и где график достигает максимума и минимума.

а) 2 стр. до 4 шт.
б) -4 р до 0
в) -3 р к стр.
V. Сохраните файл GSP. Назовите его coswavesmu.gsp, где сму ваши инициалы. Закройте файл.
Ключ учителя для задания для учащихся 2
И.
2. В ячейке A2 введите «0». В ячейке A3, введите «=A2+pi()/ 4». Перетащите, чтобы заполнить строку 10.
3. В ячейке B2 введите «=cos(A2)». Перетащите, чтобы заполнить строку 10.
Вот пример таблицы:
| 0 | 1 |
| 0,7854 | 0,7071 |
| 1,5710 | 0 |
| 2,3562 | -0,7071 |
3. 1416 1416 | -1 |
| 3,9270 | -0,7071 |
| 4,7124 | 0 |
| 5.4978 | 0,7071 |
| 6.2832 | 1 |
Обратите внимание, что значения y следуют шаблону!!
II.
4. Вот пример графика:
Домен графика — [0,2p], а диапазон равно [-1,1].
III.
2. Вот пример таблицы:
| -6,2832 | 1 |
| -5,4978 | 0,7071 |
| -4,7124 | 0 |
| -3,9270 | -0,7071 |
| -3,1416 | -1 |
| -2,3562 | -0,7071 |
| -1,5710 | 0 |
| -0,7854 | 0,7071 |
6. 2832 2832 | 1 |
Вот пример графика:
Обратите внимание, что две части графика идентичны.
IV.
а)
б)
в)
Студенческая практика
1. Нарисуйте следующие функции над данный домен. Будьте внимательны к тому, где график пересекает ось X и где график достигает своих максимальных и минимальных точек.
а) у = cosx, [-2р, р]
б) у = sinx, [0, 3p]
в) у = sinx, [-р, р]
г) у = cosx, [р, 3р]
2. Дайте уравнение функции и область определения для следующих графиков.
а)
б)
в)
Ключ учителя для студенческой практики
1.
а)
б)
в)
г)
2.
а) у = sinx, [-3p, -p]
б) у = cosx, [р, 2р]
в) у = cosx, [-р, р]
Возврат на домашнюю страницу Шеннон
График синуса и косинуса — тригонометрия
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
Помощь по тригонометрии » Тригонометрические функции и графики » Тригонометрические графики » График синуса и косинуса
Показанная ниже функция имеет амплитуду ___________ и период _________.
Возможные ответы:
Правильный ответ:
Объяснение:
Амплитуда всегда является положительным числом и определяется числом перед тригонометрической функцией.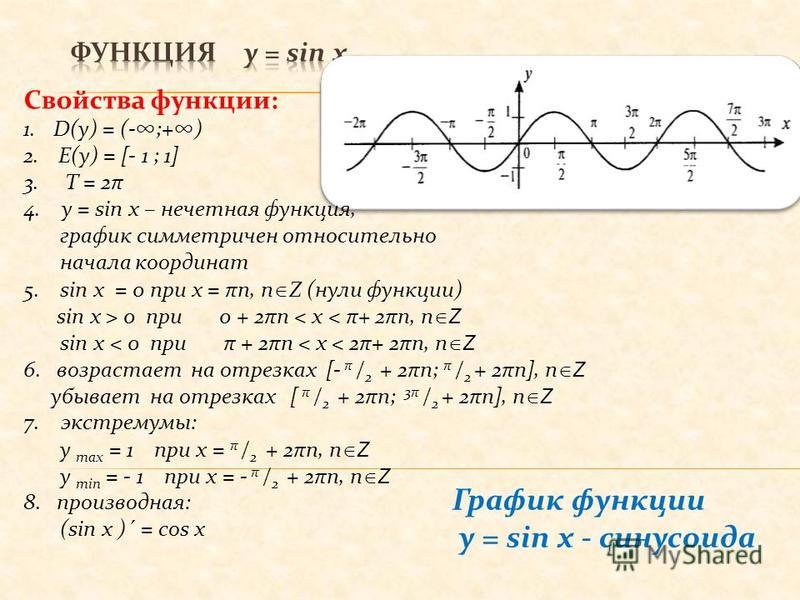 В данном случае амплитуда равна 4. Период определяется как , где b – число перед x. В этом случае период .
В данном случае амплитуда равна 4. Период определяется как , где b – число перед x. В этом случае период .
Сообщить об ошибке
Это график какой функции?
Возможные ответы:
Правильный ответ:
Объяснение:
Амплитуда синусоидальной функции увеличилась на 3, так что это коэффициент для . +2 показывает, что начало функции теперь находится в точке вместо
Сообщить об ошибке
Какой из следующих графиков не имеет -перехвата в точке ?
Возможные ответы:
Правильный ответ:
Объяснение:
Y-пересечение — это значение y, когда .
Напомним, что косинус — это значение единичного круга.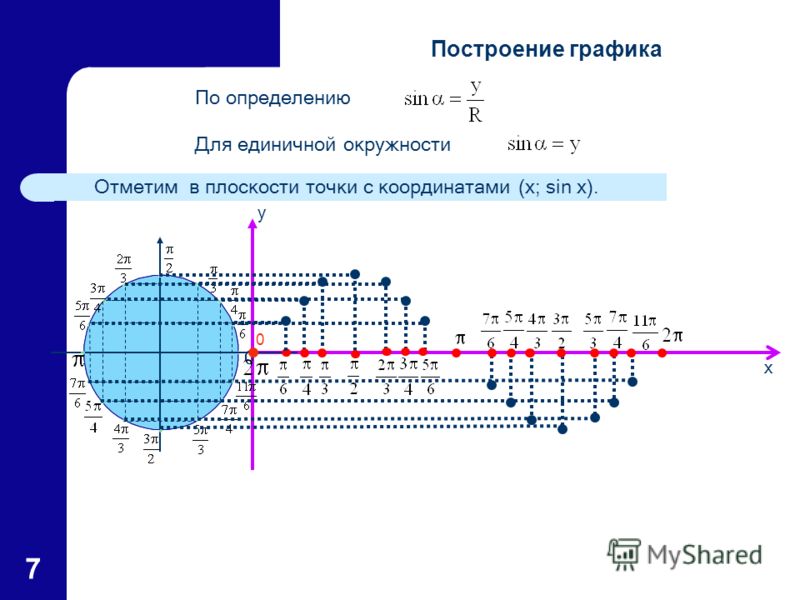 Так, так и работает.
Так, так и работает.
Секанс является обратной величиной косинуса, поэтому он также работает.
Также напомню, что . Таким образом, единственным ответом, который не является эквивалентным, является .
Сообщить об ошибке
Какой график правильно иллюстрирует данное уравнение?
Возможные ответы:
Правильный ответ:
Объяснение:
Самый простой способ решить подобную задачу — определить, где будет располагаться конкретная точка на графике, а затем сравнить это с нашими вариантами ответов. Сначала мы должны найти значение y, когда значение x равно нулю. Мы начнем с подстановки нуля вместо переменной x в нашем уравнении.
Теперь, когда мы вычислили значение y, мы знаем, что правильный график должен иметь следующую точку:
К сожалению, два из наших графиков включают эту точку; таким образом, нам нужно выбрать вторую точку.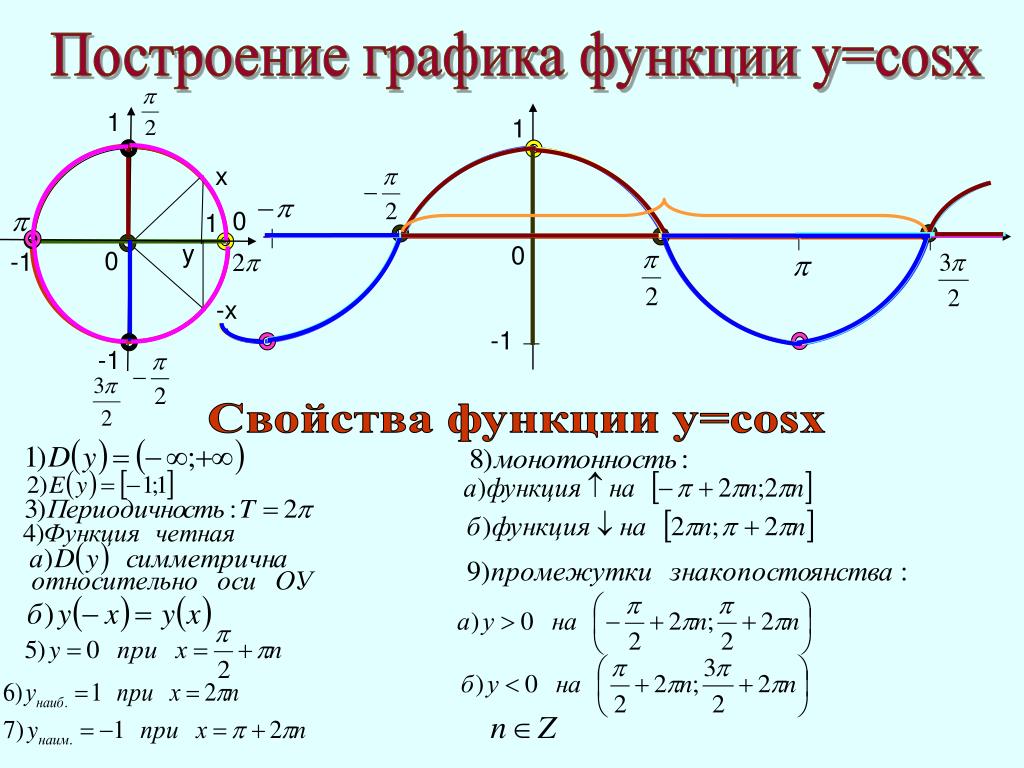
Давайте найдем значение y, когда переменная x равна следующему:
Начнем с подстановки этого значения в исходное уравнение.
Теперь нам нужно исследовать два оставшихся варианта для следующей точки:
К сожалению, оба наших оставшихся графа также имеют эту точку; следовательно, нам нужно выбрать другое значение x. Предположим, что переменная x равна следующему:
Теперь мы должны подставить это значение в наше данное уравнение.
Теперь мы можем найти график со следующей точкой:
Мы сузились до окончательного ответа; таким образом, следующий график верен:
Сообщить об ошибке
Пусть функция определена следующим образом:
.
3 в приведенной выше функции влияет на какой атрибут графика ?
Возможные ответы:
Период
Вертикальный сдвиг
Фазовый сдвиг
Амплитуда
Правильный ответ:
Вертикальный сдвиг
Объяснение:
Период функции обозначается коэффициентом перед ; здесь период неизменен.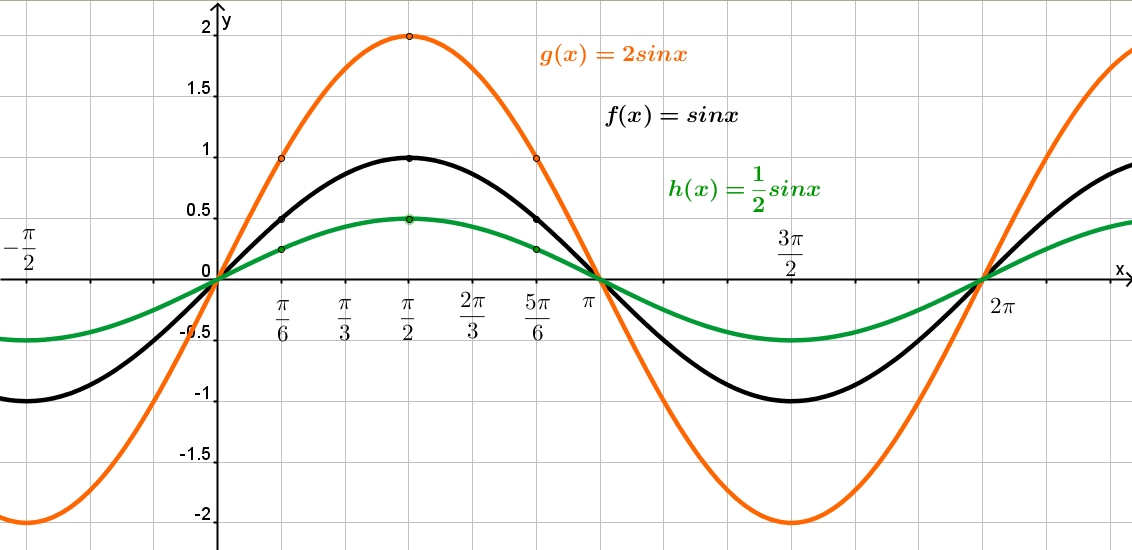
Амплитуда функции определяется коэффициентом перед ; здесь амплитуда равна 2.
Сдвиг фазы задается значением, добавляемым или вычитаемым внутри функции; здесь сдвиг на единицу вправо.
Единственным неисследованным атрибутом графика является сдвиг по вертикали, поэтому 3 — это сдвиг графика по вертикали.
Сообщить об ошибке
Какое уравнение для приведенной выше функции, увеличенное ниже?
Возможные ответы:
Правильный ответ:
Объяснение:
Амплитуда синусоидальной функции равна если не усилена константой перед уравнением. В этом случае амплитуда равна , поэтому постоянная фронта равна .
График движется через начало координат, так что это либо синусоидальный, либо сдвинутый косинусоидальный график.
Повторяется один раз в каждом , в отличие от обычного , поэтому период удваивается, константа рядом с переменной равна .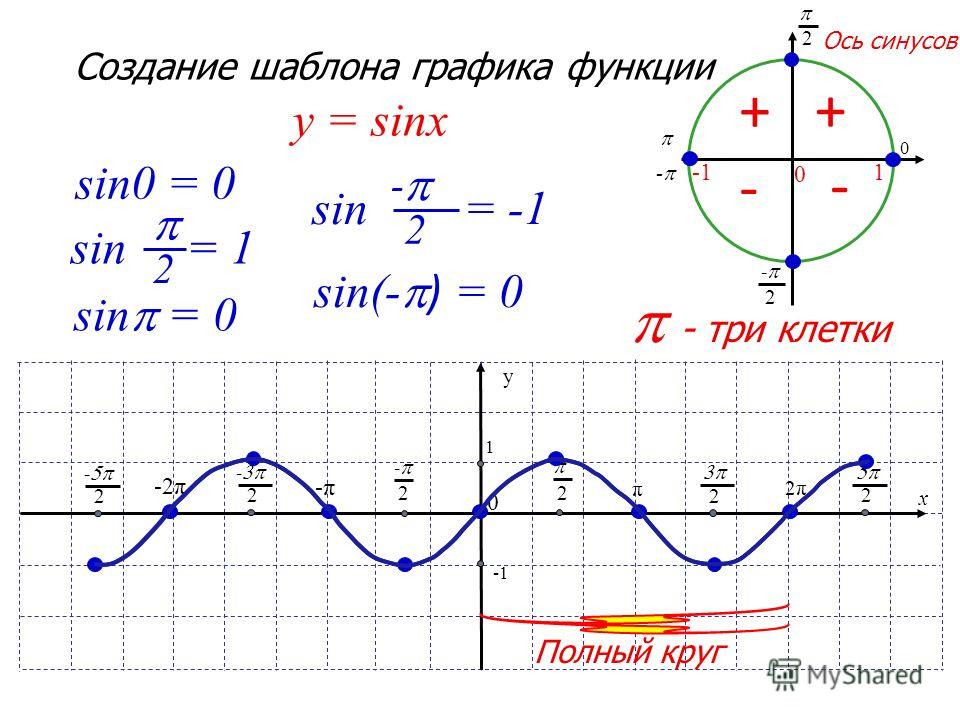
Единственный ответ, в котором найдены правильные значения амплитуды и периода:
Сообщить об ошибке
Какова область определения функции синуса? Какова область определения функции косинуса?
Возможные ответы:
Область синуса:
Область определения косинуса:
Область определения синуса:
Область определения косинуса: все действительные числа
Область определения синуса: все действительные числа
Область определения косинуса: все действительные числа
Область определения синуса: все действительные числа
Область определения косинуса:
Область синуса: все действительные числа
Область определения косинуса: все действительные числа
Объяснение:
И синусоидальные, и косинусоидальные функции продолжаются бесконечно влево и вправо при просмотре на графике.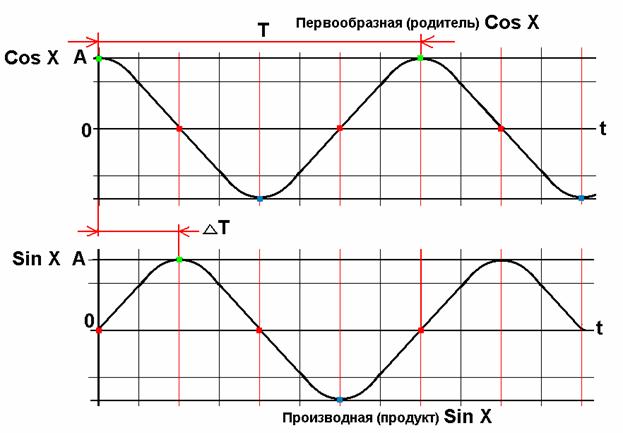 По этой причине каждая из этих функций имеет области определения «всех действительных чисел».
По этой причине каждая из этих функций имеет области определения «всех действительных чисел».
Альтернативно, каждая из этих функций находится в диапазоне от -1 до 1 в направлении y. Все неправильные ответы включают , что является диапазоном функций синуса и косинуса.
Сообщить об ошибке
Что из следующего правильно переводит функцию в ?
Возможные ответы:
Сдвиг на 1 единицу вверх
Сдвиг влево единицы
Сдвиг на 1 единицу вниз
Сдвиг вправо на единицу
Сдвиг0011
Правильный ответ:
Сдвиг влево единиц
Объяснение:
График показан красным цветом ниже, а график показан синим цветом ниже. Поскольку функция является периодической, существует бесконечно много преобразований, которые можно было бы преобразовать в , но ниже есть только один вариант ответа, который является правильным, и это «сдвиг влево единиц».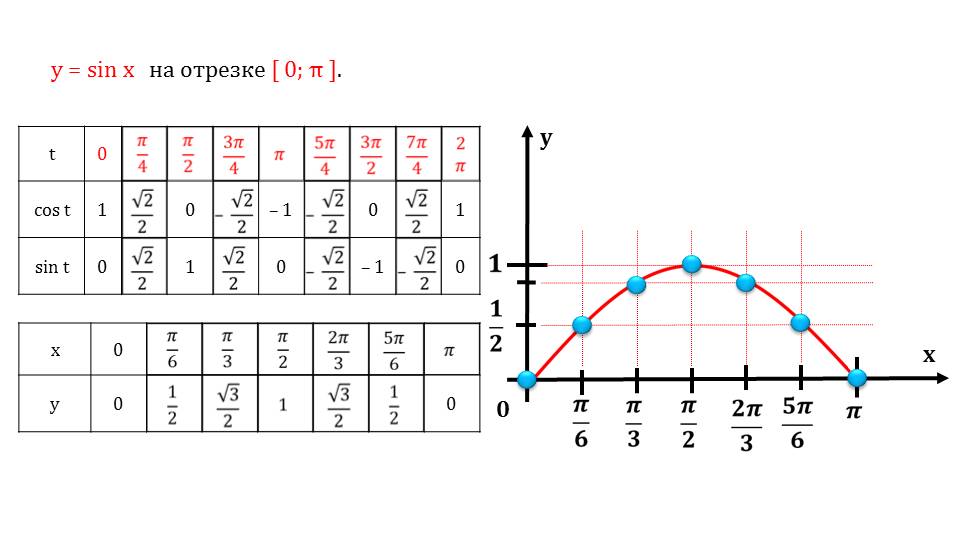 Согласно графику, смещение единиц измерения вправо также было бы правильным, но это не вариант ответа.
Согласно графику, смещение единиц измерения вправо также было бы правильным, но это не вариант ответа.
Сообщить об ошибке
Какой из следующих графиков представляет функцию ?
Возможные ответы:
Правильный ответ:
Объяснение:
График это:
Этот график претерпевает три преобразования. Сначала возьмите график , выделенный синим цветом ниже, и переверните его по оси x. Мы делаем это из-за отрицательного знака перед функцией косинуса. Вы можете увидеть полученный график зеленым цветом ниже. Далее мы хотим растянуть график в 2 раза, так как наша амплитуда равна 2 (мы получаем это из коэффициента перед функцией косинуса). Вы можете увидеть получившийся график фиолетовым цветом ниже.
Наконец, нам нужно сдвинуть график вверх на 1 единицу. Это представлено черным графиком ниже.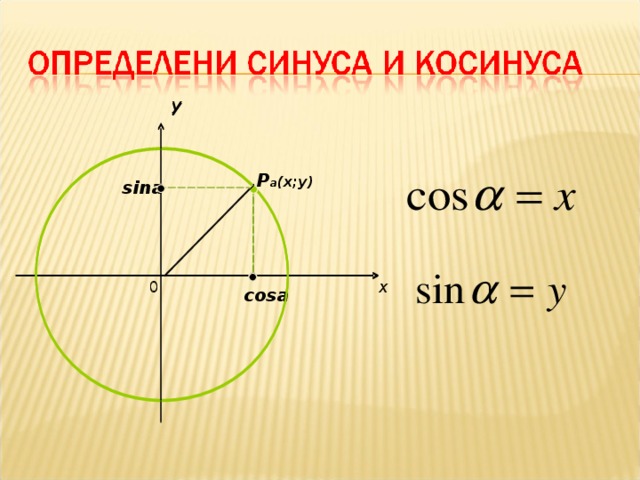
Неправильные ответы отображают графики функций , , и .
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по тригонометрии
6 Диагностические тесты 155 практических тестов Вопрос дня Карточки Learn by Concept
График синусов и косинусов с использованием Python
График синуса и косинуса с использованием Python
Знакомство с графиком синус/косинус
x = 0° (тогда как синусоида ( y = sin ( x )) начинается с амплитуды y = 0). Мы говорим, что косинусоидальная кривая — это синусоида, сдвинутая влево на 90°. График синуса и косинуса подобен волне, которая вечно колеблется между -1 и 1, в форме, которая повторяется каждые 360° (2π) единиц.
Реализация программы
В этом руководстве я использовал программное обеспечение Python 3.5.2 (64-разрядная версия) и 7 модулей: MatPlotLib 2.0.2, PyParsing 2.2.0, Python-DateUtil 2.6.1, PyTZ 2017.2, SetupTools 36.2 .0, Cycler 0.10.0 и NumPy-MKL 1.13.1, реализованные в операционной системе Windows 10 Enterprise. 7 модулей выбираются на основе совместимости версии и разрядности Python и ОС.
Исходный код
импортировать numpy как np
импортировать matplotlib.pyplot как plt
X = np.linspace(-np.pi, np.pi, 256, конечная точка = True)
C, S = np.cos(X), np.sin(X)
plt.plot(X, C, цвет = "синий", ширина линии = 1,
стиль линии = "-", метка = r'$y = cos(x)$')
plt.plot(X, S, цвет = "красный", ширина линии = 1,
стиль линии = "-", метка = r'$y = sin(x)$')
plt.legend(loc = 'вверху слева')
топор = plt.gca()
ax.spines['право'].set_color('нет')
ax.spines['top'].set_color('none')
ax.yaxis.set_ticks_position('слева')
ax.xaxis.set_ticks_position('внизу')
ax. \circ$', r'$-9\circ$'])
plt.ylim (C.min() * 1,1, C.max() * 1,1)
plt.yticks([-1, 1], [r'$-1$', r'$+1$'])
plt.show()
\circ$', r'$-9\circ$'])
plt.ylim (C.min() * 1,1, C.max() * 1,1)
plt.yticks([-1, 1], [r'$-1$', r'$+1$'])
plt.show() Самые популярные посты
Калькулятор счетов TNEB
நீங்கள் இருந்தபடியே உங்கள் மின் உபயோக கட்டணத் தொகை சுலபமாக அறிந்து கொள்ளலாம். Калькулятор счетов TNEB – 2022 (пересмотрено 09 сентября)., 2022) Только для внутреннего использования Потребляемые единицы: Единицы ( ед. ) Субсидия (≤ 100 ед. ) Диапазон единиц Стоимость единицы продукции От до ≤ 100 ₹ 4,50 × ед. ₹ 450 1 100 ₹ 0.00 101
Читать далее
Технические вопросы
1. Вас попросили просмотреть инструкции в файле .PDF, но файл не открывается. Каков типичный шаг по устранению этой проблемы? Переустановите или обновите Adobe Reader. Запросите еще одну копию файла.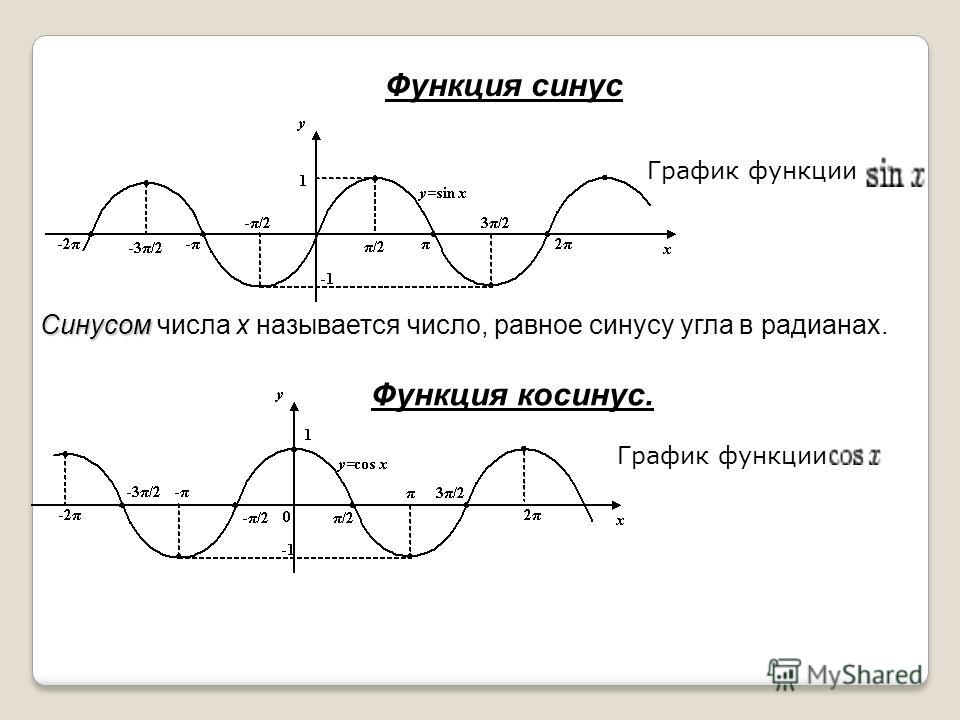 Откройте файл с помощью Блокнота. Преобразуйте файл в другой формат. 2. Для чего в Windows Vista, Windows 7 или Windows 8 используется Snipping Tool? Для создания аудиофрагментов Для обрезки фотографий, загруженных с камеры Для редактирования фильмов Для захвата и создания скриншотов 3. Приложение не отвечает; как бы вы заставили приложение закрыться? Перезагрузите компьютер. Щелкните красный значок X в приложении. Откройте диспетчер задач, выберите приложение и нажмите «Завершить задачу». Откройте «Программы и компоненты», выберите приложение и нажмите «Удалить». 4. В Windows Vista, Windows 7 и Windows 8, где недавно загруженные файлы сохраняются по умолчанию? C:\Пользователи\имя пользователя\Загрузки\ C:\Documents and Settings\имя пользователя\Загрузки\ C:\Program Files\ C:\P
Откройте файл с помощью Блокнота. Преобразуйте файл в другой формат. 2. Для чего в Windows Vista, Windows 7 или Windows 8 используется Snipping Tool? Для создания аудиофрагментов Для обрезки фотографий, загруженных с камеры Для редактирования фильмов Для захвата и создания скриншотов 3. Приложение не отвечает; как бы вы заставили приложение закрыться? Перезагрузите компьютер. Щелкните красный значок X в приложении. Откройте диспетчер задач, выберите приложение и нажмите «Завершить задачу». Откройте «Программы и компоненты», выберите приложение и нажмите «Удалить». 4. В Windows Vista, Windows 7 и Windows 8, где недавно загруженные файлы сохраняются по умолчанию? C:\Пользователи\имя пользователя\Загрузки\ C:\Documents and Settings\имя пользователя\Загрузки\ C:\Program Files\ C:\P
Читать далее
Простой серверный и клиентский чат с использованием Python
В языке Python сокет (или сетевой сокет) — это модуль, используемый для связи между двумя компьютерами. Он предоставляет два типа интерфейса для доступа к сети, а именно низкоуровневый (подключения, зависящие от платформы — пример: Telnet) и высокоуровневый (подключения, зависящие от приложения — пример: HTTP, FTP, SMTP и т.

 Фазовый угол. Сдвиг по фазе.
Фазовый угол. Сдвиг по фазе.
 )
) слева.
слева.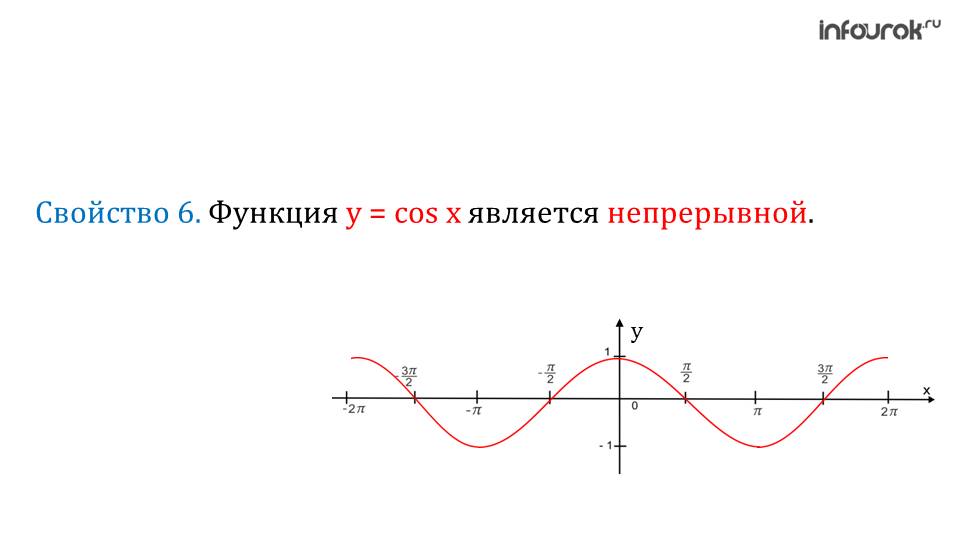 слева).
слева).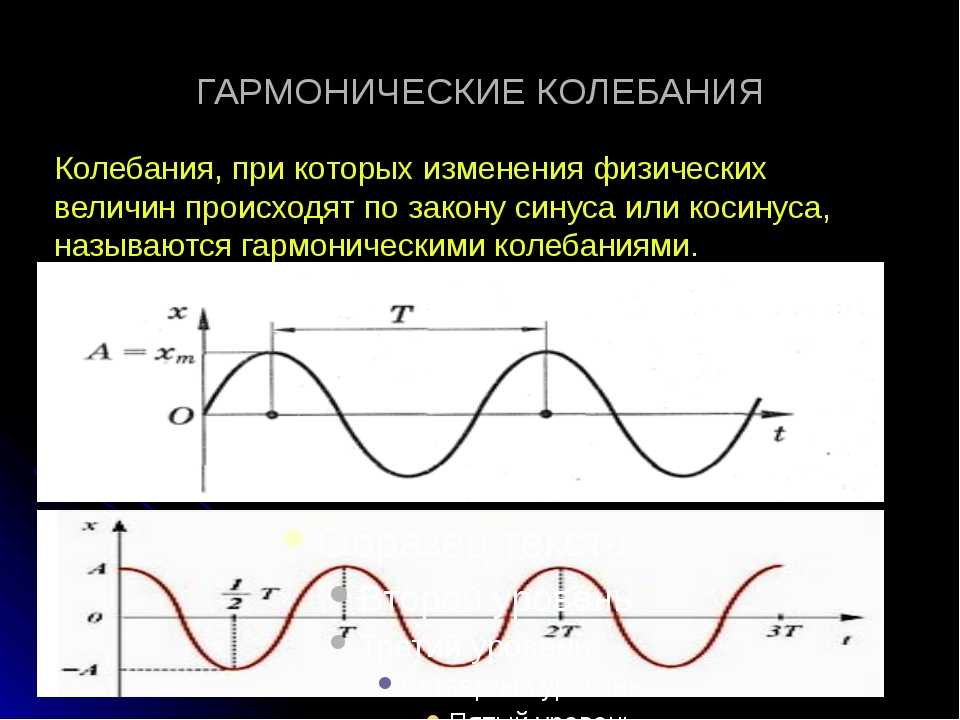 е. 233o .
е. 233o . Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.
Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.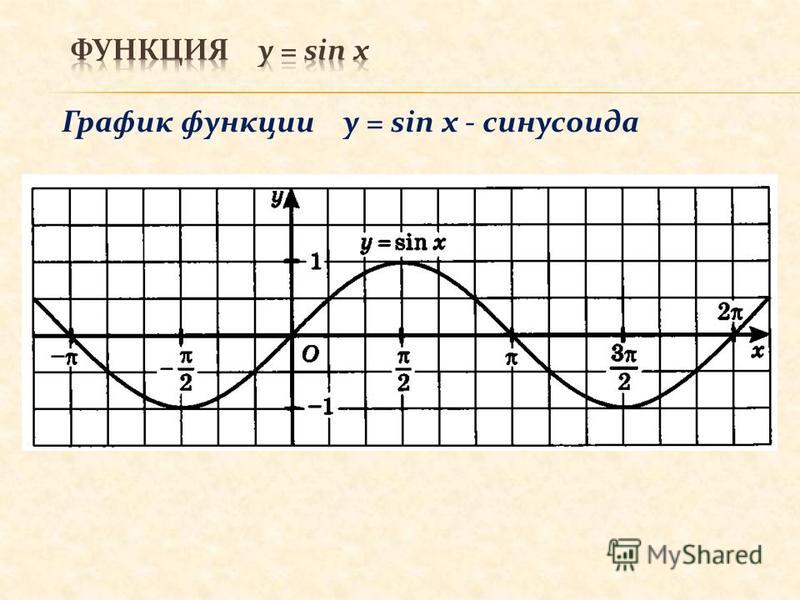 y=cosA и y=cos(1/2)A (косинусоиды).
y=cosA и y=cos(1/2)A (косинусоиды).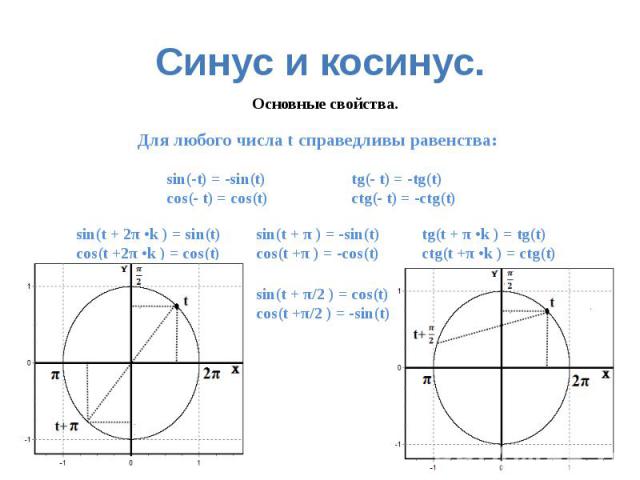 Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для y=5cos2A амплитуда равна 5, а период — 360o/2= 180o.
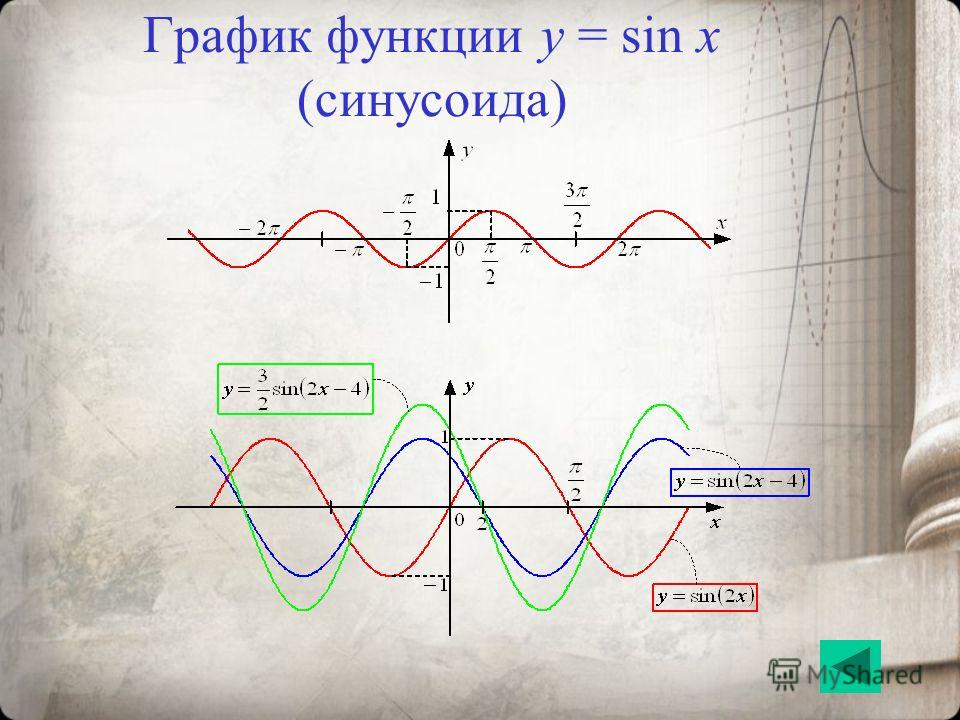
Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды — 4. Аналогично для y=5cos2A амплитуда равна 5, а период — 360o/2= 180o. Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α — сдвиг фазы относительно y=sinA и y=cosA.
Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α — сдвиг фазы относительно y=sinA и y=cosA.
 е. на π/6 радиан или на 30o
е. на π/6 радиан или на 30o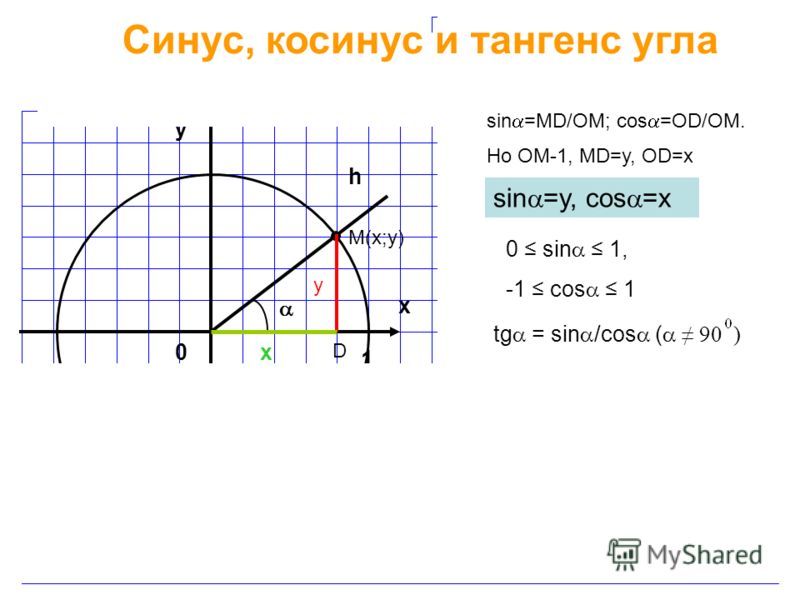
 = (0,26*180/π)o = 14,9o.
= (0,26*180/π)o = 14,9o.

 в диапазоне от 0p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы
используя радианы в качестве наших единиц.
в диапазоне от 0p до 2p с шагом p/4. Помните, что x представляет угловую меру — мы
используя радианы в качестве наших единиц.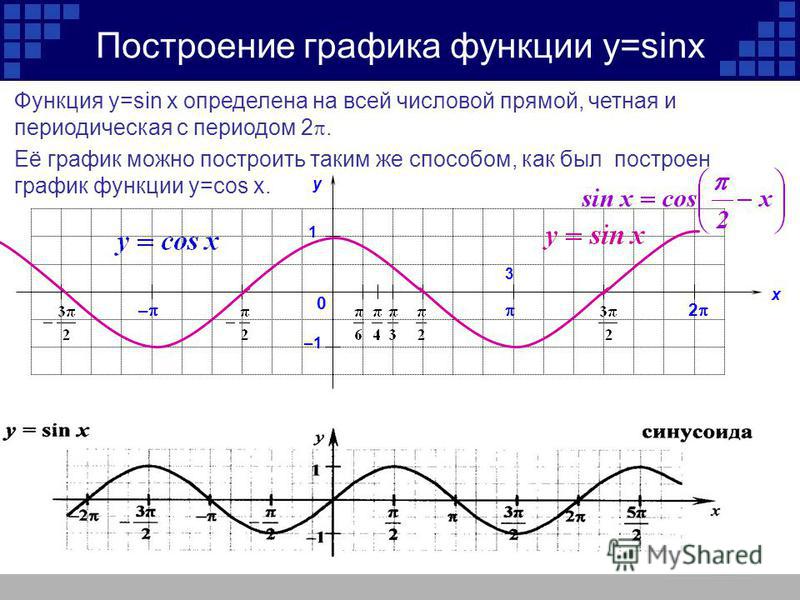 Затем выберите
3-й, 4-й и 5-й пункты и сделайте то же самое. Повторите процесс
для 5-го, 6-го и 7-го, а затем 7-го, 8-го и 9-гой точки.
Затем выберите
3-й, 4-й и 5-й пункты и сделайте то же самое. Повторите процесс
для 5-го, 6-го и 7-го, а затем 7-го, 8-го и 9-гой точки.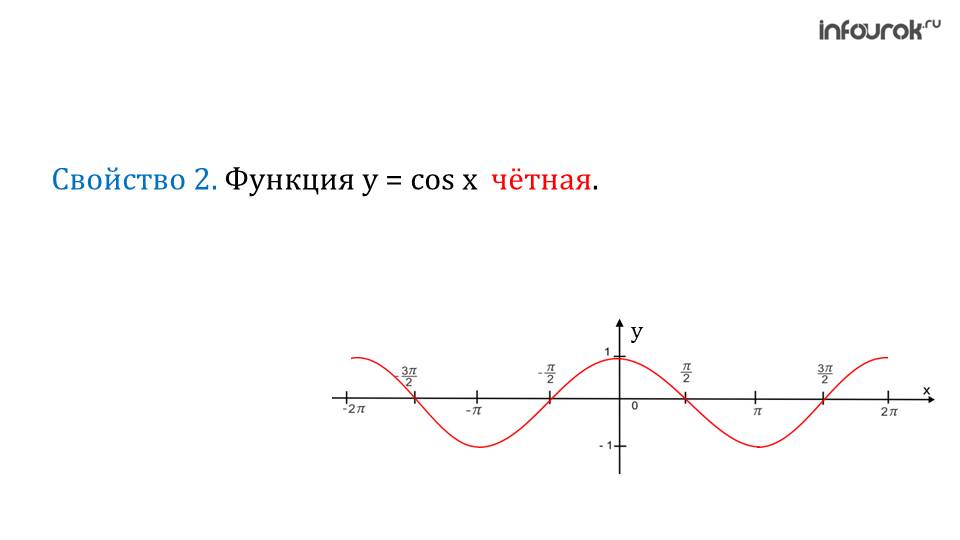 Будьте внимательны к тому, где график пересекает ось x и где
график достигает максимума и минимума.
Будьте внимательны к тому, где график пересекает ось x и где
график достигает максимума и минимума. 
 \circ$', r'$-9\circ$'])
plt.ylim (C.min() * 1,1, C.max() * 1,1)
plt.yticks([-1, 1], [r'$-1$', r'$+1$'])
plt.show()
\circ$', r'$-9\circ$'])
plt.ylim (C.min() * 1,1, C.max() * 1,1)
plt.yticks([-1, 1], [r'$-1$', r'$+1$'])
plt.show()