______
Похожие вопросы
Найдите корень уравнения корень из 5x+74=8…
Срочно решить уравнение 527346-(×-29865)=349219…
Помогите решить значение выражение 13770000:450-142*4560:213=плиз
…
Помогите пожалуйста. номер 2,3,4,5…
Срочно решить уравнение ×÷7+39816=41027…
Помогите решить задачу номер 5 ,срочноооо…
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Химия
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Қазақ тiлi
Беларуская мова
Информатика
Экономика
Музыка
Право
Французский языкНемецкий язык
МХК
ОБЖ
Психология
Косинус икс умножить на синус икс.
 Уравнение sin x = a
Уравнение sin x = aГде были рассмотрены задачи на решение прямоугольного треугольника, я пообещал изложить приём запоминания определений синуса и косинуса. Используя его, вы всегда быстро вспомните – какой катет относится к гипотенузе (прилежащий или противолежащий). Решил в «долгий ящик не откладывать», необходимый материал ниже, прошу ознакомиться 😉
Дело в том, что я не раз наблюдал, как учащиеся 10-11 классов с трудом вспоминают данные определения. Они прекрасно помнят, что катет относится к гипотенузе, а вот какой из них — забывают и путают. Цена ошибки, как вы знаете на экзамене – это потерянный бал.
Информация, которую я представлю непосредственно к математике не имеет никакого отношения. Она связана с образным мышлением, и с приёмами словесно-логической связи. Именно так, я сам, раз и на всегда запомнил данные определения. Если вы их всё же забудете, то при помощи представленных приёмов всегда легко вспомните.
Напомню определения синуса и косинуса в прямоугольном треугольнике:
Косинус острого угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе:
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Итак, какие ассоциации у вас вызывает слово косинус?
Наверное, у каждого свои 😉 Запоминайте связку:
Таким образом, у вас сразу в памяти возникнет выражение –
«… отношение ПРИЛЕЖАЩЕГО катета к гипотенузе ».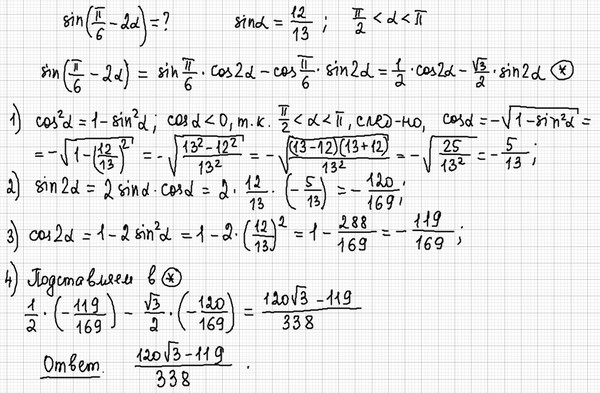
Проблема с определением косинуса решена.
Если нужно вспомнить определение синуса в прямоугольном треугольнике, то вспомнив определение косинуса, вы без труда установите, что синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе. Ведь катетов всего два, если прилежащий катет «занят» косинусом, то синусу остаётся только противолежащий.
Как быть с тангенсом и котангенсом? Путаница та же. Учащиеся знают, что это отношение катетов, но проблема вспомнить какой к которому относится – то ли противолежащий к прилежащему, то ли наоборот.
Определения:
Тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему:
Как запомнить? Есть два способа. Один так же использует словесно-логическую связь, другой – математический.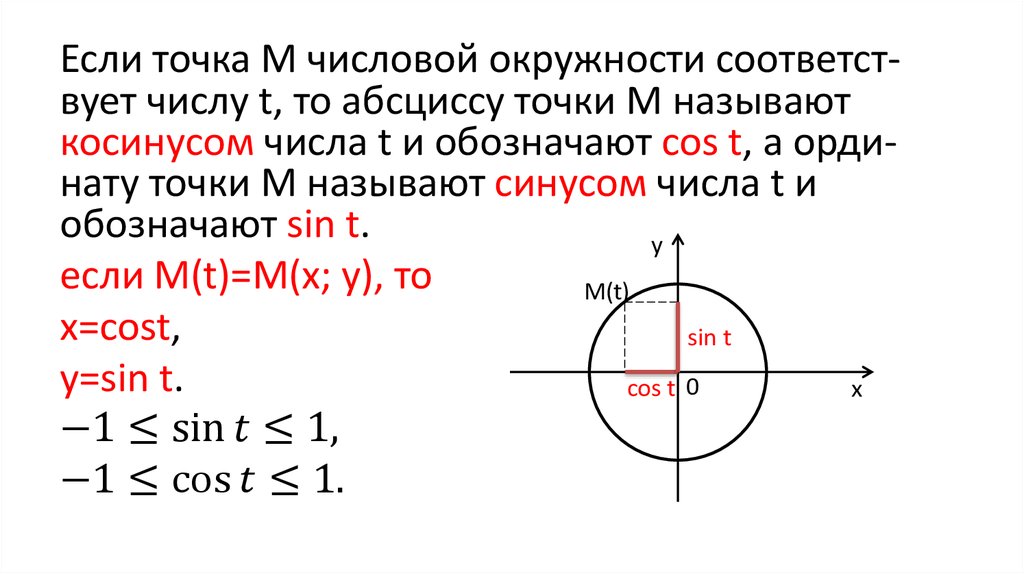
СПОСОБ МАТЕМАТИЧЕСКИЙ
Есть такое определение – тангенсом острого угла называется отношение синуса угла к его косинусу:
*Запомнив формулу, вы всегда сможете определить, что тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему.
Аналогично. Котангенсом острого угла называется отношение косинуса угла к его синусу:
Итак! Запомнив указанные формулы вы всегда сможете определить, что:
— тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему
— котангенс острого угла в прямоугольном треугольнике — это отношение прилежащего катета к противолежащему.
СПОСОБ СЛОВЕСНО-ЛОГИЧЕСКИЙ
О тангенсе. Запомните связку:
То есть если потребуется вспомнить определение тангенса, при помощи данной логической связи, вы без труда вспомните, что это
«… отношение противолежащего катета к прилежащему»
Если речь зайдёт о котангенсе, то вспомнив определение тангенса вы без труда озвучите определение котангенса –
«… отношение прилежащего катета к противолежащему»
Есть интересный приём по запоминанию тангенса и котангенса на сайте »
Математический тандем
» , посмотрите.
СПОСОБ УНИВЕРСАЛЬНЫЙ
Можно просто зазубрить. Но как показывает практика, благодаря словесно-логическим связкам человек запоминает информацию надолго, и не только математическую.
Надеюсь, материал был вам полезен.
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Значения синуса заключены в промежутке [-1; 1], т.е. -1 ≤ sin α ≤ 1. Поэтому если |а| > 1, то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 корней не имеет.
Обратимся к некоторым задачам.
Решить уравнение sin x = 1/2.
Решение.
Отметим, что sin x – это ордината точки единичной окружности, которая получена в результате поворота точки Р (1; 0) на угол х вокруг начала координат.
Ордината, равная ½, присутствует у двух точек окружности М 1 и М 2 .
Так как 1/2 = sin π/6, то точка М 1 получается из точки Р (1; 0) посредством поворота на угол х 1 = π/6, а также на углы х = π/6 + 2πk, где k = +/-1, +/-2, …
Точка М 2 получается из точки Р (1; 0) в результате поворота на угол х 2 = 5π/6, а также на углы х = 5π/6 + 2πk, где k = +/-1, +/-2, …, т.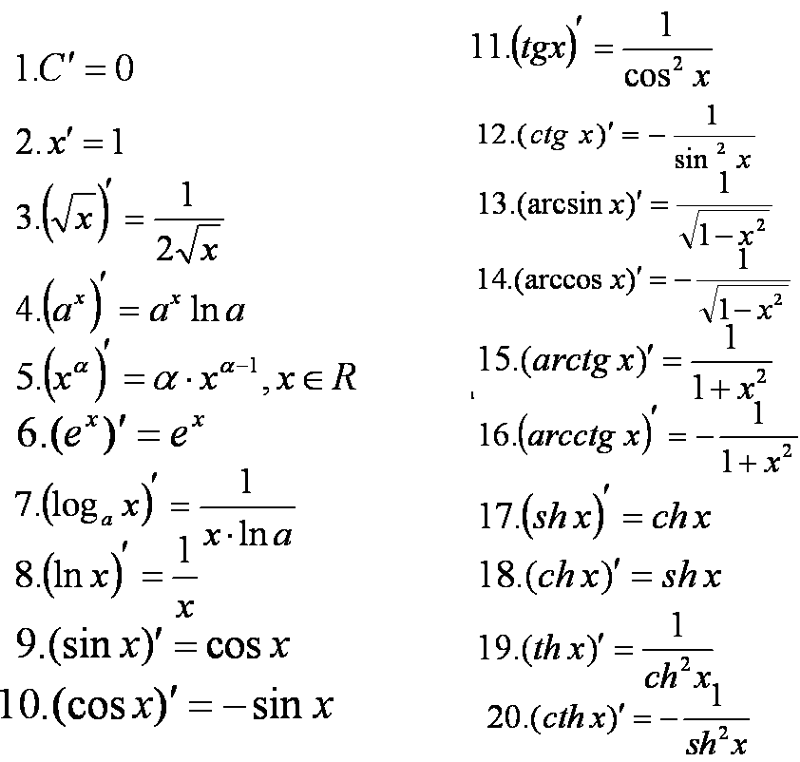
Итак, все корни уравнения sin х = 1/2 можно найти по формулам х = π/6 + 2πk, х = π – π/6 + 2πk, где k € Z.
Эти формулы могут объединиться в одну: х = (-1) n π/6 + πn, где n € Z (1).
Действительно, если n – четное число, т.е. n = 2k, то из формулы (1) получаем х = π/6 + 2πk, а если n – нечетное число, т.е. n = 2k + 1, то из формулы (1) получаем х = π – π/6 + 2πk.
Ответ. х = (-1) n π/6 + πn, где n € Z.
Решить уравнение sin x = -1/2.
Решение.
Ординату -1/2 имеют две точки единичной окружности М 1 и М 2 , где х 1 = -π/6, х 2 = -5π/6. Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.
Эти формулы мы можем объединить в одну: х = (-1) n (-π/6) + πn, n € Z (2).
Действительно, если n = 2k, то по формуле (2) получаем х = -π/6 + 2πk, а если n = 2k – 1, то по формуле (2) находим х = -5π/6 + 2πk.
Ответ. х = (-1) n (-π/6) + πn, n € Z.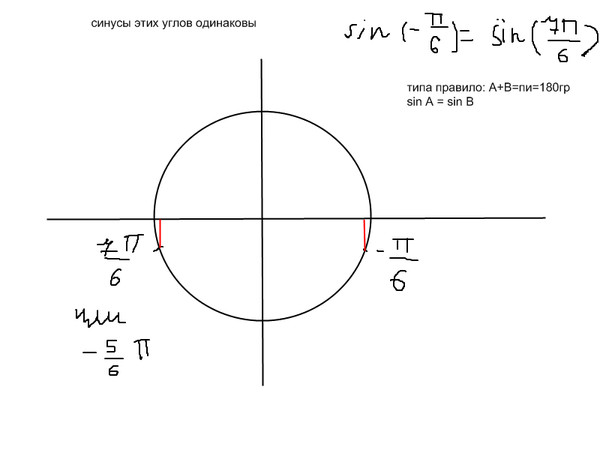
Таким образом, каждое из уравнений sin x = 1/2 и sin x = -1/2 имеет бесконечное множество корней.
На отрезке -π/2 ≤ х ≤ π/2 каждое из этих уравнений имеет только один корень:
х 1 = π/6 – корень уравнения sin x = 1/2 и х 1 = -π/6 – корень уравнения sin x = -1/2.
Число π/6 называют арксинусом числа 1/2 и записывают: arcsin 1/2 = π/6; число -π/6 называют арксинусом числа -1/2 и пишут: arcsin (-1/2) = -π/6.
Вообще уравнение sin x = а, где -1 ≤ а ≤ 1, на отрезке -π/2 ≤ х ≤ π/2 имеет лишь один корень. Если а ≥ 0, то корень заключен в промежутке ; если а
Таким образом, арксинусом числа а € [–1; 1] называется такое число а € [–π/2; π/2], синус которого равен а.
аrcsin а = α, если sin α = а и -π/2 ≤ х ≤ π/2 (3).
Например, аrcsin √2/2 = π/4, так как sin π/4 = √2/2 и – π/2 ≤ π/4 ≤ π/2;
аrcsin (-√3/2) = -π/3, так как sin (-π/3) = -√3/2 и – π/2 ≤ – π/3 ≤ π/2.
Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что корни уравнения sin х = а, где |а| ≤ 1, выражаются формулой
х = (-1) n аrcsin а + πn, n € Z (4).
Также мы можем доказать, что для любого а € [-1; 1] справедлива формула аrcsin (-а) = -аrcsin а.
Из формулы (4) следует, что корни уравнения
sin х = а при а = 0, а = 1, а = -1 можно находить по более простым формулам:
sin х = 0 х = πn, n € Z (5)
sin х = 1 х = π/2 + 2πn, n € Z (6)
sin х = -1 х = -π/2 + 2πn, n € Z (7)
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 (x , y).
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.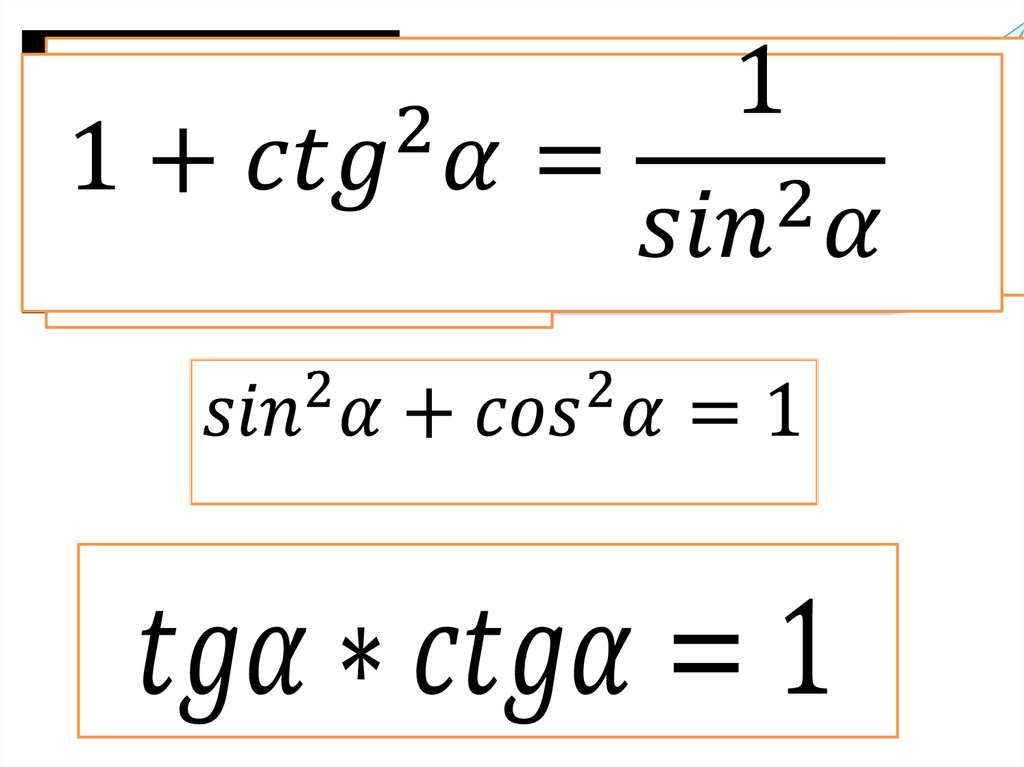
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Как найти синус?
Изучение геометрии помогает развивать мышление. Этот предмет обязательно входит в школьную подготовку. В жизнедеятельности знание этого предмета может пригодиться — например, при планировке квартиры.
Из истории
В рамках курса геометрии изучается также тригонометрия, которая исследует тригонометрические функции. В тригонометрии мы изучаем синусы, косинусы, тангенсы и котангенсы угла.
Но на данный момент начнем с самого простого — синуса. Давайте рассмотрим более детально самое первое понятие — синус угла в геометрии. Что такое синус и как его найти?
Понятие «синус угла» и синусоиды
Синус угла — это соотношение значений противоположного катета и гипотенузы прямоугольного треугольника. Это прямая тригонометрическая функция, которая на письме обозначается как «sin (x)», где (х) — угол треугольника.
На графике синус угла обозначается синусоидой со своими особенностями. Синусоида выглядит как непрерывная волнообразная линия, которая лежит в определенных рамках на плоскости координат. Функция нечетная, поэтому симметрична относительно 0 на плоскости координат (выходит из начала отсчета координат).
Область определения этой функции лежит в диапазоне от -1 до +1 на декартовой системе координат. Период функции синус угла составляет 2 Пи. Это означает, что каждые 2 Пи рисунок повторяется, и синусоида проходит полный цикл.
Уравнение синусоиды
- sin х = a / c
- где а — противолежащий к углу треугольника катет
- с — гипотенуза прямоугольного треугольника
Свойства синуса угла
- sin (x) = — sin (x). Эта особенность демонстрирует, что функция симметрична, и если отложить на системе координат в обе стороны значения х и (-х), то ординаты этих точек будут противоположными. Они будут находиться на равном расстоянии друг от друга.

- Еще одной особенностью этой функции является то, что график функции возрастает на отрезке [- П/2 + 2 Пn]; [П/2 + 2Пn], где n — любое целое число. Убывание графика синуса угла будет наблюдаться на отрезке: [ П/2 + 2 Пn]; [ 3П/2 + 2Пn].
- sin (x) > 0, когда х лежит в диапазоне (2Пn, П + 2Пn)
- (x)
Значения синусов угла определяются по специальным таблицам. Созданы такие таблицы для облегчения процесса подсчета сложных формул и уравнений. Она легка в использовании и содержит значения не только функции sin (x), но также и значения других функций.
Более того, таблица стандартных значений этих функций включена к обязательному изучению на память, как таблица умножения. Особенно это актуально для классов с физико-математическим уклоном. В таблице можно увидеть значения основных используемых в тригонометрии углов: 0, 15, 30, 45, 60, 75, 90, 120, 135, 150, 180, 270 и 360 градусов.
Также существует таблица, определяющая значения тригонометрических функций нестандартных углов. Пользуясь разными таблицами, можно без труда вычислить синус, косинус, тангенс и котангенс некоторых углов.
Пользуясь разными таблицами, можно без труда вычислить синус, косинус, тангенс и котангенс некоторых углов.
С тригонометрическими функциями составляются уравнения. Решать эти уравнения легко, если знать простые тригонометрические тождества и приведения функций, например, такие, как sin (П/2 + х) = cos (x) и другие. Для таких приведений также составлена отдельная таблица.
Как найти синус угла
Когда стоит задача найти синус угла, а по условию у нас есть только косинус, тангенс, или котангенс угла, мы легко можем вычислить нужное с помощью тригонометрических тождеств.
- sin 2 x + cos 2 x = 1
Исходя из этого уравнения, мы можем найти как синус, так и косинус, в зависимости от того, какое значение неизвестно. У нас получится тригонометрическое уравнение с одним неизвестным:
- sin 2 x = 1 — cos 2 x
- sin x = ± √ 1 — cos 2 x
- ctg 2 x + 1 = 1 / sin 2 x
Из этого уравнения можно найти значение синуса, зная значение котангенса угла. Для упрощения замените sin 2 x = у, и тогда у вас получится простое уравнение. Например, значение котангенса равно 1, тогда:
Для упрощения замените sin 2 x = у, и тогда у вас получится простое уравнение. Например, значение котангенса равно 1, тогда:
- 1 + 1 = 1/у
- 2 = 1 / у
- 2у = 1
- у = 1/2
Теперь выполняем обратную замену игрека:
- sin 2 x = ½
- sin x = 1 / √2
Поскольку мы взяли значение котангенса для стандартного угла (45 0), полученные значения можно проверить по таблице .
Если у вас дано значение тангенса, а нужно найти синус, поможет еще одно тригонометрическое тождество:
- tg x * ctg x = 1
Из этого следует, что:
- ctg x = 1 / tg x
Для того чтобы найти синус нестандартного угла, например, 240 0 , необходимо воспользоваться формулами приведения углов. Мы знаем, что π у нас соответствует 180 0 . Таким образом, мы выразим наше равенство с помощью стандартных углов путем разложения.
- 240 0 = 180 0 + 60 0
Нам необходимо найти следующее: sin (180 0 + 60 0). В тригонометрии есть формулы приведения, которые в данном случае пригодятся. Это формула:
Это формула:
- sin (π + х) = — sin (х)
Таким образом, синус угла 240 градусов равен:
- sin (180 0 + 60 0) = — sin (60 0) = — √3/2
В нашем случае, х = 60, а П, соответственно, 180 градусам. Значение (-√3/2) мы нашли по таблице значений функций стандартных углов.
Таким образом можно разложить нестандартные углы, например: 210 = 180 + 30.
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу.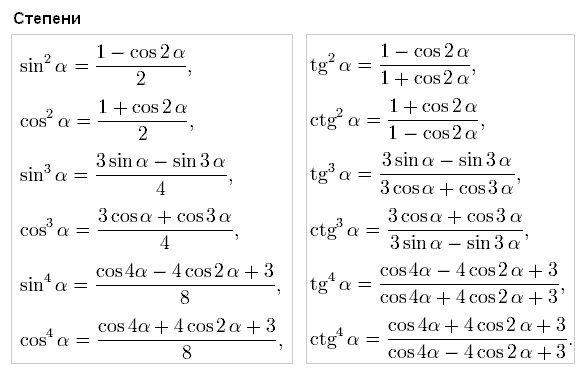 Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее.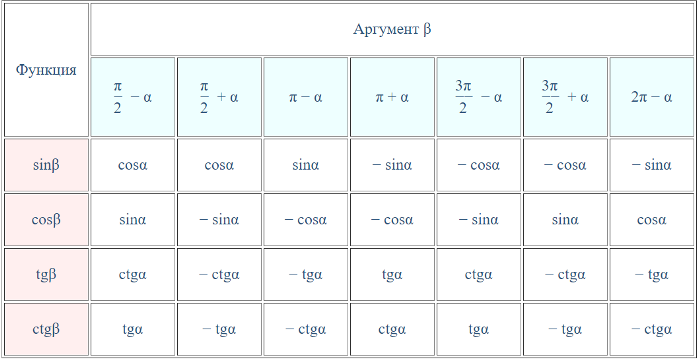 Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла.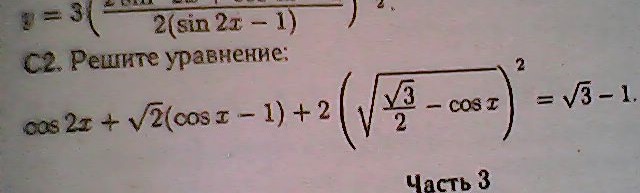 Выглядит она так.
Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.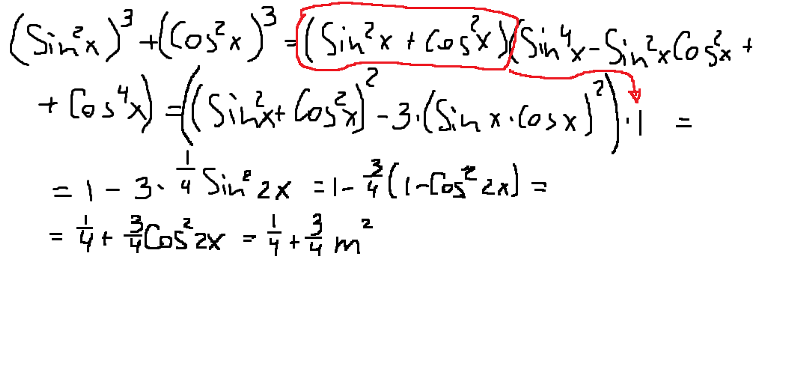 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Сколько будет \\[\\sin (x)\\] умножить на \\[\\sin (x)\\]?
Ответить
Проверено
174k+ просмотров
Подсказка: В этой задаче нам нужно решить тригонометрическую функцию, используя тригонометрическое тождество Пифагора.

