Синус косинус тангенс двойного угла: HTTP 404 Resource not found

косинус, синус и тангенс двойного угла

Формулы сложения позволяют выразить sin(2*a), cos(2*a) и tg(a) через тригонометрические функции угла a.

1. cos(a+b) = cos(a)*cos(b) — sin(a)*sin(b).

2. sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b).

3. tg(a+b) = (tg(a) +tg(b))/(1-tg(a)*tg(b)).

Положим в этих формулах a = b. В результате получим следующие тождества:

1. sin(2*a) = 2*sin(a)*cos(a).

2. cos(2*a) = (cos(a)) 2 — (sin(a)) 2 .

3. tg(2*a) = (2*tg(a))/(1-(tg(a)) 2).

Данные тождества получили название формул двойного угла. Рассмотрим несколько примеров применения формул двойного угла.

Пример 1. Найти значение sin(2*a), зная, что cos(a) = -0,8 и a — угол 3 четверти. Решение:

Сначала вычислим sin(a). Так как угол а третья четверть, то синус в третей четверти будет отрицательным:

sin(a) = -v(1-(cos(a)) 2) = -v(1-0,64) = -v0,36 = -0,6.

По формуле синуса двойного угла имеем:

sin(2*a) = 2*sin(a)*cos(a) = 2*sin(a)*cos(a) = 2*(-0,6)*(-0,8) = 0,96.

Ответ: sin(2*a) = 0,96.

Пример 2. Упростить выражение sin(a)*(cos(a)) 3 — (sin(a)) 3 *cos(a). Решение:

Вынесем за скобки sin(a)*cos(a). Получим:

sin(a)*(cos(a)) 3 — (sin(a)) 3 *cos(a) = sin(a)*cos(a)*(cos(a)) 2 — (sin(a)) 2).

Теперь воспользуемся формулами двойного угла:

= (1/2)*(2*sin(a)*cos(a))*cos(2*a) = (1/2)*sin(2*a)*sin(2*a) = (1/4)*sin(4*a).

Ответ: sin(a)*(cos(a)) 3 — (sin(a)) 3 *cos(a) = (1/4)*sin(4*a).

Используя формулы двойного угла можно получить следующие выражения

1 — cos(2*a) = 2*(sin(a)) 2 ,

1 + cos(2*a) = 2*(cos(a)) 2 .

Иногда при решении примеров бывает очень удобно использовать эти формулы. Рассмотрим следующий пример:

Пример 3. Упростить выражение (1-cos(a))/(1+cos(a)). Решение:

Применим формулы, записанные выше, для выражений (1-cos(a)) и (1+cos(a)). Для этого прежде представим угол а в виде следующего произведения 2*(a/2).

В результате преобразований получаем:

(1-cos(a))/(1+cos(a)) = (2*(sin(a/2)) 2)/(2*(cos(a/2)) 2),

Используя определение тангенса имеем:

(2*(sin(a/2)) 2)/(2*(cos(a/2)) 2)= (tg(a/2)) 2 .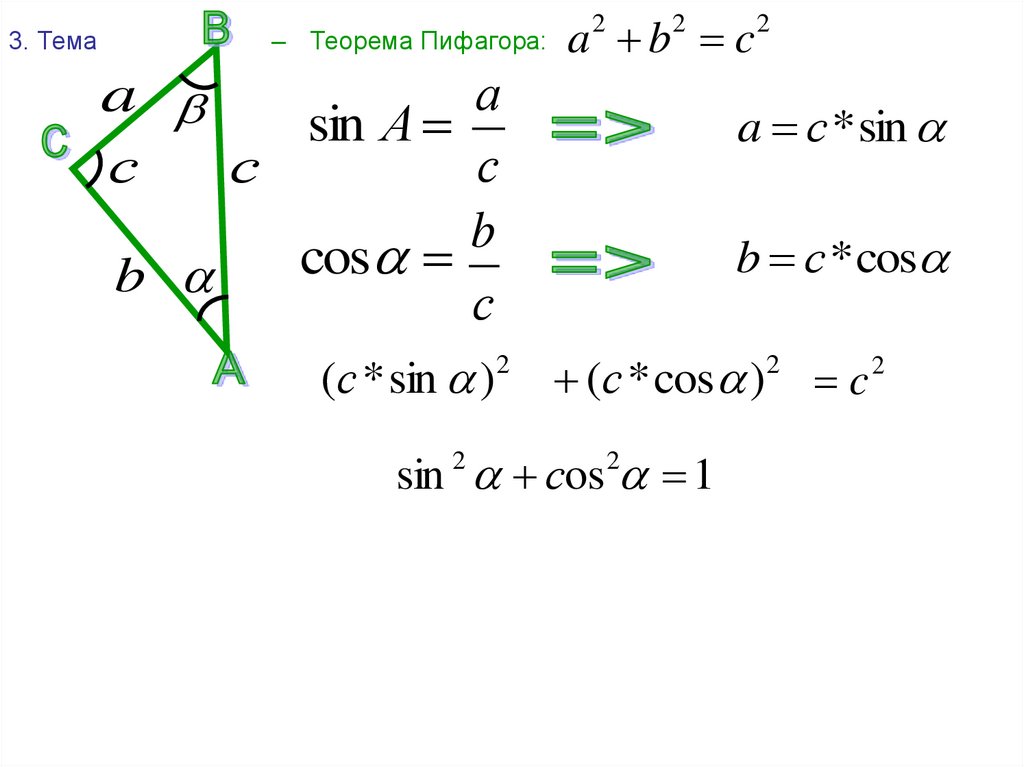

Ответ: (1-cos(a))/(1+cos(a))= (tg(a/2)) 2 .

Самые часто задаваемые вопросы

Возможно ли, изготовить печать на документе по предоставленному образцу? Ответ Да, возможно. Отправьте на наш электронный адрес скан-копию или фото хорошего качества, и мы изготовим необходимый дубликат.

Какие виды оплаты вы принимаете? Ответ Вы можете оплатить документ во время получения на руки у курьера, после того, как проверите правильность заполнения и качество исполнения диплома. Также это можно сделать в офисе почтовых компаний, предлагающих услуги наложенного платежа.
Все условия доставки и оплаты документов расписаны в разделе «Оплата и доставка». Также готовы выслушать Ваши предложения по условиям доставки и оплаты за документ.

Могу ли я быть уверена, что после оформления заказа вы не исчезнете с моими деньгами? Ответ В сфере изготовления дипломов у нас достаточно длительный опыт работы. У нас есть несколько сайтов, который постоянно обновляются. Наши специалисты работают в разных уголках страны, изготавливая свыше 10 документов день. За годы работы наши документы помогли многим людям решить проблемы трудоустройства или перейти на более высокооплачиваемую работу. Мы заработали доверие и признание среди клиентов, поэтому у нас совершенно нет причин поступать подобным образом. Тем более, что это просто невозможно сделать физически: Вы оплачиваете свой заказ в момент получения его на руки, предоплаты нет.

Могу я заказать диплом любого ВУЗа? Ответ В целом, да. Мы работаем в этой сфере почти 12 лет. За это время сформировалась практически полная база выдаваемых документов почти всех ВУЗов страны и за разные года выдачи. Все, что Вам нужно – выбрать ВУЗ, специальность, документ, и заполнить форму заказа.

Что делать при обнаружении в документе опечаток и ошибок? Ответ Получая документ у нашего курьера или в почтовой компании, мы рекомендуем тщательно проверить все детали. Если будет обнаружена опечатка, ошибка или неточность, Вы имеете право не забирать диплом, при этом нужно указать обнаруженные недочеты лично курьеру или в письменном виде, отправив письмо на электронную почту.
В кратчайшие сроки мы исправим документ и повторно отправим на указанный адрес. Разумеется, пересылка будет оплачена нашей компанией.
Чтобы избежать подобных недоразумений, перед тем, как заполнять оригинальный бланк, мы отправляем на почту заказчику макет будущего документа, для проверки и утверждения окончательного варианта. Перед отправкой документа курьером или почтой мы также делаем дополнительное фото и видео (в т. ч. в ультрафиолетовом свечении), чтобы Вы имели наглядное представление о том, что получите в итоге.

Что нужно сделать, чтобы заказать диплом в вашей компании? Ответ Для заказа документа (аттестата, диплома, академической справки и др.) необходимо заполнить онлайн-форму заказа на нашем сайте или сообщить свою электронную почту, чтобы мы выслали вам бланк анкеты, который нужно заполнить и отправить обратно нам.
Если вы не знаете, что указать в каком-либо поле формы заказа/анкеты, оставьте их незаполненными. Всю недостающую информацию мы потому уточним в телефонном режиме.

Последние отзывы

Torywild:

Купить диплом в вашей компании я решила, когда переехала в другой город, а среди своих вещей не смогла найти свой диплом. Без него меня бы не взяли на хорошую высокооплачиваемую работу. Ваш консультант меня заверила, что данная информация не разглашается, и документ никто не отличит от оригинала. Сомнения не оставляли, но пришлось рискнуть. Понравилось, что не нужна предоплата. В общем, получила диплом вовремя и меня не обманули. Спасибо!

Оксана Ивановна:

Когда у меня украли диплом, я ужасно расстроилась. Ведь меня как раз в это время уволили, а найти сейчас хорошую работу без диплома о высшем образовании практически невозможно. Благо, соседка подсказала обратиться в вашу организацию. Сначала я отнеслась с недоверием, но решила рискнуть. Позвонила менеджеру компании, объяснила свою ситуацию. И мне повезло! Все сделали оперативно, а главное, пообещали не разглашать мою тайну. Меня волновало, чтобы впоследствии не всплыл факт покупки мной диплома.

Маша Кутенкова:

Спасибо за работу! Заказывала диплом 1991 года. Когда стали поднимать документы, оказалось, что опыта мало, нужна и бумага, подтверждающая образование. У меня ее не было, причем начальница это знала, и сама порекомендовала вашу компанию (видать, сотрудник я ничего так). На документе она мне указала на детали – мол, в каких годах используют тушь или чернила, толщина подписи и т. д. Спасибо за дотошность и качество!

LenOK:

Начитавшись историй о позорных увольнениях сотрудников, у которых дипломы напечатаны на цветном принтере, я пошла подавать документы в универ. Увы, бюджета нет, денег учиться и оплачивать сессии тоже нет, пришлось рисковать. Хотя я очень рада, что познакомилась с вашей компанией. Хоть меня и не взяли на работу с вашим дипломом, ввиду несдачи практического блока, это не ваша вина. Как найду новое место – сразу к вам, без промедлений!

Jerry Terry:

Наблюдая, с каким конфузом вылетел мой коллега с работы за поддельный диплом, было страшно последовать его примеру. Если бы не кума, которая заказывала у вас – не рискнула бы. Она заверила, что здесь все гладко, и моя фамилия будет везде, где надо. На все про все у меня было 4 дня. Спасибо вам за скорость – справились за 3, еще и успели дотошно изучить способы подделки документов, но ваш бланк не подходит под подделку, значит, сойдет за оригинал.

Андрей:

Никогда бы не мог подумать, что придется покупать диплом. Дочь после школы уехала в Польшу на заработки, когда вернулась через 5 лет, захотела устроиться дизайнером одежды в местный дом моды. Без диплома никто брать ее на работу не хотел. Понимал, что, если не устроится на эту работу, опять уедет. Прошарился вечер в интернете, и на утро с документами дочери был уже в офисе. Через неделю вместе с ней забрал диплом, и она наконец-то осталась работать в своем городе на желанной должности. Не представляете, как я вам благодарен!

Вы можете заказать подробное решение вашей задачи !!!

Формулы двойного угла дают возможность выразить тригонометрические функции (синус, косинус, тангенс, котангенс) угла ` 2\alpha` через эти самые функции угла `\alpha`.

2 \alpha-1}=` `\frac 2{ \ ctg \ \alpha-tg \ \alpha}`
`ctg \ 2\alpha=\frac { \ ctg \ \alpha-tg \ \alpha}2`

Формулы для косинуса и синуса двойного угла выполняются для любого угла `\alpha`. Формулы для тангенса двойного угла справедливы для тех `\alpha`, при которых определен `tg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi4+\frac\pi2 n, \ n \in Z`. Аналогично, для котангенса они имеют место для тех `\alpha`, при которых определен `ctg \ 2\alpha`, то есть при ` \alpha\ne\frac\pi2 n, \ n \in Z`.

Доказательство формул двойного угла

Все формулы двойного угла выводятся из формул сумы и разности углов тригонометрических функций.

Возьмем две формулы, для сумы углов синуса и косинуса:

`sin(\alpha+\beta)=` `sin \ \alpha\ cos \ \beta+cos \ \alpha\ sin \ \beta` и `cos(\alpha+\beta)=` `cos \ \alpha\ cos \ \beta-sin \ \alpha\ sin \ \beta`. Возьмем `\beta=\alpha`, тогда `sin(\alpha+\alpha)=` `sin \ \alpha\ cos \ \alpha+cos \ \alpha\ sin \ \alpha=2 \ sin \ \alpha \ cos \ \alpha`, аналогично `cos(\alpha+\alpha)=` `cos \ \alpha\ cos \ \alpha-sin \ \alpha\ sin \ \alpha=cos^2 \alpha-sin^2 \alpha`, что и доказывает формулы двойного угла для синуса и косинуса.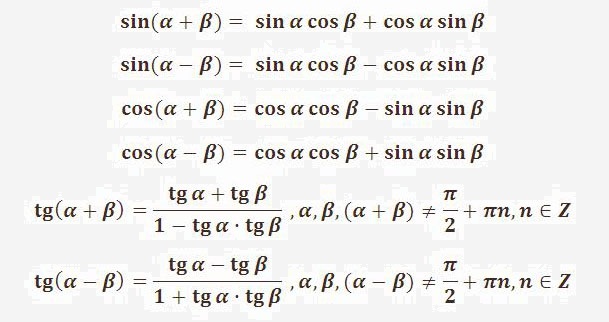

2 \alpha-1}`.

Для доказательства формул угла ` 4\alpha` можно представить его как ` 2 \cdot 2\alpha` и примерить два раза формулы двойного угла.

Для вывода аналогичных равенств для угла ` 5\alpha` можно записать его, как ` 3\alpha + 2\alpha` и применить тождества суммы и разности углов и двойного и тройного угла.

Аналогично выводятся все формулы для других кратных углов, то нужны они на практике крайне редко.

В тригонометрии многие формулы легче вывести, чем вызубрить. Косинус двойного угла — замечательная формула! Она позволяет получить формулы понижения степени и формулы половинного угла.

Итак, нам нужны косинус двойного угла и тригонометрическая единица:

Они даже похожи: в формуле косинуса двойного угла — разность квадратов косинуса и синуса, а в тригонометрической единице — их сумма. Если из тригонометрической единицы выразить косинус:

и подставить его в косинус двойного угла, то получим:

Это — еще одна формула косинуса двойного угла:

Эта формула — ключ к получению формулы понижения степени:

Итак, формула понижения степени синуса:

Если в ней угол альфа заменить на половинный угол альфа пополам, а двойной угол два альфа — на угол альфа, то получим формулу половинного угла для синуса:

Теперь из тригонометрической единицы выразим синус:

Подставим это выражение в формулу косинуса двойного угла:

Получили еще одну формулу косинуса двойного угла:

Эта формула — ключ к нахождению формулы понижения степени косинуса и половинного угла для косинуса.

Таким образом, формула понижения степени косинуса:

Если в ней заменить α на α/2, а 2α — на α, то получим формулу половинного аргумента для косинуса:

Так как тангенс — отношение синуса к косинусу то формула для тангенса:

Котангенс — отношение косинуса к синусу. Поэтому формула для котангенса:

Конечно, в процессе упрощения тригонометрических выражений формулы половинного угла или понижения степени нет смысла каждый раз выводить. Гораздо проще перед собой положить листик с формулами. И упрощение продвинется быстрее, и зрительная память включится на запоминание.

Но несколько раз вывести эти формулы все же стоит. Тогда вы будете абсолютно уверены в том, что на экзамене, когда нет возможности воспользоваться шпаргалкой, вы без труда их получите, если возникнет необходимость.

Формулы двойного угласлужат для выражения синусов, косинусов, тангенсов, котангенсов угла со значением 2 α , используя тригонометрические функции угла α . Данная статья познакомит со всеми формулами двойного угла с доказательствами. Будут рассмотрены примеры применения формул. В заключительной части будут показаны формулы тройного, четверного углов.

Yandex.RTB R-A-339285-1

Список формул двойного угла

Для преобразования формул двойного угла следует помнить о том, что углы в тригонометрии имеют вид n α записи, где n является натуральным числом, значение выражение записывается без скобок. Таким образом, считается, что запись sin n α имеет то же значение, что и sin (n α) . При обозначении sin n α имеем аналогичную запись (sin α) n . Использование записи применимо для всех тригонометрических функций со степенями n .

Ниже приведены формулы двойного угла:

sin 2 α = 2 · sin α · cos α cos 2 α = cos 2 α — sin 2 α , cos 2 α = 1 — 2 · sin 2 α , cos 2 α = 2 · cos 2 α — 1 t g 2 α = 2 · t g α 1 — t g 2 α c t g 2 α — c t g 2 α — 1 2 · c t g α

Отметим, что данные формулы sin и cos применимы с любым значением угла α . Формула тангенса двойного угла справедлива при любом значении α , где t g 2 α имеет смысл, то есть α ≠ π 4 + π 2 · z , z является любым целым числом. Котангенс двойного угла существует при любом α , где c t g 2 α определен на α ≠ π 2 · z .

Косинус двойного угла имеет тройную запись двойного угла. Все они являются применимыми.

Доказательство формул двойного угла

Доказательство формул берет начало из формул сложения. Применим формулы синуса суммы:

sin (α + β) = sin α · cos β + cos α · sin β и косинуса суммы cos (α + β) = cos α · cos β — sin α · sin β . Предположим, что β = α , тогда получим, что

sin (α + α) = sin α · cos α + cos α · sin α = 2 · sin α · cos α и cos (α + α) = cos α · cos α — sin α · sin α = cos 2 α — sin 2 α

Таким образом доказываются формулы синуса и косинуса двойного угла sin 2 α = 2 · sin α · cos α и cos 2 α = cos 2 α — sin 2 α .

Остальные формулы cos 2 α = 1 — 2 · sin 2 α и cos 2 α = 2 · cos 2 α — 1 приводят к виду cos 2 α = cos 2 α = cos 2 α — sin 2 α , при замене 1 на сумму квадратов по основному тождеству sin 2 α + cos 2 α = 1 . Получаем, что sin 2 α + cos 2 α = 1 . Так 1 — 2 · sin 2 α = sin 2 α + cos 2 α — 2 · sin 2 α = cos 2 α — sin 2 α и 2 · cos 2 α — 1 = 2 · cos 2 α — (sin 2 α + cos 2 α) = cos 2 α — sin 2 α .

Для доказательства формул двойного угла тангенса и котангенса применим равенства t g 2 α = sin 2 α cos 2 α и c t g 2 α = cos 2 α sin 2 α . После преобразования получим, что t g 2 α = sin 2 α cos 2 α = 2 · sin α · cos α cos 2 α — sin 2 α и c t g 2 α = cos 2 α sin 2 α = cos 2 α — sin 2 α 2 · sin α · cos α . Разделим выражение на cos 2 α , где cos 2 α ≠ 0 с любым значением α , когда t g α определен. Другое выражение поделим на sin 2 α , где sin 2 α ≠ 0 с любыми значениями α , когда c t g 2 α имеет смысл. Чтобы доказать формулу двойного угла для тангенса и котангенса, подставим и получим:

Формулы сложения, формулы двойного угла

Используй поиск, чтобы найти научные материалы и собрать список литературы

База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны

Содержание статьи

1. Формулы сложения

2. Синус, косинус и тангенс двойного угла

3. Решение прямоугольных треугольников.

Формулы сложения

Основные формулы сложения представляют собой тригонометрические функции суммы и разности углов:

Синус, косинус и тангенс двойного угла

Синус, косинус и тангенс двойного угла представляют собой частный случай тригонометрических функций кратных углов, а также тригонометрических функций половинных углов.

Формулы кратных углов:

Формулы половинных углов:

Замечание

В этих формулах перед знаком радикала должен быть поставлен знак $»+»$ или $»-«$ в зависимости от того, в какой четверти находится угол $\frac{\alpha }{2} $.

Решение прямоугольных треугольников.

Задачи на решение прямоугольных треугольников распределяются на две основные группы:

1. заданы две стороны прямоугольного треугольника; требуется определить третью сторону и оба острых угла;

2. заданы сторона и острый угол прямоугольного треугольника; требуется определить две остальные стороны и второй острый угол. \circ -A$. Для вычисления значения тангенса угла $B$ используем калькулятор Windows. Вычисление второго катета: $b=a\cdot tgB$. Для вычисления значения синуса угла $A$ используем калькулятор Windows. Вычисление гипотенузы: $c=\frac{a}{\sin A} $.

   Замечание 1

   Для решения представленных задач могут быть использованы и другие цепочки действий. Так, например, в задаче 4 для вычисления гипотенузы можно использовать теорему Пифагора. И т.п.

   Сообщество экспертов Автор24

   Автор этой статьи Дата последнего обновления статьи: 02.03.2022

   Выполнение любых типов работ по математике

   Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами

   Подбор готовых материалов по теме

   Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы

   Использование тождества двойного угла для косинуса

   Тождества для углов, вдвое превышающих один из общих углов (двойные углы), часто используются в триггерах. Эти тождества позволяют вам иметь дело с большим углом в терминах меньшего и более управляемого.

   Функция двойного угла записывается, например, как sin 2θ, cos 2α или tan 2 x , где 2θ, 2α и 2 x — меры угла, и предполагается, что вы имеете в виду sin (2θ), cos(2α) или tan(2 х ). Поскольку тангенс равен отношению синуса и косинуса, его идентичность исходит из тождества их двойного угла.

   Тождества двойного угла находят функцию для удвоенного угла θ. Обратите внимание, что функция косинуса имеет три разные версии идентичности двойного угла.

   Нахождение косинуса удвоенного угла проще, чем нахождение других значений функции, потому что у вас есть три версии на выбор. Вы делаете свой выбор в зависимости от того, какая информация доступна и что проще всего вычислить. Чтобы показать вам, откуда берется первое из тождеств двойного угла для косинуса, в этом примере используется тождество суммы углов для косинуса. Поскольку два угла равны, вы можете заменить β на α, поэтому cos (α + β) = cosα cosβ – sinβ становится равным

   Чтобы получить вторую версию, используйте первое тождество Пифагора, sin ² + cos ² = 1. Решив sin ² , вы получите sin ² = 1 – cos ² . Подставив этот результат обратно в тождество двойного угла для косинуса и упростив, вы получите

   Чтобы найти последнюю версию тождества двойного угла для косинуса, решите первое тождество Пифагора для cos ² α, что даст вам cos ² α = 1 – sin ² α. Затем подставьте этот результат в первое тождество суммы углов для косинуса:

   Самым большим преимуществом наличия трех разных тождеств для косинуса двойного угла является то, что вы можете найти косинус только с одним другим значением функции. С другой стороны, тождества суммы и разности для синуса и косинуса, а также тождество двойного угла для синуса включают как синус, так и косинус углов.

   Вот пример, демонстрирующий это преимущество. Найдите cos 2α; угол α находится в четвертом квадранте, а sinα = –0,45.

   1. Выберите подходящую двухугольную идентичность.

      Поскольку значение синуса известно, используйте cos 2α = 1 – 2sin ² α.

   2. Вставьте данное значение в формулу и упростите.

   Полученный косинус положителен. Косинус положителен в первом и четвертом квадрантах, так как же узнать, в каком из этих двух квадрантов лежит конечная сторона этого двойного угла? Вернитесь к началу задачи — вы знаете, что исходный угол находится в четвертом квадранте. Угол в четвертом квадранте составляет от 270 до 360 градусов. Если вы удвоите эти числа (потому что вы работаете с двойным углом), вы получите 540 градусов и 720 градусов. Углы между этими двумя значениями лежат в третьем и четвертом квадрантах. Косинус положителен в четвертом квадранте, поэтому этот двойной угол лежит в четвертом квадранте.

   Эту статью можно найти в категории:

   • Тригонометрия ,

   тригонометрия — Использование единичного круга для доказательства формул двойного угла для синуса и косинуса?

   спросил 10 лет, 6 месяцев назад

   Изменено 6 лет, 10 месяцев назад

   Просмотрено 14 тысяч раз

   $\begingroup$

   Как использовать единичный круг для доказательства формул двойного угла для синуса и косинуса?

   • тригонометрия

   $\endgroup$

   4

   $\begingroup$

   Посмотрите на эту цифру:

   $\endgroup$

   4

   $\begingroup$

   Вот один из вариантов. Допустим, мы хотим найти $\sin 2\theta$ и $\cos 2\theta$. Нарисуйте единичную окружность в обычной системе координат $x$-$y$, а также введите новую систему координат $x’$-$y’$, повернутую на $\theta$ по часовой стрелке на вокруг начала координат. Важно, что единичный круг в системе $xy$ и в системе $x’y’$ один и тот же:

   Соотношение между двумя системами координат равно $$ x’ = x\cos\theta — y\sin\theta \qquad y’=x\sin\theta + y\cos\theta $$ 92 \qquad \sin2\theta = \cos(\theta)\sin(\theta) + \sin(\theta)\cos(\theta)$$

   $\endgroup$

   3

   $\begingroup$

   По сути, это доказательство Кристиана Блаттера с некоторыми незначительными отличиями, но мне нравится интерпретация области, которую оно использует, и историческая связь. Это также немного объясняет связь доказательства Кристиана Блаттера с кругом. Эта версия дает формулу двойного угла только для $\sin$.

   Прямоугольный треугольник с гипотенузой $1$ и углом $\theta$ имеет площадь $\frac{1}{2}\cos\theta\sin\theta.$ Четыре таких треугольника вместе имеют площадь $2\cos\theta\sin\ theta.$ Расположите четыре прямоугольных треугольника так, чтобы получилась фигура в форме воздушного змея.

   Две диагонали фигурки в виде воздушного змея (обозначены сплошными линиями) перпендикулярны, а площадь фигуры равна половине произведения их длин. Но одна диагональ имеет длину $1$, а другая — $2\sin2\theta$. Формула двойного угла для $\sin$ выглядит следующим образом.

   Мой интерес к этому доказательству отчасти исторический. Впишите правильный $n$-угольник в единичную окружность. Пусть $\ell_n$ — длина стороны $n$-угольника. Этот $n$-угольник можно разбить на $n$ равнобедренных треугольников с длинами сторон $1,$ $1,$ $\ell_n.$

   Теперь составьте из $n$ воздушных змеев правильный $2n$-угольник. .

   Диагонали этих воздушных змеев равны $1$ и $\ell_n$.

   No related posts.