Вопросы для проверки
Формулы тройных углов
Обратные тригонометрические функции
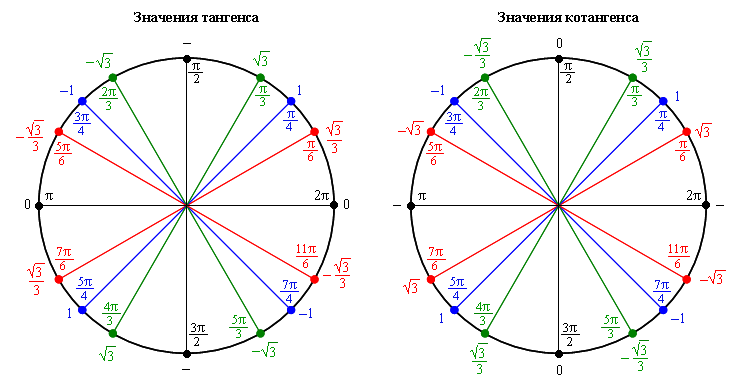
Некоторые значения тригонометрических функций
таблица 3
Аргумент | Функция | |||
sin | cos | tg | ctg | |
15 | ||||
18 | ||||
36 | ||||
54 | ||||
72 | ||||
| 75 | ||||
1.
Что
такое числовая окружность?
2. Перечислите признаки числовой окружности.
3. Какая величина принимается за единицу измерения при градусном измерении углов?
4. Что такое радиан?
5. По каким формулам переводят градусную меру угла в радианную и наоборот?
6. Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.
7. Почему ошибочна запись = 180?
8. При каком условии длина дуги равна ее радианной мере?
9. Какой угол называется углом поворота?
10. Какой угол поворота называется положительным? отрицательным?
11. Задайте формулой общий вид углов поворота.
12. Сформулируйте правило «полного оборота».
13. Какие функции называются тригонометрическими?
14. Дайте определение функции синус; косинус; тангенс; котангенс.
15. При каких углах не определен тангенс? котангенс?
16.
Назовите
значения тригонометрических функций
углов 30,
45,
60.
17. Какие значения может принимать синус? косинус? тангенс? котангенс?
18. Определите знаки тригонометрических функций в зависимости от того, в какой четверти находится аргумент.
19. Какие из тригонометрических функций являются четными, какие – нечетными?
20. Чему равен период синуса? косинуса? тангенса? котангенса?
1. Числовая прямая
Алгебраические функции — это функции, заданные аналитическим выражением, в записи которого используются алгебраические операции над числами и переменной (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня).
у = 2х + 3,
Числовая прямая — это математическая модель для представления чисел, в которой каждое число соответствует точке на прямой, причем расстояние от точки до начала отсчета равно модулю числа:
Признаки числовой прямой:
1) начало отсчета;
2) единичный отрезок;
3) положительное
направление (стрелка).
11. Простейшие тригонометрические неравенства
Чтобы решить простейшее тригонометрическое неравенство нужно:
1. Провести прямую к линии соответствующей функции.
2. Выделить дугу, на которой лежат решения неравенства.
3. Найти концы этой дуги, помня, что обход совершается против часовой стрелки от меньшего числа к большему.
4. Прибавить к концам интервала числа, кратные периоду функции.
Решить неравенство
Решение.
Все решения, удовлетворяющие заданному неравенству, лежат на дуге l. Найдем ее концы:
С учетом периода синуса, запишем ответ:
.
Ответ:
10. Простейшие тригонометрические уравнения
Если правая часть уравнения — отрицательное число, то следует воспользоваться свойствами соответствующих обратных тригонометрических функций, тогда:
При а = 1; 0; –1 решение уравнения записывается в виде (n Z):
что это такое в алгебре, как найти, вывод уравнения, формула и примеры
Числовая окружность — что это такое в алгебре
Функции, описывающие различные процессы, можно разделить на алгебраические и не алгебраические.
Для первых зависимость значения функции от значения ее аргумента изображается аналитически — в виде формулы.
Рассмотрим случай, который можно описать с помощью не алгебраической функции.
Автомобиль едет по кольцевой дороге. Где будет находиться автомобиль спустя заданное время? Как определить конечную точку пути, если известна величина его перемещения?
В приведенном примере параметры движения удобно задавать в виде точек на окружности, при этом радиус окружности будет равен радиусу кольцевой дороги. Тогда точке, определяющей положение автомобиля в данный момент времени, будет соответствовать некоторое действительное число на окружности. По заданной точке и числу можно определить параметры движения.
ОпределениеЧисловой окружностью называют окружность, у которой установлено соответствие между точками на окружности и действительными числами.
Числовую окружность можно считать математической моделью функций, используемых в тригонометрии (синус, косинус, тангенс, котангенс).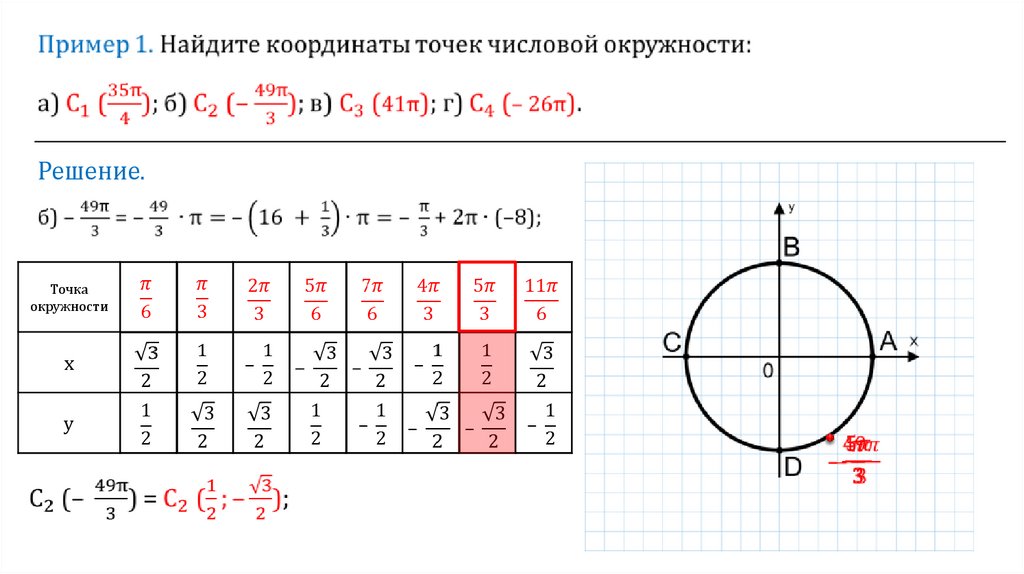
Общий вид и длина числовой окружности
Любую окружность можно использовать как числовую, при условии соблюдения следующих основных правил:
- выбрано начало отсчета;
- определено положительное направление отсчета;
- задан масштаб.
Часто в качестве числовой берут окружность с радиусом, равным 1. Такую окружность называют единичной.
Вычислим длину единичной окружности по формуле: L=2πR. Поскольку R=1, получим: L=2π. Разделим круг на четыре части, которые образуют четыре дуги:AB⏜,BC⏜, CD⏜, DA⏜. За положительное направление примем направление против часовой стрелки, то есть дугаAB⏜ образует первую четверть,AB⏜ — вторую, AB⏜ — третью, AB⏜ — четвертую.
Точки A, B, C, D принято не включать в границы четвертей. Дуги AB⏜, BC⏜, CD⏜, DA⏜ аналогичны интервалам на числовой прямой.
Главное свойство числовой окружности
Если рассматривать числовую прямую, то каждой точке на прямой соответствует единственное действительное число.
Однако это утверждение не справедливо в случае числовой окружности.
Возьмем некоторое действительное число t, на единичной окружности ему будет соответствовать точка N. Теперь найдем точку, которая задается числом t+2π. Для этого от точки N отложим дугу, равную 2π. Так как длина единичной окружности равна 2π, то заданная дуга — это один полный оборот. Получили, что числу t+2π соответствует та же точка N, как и числам t+4π , t+6π, t-8π и т. д.
Отсюда главное свойство числовой окружности:
На числовой окружности действительному числу t соответствует единственная точка N на окружности. Точке N соответствует бесконечное множество действительных точек вида: t+2πk, k∈Z,где Z — множество целых чисел.
Вывод уравнения, как найти координаты
Расположим единичную окружность на координатной плоскости так, чтобы центр круга совпадал с точкой начала координат, радиус окружности примем за масштабную единицу.
Тогда любая произвольная точка на окружности будет иметь координаты: N (xN, yN).
Уравнение окружности имеет вид: x2+y2=R2. При R=1, получим уравнение единичной окружности:
Формулаx2+y2=1
ПримечаниеИз определения и формулы единичной окружности можно сделать вывод, что координаты любой точки на окружности находятся в промежутках -1≤ x≤ 1 и -1≤ y≤ 1.
На конкретном примере кратко рассмотрим алгоритм нахождения координат точки.
Пример 1Пусть на единичной окружности задана точка F, которой соответствует число π4 .
Опустим перпендикуляр FL из точки F на ось абсцисс. Дуга AF⏜ равна половине дуги первой четверти, а значит, угол ∠LOF=45°. Тогда треугольник △LOF — равнобедренный, так как углы при стороне OF равны между собой. Катет OL равен координате x, а катет FL — координате y. Составим систему:
x=yx2+y2=1
При решении системы уравнений необходимо учитывать, что точка F находится в первой четверти, то есть x>0 и y>0.
Решением системы и координатами точки F будут: x=22иy=22.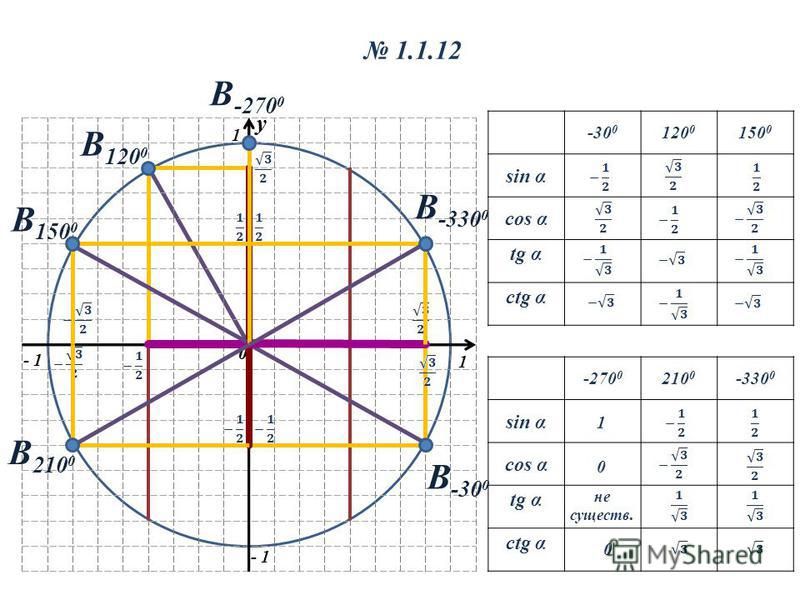
Аналогичным образом через прямоугольные треугольники находятся координаты любой точки на числовой окружности.
Для удобства расчетов сделаем два макета единичной окружности. Для первого макета разделим каждую четверть пополам и запишем координаты получившихся точек.
Для второго макета будем делить каждую четверть на три части. Аналогично в таблице укажем координаты каждой из точек.
Примеры решения задач для решения в 10 классе
Пример 2Не пользуясь представленной таблицей значений, найти координаты точки L, которой на числовой окружности соответствует число 5π6.
Решение.
Опустим из точки L перпендикуляр LK на ось абсцисс и построим прямоугольный треугольник △OLK.
Угол, который образует гипотенуза OL с осью абсцисс, равен 150°.
Тогда угол ∠LOK будет равен 30°.
Из определения синуса:sin(30°)=LKOL.
Учитывая, что катет LK равен координате y, а гипотенуза OL — радиусу на единичной окружности, составим и решим систему уравнений:
sin(30°)=y1x2+y2=1→ y=12×2+14=1→y=12x=±32
Необходимо выбрать знаки для найденных координат.
Точка L находится во второй четверти, значит x<0 и y>0. Тогда координатами точки L будут являться:x=-32,y=12.
Ответ:L (-32;12).
Пример 3Найти точки на единичной окружности, которые соответствуют абсциссе -12.
Решение.
На координатной плоскости проведем прямую x=-12. Прямая пересекает окружность в двух точках L и L_1.
По таблице определим, что точке L соответствует число 2π3, а точке L_1 — число 4π3.
Воспользуемся основным свойством числовой окружности и запишем две серии решений:
2π3+2πk,4π3+2πk, k∈Z.
Ответ: 2π3+2πk,4π3+2πk, k∈Z.
Пример 4На единичной окружности отмечена точка L, которой соответствует число 22π18.
Известно, что синус ∠BOL равен 0,766. Найти координату x заданной точки.
Решение.
Из точки L опустим перпендикуляр LM на ось абсцисс. Значение координаты x равно длине катета OM прямоугольного треугольника △LOM.
По определению косинуса угла: cos(∠MOL)=OMOL.
Значение косинуса получим из формулы приведения:sin(π2+α)=cosα .