| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | cos(pi/2) | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | ||
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |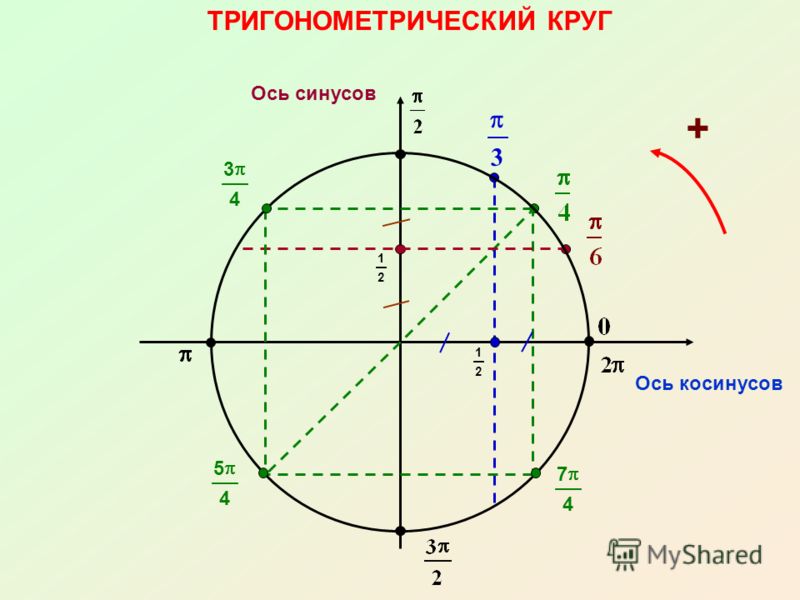
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |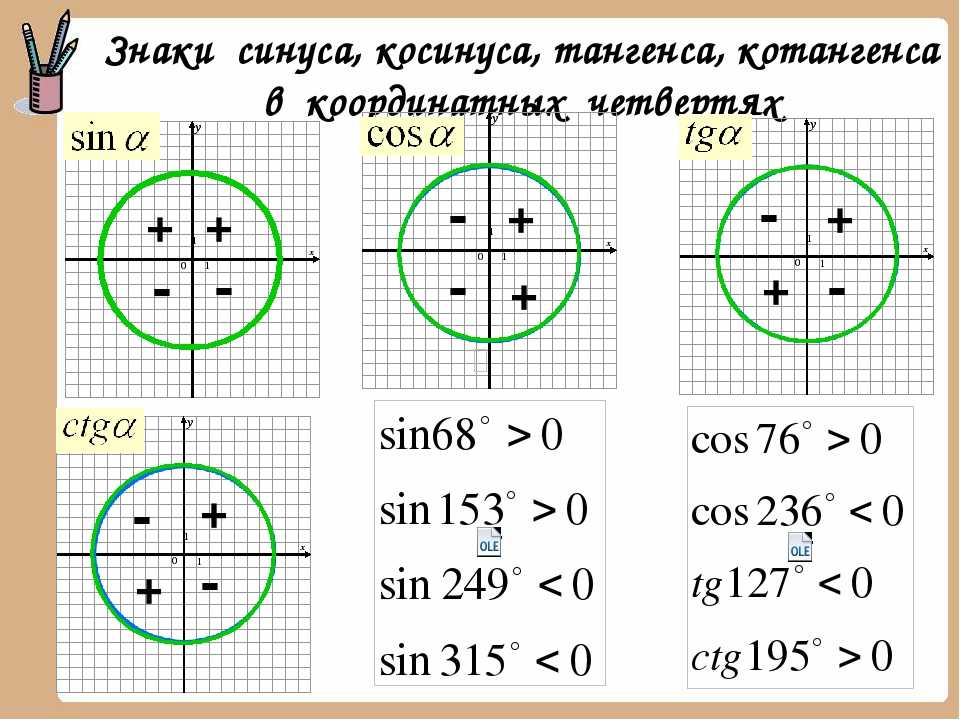
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | sin((4pi)/3) | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |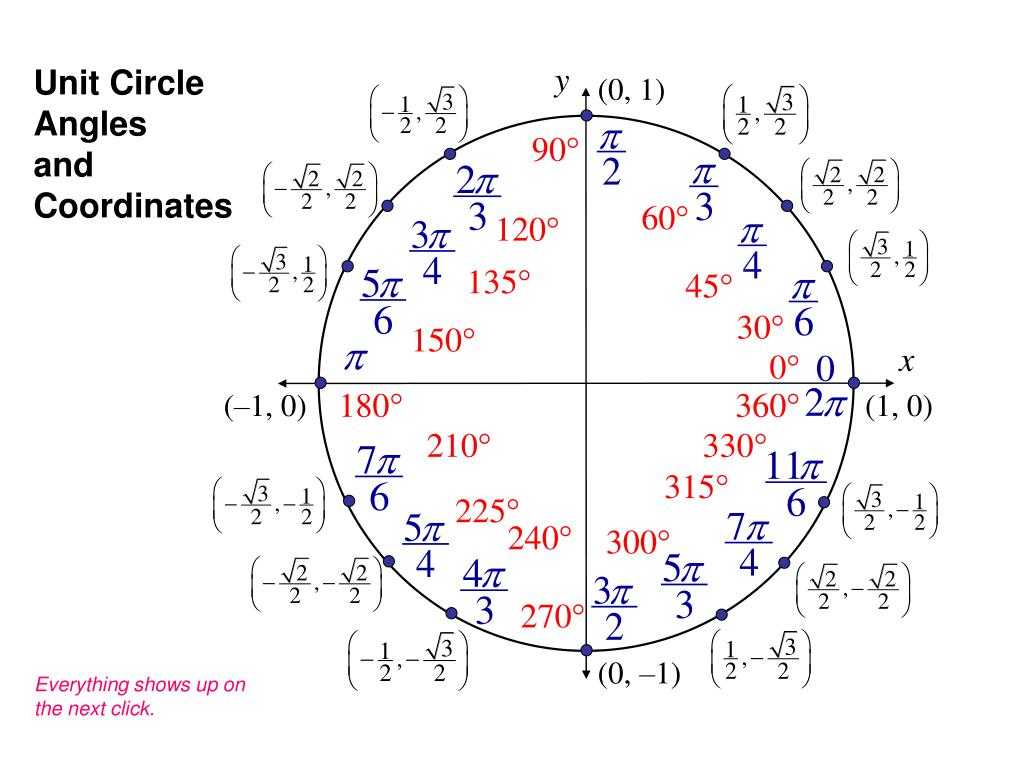
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
9 класс. Геометрия. Соотношения между сторонами и углами треугольника. Синус, косинус и тангенс угла. — Синус, косинус и тангенс угла. Основное тригонометрическое тождество.
Комментарии преподавателяКак измерить высоту дерева ? Как найти расстояние до недоступной точки , вершины дерева (рис.
1)?
Рис. 1. Наглядный пример из 8 класса о введении тригонометрических функций острого угла
Рис. 2. Прямоугольный треугольник АВС
Пусть задан треугольник (рис. 2), a; – катеты, – гипотенуза, – угол.
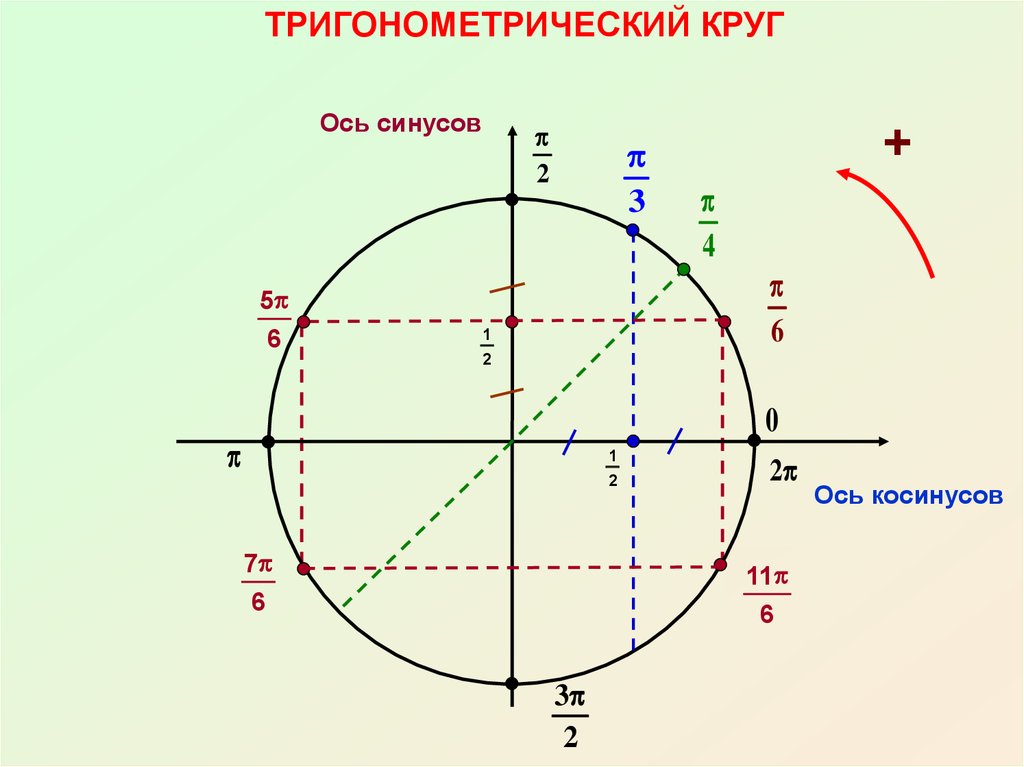
Поместим единичную полуокружность в координатную плоскость (рис. 3).
1. Рассмотрим , в нем , где , т. е. это прямоугольный треугольник, угол – острый.
Рис. 3. Единичная окружность в координатной плоскости
Синусом угла называется отношение противолежащего катета гипотенузе :
Но гипотенуза , поэтому:
– ордината точки :
но , значит:
– абсцисса точки единичной полуокружности.
Синус острого угла – это ордината, а косинус – это абсцисса точки первой четверти.
Точка имеет единственную пару координат , – это косинус , – синус .
Но абсциссу и ординату имеют все точки полуокружности.
2. Рассмотрим любой (рисунок 4), из отрезка .
Рис. 4. единичной окружности в координатной плоскости
Его луч определяет единственную точку на полуокружности, ординату назовем синусом , а абсциссу – его косинусом.
примем, что – это отношение к :
Дано:
Найти:
Решение
Рис. 5. Единичная окружность в координатной плоскости
(рис. 5)
По определению, точка с координатами (0;1) есть точка с координатами :
Примечание: т. к. есть 0, то не существует:
Ответ:.
Задача решена.
Дано:
Найти:
Решение
Рис. 6. Единичная окружность в координатной плоскости
(рис. 6)
Ответ: ; ; .
Задача решена.
Рассмотрим некоторые свойства единичной полуокружности (рис. 7).
Она проецируется на ось в отрезок , а на ось в отрезок , отсюда вывод:
Рис.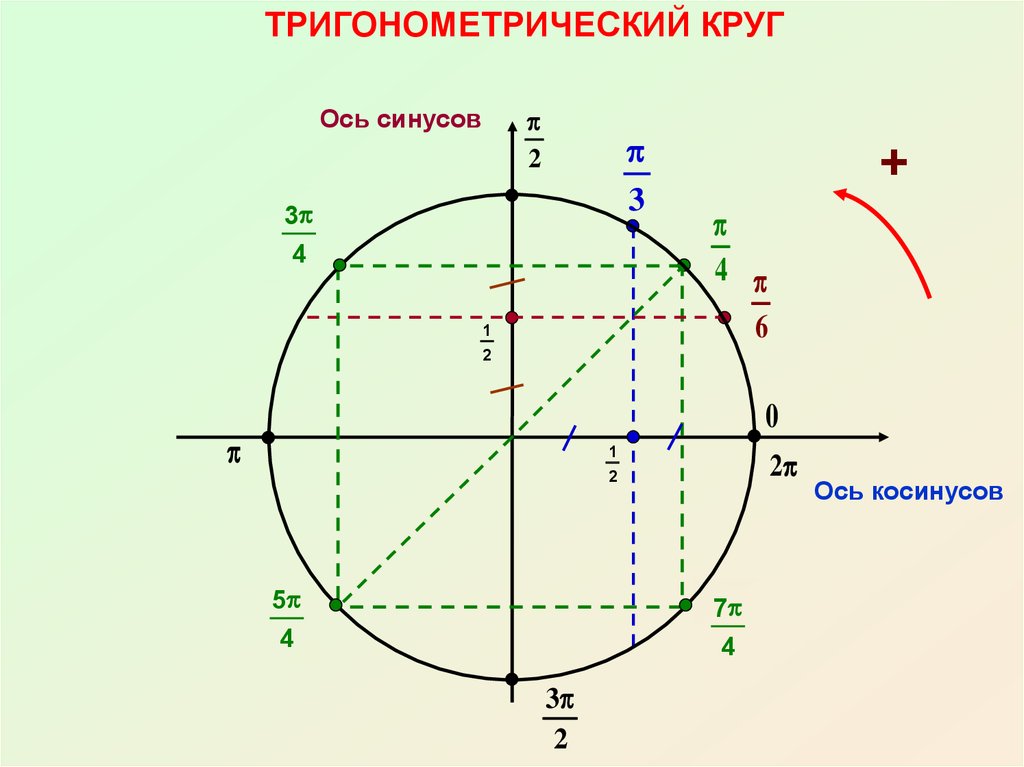
7. Единичная полуокружность в координатной плоскости
В частности, косинус тупого угла отрицателен.
Уравнение единичной окружности с центром в точке и :
Для
Именно это соотношение называют основным тригонометрическим тождеством.
Рассмотрим связь тангенса и косинуса.
Если , то из основного тригонометрического тождества имеем:
Такова связь между косинусом и тангенсом.
Пусть .
Тогда из основного тригонометрического тождества найдем связь между котангенсом и синусом:
Проверьте самостоятельно их справедливость с помощью единичной полуокружности.
Вывод
Мы вспомнили, что такое синус, косинус и тангенс для острых углов, узнали, что такое для углов от до , рассмотрели простейшие свойства введённых функций и основные формулы, которые связывают между собой синус, косинус, тангенс и котангенс, причем для всех углов от до .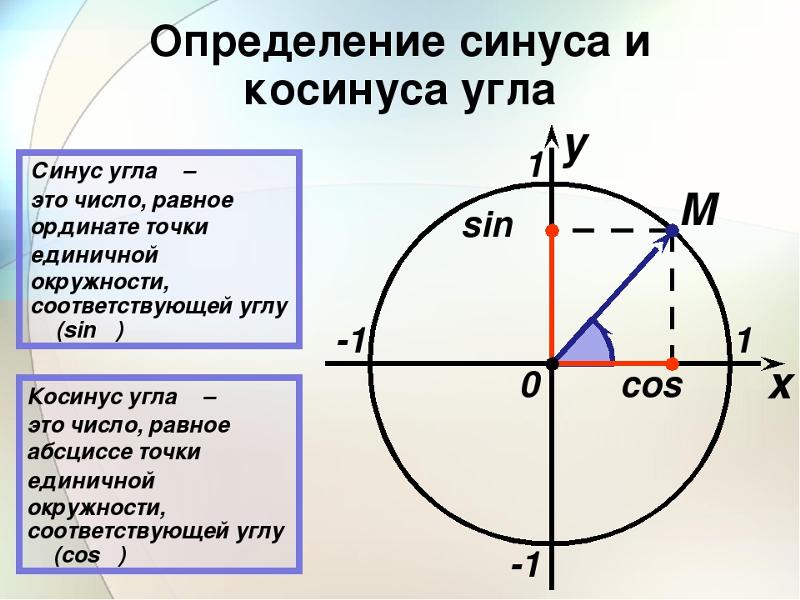
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/9-klass/sinus-kosinus-i-tangens-ugla/sinus-kosinus-i-tangens-ugla-osnovnoe-trigonometricheskoe-tozhdestvo
http://nsportal.ru/sites/default/files/2015/01/06/sinus_kosinus_i_tangens.pptx
http://dok.opredelim.com/pars_docs/refs/16/15413/img2.jpg
http://5klass.net/datas/algebra/Trigonometricheskie-funktsii/0007-007-Svojstva-sinusa-kosinusa-tangensa-i-kotangensa.jpg
http://math-box.net/wp-content/plugins/download-form/force_download.php?id=186&token=0b3565eedfb35781a1d4c4e15805a63f
http://www.azdekor.ru/Spektr/SREDN_SKOOL/MATEM/N109/images/geom_9_5.jpg
http://www.cleverstudents.ru/trigonometry/basic_trigonometric_identities.html
http://onlinegdz.net/test-sinus-kosinus-tangens-kotangens-ugla-geometriya-9-klass-atanasyan/
Unit Circle — JavaTpoint
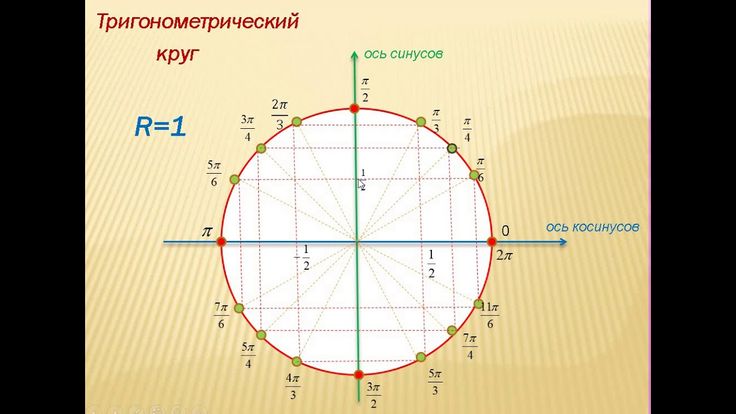
следующий → ← предыдущая В геометрии единичный круг — это особый тип круга. В этом разделе мы узнаем что такое единичный круг, части единичного круга, и как найти точки единичной окружности . Что такое единичный круг?Окружность с радиусом единиц называется единичной окружностью. Это означает, что круг, радиус которого равен 1 единице, называется окружностью единиц Другими словами, любая прямая линия, проведенная из центра в любую точку на краю круга, длина этой линии всегда будет равна 1. Точки единичного круга Точки единичного круга облегчают нам математику. Например, в единичном круге для любого угла θ тригонометрические значения для синуса и косинуса явно представляют собой не что иное, как sin (θ) = y и cos (θ) = x. Чтобы понять точки единичного круга, сначала изучим систему квадрантов в тригонометрии. На следующем рисунке показаны четыре квадранта.
На следующем рисунке показано, какой квадрант будет иметь положительное или отрицательное значение синуса и косинуса. Теперь перейдите к единичному кругу. Сначала проводим две секущие по вертикали и по горизонтали. Он делит круг на четыре квадранта (против часовой стрелки), обозначенные как 1 -й -й, 2-й -й -й, 3-й -й -й, 4-й -й -й квадранты соответственно. Запишите координаты каждой точки пересечения. Мы можем определить тригонометрические функции синуса и косинуса на единичной окружности. Подставив значения x и y на косинус и синус соответственно, получим: cos 2 θ+sin 2 θ=1 Из единичного круга видно, что значения синуса и косинуса никогда не будут больше чем 1 или на меньше -1 . Следовательно, значения синуса и косинуса лежат между 1 и -1. Когда мы достигаем одной четверти и трех четвертей окружности (означает 90°, 180°, 270°), мы не определяем касательную для этих углов. Теперь мы далее разделим каждый квадрант на четыре части. Эти части образуют углы 0°, 30°, 45°, 60° и 9°.0°. Примечание: Мы не будем рассматривать 0°, 90°, 180° и 270° в любом квадранте. Это только для понимания.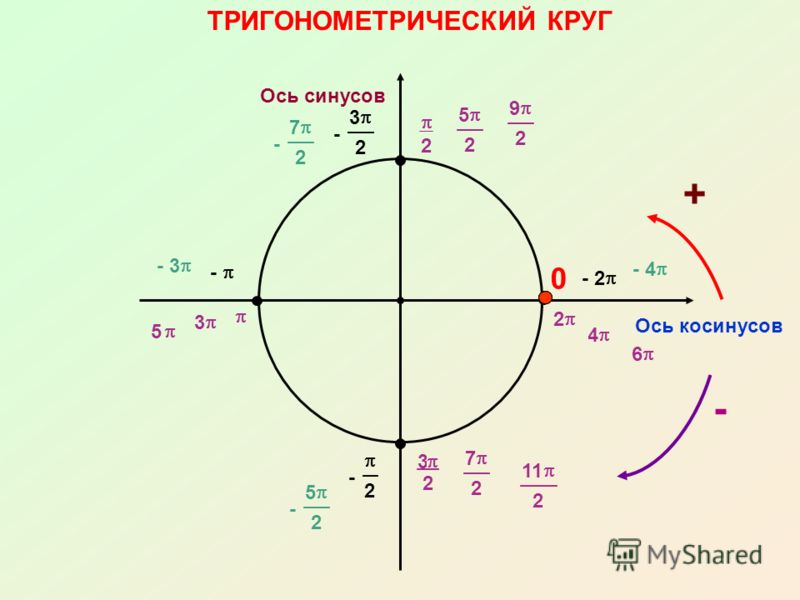 Чтобы записать значения других углов всех квадрантов, мы должны запомнить значения триг-функции.Когда мы сделали все вышеперечисленные шаги, первый квадрант выглядит следующим образом: Следующий единичный круг, показывающий координаты определенных точек. Следующая тема# ← предыдущая следующий → |
Он используется для объяснения тригонометрической концепции. Мы можем использовать его для объяснения всех возможных мер углов от 0 до 360 градусов. Вкратце, единичный круг обозначает все возможные углы, которые существуют с положительными и отрицательными значениями.
Предположим, что (x, y) — точка на единичной окружности, а хорды от центра до точки (x, y) составляют угол θ градусов от оси x, как показано на следующем рисунке. Тогда уравнение x 2 +y 2 =1 дает следующее соотношение: PDF КРУГОВАЯ ТРИГОНОМЕТРИЯ Обзор устройства Это устройство рассматривает углы и измерения углов. Вы рассмотрите специальные прямоугольные треугольники и примените их к изучению круговой тригонометрии. Измерение угла На плоскости угол образуется путем вращения луча, называемого начальной стороной угла, вокруг его конечной точки, пока он не совпадет с другим лучом, называемым конечной стороной. Мерой угла в стандартном положении является величина поворота от начальной стороны до конечной стороны. Если угол вращается против часовой стрелки, мера положительна . Если угол вращается по часовой стрелке, мера равна минус . *Один оборот равен 360º. Два угла в стандартном положении составляют котерминальных углов , если они имеют одну и ту же конечную сторону.
Базовые углы Для любого угла θ в стандартном положении опорный угол θ ref является положительным острым углом, образованным конечной стороной θ и ближайшей частью оси x . Базовый угол любого угла можно найти с помощью следующего: Если крайняя сторона θ находится в квадранте III, тогда опорный угол любого угла можно найти, используя следующее:
Тригонометрические значения (07:08) S вверх! Перейдите к вопросам № 6–9 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. Градусы и радианы Градусы углов широко используются в инженерии, геодезии и навигации. Другая единица измерения угла называется радиан , которая лучше подходит для определенных математических разработок, научной работы и инженерных приложений. Радианная мера угла равна длине дуги на единичной окружности (окружности с центром в начале координат и радиусом 1), которую пересекает угол в стандартном положении. Длина окружности любого круга равна 2π r , где r — радиус окружности. Таким образом, длина окружности единичного круга равна 2π(1) или 2π радианам. Следовательно, угол, представляющий один полный оборот окружности, равен 2π радианам или 360°. Таким образом, угол 180° = π радиан, а 90° = . Вы можете конвертировать градусы в радианы и наоборот.
S топ! Перейдите к вопросам № 10–17 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. Круговой Тригонометрия Тригонометрия изучает углы и треугольники. Слово тригонометрия происходит от греческих слов, означающих «мера треугольника». В тригонометрии обычно используются углы, меры которых кратны 30° и 45°. Эти угловые меры эквивалентны радианным мерам и соответственно. Критические значения в квадранте I следующие: Если вы помните, что 180° = π радиан, легко запомнить другие углы. 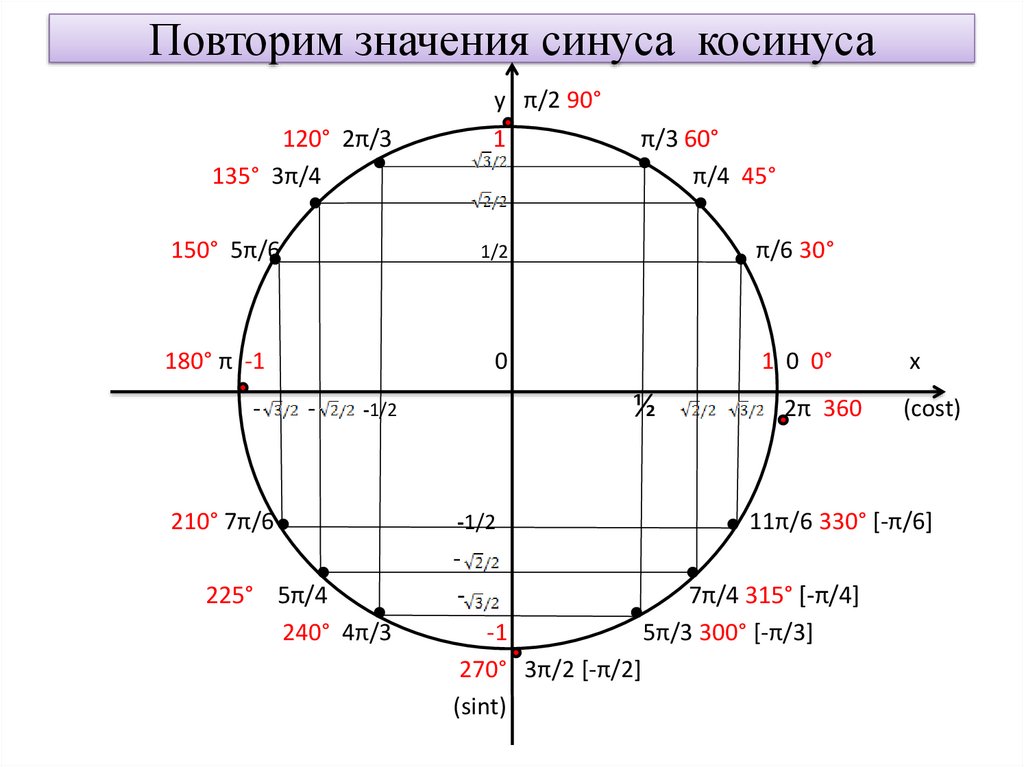 Кроме того, все кратные целым числам также будут критическими значениями для всех углов ≤ 360°. Например: Единичный круг с критическими значениями, помеченными в радианах и градусах, показан ниже: Соотношения синуса (sin), косинуса (cos) и тангенса (tan) основаны на свойствах прямоугольных треугольников. Эти три коэффициента являются наиболее распространенными триггерными коэффициентами. Есть определенные углы, точные триггерные функции которых можно найти без калькулятора. 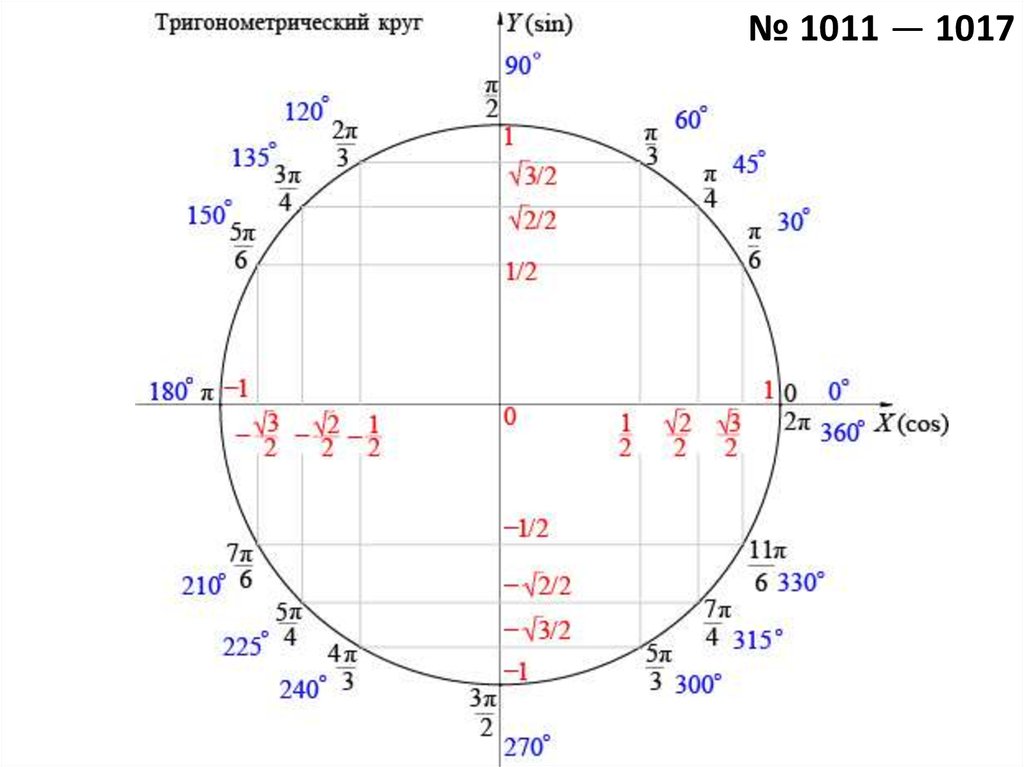 Эти углы составляют 30°, 45°, 60° и любой угол, имеющий любой из этих трех углов в качестве опорных. Отношения длин сторон каждого треугольника показаны ниже. В этом разделе вам будет полезно узнать точные значения sin, cos и tan этих углов.Шесть триггерных функций (02:33) Шесть триггерных функций и многое другое (12:13) Решение прямоугольных треугольников (04:15) Особые прямоугольные треугольники (04:25) Полярные координаты: Сигналы радара (05:12) Прямоугольные треугольники в квадранте 1 На приведенной ниже диаграмме прямоугольный треугольник можно вписать в окружность следующим образом. Для угла в стандартном положении конечная сторона угла на единичной окружности попадает в точку, x -координата — это косинус угла, а y -координата является синусом угла, то есть cos θ = x и sin θ = y . На приведенной выше диаграмме гипотенуза треугольника также является радиусом окружности. Если допустить r = 1 и выбрать один из особых прямоугольных треугольников для вписания в каждый квадрант окружности, то можно установить тригонометрические значения для каждого критического значения от 0 до r до 2π r .
Полярные координаты: сигналы радара (05:12) S топ! Перейдите к вопросам № 18–20 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. 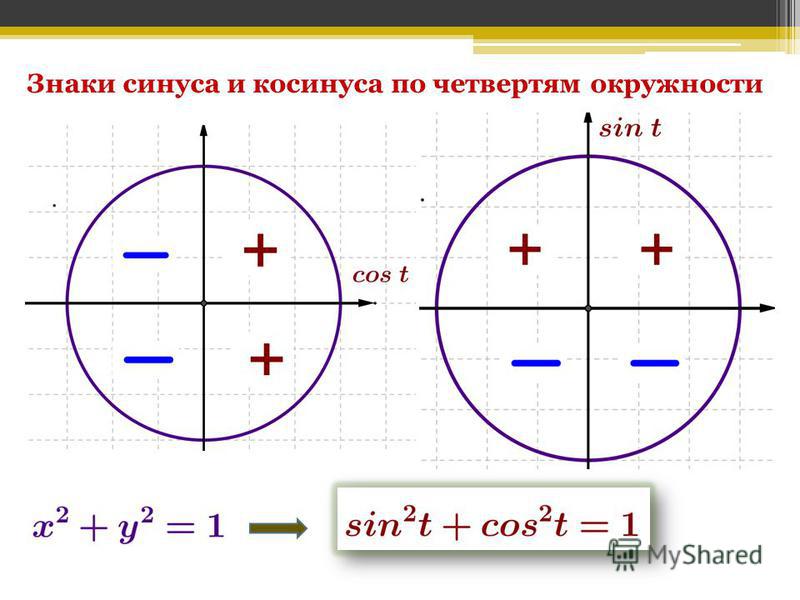 Прямоугольные треугольники и опорные углы в квадрантах № 2, 3, 4 Поскольку специальные прямоугольные треугольники вписаны в квадранты № 2, 3 и 4, стороны треугольников принимают значения, отражающие направление взято для того, чтобы радиус (гипотенуза) пересекал критическое значение на единичной окружности.
В таблице ниже приведены знаки тригонометрических соотношений для каждого квадранта.
Единичный круг (07:07) Останавливаться! Перейдите к вопросам № 21–38 по этому разделу, затем вернитесь, чтобы перейти к следующему разделу. Тригонометрические соотношения для квадрантных углов Если крайняя сторона угла в стандартном положении совпадает с одной из осей, он называется квадрантным углом. В предыдущем обсуждении вписанные треугольники использовались для оценки тригонометрических отношений углов, найденных в каждом квадранте единичной окружности. Однако угловые меры 0, π
, , и 2π (0°, 90°, 180°, 270°, 360°) не находятся «внутри» ни одного из квадрантов № 1, 2, 3 или 4. Положение каждого из этих углов на единичной окружности равно найдено либо на x или y — оси, которые являются граничными линиями между четырьмя квадрантами. |
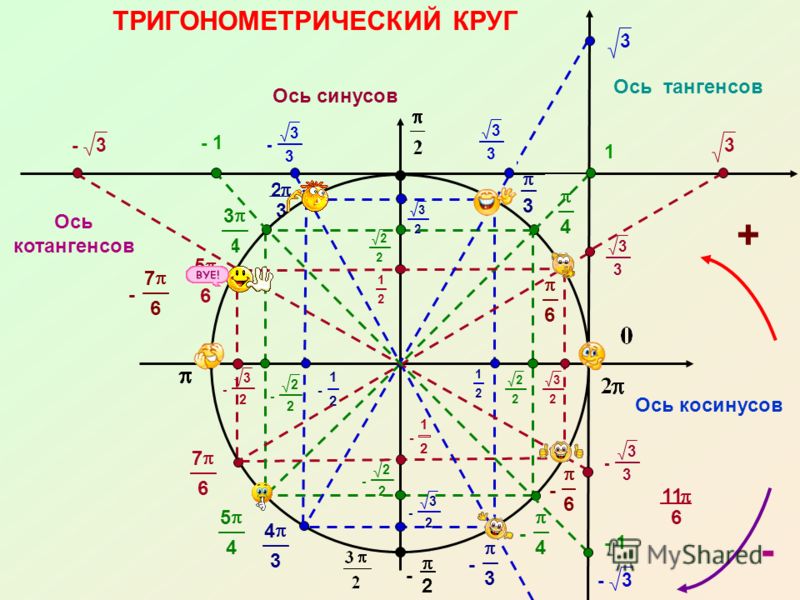Угол в стандартная позиция , если вершина находится в начале координат и ее начальная сторона проходит вдоль положительной оси x . 
