Почему синус пи равен 0
Синус числа ПИ — что это?
Следим мысленно за радиус- вектором, вращая его против часовой, начинаем от нуля до пи/2,потом- в конце второго квадранта в точке= равной пи градусов, нужный катет превращается в точку, то есть в нуль, его отношение к любой величине равно нулю, значит и синус 180 градусов= 0.
Число Пи не может быть выражено точно, это может быть 3,14. и 3,1415 и так далее до бесконечности. Правильно было написать «Синус угла Пи — это ?». Тогда правильный ответ 0.
На самом деле термин «синус» в европейских языках возник в результате ошибки переводчика. Он переводил (дело было в средневековье, в XII веке) математические труды с арабского языка на латинский. В те времена арабы преуспели в математике, и европейцы широко пользовались переводами математических трудов с арабского на латынь. Кстати, в арабский язык многие математические термины попали в результате переводов математических трудов древних греков. Так случилось и с понятием синуса.
Термин был в трудах александрийских математиков, работавших в первых веках новой эры и разработавших начатки тригонометрии. В их трудах было слово «хорда», которая по-гречески означала струну, а также тетиву (колебания струны ведь связано с функцией синуса, но понятия функций тогда не было). Перевод с древнегреческого на арабский сделал персидский математик Аль-Хорезми (от этого имени произошел термин «алгоритм» — об этом недавно был вопрос на БВ). Хорезми перевел термин правильно — арабским термином «джейяб». А вот европейский переводчик неверно понял огласовку этого термина (которая указывает на произношение гласных звуков) и прочитал его как «джиба» (залив, бухта). В результате такого «перевода» и появился латинский термин sinus. По другой версии, термин попал в европейские языки окольным путем, через Индию и санскрит. Но искажение термина все равно случилось.
Я так понял, что задача сводится к тому, что нам неизвестен угол треугольника, и нам нужно его найти.
Для того чтобы найти синус угла, а затем и сам угол в произвольном треугольнике, необходимо знать длины двух сторон: стороны, противолежащей искомому углу, и какой-либо другой стороны — и ещё величину угла, противолежащего этой последней стороне.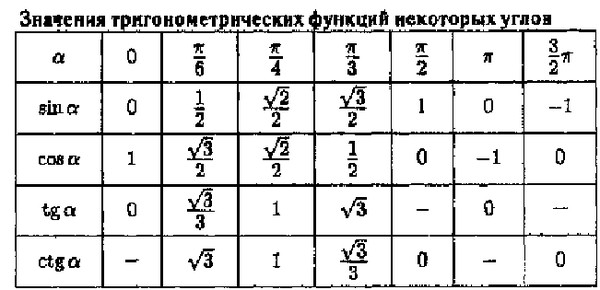
А затем нужно применить теорему синусов.
Обозначим искомый (неизвестный) угол как A, противолежащую сторону — a, другую известную сторону — b, известный противолежащий этой стороне угол — B.
По теореме синусов: a/sin(A) = b/sin(B).
Отсюда: sin(A) = a * sin(B)/b;
A = arcsin[a * sin(B)/b].
Непосредственно многим людям тригонометрические функции не нужны,точнее как- будто бы не нужны.Но вся техника стоит на синусах и косинусах,электроэнергия ,переменный ток изменяется по синусоидальному закону,многие процессы в природе описываются с применением тригонометрии.Даже в повседневной жизни на постройке своего дома и то нужно применять синусы непосредственно.Опосредственно без них нельзя уже обойтись человечеству.
Вспомним, что синус угла в прямоугольном треугольнике равен отношению противолежащего катета к гипотенузе, а косинус — прилежащего. Теперь будем уменьшать этот угол. Гипотенуза будет «ложиться» на прилежащий катет, всё больше сокращая противолежащий.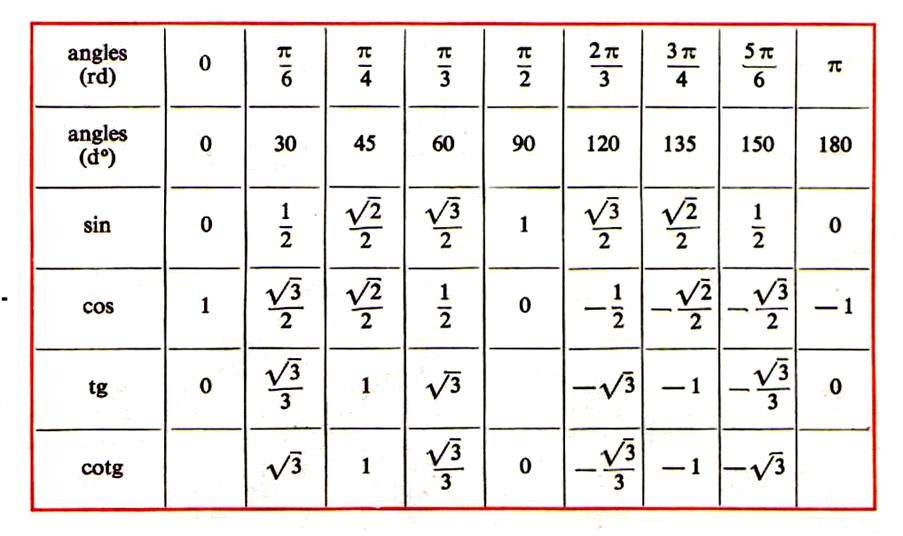
Когда угол «схлопнется» полностью, станет равен нулю, противолежащий катет исчезнет совсем, а гипотенуза сольётся с прилежащим катетом. То есть, синус станет равен нулю, а косинус — единице.
sin0=0, cos0=1.
Будем считать что 120 и 150 это аргументы функций. Также предположим что по умолчанию между функциями и числом 12 опущен знак [*].
Таблица значений тригонометрических функцийДля определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.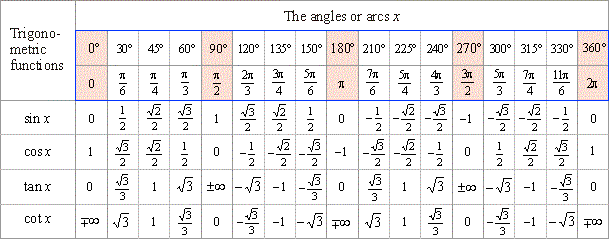
Синус пи, косинус пи, тангенс пи и других углов в радианах
Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.
Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.
Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.
Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.
2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.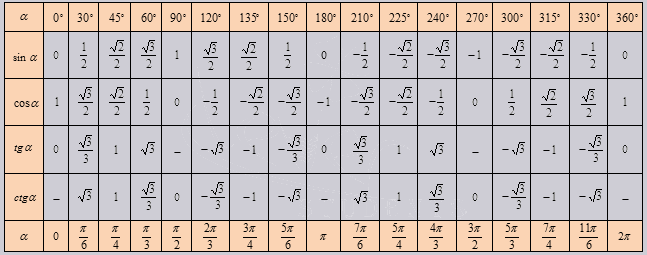
3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.
sin пи найти
Здравствуйте!
Я хочу попросить Вам помочь мне разобраться с темой синусов. А точнее с одним из примеров, который у меня вызвал трудность. Этот пример выглядит так: sin пи найти. А что с ним делать и самое главное — как, для меня непонятно! Помогите пожалуйста разобраться с этим!
Здравствуйте! Ваш вопрос очень интересный и актуальный в наше время, но я всё-таки надеюсь, что мы сможем Вам помочь с этим разобраться. Нам с вами нужно решить такую задачку: найти sin пи найти .
Для углов от 0 до 360 градусов практически любое значение cos или sin можно с лёгкостью найти в соответствующих табличках, которые существуют и распространены, как например такие значения:
Но у нас с Вами не косинус (cos), а синус. Давайте сначала разберёмся, что такое синус угла.
Синусом является одной из тригонометрических функцией, которая представляет собой отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.
Если мы с Вами начинаем говорить о значении синуса пи (pi) , то для этого мы воспользуемся таблицей, о которой уже вспоминали выше:
Надеюсь, теперь Вам стало более понятно, как решаются подобные задания и в дальнейшем у Вас больше не будет возникать подобных вопросов. Удачи Вам в вашем желании научиться чему-нибудь новому!
Ответ:
Ваш компьютер не может выполнять настоящие математические операции, потому что он не может использовать реальные числа. Будь осторожен!
Хранить целые числа в компьютере легко, вы просто записываете их в системе счисления 2. Это немедленно дает вам рациональные числа (также известные как дроби), потому что вы можете хранить числитель и знаменатель как целые числа.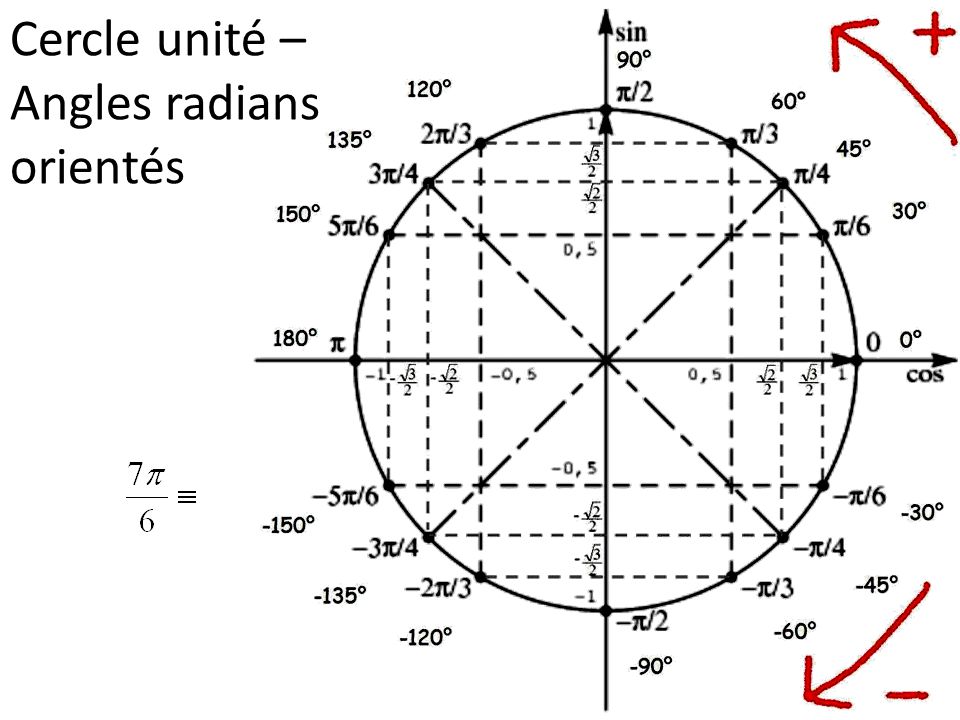
Но как хранить действительные числа (под которыми я действительно подразумеваю иррациональные числа, поскольку мы уже рассмотрели рациональное подмножество). Возьмем, к примеру, самое известное иррациональное число: $\pi$. Будучи иррациональным, $\pi$ требует для представления бесконечное количество цифр (см. здесь первый миллион цифр). Это относится к любой системе счисления, поэтому, если мы хотим хранить $\pi$ в системе счисления 2, нам потребуется бесконечное количество битов в памяти. Ясно, что это не практично. 90.$$Система с плавающей запятой в первую очередь определяется ее точностью $P$ (количество цифр, хранящихся в мантиссе). Поскольку перед точкой может стоять только одна цифра, числа меньше 1 или больше 10 представляются путем изменения целочисленного показателя степени. Чтобы получить более точный результат вычислений, вы просто увеличиваете точность $P$ чисел, которые используете для его вычисления. Современные компьютеры повсеместно соответствуют стандарту с плавающей запятой IEEE 754, в котором изложены правила арифметики с плавающей запятой.
2).\end{equation}Подставляя ответ B и решая $x$, мы получаем\begin{equation}\texttt{math.pi}=\pi — 1,22464679{-16},\end{equation}что немного меньше $\pi$.
TLDR : Если вы ученый, то, вероятно, многие из ваших результатов являются числовыми и компьютерными. Но ваш компьютер не может выполнять арифметические операции с действительными числами, потому что он не может использовать действительные числа. Когда ваш компьютер говорит, что ответ равен 3e-16, это может быть очень точным результатом, и ответ действительно может быть маленьким, отличным от нуля числом. Но более вероятно, что 3e-16 происходит из-за ошибки округления, и фактический ответ должен быть равен нулю. По этой причине некоторые выражения очень плохи и не должны использоваться (например, $1-\cos(x)$). Понимание того, почему такие выражения плохи, требует более глубокого изучения арифметики с плавающей запятой. Я настоятельно рекомендую для начала прочитать книгу Дэвида Голдберга «Что каждый компьютерный ученый должен знать об арифметике с плавающей запятой» и посмотреть, к чему она вас приведет.
В конечном счете, вы должны предположить, что каждый числовой результат имеет некоторую ошибку с плавающей запятой. И если вы не будете осторожны, эта ошибка с плавающей запятой может стать очень большой. Так что будь осторожен.
what-csc-in-math — Googlesuche
AlleBilderVideosNewsMapsShoppingBücher
suchoptionen
Таким образом, косеканс угла равен отношению длины гипотенузы к длине стороны, противоположной углу. Косеканс сокращенно обозначается как csc. csc θ = гипотенуза / сторона, противоположная θ Кроме того, мы знаем, что косеканс является величиной, обратной синусу, т. е. csc θ = 1/sin θ
Что такое тригонометрия CSC? — JEE Q & A — Byjus
byjus.com › jee-questions › what-is-csc-trigonometry
Hervorgehobene Snippets
Ähnliche Fragen
Чему также равно csc?
Является ли csc sin или cos?
Для чего используется csc в математике?
Является ли csc тем же, что и cos?
Косеканс (csc) — Тригонометрическая функция — Открытый справочник по математике
www.
mathopenref.com › косеканс
В прямоугольном треугольнике косеканс угла равен длине гипотенузы, деленной на длину противоположной стороны . В формуле это сокращается до …
Определение косеканса (Иллюстрированный математический словарь) — Math is Fun стороны, противоположной углу.
косеканс | математика — Encyclopedia Britannica
www.britannica.com › Наука › Математика
котангенс (cot), секанс (sec) и косеканс (csc). Эти шесть тригонометрических функций по отношению к прямоугольному треугольнику показаны на рисунке.
Формула косеканса, функции и примеры | Что такое… — Study.com
study.com › академия › урок › косеканс-определение-…
18.01.2022 · В прямоугольном треугольнике косекансом называется отношение гипотенузы к противоположная сторона угла. Косеканс обозначается или сокращается как CSC …
Bilder
Alle anzeigen
Alle anzeigen
Csc Sec Cot — Formula, Table, Domain, Graph, Examples — Cuemath
www.
cuemath.com › тригонометрия › косеканс-секанс…
Csc Sec Cot – это сокращенная форма записи тригонометрических функций функций косеканса, секанса и котангенса. У нас в основном шесть тригонометрических …
Формула, график, домен, диапазон | Функция косеканса — Cuemath
www.cuemath.com › тригонометрия › функция косеканса…
Косеканс — одна из шести основных тригонометрических функций, сокращенно обозначаемая как csc x или cosec x, где x — угол. В прямоугольном треугольнике косеканс …
Секанс (sec), косеканс (csc) и котангенс (cot) пример — YouTube
www.youtube.com › смотреть
13.07.2015 · Пропустили предыдущий урок? https://www.khanacademy.org/math/trig… Тригонометрия по Хану…
Дауэр: 4:44
Прислан: 13.07.2015
Секанс (сек), косеканс (csc) и котангенс ( детская кроватка) | Chitown Tutoring
chitowntutoring.com › секанс-сек-косеканс-csc-и-котангенс-кот
08.12.