Формулы, применяемые как для синуса, так и косинуса половинного угла не зависит от заданного значения угла α. Для тангенса в независимости от угла α определяется следующим видом \[\tan \frac{\alpha}{2}\], где значение угла a≠π+2π•z, а значение z равняется любому целому числу. Значение выражения 1+cosα не должно быть равно нулю. Формула котангенса угла будет считаться верной, если любой угол α, где имеет место быть половинный угол α в тригонометрии, принимает следующий вид α ≠2π•z.
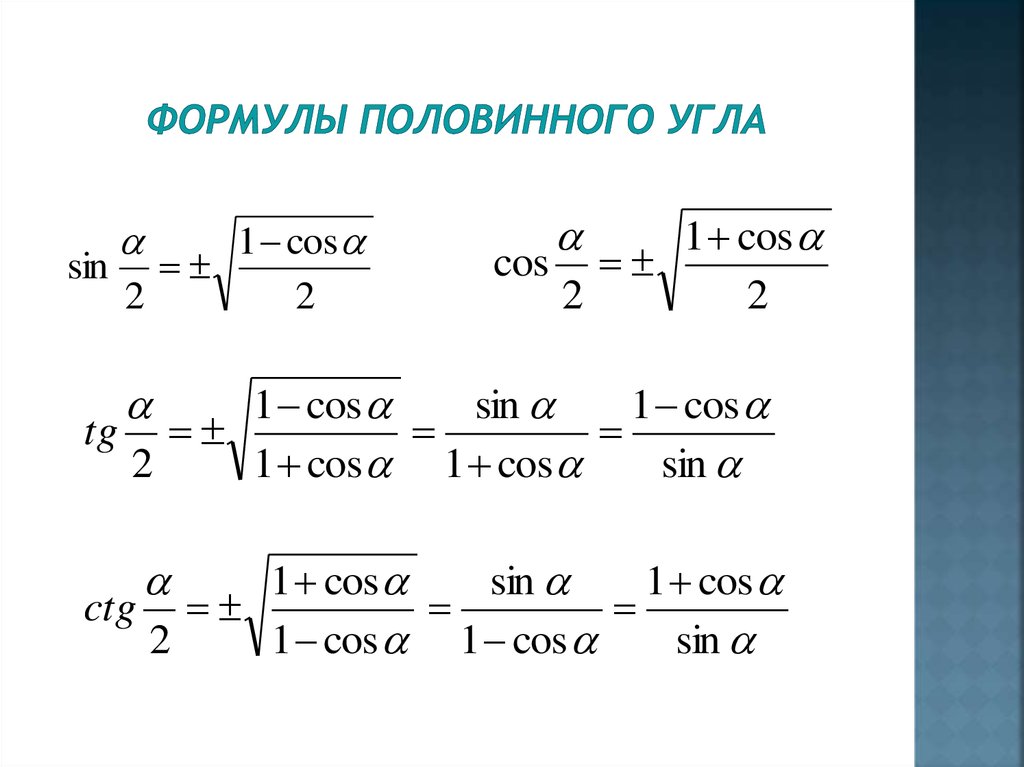
Самыми важными тригонометрическими формулами половинного угла являются тригонометрических функций с квадратами, которые могут быть выведены и через положительные, и отрицательное значение арифметического квадратного корня. Получаются следующие формулы половинного угла:
\[ \frac{\sin \sin \alpha}{2}=\pm \frac{\sqrt{1-\cos \alpha}}{\sqrt{2}}, \frac{\cos \cos \alpha}{2}=\pm \frac{\sqrt{1+\cos \alpha}}{\sqrt{2}}, \quad \tan \frac{\alpha}{2}=\frac{\sqrt{1-\cos \alpha}}{\sqrt{1+\cos \alpha}}, \cot \frac{\alpha}{2}=\frac{\sqrt{1+\cos \alpha}}{\sqrt{1-\cos \alpha}} \]
Знак «-» свидетельствуют о том, что тригонометрическая функция определяется четвертью угла \[\frac{\alpha}{2}\]
Доказательство тригонометрических функций половинного угла
Доказательство тригонометрических формул половинного угла строится на основании формулы косинуса двойного угла \[\cos \alpha=1-2 \times \frac{\alpha}{2}\] и \[\cos \alpha=2 \times \frac{\alpha}{2}-1\].
{\circ}=\frac{\sqrt{2+\sqrt{3}}}{2}\]
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Рассмотрим ещё одно задание.
Необходимо вычислить значение указанного выражения \[\frac{4 \cos \alpha}{2}+2 \cos \alpha+5\], где \[\cos \alpha=\frac{1}{8}\].
Решение:
Нужно использовать ту же самую формулу, которую применяли в первом примере \[\frac{\cos \alpha}{2}=\pm \frac{\sqrt{1+\cos \alpha}}{\sqrt{2}}\]. Подставим значение косинуса, упростим данное выражение:
\[ \frac{4 \sqrt{1+\cos \alpha}}{\sqrt{2}}+2 \cos \alpha+5=\frac{4 \sqrt{1+\frac{1}{8}}}{\sqrt{2}}+2 \times \frac{1}{8}+5=\frac{4 \sqrt{9}}{\sqrt{16}}+\frac{1}{4}+5=8 \frac{1}{4} \]
Ответ: \[\frac{4 \cos \alpha}{2}+2 \cos \alpha+5=8 \frac{1}{4}\].
Применяя формулы тригонометрического половинного угла, нужно учитывать, что угол может быть и нестандартного вида a2 и a, а его нужно будет привести к такому стандартному виду.
Главным пунктом является то, что аргумент в правой части должен быть в два раза больше, чем в левой. В противном случае применить формулу не получится.
Если тождество записано в таком виде \[7 \alpha=\frac{1-\cos 14 \alpha}{2}\] или \[\frac{5 a}{17}=\frac{1-\frac{\cos \cos 10 \alpha}{17}}{2}\], то формулу применять можно.
Для того чтобы научиться правильно преобразовать и применять описанные выше формулы, нужна пристально изучить тему функции тригонометрических выражений. Не каждое выражение поддается преобразованию. И особое внимание нужно обратить на то, что значение углов тригонометрических функций зависит от их нахождения в разных четвертях для определения положительного и отрицательного знака выражения.
Синус, косинус и тангенс половинного угла»
Дата проведения: Тема урока: «Синус, косинус и тангенс половинного угла»
Тип урока: урок усвоения новых знаний
Цели урока: 1) образовательная: Показать как с помощью основного тригонометрического тождества и формул двойного угла выводится формулы для половинного угла; сформировать умения применять полученные формулы при упрощении и вычислении тригонометрических выражений.
2) развивающая: Развивать алгоритмическое мышление, память, умение излагать мысли, делать выводы, обобщения; содействовать рациональной организации труда.
3)воспитательная: Воспитать внимательность, наблюдательность, трудолюбие и заинтересованность учащихся новым материалом
Оборудование: компьютер, учебники, тетради
Литература: А.Ш.Алиев, А.Н.Колмогов
Ход урока:
- Организационный момент: приветствие, проверка готовности к уроку. (1 мин
Эпиграф к уроку.
Нельзя математику изучить,
наблюдая, как это делает другой.
2)Повторение
-какие формулы мы вчера прошли?
-для каких функций?
3)Новая тема
3)Закрепление
Зная, что ,.
Решение. Формула половинного угла для косинуса имеет вид , тогда .
Ответ: .
4.Итог урока
Оценивание. Д/задание
Просмотр содержимого документа
«Синус, косинус и тангенс половинного угла»»
Дата проведения:
Тема урока: «Синус, косинус и тангенс половинного угла»
Тип урока: урок усвоения новых знаний
Цели урока: 1) образовательная: Показать как с помощью основного тригонометрического тождества и формул двойного угла выводится формулы для половинного угла; сформировать умения применять полученные формулы при упрощении и вычислении тригонометрических выражений.
2) развивающая: Развивать алгоритмическое мышление, память, умение излагать мысли, делать выводы, обобщения; содействовать рациональной организации труда.
3)воспитательная: Воспитать внимательность, наблюдательность, трудолюбие и заинтересованность учащихся новым материалом
Оборудование: компьютер, учебники, тетради
Литература: А.Ш.Алиев, А.Н.Колмогов
Ход урока:
Организационный момент: приветствие, проверка готовности к уроку. (1 мин
Эпиграф к уроку.
Нельзя математику изучить,
наблюдая, как это делает другой.
2)Повторение
-какие формулы мы вчера прошли?
-для каких функций?
3)Новая тема
3)Закрепление
Зная, что ,.
Решение. Формула половинного угла для косинуса имеет вид , тогда . Итак, значение квадрата косинуса 15 градусов найдено, осталось по нему найти значение самого косинуса.
Так как угол 15 градусов является углом первой координатной четверти, то косинус этого угла должен быть положительным (при необходимости смотрите раздел теории знаки синуса, косинуса, тангенса и котангенса по четвертям). Таким образом, так как , то .
Ответ: .
4.Итог урока
Оценивание. Д/задание
тригонометрия — Формула тангенса половины угла
спросил
Изменено 5 лет, 11 месяцев назад
Просмотрено 902 раза
$\begingroup$
Итак, мы начнем со следующей формулы тангенса половины угла: $$ \tan\left(\frac \theta2\right) = \pm\sqrt{\frac {1 — \cos \theta}{1 + \cos \theta}} $$
Если я произведу некоторые алгебраические манипуляции, я получу следующее: $$ \tan \left(\frac \theta2\right)= \pm\frac {1 — \cos \theta} {\sin \theta}$$
Согласно тригонометрии Майкла Коррала знак минус невозможен, поэтому Я получаю только:
$$ \tan \left(\frac \theta2\right)= \frac {1 — \cos \theta} {\sin \theta} $$
Не могли бы вы объяснить, почему это так? истинный?
- тригонометрия
$\endgroup$
$\begingroup$
Суетливость по поводу $\pm$ возникает из-за того, что $\tan \frac\theta2$ может быть как положительным, так и отрицательным, тогда как квадратный корень всегда считается положительным.
Ваши алгебраические манипуляции с $\sqrt{\frac{1-\cos\theta}{1+\cos\theta}}$ в порядке, за исключением последнего шага: результат должен быть $\left|\frac{1-\ cos\theta}{\sin\theta}\right|$, как в выводе @haqnatural, что приводит к
$$
\tan\frac\theta2 = \pm\left|\frac{1-\cos\theta}{\sin\theta}\right|.\tag1
$$
Уравнение (1) верно, но не приближает нас к решению вопроса о том, какой знак выбрать! Один из способов решить это — рассмотреть разные диапазоны $\theta$, как в ответе @imranfat. 92т
$$
и
$$\sin2t = 2\sin t\cos t.$$
$\endgroup$
$\begingroup$ Один из способов решить эту проблему — посмотреть на знаковый результат $tan\theta/2$. Это происходит, если $\theta$ находится на интервале $(\pi,2\pi)$. Другими словами, когда $\theta$ (не $\theta/2$!!) находится в квадранте 3 или 4, $tan\theta/2<0$. Теперь в $\frac{1-cos\theta}{sin\theta}$ числитель положителен, поэтому рассмотрим знаменатель.
Синусоидальный график дает отрицательные значения, когда $\theta$ находится в Q3 или Q4, поэтому результат отрицательный. Аналогично для углов, заданных в квадрантах 1 и 2, результат синуса положительный. Теперь для выражения, содержащего квадратный корень, автор ставит плюс/минус впереди, но читателю необходимо определить рассматриваемый квадрант, а затем выбрать правильный знак. В противном случае правильным тождеством является $tan\theta/2=\frac{1-cos\theta}{sin\theta}$ без абсолютных значений.
$\endgroup$
Вывод для Sin, Cos и Tan с доказательством
Стороны треугольников, а также сами углы изучаются в тригонометрии. Он специально использует прямоугольные треугольники. Чтобы определить углы и стороны треугольника, примените тригонометрические отношения. Одной из составляющих математики являются тригонометрические соотношения. И треугольник, и полуугол можно рассчитать по множеству формул.
Что такое формула половинного угла?
Формула половинного угла в выражениях половинной ширины обычно выражается как \(\frac{\theta}{2}, \frac{x}{2}, \frac{A}{2}\) и т.
д., где полуширины являются частичными углами. Формулы половинного угла используются для нахождения точного значения тригонометрических соотношений для таких углов, как 22,5° (половина стандартного угла в 45°), 15° (половина стандартного угла в 30°) и так далее.
Из таблицы тригонометрических функций знать значения тригонометрических функций (sin, cos, tan, cot, sec, cosec) для таких углов, как 0°, 30°, 45°, 60°, 90°. Однако, чтобы узнать точные значения sin 22,5°, tan 15° и т. д., очень полезны формулы половинного угла. Это также полезно для доказательства множественных тригонометрических тождеств. Существуют формулы полуширины, полученные из формулы двойной ширины, выраженной в полуширине \(\ frac{\theta}{2}, \frac{x}{2}, \frac{A}{2}\) , и так далее.
Тождества половинных углов
Здесь представлены тождества половинных углов всех тригонометрических функций.
Формула половинного угла для синуса
\(sin\frac{\theta}{2}=+\sqrt{\frac{1-cos\theta}{2}}\) ……….
. for \(\ frac{\theta}{2}\) в квадранте I или квадранте II
\(sin\frac{\theta}{2}=-\sqrt{\frac{1-cos\theta}{2}}\) ……….. for \(\frac{\theta}{2 }\) в квадранте III или квадранте IV
Формула половинного угла для косинуса
\(cos\frac{\theta}{2}=+\sqrt{\frac{1+cos\theta}{2}}\) ……….. для \(\frac{\theta}{2}\) в квадранте I или квадранте IV
\(cos\frac{\theta}{2}=-\sqrt{\frac{1+cos \theta}{2}}\) ……….. для \(\frac{\theta}{2}\) в квадранте II или квадранте III
Формула половинного угла для касательной
\(tan\frac{\ theta}{2}=+\sqrt{\frac{1-cos\theta}{1+cos\theta}}\) ……….. for \(\frac{\theta}{2}\) в квадранте I или квадрант III
\(tan\frac{\theta}{2}=-\sqrt{\frac{1-cos\theta}{1+cos\theta}}\) ……….. for \(\frac{\ theta}{2}\) в квадранте II или квадранте IV
Формула половинного угла для гиперболического синуса
\(sin\frac{x}{2}=+\sqrt{\frac{1-coshx}{2}} \) …………… для \(x\geq0\)
\(sin\frac{x}{2}=-\sqrt{\frac{1-coshx}{2}}\) ………… … for \(x\leq0\)
Формула половинного угла для гиперболического косинуса
\(cosh\frac{x}{2}=+\sqrt{\frac{1+coshx}{2}}\)
Формула половинного угла для гиперболического тангенса
\(tanh\frac{x}{2}=+\sqrt{\frac{1-coshx}{1+coshx}}\) …………… для \(x\geq0\)
\( tanh\frac{x}{2}=-\sqrt{\frac{1-coshx}{1+coshx}}\) …………… for \(x\leq0\)
Вывод формул половинного угла с использованием Double Формулы углов
Формулы двойных углов используются для получения формул половинных углов.
Формулы двойного угла представляют двойные углы, такие как \(2\theta\), 2A и 2x. Формулы двойного угла известны как sin, cos и tan.
\(sin2x = 2sinxcosx\)
92(\frac{A}{2}) = \frac{1 + cosA}{2}\)\(cos\frac{A}{2}=+\sqrt{\frac{1+cosA}{ 2}}\) ……….. для \(\frac{A}{2}\) в квадранте I или квадранте IV
\(cos\frac{A}{2}=-\sqrt{\frac{ 1+cosA}{2}}\) ……….. для \(\frac{A}{2}\) в квадранте II или квадранте III
Формула половинного угла Tan Proof
Мы используем формулу половинного угла sin и cos, чтобы узнать формулу половинного угла tan. Мы знаем, что
\(tan\frac{A}{2}=\frac{sin\frac{A}{2}}{cos\frac{A}{2}}\)
\(sin\frac{A}{2}=\pm\sqrt{\frac{1-cosA}{2}}\)
\(cos\frac{A}{2}=\pm\sqrt{ \frac{1+cos\theta}{2}}\)
\(tan\frac{A}{2}=\frac{\pm\sqrt{\frac{1-cosA}{2}}}{ \pm\sqrt{\frac{1+cosA}{2}}}\)
\(tan\frac{A}{2}=\frac{\sqrt{\frac{1-cosA}{2}} }{\sqrt{\frac{1+cosA}{2}}}\)
Таким образом,
\(tan\frac{A}{2}=+\sqrt{\frac{1-cosA}{1 +cosA}}\) ……….
2(\frac{A}{2}) – 1\) 92)}{2bc}\)
\(= (\frac{1}{2})\frac{(a + b − c)(a + c − b)}{2bc}\)
\( = (\frac{1}{2})\frac{[(a + b + c) — 2c][(a + b + c) — 2b]}{2bc}\)
\(= (\ frac {1}{2})\frac{(2s − 2c)(2s − 2b)}{2bc}\)
\(= \frac{(s − b)(s − c)}{bc}\)
\({\implies}sin(\frac{A}{2}) = \sqrt{[\frac{(s − b)(s − c)}{bc}]}\)
Важные моменты для Помните
Вот ключевые моменты, которые вы должны помнить.
Вы можете использовать формулы половинного угла, чтобы узнать значения половинных значений тригонометрических величин. Три формулы:
\(sin\frac{\theta}{2}=\sqrt{\frac{1-cos\theta}{2}}\)
\(cos\frac{\theta}{2}=\sqrt {\ frac {1 + cos \ theta} {2}} \)
\ (tan \ frac {\ theta} {2} = \ sqrt {\ frac {1-cos \ theta} {1 + cos \ theta} }\)
Решенный пример формулы половины угла
Вот несколько решенных примеров формулы половины угла тригонометрии.
Решено Пример 1: Найдите точное значение следующего выражения: sin(22,5°)
Решение:
\(sin\frac{\theta}{2}=\sqrt{\frac{1- cos\тета}{2}}\) 9{2}+ \cos{{x}}\)
\(\displaystyle={2}{\left(\frac{{{1}- \cos{{x}}}}{{2}}\ справа)}+ \cos{{x}}\)
\(\displaystyle={1}- \cos{{x}}+ \cos{{x}}\)
\(\displaystyle={1 }\)
\(\displaystyle=\text{RHS}\)
Следовательно, доказано.
Надеюсь, что эта статья о формулах половинного угла была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о формулах половинного угла
В.1 Как найти половинный угол в тригонометрии?
Ans.1 Формулы двойного угла используются для получения формул половинного угла. Формулы двойного угла представляют двойные углы, такие как \(2\theta\), 2A и 2x. Заменяя x на \(\frac{A}{2}\) в обеих частях каждого уравнения в формуле двойного угла, мы находим половинный угол в тригонометрии.
В.2 Для чего используется формула половинного угла?
Ans.2 Формулы половинного угла используются для нахождения точного значения тригонометрических соотношений для таких углов, как 22,5° (половина стандартного угла 45°), 15° (половина стандартного угла 30°), и так далее.
В.3 Как выводится формула половинного угла?
Ответ 3 Заменив x на \(\frac{A}{2}\) в обеих частях каждого уравнения в формуле двойного угла, мы найдем половину угла в тригонометрии.